Assessing Protection Strategies for Urban Rail Transit Systems: A Case-Study on the Central London Underground
Abstract
:1. Introduction
2. Literature Review
2.1. Single-Asset Metrics for Fortification
2.2. Systemic Approach to Fortification
3. Methodology
3.1. Sequential Approach
3.2. Integrated Approach
- N is the set of network nodes, indexed by i, s or d,
- A is the set of network arcs,
- is the set of paths connecting nodes s and d, indexed by p,
- , is the set of nodes in path p,
- is the length of path p,
- is the length of the longest path connecting nodes s and d,
- is the amount of passenger flow travelling from node s to node d,
- D is the maximum number of nodes that can be disrupted simultaneously,
- B is the amount of budget available for protection,
- is a penalty cost incurred when nodes s and d are disconnected,
- are constants used to normalise path and flow objectives, respectively,
- are real coefficients used to weight connectivity, path and flow objectives, respectively, whose sum is equal to 1.
- is equal to 1 if node i is protected, 0 otherwise,
- is equal to 1 if node i is disrupted, 0 otherwise,
- is the length of the shortest non-disrupted path from node s to node d,
- is equal to 1 if there is no connection between nodes s and d, 0 otherwise.
4. Central London Underground: A Case Study
5. Discussion
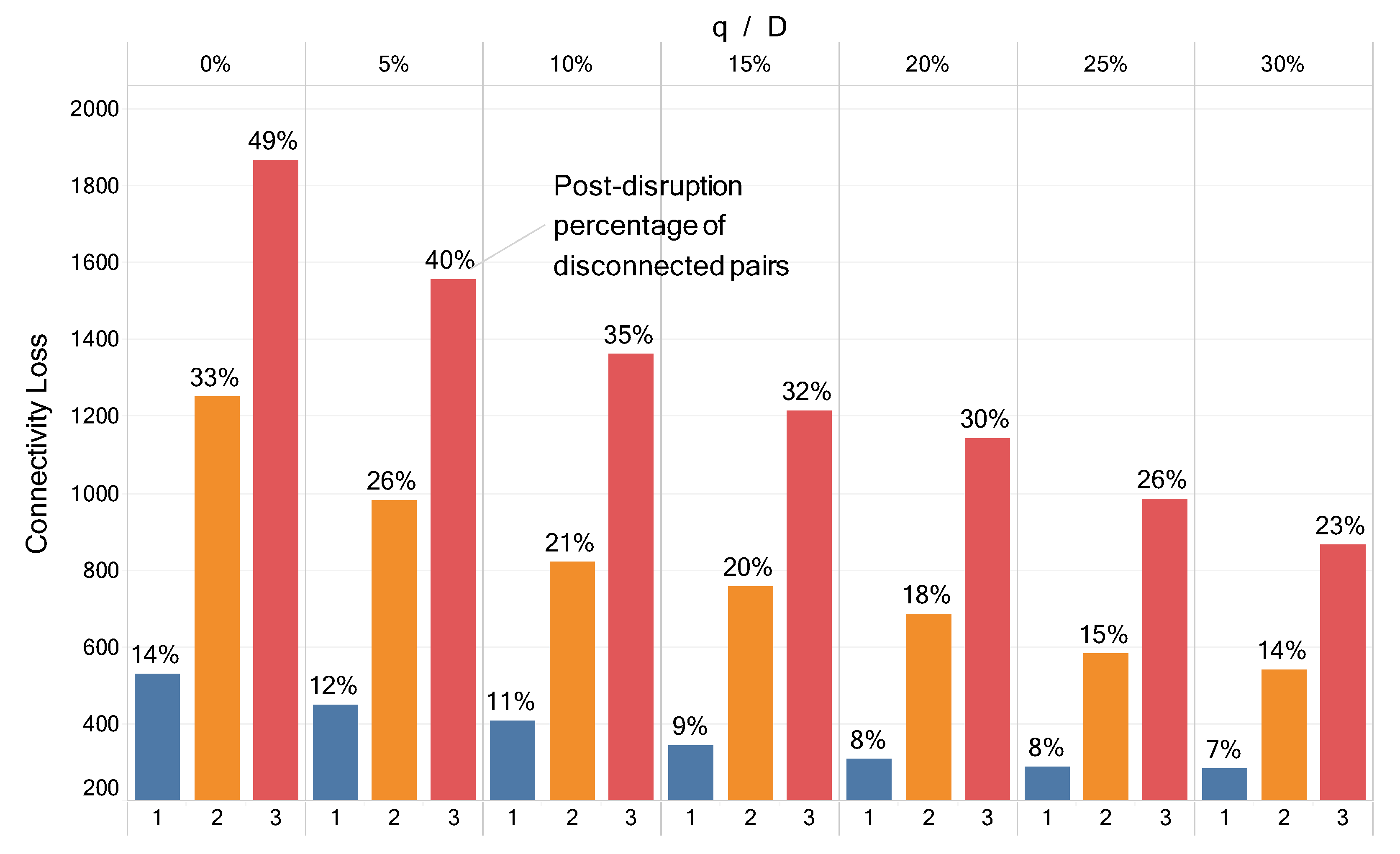
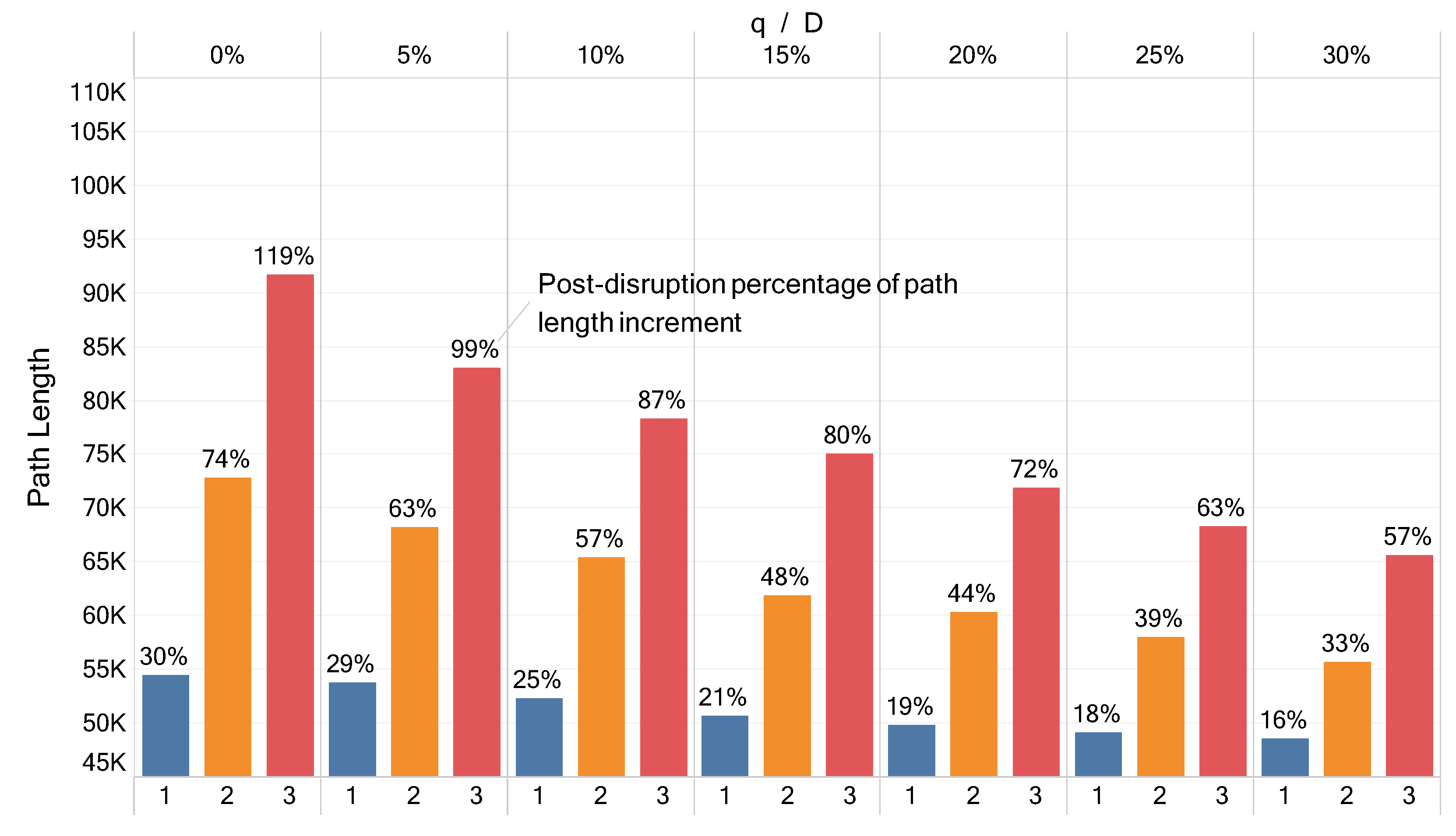
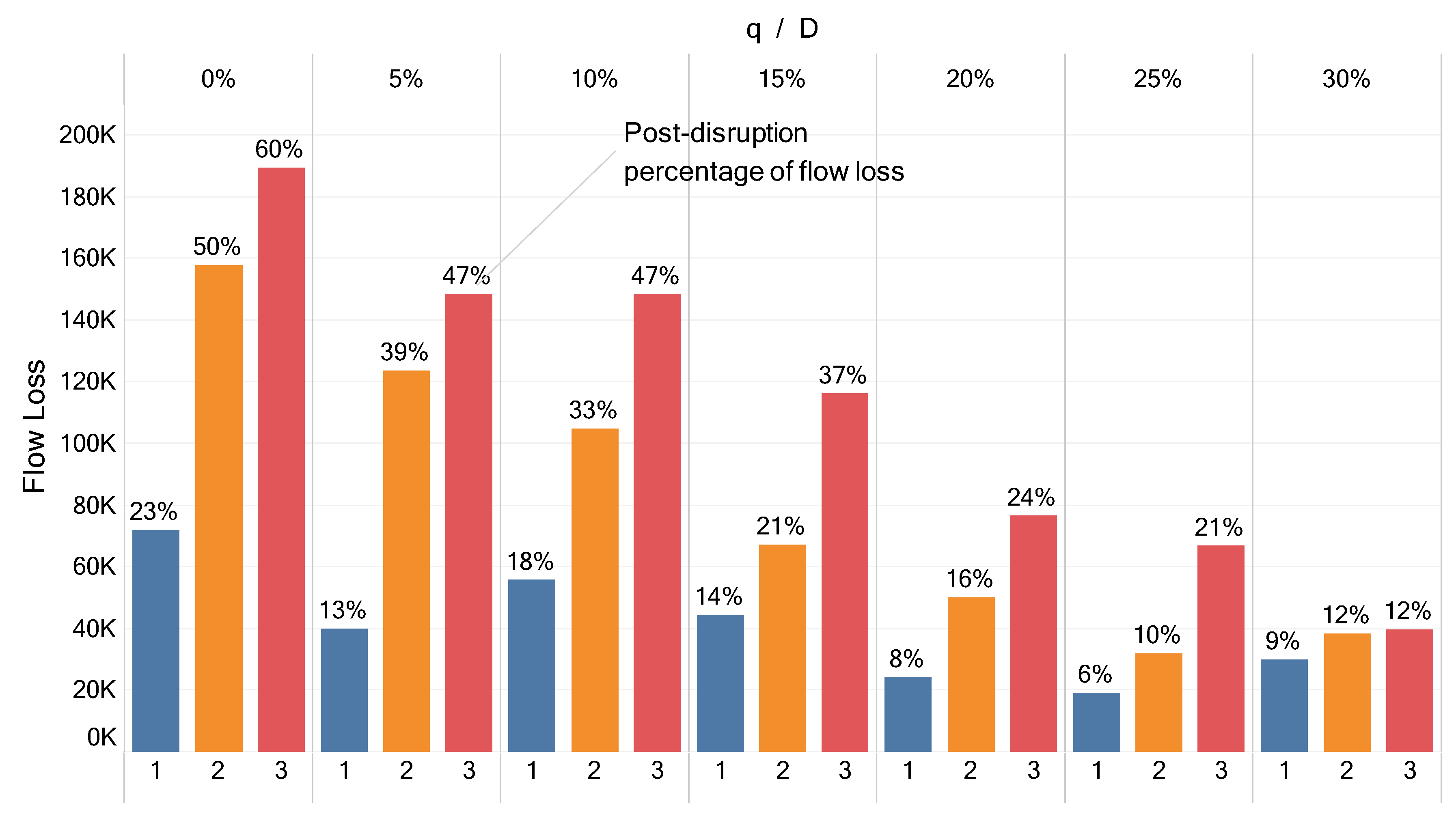
5.1. Sequential Approach Analysis
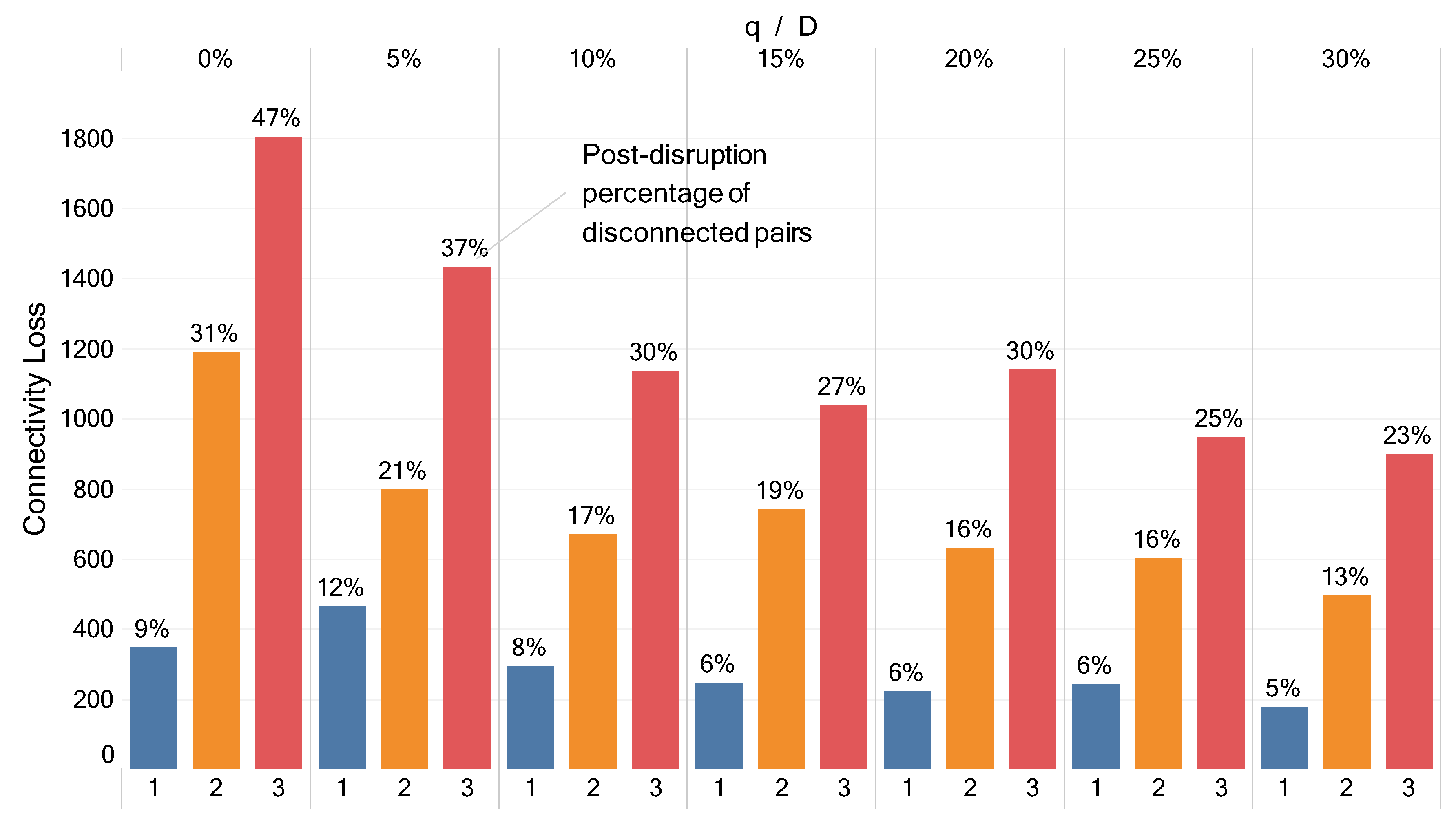
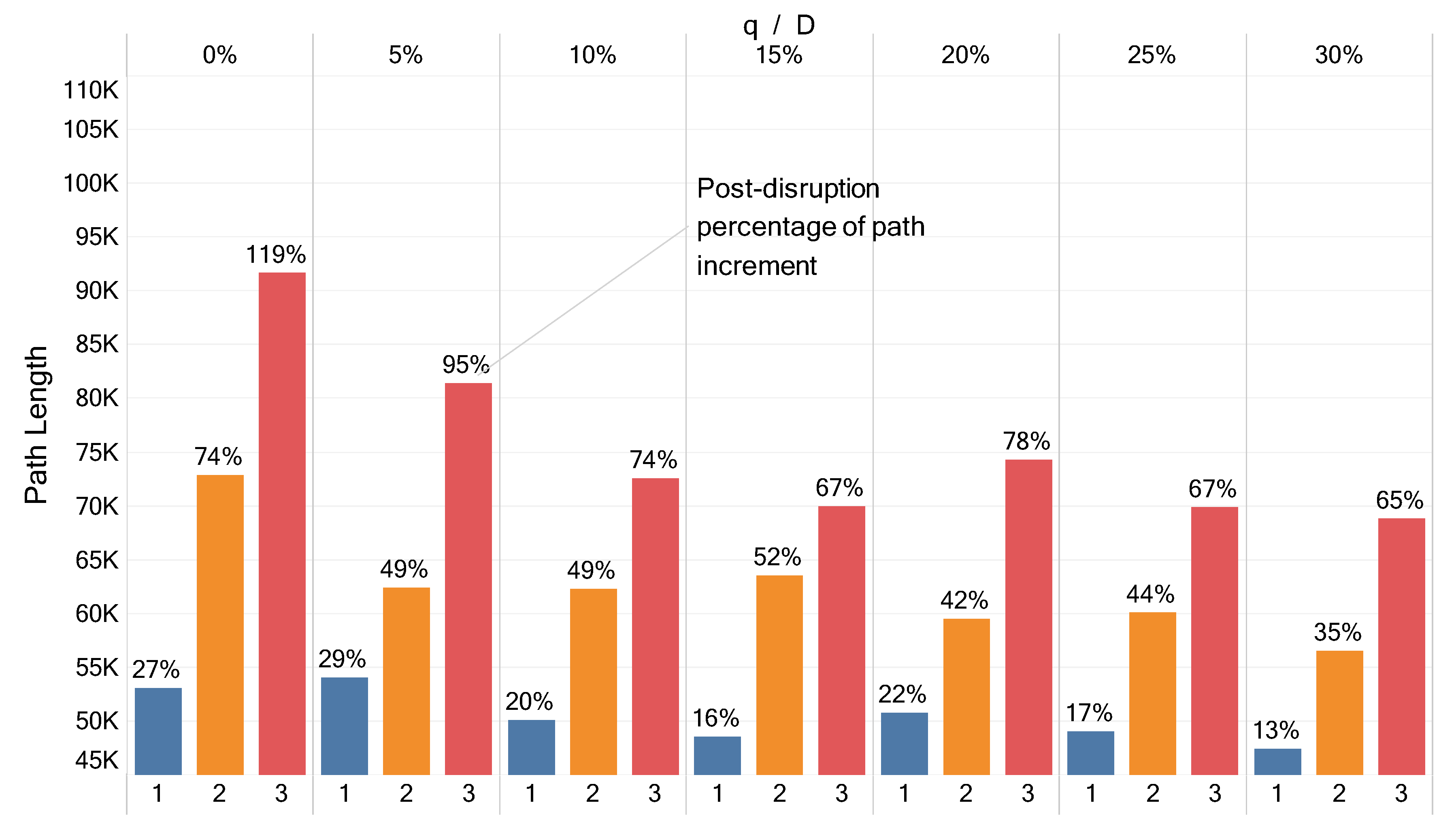
5.2. Integrated Approach Analysis
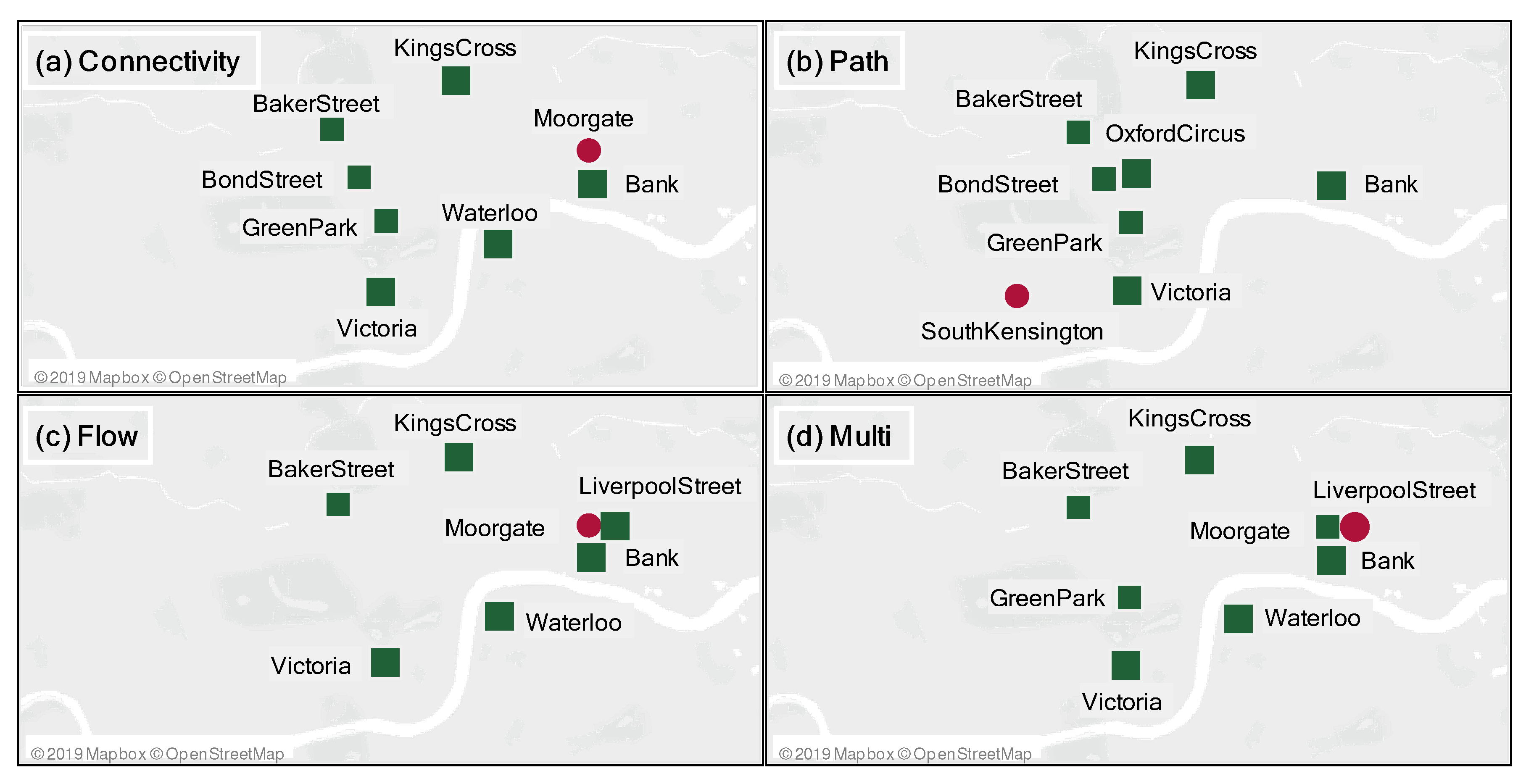
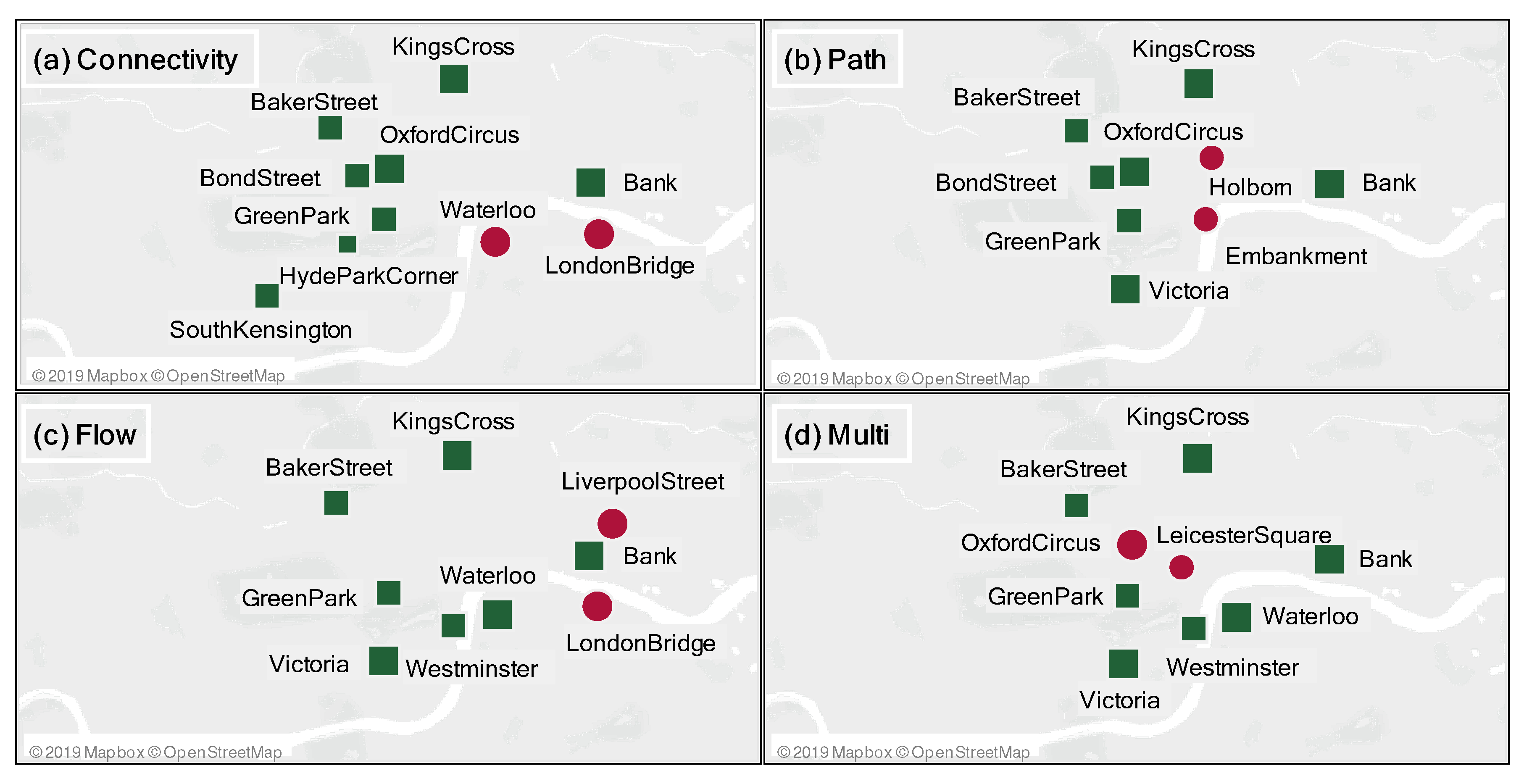
- connectivity-based model ( = 1, = 0, and = 0), referred to as ;
- path-based model ( = 0, = 1, and = 0), referred to as ;
- flow-based model ( = 0, = 0, and = 1), referred to as ; and
- multi-criteria model with equal weights model ( = 0.33, = 0.33, and = 0.33), referred to as .
5.3. Comparing Sequential and Integrated Approaches
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rodgers, L.; Qurashi, S.; Connor, S. 7 July London bombings: What happened that day? BBC, 3 July 2015. [Google Scholar]
- Eardley, N. Rail passengers face some delays at King’s Cross station. BBC, 29 December 2014. [Google Scholar]
- Weaver, M. Hospital, rail lines and roads flooded after heavy rain in England. Guardian, 11 June 2019. [Google Scholar]
- Derrible, S.; Kennedy, C. The complexity and robustness of metro networks. Phys. A Stat. Mech. Its Appl. 2010, 389, 3678–3691. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, M.; Liu, H.; Xu, X. Networked characteristics of the urban rail transit networks. Phys. A Stat. Mech. Its Appl. 2013, 392, 1538–1546. [Google Scholar] [CrossRef]
- Francis, R.; Bekera, B. A metric and frameworks for resilience analysis of engineered and infrastructure systems. Reliab. Eng. Syst. Saf. 2014, 121, 90–103. [Google Scholar] [CrossRef]
- Wang, X.; Koç, Y.; Derrible, S.; Ahmad, S.N.; Pino, W.J.; Kooij, R.E. Multi-criteria robustness analysis of metro networks. Phys. A Stat. Mech. Its Appl. 2017, 474, 19–31. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, S.; Wang, X. Comparison analysis on vulnerability of metro networks based on complex network. Phys. A Stat. Mech. Its Appl. 2018, 496, 72–78. [Google Scholar] [CrossRef]
- Starita, S.; Esposito Amideo, A.; Scaparra, M.P. Assessing Urban Rail Transit Systems Vulnerability: Metrics vs. interdiction Models. In International Conference on Critical Information Infrastructures Security; D’Agostino, G., Scala, A., Eds.; Springer: Cham, Switerland, 2018; pp. 144–155. [Google Scholar]
- Rueda, D.F.; Calle, E.; Marzo, J.L. Robustness comparison of 15 real telecommunication networks: Structural and centrality measurements. J. Netw. Syst. Manag. 2017, 25, 269–289. [Google Scholar] [CrossRef]
- Wood, R.K. Deterministic Network Interdiction. Math. Comput. Model. 1993, 17, 1–18. [Google Scholar] [CrossRef]
- Scaparra, M.P.; Church, R.L. A bilevel mixed-integer program for critical infrastructure protection planning. Comput. Oper. Res. 2008, 35, 1905–1923. [Google Scholar] [CrossRef]
- Cappanera, P.; Scaparra, M.P. Optimal allocation of protective resources in shortest-path networks. Transp. Sci. 2011, 45, 64–80. [Google Scholar] [CrossRef]
- Scaparra, M.P.; Church, R.L. Protecting supply systems to mitigate potential disaster: A model to fortify capacitated facilities. Int. Reg. Sci. Rev. 2012, 35, 188–210. [Google Scholar] [CrossRef]
- Dempe, S. Foundations of Bilevel Programming; Kluwer Academie Publishers: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Xing, Y.; Lu, J.; Chen, S.; Dissanayake, S. Vulnerability analysis of urban rail transit based on complex network theory: A Case study of Shanghai Metro. Public Transp. 2017, 9, 501–525. [Google Scholar] [CrossRef]
- Rochat, Y. Closeness centrality extended to unconnected graphs: The harmonic centrality index. In Proceedings of the 6th Applications of Social Network Analysis Conference (ASNA 2009), Zurich, Switzerland, 26–28 August 2009. [Google Scholar]
- Latora, V.; Marchiori, M. Efficient behavior of small-world networks. Phys. Rev. Lett. 2001, 87, 198701. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Zhao, Y.; Lu, Q.C. Vulnerability analysis of urban rail transit networks: A case study of Shanghai, China. Sustainability 2015, 7, 6919–6936. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Zhou, M.; Li, F.; Sun, C. Robustness assessment of urban rail transit based on complex network theory: A case study of the Beijing Subway. Saf. Sci. 2015, 79, 149–162. [Google Scholar] [CrossRef]
- Kim, H.; Song, Y. An integrated measure of accessibility and reliability of mass transit systems. Transportation 2018, 45, 1075–1100. [Google Scholar] [CrossRef]
- Wollmer, R. Removing arcs from a network. Oper. Res. 1964, 12, 934–940. [Google Scholar] [CrossRef]
- Fulkerson, D.R.; Harding, G.C. Maximizing the minimum source-sink path subject to a budget constraint. Math. Program. 1977, 13, 116–118. [Google Scholar] [CrossRef]
- Israeli, E.; Wood, R.K. Shortest-path network interdiction. Netw. Int. J. 2002, 40, 97–111. [Google Scholar] [CrossRef]
- Bayrak, H.; Bailey, M.D. Shortest path network interdiction with asymmetric information. Netw. Int. J. 2008, 52, 133–140. [Google Scholar] [CrossRef]
- Borrero, J.S.; Prokopyev, O.A.; Saure, D. Sequential shortest path interdiction with incomplete information. Decis. Anal. 2015, 13, 68–98. [Google Scholar] [CrossRef]
- Sefair, J.A.; Smith, J.C. Dynamic shortest-path interdiction. Networks 2016, 68, 315–330. [Google Scholar] [CrossRef]
- Cormican, K.J.; Morton, D.P.; Wood, R.K. Stochastic network interdiction. Oper. Res. 1998, 46, 184–197. [Google Scholar] [CrossRef]
- Myung, Y.S.; Kim, H.J. A cutting plane algorithm for computing k-edge survivability of a network. Eur. J. Oper. Res. 2004, 156, 579–589. [Google Scholar] [CrossRef]
- Murray, A.T.; Matisziw, T.C.; Grubesic, T.H. Critical network infrastructure analysis: Interdiction and system flow. J. Geogr. Syst. 2007, 9, 103–117. [Google Scholar] [CrossRef]
- Grubesic, T.H.; Matisziw, T.C.; Murray, A.T.; Snediker, D. Comparative approaches for assessing network vulnerability. Int. Reg. Sci. Rev. 2008, 31, 88–112. [Google Scholar] [CrossRef]
- Brown, G.; Carlyle, M.; Salmeron, J.; Wood, K. Defending critical infrastructure. Interfaces 2006, 36, 530–544. [Google Scholar] [CrossRef]
- Aksen, D.; Piyade, N.; Aras, N. The budget constrained r-interdiction median problem ith capacity expansion. Cent. Eur. J. Oper. Res. 2010, 18, 269–291. [Google Scholar] [CrossRef]
- Liberatore, F.; Scaparra, M.P.; Daskin, M.S. Analysis of facility protection strategies against an uncertain number of attacks: The stochastic R-interdiction median problem with fortification. Comput. Oper. Res. 2011, 38, 357–366. [Google Scholar] [CrossRef]
- Losada, C.; Scaparra, M.P.; O’Hanley, J. Optimizing system resilience: A facility protection model with recovery time. Eur. J. Oper. Res. 2012, 217, 519–530. [Google Scholar] [CrossRef]
- Sadeghi, S.; Seifi, A.; Azizi, E. Trilevel shortest path network interdiction with partial fortification. Comput. Ind. Eng. 2017, 106, 400–411. [Google Scholar] [CrossRef]
- Lozano, L.; Smith, J.C.; Kurz, M.E. Solving the traveling salesman problem with interdiction and fortification. Oper. Res. Lett. 2017, 45, 210–216. [Google Scholar] [CrossRef] [Green Version]
- Binder, S.; Maknoon, Y.; Bierlaire, M. The multi-objective railway timetable rescheduling problem. Transp. Res. Part C 2017, 78, 78–94. [Google Scholar] [CrossRef] [Green Version]
- Shakibayifar, M.; Sheikholeslami, A.; Corman, F.; Hassannayebi, E. An integrated rescheduling model for minimizing train delays in the case of line blockage. Oper. Res. 2017, 1–29. [Google Scholar] [CrossRef]
- Xu, P.; Corman, F.; Peng, Q.; Luan, X. A Timetable rescheduling approach and transition phases for high speed railway traffic during disruptions. Transp. Res. Rec. 2017, 2607, 82–92. [Google Scholar] [CrossRef] [Green Version]
- Xu, P.; Corman, F.; Peng, Q.; Luan, X. A train rescheduling model integrating speed management during disruptions of high-speed traffic under a quasi-moving block system. Transp. Res. Part B 2017, 104, 638–666. [Google Scholar] [CrossRef]
- Botte, M.; D’Acierno, L. Dispatching and rescheduling tasks and their interactions with travel demand and the energy domain: Models and algorithms. Urban Rail Transit 2018, 4, 163–197. [Google Scholar] [CrossRef]
- Jin, J.G.; Lu, L.; Sun, L.; Yin, J. Optimal allocation of protective resources in urban rail transit networks against intentional attacks. Transp. Res. Part E Logist. Transp. Rev. 2015, 84, 73–87. [Google Scholar] [CrossRef]
- Sarhadi, H.; Tulett, D.M.; Verma, M. A defender-attacker-defender approach to the optimal fortification of a rail intermodal terminal network. J. Transp. Secur. 2015, 8, 17–32. [Google Scholar] [CrossRef]
- Sarhadi, H.; Tulett, D.M.; Verma, M. An analytical approach to the protection planning of a rail intermodal terminal network. Eur. J. Oper. Res. 2017, 257, 511–525. [Google Scholar] [CrossRef]
- Scaparra, M.P.; Starita, S.; Sterle, C. Optimizing investment decisions for railway systems protection. In Railway Infrastructure Security; Springer: Cham, Switerland, 2015; pp. 215–233. [Google Scholar]
- Starita, S.; Scaparra, M.P. Optimizing dynamic investment decisions for railway systems protection. Eur. J. Oper. Res. 2016, 248, 543–557. [Google Scholar] [CrossRef] [Green Version]
- Starita, S.; Scaparra, M.P. Passenger railway network protection: A model with variable post-disruption demand service. J. Oper. Res. Soc. 2018, 69, 603–618. [Google Scholar] [CrossRef] [Green Version]
- Transport For London. TfL Annual Reports and Statement of Accounts 2017–18. Available online: http://content.tfl.gov.uk/tfl-annual-report-and-statement-of-accounts-2017-18.pdf (accessed on 18 September 2019).
- O’Hanley, J.R.; Church, R.L. Designing robust coverage networks to hedge against worst-case facility losses. Eur. J. Oper. Res. 2011, 209, 23–36. [Google Scholar] [CrossRef]




| ND | HC | NV | NB | PF |
| King’s Cross | OxfordCircus | GreenPark | GreenPark | Bank |
| Bank | GreenPark | OxfordCircus | OxfordCircus | King’s Cross |
| BakerStreet | Bank | Bank | LeicesterSquare | Waterloo |
| Waterloo | BakerStreet | BakerStreet | PiccadillyCircus | Victoria |
| OxfordCircus | Embankment | King’s Cross | Embankment | LiverpoolStreet |
| Moorgate | King’s Cross | Embankment | TottenhamCourtRoad | BakerStreet |
| GreenPark | LeicesterSquare | Victoria | CharingCross | Moorgate |
| Embankment | Holborn | BondStreet | King’s Cross | LondonBridge |
| LiverpoolStreet | TottenhamCourtRoad | Waterloo | Westminster | Paddington |
| Aldgate | Waterloo | Holborn | WarrenStreet | Farringdon |
| ST | IM | SV | WA | WI |
| Bank | GreenPark | Bank | Bank | King’s Cross St Pancras |
| King’s Cross | OxfordCircus | King’s Cross | King’s Cross | Bank |
| Waterloo | LeicesterSquare | Waterloo | Waterloo | Waterloo |
| BakerStreet | PiccadillyCircus | Victoria | Victoria | BakerStreet |
| Moorgate | Embankment | BakerStreet | BakerStreet | GreenPark |
| LiverpoolStreet | TottenhamCourtRoad | Moorgate | LiverpoolStreet | OxfordCircus |
| Victoria | CharingCross | GreenPark | Moorgate | Moorgate |
| GreenPark | King’s Cross | OxfordCircus | OxfordCircus | Victoria |
| OxfordCircus | Westminster | LiverpoolStreet | GreenPark | Embankment |
| Paddington | WarrenStreet | LondonBridge | LondonBridge | LiverpoolStreet |
| ND | HC | NV | NB | PF |
| GoodgeStreet | Barbican | Southwark | EdgwareRoad(Bak) | LeicesterSquare |
| EdgwareRoad(Bak) | LambethNorth | Angel | Aldgate | Queensway |
| CoventGarden | EdgwareRoad(Cir) | LambethNorth | TowerHill | RussellSquare |
| ChanceryLane | SloaneSquare | Borough | LambethNorth | LambethNorth |
| CannonStreet | Bayswater | TowerHill | Borough | Borough |
| Blackfriars | Borough | EdgwareRoad(Bak) | Elephant-Castle | GoodgeStreet |
| Bayswater | Pimlico | Elephant-Castle | Pimlico | RegentsPark |
| Angel | EarlsCourt | Vauxhall | EarlsCourt | CoventGarden |
| Vauxhall | Vauxhall | EarlsCourt | Vauxhall | Bayswater |
| AldgateEast | AldgateEast | AldgateEast | AldgateEast | EdgwareRoad(Bak) |
| ST | IM | SV | WA | WI |
| Queensway | EdgwareRoad(Bak) | GoodgeStreet | HydeParkCorner | Southwark |
| AldgateEast | Aldgate | Queensway | RussellSquare | TowerHill |
| RussellSquare | TowerHill | AldgateEast | GoodgeStreet | EdgwareRoad(Bak) |
| LambethNorth | LambethNorth | RussellSquare | Queensway | Pimlico |
| Borough | Borough | CoventGarden | LambethNorth | Elephant-Castle |
| GoodgeStreet | Elephant-Castle | RegentsPark | RegentsPark | LambethNorth |
| RegentsPark | Pimlico | LambethNorth | CoventGarden | Borough |
| CoventGarden | EarlsCourt | Borough | Borough | EarlsCourt |
| Bayswater | Vauxhall | Bayswater | Bayswater | Vauxhall |
| EdgwareRoad(Bak) | AldgateEast | EdgwareRoad(Bak) | EdgwareRoad(Bak) | AldgateEast |
| Model | Connectivity | Path | Flow | Multi | AVG | Max |
|---|---|---|---|---|---|---|
| 0% | 1% | 41% | 6% | 12% | 41% | |
| 6% | 0% | 52% | 10% | 17% | 52% | |
| 22% | 7% | 0% | 9% | 10% | 22% | |
| 6% | 2% | 20% | 0% | 7% | 20% |
| Connectivity | Path | Flow | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | Metric | Metric | |||||||||||||||
| D | q | IM | ND | ST | WI | HC | IM | NB | NV | SV | WA | WI | PF | ST | SV | WA | WI |
| 1 | 5% | 18% | 18% | 18% | 18% | 1% | 1% | 1% | 1% | 1% | 1% | 1% | 0% | 0% | 0% | 0% | 0% |
| 10% | 30% | 10% | 10% | 10% | 4% | 4% | 4% | 4% | 3% | 3% | 4% | 0% | 12% | 0% | 0% | 12% | |
| 15% | 54% | 31% | 31% | 31% | 7% | 7% | 7% | 2% | 2% | 6% | 7% | 0% | 27% | 13% | 0% | 27% | |
| 20% | 71% | 46% | 20% | 20% | 9% | 9% | 9% | 2% | 3% | 3% | 3% | 0% | 13% | 13% | 13% | 68% | |
| 25% | 55% | 7% | 28% | 28% | 11% | 11% | 11% | 3% | 3% | 5% | 5% | 0% | 23% | 13% | 9% | 23% | |
| 30% | 58% | 9% | 31% | 31% | 12% | 12% | 12% | 4% | 4% | 6% | 6% | 0% | 0% | 34% | 18% | 52% | |
| AVG | 48% | 20% | 23% | 23% | 7% | 7% | 7% | 3% | 3% | 4% | 4% | 0% | 13% | 12% | 7% | 30% | |
| 2 | 5% | 27% | 6% | 6% | 6% | 7% | 7% | 7% | 7% | 3% | 3% | 3% | 4% | 4% | 4% | 4% | 4% |
| 10% | 52% | 27% | 27% | 27% | 1% | 11% | 11% | 1% | 8% | 8% | 8% | 0% | 2% | 0% | 0% | 2% | |
| 15% | 65% | 8% | 19% | 8% | 6% | 18% | 18% | 4% | 10% | 14% | 6% | 24% | 7% | 3% | 24% | 27% | |
| 20% | 46% | 20% | 12% | 12% | 9% | 13% | 13% | 1% | 6% | 6% | 6% | 59% | 0% | 0% | 0% | 28% | |
| 25% | 72% | 26% | 32% | 32% | 12% | 17% | 17% | 4% | 5% | 11% | 11% | 52% | 15% | 15% | 15% | 14% | |
| 30% | 52% | 36% | 42% | 42% | 17% | 17% | 17% | 8% | 10% | 15% | 15% | 26% | 26% | 26% | 26% | 24% | |
| AVG | 52% | 21% | 23% | 21% | 8% | 14% | 14% | 4% | 7% | 9% | 8% | 27% | 9% | 8% | 11% | 17% | |
| 3 | 5% | 16% | 1% | 1% | 1% | 5% | 5% | 5% | 5% | 2% | 2% | 2% | 5% | 5% | 5% | 5% | 5% |
| 10% | 32% | 16% | 16% | 16% | 2% | 11% | 11% | 2% | 8% | 8% | 9% | 14% | 14% | 14% | 14% | 14% | |
| 15% | 48% | 4% | 26% | 4% | 3% | 16% | 16% | 1% | 11% | 13% | 3% | 30% | 5% | 5% | 30% | 5% | |
| 20% | 36% | 11% | 9% | 9% | 7% | 16% | 16% | 5% | 6% | 6% | 6% | 40% | 0% | 0% | 0% | 9% | |
| 25% | 42% | 23% | 23% | 26% | 13% | 16% | 16% | 8% | 10% | 10% | 11% | 61% | 20% | 17% | 17% | 16% | |
| 30% | 46% | 36% | 40% | 43% | 17% | 17% | 17% | 12% | 15% | 15% | 16% | 21% | 21% | 27% | 23% | 27% | |
| AVG | 37% | 15% | 19% | 17% | 8% | 13% | 13% | 5% | 9% | 9% | 8% | 29% | 11% | 11% | 15% | 13% | |
| AVG | 46% | 19% | 22% | 20% | 8% | 11% | 11% | 4% | 6% | 8% | 7% | 19% | 11% | 11% | 11% | 20% | |
| Metric | q | ||||||
|---|---|---|---|---|---|---|---|
| D | 5% | 10% | 15% | 20% | 25% | 30% | |
| WI | 1 | 0% | 8% | 21% | 12% | 8% | 9% |
| 2 | 3% | 15% | 2% | 2% | 11% | 20% | |
| 3 | 0% | 13% | 3% | 2% | 15% | 29% | |
| AVG | 1% | 12% | 8% | 5% | 11% | 19% | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esposito Amideo, A.; Starita, S.; Scaparra, M.P. Assessing Protection Strategies for Urban Rail Transit Systems: A Case-Study on the Central London Underground. Sustainability 2019, 11, 6322. https://doi.org/10.3390/su11226322
Esposito Amideo A, Starita S, Scaparra MP. Assessing Protection Strategies for Urban Rail Transit Systems: A Case-Study on the Central London Underground. Sustainability. 2019; 11(22):6322. https://doi.org/10.3390/su11226322
Chicago/Turabian StyleEsposito Amideo, Annunziata, Stefano Starita, and Maria Paola Scaparra. 2019. "Assessing Protection Strategies for Urban Rail Transit Systems: A Case-Study on the Central London Underground" Sustainability 11, no. 22: 6322. https://doi.org/10.3390/su11226322





