Inertia Provision and Small Signal Stability Analysis of a Wind-Power Generation System Using Phase-Locked Synchronized Equation

Abstract

The inertia and damping of the modern power system are consistently decreased when wind energy has a high penetration level into the grid. This paper proposes a novel solution through transforming the wind turbine generator into an equivalent motion equation mimicking the basic characteristics of the synchronous generator (SG). This synchronized equation builds upon the phase-locked loop (PLL) model of the doubly-fed induction generator (DFIG), which characterizes the inertia constant, damping coefficient, and synchronizing torque. Thanks to this work, the dynamic performance of the inverter-based asynchronous generator could be analyzed from the perspective of the classical rotor motion equation. It further enables us to employ the analogy method to provide the DFIG with automated frequency response ability and to estimate the inertia constant quantitatively. Results also manifest that based on the synchronized equation, the PLL forms a power system stabilizer to enhance the power system oscillation. Hence, parameters tuning in PLL for coordinating inertia provision and damping enhancement are introduced. The contribution of this study lies in that the equivalent synchronized equation is established to optimize the system operation without alterations in the existing control structure of the DFIG. The theoretical analysis and the strategy are verified through the power system simulator.

1. Introduction

The wind power generation system offers solutions to energy shortage and environmental contamination with the effective application of the clean, abundant, ever-renewable wind energy [1]. The globally installed wind power capacity has reached up to 539 GW since 2017 [2], which significantly reduces the dependency on fossil energy and greenhouse gas emissions. Among the current wind power technology, the doubly-fed induction generator (DFIG) based wind power generation system presents obvious dominance with high energy transfer efficiency, flexible grid connection, and power decoupling control [3,4,5]. Nevertheless, the power system with high wind energy penetration experiences significant transitions in dynamic and transient characteristics [6]. Different from the synchronous generators (SGs), the DFIG operates at the maximum power producing point for a given wind speed [7]. For this reason, the system frequency is decoupled from the partially rated power converter, which results in a loss of ability in the DFIG to provide inertia and frequency support [8,9]. The reduced inertia has also presented challenges to the system small signal stability [10,11]. This paper aims to improve both the inertia and oscillation damping of the power grid.

Inertia provision strategies are basically classified into three types: the virtual inertia control (VIC), the virtual synchronous generator (VSG) technology, and the phase-locked loop (PLL)-based inertia emulation method. (i) The VIC introduces the frequency deviation into the active power controller and employs the stored energy to suppress frequency drops [12]. The basic controller for VIC includes the droop control [13], the differential control [14], and the proportional plus derivative control [15]. In addition, the inertia emulation strategy by switching the maximum power point tracking (MPPT) curve is proposed to improve the robustness of the controller [16]. In [17], an enhanced frequency support technique was proposed utilizing the superconducting magnetic energy storage (SMES) preserved in the permanent magnet synchronous generator (PMSG). The fast response ability of SMES provides the PMSG with higher inertia provision and less stress in the rotational mass. In addition to inertia emulation, the impacts of VIC on the small signal stability of the power system were analyzed in [18,19]. Under receiving and feeding networks, the VIC may either improve the oscillation damping or produce negative damping for the power grid. (ii) The VSG technology controls the inverter-based renewable energy sources to mimic the essential behavior of the SG [20]. Provided with the virtual inertia and the frequency droop control, the VSG takes the same responsibility to attenuate the power imbalance as the SG does. Aiming at the system small signal stability with the application of the VSG, the parameters design of the power loop is explored to analyze and improve the stability margin [21,22]. Superior to the VIC, the VSG technology is equipped with the damping and reactive power control to suppress the power oscillation. However, more complex inverter control algorithms and fault current limiting schemes are required for the VSG. (iii) The PLL-based inertia emulation method adopts the controlled delay lock technology, which provides the wind turbine generator (WTG) with the automated frequency response ability [23]. The current researches have calculated the inertia time constant of WTG with the frequency-domain expression [24,25]. Meanwhile, the separate effect of the PLL parameter on the small signal stability of the power system has been studied [26,27]. The existing research findings illustrate that the inertia of WTG could be enhanced by decreasing the parameters in PLL with a constant ratio [23]. However, this approach only ensures that the internal stability of PLL remains unchanged [27]. Based on the previous researches, this paper focuses on improving both the inertia and damping through changing the phased-locked mechanism in PLL.

The PLL-based inertia emulation has a number of advantages compared with the VIC and VSG in that (i) the parameters tuning in PLL makes the DFIG respond to frequency disturbance spontaneously without alterations or modifications in the existing active power control loop; (ii) the standard and technologies for the existing PLL-based voltage-source converter are quite mature; and (iii) the equivalent motion equation is established based on the phase-locked mechanism, so that the DFIG responds to the frequency excursion in the same way as the SG does. Therefore, the inertia time constant of the DFIG has physical significance and could be quantified.

However, modification of parameters in PLL is likely to have a significant impact on the system damping and locking accuracy of PLL. The unresolved issues for the PLL-based inertia emulation also include establishing the equivalent swing equation of WTG to reveal its motion mechanism, obtaining the time-domain expression of the inertia time constant of WTG to estimate precisely its inertial response ability, and clarifying synthetic effects of PLL parameters on small signal stability of the power system. Aiming at these problems, this paper derives the time-domain expression of inertia constant of the DFIG by establishing the PLL-synchronized swing equation. The inertia emulation and parameters optimization strategy are proposed to realize better frequency response performance and high oscillation damping of the power system at the same time.

Section 2 “Materials and Methods” is organized as follows: In Section 2.1, the synchronized swing equation of the DFIG is established based on the PLL model. In Section 2.2, the physical significance of the equivalent inertia is discussed, and the inertia emulation strategy is proposed though parameters tuning. In Section 2.3, the internal stability of PLL and its impacts on the global stability of the multi-machine system are analyzed in detail. The parameters optimization strategy is proposed to improve the inertial response ability of the DFIG while maintaining strong oscillation damping. In Section 3 “Simulation Results”, the mechanisms analysis and the strategy are verified through the simulations in Power System Simulator for Engineering (PSS/E).

2. Materials and Methods

The description of the variables used through the text is listed as follows:

KP_PLL, KI_PLL	Proportional plus integral (PI) control parameters of PLL.
uds, uqs	Stator voltage in the dq reference frame.
ids, iqs	Stator current in the dq reference frame.
δpll, ωpll	Phase angle of PLL, phase-locked angular velocity.
δg, ωg	Power angle of SG, rotor angular velocity of SG.
δw, θin	Phase angle of stator voltage, relative phase angle between Uw and E.
Uw, E, U	Stator voltage vector, internal voltage vector, voltage of infinite bus.
Hw, Hg	Inertia time constant of wind power plant (WPP), inertia time constant of SG.
Dw, Dg	Damping coefficient of WPP, damping coefficient of SG.
Pw, Pg	Active power output of WPP, active power output of SG.
sr, ω0	Slip ratio of DFIG, reference angular velocity of the power system.

2.1. Establishment of PLL-Synchronized Swing Equation of the DFIG

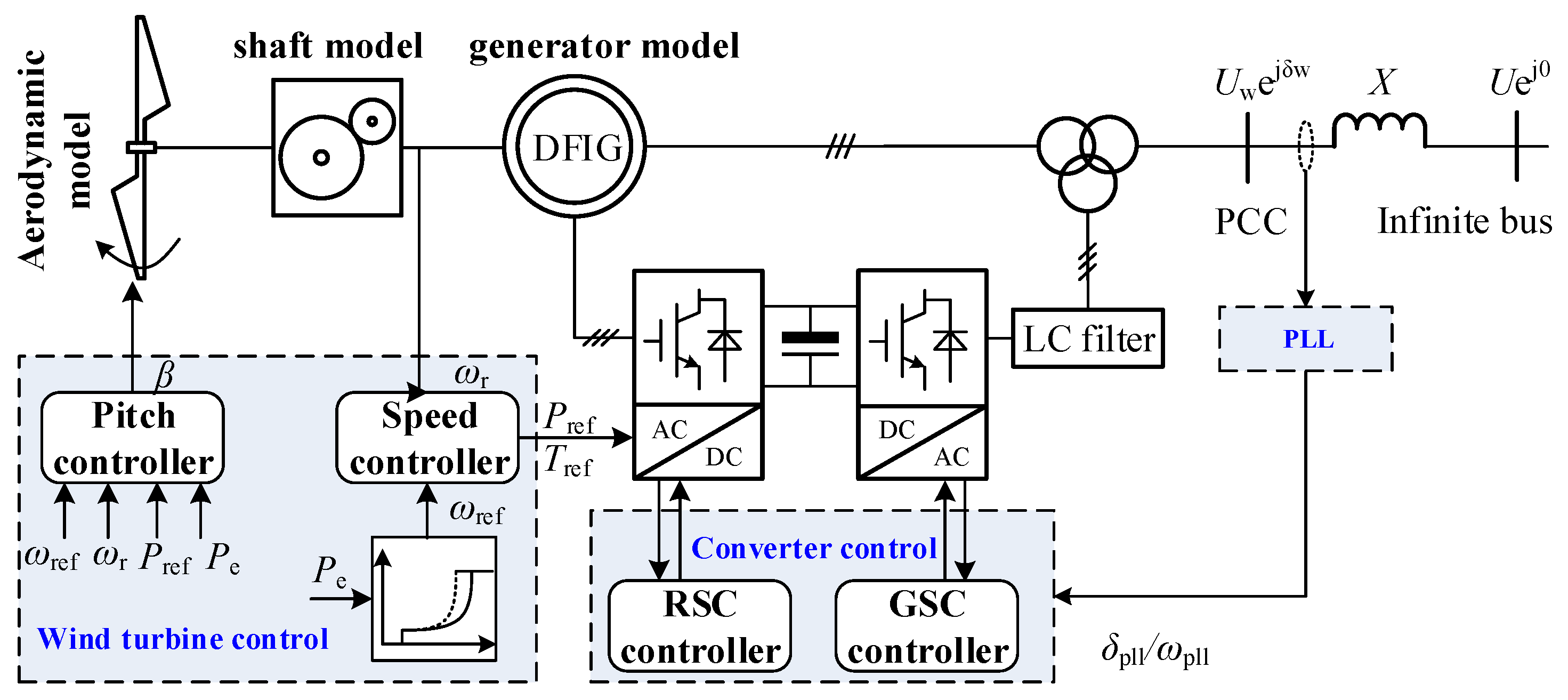
2.1.1. Introduction of the DFIG Control Structure

This section aims to introduce the control structure of the doubly-fed induction generator (DFIG). As is shown in Figure 1, the control structure of the DFIG is composed of the physical model and the control model [23]. The physical model includes the aerodynamic, shaft, and generator models. The control model includes the pitch angle control, maximum power point tracking, speed control, and the converter control models. According to [28], the specific differential equations of the physical models and the control models of the DFIG have been studied in detail. In addition, the phase-locked loop (PLL) model is utilized to track the voltage angle and frequency in the point of common coupling (PCC). The PLL model forms an important basis for the voltage-oriented control, the power-decoupling control, and the constant-frequency operation of the DFIG. However, the mechanisms of the PLL model on output characteristics of the DFIG have not been studied fully.

This paper focuses on the mechanisms of the PLL model alone on the output characteristics of the DFIG. According to [23], the active power increments of the DFIG are determined by two parts: the active power control loop and the PLL control loop, which are shown in Figure 2. The active power control loop produces the internal phase angle increment Δθ_in. Whereas the PLL control loop produces the phase-locked angle increment Δδ_pll. The sum of Δθ_in and Δδ_pll constitutes the synthetic power angle variation Δδ_in, which directly influences the active power output of the DFIG. The dynamics of the active power control loop is neglected to highlight the effects of the PLL model. Therefore, there is Δθ_in = 0 and Δδ_pll = Δδ_in in this paper.

Generally, the PLL model consists of an integration element 1/s and a proportional plus integral (PI) control. Figure 2 shows the transfer function block diagram of the PLL model in PSS/E [29]. Accordingly, the differential equation of the PLL model is expressed as [26]:

$$\frac{1}{{\omega }_0}{\dot{\delta }}_{\mathrm{pll}}={\omega }_{\mathrm{pll}}=K_{\mathrm{I}\_\mathrm{PLL}}\cdot K_{\mathrm{P}\_\mathrm{PLL}}{x}_{\mathrm{pll}}-K_{\mathrm{P}\_\mathrm{PLL}}{u}_{\mathrm{ds}}$$

(1)

As is shown in (1) and Figure 2, δ_pll is the phase-locked angle; ${\dot{\delta }}_{\mathrm{pll}}$ is the first-order derivative of δ_pll, ω_pll is the phase-locked angular velocity; ω₀ = 2πf₀ is the reference angular velocity of the power system; K_{P_PLL} and K_{I_PLL} are the proportional gain and integral gain, respectively; x_pll is the intermediate state variable and satisfies ${\dot{x}}_{\mathrm{pll}}=-u_{\mathrm{ds}}$, and u_ds denotes the d-axis stator voltage amplitude.

2.1.2. Establishment of Swing Equation of the DFIG Based on PLL

According to [30], the rotor motion equation of SG could be regarded as a modified PLL, which ensures the synchronous operation between the SG and the power system. Based on this, this section attempts to derive the equivalent swing equation of the DFIG based on the PLL equation in (1). Basically, the PLL model measures the voltage phase angle at PCC to realize voltage-oriented control. As is shown in Figure 3, the voltage vector U_w at PCC locates in the dq synchronous reference frame, and the dq-axis stator voltage vectors u_ds and u_qs locate in the dq PLL reference frame, respectively [24]. The d(ω_pll)-axis and q(ω_pll)-axis rotate with the angular velocity of ω_pll, and the q(ω₀)-axis and d(ω₀)-axis rotate with the angular velocity of ω₀. δ_w is the initial phase angle of U_w, and δ_pll is also the initial phase angle of u_qs. E is the internal voltage vector of the DFIG. θ_in is the angle difference between E and u_qs.

According to Figure 3, the voltage amplitudes of u_qs and u_ds are expressed as [31]:

$$\{\begin{array}{l}{u}_{\mathrm{ds}}=U_{\mathrm{w}}\sin ({\delta }_{\mathrm{pll}}-{\delta }_{\mathrm{w}})\\ u_{\mathrm{qs}}=U_{\mathrm{w}}\cos ({\delta }_{\mathrm{pll}}-{\delta }_{\mathrm{w}})\end{array}$$

(2)

In the steady state, u_qs coincides with U_w based on the voltage-oriented control. Therefore, u_ds = 0, u_qs = U_w, and δ_w − δ_pll = 0. In the following analysis, δ_w and δ_pll denote their initial values whereas Δδ_w and Δδ_pll denote their variations.

During the dynamic process, however, the variations of the voltage phase angle are produced (represented by Δδ_w and Δδ_pll). Hence, u_qs, and u_ds locate on the q(ω_pll)-axis and d(ω_pll)-axis, respectively. The increment equations of u_qs, and u_ds are calculated as:

$$\{\begin{array}{l}\mathsf{\Delta }{u}_{\mathrm{ds}}=U_{\mathrm{w}}\cos ({\delta }_{\mathrm{pll}}-{\delta }_{\mathrm{w}})\mathsf{\Delta }{\delta }_{\mathrm{pll}}-U_{\mathrm{w}}\cos ({\delta }_{\mathrm{pll}}-{\delta }_{\mathrm{w}})\mathsf{\Delta }{\delta }_{\mathrm{w}}=U_{\mathrm{w}}(\mathsf{\Delta }{\delta }_{\mathrm{pll}}-\mathsf{\Delta }{\delta }_{\mathrm{w}})\\ \mathsf{\Delta }{u}_{\mathrm{qs}}=-U_{\mathrm{w}}\sin ({\delta }_{\mathrm{pll}}-{\delta }_{\mathrm{w}})\mathsf{\Delta }{\delta }_{\mathrm{pll}}+U_{\mathrm{w}}\sin ({\delta }_{\mathrm{pll}}-{\delta }_{\mathrm{w}})\mathsf{\Delta }{\delta }_{\mathrm{w}}=0\end{array}$$

(3)

Furthermore, the active power output of the DFIG is expressed as [32]:

$$P_{\mathrm{w}}\approx (1-s_{\mathrm{r}})(u_{\mathrm{ds}}{i}_{\mathrm{ds}}+u_{\mathrm{qs}}{i}_{\mathrm{qs}})$$

(4)

where s_r is the slip ratio; i_ds is the d-axis stator current; i_qs is the q-axis stator current. Neglecting the dynamic variations of s_r, i_ds, and i_qs, the increment equation of P_w is expressed as:

$$\mathsf{\Delta }{P}_{\mathrm{w}}\approx (1-s_{\mathrm{r}})(\mathsf{\Delta }{u}_{\mathrm{ds}}{i}_{\mathrm{ds}}+\mathsf{\Delta }{u}_{\mathrm{qs}}{i}_{\mathrm{qs}})=(1-s_{\mathrm{r}})\mathsf{\Delta }{u}_{\mathrm{ds}}{i}_{\mathrm{ds}}$$

(5)

According to (1), the intermediate state variable x_pll is represented by −u_ds/s (s is the Laplacian operator), so the increment equation of PLL in (1) is calculated as:

$$\mathsf{\Delta }{\omega }_{\mathrm{pll}}=-K_{\mathrm{I}\_\mathrm{PLL}}{K}_{\mathrm{P}\_\mathrm{PLL}}\frac{\mathsf{\Delta }{u}_{\mathrm{ds}}}{s}-K_{\mathrm{P}\_\mathrm{PLL}}\mathsf{\Delta }{u}_{\mathrm{ds}}$$

(6)

As is indicated in (5) and (6), Δu_ds establishes the relationship between the active power equation and the PLL equation. The expression of Δu_ds is calculated as Δu_ds = −Δω_pll/(K_{P_PLL} + K_{I_PLL}K_{P_PLL}/s), which is substituted into (5) to obtain the transfer function of PLL. In addition, the equivalent transformations are implemented to make the transfer function of PLL have the same mathematical form as the swing equation:

$$(-\mathsf{\Delta }{P}_{\mathrm{w}}-\frac{\mathsf{\Delta }{P}_{\mathrm{w}}}{\mathsf{\Delta }{\delta }_{\mathrm{pll}}}\cdot \frac{{\omega }_0}{K_{\mathrm{I}\_\mathrm{PLL}}}\cdot \mathsf{\Delta }{\omega }_{\mathrm{pll}})\cdot \frac{K_{\mathrm{I}\_\mathrm{PLL}}{K}_{\mathrm{P}\_\mathrm{PLL}}}{(1-s_{\mathrm{r}})i_{\mathrm{ds}}\cdot s}=\mathsf{\Delta }{\omega }_{\mathrm{pll}}=\frac{s}{{\omega }_0}\mathsf{\Delta }{\delta }_{\mathrm{pll}}$$

(7)

where ΔP_w/Δδ_pll denotes the synchronizing torque of the DFIG. In this paper, ΔP_w/Δδ_pll is defined as T_s. The block diagram of the transfer function of (7) is illustrated in Figure 4a. The block diagram of the transfer function of the rotor motion equation of the SG is also illustrated in Figure 4b [33] for comparison.

Accordingly, the transfer function in (7) could also be written in the form of the differential equation:

$$M_{\mathrm{w}}\mathsf{\Delta }{\ddot{\delta }}_{\mathrm{pll}}=-\mathsf{\Delta }{P}_{\mathrm{w}}-D_{\mathrm{w}}\mathsf{\Delta }{\omega }_{\mathrm{pll}},\mathrm{where}{M}_{\mathrm{w}}=\frac{(1-s_{\mathrm{r}})i_{\mathrm{ds}}}{K_{\mathrm{I}\_\mathrm{PLL}}{K}_{\mathrm{P}\_\mathrm{PLL}}{\omega }_0},D_{\mathrm{w}}=\frac{T_{\mathrm{s}}{\omega }_0}{K_{\mathrm{I}\_\mathrm{PLL}}}$$

(8)

where ${\ddot{\delta }}_{\mathrm{pll}}$ is the second-order derivative of δ_pll.

Comparing the transfer function of the DFIG in Figure 4a with the transfer function of the SG in Figure 4b, it could reasonably conclude that D_w corresponds to the damping coefficient D_g, whereas M_w corresponds to the inertia constant M_g. In addition, δ_pll and ω_pll are the state variables, which have the same dynamic characteristics as the rotor angle δ_g and the rotor speed ω_g of the SG. Therefore, Equation (8) is defined as the swing equation of the DFIG, which is established on the PLL model, the active power equation, and the voltage-oriented control from (1) to (5). According to (8), the swing equation of the DFIG has the same components with the rotor motion equation, including the inertia constant, the damping coefficient, the synchronizing torque, and the power angle. In the next sections, the physical significance of the model will be explained further, and the accuracy of the model will be verified in the simulations of inertia provision and damping analysis.

2.2. Inertia Provisions Using the PLL-Synchronized the DFIG Model

2.2.1. Physical Significance of the Proposed Swing Equation of the DFIG

It is well known that the decoupling between the converter controls of the DFIG and system frequency results in no inertia response of the DFIG. The PLL model, however, produces the phase angle variations of Δδ_w − Δδ_pll between the internal voltage vector E and the voltage vector U_w at PCC, which changes the output characteristics of the DFIG during the dynamic process. According to Figure 3, q(ω_pll)-axis coincides with q(ω₀)-axis, and E has the same angular velocity with U_w in the steady state. However, under the frequency step down scenario, for instance, the PLL cannot accurately lock the grid voltage angle in real-time. Q(ω₀) will lag behind q(ω_pll) due to the decrease in system frequency. The angle difference between E and U_w increases from θ_in to θ_in + Δδ_w − Δδ_pll. The increase of phase angle difference contributes to the increase of active power output of the DFIG. Consequently, the PLL provides the DFIG with the ability to respond to the frequency disturbance. The response capability for frequency excursion is described by the inertia constant in (8).

2.2.2. Inertia Emulation Using the PLL-Synchronized Swing Equation

Note that the typical values of PLL parameters are K_{P_PLL} = 40 and K_{I_PLL} = 100 [27]. According to (8), the value of M_w is small enough to be neglected under typical values, which explains why the DFIG could not respond to the frequency excursion under the general state. If both of K_{P_PLL} and K_{I_PLL} decrease, M_w will increase, and the inertial response ability for the DFIG will be enhanced.

Based on the inertia expression in (8) and the DFIG model in Figure 1, Figure 5 shows the variation surface of inertia time constant H_w (2H_w/ω₀ = M_w) with K_{P_PLL} and K_{I_PLL}. The system parameters refer to Appendix A. According to Figure 5, if K_{P_PLL} or K_{I_PLL} is larger than 5, H_w approaches to 0. Whereas if both of K_{P_PLL} and K_{I_PLL} decrease to smaller than 5, H_w increases rapidly. Therefore, the DFIG has a sufficient inertia response ability only when both K_{P_PLL} and K_{I_PLL} are small enough. This result offers the possibility for improving the inertia provision of the DFIG just by changing the parameters in PLL.

The inertia provision strategy based on PLL has many unique advantages compared with the virtual inertia control, such as (i) emulating the kinetic characteristics of the rotor rotational mass based on the physical model of the swing equation, which provides the DFIG with the same inertia response characteristics with the SG; (ii) enabling us to obtain the quantitative expression of the inertia time constant of the DFIG; (iii) without changing the control structure nor adding more control loops in the DFIG. However, changing K_{P_PLL} and K_{I_PLL} might also result in adverse effects, including low locking accuracy of PLL and weak oscillation damping. The following parts focus on the impacts of K_{P_PLL} and K_{I_PLL} on the small signal stability of the power system, and research on the parameters tuning for coordination between the inertia provisions and damping enhancement.

2.3. Small Signal Stability Analysis Using PLL-synchronized Swing Equation

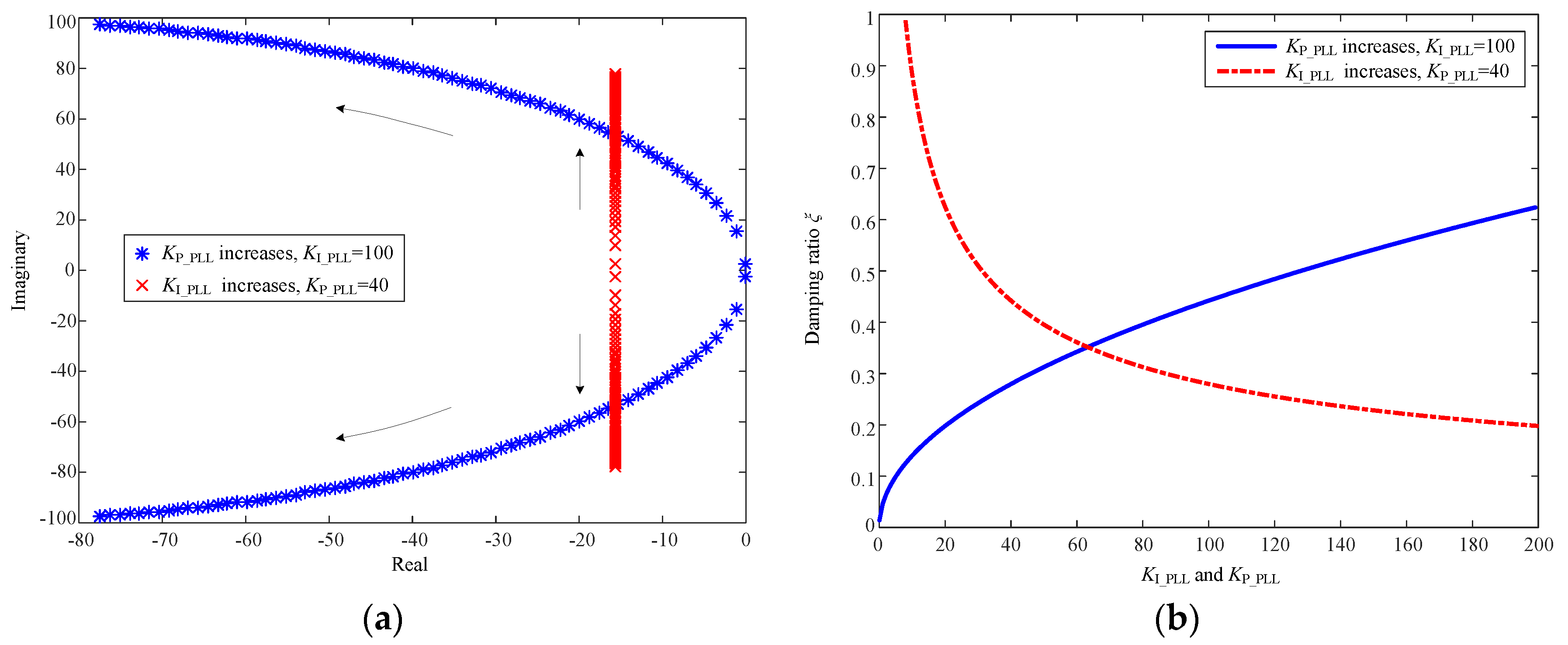
2.3.1. Internal Stability of PLL Model

The single-DFIG infinite bus system could be employed to analyze the internal stability of the PLL-synchronized swing equation. Based on the single-DFIG infinite bus system in Figure 1, this part focuses on the impacts of K_{P_PLL} and K_{I_PLL} on the locking accuracy and the internal stability of PLL. According to Figure 1, the active power increment ΔP_w is calculated as in (9) according to the active power balance equation [16].

$$\mathsf{\Delta }{P}_{\mathrm{w}}=\frac{U_{\mathrm{w}}U\cos {\delta }_{\mathrm{pll}}}{X}\cdot f\cdot \mathsf{\Delta }{\delta }_{\mathrm{pll}}=T_{\mathrm{s}}\cdot \mathsf{\Delta }{\delta }_{\mathrm{pll}},\mathrm{where}f=\frac{(1-s_{\mathrm{r}})i_{\mathrm{ds}}}{(1-s_{\mathrm{r}})i_{\mathrm{ds}}+U\cos {\delta }_{\mathrm{w}}/X}$$

(9)

where U is the voltage amplitude in the infinite bus, U_w is the voltage amplitude at PCC, X is the reactance of the transmission line, and the resistance is neglected.

The complete differential equation of the single-DFIG infinite bus system is obtained by combining (8) and (9). Solving the corresponding characteristic equation, the damping ratio ξ and the response time t_r [34] of PLL are expressed as (ω₀ = 1):

$$\xi =\frac{D_{\mathrm{w}}}{2\sqrt{T_{\mathrm{s}}{M}_{\mathrm{w}}}}=\sqrt{\frac{T_{\mathrm{s}}{K}_{\mathrm{P}\_\mathrm{PLL}}}{4(1-s_{\mathrm{r}})i_{\mathrm{ds}}{K}_{\mathrm{I}\_\mathrm{PLL}}}}$$

(10)

$$t_{\mathrm{r}}\propto \frac{2(1-s_{\mathrm{r}})i_{\mathrm{ds}}}{T_{\mathrm{s}}{K}_{\mathrm{P}\_\mathrm{PLL}}}$$

(11)

According to (10), the damping ratio ξ is proportional to K_{P_PLL}, whereas inversely proportional to K_{I_PLL}. Note that the damping ratio ξ is proportional to K_{P_PLL}/K_{I_PLL}. To improve the inertial response ability of the DFIG, K_{P_PLL} and K_{I_PLL} could be set as small enough values but maintain the same ratio (K_{I_PLL}/K_{P_PLL} = 100/40). In this case, the damping properties of PLL would not change.

As is indicated in (11), the response time t_r is inversely proportional to K_{P_PLL}. The increase of t_r means that it takes more time for PLL to lock the system voltage angle and frequency. Therefore, the decrease of K_{P_PLL} improves the inertial response ability of the DFIG, but slows down the response rate and reduces the locking accuracy of PLL at the same time.

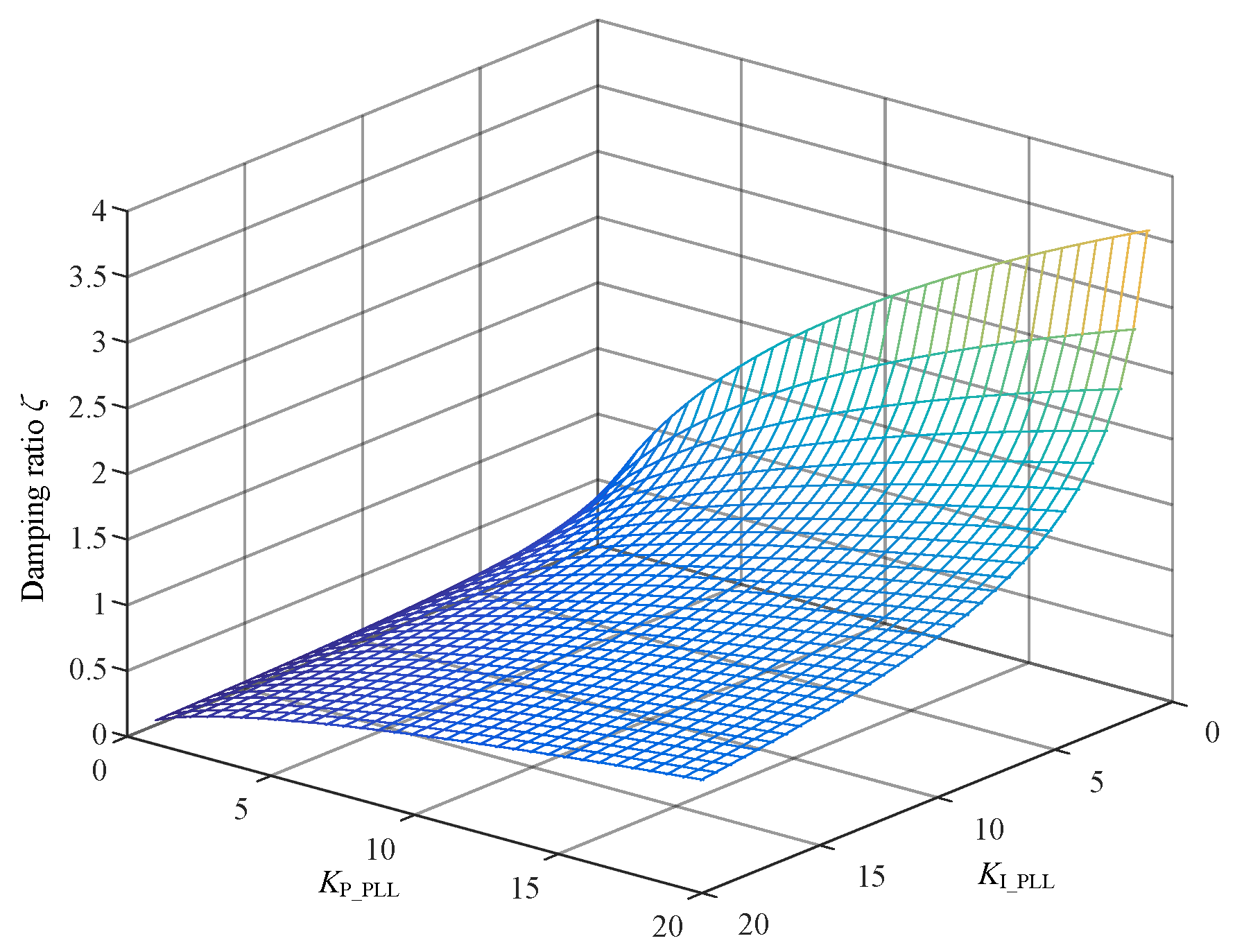
2.3.2. Small Signal Stability of Wind-Integrated Power System

This section analyzes the impacts of the PLL-synchronized swing equation of the DFIG on global stability of the multi-machine power system. As is shown in Figure 6, the single-machine infinite bus system integrated with a DFIG-based wind farm is served as the test model. The system parameters refer to Appendix A. Since the PLL-synchronized swing equation of the DFIG is established resembling the conventional SG, the system is composed of two swing equations with the same structure. If Δδ_s = Δδ_g − Δδ_pll is defined as the synthetic power angle of the system, the simultaneous differential equation of the system could be established by subtracting the swing equation of the DFIG from that of the SG.

In the two-machine infinite bus system in Figure 6, the swing equation of the SG is expressed as in (12) where ΔP_g is derived from the active power balance equation [16]:

$$\mathsf{\Delta }{\ddot{\delta }}_{\mathrm{g}}+\frac{D_{\mathrm{g}}}{M_{\mathrm{g}}}\mathsf{\Delta }{\dot{\delta }}_{\mathrm{g}}+\frac{\mathsf{\Delta }{P}_{\mathrm{g}}}{M_{\mathrm{g}}}=0,\mathsf{\Delta }{P}_{\mathrm{g}}=\frac{E{U}_{\mathrm{w}}\cos ({\delta }_{\mathrm{g}}-{\delta }_{\mathrm{w}})}{X_1}f(\mathsf{\Delta }{\delta }_{\mathrm{g}}-\mathsf{\Delta }{\delta }_{\mathrm{pll}})$$

(12)

In the same way, the swing equation of the DFIG is expressed as in (13) where ΔP_g is also derived from the active power balance equation [16].

$$\mathsf{\Delta }{\ddot{\delta }}_{\mathrm{pll}}+\frac{D_{\mathrm{w}}}{M_{\mathrm{w}}}\mathsf{\Delta }{\dot{\delta }}_{\mathrm{pll}}+\frac{\mathsf{\Delta }{P}_{\mathrm{w}}}{M_{\mathrm{w}}}=0,\mathsf{\Delta }{P}_{\mathrm{w}}=\frac{U_{\mathrm{w}}E\cos ({\delta }_{\mathrm{w}}-{\delta }_{\mathrm{g}})}{X_1}f(\mathsf{\Delta }{\delta }_{\mathrm{pll}}-\mathsf{\Delta }{\delta }_{\mathrm{g}})$$

(13)

where δ_g, D_g, and M_g are the rotor angle, the damping coefficient, and the inertia constant of the SG, respectively; ${\ddot{\delta }}_{\mathrm{g}}$ and ${\dot{\delta }}_{\mathrm{g}}$ are the second-order and first-order derivatives of ${\delta }_{\mathrm{g}}$, respectively; X₁ is the reactance between the SG and DFIG; and X₂ is the reactance of the transmission line between the PCC and the infinite bus. If the transmission power on X₂ reaches its total transfer capacity (TTC), the coefficient f satisfies f ≈ (1-s_r)⋅i_ds/[Ecos(δ_g − δ_w)/X₁ + (1 − s_r)⋅i_ds].

It is assumed that the system has uniform damping: D_g/M_g ≈ D_w/M_w. This assumption is reasonable especially for small values of K_{P_PLL} and K_{I_PLL} and for two large power grids interconnected with long distance transmission lines. Based on the swing equations of the DFIG and SG, the simultaneous differential equation of the system is obtained by subtracting (13) from (12):

$$\mathsf{\Delta }{\ddot{\delta }}_{\mathrm{s}}+\frac{1}{2}\left(\frac{D_{\mathrm{g}}}{M_{\mathrm{g}}}+\frac{D_{\mathrm{w}}}{M_{\mathrm{w}}}\right)\mathsf{\Delta }{\dot{\delta }}_{\mathrm{s}}+\left(\frac{M_{\mathrm{g}}+M_{\mathrm{w}}}{M_{\mathrm{g}}{M}_{\mathrm{w}}}\right)\frac{E{U}_{\mathrm{w}}\cos ({\delta }_{\mathrm{g}}-{\delta }_{\mathrm{w}})}{X_1}f\mathsf{\Delta }{\delta }_{\mathrm{s}}=0$$

(14)

Equation (14) is employed to analyze the damping properties of the multi-machine power system. The differences between (14) and (8) are that (14) embodies the interactive influences between the DFIG and SG, whereas Equation (8) only reflects the internal stability of PLL. Through solving the characteristic equation of (14), the damping ratio is expressed as:

$$\xi =\frac{1}{4}\left(\frac{D_{\mathrm{g}}}{M_{\mathrm{g}}}+\frac{D_{\mathrm{w}}}{M_{\mathrm{w}}}\right)/\sqrt{\left(\frac{1}{M_{\mathrm{g}}}+\frac{1}{M_{\mathrm{w}}}\right)\frac{E{U}_{\mathrm{w}}\cos ({\delta }_{\mathrm{g}}-{\delta }_{\mathrm{w}})f}{X_1}}$$

(15)

To analyze the impacts of K_{I_PLL} and K_{P_PLL} on the small signal stability of the two-machine infinite bus system, the variations of eigenvalues and damping ratios with K_{I_PLL} and K_{P_PLL} are illustrated in Figure 7a,b, respectively.

According to Figure 7a, the real parts of the eigenvalues move away from the original point when K_{P_PLL} increases, whereas the real parts are not affected by K_{I_PLL}. According to Figure 7b, the damping ratios increase when K_{P_PLL} increase, whereas decrease when K_{I_PLL} increase. Therefore, the PLL-based swing equation of the DFIG might deteriorate the small signal stability of the system with large K_{I_PLL} and small K_{P_PLL}.

As is discussed in Section 2.3.1, the internal stability of the PLL would not change if K_{I_PLL} and K_{P_PLL} decrease with a constant K_{I_PLL}/K_{P_PLL} ratio. As for the global stability of the multi-machine system, the combined effects of K_{I_PLL} and K_{P_PLL} should be analyzed further.

According to (15), the damping ratio of the multi-machine power system is not merely relative to K_{I_PLL}/K_{P_PLL}. For ease of analysis, the damping ratio of (15) is rewritten as:

$$\xi =\frac{a{K}_{\mathrm{P}\_\mathrm{PLL}}}{\sqrt{b+c{K}_{\mathrm{P}\_\mathrm{PLL}}{K}_{\mathrm{I}\_\mathrm{PLL}}}}=\sqrt{\frac{a}{\frac{b}{K_{\mathrm{P}\_\mathrm{PLL}}^2}+c\frac{K_{\mathrm{I}\_\mathrm{PLL}}}{K_{\mathrm{P}\_\mathrm{PLL}}}}}$$

(16)

$\mathrm{where}a=\frac{1}{2}\frac{T_{\mathrm{s}}}{i_{\mathrm{ds}}(1-s_{\mathrm{r}})},b=\frac{E{U}_{\mathrm{w}}\cos ({\delta }_{\mathrm{g}}-{\delta }_{\mathrm{w}})f}{M_{\mathrm{g}}{X}_1},c=\frac{E{U}_{\mathrm{w}}\cos ({\delta }_{\mathrm{g}}-{\delta }_{\mathrm{w}})f}{i_{\mathrm{ds}}(1-s_{\mathrm{r}})X_1}$.

As is indicated in (16), if K_{I_PLL} and K_{P_PLL} are large enough, $b/K_{\mathrm{P}\_\mathrm{PLL}}^2$ is small enough to be neglected compared with $c{K}_{\mathrm{I}\_\mathrm{PLL}}/K_{\mathrm{P}\_\mathrm{PLL}}$. In this condition, the damping ratio ξ remains nearly unchanged when K_{I_PLL} and K_{P_PLL} decrease with a constant K_{I_PLL}/K_{P_PLL} ratio. Whereas if K_{P_PLL} and K_{I_PLL} are small enough, $b/K_{\mathrm{P}\_\mathrm{PLL}}^2$ is comparable with $c{K}_{\mathrm{I}\_\mathrm{PLL}}/K_{\mathrm{P}\_\mathrm{PLL}}$ and cannot be neglected. In this case, the damping ratio ξ decreases with the decrease of K_{P_PLL} even if K_{I_PLL}/K_{P_PLL} = constant.

Figure 8 describes the variation surface of damping ratios with K_{I_PLL} and K_{P_PLL} in the two-machine infinite bus system. The same conclusions could be drawn that the damping ratio decreases when K_{I_PLL} increases and K_{P_PLL} decreases. When K_{P_PLL} is small enough, ξ is down to nearly zero even if K_{I_PLL}/K_{P_PLL} = constant. The decrease of K_{I_PLL} and K_{P_PLL} with the same ratio for improving the inertial response ability of the DFIG, however, would eventually deteriorate the system damping.

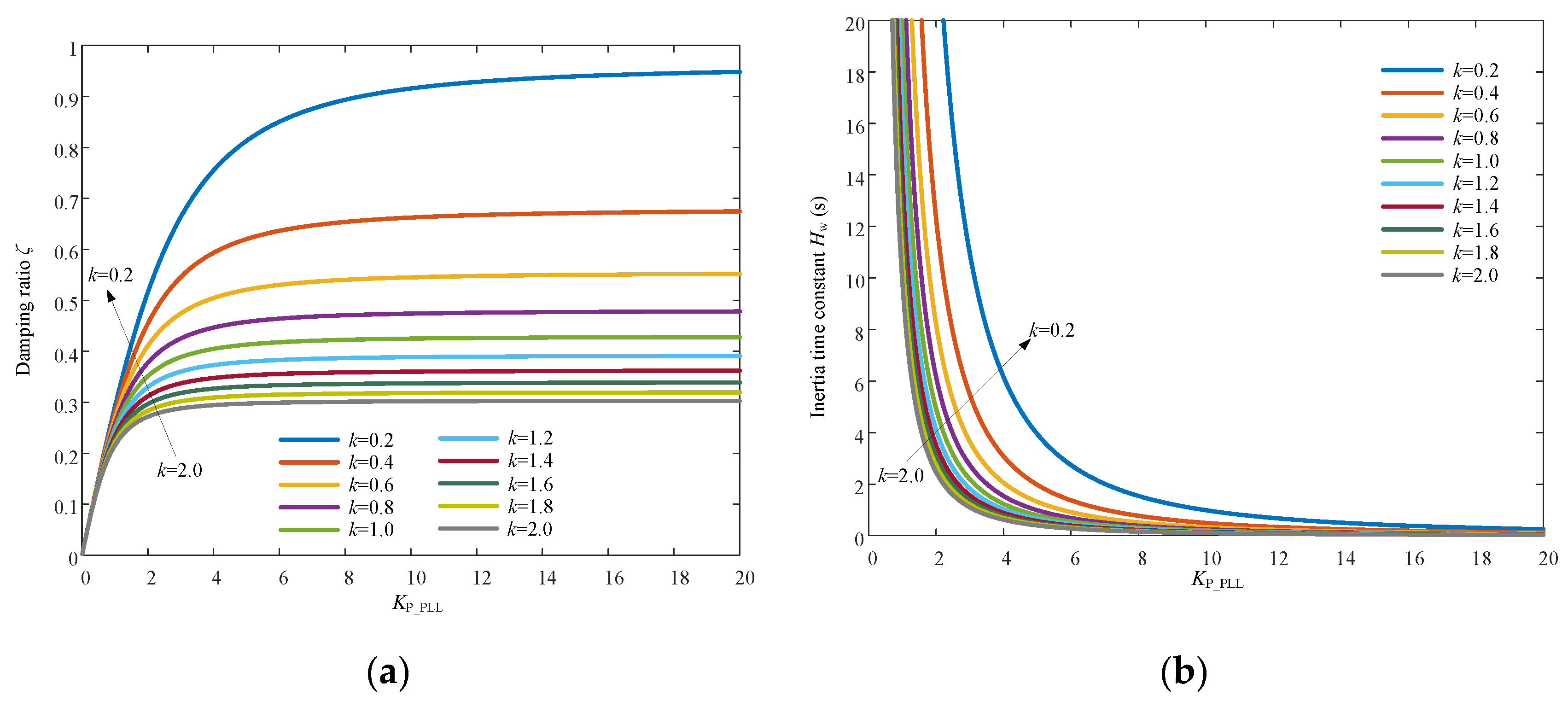
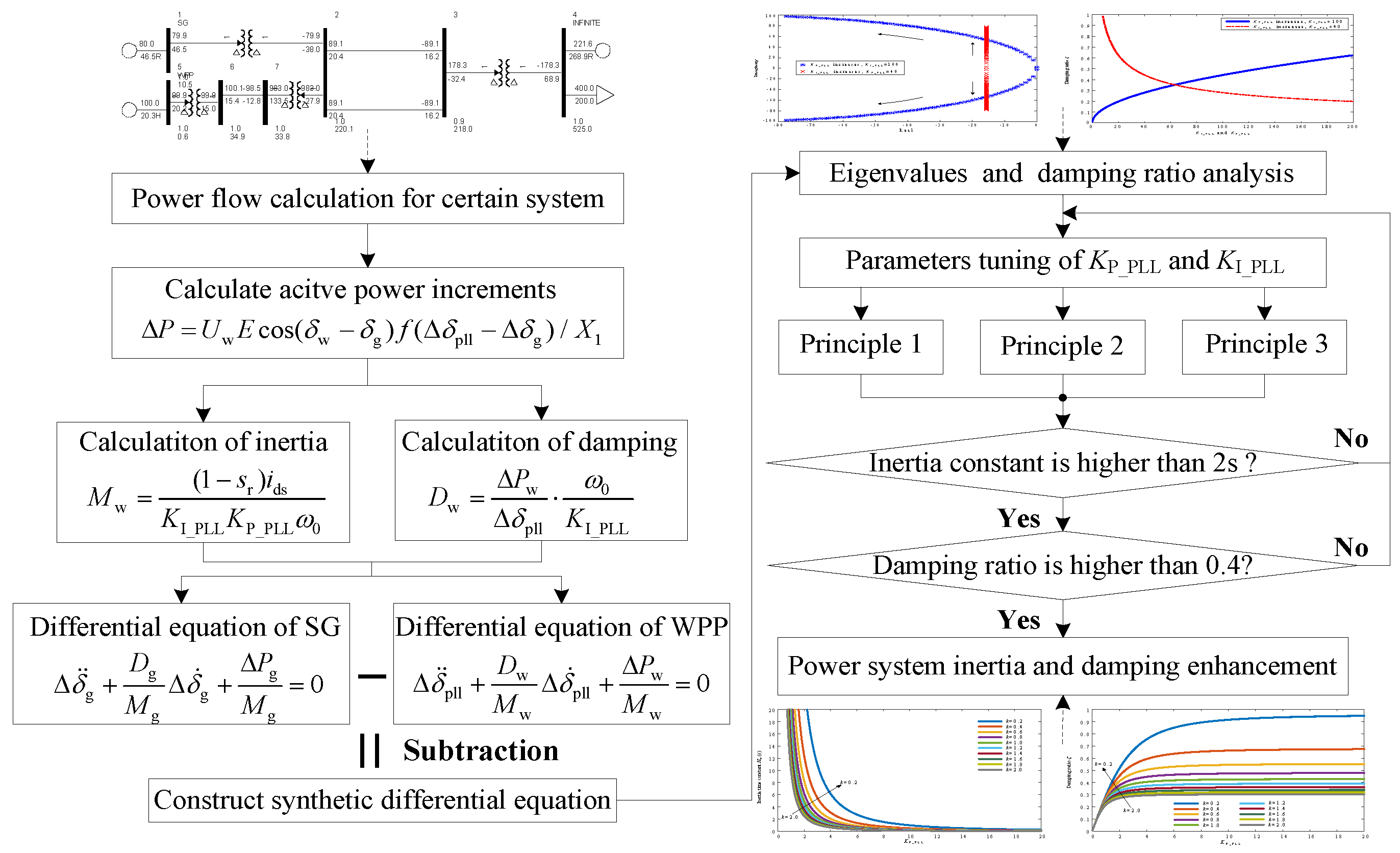
2.3.3. Parameters Optimization for Damping Enhancement and Inertia Provision

In fact, if K_{I_PLL} and K_{P_PLL} are tuned properly, a large inertia time constant and an ideal damping ratio could be realized at the same time. This section proposes three principles for parameters optimization of PLL to solve the contradiction between inertial provisions and damping reduction caused by the decreases of K_{I_PLL} and K_{P_PLL}.

Figure 9a,b illustrate the variation curves of inertia time constants and damping ratios under different ratio of k = K_{I_PLL}/K_{P_PLL} (k is set as 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, and 2.0, respectively). The decrease of K_{P_PLL} decreases the system damping even if K_{I_PLL}/K_{P_PLL} = constant. In addition, the decrease of K_{P_PLL} also reduces the locking accuracy of PLL according to Section 2.3.1. Thus, the first principle for the parameters tuning in PLL is that K_{P_PLL} should not be too small, to decrease the steady-state error of PLL and avoid system instability.

Fortunately, the decrease of K_{I_PLL} (corresponded with the smaller k in Figure 9) could improve both of system damping and inertial response ability of the DFIG simultaneously. Furthermore, K_{I_PLL} has no effects on the response rate of PLL according to (11). Therefore, the second principle for the parameters tuning in PLL is that the ratio of K_{I_PLL} to K_{P_PLL} is set as small as possible. This principle brings out three benefits: (i) improving the response rate of PLL (increasing K_{P_PLL}); (ii) damping enhancement (increasing K_{P_PLL} and decreasing K_{I_PLL}), and (iii) sufficient inertial provisions (decreasing K_{I_PLL}).

The third principle for parameters tuning in PLL is based on the performance requirements of the power system. The requirements are that wind power plants (WPPs) should respond to the frequency, which is equivalent to at least 2 s of inertia time constant [35], and the damping ratio of the system should be higher than 0.4 [34]. If K_{P_PLL} and K_{I_PLL} are tuned properly based on the principles above, acceptable damping and sufficient inertia response ability could be realized at the same time. Taking the variation curves of H_w and ξ with k = 0.2 in Figure 9 for example, if K_{P_PLL} is set as 4 and K_{I_PLL} is set as 0.8, the inertia time constant of H_w is larger than 6 s, and the damping ratio is not lower than 0.7.

The main steps for parameters tuning are shown in Figure 10. For a certain power system integrated with WPPs, the first step is to calculate the power flow of the whole system. Based on this, the active power increments of both wind farms ΔP_w and SGs ΔP_g are obtained with the power balance equation. The second step is to estimate the equivalent inertia time constant H_w and damping coefficient D_w of the wind farm according to (8). H_w, D_w, and ΔP_w constitute the basic elements of swing equation of the WPP in (13). Accordingly, the simultaneous differential equation of the whole system is established by subtracting the swing equation of the WPP from that of the SG, which is implemented as described in (14). Solving the characteristic equation, the eigenvalues and the damping ratio are obtained, which are strongly correlated to K_{P_PLL} and K_{I_PLL} according to (16). Therefore, the three principles for parameters tuning in PLL are introduced to ensure that the inertia time constant of the WPP is larger than 2 s and the damping ratio of the whole system is not lower than 0.4. Eventually, the parameters optimization in the PLL-synchronized swing equation offers better frequency recovery performance and higher damping capacity for the power system.

3. Simulation Results

Based on the analysis above, the DFIG is provided with sufficient inertial response ability with proper parameters tuning in PLL. Meanwhile, the proportional gain and integral gain have different impacts on the system damping and should be set following certain principles. For this work, the time domain simulations in PSS/E are conducted to verify (i) the frequency response ability of the DFIG with different K_{I_PLL} and K_{P_PLL}, (ii) the variation of the system damping with different K_{I_PLL} and K_{P_PLL}, and (iii) the effectiveness of parameters optimization for K_{I_PLL} and K_{P_PLL}.

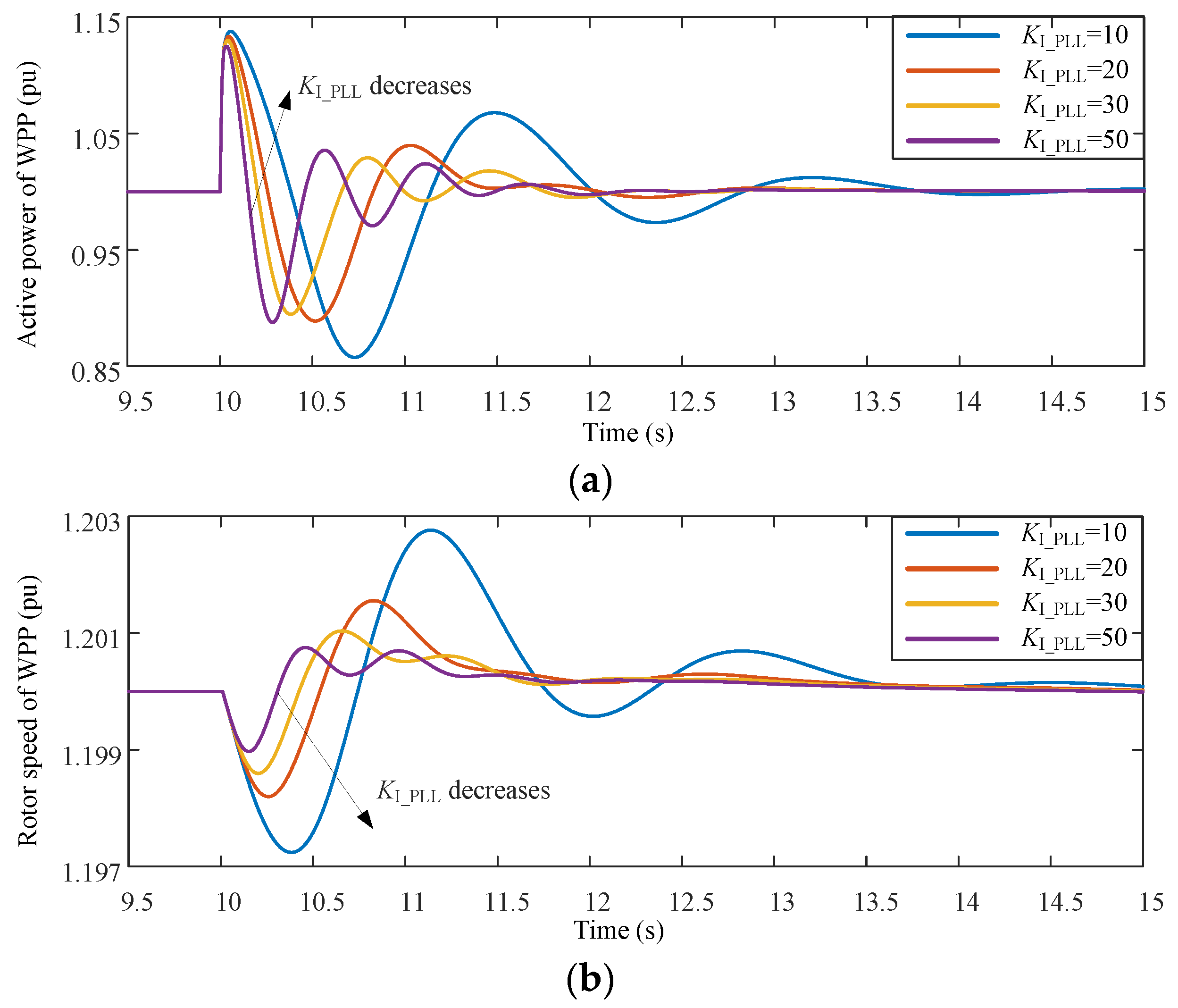
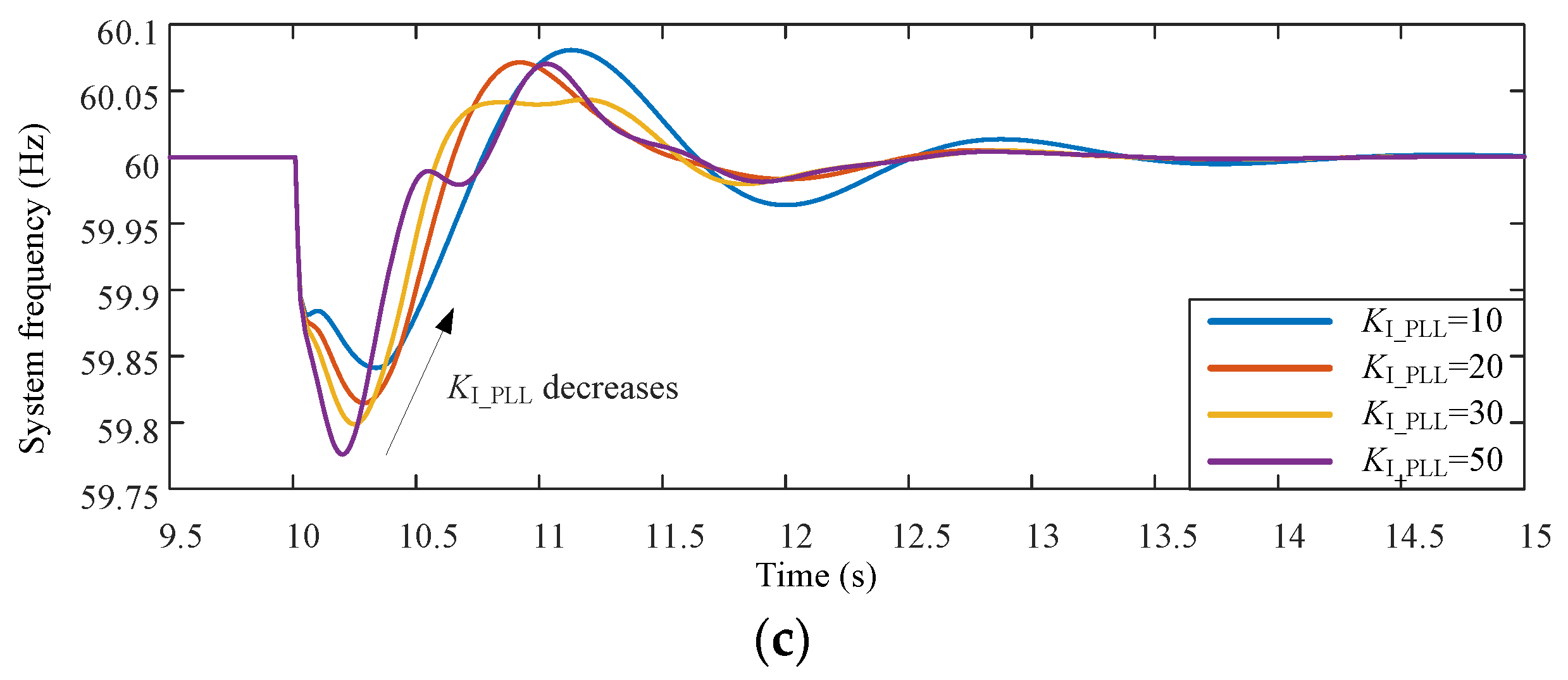
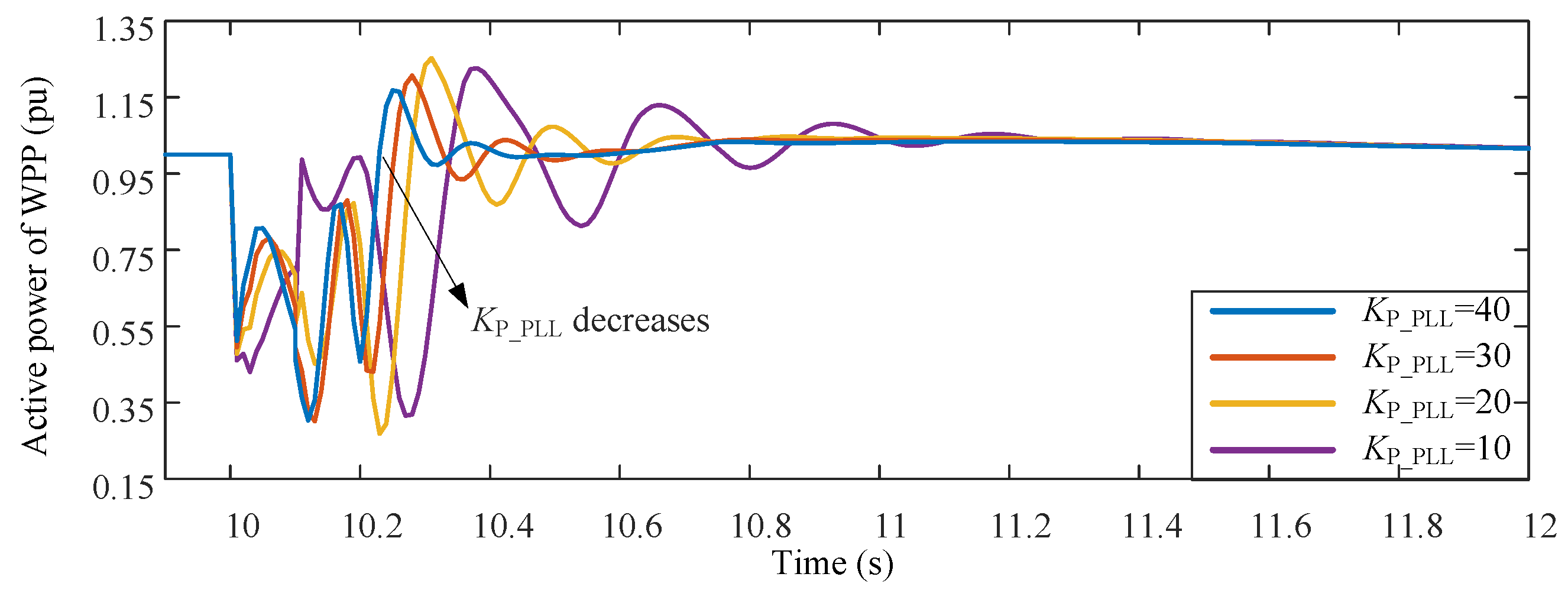
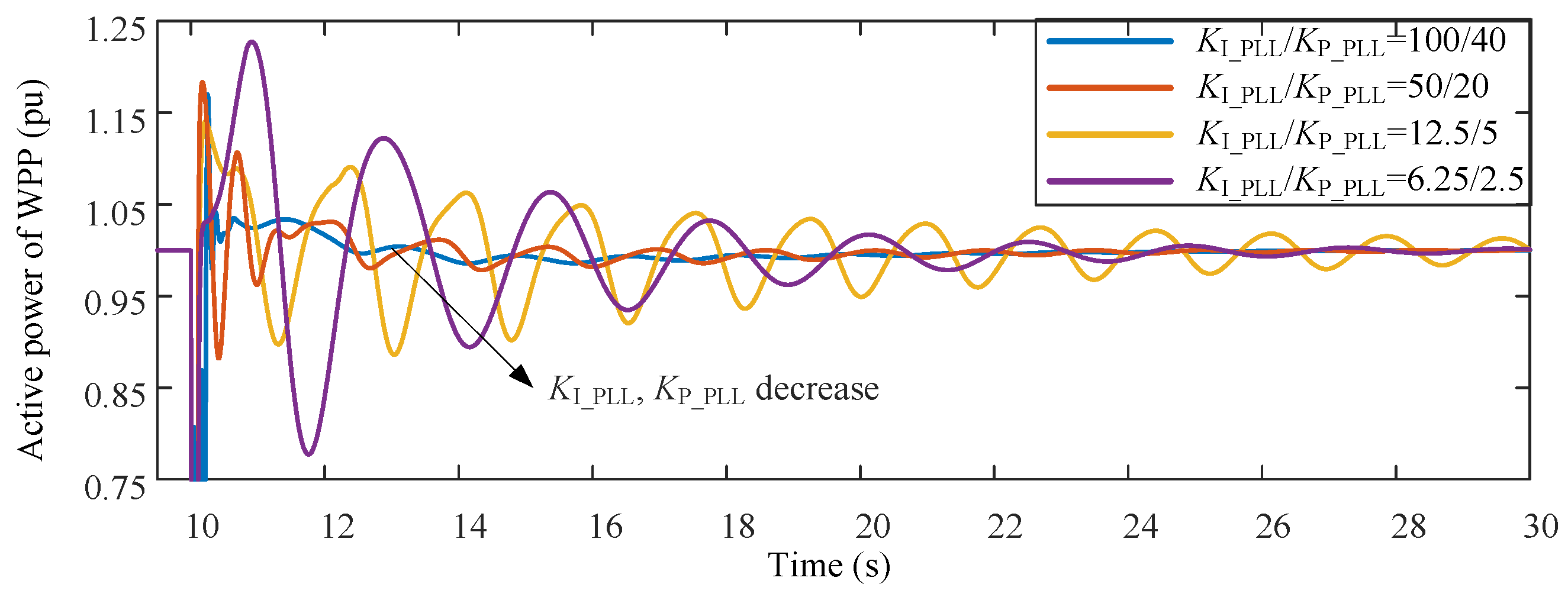
3.1. Simulations in Single-Machine Infinite Bus System With a WPP

This section simulates the impacts of K_{I_PLL} and K_{P_PLL} on the inertial response ability of the DFIG and the system damping in the single-machine infinite bus system integrated with a wind power plant (WPP). As is shown in Figure 11, the WPP on Bus 5, which consists of 67 unit 1.5 MW DFIG, is integrated into the single-machine infinite bus system through the two-stage transformer. The DFIG is represented by the generic WT3 model in PSS/E. It is assumed that each DFIG in the WPP has the same output characteristics, so the WPP is equivalent to a single wind turbine generator with the sum of the capacity of each DFIG unit. The synchronous generator on Bus 1 is represented by the round rotor generator model, whereas the synchronous generator on the infinite Bus 4 is represented by the classical generator model. The reference capacity of the system is 100 MVA, and the load power is 400 MW. The penetration rate of wind power is 24.94%. The power flow data of the system is shown in the circuit diagram in Figure 11, and the model parameters refer to the [29].

Based on this wind-integrated power system, five cases are conducted, that is: case1 tests the influences of K_{P_PLL} on inertial responses, case2 tests the influences of K_{I_PLL} on inertia responses, case3 tests the influences of K_{P_PLL} on system damping, case4 tests the influence of K_{I_PLL} on system damping, and case5 tests the joint effects of K_{I_PLL} and K_{P_PLL} on system damping. The fault scenarios in case1 and case2 are set as the active load on Bus 4 decreasing from 400MW to 350MW at 10 s. The fault scenarios in case3–case5 are set as a three-phase short circuit fault occurring at Bus 3 at 10 s and being cleared after 0.1 s.

In case1, K_{I_PLL} is set as five and K_{P_PLL} is set as 6, 10, 15, and 25 respectively. Figure 12a–c show the time domain waveforms of the active power of the WPP, rotor speed of the WPP, and the system frequency. According to Figure 12a, the instantaneous active power increment at 10 s manifests that the WPP could respond to frequency fluctuation after the parameters tuning of PLL. In addition, the amplitude of active power increases with the decrease of K_{P_PLL}, which indicates that the decrease of K_{P_PLL} improves the inertial response ability. As shown in Figure 12b, the declines of the rotor speed of the WPP at the initial stage of frequency excursion is due to the utilization of the kinetic energy of the wind turbine rotor. The smaller value of K_{P_PLL} is, the deeper the decline of rotor speed is. The active power increment from the WPP eases the active power imbalance of system, and inhibits the declines of system frequency, as is shown in Figure 12c.

In case2, K_{P_PLL} is set as 4 and K_{I_PLL} is set as 10, 20, 30, and 50 respectively. Figure 13a–c show the variations of the active power of the WPP, rotor speed of the WPP, and system frequency. Figure 13a indicates that the decrease of K_{I_PLL} increases both the amplitude and duration of active power supporting of the WPP. Note that the additional energy produced from the WPP is the product of active power and time. More additional energy contributed to the system results in more utilization of kinetic energy from the rotating mass of the turbine blades. Thus, the rotor speed of the WPP declines with a decrease of K_{I_PLL}, as shown in Figure 13b. According to Figure 13c, with lower values of K_{I_PLL}, more additional active power from the WPP is produced to alleviate the power shortage in the system, which inhibits the declines of system frequency.

To conclude, the inertia of the WPP is inversely proportional to K_{I_PLL} and K_{P_PLL}. The proportional gain and integral gain in PLL could be decreased simultaneously to improve the inertial response ability of the DFIG. The time domain simulation has the same results as that of the theoretical analysis in Section 2.2.

From case3 to case5, the impacts of K_{P_PLL} and K_{I_PLL} on small signal stability of the system are studied. Considering that the electrical quantities in the same case have similar damping properties, the time domain waveforms of the active power of the WPP are employed to illustrate the damping properties of the system.

In case3, K_{I_PLL} is set as 100, and K_{P_PLL} is set as 10, 20, 30, and 40, respectively. Figure 14 shows the oscillation curves of the active power of the WPP with different values of K_{P_PLL}. The active power of the WPP fluctuate more intensely and spends longer time recovering from oscillation state to steady state with smaller K_{P_PLL}. Therefore, the system damping is weakened with the decrease of K_{P_PLL}. This result illustrates that the proportional gain in PLL cannot be set too small and the inertial response ability of the DFIG has an upper limit constrained by system stability.

In case4, K_{P_PLL} is set as 1, and K_{I_PLL} is set as 100, 200, 300, and 400, respectively. Figure 15 shows the oscillation curves of the active power of WPP with different values of K_{I_PLL}. As shown in Figure 15, the active power has larger oscillation amplitudes and longer transient time with larger values of K_{I_PLL}. Further, larger K_{I_PLL} contributes to larger oscillation frequency and lower damping of the system, which corresponds with the theoretical results in Figure 7. Therefore, the decrease of K_{I_PLL} is beneficial to both damping and inertia provision of the system.

In case5, the ratio of K_{I_PLL} to K_{P_PLL} maintains constant: k = 2.5. K_{I_PLL}/K_{P_PLL} are set as 100/40, 50/20, 12.5/5, 6.25/2.5, respectively. This case is conducted to verify that decreasing K_{I_PLL} and K_{P_PLL} with constant ratio k would still deteriorate the system damping. Figure 16 shows the oscillation curves of the active power of the WPP with different K_{I_PLL} and K_{P_PLL}. It is obvious that typical values of K_{I_PLL} and K_{P_PLL} (100, 40) correspond with strong damping and quick recovery from oscillation to stability, whereas smaller K_{I_PLL} and K_{P_PLL} result in lower damping and even instability of the system.

The detailed inertia time constants of the WPP in case1–case2 and damping ratios in case3–case5 are described in

Table 1. Inertia time constants in case1–case2 and damping ratios in case3–case5.

Case1		Case2		Case3		Case4		Case5
KI_PLL = 5		KP_PLL = 4		KI_PLL = 100		KP_PLL = 1		KI_PLL/KP_PLL = 2.5
KP_PLL	Hw (s)	KI_PLL	Hw (s)	KP_PLL	ξ	KI_PLL	ξ	KI_PLL/KP_PLL	ξ
6	0.6572	10	0.4929	10	0.1798	100	0.0868	100/40	0.3139
10	0.3942	20	0.2465	20	0.2387	200	0.0712	50/20	0.3044
15	0.2629	30	0.1643	30	0.2803	300	0.0675	12.5/5	0.2603
25	0.1577	50	0.0986	40	0.3139	400	0.0664	6.25/2.5	0.1096

.

The simulation results above verify that smaller K_{I_PLL} and K_{P_PLL} contribute to sufficient inertial response ability of the DFIG, whereas decrease the system damping instead. Aiming at this contradiction, K_{P_PLL} should be set a little larger, and K_{I_PLL} should be set a little smaller following the three principles in Section 2.3.3. The parameters optimization is applied to the following actual NYPS-NETS power system.

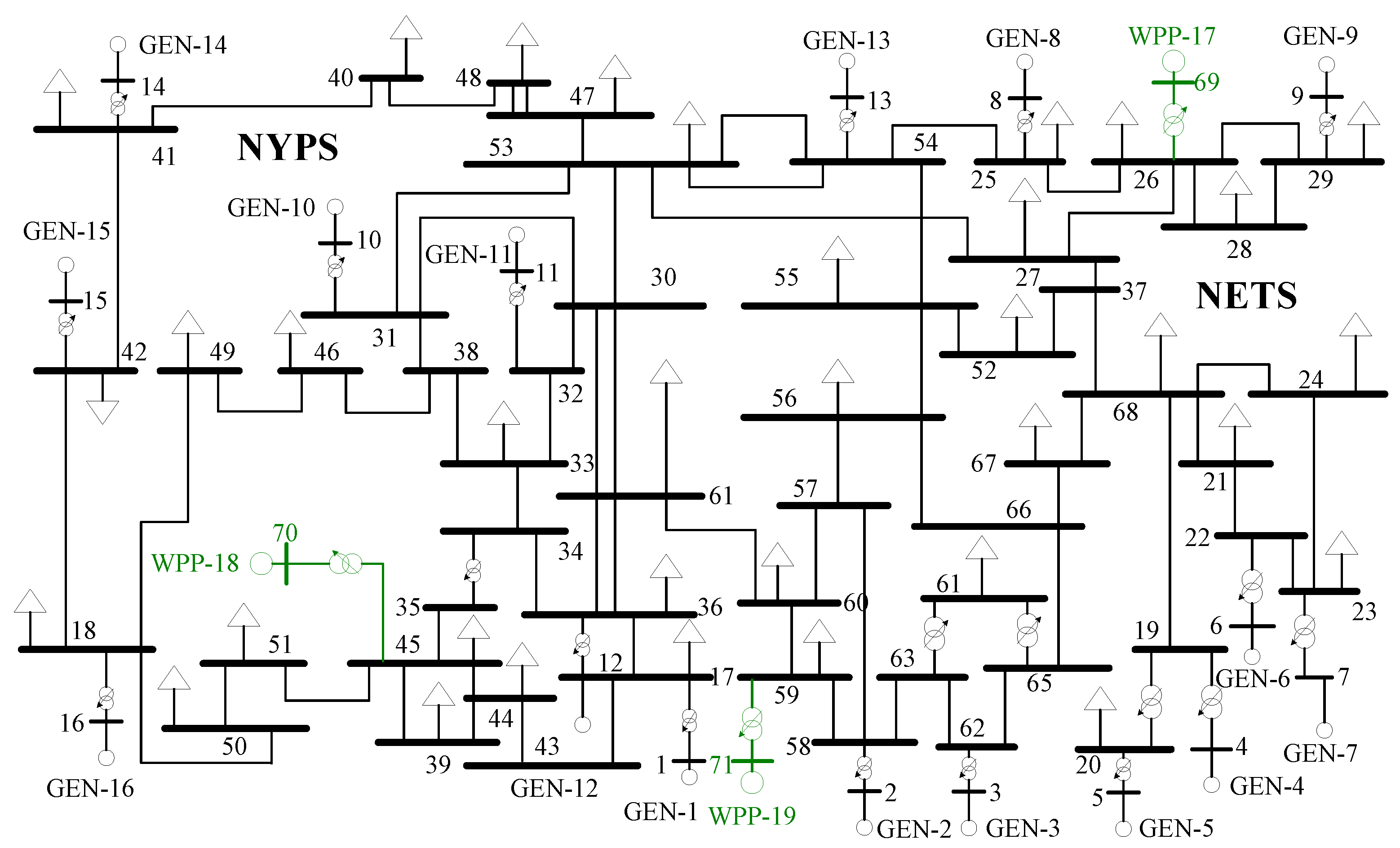
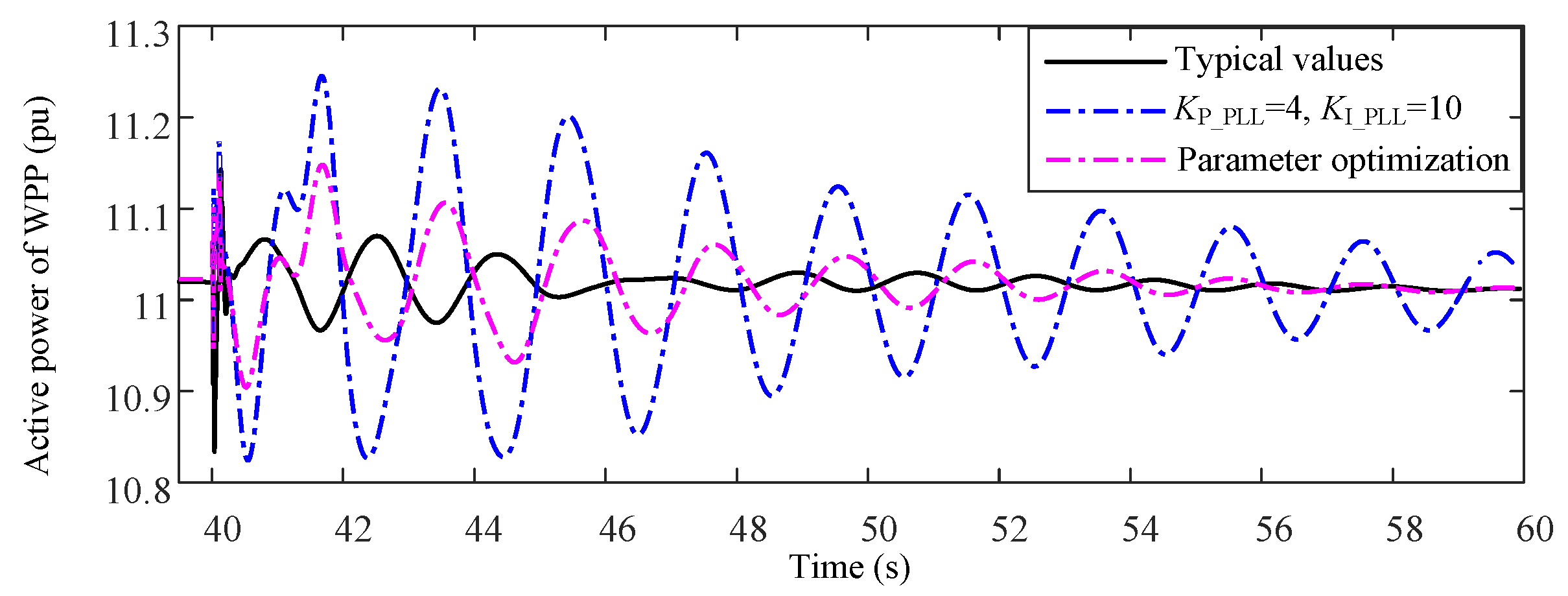
3.2. Simulations in NYPS-NETS Power System With WPPs Integration

This section tests the effectiveness of parameters optimization of PLL on the inertial response ability of the WPP and the damping ratio in NYPS-NETS power system [36]. Figure 17 displays the network structure of NYPS-NETS power system, which consists of two areas: New York Power System and New England Test System. To meet rising demand for wind power penetration in the future system in 2024, three WPPs are integrated into the system, which contributes to 15% wind power penetration levels.

Table 2. Locations and capacities of wind power plants (WPPs).

PCC	WPP-Number	Capacity
Bus-69	WPP-17	1110 MVA
Bus-45	WPP-18	1110 MVA
Bus-59	WPP-19	1110 MVA

describes the locations and capacities of the three WPPs.

The parameters in PLL are set as: (i) K_{I_PLL}/K_{P_PLL} = 100/40 (Typical values); (ii) K_{I_PLL}/K_{P_PLL} = 10/4; (iii) K_{I_PLL}/K_{P_PLL} = 12/2.5 (parameters optimization) to highlight the advantages of the proposed parameters optimization strategy. For comparing the inertial response ability under different parameters tuning of K_{P_PLL} and K_{I_PLL}, 500 MW of active-load power is added on Bus-59 at 40 s. The WPP-19 is taken as the observing object to reflect the performance of the system.

Figure 18a–c show the time domain waveforms of the active power of WPP-19, rotor speed of WPP-19, and the system frequency. When K_{P_PLL} and K_{I_PLL} are taken as the typical values (black curves), there are few inertial responses in WPP-19 after the frequency drop. The active power of WPP-19 fails to respond to the frequency deviations and has no contributions to the power imbalance of the system. The rotor speed of WPP-19 remains nearly unchanged, so there is no kinetic energy from the wind turbine rotor injected into the system. Consequently, the system frequency nadir reaches 59.85 Hz. In contrast, if K_{P_PLL} and K_{I_PLL} are decreased to 4 and 10 with constant ratio: K_{I_PLL}/K_{P_PLL} = 2.5, the WPP-19 is provided with sufficient inertial response ability (blue dashed curves). The active power of WPP-19 increases to 12.3 p.u. at the initial stage of the disturbance, and declines gradually to release the kinetic energy from the wind turbine rotor. The inertial response of WPPs restrains the system frequency decline, so the system frequency nadir increases to 59.9 Hz.

The system damping under different parameters tuning of PLL is tested by adding a three-phase short circuit fault in line 25–26 at 40 s and tripping the line after 0.1 s. Figure 19 shows the oscillation curves of the active power of WPP-19. Comparing the black curve with the blue dashed curve in Figure 19, it indicates that decreasing K_{I_PLL} and K_{P_PLL} simultaneously deteriorates the system damping even if K_{I_PLL}/K_{P_PLL} = constant. Focusing on this problem, the parameters in PLL are adjusted by increasing K_{P_PLL} and decreasing K_{I_PLL} based on the principles in Section 2.3.3. The proper PLL parameters adopted in this system are K_{P_PLL} = 12, K_{I_PLL} = 2.5. As is illustrated by the pink dashed curves in Figure 18 and Figure 19, WPP-19 is provided with sufficient inertial response ability compared with K_{P_PLL} = 10, K_{I_PLL} = 4. Meanwhile, the damping properties of the active power of WPP-19 is also enhanced and recover to the equal level of the typical-values condition (K_{P_PLL} = 100, K_{I_PLL} = 40).

Table 3. Inertia time constants and damping ratios.

KI_PLL, KP_PLL	Inertia Constant	Damping Ratio
100, 40	0.0452 s	0.68
10, 4	4.8183 s	0.33
12, 2.5	6.0243 s	0.69

describes the inertia time constant of WPP-19 and the damping ratios of the dominant modes of the active power of WPP-19. After the parameters’ optimization of PLL, WPP-19 is provided with larger inertia time constant (6.0243 s) and stronger damping properties (0.69) compared with the cases of typical values and decreasing K_{I_PLL} and K_{P_PLL} with a constant ratio.

4. Discussion

Based on the theoretical analysis and simulation results above, proper parameters tuning could increase both the inertial response ability of the DFIG and the small signal stability of the power system. The common research findings are obtained in [25] that decreasing the parameters in PLL with a constant ratio has no effects on the internal stability of PLL. However, this paper further illustrates that the small signal stability of the whole system is deteriorated under these parameters tuning. Consequently, the parameters optimization is proposed to solve the contradiction. Compared with [23], the inertia time constants calculated in this paper are the time-domain expressions, which could estimate precisely the inertial response ability of the certain wind farms. Based on the research results in [26,27], the paper not only clarifies the effects of K_{I_PLL} and K_{P_PLL} on the small signal stability of the power system but also investigates the internal relationship between the PLL and the inertia provision. Therefore, the synthetic effects of K_{I_PLL} and K_{P_PLL} on inertia and damping are studied, respectively, in detail. The main innovation the paper is establishing the PLL-synchronized DFIG model, which imitates the motion of the SG and could give an all-around illustration for inertia and damping characteristics in the wind-integrated power system.

The current limitation of the paper is that the PLL-synchronized DFIG model only considers the dynamics of PLL and voltage-oriented control. The future research works will focus on establishing a more complex mathematical form of the model considering the dynamics of the inverter control and the driving chain. Referring to the power system stabilizer (PSS) in the traditional synchronous generator, the advanced damping controller for the PLL-based DFIG model could also be studied further for withstanding weak damping caused by higher penetration of renewable energy sources.

5. Conclusions

Aiming at reduced inertia and weak damping properties of the wind-integrated power system, this paper derives the synchronized swing equation of the DFIG based on the dynamic models of PLL. There is a similarity in mathematical form between the proposed swing equation and the rotor motion equation of the SG, which embodies the inertia constant, the damping coefficient, and the synchronizing torque. Thanks to this work, the inverter-based asynchronous wind generator is regarded as the SG, and the dynamic characteristics of the power system could be described by a series of synchronous motion equations. Then the inertia estimation of the DFIG and system damping analysis is conducted based on the PLL-synchronized swing equation. The conclusions are summarized as follows:

(i)

The equivalent inertia of the DFIG is inversely proportional to both the proportional and integral gains of PLL. The proportional and integral gains should be small enough for providing the DFIG sufficient inertial response ability.

(ii)

The internal stability of PLL will not change if the proportional and integral gains decrease with the constant ratio. Whereas aiming at the multi-machine system, decreasing the parameters in PLL with the constant ratio cannot avoid deteriorating the damping characteristics of the whole system. The small proportional gain will also slow down the response rate and locking accuracy of PLL.

(iii)

The parameters optimization of PLL is proposed following three principles by decreasing the ratio of K_{I_PLL} to K_{P_PLL} for obtaining sufficient inertial response ability of the WPP and ideal damping properties of the system at the same.