A Short-Term Hybrid Energy System Robust Optimization Model for Regional Electric-Power Capacity Development Planning under Different Pollutant Control Pressures
Abstract
:1. Introduction
2. Energy System Analysis of Shandong Province
3. Energy System Optimization Model
3.1. Optimization Method
3.2. Model Development
- (1)
- Cost for resource consumption:
- (2)
- Cost for electricity generation:
- (3)
- Net import cost for electric power:
- (4)
- Cost for air pollutant emission:
- (5)
- Risk-aversion of the electric power system:
- (1)
- constraints regarding the electricity supply and demand balance, expressed as
- (2)
- constraints regarding the environment capacity, expressed as
- (3)
- constraints regarding the electric power production capacity, expressed as
- (4)
- constraints regarding the capacity expansion, expressed as
- (5)
- constraints regarding the coal mass balance, expressed as
- (6)
- constraints regarding the hydropower mass balance, expressed as
- (7)
- constraints regarding the solar mass balance, expressed as
- (8)
- constraints regarding the wind mass balance, expressed as
- (9)
- constraints regarding the biomass mass balance, expressed as
- (10)
- constraints regarding the nuclear mass balance, expressed as
- (10)
- constraints regarding risk control, expressed as
3.3. Data Collection and Scenarios Definition
4. Results and Discussion
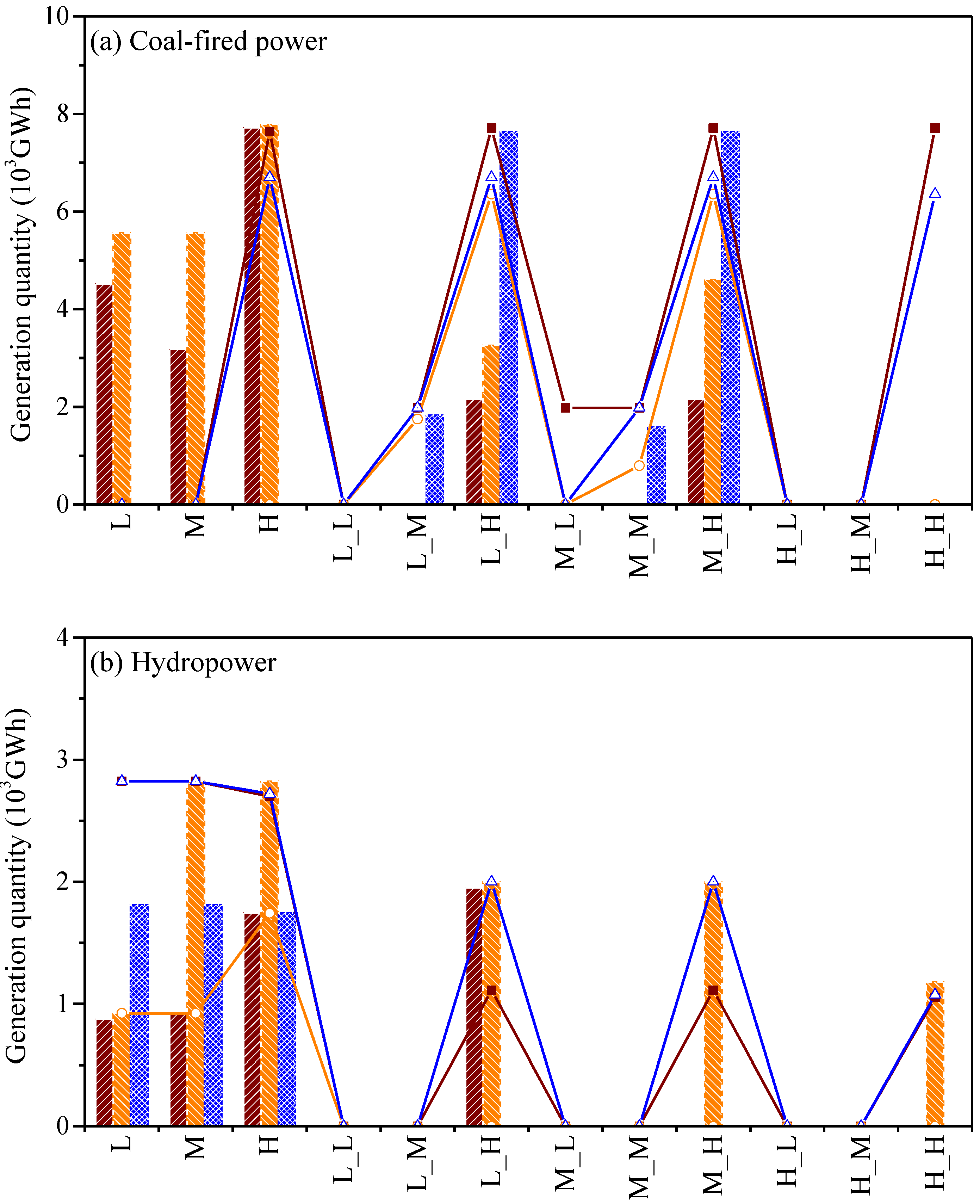
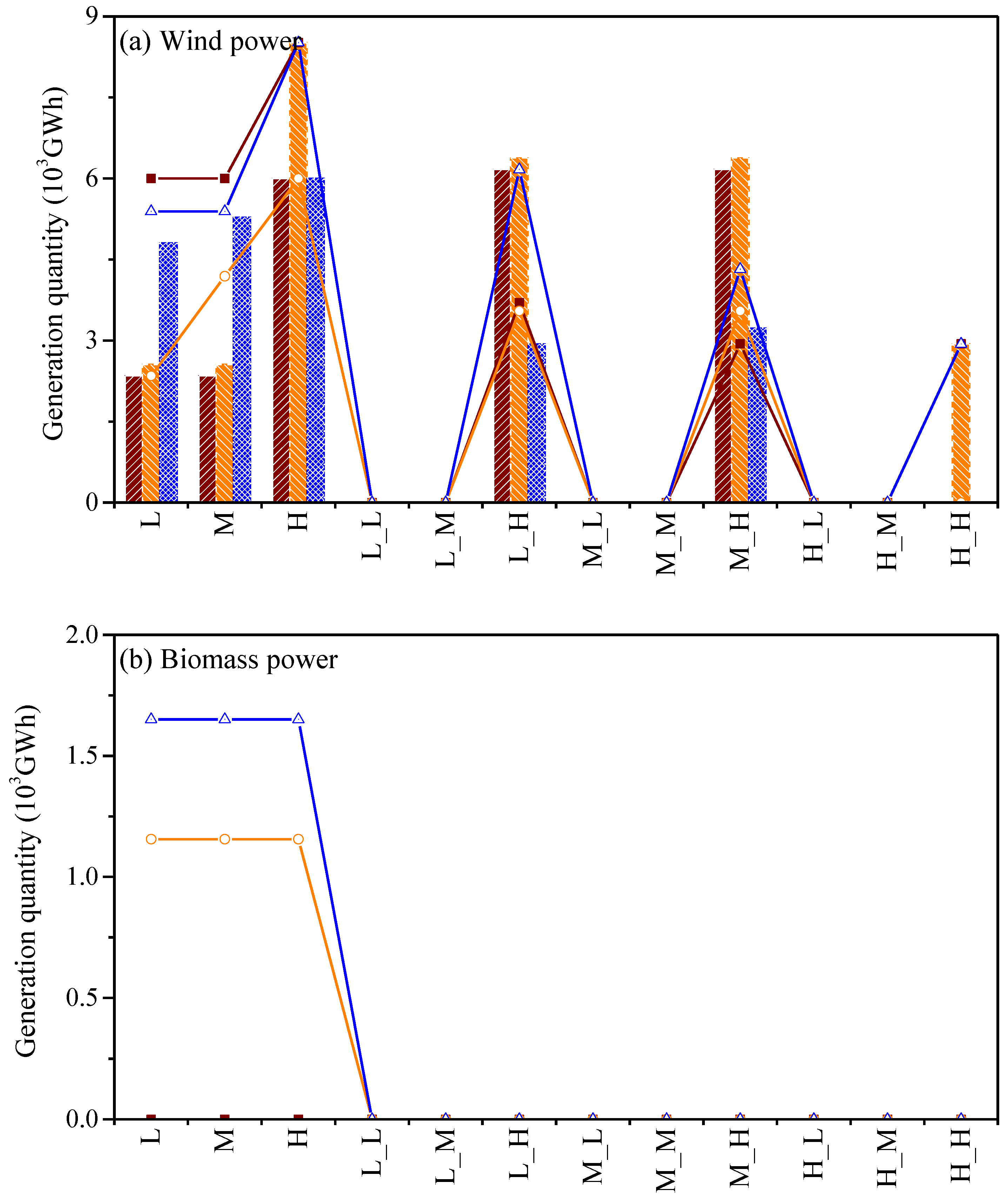
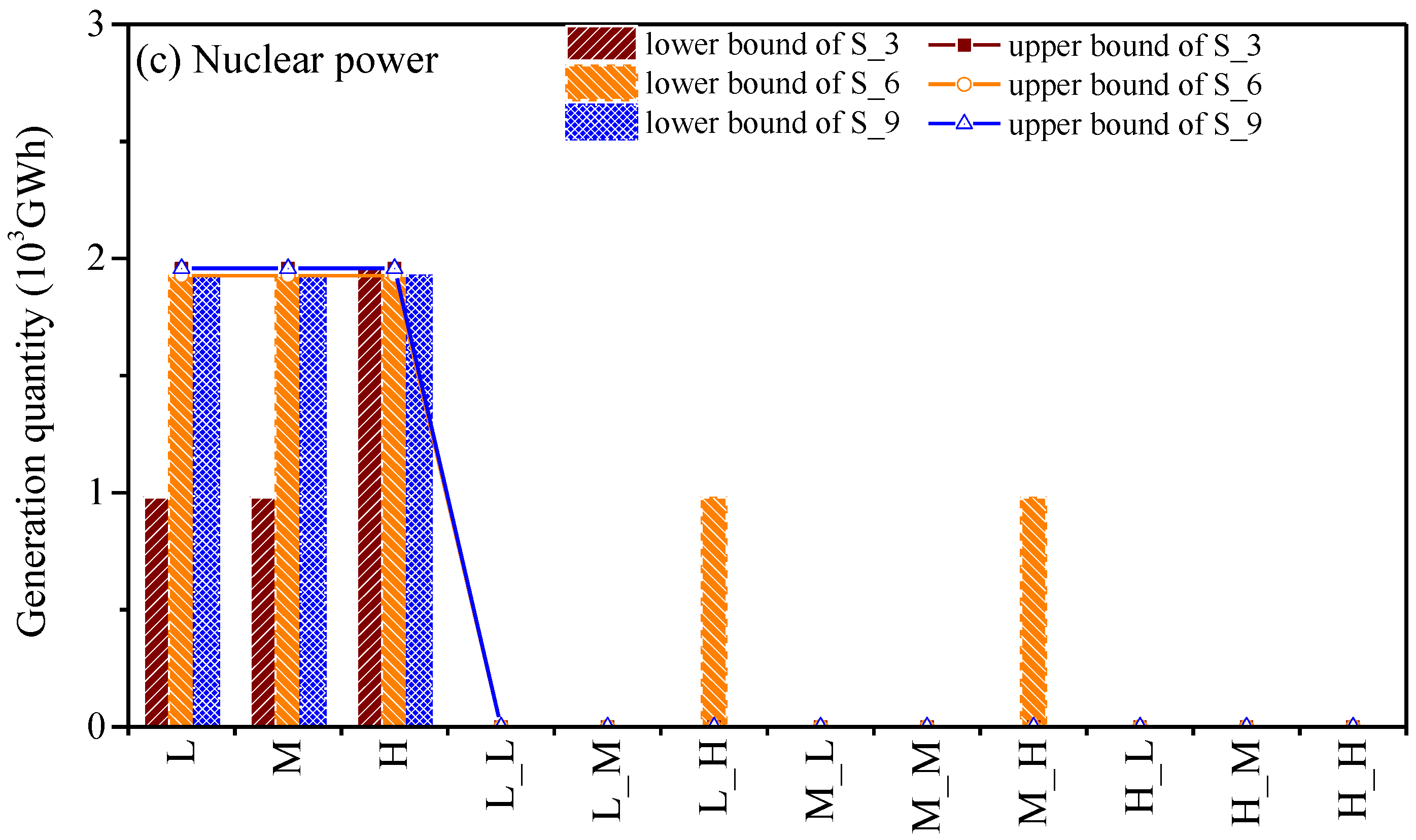
4.1. Optimized Electricity Generation in Different Emission Reduction Scenarios
4.2. Optimized Electricity Generation in Different Risk Aversion Scenarios
4.3. Capacity Expansion Schemes in Different Emission Reduction Scenarios
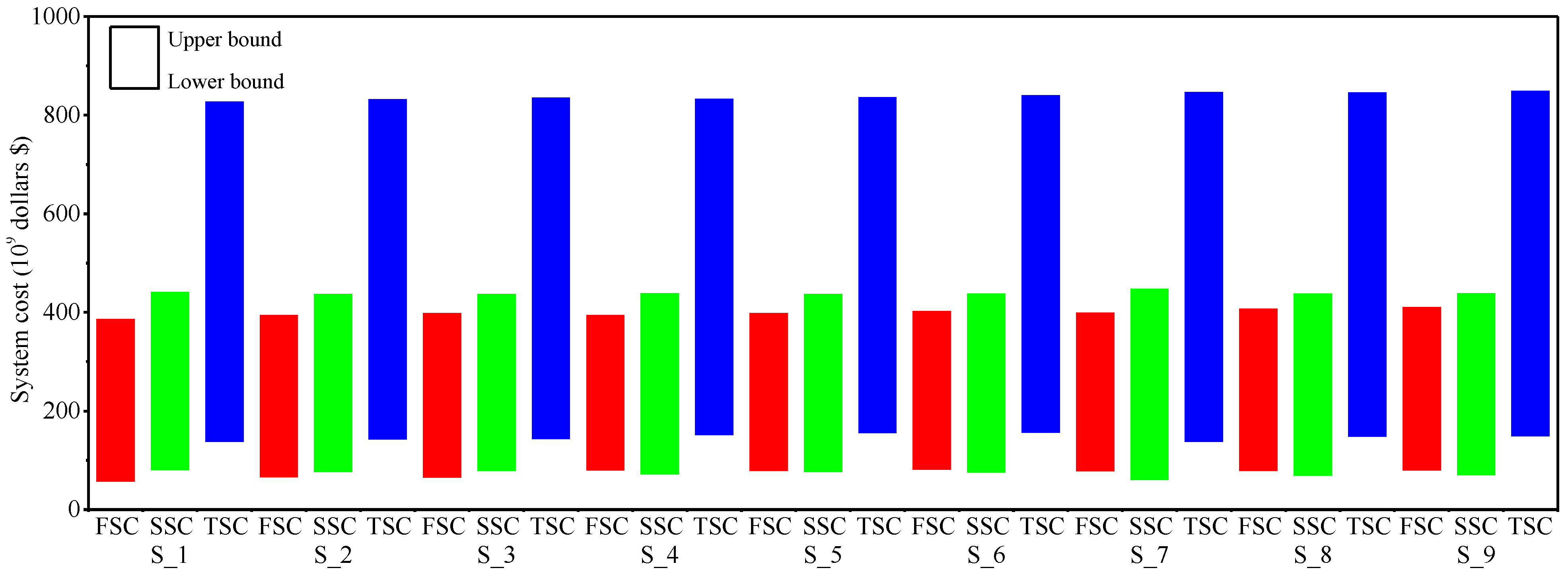
4.4. Economic Risk Analysis for the Shandong Province Energy System Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Xie, Y.; Fu, Z.; Xia, D.; Lu, W.; Huang, G.; Wang, H. Integrated Planning for Regional Electric Power System Management with Risk Measure and Carbon Emission Constraints: A Case Study of the Xinjiang Uygur Autonomous Region, China. Energies 2019, 12, 601. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Wang, J.; Zhang, L.; Liu, J.; Chen, S. Optimization of china’s electric power sector targeting water stress and carbon emissions. Appl. Energy 2020, 271, 115221. [Google Scholar] [CrossRef]
- Zhen, J.; Wu, C.; Liu, X.; Huang, G.; Liu, Z. Energy-water nexus planning of regional electric power system within an inexact optimization model in Tangshan City, China. J. Clean. Prod. 2020, 266, 121997. [Google Scholar] [CrossRef]
- Yin, J.; Huang, G.; Xie, Y.; An, Y. Carbon-subsidized inter-regional electric power system planning under cost-risk tradeoff and uncertainty: A case study of Inner Mongolia, China. Renew. Sustain. Energy Rev. 2021, 135, 110439. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, T.; Guo, F. A multi-regional energy transport and structure model for China’s electricity system. Energy 2018, 161, 907–919. [Google Scholar] [CrossRef] [Green Version]
- Karmellos, M.; Georgiou, P.; Mavrotas, G. A comparison of methods for the optimal design of Distributed Energy Systems under uncertainty. Energy 2019, 178, 318–333. [Google Scholar] [CrossRef]
- Firouzmakana, P.; Hooshmanda, R.A.; Bornapourb, M.; Khodabakhshian, A. A comprehensive stochastic energy management system of micro-CHP units, renewable energy sources and storage systems in microgrids considering demand response programs. Renew. Sustain. Energy Rev. 2019, 108, 355–368. [Google Scholar] [CrossRef]
- Wang, X.C.; Klemeša, J.J.; Dong, X.B.; Fan, W.; Xu, Z.; Wang, Y.; Varbanov, P.S. Air pollution terrain nexus, A review considering energy generation and consumption. Renew. Sustain. Energy Rev. 2019, 105, 71–85. [Google Scholar] [CrossRef]
- Wu, C.; Guan, P.; Zhong, L.; Lv, J.; Hu, X.; Huang, G.; Li, C. An optimized low-carbon production planning model for power industry in coal-dependent regions—A case study of Shandong, China. Energy 2020, 192, 116636. [Google Scholar] [CrossRef]
- Tan, Q.; Liu, Y.; Zhang, X. Stochastic optimization framework of the energy-water-emissions nexus for regional power system planning considering multiple uncertainty. J. Clean. Prod. 2020, 281, 124470. [Google Scholar] [CrossRef]
- Yu, L.; Li, Y.; Shan, B.; Huang, G.; Xu, L. A scenario-based interval-stochastic basic-possibilistic programming method for planning sustainable energy system under uncertainty: A case study of Beijing, China. J. Clean. Prod. 2018, 197, 1454–1471. [Google Scholar] [CrossRef]
- Yu, J.; Ryu, J.-H.; Lee, I.-B. A stochastic optimization approach to the design and operation planning of a hybrid renewable energy system. Appl. Energy 2019, 247, 212–220. [Google Scholar] [CrossRef]
- Fu, Y.; Huang, G.; Xie, Y.; Liao, R.; Yin, J. Planning electric power system under carbon-price mechanism considering multiple uncertainties—A case study of Tianjin. J. Environ. Manag. 2020, 269, 110721. [Google Scholar] [CrossRef]
- Yue, X.; Pyea, S.; De Carolisd, J.; Li, F.G.N.; Rogana, F.; Gallachóir, B.Ó. A review of approaches to uncertainty assessment in energy system optimization models. Energy Strategy Rev. 2018, 21, 204–217. [Google Scholar] [CrossRef]
- Ji, L.; Niu, D.X.; Huang, G.H. An inexact two-stage stochastic robust programming for residential micro-grid management-based on random demand. Energy 2014, 67, 186–199. [Google Scholar] [CrossRef]
- Chen, C.; Qi, M.; Kong, X.; Huang, G.; Li, Y. Air pollutant and CO2 emissions mitigation in urban energy systems through a fuzzy possibilistic programming method under uncertainty. J. Clean. Prod. 2018, 192, 115–137. [Google Scholar] [CrossRef]
- Boffino, L.; Conejo, A.; Sioshansi, R.; Oggioni, G. A two-stage stochastic optimization planning framework to decarbonize deeply electric power systems. Energy Econ. 2019, 84, 104457. [Google Scholar] [CrossRef]
- Guo, Q.; Nojavan, S.; Lei, S.; Liang, X. Economic-environmental analysis of renewable-based micro-grid under a CVaR-based two-stage stochastic model with efficient integration of plugin electric vehicle and demand response. Sustain. Cities Soc. 2021, 75, 103276. [Google Scholar] [CrossRef]
- Dong, C.; Huang, G.H.; Cai, Y.P.; Liu, Y. An inexact optimization modeling approach for supporting energy systems planning and air pollution mitigation in Beijing city. Energy 2012, 37, 673–688. [Google Scholar] [CrossRef]
- Zhu, H.; Huang, W.; Huang, G. Planning of regional energy systems: An inexact mixed-integer fractional programming model. Appl. Energy 2014, 113, 500–514. [Google Scholar] [CrossRef]
- Lei, Y.; Wang, D.; Jia, H.; Li, J.; Chen, J.; Li, J.; Yang, Z. Multi-stage stochastic planning of regional integrated energy system based on scenario tree path optimization under long-term multiple uncertainties. Appl. Energy 2021, 300, 117224. [Google Scholar] [CrossRef]
- Balbás, A.; Balbás, B.; Balbás, R. Differential equations connecting VaR and CVaR. J. Comput. Appl. Math. 2017, 326, 247–267. [Google Scholar] [CrossRef] [Green Version]
- Chai, S.L.; Zhou, P. The Minimum-CVaR strategy with semi-parametric estimation in carbon market hedging problems. Energy Econ. 2018, 76, 64–75. [Google Scholar] [CrossRef]
- Ju, L.W.; Tan, Q.L.; Lu, Y.; Tan, Z.F.; Zhang, Y.X.; Tan, Q.K. A CVaR-robust-based multi-objective optimization model and three-stage solution algorithm for a virtual power plant considering uncertainties and carbon emission allowances. Int. J. Electr. Power Energy Syst. 2019, 107, 628–647. [Google Scholar] [CrossRef]
- Huang, R.; Huang, G.; Cheng, G.; Dong, C. Regional heuristic interval recourse power system analysis for electricity and environmental systems planning in Eastern China. Resour. Conserv. Recycl. 2017, 122, 185–201. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, W.; Li, H.; Liu, B.; Zhang, Z.; Wang, X. Multi-stage stochastic programming based offering strategy for hydrogen fueling station in joint energy, reserve markets. Renew. Energy 2021, 180, 605–615. [Google Scholar] [CrossRef]
- Pflug, G.C. Some remarks on the value-at-risk and the conditional value-at-risk. In Probabilistic Constrained Optimization; Springer: Berlin/Heidelberg, Germany, 2000; pp. 272–281. [Google Scholar]
- Rockafellar, R.T.; Uryasev, S. Optimization of conditional value-at-risk. J. Risk 2000, 2, 21–41. [Google Scholar] [CrossRef] [Green Version]
- Rockafellar, R.T.; Uryasev, S. Conditional value-at-risk for general loss distributions. J. Bank. Financ. 2002, 26, 1443–1471. [Google Scholar] [CrossRef]
- Shandong Municipal Bureau of Statistics, National Bureau of Statistics Survey Office in Shandong. Shandong Statistical Yearbook. 2010–2018; China Statistics Press: Qingdao, China, 2018. [Google Scholar]
- Mondal, A.H.; Ringler, C. Long-term optimization of regional power sector development: Potential for cooperation in the Eastern Nile region? Energy 2020, 201, 117703. [Google Scholar] [CrossRef]
- Liu, J.; Lin, Q.; Huang, G.; Wu, Q.; Li, H. Energy systems planning and GHG-emission control under uncertainty in the province of Liaoning, China—A dynamic inexact energy systems optimization model. Int. J. Electr. Power Energy Syst. 2013, 53, 142–158. [Google Scholar] [CrossRef]
- Li, M.; Dalia, P.-E.; Zhang, J. Policies to promote energy efficiency and air emissions reductions in China’s electric power generation sector during the 11th and 12th five-year plan periods: Achievements, remaining challenges, and opportunities. Energy Policy 2018, 125, 429–444. [Google Scholar] [CrossRef]
- Wang, M.; Mao, X.; Gao, Y.; He, F. Potential of carbon emission reduction and financial feasibility of urban rooftop photovoltaic power generation in Beijing. J. Clean. Prod. 2018, 203, 1119–1131. [Google Scholar] [CrossRef]
- Li, T.; Li, Z.; Li, W. Scenarios analysis on the cross-region integrating of renewable power based on a long-period cost-optimization power planning model. Renew. Energy 2020, 156, 851–863. [Google Scholar] [CrossRef]







| Conversion Technology | Time Period | ||
|---|---|---|---|
| t = 1 | t = 2 | ||
| Regular and surplus costs for power generation of each power conversion technology (USD 103/GWh) | |||
| Coal-fired power | Regular cost, | [23.1, 25.4] | [23.9, 26.2] |
| Surplus cost, | [9.9, 10.5] | [10.4, 11.1] | |
| Hydropower | Regular cost, | [13.1,14.6] | [12.4, 13.9] |
| Surplus cost, | [5.6, 6.6] | [5.8, 7.2] | |
| Photovoltaic power | Regular cost, | [8.5, 9.4] | [8.3, 9.0] |
| Surplus cost, | [3.6, 4.0] | [3.6, 4.4] | |
| Wind power | Regular cost, | [6.4, 8.6] | [6.2, 8.2] |
| Surplus cost, | [2.9, 3.2] | [3.1, 3.4] | |
| Biomass power | Regular cost, | [28.3, 30.0] | [29.9, 31.7] |
| Surplus cost, | [14.7, 15.6] | [15.9, 16.2] | |
| Nuclear power | Regular cost, | [7.2, 8.5] | [6.8, 8.1] |
| Surplus cost, | [3.5, 4.0] | [3.2, 3.7] | |
| Fixed (USD 106) and variable (USD 106/GW) costs for capacity expansion | |||
| Coal-fired power | Fixed cost, | [816.0, 96.0] | [757.4, 891.0] |
| Variable cost, | [544.2, 640.3] | [522.5, 614.9] | |
| Hydropower | Fixed cost, | [2065.5, 2430.0] | [2021.3, 2378.0] |
| Variable cost, | [1380.6, 1624.2] | [1394.4, 1640.4] | |
| Photovoltaic power | Fixed cost, | [2159.0, 2540.0] | [1981.4, 2331.0] |
| Variable cost, | [1439.5, 1693.6] | [1367.5, 1608.9] | |
| Wind power | Fixed cost, | [1704.3, 1583.6] | [2005.0, 1863.0] |
| Variable cost, | [1137.9, 1338.7] | [1092.4, 1285.2] | |
| Biomass power | Fixed cost, | [1856.4, 2184.0] | [1746.8, 2055.0] |
| Variable cost, | [1210.0, 1423.5] | [1178.7, 1386.7] | |
| Nuclear power | Fixed cost, | [2082.5, 2450.0] | [1787.6, 2103.0] |
| Variable cost, | [1389.8, 1635.0] | [1232.5, 1450.0] | |
| Operation time for generation technology p in period t (h) | |||
| Coal-fired power | [16,800, 17,400] | [16,800, 17400] | |
| Hydropower | [11,700, 12,000] | [11,700, 12,000] | |
| Photovoltaic power | [2700, 3000] | [2700, 3000] | |
| Wind power | [8700, 9000] | [8700, 9000] | |
| Biomass power | [13,800, 14,400] | [13,800, 14,400] | |
| Nuclear power | [18,900, 19,200] | [18,900, 19,200] | |
| Demand Sector | Demand Level | Probability (%) | Electricity Demand (103 GWh) | |
|---|---|---|---|---|
| t = 1 | t = 2 | |||
| Agriculture | L | 20 | [25.4, 25.9] | [31.7, 32.8] |
| M | 60 | [27.9, 28.4] | [34.7, 35.9] | |
| H | 20 | [30.3, 30.8] | [37.7, 39.0] | |
| Industrial | L | 20 | [864.0, 880.5] | [1075.6, 1113.8] |
| M | 60 | [946.6, 963.2] | [1178.5, 1218.4] | |
| H | 20 | [1029.3, 1045.8] | [1281.5, 1323.0] | |
| Building industry | L | 20 | [9.8, 10.0] | [12.2, 12.7] |
| M | 60 | [10.8, 10.9] | [13.38, 13.8] | |
| H | 20 | [11.7, 11.9] | [14.6, 15.0] | |
| Transportation | L | 20 | [17.6, 17.9] | [21.9, 22.7] |
| M | 60 | [19.3, 19.5] | [24.0, 24.8] | |
| H | 20 | [21.0, 21.3] | [26.1, 27.0] | |
| Business | L | 20 | [82.1, 83.7] | [102.2, 105.8] |
| M | 60 | [90.0, 91.5] | [112.0, 115.8] | |
| H | 20 | [97.8, 99.4] | [121.8, 125.7] | |
| Residential | L | 20 | [122.2, 124.5] | [152.1, 157.5] |
| M | 60 | [133.9, 136.2] | [166.7, 172.3] | |
| H | 20 | [145.6, 147.9] | [181.3, 187.1] | |
| Scenario | Risk Aversion Parameter | Emission Reduction Target |
|---|---|---|
| Scenario 1 (S_1) | 0.05 | 0% |
| Scenario 2 (S_2) | 0.05 | 7% |
| Scenario 3 (S_3) | 0.05 | 15% |
| Scenario 4 (S_4) | 0.5 | 0% |
| Scenario 5 (S_5) | 0.5 | 7% |
| Scenario 6 (S_6) | 0.5 | 15% |
| Scenario 7 (S_7) | 10 | 0% |
| Scenario 8 (S_8) | 10 | 7% |
| Scenario 9 (S_9) | 10 | 15% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, J.; Liao, C.; Ji, L.; Xie, Y.; Yu, Y.; Yin, J. A Short-Term Hybrid Energy System Robust Optimization Model for Regional Electric-Power Capacity Development Planning under Different Pollutant Control Pressures. Sustainability 2021, 13, 11341. https://doi.org/10.3390/su132011341
Cui J, Liao C, Ji L, Xie Y, Yu Y, Yin J. A Short-Term Hybrid Energy System Robust Optimization Model for Regional Electric-Power Capacity Development Planning under Different Pollutant Control Pressures. Sustainability. 2021; 13(20):11341. https://doi.org/10.3390/su132011341
Chicago/Turabian StyleCui, Jixian, Chenghao Liao, Ling Ji, Yulei Xie, Yangping Yu, and Jianguang Yin. 2021. "A Short-Term Hybrid Energy System Robust Optimization Model for Regional Electric-Power Capacity Development Planning under Different Pollutant Control Pressures" Sustainability 13, no. 20: 11341. https://doi.org/10.3390/su132011341






