Research on the Optimization Model of Railway Emergency Rescue Network Considering Space-Time Accessibility
Abstract
:1. Introduction
2. Analysis of Railway Rescue Transportation Network and Space-Time Accessibility
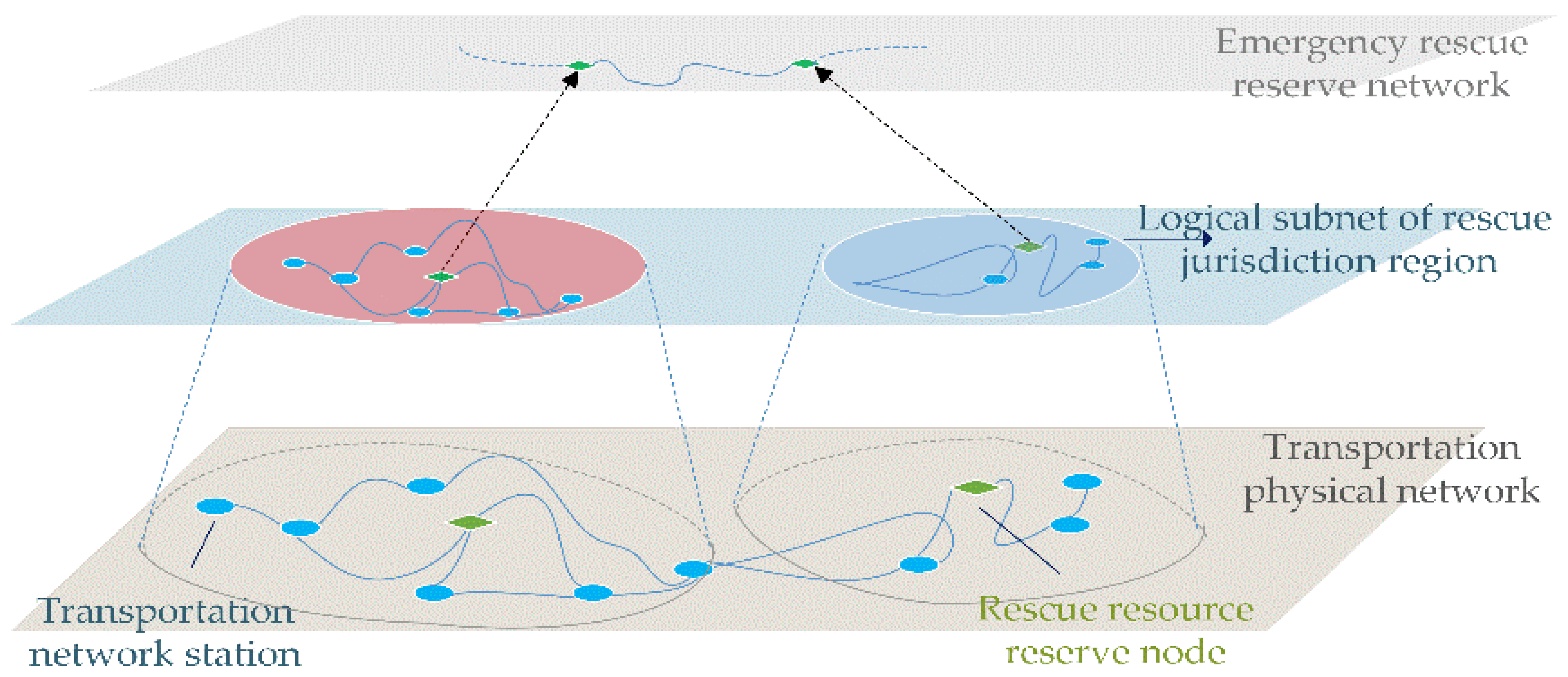
2.1. Construction of Railway Emergency Rescue Transportation Network
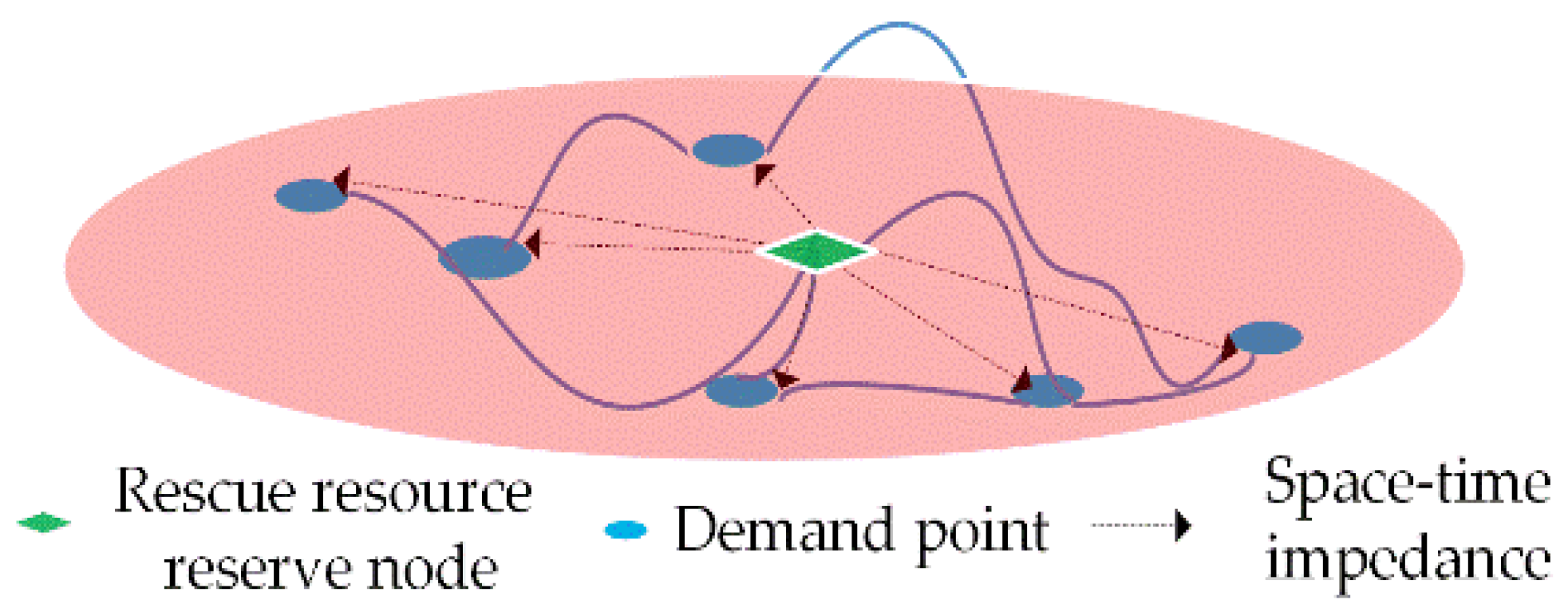
2.2. Accessibility Identification of Rescue Resource Reserve Nodes in Emergency Rescue Network
2.3. Space-Time Accessibility Identification of Emergency Rescue Network Edges
3. Maintenance Allocation Strategy Model of Railway Emergency Rescue Network
3.1. Risk Model Considering Space-Time Accessibility
3.2. Objective Function of Maintenance Allocation Strategy Model
3.3. Methodology for Solving the Maintenance Allocation Policy Model
4. Examples and Results
4.1. Case Overview
4.2. Maintenance Allocation Model Construction
4.2.1. Space-Time Accessibility of Emergency Rescue Network
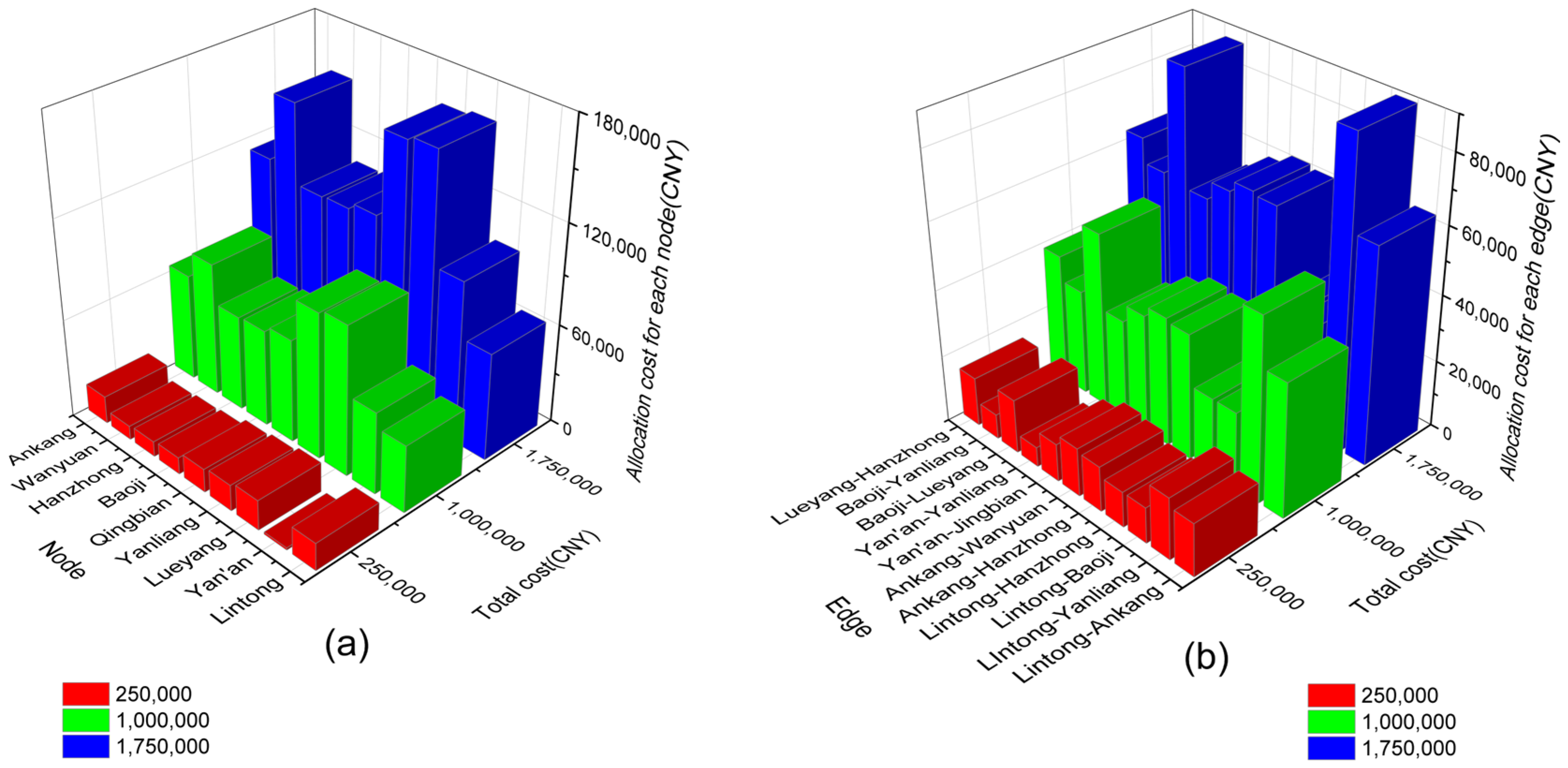
4.2.2. Reserve Node and Edge Maintenance Strategy Allocation Results
4.3. Analysis of Results
4.3.1. Reserve Node and Edge Maintenance Allocation Results
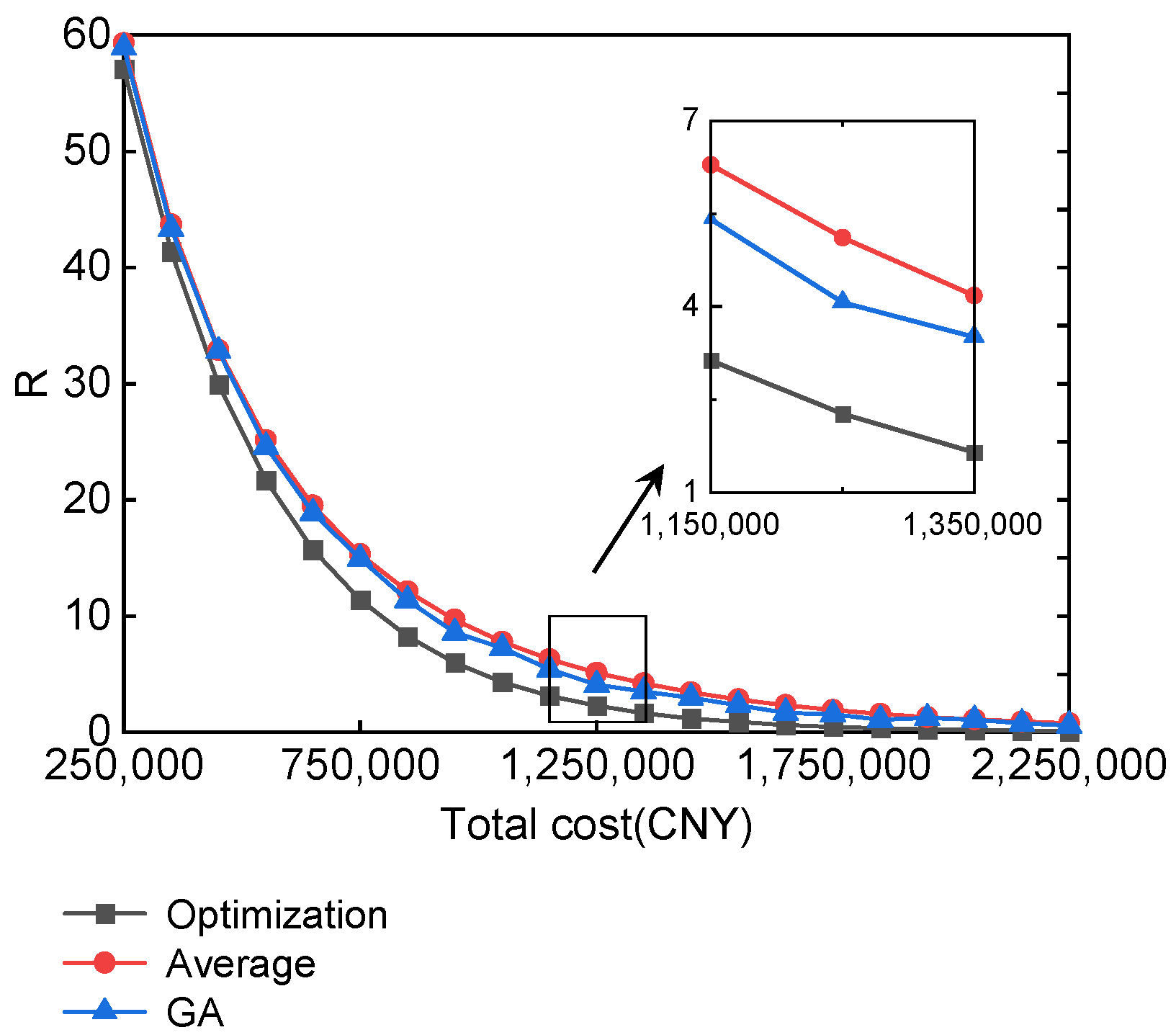
4.3.2. Comparative Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, C.; Gao, Y.; Yang, L.; Gao, Z.; Qi, J. Joint optimization of train scheduling and maintenance planning in a railway network: A heuristic algorithm using Lagrangian relaxation. Transport. Res. B-Meth. 2020, 134, 64–92. [Google Scholar] [CrossRef]
- D’Ariano, A.; Meng, L.; Centulio, G.; Corman, F. Integrated stochastic optimization approaches for tactical scheduling of trains and railway infrastructure maintenance. Comput. Ind. Eng. 2019, 127, 1315–1335. [Google Scholar] [CrossRef]
- Aken, S.; Bešinović, N.; Goverde, R. Designing alternative railway timetables under infrastructure maintenance possessions. Transport. Res. B-Meth. 2017, 98, 224–238. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y.; Sun, C.; Liu, Y. Accessibility impact of the present and future high-speed rail network: A case study of Jiangsu Province, China. J. Transp. Geogr. 2016, 54, 161–172. [Google Scholar] [CrossRef]
- Shatanawi, M.; Mészáros, F. Implications of the Emergence of Autonomous Vehicles and Shared Autonomous Vehicles: A Budapest Perspective. Sustainability 2022, 14, 10952. [Google Scholar] [CrossRef]
- Martín, B.; Ortega, E.; de Isidro, Á.; Iglesias-Merchan, C. Improvements in high-speed rail network environmental evaluation and planning: An assessment of accessibility gains and landscape connectivity costs in Spain. Land Use Pol. 2021, 103, 105321. [Google Scholar] [CrossRef]
- Li, S.; Duan, H.; Smith, T.; Hu, H. Time-varying accessibility to senior centers by public transit in Philadelphia. Transport. Res. A-Pol. 2021, 151, 245–258. [Google Scholar] [CrossRef]
- Cortés, Y. Spatial Accessibility to Local Public Services in an Unequal Place: An Analysis from Patterns of Residential Segregation in the Metropolitan Area of Santiago, Chile. Sustainability 2021, 13, 442. [Google Scholar] [CrossRef]
- Cheng, W.; Wu, J.; Moen, W.; Hong, L. Assessing the spatial accessibility and spatial equity of public libraries’ physical locations. Libr. Inform. Sci. Res. 2021, 43, 101089. [Google Scholar] [CrossRef]
- El-Maissi, A.M.; Argyroudis, S.A.; Kassem, M.M.; Leong, L.V.; Mohamed Nazri, F. An Integrated Framework for the Quantification of Road Network Seismic Vulnerability and Accessibility to Critical Services. Sustainability 2022, 14, 12474. [Google Scholar] [CrossRef]
- Shahparvari, S.; Fadaki, M.; Chhetri, P. Spatial accessibility of fire stations for enhancing operational response in Melbourne. Fire Saf. J. 2020, 117, 10314. [Google Scholar] [CrossRef]
- KC, K.; Corcoran, J.; Chhetri, P. Measuring the spatial accessibility to fire stations using enhanced floating catchment method. Socio-Econ. Plan. Sci. 2020, 69, 100673. [Google Scholar] [CrossRef]
- Wei, Z.; Bai, J.; Feng, R. Evaluating the spatial accessibility of medical resources taking into account the residents’ choice behavior of outpatient and inpatient medical treatment. Socio-Econ. Plan. Sci. 2022, 83, 101336. [Google Scholar] [CrossRef]
- Li, M.; Wang, F.; Kwan, M.; Chen, J.; Wang, J. Equalizing the spatial accessibility of emergency medical services in Shanghai: A trade-off perspective. Comput. Environ. Urban Syst. 2022, 92, 101745. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhong, Q.; Yin, Y.; Yan, X.; Peng, Q. A Fast Approach for Reoptimization of Railway Train Platforming in Case of Train Delays. J. Adv. Transport. 2020, 2020, 5609524. [Google Scholar] [CrossRef]
- Bababeik, M.; Khademi, N.; Chen, A. Increasing the resilience level of a vulnerable rail network: The strategy of location and allocation of emergency relief trains. Transport. Res. E 2018, 119, 110–128. [Google Scholar] [CrossRef]
- Lv, H.; Peng, X.; Xu, H.; Zhang, J. Research on the site selection of railway superlong tunnel emergency rescue station. J. Railw. Eng. Soc. 2020, 37, 59–64. [Google Scholar]
- Cheng, Y.; Liang, Z. A strategic planning model for the railway system accident rescue problem. Transport. Res. E 2014, 69, 75–96. [Google Scholar] [CrossRef]
- Li, S.; Xu, J. Research on coordination method of scenario conflict in railway emergency rescue group decision-making. J. Chin. Railw. Soc. 2019, 41, 32–39. [Google Scholar]
- Liu, L.; Yang, X. Travel Time Reliability-Based Rescue Resource Scheduling for Accidents Concerning Transport of Dangerous Goods by Rail. Algorithms 2021, 14, 325. [Google Scholar] [CrossRef]
- Chen, D.; Sun, Y.; Li, J.; Ni, S. Construction of evaluation index system for emergency rescue capacity of rail transit under serious epidemic situation. J. Traffic Transp. Eng. 2020, 20, 129–138. [Google Scholar]
- Sun, J.; Cao, H.; Geng, B. Demand Prediction of Railway Emergency Resources Based on Case-Based Reasoning. J. Adv. Transport. 2021, 2021, 6666631. [Google Scholar] [CrossRef]
- France-Mensah, J.; O’Brien, W. Budget allocation models for pavement maintenance and rehabilitation: Comparative case study. J. Manag. Eng. 2021, 34, 05018002. [Google Scholar] [CrossRef]
- Ramachandran, S.; Rajendran, C.; Amirthalingam, V. Decision support system for the maintenance management of road network considering multi-criteria. Int. J. Pavement Res. Technol. 2019, 12, 325–335. [Google Scholar] [CrossRef]
- Wei, Y.; Jin, L.; Xu, M. Instructions for planning emergency shelters and open spaces in China: Lessons from global experiences and expertise. Int. J. Disaster Risk Reduct. 2020, 51, 101813. [Google Scholar] [CrossRef]
- Tsenga, W.; Shen, T.; Hsieh, P. Theory establishment and data preparedness for modeling emergency medical service in case of a mass casualty incidents in road tunnels. Procedia Eng. 2018, 211, 36–45. [Google Scholar] [CrossRef]
- Hamshary, E.; Abouhamad, M.; Marzouk, M. Integrated maintenance planning approach to optimize budget allocation for subway operating systems. Tunn. Undergr. Sp. Technol. 2022, 121, 104322. [Google Scholar] [CrossRef]
- Sun, B.; Liu, J.; Hao, J. Maintenance Decision-Making of an Urban Rail Transit System in a Regionalized Network-Wide Perspective. Sustainability 2020, 12, 9734. [Google Scholar] [CrossRef]
- Xu, L.; Wang, C.; Dong, W.; Sun, X. A Method for Optimal Allocation of Regional Rail Transit Emergency Resources Based on Resource Sharing. J. Phys. Conf. Ser. 2018, 1624, 042037. [Google Scholar] [CrossRef]
- Zhang, G.; Song, L.; Wang, H.; Hu, C.; Wang, N. Location-assistant content distribution scheme for emergency rescue. Int. J. Distrib. Sens. Netw. 2018, 14, 1550147718800464. [Google Scholar] [CrossRef] [Green Version]
- Feng, J.; Gai, W.; Li, J. Multi-objective optimization of rescue station selection for emergency logistics management. Saf. Sci. 2019, 120, 276–282. [Google Scholar] [CrossRef]
- Tang, Z.; Qin, J.; Sun, J. Railway emergency resource dispatching optimization based on fuzzy satisfaction degree under the priority principle. J. Intell. Fuzzy. Syst. 2017, 33, 2677–2686. [Google Scholar] [CrossRef]
- Fecarotti, C.; Andrews, J.; Pesenti, R. A mathematical programming model to select maintenance strategies in railway networks. Reliab. Eng. Syst. Saf. 2021, 216, 107940. [Google Scholar] [CrossRef]
- Jia, L.; Wang, L.; Qin, Y. Resource Allocation on High-Speed Railway Emergency Management. In High-Speed Railway Operation under Emergent Conditions. Advances in High-Speed Rail Technology; Springer: Berlin, Heidelberg, 2022; pp. 265–286. [Google Scholar]




| Node | Lintong | Yan’an | Lueyang | Yanliang | Jingbian | Baoji | Hanzhong | Wanyuan | Ankang | ||
| 9.6700 | 3.9302 | 10.1202 | 9.3524 | 7.4984 | 6.1247 | 5.8570 | 7.3292 | 8.4631 | |||
| Edge | Lintong-Ankang | Lintong-Yanliang | Lintong-Baoji | Lintong- Hanzhong | Ankang- Hanzhong | Ankang-Wanyuan | Yan’an- Jingbian | Yan’an-Yanliang | Baoji- Lueyang | Baoji- Yanliang | Lueyang-Hanzhong |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 2 | 3 | 2 | |
| 9.0643 | 9.5112 | 7.8974 | 7.7635 | 7.1578 | 7.8776 | 5.7143 | 3.3207 | 8.1225 | 3.8693 | 7.9886 |
| [CNY] | [CNY] | ||||||
|---|---|---|---|---|---|---|---|
| 250,000(gz) | 1,000,000(gz) | 17,500,000(gz) | 250,000(gz) | 1,000,000(gz) | 17,500,000(gz) | ||
| Lintong | 16,585 | 40,779 | 64,972 | Lintong-Ankang | 15,938 | 40,132 | 64,325 |
| Yan’an | 1300 | 49,688 | 98,075 | Lintong-Yanliang | 18,547 | 54,838 | 91,128 |
| Lueyang | 18,162 | 90,743 | 163,323 | Lintong-Baoji | 10,746 | 22,843 | 34,939 |
| Yanliang | 15,795 | 88,376 | 160,956 | Lintong-Hanzhong | 10,660 | 22,757 | 34,854 |
| Jingbian | 14,220 | 62,608 | 110,995 | Ankang-Hanzhong | 13,577 | 37,770 | 61,964 |
| Baoji | 10,173 | 58,560 | 106,947 | Ankang-Wanyuan | 14,535 | 38,729 | 62,922 |
| Hanzhong | 9279 | 57,667 | 106,054 | Yan’an-Jingbian | 11,325 | 35,518 | 59,712 |
| Wanyuan | 8349 | 80,929 | 153,510 | Yan’an-Yanliang | 5897 | 30,090 | 54,284 |
| Ankang | 16,630 | 65,017 | 113,405 | Baoji-Lueyang | 16,180 | 52,470 | 88,760 |
| Baoji-Yanliang | 7426 | 31,619 | 55,813 | ||||
| Lueyan-Hanzhong | 14,675 | 38,869 | 63,062 | ||||
| Algorithm | Risk R | CPU Time | ||
|---|---|---|---|---|
| Optimization allocation algorithm | 75.5656 | 49.4344 | 2.2675 | 1 s |
| Average allocation algorithm | 56.25 | 68.75 | 5.1124 | 1 s |
| GA allocation algorithm | 63.3879 | 61.6121 | 4.0681 | 23 s |
| [CNY] | [CNY] | ||||||
|---|---|---|---|---|---|---|---|
| Optimization | Average | GA | Optimization | Average | GA | ||
| Lintong | 48,843 | 62,500 | 71,239 | Lintong-Ankang | 48,196 | 62,500 | 56,323 |
| Yan’an | 65,817 | 62,500 | 69,971 | Lintong-Yanliang | 66,934 | 62,500 | 52,377 |
| Lueyang | 114,936 | 62,500 | 94,448 | Lintong-Baoji | 26,875 | 62,500 | 60,421 |
| Yanliang | 112,569 | 62,500 | 66,254 | Lintong-Hanzhong | 26,789 | 62,500 | 62,454 |
| Jingbian | 78,737 | 62,500 | 65,872 | Ankang-Hanzhong | 45,835 | 62,500 | 50,482 |
| Baoji | 74,689 | 62,500 | 61,112 | Ankang-Wanyuan | 46,793 | 62,500 | 51,207 |
| Hanzhong | 73,796 | 62,500 | 49,856 | Yan’an-Jingbian | 43,583 | 62,500 | 70,992 |
| Wanyuan | 105,123 | 62,500 | 93,767 | Yan’an-Yanliang | 38,155 | 62,500 | 50,273 |
| Ankang | 81,146 | 62,500 | 61,361 | Baoji-Lueyang | 64,567 | 62,500 | 60,319 |
| Baoji-Yanliang | 39,684 | 62,500 | 59,023 | ||||
| Lueyang-Hanzhong | 46,933 | 62,500 | 42,251 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, J.; Shang, M.; Dang, J. Research on the Optimization Model of Railway Emergency Rescue Network Considering Space-Time Accessibility. Sustainability 2022, 14, 14503. https://doi.org/10.3390/su142114503
Zuo J, Shang M, Dang J. Research on the Optimization Model of Railway Emergency Rescue Network Considering Space-Time Accessibility. Sustainability. 2022; 14(21):14503. https://doi.org/10.3390/su142114503
Chicago/Turabian StyleZuo, Jing, Mengxing Shang, and Jianwu Dang. 2022. "Research on the Optimization Model of Railway Emergency Rescue Network Considering Space-Time Accessibility" Sustainability 14, no. 21: 14503. https://doi.org/10.3390/su142114503






