Spatial Structure of China’s Green Development Efficiency: A Perspective Based on Social Network Analysis
Abstract
:1. Introduction
2. Methods and Data
2.1. Measurement of GDE
2.1.1. Super-EBM Model
2.1.2. Evaluation System
2.2. Social Network Analysis
2.2.1. Building a Spatial Correlation Network
2.2.2. Overall Network Structure Characteristics
2.2.3. Centrality
2.2.4. Cohesive Subgroups
2.3. Analysis of Influencing Factors
2.3.1. The QAP Correlation
2.3.2. Geographical Detector
2.3.3. Influencing Factors Variables
2.4. Data Source and Processing
3. Results
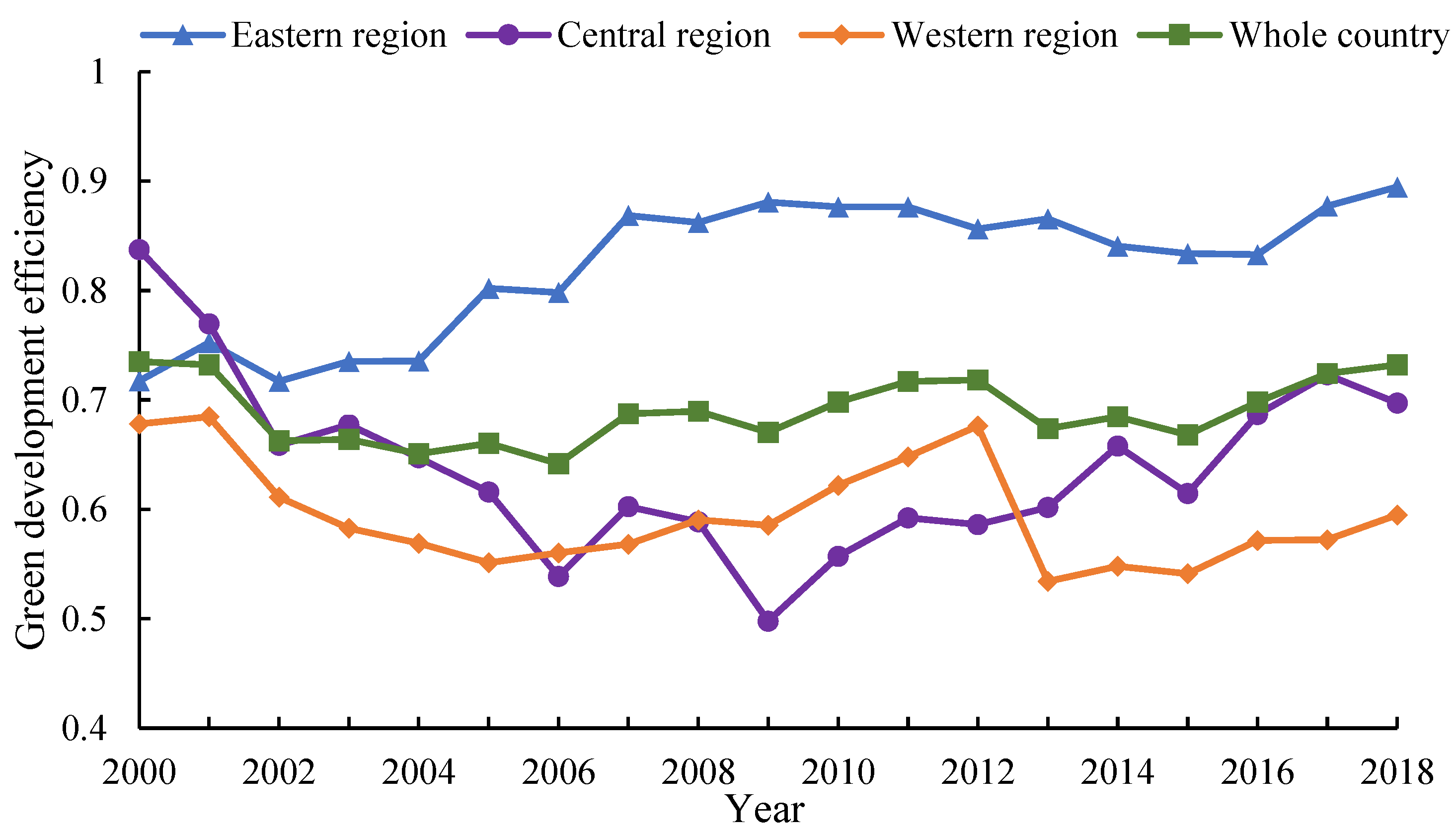
3.1. Calculation Results of GDE
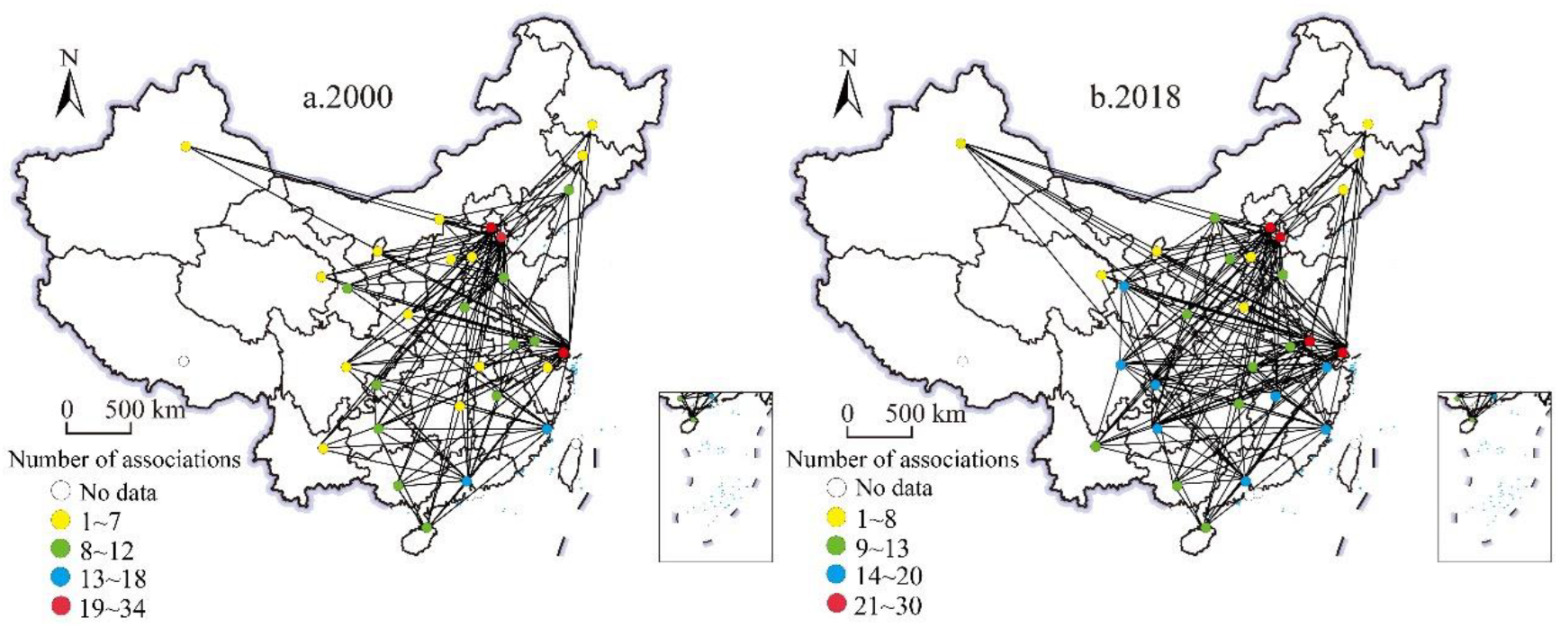
3.2. Spatial Correlation Network Analysis of GDE in China
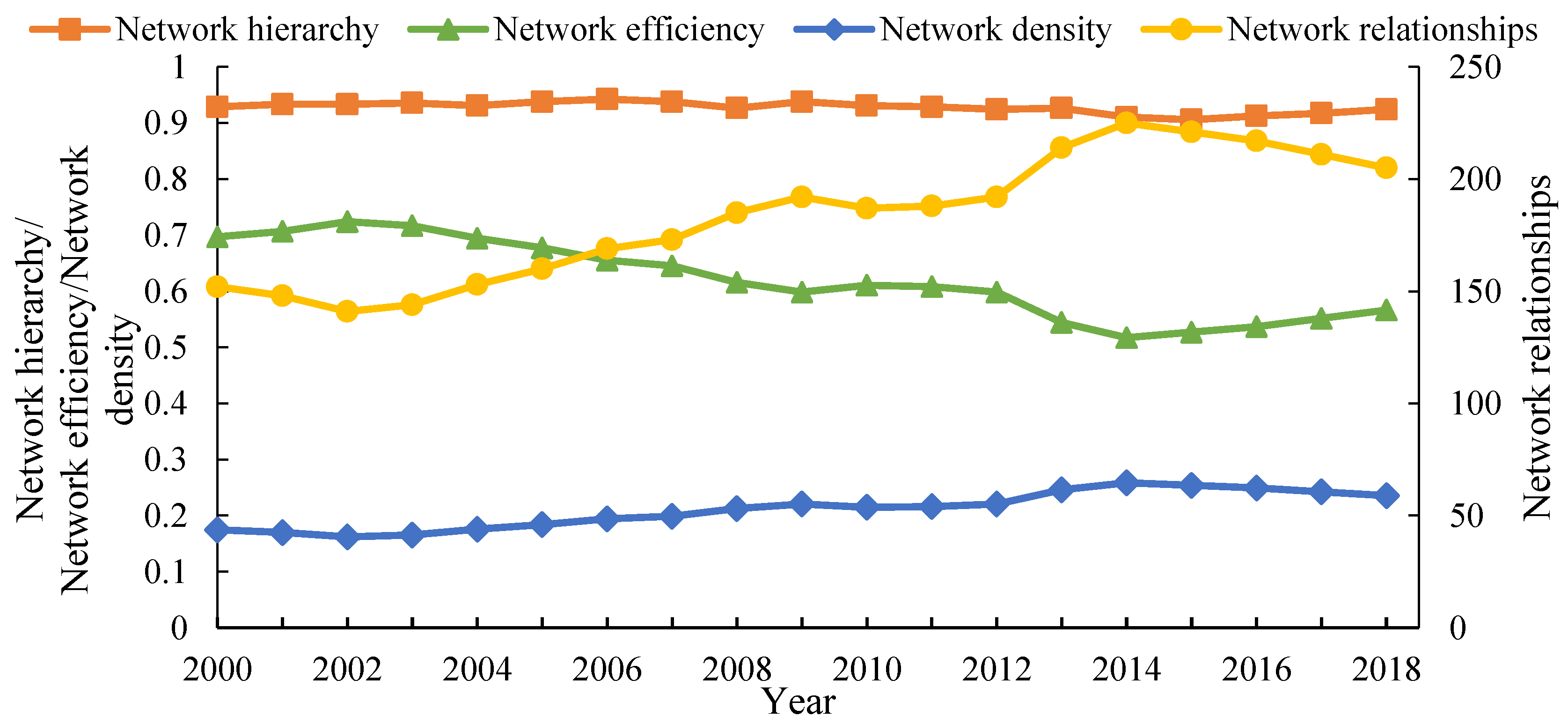
3.2.1. Overall Network Structure
3.2.2. Centrality Analysis
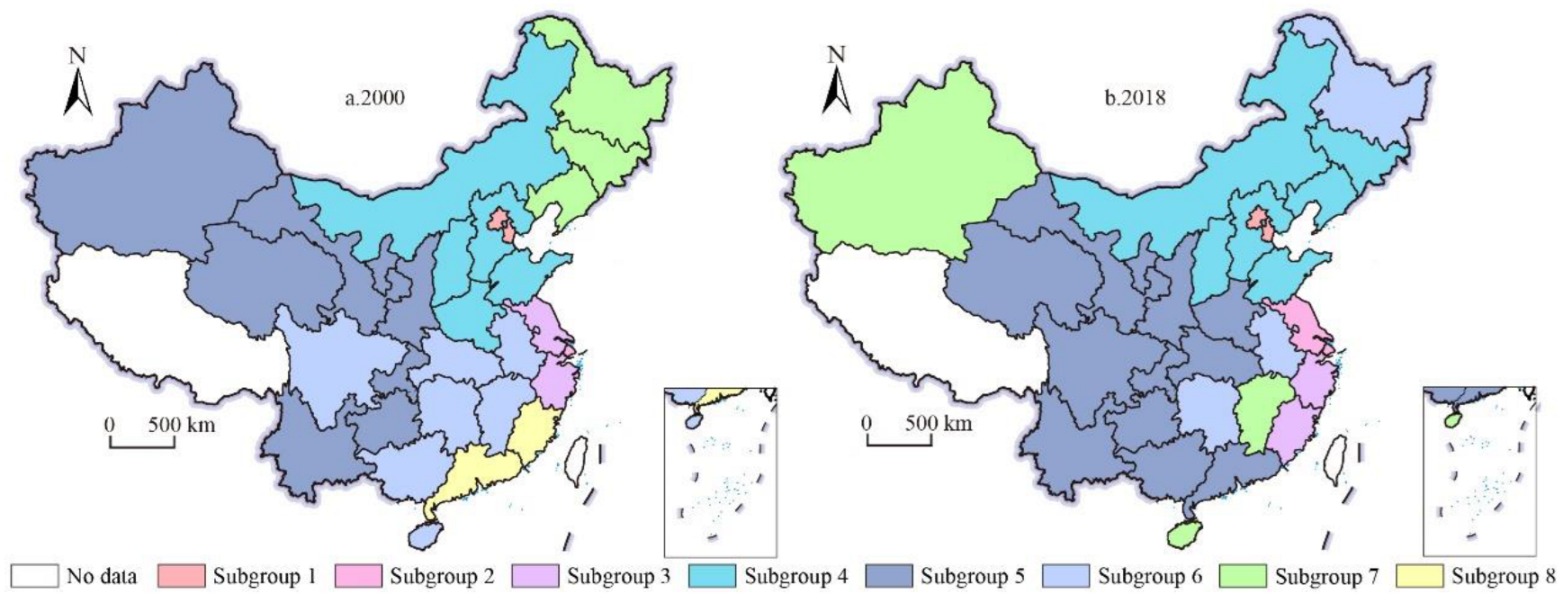
3.2.3. Cohesive Subgroups Analysis
3.3. Analysis of Influencing Factors
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Z.; Zheng, K.; Zhong, Q. Comprehensive evaluation and spatial-temporal pattern of green development in Hunan Province, China. Sustainability 2022, 14, 6819. [Google Scholar] [CrossRef]
- Zakari, A.; Khan, I.; Tan, D.; Alvarado, R.; Dagar, V. Energy efficiency and sustainable development goals (SDGs). Energy 2022, 239, 122365. [Google Scholar] [CrossRef]
- United Nations. In Proceedings of the 2008 United Nations Climate Change Conference, Poznań, Poland, 1–12 December 2008; Available online: https://baike.baidu.com/item/%E7%BB%BF%E8%89%B2%E6%96%B0%E6%94%BF/971528 (accessed on 6 August 2022).
- OECD. Towards Green Growth: A Summary for Policy Makers; Organisation for Economic Co-operation and Development (OECD): Paris, France, 2011. [Google Scholar]
- UNEP. Towards a Green Economy: Pathways to Sustainable Development and Poverty Eradication—A Synthesis for Policy Makers; UNEP: Nairobi, Kenya, 2011. [Google Scholar]
- Jänicke, M. “Green growth”: From a growing eco-industry to economic sustainability. Energy Policy 2012, 48, 13–21. [Google Scholar] [CrossRef]
- Sun, C.; Tong, Y.; Zou, W. The evolution and a temporal-spatial difference analysis of green development in China. Sustain. Cities Soc. 2018, 41, 52–61. [Google Scholar] [CrossRef]
- Li, C.; Song, L. Regional differences and spatial convergence of green development in China. Sustainability 2022, 14, 8511. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, Y.; Cao, X.; Wang, C.; Wang, Y.; Zhang, M.; Ferrier, R.C.; Jenkins, A.; Yuan, J.; Bailey, M.J.; et al. Forty years of reform and opening up: China’s progress toward a sustainable path. Sci. Adv. 2019, 5, eaau9413. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Zhang, C.; Kafy, A.; Tan, S. Simulating the relationship between land use/cover change and urban thermal environment using machine learning algorithms in Wuhan City, China. Land 2022, 11, 14. [Google Scholar] [CrossRef]
- Gai, M.; Wang, X.; Qi, C. Spatiotemporal evolution and influencing factors of ecological civilization construction in China. Complexity 2020, 2020, 8829144. [Google Scholar] [CrossRef]
- Lu, P.; Liu, J.; Wang, Y.; Ruan, L. Can industrial agglomeration improve regional green total factor productivity in China? An empirical analysis based on spatial econometrics. Growth Chang. 2021, 52, 1011–1039. [Google Scholar] [CrossRef]
- Huang, M.; Ding, R.; Xin, C. Impact of technological innovation and industrial-structure upgrades on ecological efficiency in China in terms of spatial spillover and the threshold effect. Integr. Environ. Assess. Manag. 2020, 17, 852–865. [Google Scholar] [CrossRef]
- Lu, X.; Qu, Y.; Sun, P.; Yu, W.; Peng, W. Green transition of cultivated land use in the Yellow River Basin: A perspective of green utilization efficiency evaluation. Land 2020, 9, 475. [Google Scholar] [CrossRef]
- Xue, L.; Zheng, Z.; Meng, S.; Li, M.; Li, H.; Chen, J. Carbon emission efficiency and spatio-temporal dynamic evolution of the cities in Beijing-Tianjin-Hebei Region, China. Environ. Dev. Sustain. 2022, 24, 7640–7664. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, P. Has the level of green development in the northwestern provinces of China truly improved? A case study of Shaanxi. Sustain. Cities Soc. 2019, 51, 101779. [Google Scholar] [CrossRef]
- Weng, Q.; Qin, Q.; Li, L. A comprehensive evaluation paradigm for regional green development based on “Five-Circle Model”: A case study from Beijing-Tianjin-Hebei. J. Clean. Prod. 2020, 277, 124076. [Google Scholar] [CrossRef]
- Xiao, Y.; Chen, J.; Wang, X.; Lu, X. Regional green development level and its spatial spillover effects: Empirical evidence from Hubei Province, China. Ecol. Indic. 2022, 143, 109312. [Google Scholar] [CrossRef]
- Zhang, H.; Geng, Z.; Yin, R.; Zhang, W. Regional differences and convergence tendency of green development competitiveness in China. J. Clean. Prod. 2020, 254, 119922. [Google Scholar] [CrossRef]
- Tong, C.; Ding, S.; Wang, B.; Yang, S. Assessing the target-availability of China’s investments for green growth using time series prediction. Phys. A Stat. Mech. Appl. 2020, 537, 122724. [Google Scholar] [CrossRef]
- Houssini, K.; Geng, Y. Measuring Morocco’s green growth performance. Environ. Sci. Pollut. Res. 2022, 29, 1144–1154. [Google Scholar] [CrossRef]
- Lu, W.; Zhang, G. Green development efficiency of urban agglomerations in a developing country: Evidence from Beijing-Tianjin-Hebei in China. Environ. Dev. Sustain. 2022, 4, 1–24. [Google Scholar] [CrossRef]
- Cooper, W.W.; Rhodes, E. Short communication: Measuring the efficiency of decision-making units. Eur. J. Oper. Res. 1979, 3, 339. [Google Scholar]
- Yang, L.; Wang, K.L.; Geng, J.C. China’s regional ecological energy efficiency and energy saving and pollution abatement potentials: An empirical analysis using epsilon-based measure model. J. Clean. Prod. 2018, 194, 300–308. [Google Scholar] [CrossRef]
- Cuiyun, C.; Chazhong, G. Green development assessment for countries along the belt and road. J. Environ. Manag. 2020, 263, 110344. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.; Tong, Z.; Du, W.; Zhang, J.; Liu, X.; Yang, Z. Comprehensive evaluation of green development in Dongliao river basin from the integration system of “Multi-dimensions”. Sustainability 2021, 13, 4785. [Google Scholar] [CrossRef]
- Chen, Z.; Li, X.; Xia, X. Measurement and spatial convergence analysis of China’s agricultural green development index. Environ. Sci. Pollut. Res. 2021, 28, 19694–19709. [Google Scholar] [CrossRef] [PubMed]
- Huang, M.; Li, S. The analysis of the impact of the Belt and Road initiative on the green development of participating countries. Sci. Total Environ. 2020, 722, 137869. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, R.; Liu, L.; Ren, Y. A spatial effect study on financial agglomeration promoting the green development of urban agglomerations. Sustain. Cities Soc. 2021, 70, 102900. [Google Scholar] [CrossRef]
- Xie, H.; Ouyang, Z.; Choi, Y. Characteristics and influencing factors of green finance development in the Yangtze river delta of China: Analysis based on the spatial durbin model. Sustainability 2020, 12, 9753. [Google Scholar] [CrossRef]
- Tone, K.; Tsutsui, M. An epsilon-based measure of efficiency in DEA—A third pole of technical efficiency. Eur. J. Oper. Res. 2010, 207, 1554–1563. [Google Scholar] [CrossRef]
- Fan, J.; Xiao, Z. Analysis of spatial correlation network of China’s green innovation. J. Clean. Prod. 2021, 299, 126815. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Y.; Xu, C.; Yang, Y. Towards a sustainable grain production network: An empirical study from Northeast China. Sustainability 2022, 14, 8849. [Google Scholar] [CrossRef]
- Shaharudin, M.S.; Fernando, Y.; Chiappetta Jabbour, C.J.; Sroufe, R.; Jasmi, M.F.A. Past, present, and future low carbon supply chain management: A content review using social network analysis. J. Clean. Prod. 2019, 218, 629–643. [Google Scholar] [CrossRef]
- Andersen, P.; Petersen, N.C. A procedure for ranking efficient units in data envelopment analysis. Manage. Sci. 1993, 39, 1261–1264. [Google Scholar] [CrossRef]
- Lyu, X.; Peng, W.; Yu, W.; Xin, Z.; Niu, S.; Qu, Y. Sustainable intensification to coordinate agricultural efficiency and environmental protection: A systematic review based on metrological visualization. J. Land Use Sci. 2021, 16, 313–338. [Google Scholar] [CrossRef]
- Li, H.; He, F.; Deng, G. How does environmental regulation promote technological innovation and green development? New evidence from China. Polish J. Environ. Stud. 2019, 29, 689. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Yi, Z.; Jia, J. The efficiency evolution and risks of green development in the Yangtze River Economic Belt, China. Sustainability 2022, 14, 10417. [Google Scholar] [CrossRef]
- Zhao, L.; Gao, X.; Jia, J.; Zhang, Y. Analyzing inclusive green growth in China: A perspective of relative efficiency. Environ. Sci. Pollut. Res. 2022, 22, 23155. [Google Scholar] [CrossRef]
- Liu, R.; Chen, D.; Yang, S.; Chen, Y. Evaluation of green development efficiency of the major cities in Gansu Province, China. Sustainability 2021, 13, 3034. [Google Scholar] [CrossRef]
- Liu, K.; Shi, D.; Xiang, W.; Zhang, W. How has the efficiency of China’s green development evolved? An improved non-radial directional distance function measurement. Sci. Total Environ. 2022, 815, 152337. [Google Scholar] [CrossRef]
- Yang, T.; Zhou, K.; Zhang, C. Spatiotemporal patterns and influencing factors of green development efficiency in China’s urban agglomerations. Sustain. Cities Soc. 2022, 85, 104069. [Google Scholar] [CrossRef]
- Gao, H.; Zhao, L. Green development level measurement and spatial difference analysis of Yangtze River Economic Belt. Sci. Technol. Prog. Policy 2019, 36, 46–53. [Google Scholar]
- Cui, H.; Liu, Z. Spatial-temporal pattern and influencing factors of the urban green development efficiency in Jing-Jin-Ji Region of China. Polish J. Environ. Stud. 2021, 2, 1079–1093. [Google Scholar] [CrossRef] [PubMed]
- Yue, L.; Xue, D. Spatiotemporal change of urban green development efficiency in the Yellow River Basin and influencing factors. Resour. Sci. 2020, 42, 2274–2284. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, D.; Xu, M.; Yang, M.; Zou, W. Capital misallocation, technological innovation, and green development efficiency: Empirical analysis based on China provincial panel data. Environ. Sci. Pollut. Res. 2022, 4, 65535–65548. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Liu, Q.; Xu, J.; Fujiki, Y. Evolution characteristics of the spatial network structure of tourism efficiency in China: A province-level analysis. J. Destin. Mark. Manag. 2020, 18, 100509. [Google Scholar] [CrossRef]
- Chen, B.; Wu, C.; Huang, X.; Yang, X. Examining the relationship between urban land expansion and economic linkage using coupling analysis: A case study of the Yangtze River Economic Belt, China. Sustainability 2020, 12, 1227. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Shao, X.; Tang, M.; Lan, H. Spatio-temporal evolution of green innovation network and its multidimensional proximity analysis: Empirical evidence from China. J. Clean. Prod. 2021, 283, 124649. [Google Scholar] [CrossRef]
- Wang, F.; Wu, L.; Zhang, F. Network structure and influencing factors of agricultural science and technology innovation spatial correlation network—A study based on data from 30 provinces in China. Symmetry 2020, 12, 1773. [Google Scholar] [CrossRef]
- Gan, C.; Voda, M.; Wang, K.; Chen, L.; Ye, J. Spatial network structure of the tourism economy in urban agglomeration: A social network analysis. J. Hosp. Tour. Manag. 2021, 47, 124–133. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, H.; Wang, Z.; Dai, X. The improvement path for regionally coordinated green development: Evidence from social network analysis. Int. J. Environ. Res. Public Health 2022, 19, 1703. [Google Scholar] [CrossRef]
- Hsu, C.W.; Lin, C.Y. Using social network analysis to examine the technological evolution of fermentative hydrogen production from biomass. Int. J. Hydrogen Energy 2016, 41, 21573–21582. [Google Scholar] [CrossRef]
- Freeman, L.C. Centrality in social networks. Soc. Netw. 1979, 1, 215–239. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Zhang, Y.; Sang, Z.; Wang, W.; Zhang, L.; Li, M. Connection characteristics and hierarchical structure of China’s Urban Network-Based on the communications technology service industry. Complexity 2022, 10, 61433293. [Google Scholar] [CrossRef]
- Barnett, G.A. Encyclopedia of Social Networks; SAGE Publications: Thousand Oaks, CA, USA, 2011; pp. 523–526. [Google Scholar]
- Yue, H.; Hu, T. Geographical detector-based spatial modeling of the COVID-19 mortality rate in the continental United States. Int. J. Environ. Res. Public Health 2021, 18, 6832. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhang, X.; He, F.; Yuan, R. Regional green development level and its spatial relationship under the constraints of haze in China. J. Clean. Prod. 2019, 210, 376–387. [Google Scholar] [CrossRef]
- Zhao, P.J.; Zeng, L.e.; Lu, H.y.; Zhou, Y.; Hu, H.y.; Wei, X.Y. Green economic efficiency and its influencing factors in China from 2008 to 2017: Based on the super-SBM model with undesirable outputs and spatial Dubin model. Sci. Total Environ. 2020, 741, 140026. [Google Scholar] [CrossRef]
- Zhao, L.; Cao, N.; Han, Z.; Gao, X. Spatial correlation network and influencing factors of green economic efficiency in China. Resour. Sci. 2021, 43, 1933–1946. [Google Scholar] [CrossRef]
- Zhang, M.; Tan, S.; Zhang, X. How do varying socio-economic factors affect the scale of land transfer? Evidence from 287 cities in China. Environ. Sci. Pollut. Res. 2022, 29, 40865–40877. [Google Scholar] [CrossRef]
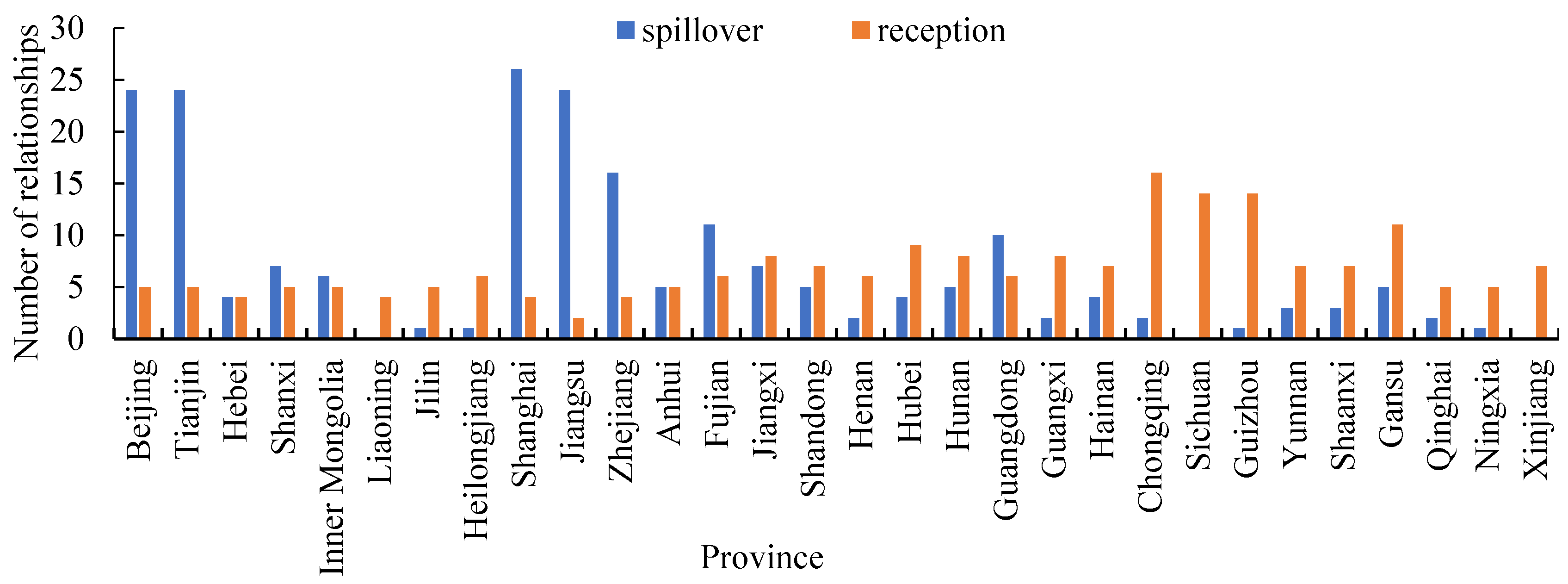

| Type of Indicator | Input & Output Elements | Variables | Data Sources |
|---|---|---|---|
| Input Indicators | Labor input | Number of employees (10 thousand people) | China Population and Employment Statistical Yearbook, statistical yearbooks of provinces and regions |
| Capital input | Stock of fixed assets (CNY 100 million) | China Statistical Yearbook | |
| Energy input | Total energy consumption (10 thousand tons of standard coal) | China Energy Statistical Yearbook | |
| Resource input | Total water consumption (100 million m3) | China Statistical Yearbook | |
| Land input | Built-up area (km2) | China Statistical Yearbook | |
| Technical input | Internal expenses for research and experimental development (CNY 10 thousand) | China Statistical Yearbook | |
| Output Indicators | Economic output | GDP (CNY billion) | China Statistical Yearbook |
| Social output | Per capita retail sales of social consumer goods (CNY), average salary of employees (CNY), average years of education (year), per capita life expectancy (years old), greening coverage of built-up areas (%) | China Statistical Yearbook, statistical yearbooks of provinces and regions | |
| Environmental undesirable output | Wastewater emissions (ten thousand tons), SO2 emissions (ten thousand tons), smoke (dust) emissions (ten thousand tons), general industrial solid waste generation (ten thousand tons) | China Statistical Yearbook and China Environmental Statistical Yearbook |
| Province | 2000 | 2018 | ||||
|---|---|---|---|---|---|---|
| Degree Centrality | Closeness Centrality | Betweenness Centrality | Degree Centrality | Closeness Centrality | Betweenness Centrality | |
| Beijing | 79.310 | 72.500 | 5.851 | 82.759 | 85.294 | 6.178 |
| Tianjin | 82.759 | 80.556 | 7.958 | 82.759 | 85.294 | 6.178 |
| Hebei | 13.793 | 46.032 | 0.158 | 20.690 | 49.153 | 0.888 |
| Shanxi | 17.241 | 46.774 | 0.189 | 27.586 | 55.769 | 1.405 |
| Inner Mongolia | 13.793 | 46.774 | 0.158 | 27.586 | 51.786 | 0.649 |
| Liaoning | 24.138 | 3.567 | 0.103 | 13.793 | 3.333 | 0 |
| Jilin | 17.241 | 3.571 | 0.246 | 17.241 | 3.448 | 0 |
| Heilongjiang | 13.793 | 3.567 | 0 | 20.690 | 3.448 | 0.062 |
| Shanghai | 93.103 | 93.548 | 13.258 | 89.655 | 90.625 | 9.486 |
| Jiangsu | 24.138 | 55.769 | 0.423 | 82.759 | 85.294 | 5.831 |
| Zhejiang | 10.345 | 49.153 | 0 | 58.621 | 65.909 | 1.771 |
| Anhui | 31.034 | 59.184 | 0.727 | 24.138 | 52.727 | 1.347 |
| Fujian | 41.379 | 59.184 | 0.603 | 48.276 | 48.333 | 3.347 |
| Jiangxi | 24.138 | 53.704 | 2.136 | 31.034 | 54.717 | 14.913 |
| Shandong | 31.034 | 59.184 | 0.747 | 31.034 | 50.000 | 4.246 |
| Henan | 20.690 | 54.717 | 0.912 | 24.138 | 34.524 | 0.142 |
| Hubei | 20.690 | 4.496 | 0.073 | 37.931 | 38.667 | 0.801 |
| Hunan | 17.241 | 4.309 | 0.088 | 34.483 | 34.940 | 1.069 |
| Guangdong | 41.379 | 4.348 | 5.203 | 37.931 | 47.541 | 9.283 |
| Guangxi | 20.690 | 4.315 | 0.088 | 31.034 | 32.955 | 0.246 |
| Hainan | 24.138 | 4.322 | 0.15 | 31.034 | 34.524 | 0.544 |
| Chongqing | 20.690 | 4.315 | 0.088 | 58.621 | 3.571 | 0.840 |
| Sichuan | 24.138 | 3.333 | 0 | 48.276 | 3.333 | 0 |
| Guizhou | 27.586 | 4.315 | 0.252 | 48.276 | 3.567 | 0.189 |
| Yunnan | 17.241 | 4.309 | 0.088 | 31.034 | 33.333 | 0.215 |
| Shaanxi | 20.690 | 3.333 | 0 | 31.034 | 4.149 | 0.183 |
| Gansu | 24.138 | 3.448 | 0.154 | 44.828 | 4.161 | 3.709 |
| Qinghai | 13.793 | 3.448 | 0 | 20.690 | 4.143 | 0 |
| Ningxia | 13.793 | 3.333 | 0 | 17.241 | 4.131 | 0 |
| Xinjiang | 10.345 | 3.333 | 0 | 24.138 | 3.333 | 0 |
| Average | 27.816 | 28.091 | 1.322 | 39.310 | 35.733 | 2.451 |
| Max | 93.103 | 93.548 | 13.258 | 89.655 | 90.625 | 14.913 |
| Min | 10.345 | 3.333 | 0 | 13.793 | 3.333 | 0 |
| Variables | Obs Value | Significa | Average | Std Dev | Minimum | Maximum | p ≥ 0 | p ≤ 0 |
|---|---|---|---|---|---|---|---|---|
| pgdp | 0.476 | 0.000 | 0.001 | 0.061 | −0.154 | 0.277 | 0.000 | 1.000 |
| inds | 0.270 | 0.000 | 0.001 | 0.070 | −0.155 | 0.259 | 0.000 | 1.000 |
| tech | 0.182 | 0.015 | 0.001 | 0.074 | −0.129 | 0.243 | 0.015 | 0.985 |
| urb | 0.409 | 0.000 | −0.001 | 0.062 | −0.155 | 0.261 | 0.000 | 1.000 |
| er | −0.095 | 0.051 | −0.000 | 0.067 | −0.160 | 0.333 | 0.949 | 0.051 |
| fina | 0.161 | 0.017 | −0.001 | 0.065 | −0.177 | 0.289 | 0.017 | 0.983 |
| res | 0.081 | 0.076 | 0.000 | 0.054 | −0.156 | 0.242 | 0.076 | 0.924 |
| Variables | pgdp | inds | tech | urb | er | fina | res |
|---|---|---|---|---|---|---|---|
| Degree centrality | 0.821 | 0.260 | 0.427 | 0.703 | 0.203 | 0.382 | 0.137 |
| Closeness centrality | 0.602 | 0.181 | 0.355 | 0.449 | 0.111 | 0.412 | 0.179 |
| Betweenness centrality | 0.327 | 0.252 | 0.146 | 0.310 | 0.154 | 0.306 | 0.197 |
| Average | 0.583 | 0.231 | 0.309 | 0.487 | 0.156 | 0.367 | 0.171 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Cao, N.; Zhang, Y.; Zhao, L. Spatial Structure of China’s Green Development Efficiency: A Perspective Based on Social Network Analysis. Sustainability 2022, 14, 16156. https://doi.org/10.3390/su142316156
Gao X, Cao N, Zhang Y, Zhao L. Spatial Structure of China’s Green Development Efficiency: A Perspective Based on Social Network Analysis. Sustainability. 2022; 14(23):16156. https://doi.org/10.3390/su142316156
Chicago/Turabian StyleGao, Xiaotong, Naigang Cao, Yushuo Zhang, and Lin Zhao. 2022. "Spatial Structure of China’s Green Development Efficiency: A Perspective Based on Social Network Analysis" Sustainability 14, no. 23: 16156. https://doi.org/10.3390/su142316156






