Effect of Fines Content on Pore Distribution of Sand/Clay Composite Soil
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental Method
3. Results and Discussion
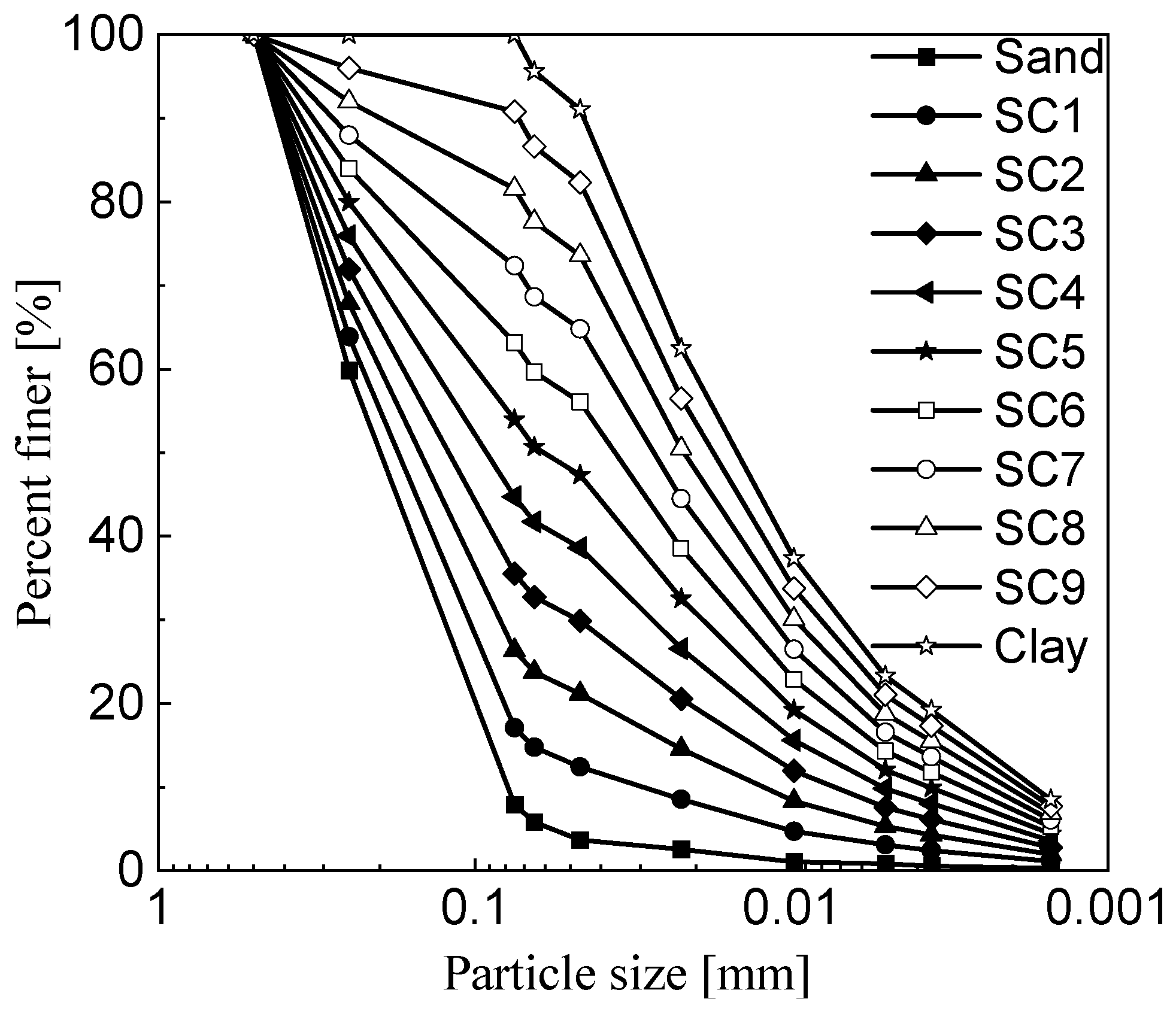
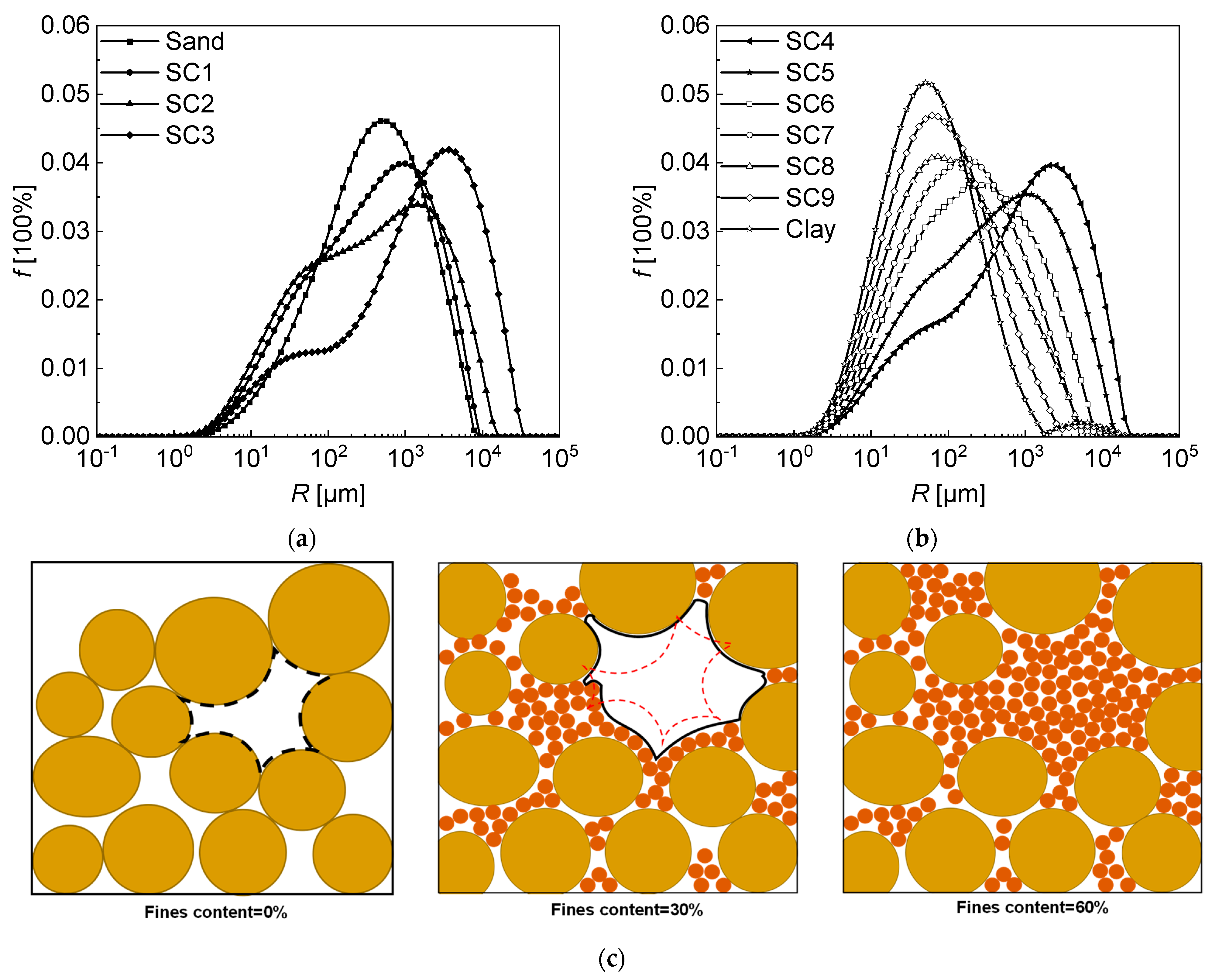
3.1. Particle Size Distribution Curves of Composite Soils with Different Fines Content
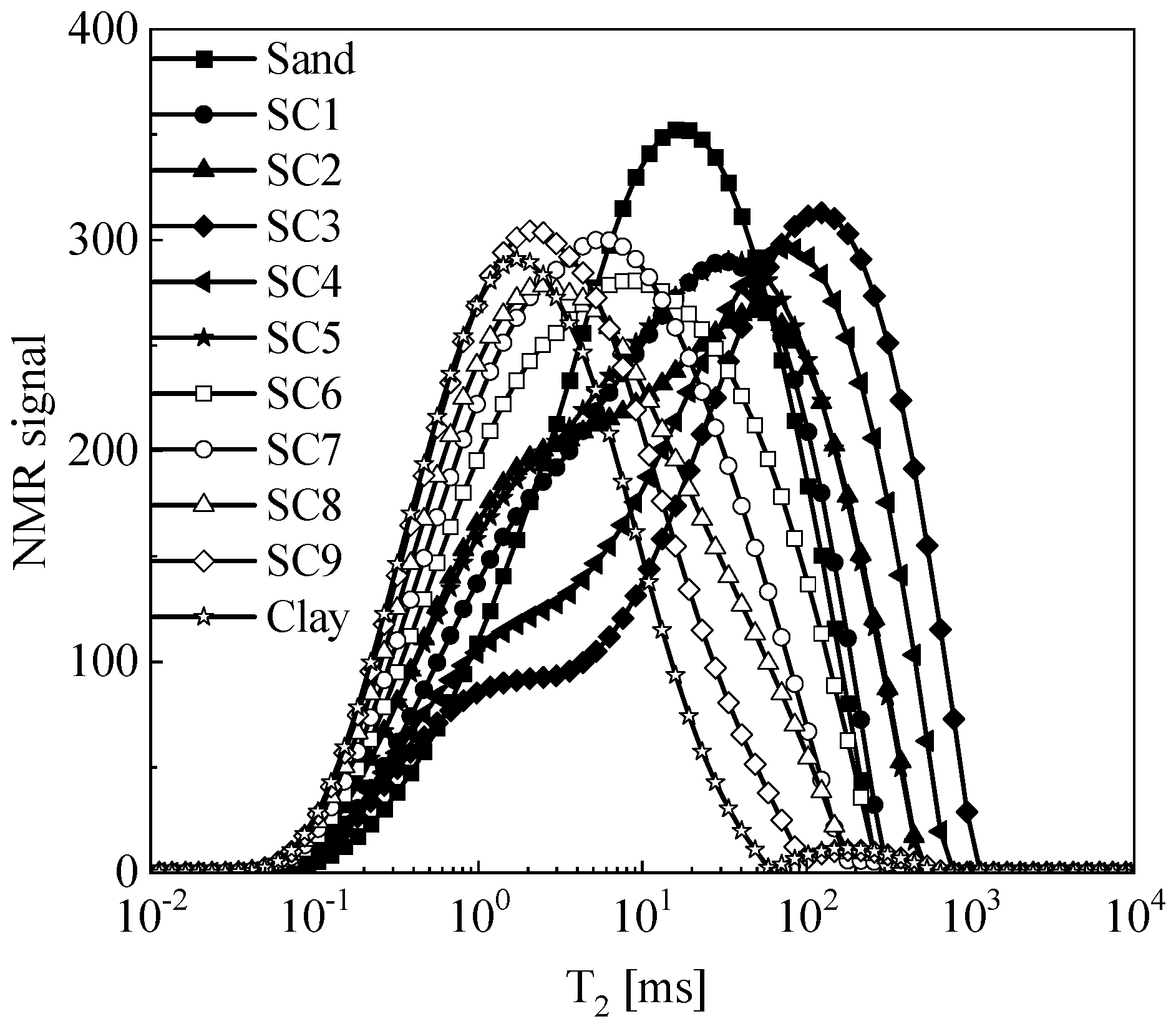
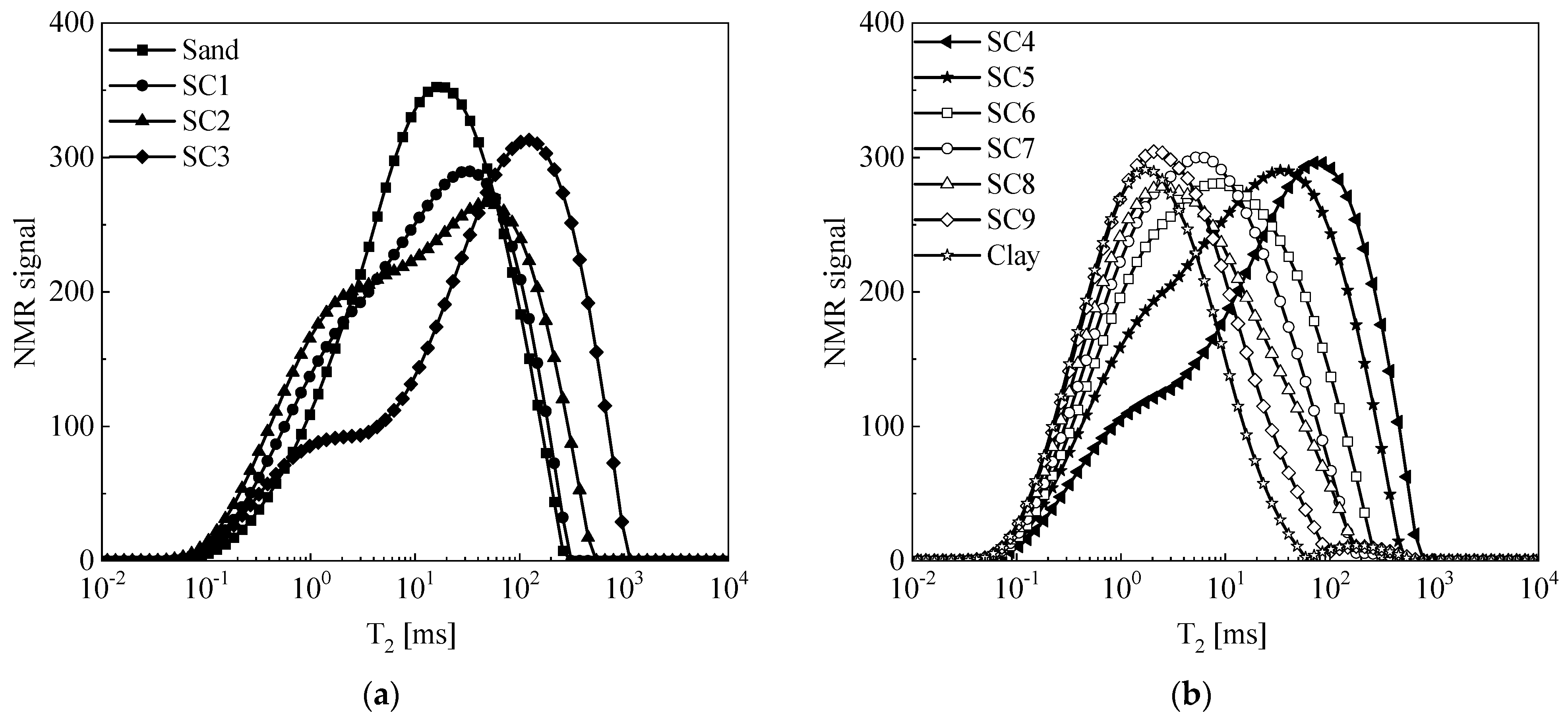
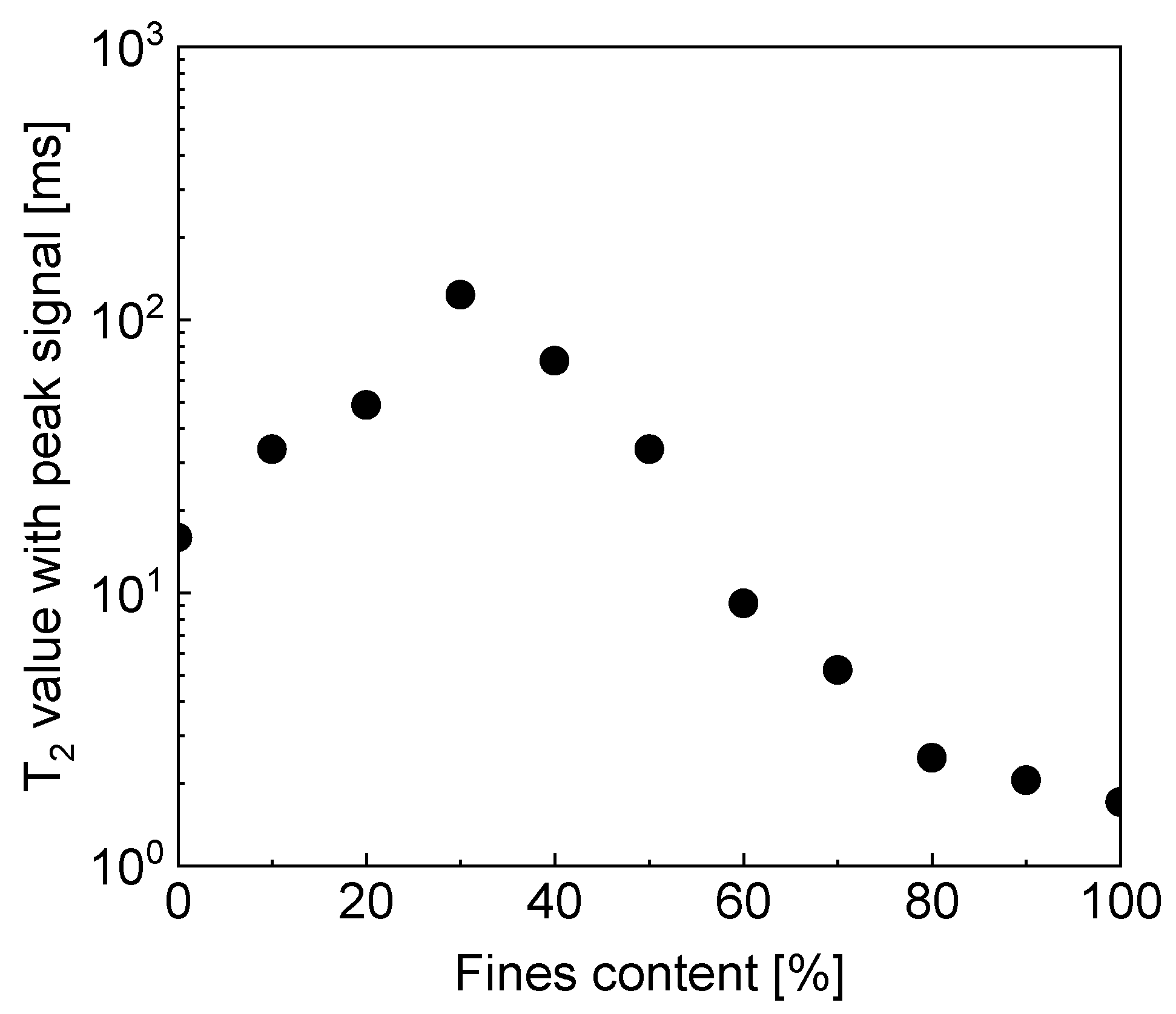
3.2. Influence of Fines Content on the T2 Distribution Curve of Composite Soil
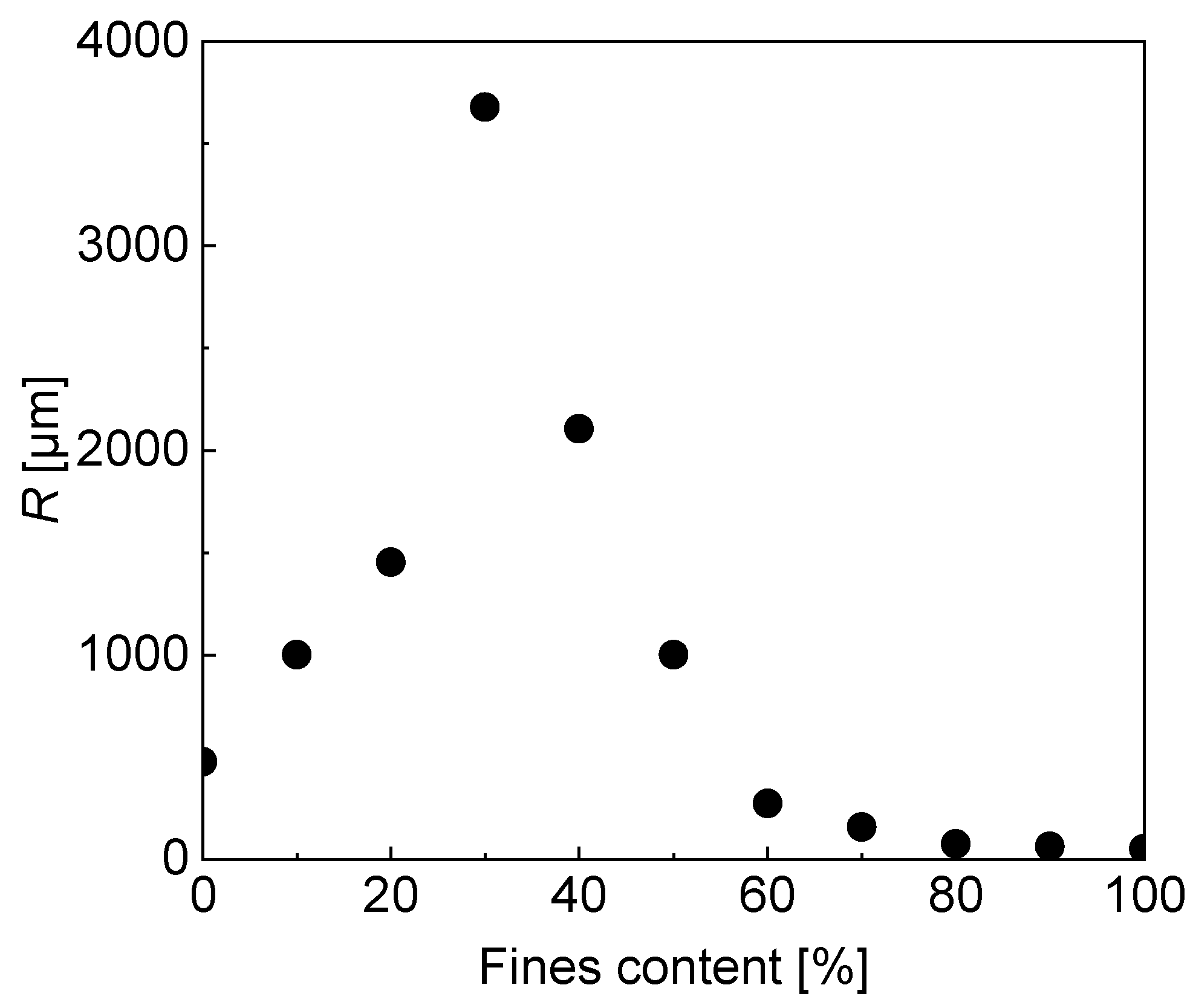
3.3. Effect of Fines Content on the Pore Size Distribution Curve of the Composite Soil
4. Discussion
5. Conclusions
- (1)
- When the fines content is relatively small (0–30%), the pore size distribution curve of the composite soil shifts to the right as the fines content increases. The proportion of small pores increases, accompanied by an increase in the size of large pores. This causes the shape of the pore size distribution curve to gradually transition from a unimodal distribution of pure sand to a bimodal distribution, composed of small pores dominated by fine particles and large pores dominated by the coarse particle skeleton. This is mainly because the addition of fine particles will cause the skeletal structure dominated by coarse particles to form a skeletal structure with locally large pores. When the fines content reaches 30%, the bimodal structure is the strongest with the most developed honeycomb pore structure, leading to the largest collapsibility of the composite soil.
- (2)
- As the fines content continues to increase beyond 30%, the pore size distribution curve begins to shift to the left; that is, the number of large pores in the composite soil decreases, and the number of small pores increases. Fine particles begin to fill the large pores, weakening the honeycomb pore structure. The pore distribution curve gradually becomes unimodal with more uniform pore size distribution.
- (3)
- As the fines content increases, the dominant pore size of the composite soil first increases and then decreases. When the fines content reaches 30%, the dominant pore size increases to its maximum value, and the corresponding local skeletal structure is the strongest. With the further increase in the fines content, the number of small pores increases while the number of large pores decreases, and the dominant pore size rapidly decreases. When the fine particle content is greater than 60–70%, the dominant pores almost no longer change. At this time, the soil becomes cohesive soil, the coarse particles are wrapped by fine particles, and the fines content has almost no influence on the dominant pore size.
- (4)
- The effect of fines content is divided into three stages, and the influence mechanism of fines content on pore structure is obtained for each stage. By characterizing the microscopic pore structure, the water retention characteristics of composite soil considering the influence of fines content can be deduced macroscopically, providing a theoretical basis for material selection and design for plant sand fixation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, D.; Xu, Z. Study on the prevention and control measures of wind and sand on a certain railway in the Middle East. Railw. Stand. Des. 2014, 58, 64–66. [Google Scholar]
- Zhang, K.; Qu, J.; Yu, Y.; Han, Q.; Wang, T.; An, Z.; Hu, F. Progress of research on wind-blown sand prevention and control of railways in China. Adv. Earth Sci. 2019, 34, 573–583. [Google Scholar]
- Zhang, Y.; Zhang, K.; Fang, Q. Research progress and prospect of plant sand fixation in China. J. Green Sci. Technol. 2020, 6, 123–124+127. [Google Scholar]
- Niu, G.; Shao, L.; Sun, D.; Wei, C.; Guo, X.; Xu, H. Evolution law of pore-size distribution in soil-water retention test. Rock. Soil. Mech. 2020, 41, 1195–1202. [Google Scholar]
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Simms, P.H.; Yanful, E.K. Predicting soil-water characteristic curves of compacted plastic soils from measured pore-size distributions. Géotechnique 2002, 52, 269–278. [Google Scholar] [CrossRef]
- Feng, S.; Chai, J.; Xu, Z.; Yuan, Q. Evaluating the mesostructural changes of laboratory created soil-rock mixtures using a seepage test based on NMR technology. J. Test. Eval. 2018, 46, 879–891. [Google Scholar] [CrossRef]
- Jiao, W.; Zhou, D.; Wang, Y. Effects of clay content on pore structure characteristics of marine soft soil. Water 2021, 13, 1160. [Google Scholar] [CrossRef]
- Appel, M.; Stallmach, F.; Thomann, H. Irreducible fluid saturation determined by pulsed field gradient NMR. J. Pet. Sci. Eng. 1998, 19, 45–54. [Google Scholar] [CrossRef]
- Gao, H.; Li, H. Determination of movable fluid percentage and movable fluid porosity in ultra-low permeability sandstone using nuclear magnetic resonance (NMR) technique. J. Pet. Sci. Eng. 2015, 133, 258–267. [Google Scholar] [CrossRef]
- Meng, M.; Ge, H.; Ji, W.; Shen, Y.; Su, S. Monitor the process of shale spontaneous imbibition in co-current and counter-current displacing gas by using low field nuclear magnetic resonance method. J. Nat. Gas Sci. Eng. 2015, 27, 336–345. [Google Scholar] [CrossRef]
- Tian, H.; Wei, C.; Wei, H.; Chen, P.; Cheng, F. A NMR-based analysis of drying processes of compacted clayey sands. Rock Soil. Mech. 2014, 35, 2129–2136. [Google Scholar]
- Brownstein, K.R.; Tarr, C.E. Importance of classical diffusion in NMR studies of water in biological cells. Phys. Rev. A 1979, 19, 2446–2453. [Google Scholar] [CrossRef]
- Benavides, F.; Leiderman, R.; Souza, A.; Carneiro, G.; Bagueira de Vasconcellos Azeredo, R. Pore size distribution from NMR and image based methods: A comparative study. J. Pet. Sci. Eng. 2020, 184, 106321. [Google Scholar] [CrossRef]
- Gao, S.; Chapman, W.G.; House, W. Application of low field NMR T2 measurements to clathrate hydrates. J. Magn. Reson. 2009, 197, 208–212. [Google Scholar] [CrossRef] [PubMed]
- Bird, N.; Preston, A.; Randall, E.; Whalley, W.; Whitmore, A. Measurement of the size distribution of water-filled pores at different matric potentials by stray field nuclear magnetic resonance. Eur. J. Soil Sci. 2005, 56, 135–143. [Google Scholar] [CrossRef]
- Jaeger, F.; Bowe, S.; Van As, H.; Schaumann, G.E. Evaluation of 1H NMR relaxometry for the assessment of pore-size distribution in soil samples. Eur. J. Soil. Sci. 2009, 60, 1052–1064. [Google Scholar] [CrossRef]
- Chen, P.; Liu, J.; Wei, C.; Xue, W. Approach to rapidly determining the water retention curves for fine-grained soils in capillary regime based on the NMR technique. J. Eng. Mech. 2017, 143, 04017032. [Google Scholar] [CrossRef]
- He, P.; Xu, Q.; Liu, J.; Li, P.; Pu, C.; Chen, D. Effect of pore size distribution on percolation characteristics of loess based on nuclear magnetic resonance technique. Sci. Technol. Eng. 2020, 20, 12355–12360. [Google Scholar]
- Wei, X. Hydraulic Path Dependence of Shear Strength and Slope Stability of Compacted Loess. Master’s Thesis, Guilin University of Technology, Guilin, China, 2021. [Google Scholar]
- Hu, R.; Li, X.; Wang, Y.; Gao, W.; Xia, J.; Li, Z.; Gao, W.; Sun, Y. Research on engineering geomechanics and structural effect of soil-rock mixture. J. Eng. Geol. 2020, 28, 255–281. [Google Scholar]
- Gao, Y.; Sun, D.; Zhang, J.; Luo, T. Temperature effect on the water retention curve of lime-treated soil during curing. Chin. J. Geotech. Eng. 2019, 41, 2191–2196. [Google Scholar]
- Tao, G.; Kong, L. Prediction of air-entry value and soil water characteristic curve of soils with different initial void ratios. Chin. J. Geotech. Eng. 2018, 40, 34–38. [Google Scholar]
- Zhang, Q.; Cao, Z.; Gu, C.; Cai, Y. Prediction of soil–water retention curves of road base aggregate with various clay fine contents. Appl. Sci. 2022, 12, 3624. [Google Scholar] [CrossRef]
- Kaothon, P.; Lee, S.-H.; Choi, Y.-T.; Yune, C.-Y. The effect of fines content on compressional behavior when using sand–kaolinite mixtures as embankment materials. Appl. Sci. 2022, 12, 6050. [Google Scholar] [CrossRef]
- Aldaood, A. Impact of fine materials on the saturated and unsaturated behavior of silty sand soil. Ain Shams Eng. J. 2020, 11, 717–725. [Google Scholar] [CrossRef]
- Hyodo, T.; Wu, Y.; Hyodo, M. Influence of fines on the monotonic and cyclic shear behaviour of volcanic soil “Shirasu”. Eng. Geol. 2022, 301, 106591. [Google Scholar] [CrossRef]
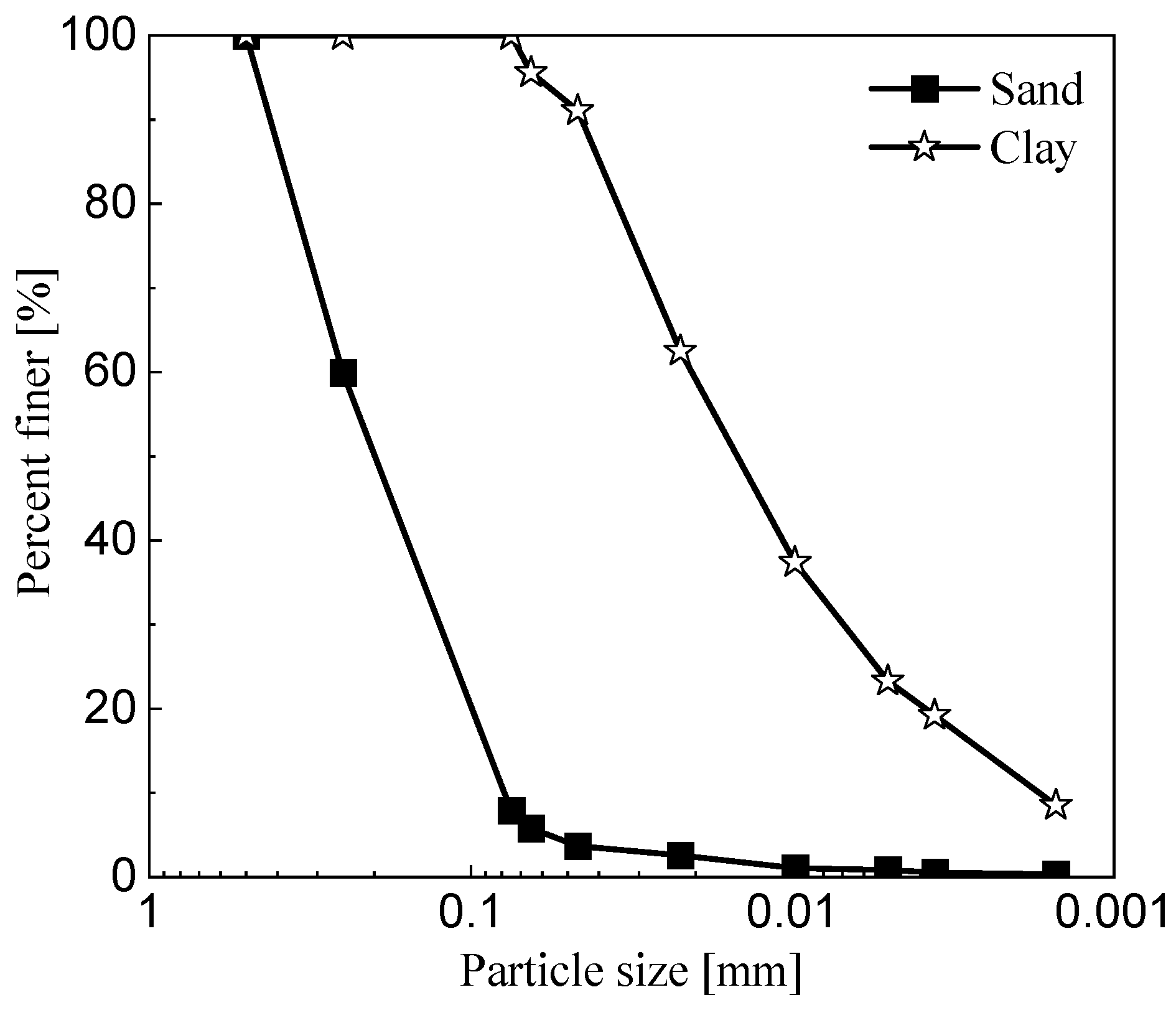


| Sand | Clay | ||
|---|---|---|---|
| Specific gravity | 2.67 | Specific gravity | 2.74 |
| Maximum void ratio | 1.02 | Liquid limit/% | 36.7 |
| Minimum void ratio | 0.62 | Plastic limit/% | 20.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Chen, P.; Yi, P.; Ma, T. Effect of Fines Content on Pore Distribution of Sand/Clay Composite Soil. Sustainability 2023, 15, 9216. https://doi.org/10.3390/su15129216
Wang M, Chen P, Yi P, Ma T. Effect of Fines Content on Pore Distribution of Sand/Clay Composite Soil. Sustainability. 2023; 15(12):9216. https://doi.org/10.3390/su15129216
Chicago/Turabian StyleWang, Mingqiang, Pan Chen, Panpan Yi, and Tiantian Ma. 2023. "Effect of Fines Content on Pore Distribution of Sand/Clay Composite Soil" Sustainability 15, no. 12: 9216. https://doi.org/10.3390/su15129216





