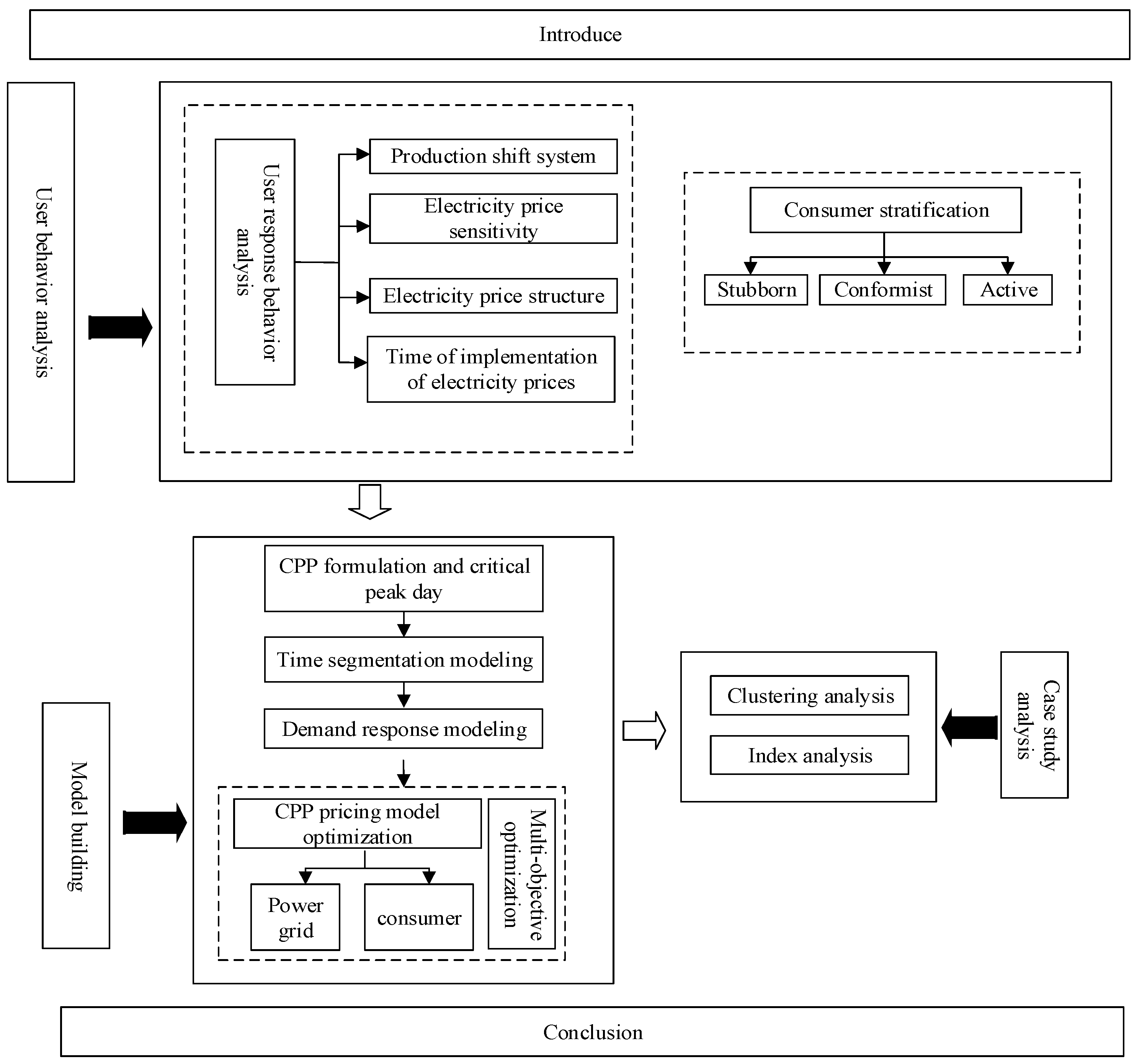
Research on Critical Peak Price Decision Optimization Considering Industrial Consumer’s Risk Appetite under the Carbon Neutrality Goal
Abstract
:1. Introduction
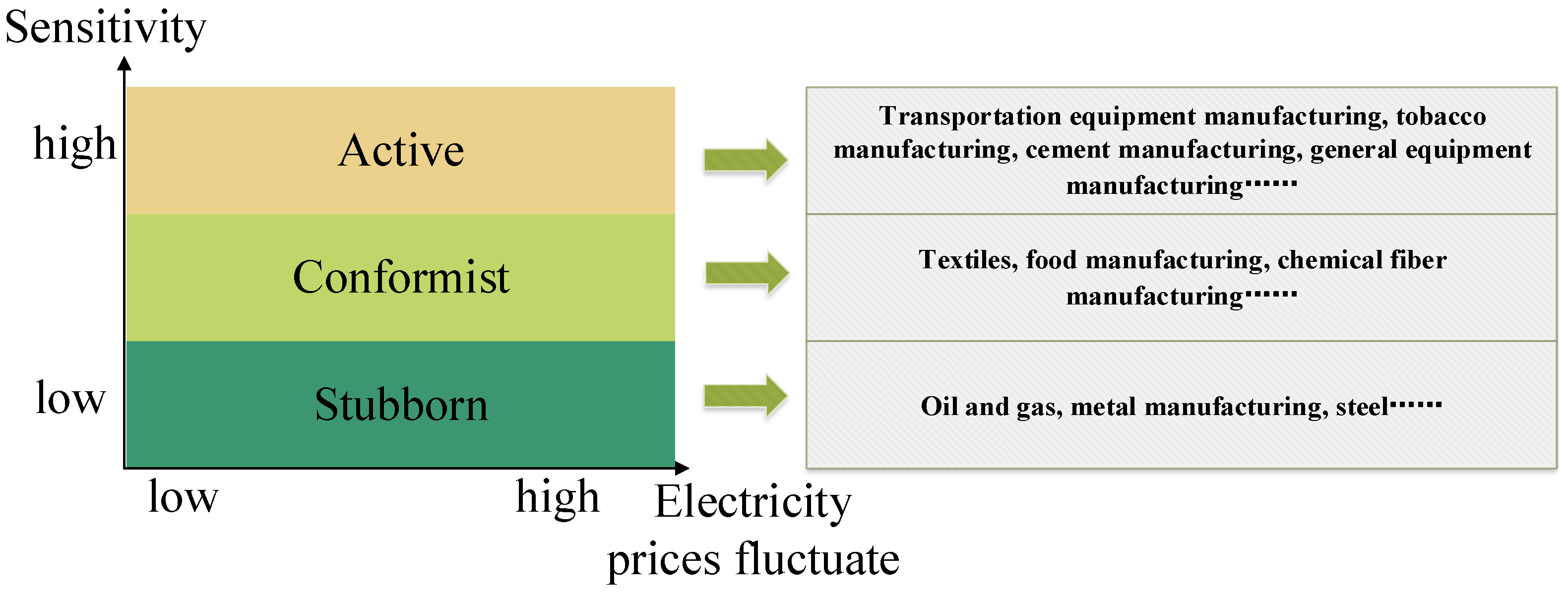
- Based on the current mechanism of China’s electricity market, refine the influencing factors such as production shift system, electricity price sensitivity factors, and electricity price structure, According to the enthusiasm of industrial enterprises in responding to electricity prices, the qualitative subdivision of industrial users into three layers: stubborn, active and conformist. The clustering method was used to quantitatively verify the stratified results.
- By constructing a multi-objective CPP optimization model, the load fluctuations and carbon emission reduction indicators before and after the implementation of CPP in the steel industry and the cement industry were compared, and the response characteristics of layered industrial users to CPP and the effect of carbon emission reduction were analyzed.
2. User Response Behavior Analysis
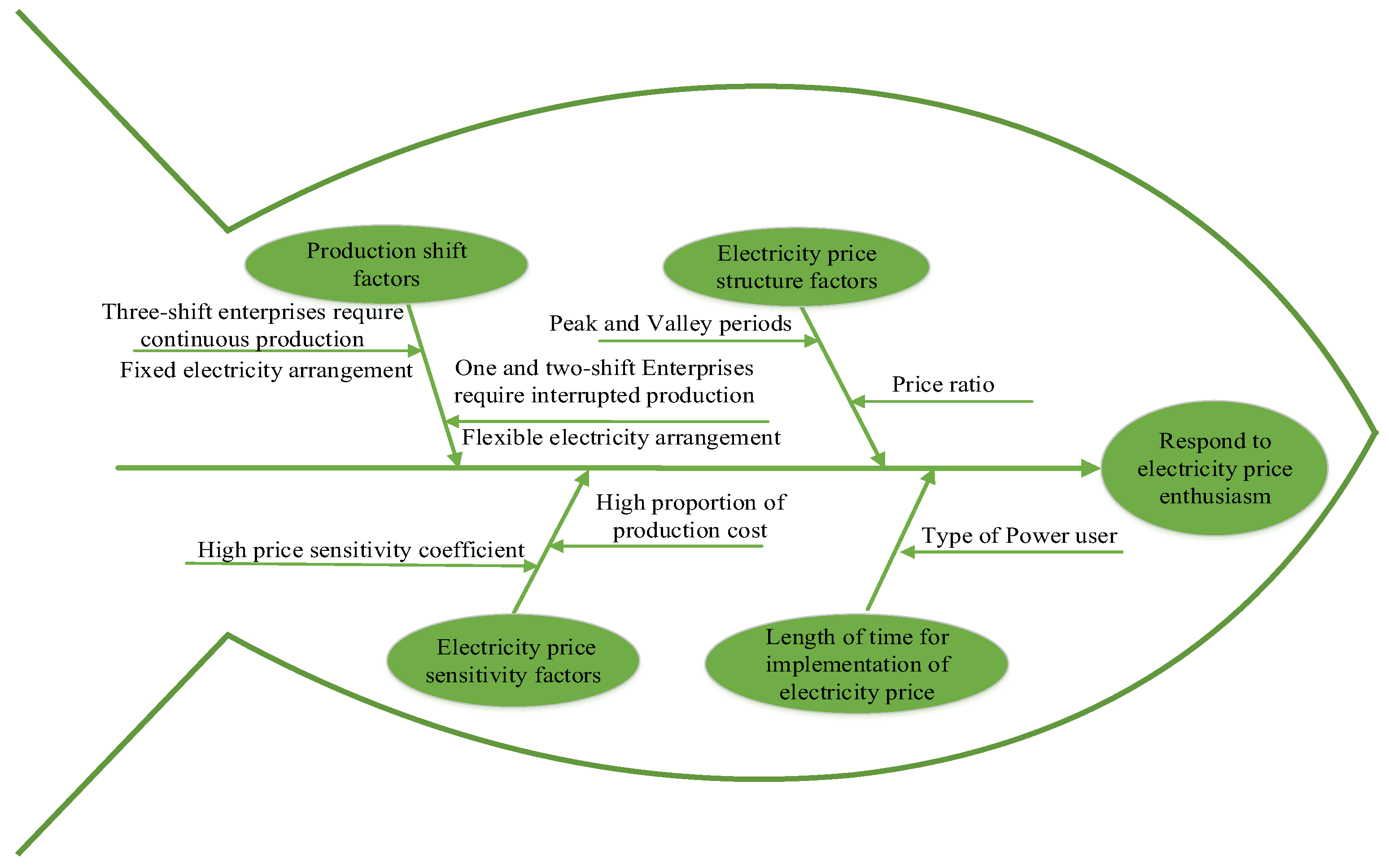
2.1. User Response Behavior Analysis
- (1)
- Production shift factors: The production shift system reflects user demand for electricity continuity. Three-shift enterprises are generally heavy industries that require continuous production, such as the steel, petroleum processing and textile industries, for which the transfer of electricity arrangements is limited by the production process; the one and two-shift systems are generally light industries that can produce intermittently, such as the food industry, and the transfer of electricity arrangements in this case is limited by the difficulty in adjusting the production arrangements of employees.
- (2)
- Electricity price sensitivity factors: The greater the electricity price sensitivity coefficient, the higher the proportion of high user electricity costs to production costs, the more sensitivity to electricity price fluctuations and the higher the enthusiasm of users to respond to differential electricity prices, such as in cement production enterprises. The proportion of electricity expenditure in industries such as food and textile processing and electronic equipment manufacturing is low, and hence, the degree of influence of electricity price fluctuations is low.
- (3)
- Electricity price structure factors: The degree of user response to CPP is significantly affected by the design of the peak and valley periods and electricity price ratios. For example, based on time-of-use electricity price (TOU), the implementation of CPP can further widen the electricity price difference so that users can transfer more electricity during critical peak hours.
- (4)
- Length of time for implementation of electricity price: In general, the difference in the speed at which different types of electricity users expand and adjust the amount of electricity increases with the implementation time of the electricity price.
2.2. Stratification of Consumer Populations
3. Model Building
3.1. CPP Formulation and Critical Peak Day
3.2. Time Segmentation Modeling
3.3. Demand Response Modeling
- 1.
- Demand price elasticity theory
- 2.
- Modeling consumer risk appetite
3.4. CPP Pricing Model Optimization
- 1.
- Objective function:
- 2.
- Constraints:
4. Case Study Analysis
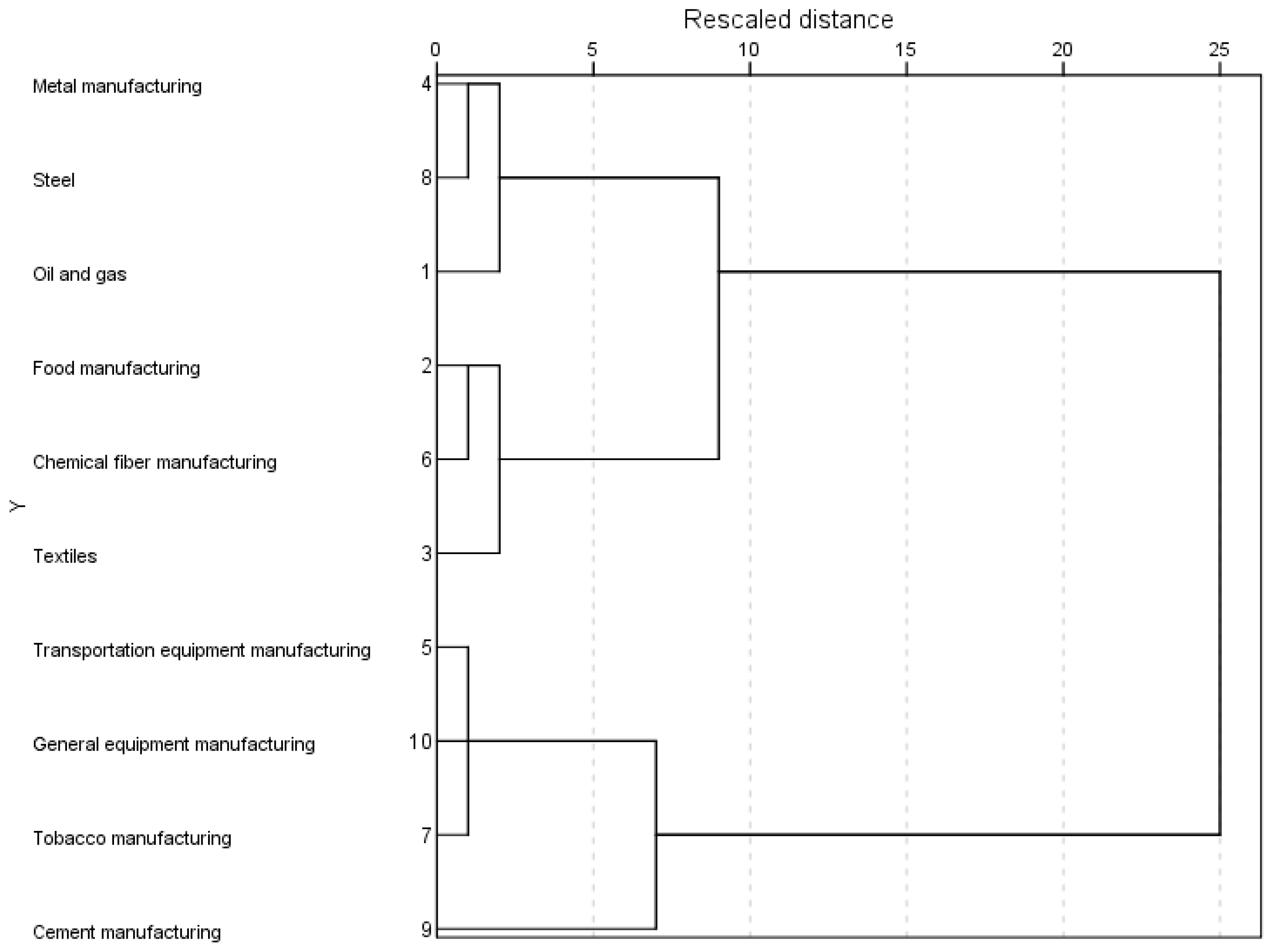
4.1. Clustering Analysis
4.2. Index Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Li, H.; Chang, M. Green energy investment, renewable energy consumption, and carbon neutrality in China. Front. Environ. Sci. 2022, 10, 1276. [Google Scholar] [CrossRef]
- Cheng, Z.; Hu, X. The effects of urbanization and urban sprawl on CO2 emissions in China. Environ. Dev. Sustain. 2023, 25, 1792–1808. [Google Scholar] [CrossRef]
- Duan, Y.W.; Yang, C.H. A Spatial Structural decomposition of Chinese and Japanese Energy consumption and CO2 Emission. Syst. Eng.—Theory Pract. 2017, 37, 2083–2090. [Google Scholar]
- Zhou, Y.M.; Feng, Y.S. China’s Electricity Price Reform and CO2 Emissions: Empirical Research and Policy Implications from the Municipal Level. Urban Environ. Stud. 2017, 11, 85–99. [Google Scholar]
- Ding, T. Joint electricity and carbon market for Northeast Asia energy interconnection. Glob. Energy Interconnect. 2020, 3, 99–110. [Google Scholar] [CrossRef]
- Hou, H.T.; Bo, X.; Cheng, Y.Y. Analysis of Carbon Emissions and Emission Reduction from Coal-Fired Power Plants Based on Dual Carbon Targets. Sustainability 2023, 15, 7369. [Google Scholar] [CrossRef]
- Karmellos, M.; Kopidou, D.; Diakoulaki, D. A decomposition analysis of the driving factors of CO2 (Carbon dioxide) emissions from the power sector in the European Union countries. Energy 2016, 94, 680–692. [Google Scholar] [CrossRef]
- Mai, L.N.; Ran, Q.Y.; Wu, H.T. A LMDI decomposition analysis of carbon dioxide emissions from the electric power sector in Northwest China. Nat. Resour. Model. 2020, 33, e12284. [Google Scholar] [CrossRef]
- Mousavi, B.; Neil, S.A.L. Driving forces of Iran’s CO2 emissions from energy consumption: An LMDI decomposition approach. Appl. Energy 2017, 206, 804–814. [Google Scholar] [CrossRef]
- Xie, P.J.; Gao, S.S.; Sun, F.H. An analysis of the decoupling relationship between CO2 emission in power industry and GDP in China based on LMDI method. J. Clean. Prod. 2019, 211, 598–606. [Google Scholar] [CrossRef]
- Liao, C.Y.; Wang, S.G.; Zhang, Y.Y. Driving forces and clustering analysis of provincial-level CO2 emissions from the power sector in China from 2005 to 2015. J. Clean. Prod. 2019, 240, 118026. [Google Scholar] [CrossRef]
- Gajowniczek, K.; Nafkha, R.; Ząbkowski, T. Seasonal peak demand classification with machine learning techniques. In Proceedings of the International Conference on Applied Mathematics & Computer Science (ICAMCS), Paris, France, 13–15 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 101–1014. [Google Scholar]
- Wang, J.; Li, H. The impact of electricity price on power-generation structure: Evidence from China. Front. Environ. Sci. 2021, 9, 733809. [Google Scholar] [CrossRef]
- Zhou, M.; Yin, Y.C.; Huang, Y.H.; Tian, S.; Li, G.Y. Dynamic Critical Peak Pricing and its Gaming Approach Considering Customers’ Response. Power Syst. Technol. 2016, 40, 3348–3354. [Google Scholar]
- Lu, Q.; Zhang, Y. A multi-objective optimization model considering users’ satisfaction and multi-type demand response in dynamic electricity price. Energy 2022, 240, 122504. [Google Scholar] [CrossRef]
- Pan, X.Y.; Pan, X.F.; Wu, X.H. Research on the heterogeneous impact of carbon emission reduction policy on R&D investment intensity: From the perspective of enterprise’s ownership structure. J. Clean. Prod. 2021, 328, 129532. [Google Scholar]
- Zheng, X.; Li, C.; Fang, X. Price sensitivity and consumers’ support for renewable energy in China. Energy 2021, 222, 119862. [Google Scholar] [CrossRef]
- Roberts, M.J.; Zhang, S.; Yuan, E. Using temperature sensitivity to estimate shiftable electricity demand. Iscience 2022, 25, 104940. [Google Scholar] [CrossRef]
- Deng, N.; Wang, B.; He, L. Does electricity price reduction bring a sustainable development of business: Evidence from fine-grained industrial electricity consumption data in China. J. Environ. Manag. 2023, 335, 117522. [Google Scholar] [CrossRef]
- Naz, M.; Iqbal, Z.; Javaid, N. Efficient power scheduling in smart homes using hybrid grey wolf differential evolution optimization technique with real time and critical peak pricing schemes. Energies 2018, 11, 384. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Gryshova, I.; Kyzym, M. Electricity Price Instability over Time: Time Series Analysis and Forecasting. Sustainability 2022, 14, 9081. [Google Scholar] [CrossRef]
- Yu, H.; Xin, X. Demand elasticity, ramsey index and cross-subsidy scale estimation for electricity price in China. Sustain. Prod. Consum. 2020, 24, 39–47. [Google Scholar] [CrossRef]
- Gou, J.; Lin, C.; Li, J. Charging strategy for electric vehicles considering consumer psychology and trip chain. Front. Energy Res. 2021, 9, 410. [Google Scholar] [CrossRef]
- Ruan, W.J.; Wang, B.B.; Li, Y.; Yang, S.C. Customer Response Behavior in Time-of-Use Price. Power Syst. Technol. 2012, 36, 86–93. [Google Scholar]


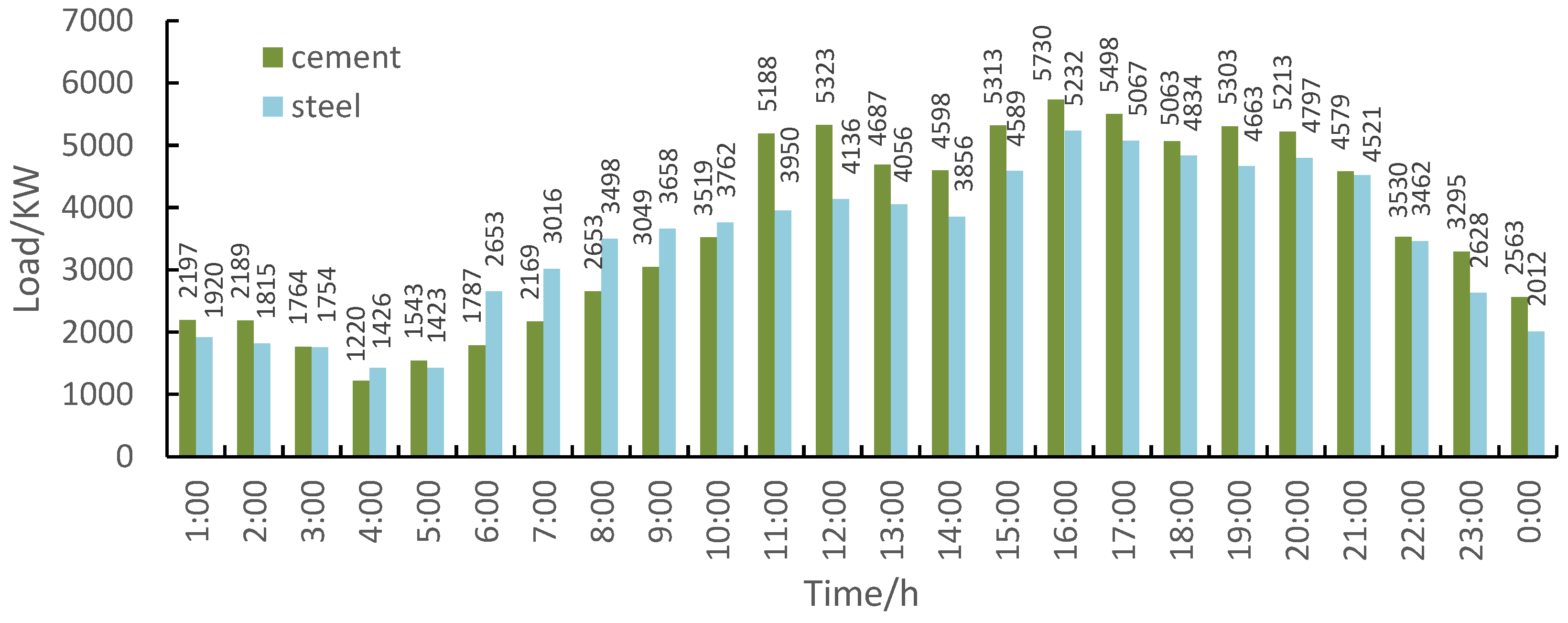


| Time | TOU | CPP | |
|---|---|---|---|
| Off-Critical Peak Days | Critical Peak Days | ||
| Valley periods | |||
| Flat periods | |||
| Peak periods | |||
| Critical-Peak periods | — | — | |
| CPP Model | Features |
|---|---|
| CPP-F | Determine in advance the maximum allowable number of days for critical-peak days, critical-peak periods and critical-peak rate systems |
| CPP-V | Based on real-time load usage, determine the maximum allowable number of days, critical-peak days and critical-peak periods |
| VPP | CPP is linked to the wholesale electricity market |
| CPR | Electricity users follow the original TOU but reduce the load at the critical peak period and avail the corresponding electricity price subsidies |
| Index | Calculation | Source or Purpose of the Data |
|---|---|---|
| Load ratio/% | =Daily load average/Daily load maximum | It is used to evaluate the load change before and after electricity price optimization, and prove the effectiveness and scientificity of electricity price optimization. |
| Power reduction rate during critical-peak hours | =(Maximum load after price optimization—Maximum original daily load)/Maximum original daily load | It is a visual representation of critical-peak load improvement and is also used as a reference indicator for clustering. |
| Save standard coal/Ton | =Total load × 0.43 × 0.001 | According to relevant information, each kWh of electricity saved can reduce 0.43 KG of standard coal, which can be used to measure the energy consumption after electricity price optimization. |
| Carbon emissions/Ton CO2 | =Total load × 0.997 × 0.001 | According to relevant information, each kWh of electricity saved can reduce 0.997 KGCO2, which can be used to measure the contribution of electricity price optimization to carbon emission reduction. |
| Carbon emissions per unit of electricity/KW·ton−1 | =Total carbon emissions/Total load × 1000 | It can be used to measure the contribution of electricity price optimization to carbon emission reduction. |
| Carbon emissions per unit of electricity cost/USD·KG−1 | =Total carbon emissions × 1000/(Total load × Average daily electricity cost) | It can be used to measure the contribution of electricity price optimization to carbon emission reduction. |
| Periods | /% | |||
|---|---|---|---|---|
| Critical-Peak | 0.015 | 0.109 | 0.913 | 1 |
| Critical-Flat | 0.023 | 0.135 | 1.12 | 3 |
| Critical-Valley | 0.023 | 0.21 | 1.204 | 2 |
| Peak-Flat | 0.03 | 0.058 | 0.283 | 6 |
| Peak-Valley | 0.05 | 0.11 | 0.513 | 8 |
| Flat-Valley | 0.06 | 0.058 | 0.4 | 4 |
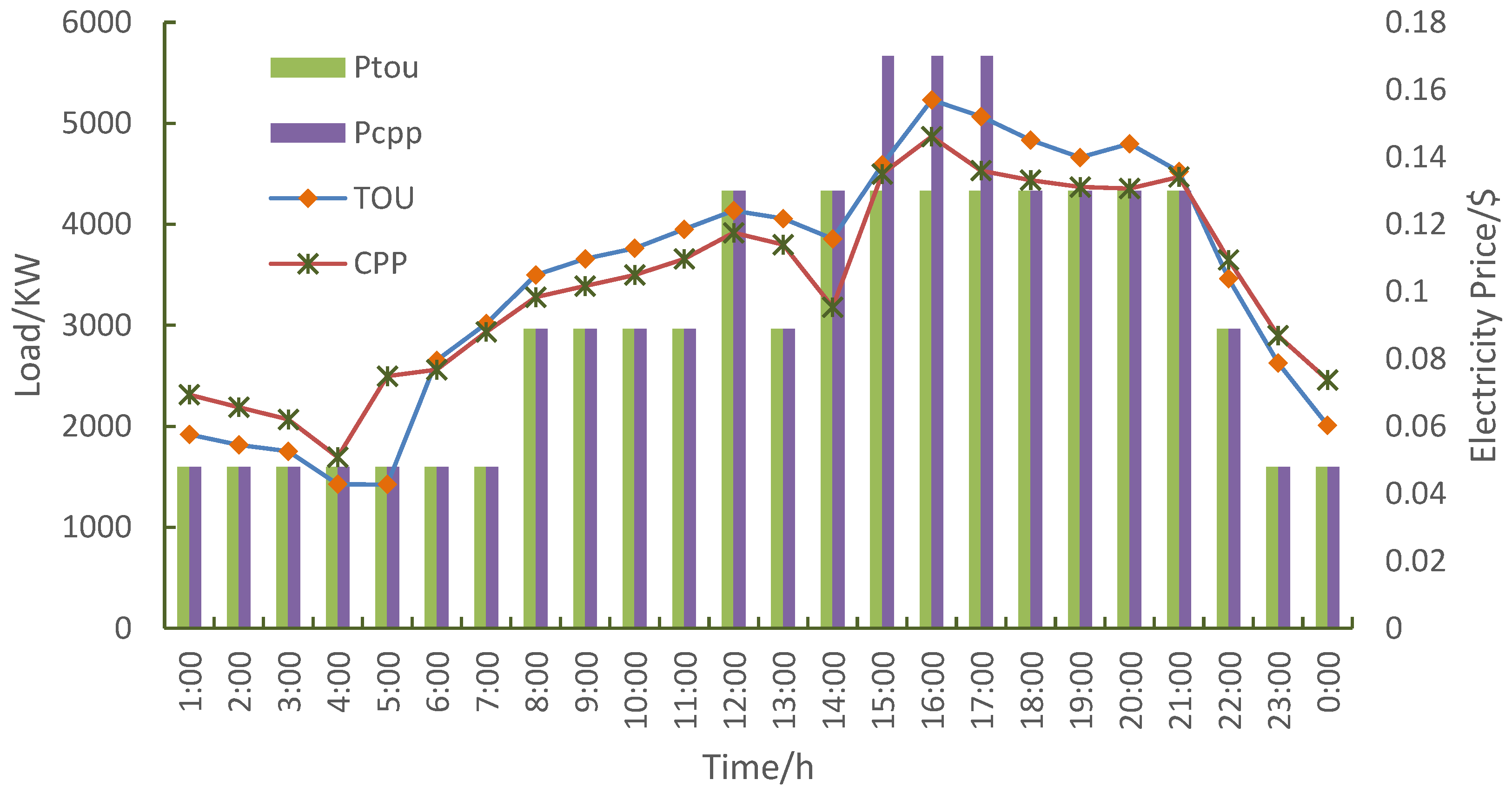
| Peaks and Valleys | TOU | CPP | ||
|---|---|---|---|---|
| Time | Price/USD/(KW·h) | Time | Price/USD/(KW·h) | |
| Peak | 11:00–12:00 14:00–21:00 | $0.13 | 11:00–12:00 14:00–15:00 17:00–21:00 | $0.13 |
| Flat | 7:00–11:00 12:00–14:00 21:00–23:00 | $0.089 | 7:00–11:00 12:00–14:00 21:00–23:00 | $0.089 |
| Valley | 23:00–7:00 | $0.048 | 23:00–7:00 | $0.048 |
| Critical-peak | 15:00–17:00 | $0.17 | ||
| Number | Industry Name | Amount of Power Reduction during Critical-Peak Hours (KW) | Power Reduction Rate during Critical-Peak Hours |
|---|---|---|---|
| 1 | Oil and gas | 95.7 | 1.4% |
| 2 | Food manufacturing | 154.3 | 8.2% |
| 3 | Textiles | 680.4 | 10.5% |
| 4 | Metal manufacturing | 183.7 | 3.9% |
| 5 | Transportation equipment manufacturing | 83.7 | 13.3% |
| 6 | Chemical fiber manufacturing | 108.6 | 6.94% |
| 7 | Tobacco manufacturing | 745.6 | 12.34% |
| 8 | Steel | 363 | 4.12% |
| 9 | Cement manufacturing | 861 | 17.68% |
| 10 | General equipment manufacturing | 780.7 | 13.8% |
| Number | Industry Name | Clustering | Distance |
|---|---|---|---|
| 1 | Oil and gas | 1 | 1.74 |
| 2 | Food manufacturing | 3 | 0.347 |
| 3 | Textiles | 3 | 1.953 |
| 4 | Metal manufacturing | 1 | 0.76 |
| 5 | Transportation equipment manufacturing | 2 | 0.98 |
| 6 | Chemical fiber manufacturing | 3 | 1.607 |
| 7 | Tobacco manufacturing | 2 | 1.94 |
| 8 | Steel | 1 | 0.98 |
| 9 | Cement manufacturing | 2 | 3.4 |
| 10 | General equipment manufacturing | 2 | 0.48 |
| Clustering | 1 | 2 | 3 |
|---|---|---|---|
| Final cluster centers | 3.14 | 14.28 | 8.55 |
| Category | Industry Name |
|---|---|
| Stubborn users | Oil and gas, metal manufacturing, steel |
| Active users | Transportation equipment manufacturing, tobacco manufacturing, cement manufacturing, general equipment manufacturing |
| Conformist users | Textiles, food manufacturing, chemical fiber manufacturing |
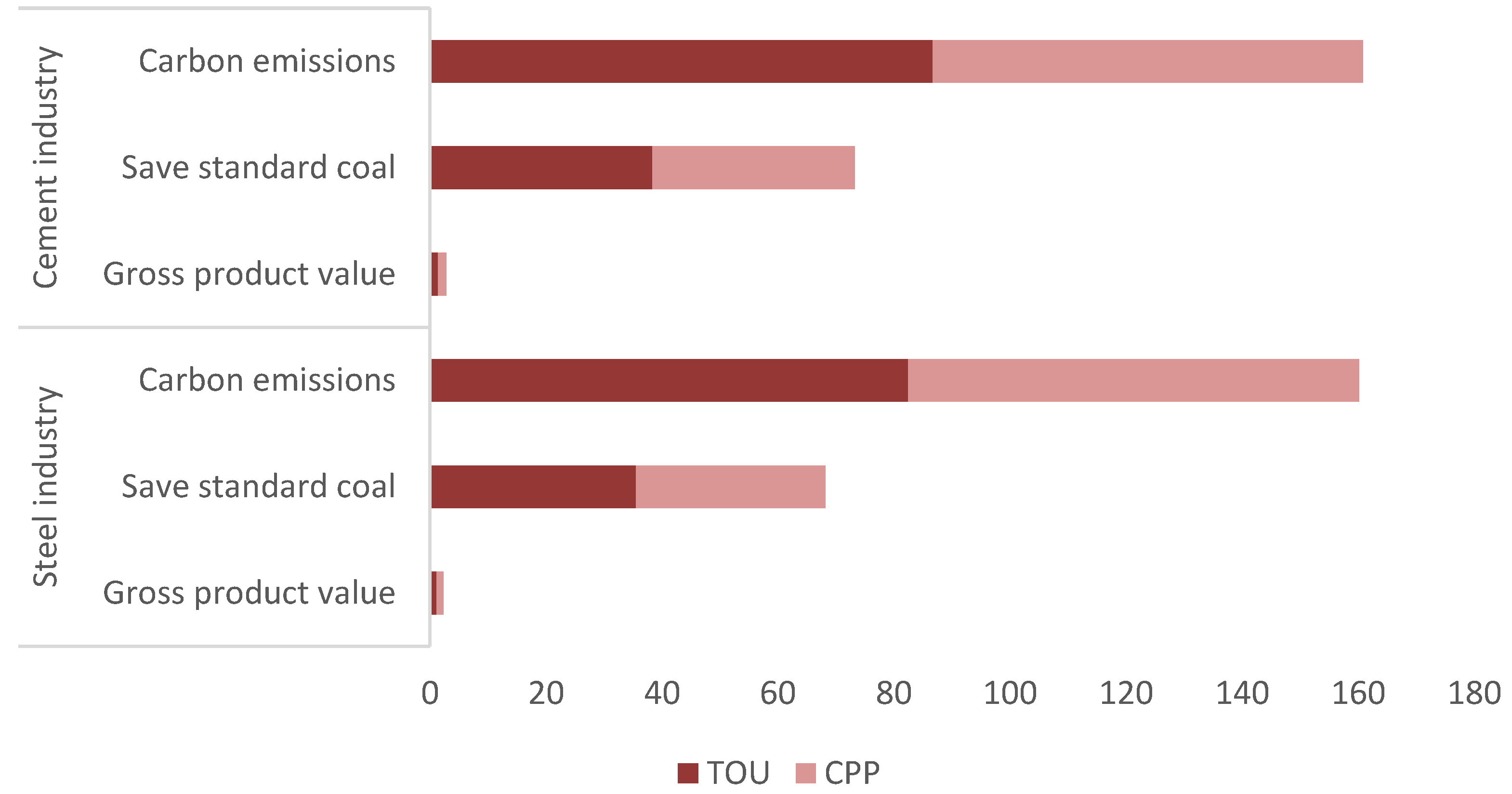
| Index | Steel Industry | Growth Rate/% | Cement Industry | Growth Rate/% | ||
|---|---|---|---|---|---|---|
| TOU | CPP | TOU | CPP | |||
| Total load/KW | 82,728 | 81,507 | −1.48 | 87,973 | 82,998 | 5.66 |
| Load ratio/% | 65.9% | 69.8% | 3.9 | 63.97% | 71.26% | 7.29 |
| Peak load/KW | 5232 | 4869 | −6.94 | 5730 | 4869 | −15.03 |
| Valley load/KW | 1423 | 1695 | 19.11 | 1220 | 2056 | 68.5 |
| Peak-to-valley difference/KW | 3809 | 3174 | −16.67 | 4510 | 2813 | −37.63 |
| Load volatility | 39.68% | 22.83% | — | 44.93% | 20.25% | — |
| Peak-to-valley difference rate of change | 72.8% | 65.19% | — | 78.7% | 51.61% | — |
| Power reduction rate during critical-peak hours | — | — | −6.94 | — | — | −15.03 |
| Average daily electricity cost /(USD/KW·h) | 0.068 | 0.067 | −1.47 | 0.068 | 0.062 | −8.82 |
| Gross product value/$M | 1.17 | 1.15 | −1.7 | 1.42 | 1.41 | −0.7 |
| Save standard coal/Ton | 35.573 | 32.603 | −8.35 | 38.356 | 34.859 | −9.12 |
| Carbon emissions/Ton CO2 | 82.480 | 77.676 | −5.82 | 86.653 | 74.200 | −14.37 |
| Carbon emissions per unit of electricity/KW·ton−1 | 0.997 | 0.953 | −4.41 | 0.985 | 0.894 | −9.24 |
| Carbon emissions per unit of electricity cost/USD·KG−1 | 14.66 | 14.22 | −0.3 | 14.49 | 14.42 | −0.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Dong, Z.; Zheng, D. Research on Critical Peak Price Decision Optimization Considering Industrial Consumer’s Risk Appetite under the Carbon Neutrality Goal. Sustainability 2023, 15, 9347. https://doi.org/10.3390/su15129347
Yu X, Dong Z, Zheng D. Research on Critical Peak Price Decision Optimization Considering Industrial Consumer’s Risk Appetite under the Carbon Neutrality Goal. Sustainability. 2023; 15(12):9347. https://doi.org/10.3390/su15129347
Chicago/Turabian StyleYu, Xiaobao, Zhenyu Dong, and Dandan Zheng. 2023. "Research on Critical Peak Price Decision Optimization Considering Industrial Consumer’s Risk Appetite under the Carbon Neutrality Goal" Sustainability 15, no. 12: 9347. https://doi.org/10.3390/su15129347





