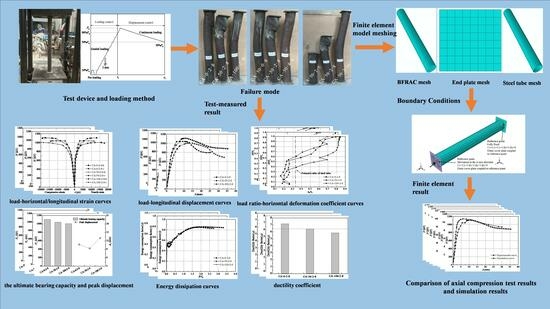
The Axial Compression Behavior of Basalt Fiber-Reinforced Recycled Aggregate Concrete-Filled Circular Steel-Tubular Column
Abstract
:1. Introduction
2. Test Overview
2.1. Specimen Design and Production
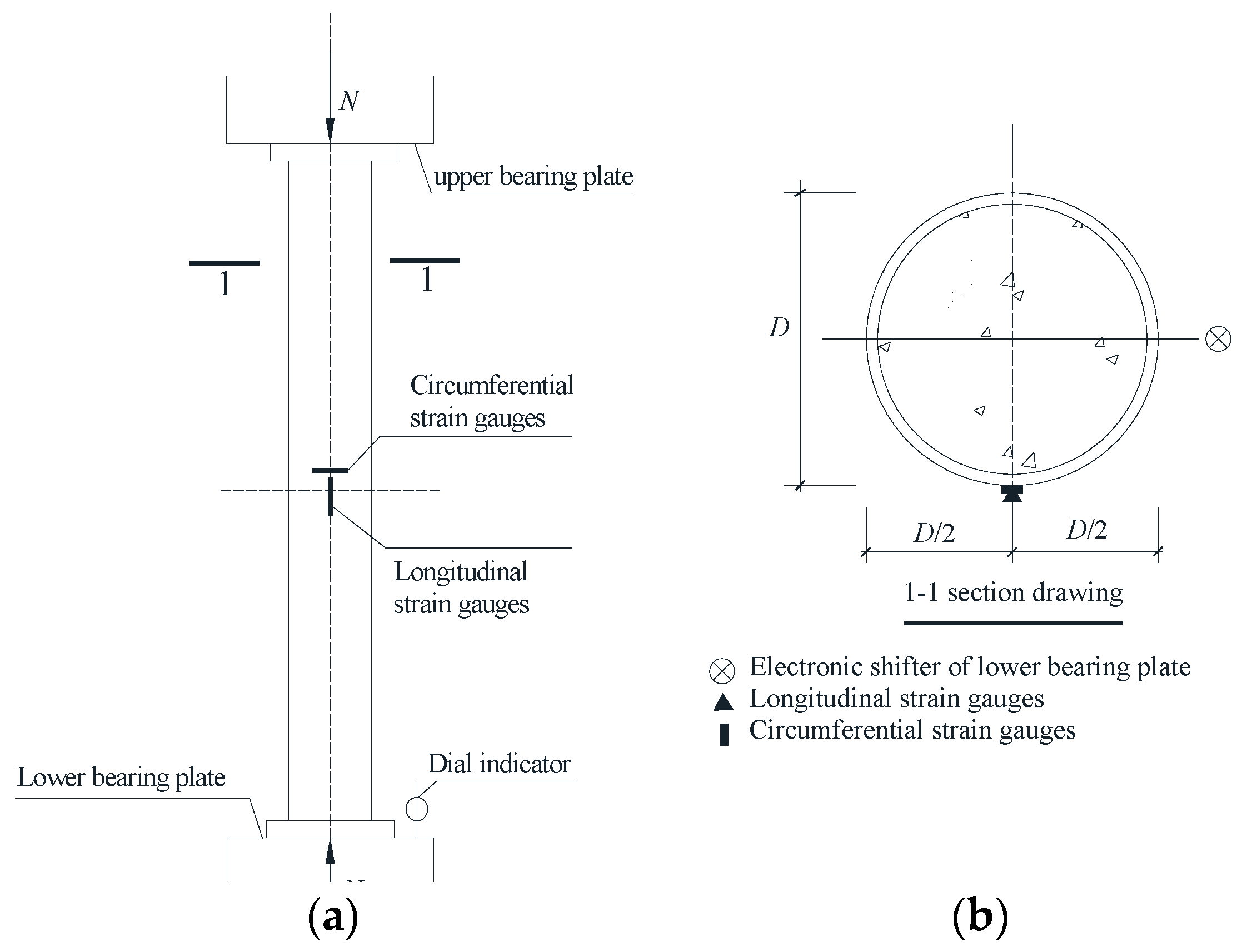
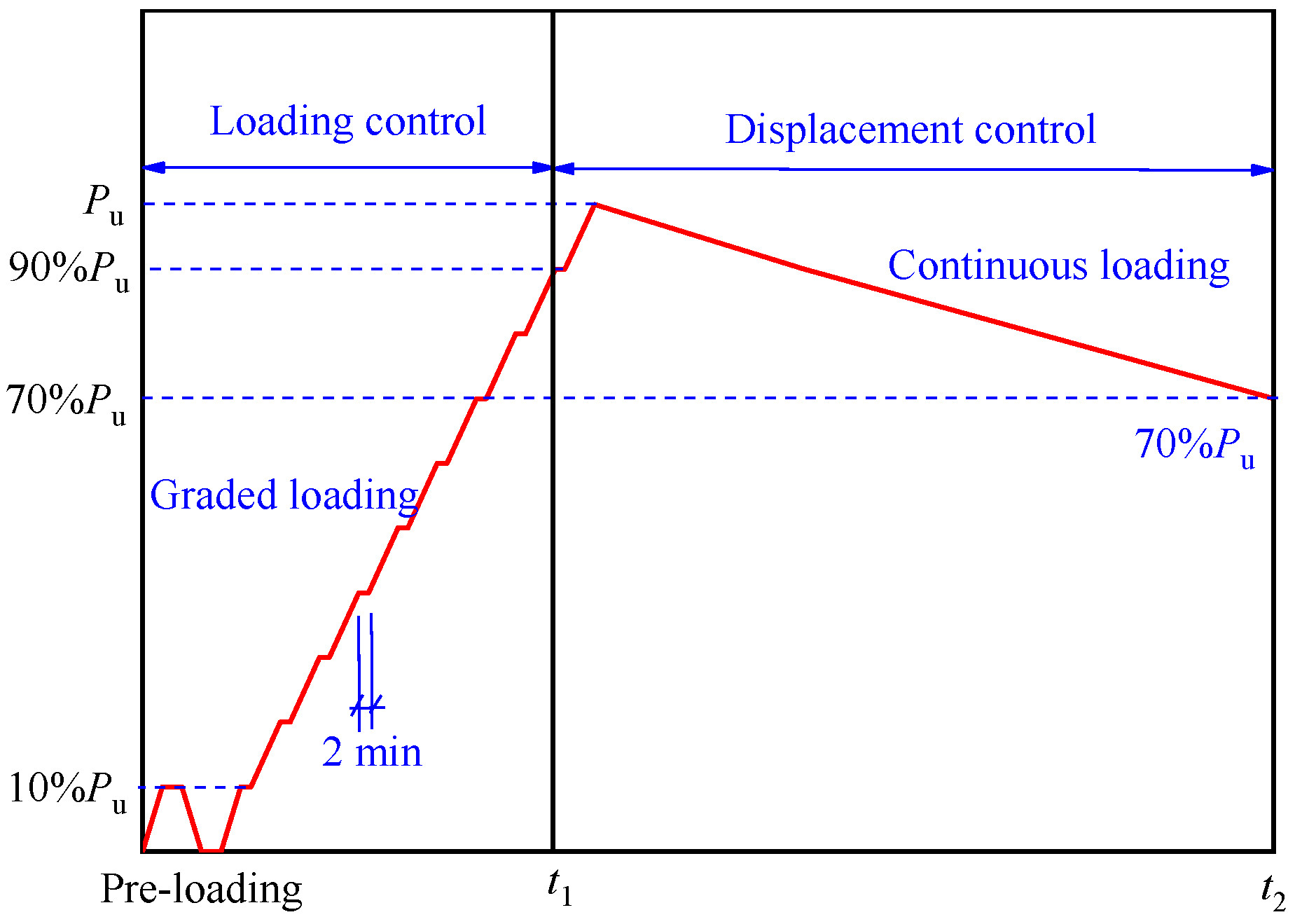
2.2. Test Device and Loading Method
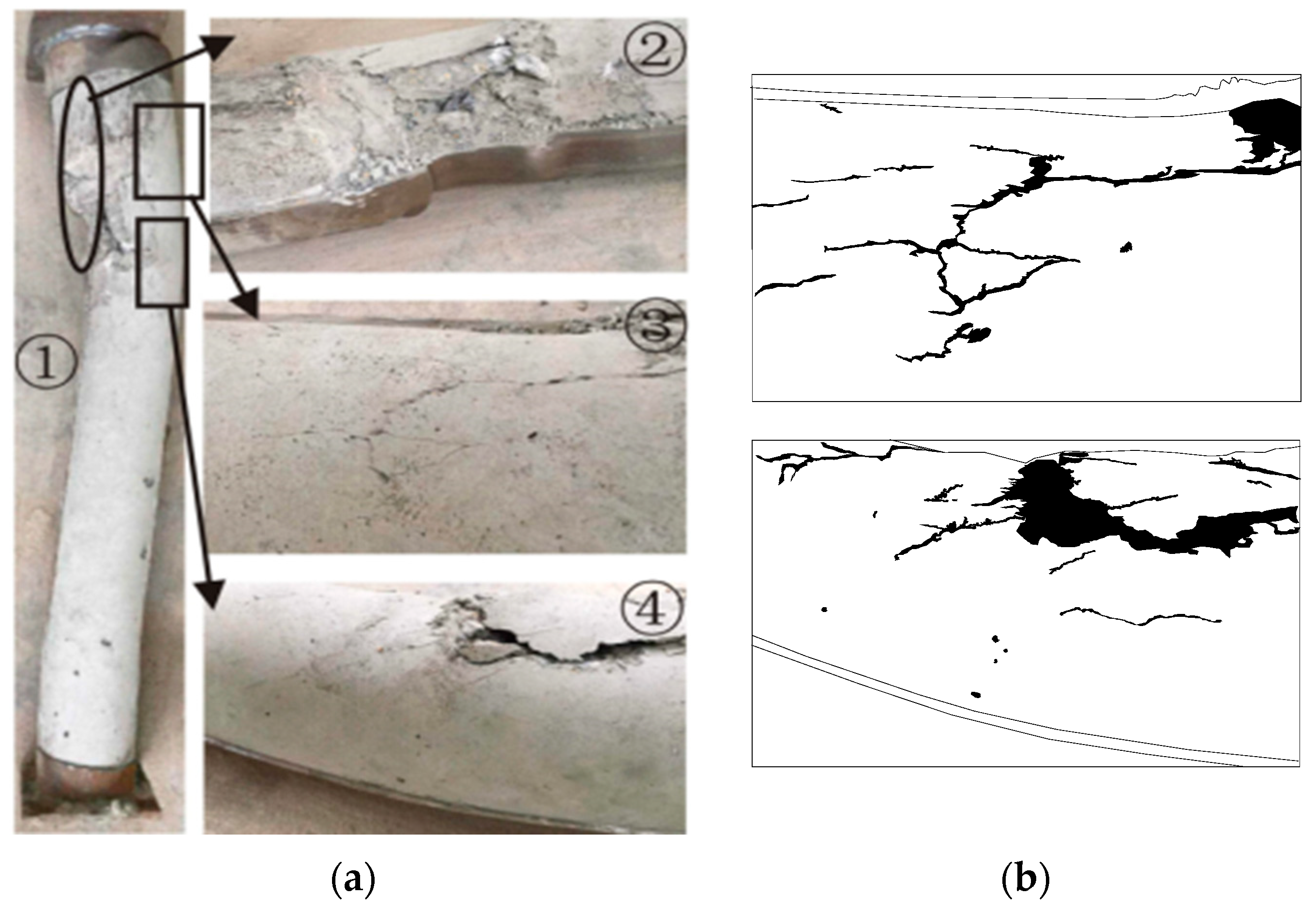
3. Loading Process and Failure Mode of C-BFRACFST Medium-Length Column under Axial Compression
4. Results and Analysis of the Axial Compression Test on C-BFRACFST Medium-Length Column
4.1. Load–Horizontal/Longitudinal Strain Curve
4.2. Load–Longitudinal Displacement Curve
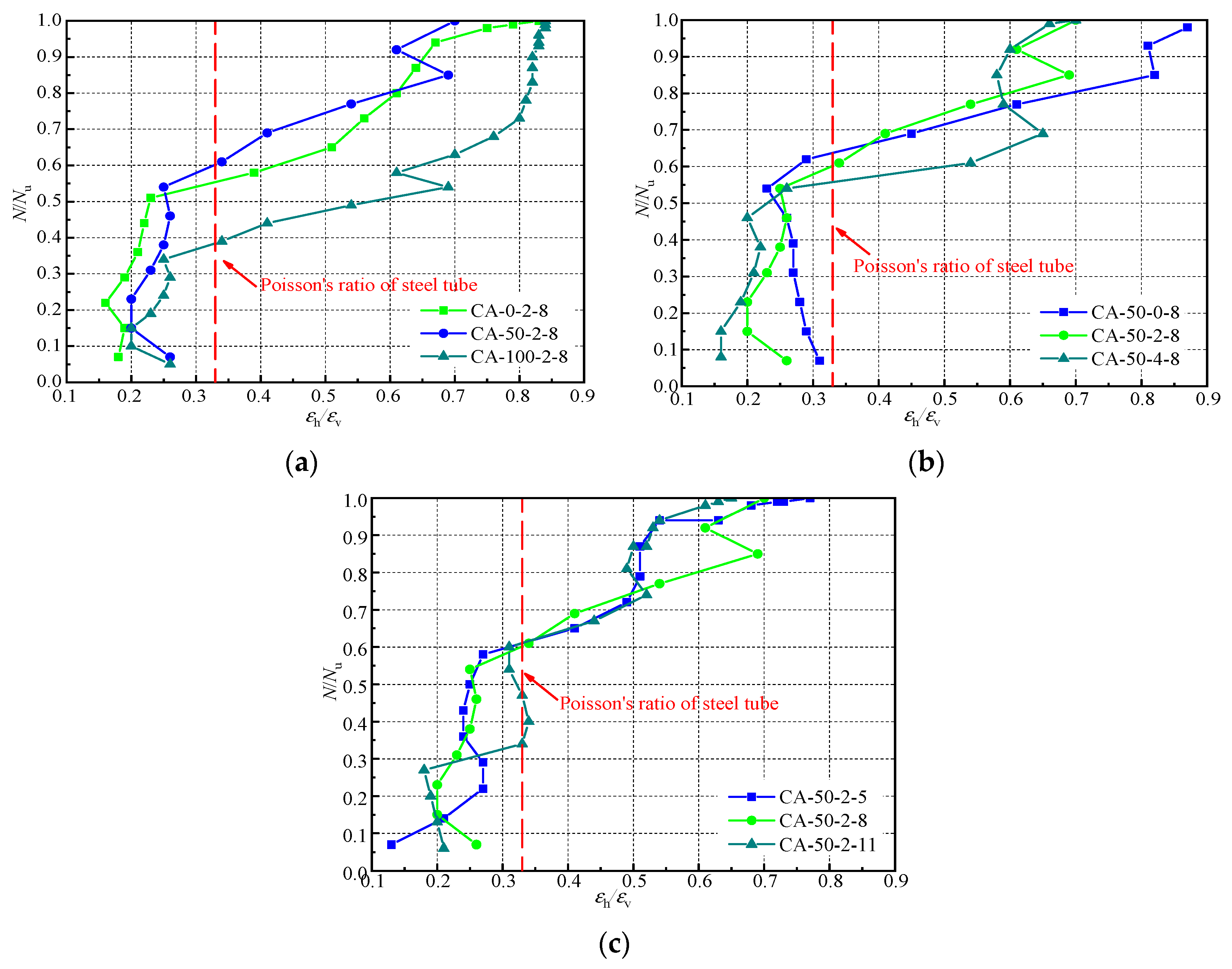
4.3. Load Ratio–horizontal Deformation Coefficient Curve
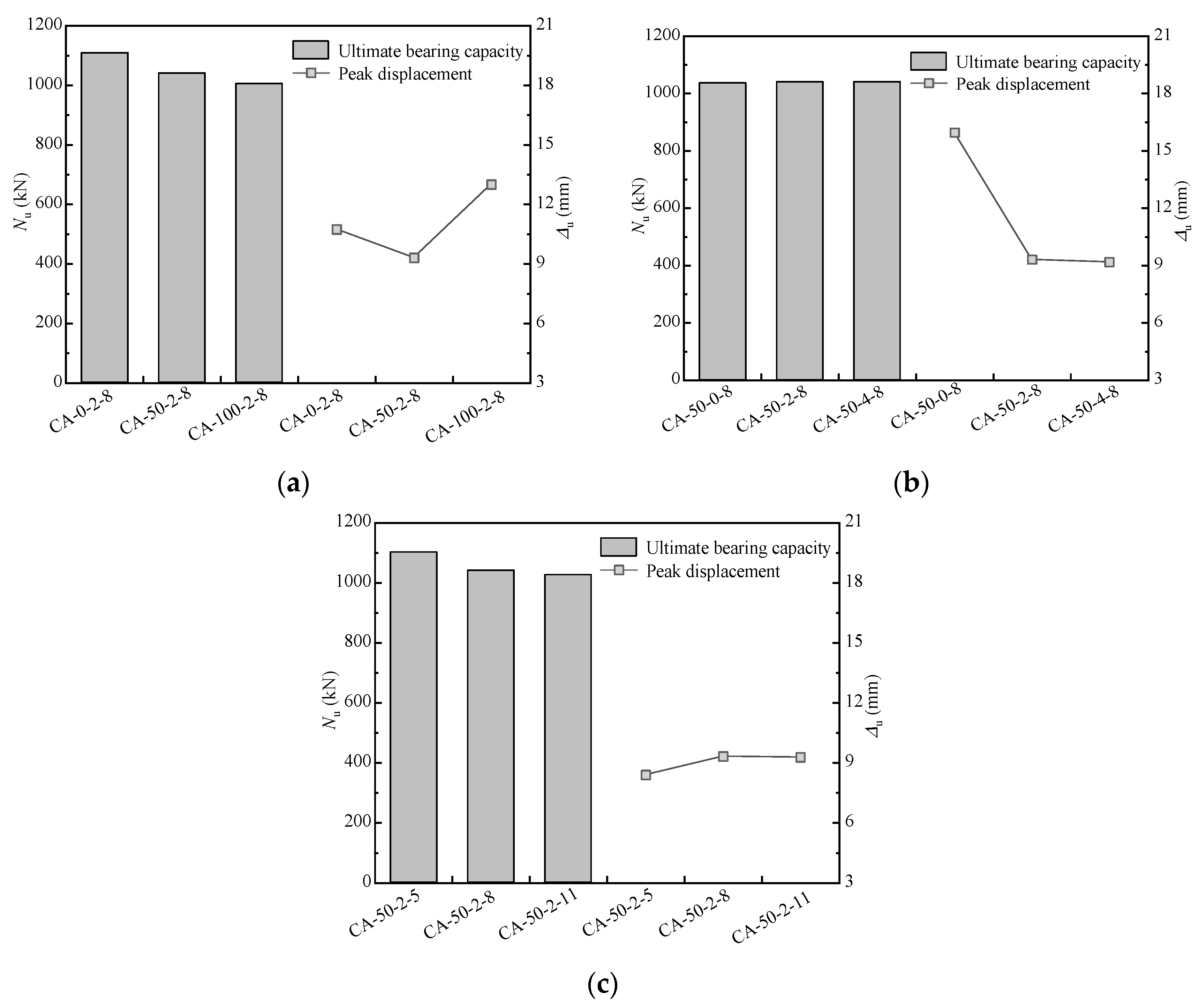
4.4. Analysis of the Effect of the Ultimate Bearing Capacity and Peak Displacement
4.5. Energy Dissipation
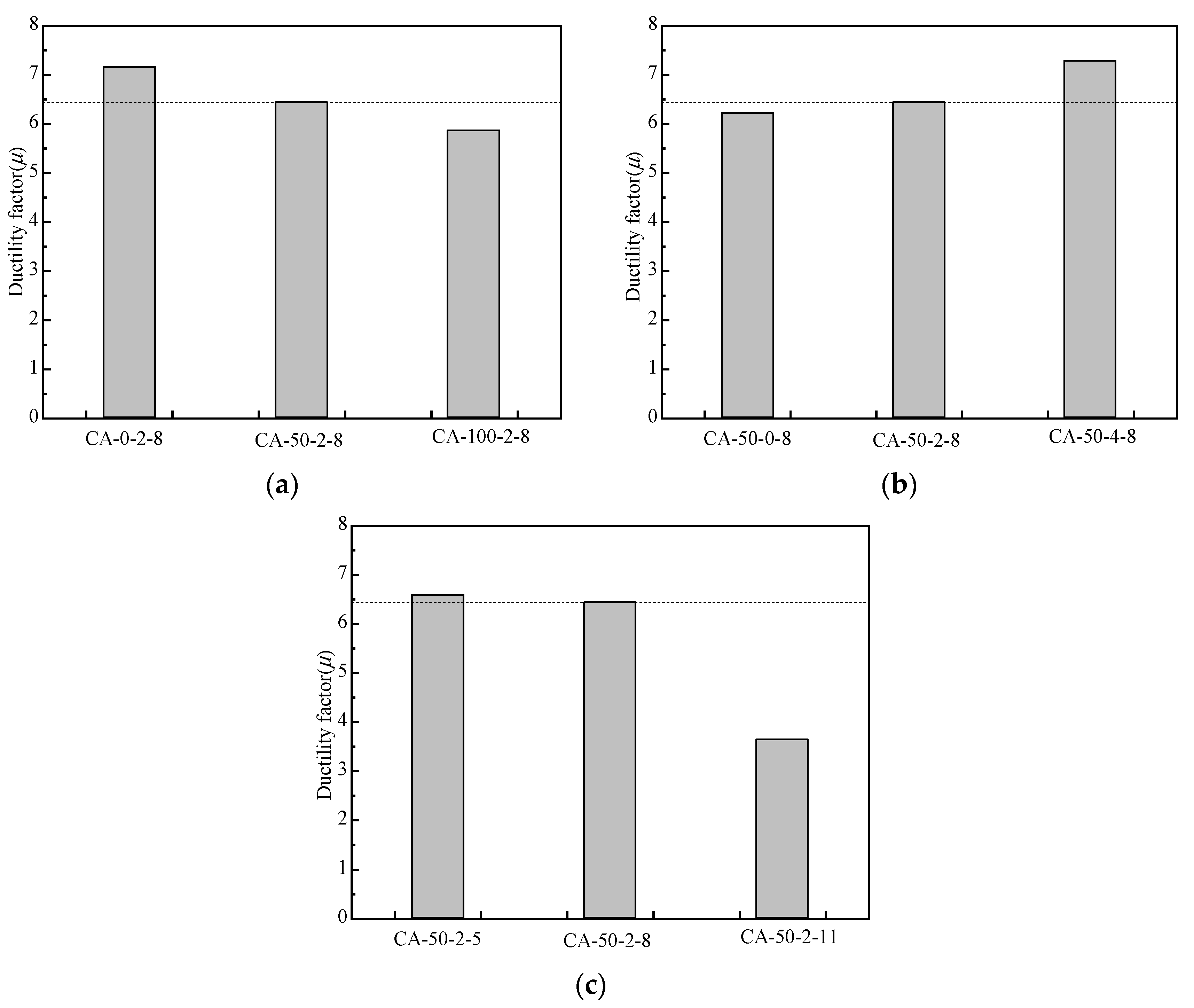
4.6. Ductility Coefficient
5. Finite Element Analysis of C-BFRACFST Medium-Length Column
5.1. Constitutive Relation of the Materials
5.1.1. Determination of the Peak Strain Correction Coefficient η
5.1.2. Determination of Effective Horizontal Compression Stress of Steel Tubes
5.1.3. Determination of Circumferential Tensile Stress fsh of Circular Steel Tubes
5.1.4. Determination of the Axial Compression Strength fcc of the Constrained Concrete
5.1.5. The Values of Peak Strain εc0, Axial Compression Strength fc0 and Elastic Modulus of Unconfined Concrete
5.2. Establishment of the Finite Element Model
5.2.1. Element Type Selection and Meshing
5.2.2. Establishment of Contact
5.2.3. Boundary Conditions
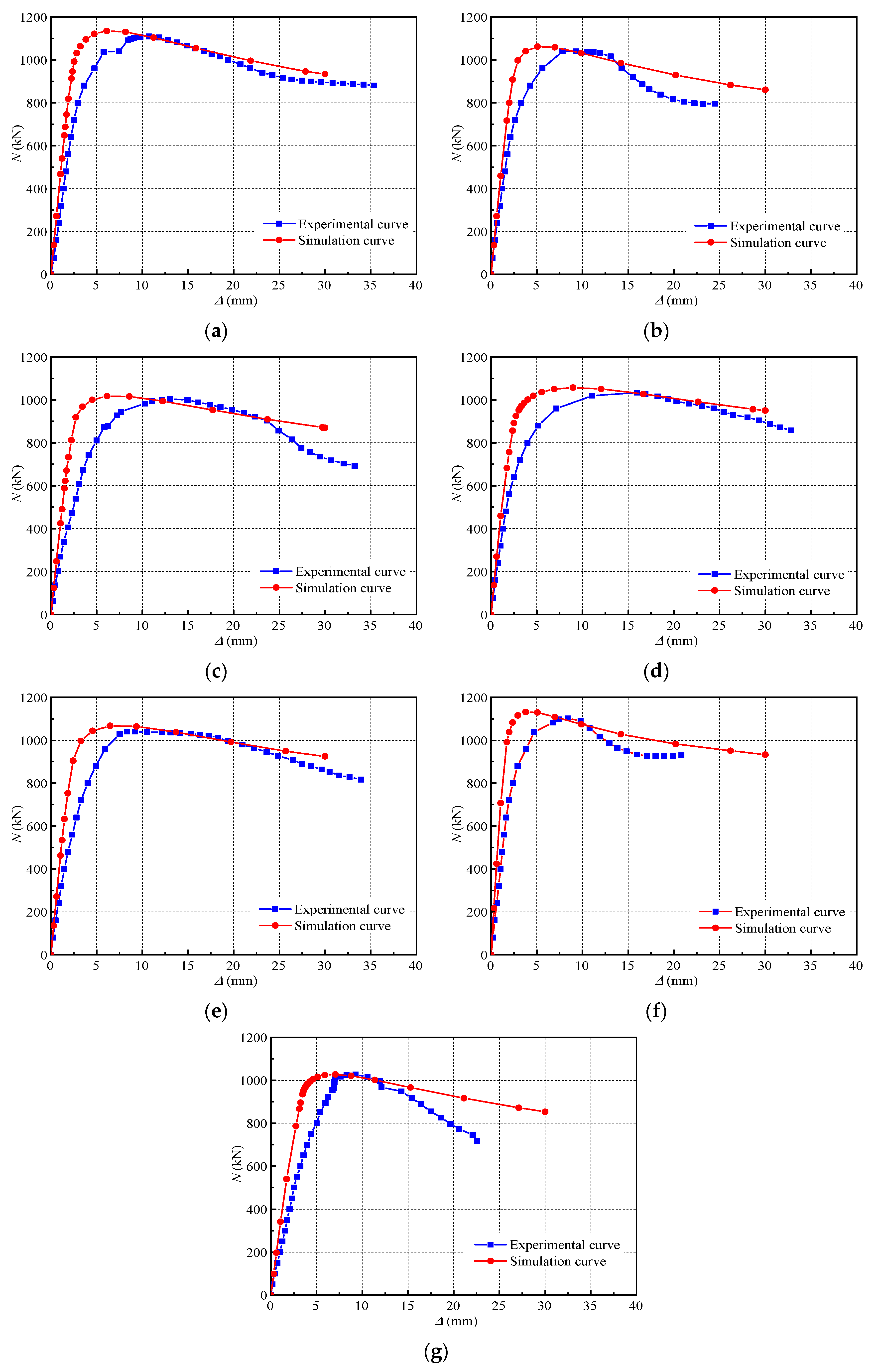
5.3. Finite Element Simulation Analysis
Comparative Analysis of ABAQUS Results
6. Conclusions
- (1)
- Under the axial compression load, instability or shear failure occurs in the columns of C-BFRACFST;
- (2)
- The ultimate bearing capacity of a specimen progressively decreases along with the recycled aggregate replacement ratio or L/D increasing and displays almost no change as the BF content increases. When the recycled aggregate replacement ratio increases from 50% to 100% or the L/D increases from 8 to 11, the ultimate bearing capacity of specimens decreases by 3.45% and 1.37%, respectively;
- (3)
- Under an axial compression load, changing the recycled aggregate replacement ratio has a minimal impact on the energy-dissipation capacity of specimens, while increasing BF content can increase the specimen energy-dissipation capacity at the later stage of bearing. Meanwhile, the energy-dissipation capacity of specimens is poor when the L/D is relatively large;
- (4)
- The displacement ductility coefficient of the C-BFRACFST column decreases with the recycled aggregate replacement ratio or L/D increasing, and gradually increases with increasing BF content. When the BF content increases from 2 kg/m3 to 4 kg/m3, the displacement ductility coefficient of specimens increases by 13.34%. However, as the recycled aggregate replacement ratio increases from 50% to 100% or the L/D increases from 8 to 11, the displacement ductility coefficient of specimens decreases by 8.91% and 43.52%, respectively;
- (5)
- In this study, the constitutive relation of core BFRAC under a constraint of circular steel tubing is derived. On this basis, a finite element model is created, and this model reflects the axial compression behavior of the C-BFRACFST column well.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, C.; Li, Y.; Zhang, J.; Li, W.; Chong, L.; Xie, Z. Performance enhancement of recycled concrete aggregate—A review. J. Clean. Prod. 2016, 112, 466–472. [Google Scholar] [CrossRef]
- Jin, R.; Li, B.; Zhou, T.; Wanatowski, D.; Piroozfar, P. An empirical study of perceptions towards construction and demolition waste recycling and reuse in China. Resour. Conserv. Recycl. 2017, 126, 86–98. [Google Scholar] [CrossRef]
- Wu, G.; Wang, L.; Yang, R.; Hou, W.; Zhang, S.; Guo, X.; Zhao, W. Pollution characteristics and risk assessment of heavy metals in the soil of a construction waste landfill site. Ecol. Inform. 2022, 70, 101700. [Google Scholar] [CrossRef]
- Kurda, R.; de Brito, J.; Silvestre, J.D. Combined effect of recycled concrete aggregates and high contents of fly ash on concrete performance. Constr. Build. Mater. 2017, 157, 554–572. [Google Scholar] [CrossRef]
- Safiullah, O.; Elhem, G.; George, W. Relationships between recycled concrete aggregates characteristics and recycled aggregates concretes performance. Constr. Build. Mater. 2016, 108, 163–174. [Google Scholar]
- Liu, B.; Feng, C.; Deng, H. Shear behavior of three types of recycled aggregate concrete. Constr. Build. Mater. 2019, 217, 557–572. [Google Scholar] [CrossRef]
- Zhang, H.; Xiao, J.; Tang, Y.; Duan, Z.; Poon, C.S. Long-term shrinkage and mechanical properties of fully recycled aggregate concrete: Testing and modelling. Cem. Concr. Compos. 2022, 130, 104527. [Google Scholar] [CrossRef]
- Van Cao, V. Experimental behaviour of recycled aggregate concrete-filled steel tubes under axial loading. Int. J. Civ. Eng. 2019, 17, 1341–1351. [Google Scholar] [CrossRef]
- Fan, C.C.; Huang, R.; Hwang, H.; Chao, S.J. Performance of concrete incorporating fine recycled aggregates from crushed concrete wastes. Constr. Build. Mater. 2016, 112, 708–715. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, S.; Wang, Y.; Geng, Y. Axial compressive behavior of recycled concrete filled steel tubular stub columns with the inclusion of crushed brick. Structures 2020, 26, 271–283. [Google Scholar] [CrossRef]
- Niu, H.C.; Cao, W.L. Full-scale testing of high-strength RACFST columns subjected to axial compression. Mag. Concr. Res. 2015, 67, 257–270. [Google Scholar] [CrossRef]
- Guan, Z.W.; Al-Husainy, A.S.; Al Teneiji, M.; Wang, Q.Y. Concentric and eccentric compression behaviour of recycled aggregate concrete filled steel tube columns strengthened with CFRP. Appl. Compos. Mater. 2022, 29, 983–1005. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, Y.; Li, S.; Xiao, L. Enhanced bond-slip behavior between recycled aggregate concrete and steel tubes under repeated loading. Structures 2021, 33, 1263–1282. [Google Scholar] [CrossRef]
- Lyu, W.Q.; Han, L.H. Investigation on bond strength between recycled aggregate concrete (RAC) and steel tube in RAC-filled steel tubes. J. Constr. Steel Res. 2019, 155, 438–459. [Google Scholar] [CrossRef]
- Nour, A.I.; Güneyisi, E.M. Prediction model on compressive strength of recycled aggregate concrete filled steel tube columns. Compos. Part B 2019, 173, 106938. [Google Scholar] [CrossRef]
- Yang, Y.F.; Hou, C. Behaviour and design calculations of recycled aggregate concrete-filled steel tube (RACFST) members. Mag. Concr. Res. 2015, 67, 611–620. [Google Scholar] [CrossRef]
- Tang, Y.C.; Li, L.J.; Feng, W.X.; Liu, F.; Liao, B. Seismic performance of recycled aggregate concrete-filled steel tube columns. J. Constr. Steel Res. 2017, 133, 112–124. [Google Scholar] [CrossRef]
- Tang, Y.C.; Li, L.J.; Feng, W.X.; Liu, F.; Zhu, M. Study of seismic behavior of recycled aggregate concrete-filled steel tubular columns. J. Constr. Steel Res. 2018, 148, 1–15. [Google Scholar] [CrossRef]
- Xu, J.J.; Chen, Z.P.; Xue, J.Y.; Chen, Y.L.; Zhang, J.T. Simulation of seismic behavior of square recycled aggregate concrete-filled steel tubular columns. Constr. Build. Mater. 2017, 149, 553–566. [Google Scholar] [CrossRef]
- Xu, J.J.; Chen, Z.P.; Zhao, X.Y.; Demartino, C.; Ozbakkaloglu, T.; Xue, J.Y. Seismic performance of circular recycled aggregate concrete-filled steel tubular columns: FEM modelling and sensitivity analysis. Thin-Walled Struct. 2019, 141, 509–525. [Google Scholar] [CrossRef]
- Huang, Y.J.; Xiao, J.Z.; Shen, L.M. Damage assessment for seismic response of recycled concrete filled steel tube columns. Earthq. Eng. Eng. Vib. 2016, 15, 607–616. [Google Scholar] [CrossRef]
- Kim, J. Influence of quality of recycled aggregates on the mechanical properties of recycled aggregate concretes: An overview. Constr. Build. Mater. 2022, 328, 127071. [Google Scholar] [CrossRef]
- Ulucan, M.; Alyamac, K.E. A holistic assessment of the use of emerging recycled concrete aggregates after a destructive earthquake: Mechanical, economic and environmental. Waste Manag. 2022, 146, 53–65. [Google Scholar] [CrossRef] [PubMed]
- Adesina, A. Performance of cementitious composites reinforced with chopped basalt fibres-An overview. Constr. Build. Mater. 2021, 266, 120970. [Google Scholar] [CrossRef]
- Jamshaid, H.; Mishra, R. A green material from rock: Basalt fiber-a review. J. Text. Inst. 2016, 107, 923–937. [Google Scholar] [CrossRef]
- Dong, J.F.; Wang, Q.Y.; Guan, Z.W.; Chai, H.K. High-temperature behaviour of basalt fibre reinforced concrete made with recycled aggregates from earthquake waste. J. Build. Eng. 2022, 48, 103895. [Google Scholar] [CrossRef]
- Li, S.P.; Zhang, Y.B.; Chen, W.J. Bending performance of unbonded prestressed basalt fiber recycled concrete beams. Eng. Struct. 2020, 221, 110937. [Google Scholar] [CrossRef]
- Zheng, Y.X.; Zhuo, J.B.; Zhang, P. A review on durability of nano-SiO2 and basalt fiber modified recycled aggregate concrete. Constr. Build. Mater. 2021, 304, 124659. [Google Scholar] [CrossRef]
- Xie, J.; Kou, S.C.; Ma, H.; Long, W.J.; Wang, Y.; Ye, T.H. Advances on properties of fiber reinforced recycled aggregate concrete: Experiments and models. Constr. Build. Mater. 2021, 277, 122345. [Google Scholar] [CrossRef]
- Katkhuda, H.; Shatarat, N. Improving the performance of recycled concrete aggregate using chopped basalt fibers and acid treatment. Constr. Build. Mater. 2017, 140, 328–335. [Google Scholar] [CrossRef]
- Dong, J.F.; Wang, Q.Y.; Guan, Z.W. Material performance of basalt fibre reinforced concrete made with recycled earthquake waste. Constr. Build. Mater. 2017, 130, 241–251. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, S.; Yang, J.; Chen, X.; Zhou, G. Experimental and finite element analyses of eccentric compression of basalt-fiber reinforced recycled aggregate concrete-filled circular steel tubular stub column. Steel Compos. Struct. 2022, 42, 617–631. [Google Scholar]
- Zhang, X.; Gao, X.; Wang, X.; Meng, E.; Wang, F. Axial compression performance of basalt-fiber-reinforced recycled-concrete-filled square steel tubular stub column. Adv. Concr. Constr. 2020, 10, 559–571. [Google Scholar]
- GB/T50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. China Architecture and Building Press: Beijing, China, 2019. (In Chinese)
- GB/T228.1-2021; Metallic Materials-Tensile Testing-Part 1: Method of Test at Room Temperature. Standards Press of China: Beijing, China, 2021. (In Chinese)
- CECS 28:2012; Technical Specification for Concrete-Filled Steel Tubular Structures. China Planning Press: Beijing, China, 2012. (In Chinese)
- Ke, X.J.; Chen, Z.P.; Xue, J.Y.; Su, Y.S. Experimental study on axial compression bearing capacity of recycled concrete-filled square steel tube short column. Eng. Mech. 2013, 30, 35–41. [Google Scholar]
- Yang, Y.L.; Yang, H.; Zhang, S.M. Compressive behavior of T-shaped concrete filled steel tubular columns. Int. J. Steel Struct. 2010, 10, 419–430. [Google Scholar] [CrossRef]
- JGJ/T 101-2015; Specification for Seismic Test of Buildings. China Architecture & Building Press: Beijing, China, 2015. (In Chinese)
- Cai, J.; Sun, G. Constitutive equation of core concrete under square steel tube restraint. J. South China Univ. Technol. (Nat. Sci. Ed.) 2008, 36, 105–109. (In Chinese) [Google Scholar]
- Han, L.H. Concrete Filled Steel Tubular Structures-Theory and Practice, 3rd ed.; Science Press: Beijing, China, 2016; pp. 109–110. (In Chinese) [Google Scholar]
- Ge, H.B.; Usami, T. Strength analysis of concrete-filled thin-walled steel box columns. J. Constr. Steel Res. 1994, 30, 259–281. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2010. (In Chinese)
- Paknahad, A.; Petre, D.G.; Leeuwenburgh, S.C.; Sluys, L.J. Interfacial characterization of poly (vinyl alcohol) fibers embedded in a calcium phosphate cement matrix: An experimental and numerical investigation. Acta Biomater. 2019, 96, 582–593. [Google Scholar] [CrossRef]
- Paknahad, A.; Goudarzi, M.; Kucko, N.W.; Leeuwenburgh, S.C.; Sluys, L.J. Calcium phosphate cement reinforced with poly (vinyl alcohol) fibers: An experimental and numerical failure analysis. Acta Biomater. 2021, 119, 458–471. [Google Scholar] [CrossRef]
- Zhao, M.Z.; Wang, Y.Y.; Lehman, D.E.; Geng, Y.; Roeder, C.W. Response and modeling of steel tubes filled with recycled fine and coarse aggregate concretes under long-term loading. J. Struct. Eng. 2021, 147, 04021166. [Google Scholar] [CrossRef]
- Meyer, Y.A.; Menezes, I.; Bonatti, R.S.; Bortolozo, A.D.; Osório, W.R. EIS investigation of the corrosion behavior of steel bars embedded into modified concretes with eggshell contents. Metals 2022, 12, 417. [Google Scholar] [CrossRef]





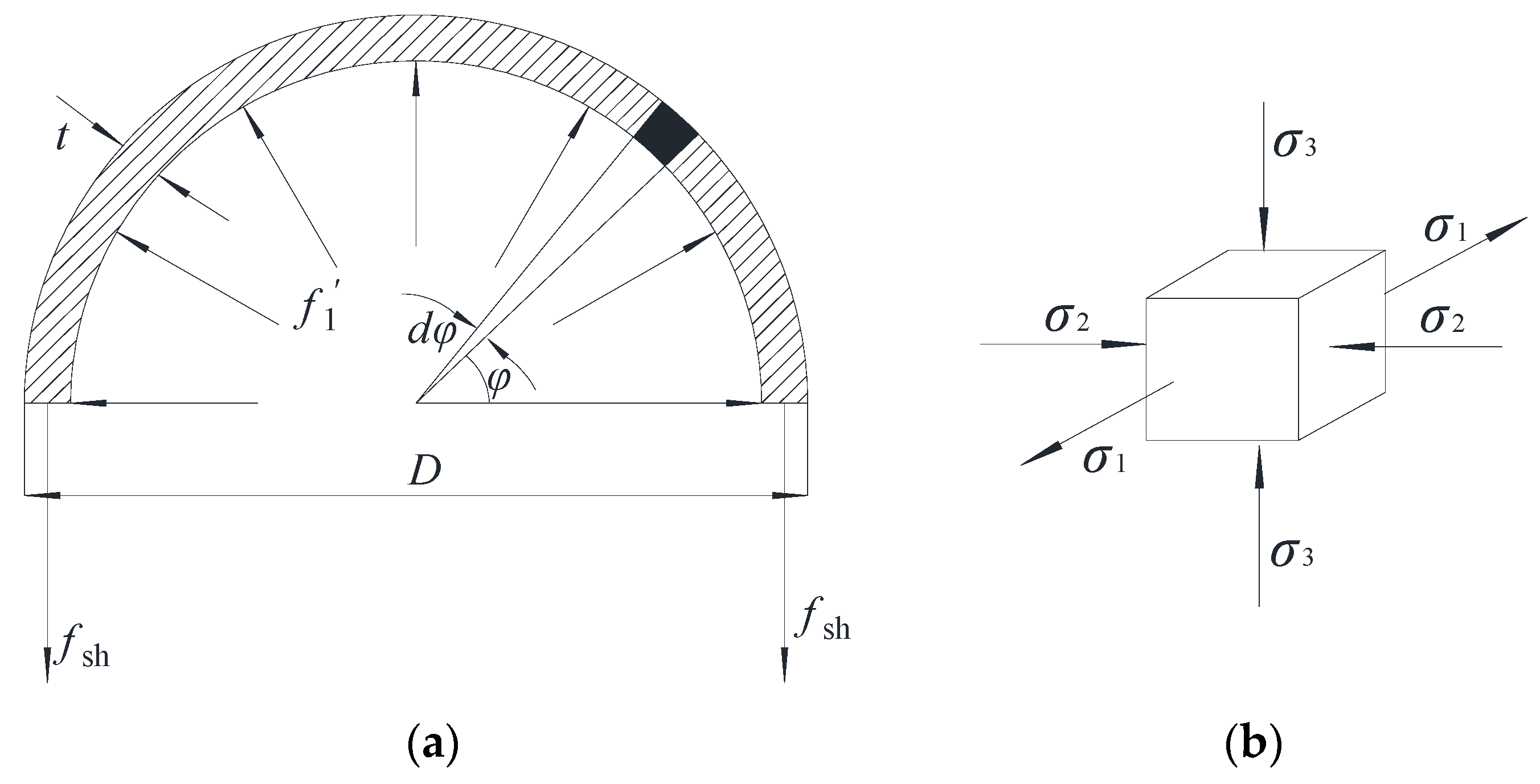


| γ (%) | W/B | Sand Ratio (%) | Water (kg/m3) | Cementitious Material (kg/m3) | Coarse Aggregate (kg/m3) | Sand (kg/m3) | Water Reducer (kg/m3) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Purified Water | Additional Water | Cement | Fly Ash | Recycled | Natural | |||||
| 0 | 0.40 | 31 | 205 | 0.0 | 427.1 | 85.4 | 0.0 | 1115.2 | 501 | 2.56 |
| 50 | 0.40 | 31 | 205 | 31.2 | 427.1 | 85.4 | 557.6 | 557.6 | 501 | 2.56 |
| 100 | 0.40 | 31 | 205 | 62.5 | 427.1 | 85.4 | 1115.2 | 0.0 | 501 | 2.56 |
| γ (%) | mBF (kg/m3) | fcu (MPa) | fc (MPa) | Ec (GPa) | νc |
|---|---|---|---|---|---|
| 0 | 2 | 52.8 | 41.5 | 33.5 | 0.22 |
| 50 | 0 | 48.5 | 34.9 | 29.2 | 0.23 |
| 2 | 50.7 | 36.1 | 31.4 | 0.20 | |
| 4 | 51.9 | 38.5 | 34.6 | 0.18 | |
| 100 | 2 | 46.1 | 32.2 | 28.3 | 0.19 |
| Specimens | L (mm) | γ (%) | mBF (kg/m3) | L/D | α | ξ | Nu (kN) | Δu (mm) |
|---|---|---|---|---|---|---|---|---|
| CA-0-2-8 | 912 | 0 | 2 | 8 | 0.1351 | 1.038 | 1109.33 | 10.74 |
| CA-100-2-8 | 912 | 100 | 2 | 8 | 0.1351 | 1.338 | 1005.33 | 13.0 |
| CA-50-2-8 | 912 | 50 | 2 | 8 | 0.1351 | 1.193 | 1041.33 | 9.31 |
| CA-50-0-8 | 912 | 50 | 0 | 8 | 0.1351 | 1.234 | 1037.64 | 15.95 |
| CA-50-4-8 | 912 | 50 | 4 | 8 | 0.1351 | 1.119 | 1041.33 | 9.18 |
| CA-50-2-5 | 570 | 50 | 2 | 5 | 0.1351 | 1.193 | 1102.87 | 8.38 |
| CA-50-2-11 | 1254 | 50 | 2 | 11 | 0.1351 | 1.193 | 1027.08 | 9.26 |
| Model Parameters | Dilation Angle | Eccentricity | fb0/fc0 | K | Viscosity Parameter |
|---|---|---|---|---|---|
| Takes values | 30° | 0.1 | 1.16 | 0.667 | 0.005 |
| Specimen Number | L (mm) | Nu (kN) | Ne (kN) | Nu/Ne |
|---|---|---|---|---|
| CA-0-2-8 | 912 | 1109.33 | 1134.98 | 0.977 |
| CA-100-2-8 | 912 | 1005.33 | 1017.72 | 0.988 |
| CA-50-2-8 | 912 | 1041.33 | 1061.50 | 0.981 |
| CA-50-0-8 | 912 | 1037.64 | 1057.55 | 0.981 |
| CA-50-4-8 | 912 | 1041.33 | 1067.19 | 0.976 |
| CA-50-2-5 | 570 | 1102.87 | 1132.04 | 0.974 |
| CA-50-2-11 | 1254 | 1027.08 | 1027.26 | 1.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Luo, C.; Wang, J.; Kuang, X.; Huang, Y. The Axial Compression Behavior of Basalt Fiber-Reinforced Recycled Aggregate Concrete-Filled Circular Steel-Tubular Column. Sustainability 2023, 15, 14351. https://doi.org/10.3390/su151914351
Zhang X, Luo C, Wang J, Kuang X, Huang Y. The Axial Compression Behavior of Basalt Fiber-Reinforced Recycled Aggregate Concrete-Filled Circular Steel-Tubular Column. Sustainability. 2023; 15(19):14351. https://doi.org/10.3390/su151914351
Chicago/Turabian StyleZhang, Xianggang, Chengyi Luo, Junbo Wang, Xiaomei Kuang, and Yajun Huang. 2023. "The Axial Compression Behavior of Basalt Fiber-Reinforced Recycled Aggregate Concrete-Filled Circular Steel-Tubular Column" Sustainability 15, no. 19: 14351. https://doi.org/10.3390/su151914351
APA StyleZhang, X., Luo, C., Wang, J., Kuang, X., & Huang, Y. (2023). The Axial Compression Behavior of Basalt Fiber-Reinforced Recycled Aggregate Concrete-Filled Circular Steel-Tubular Column. Sustainability, 15(19), 14351. https://doi.org/10.3390/su151914351