Dynamic Response of Steel–Timber Composite Beams with Varying Screw Spacing
Abstract
:1. Introduction
1.1. Steel–Timber Composite Beams as Sustainable Structural Elements
1.2. Dynamic Tests of Steel–Timber Composite Beams
2. Materials and Methods
2.1. The LVL Panels
2.2. The Steel Girders
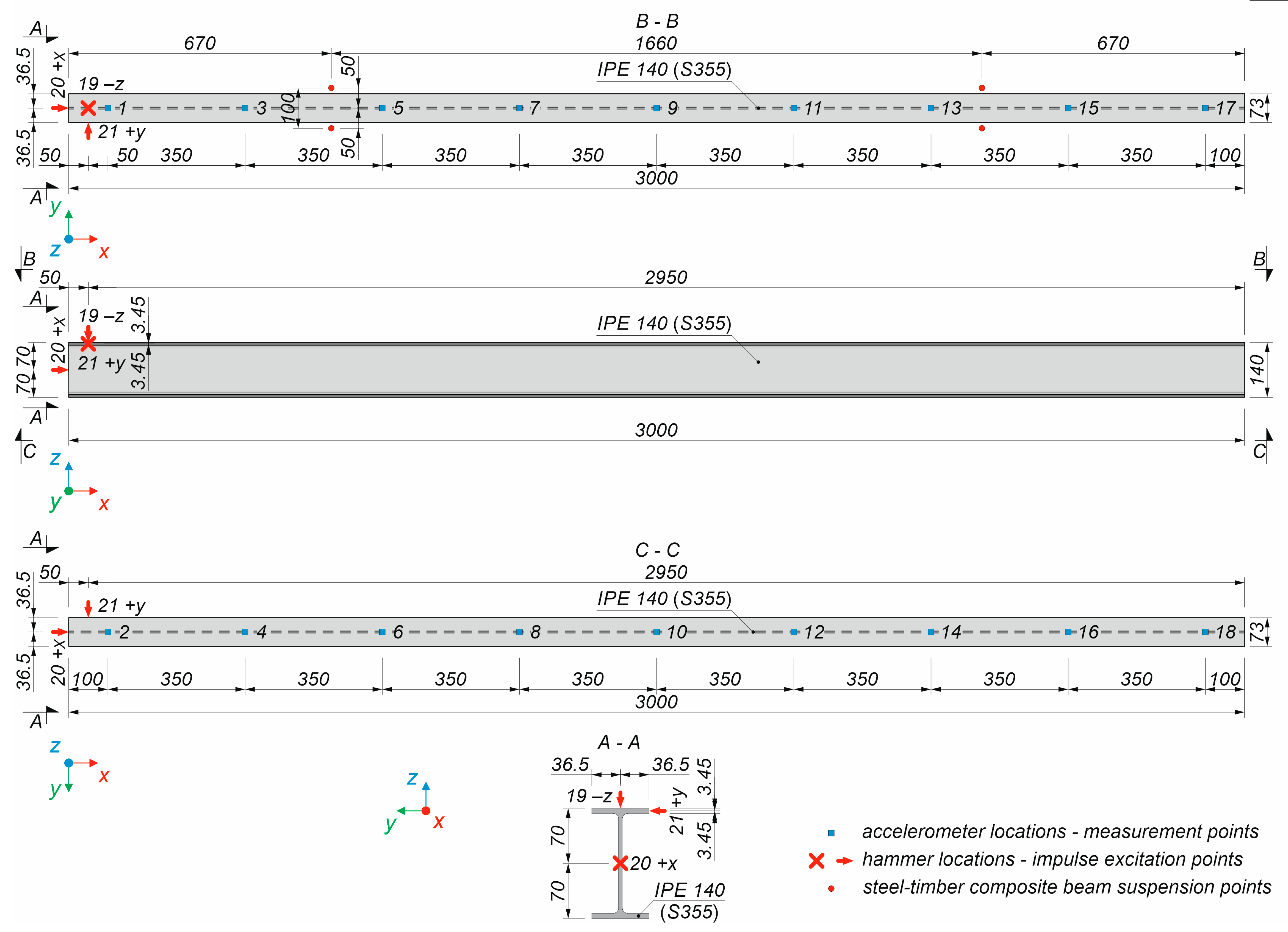
2.3. The Experimental Test of the Steel Girder
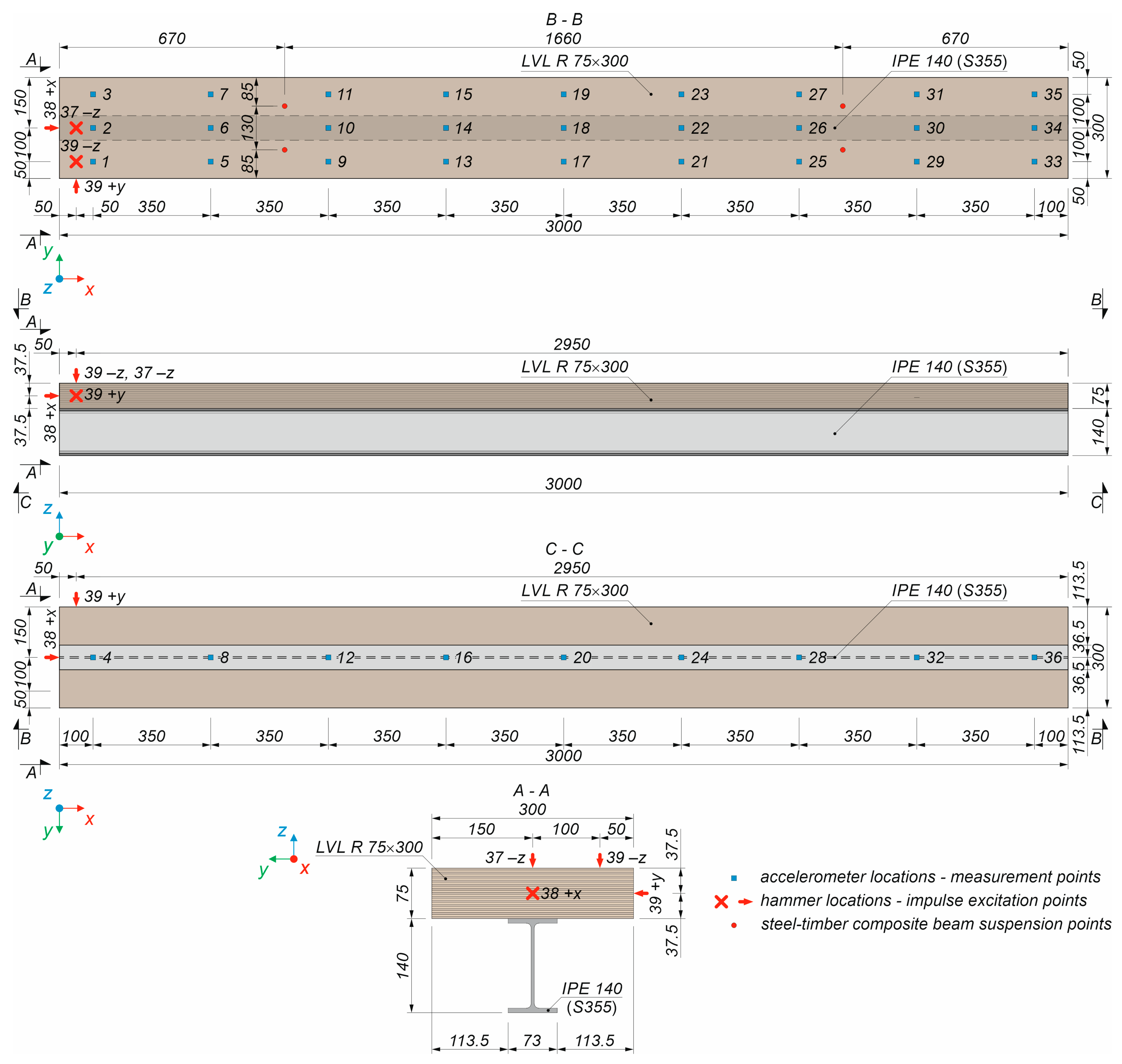
2.4. The Laboratory Tests of the Steel–Timber Composite Beams
2.5. The Numerical Models of the Steel Girder
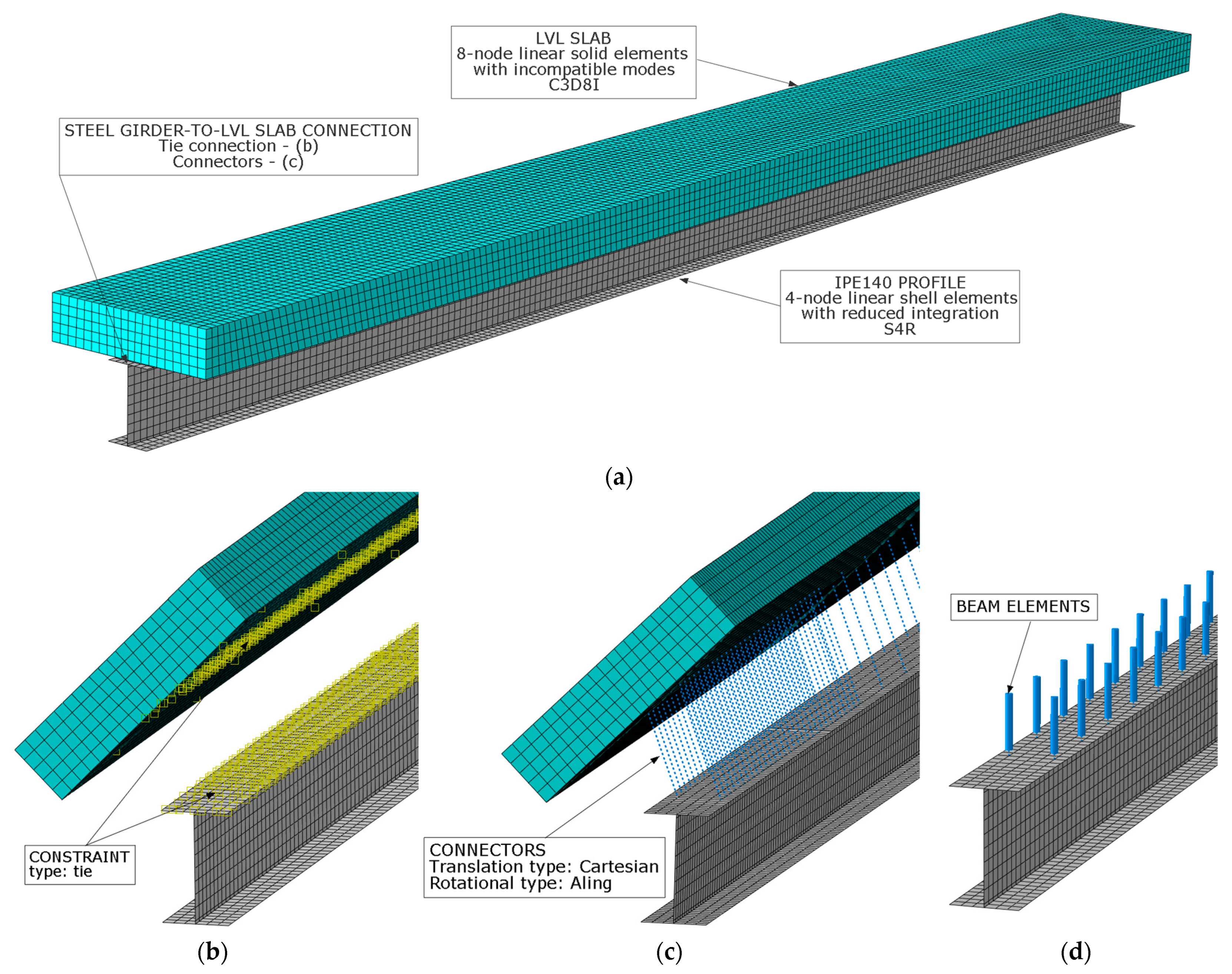
2.6. The Numerical Models of the Steel–Timber Composite Beams
3. Results
3.1. The Results of the Experimental and Numerical Analyses of the Steel Girder
3.2. The Results of the Experimental and Numerical Analyses of the Composite Beams
4. Discussion
5. Conclusions
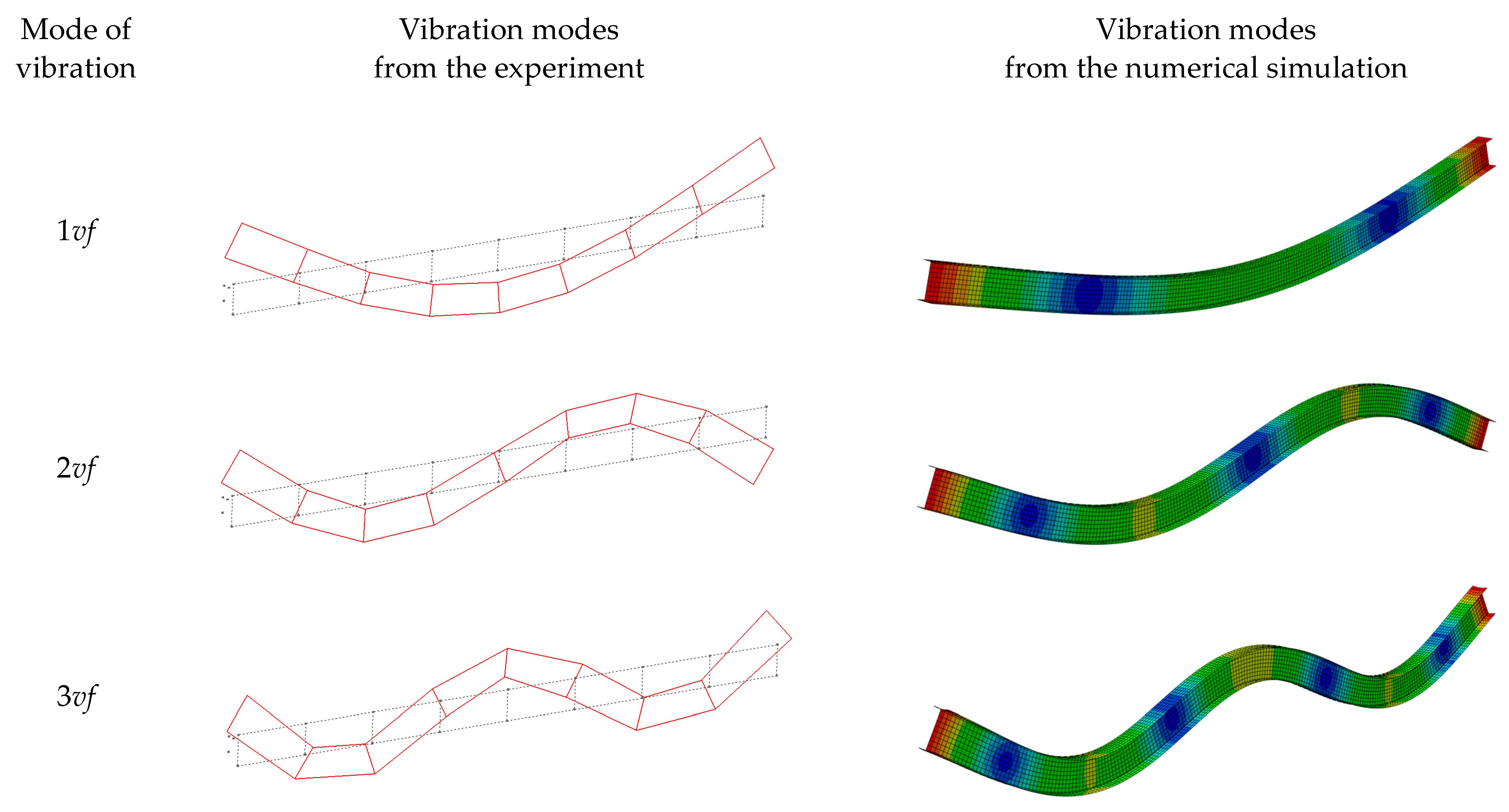
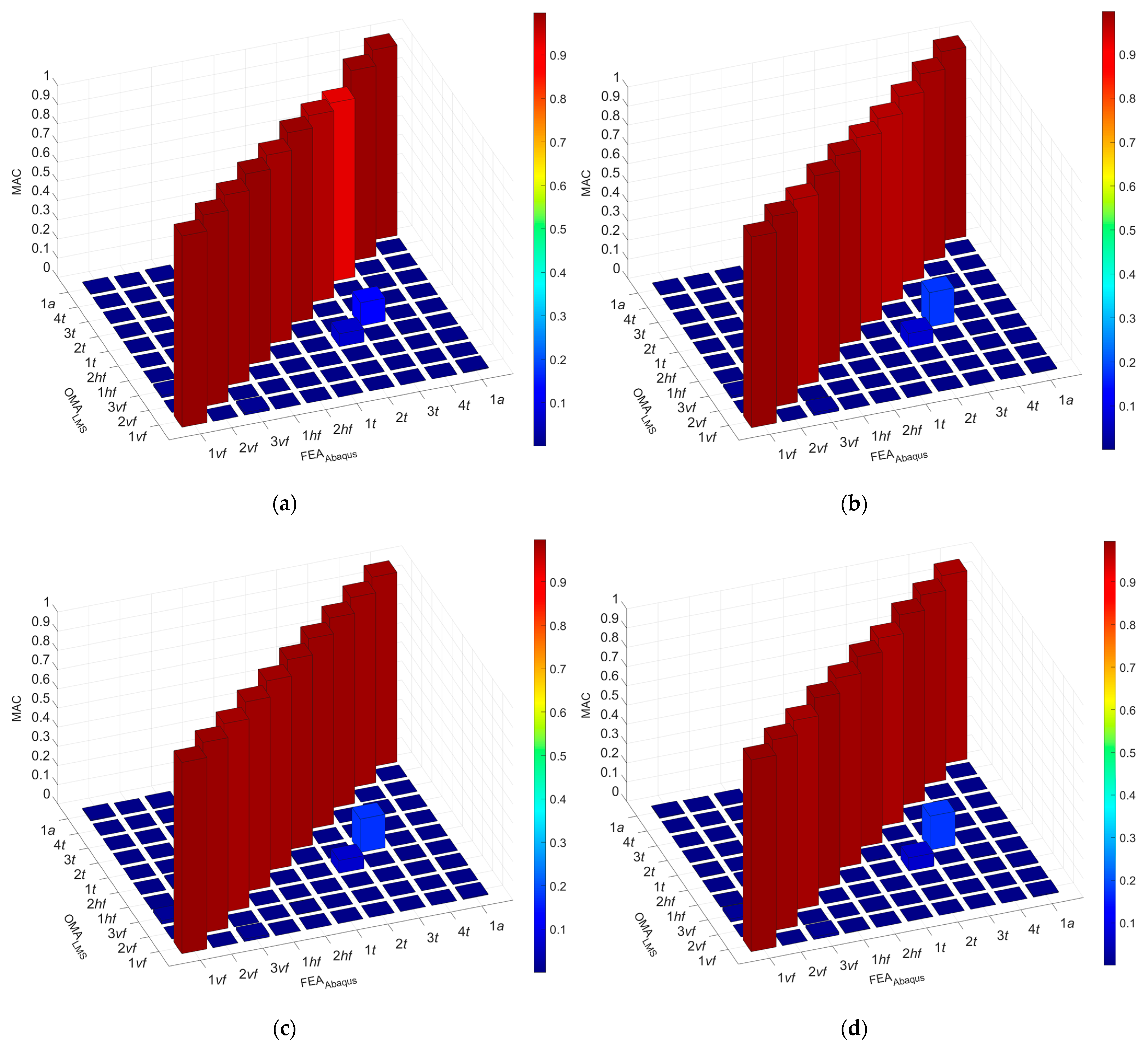
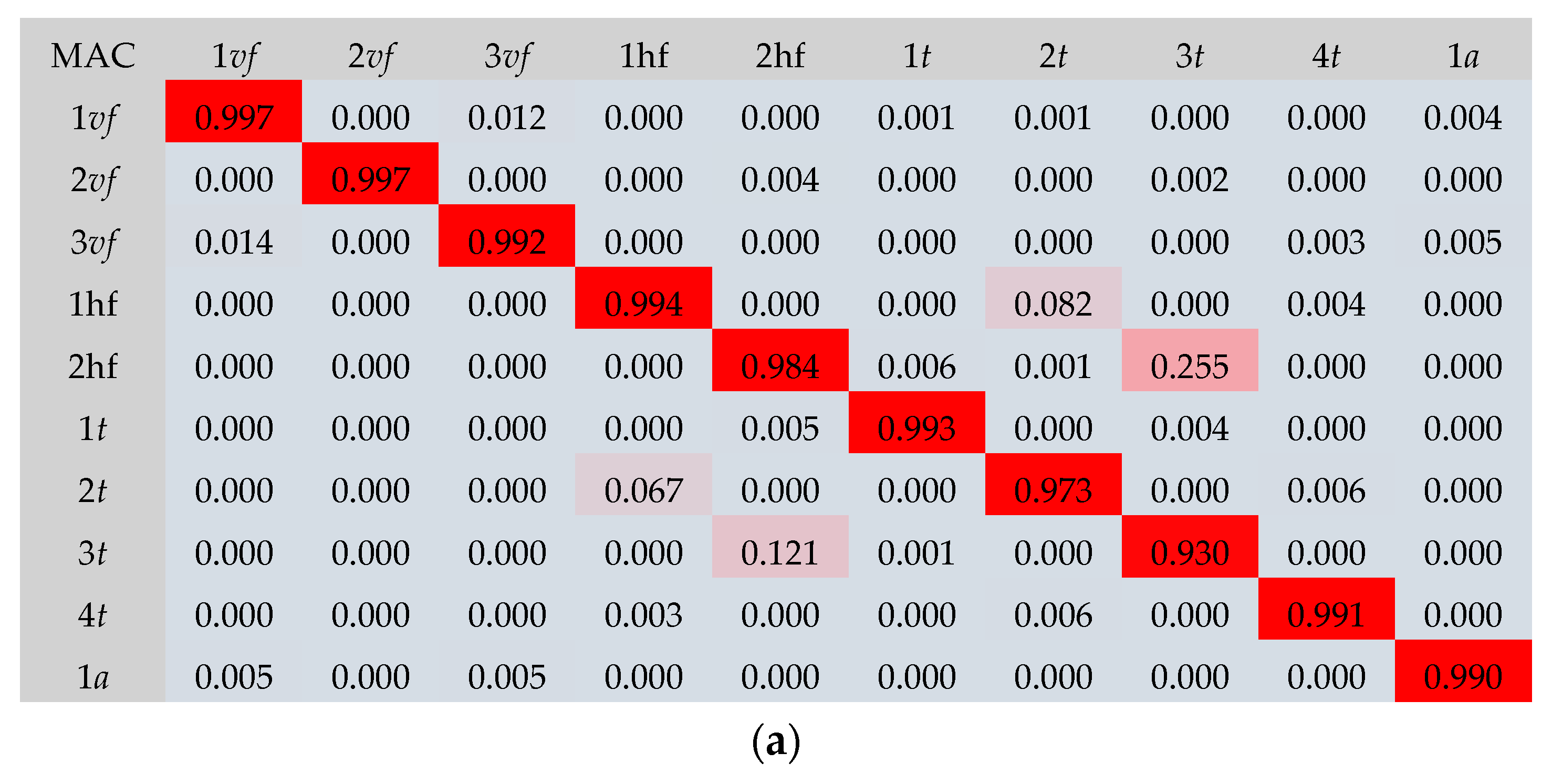
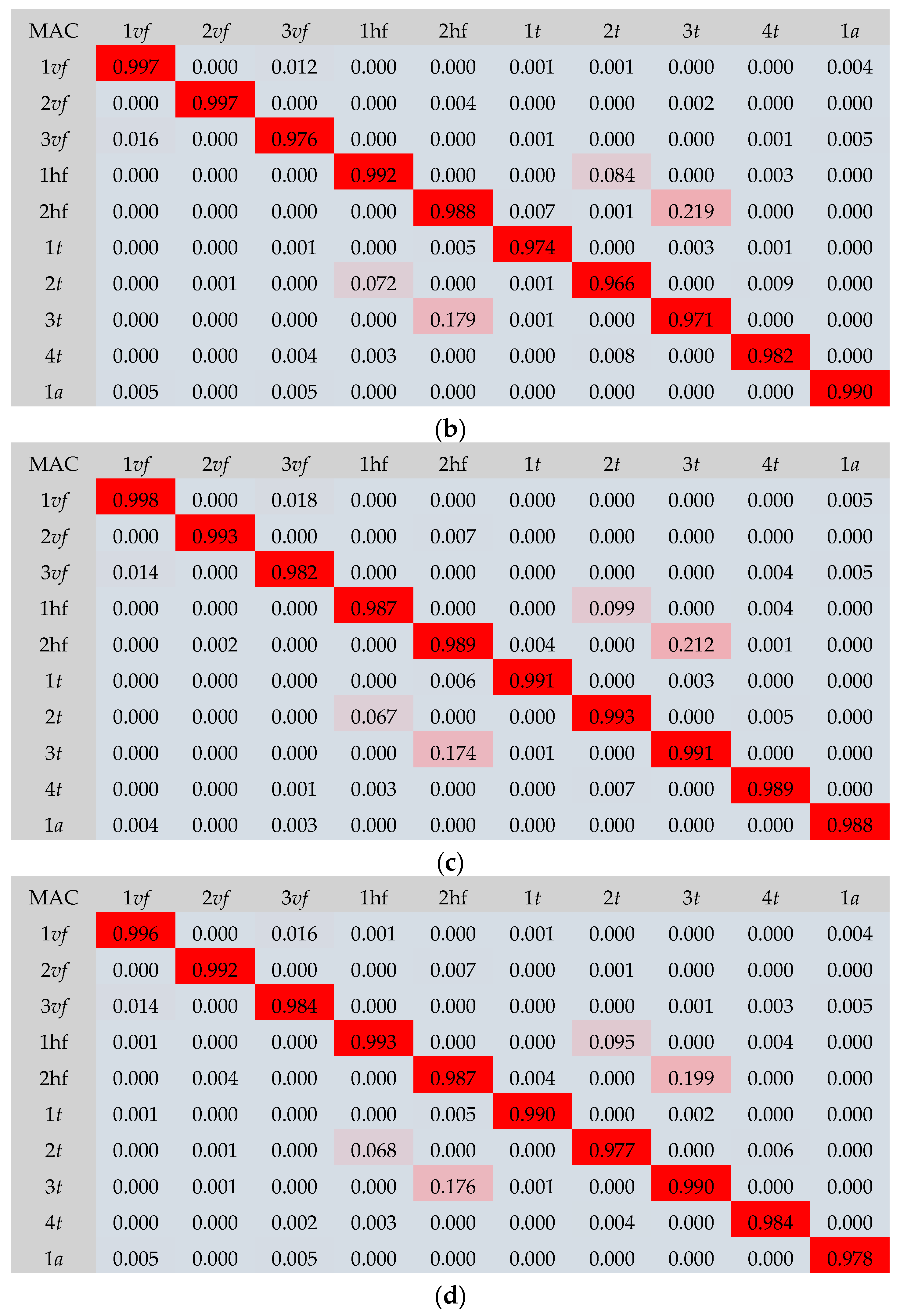
- The results of the numerical simulations corresponded to the experimental results. The frequencies obtained from the numerical analyses exhibited a high correlation with the experimental results. The MAC index values were close to 1, which resulted in high agreement between the mode shapes of vibration from the experimental tests and the numerical analyses.
- A high correlation between numerical and experimental results was possible thanks to the use of the previously developed numerical models of the steel–timber composite beam components (numerical models of the LVL slab and the steel girder). They were used to develop the numerical models of the steel–timber composite beams.
- Connection modelling was also a key parameter. The varying number of connectors resulting from the varied spacing was taken into account by connecting the LVL slab and the steel girder using discreet connectors. The possibility of slipping between the slab and the girder was allowed because the connectors were assigned displacement properties. The numerical models with discreet connectors showed lower relative errors than the numerical model with a rigid connection.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lacki, P.; Derlatka, A.; Kasza, P.; Gao, S. Numerical study of steel–concrete composite beam with composite dowels connectors. Comput. Struct. 2021, 255, 106618. [Google Scholar] [CrossRef]
- Loss, C.; Davison, B. Innovative composite steel-timber floors with prefabricated modular components. Eng. Struct. 2017, 132, 695–713. [Google Scholar] [CrossRef]
- Van Cauteren, D.; Ramon, D.; Stroeckx, J.; Allacker, K.; Schevenels, M. Design optimization of hybrid steel/timber structures for minimal environmental impact and financial cost: A case study. Energy Build. 2022, 254, 111600. [Google Scholar] [CrossRef]
- Bertino, G.; Kisser, J.; Zeilinger, J.; Langergraber, G.; Fischer, T.; Österreicher, D. Fundamentals of Building Deconstruction as a Circular Economy Strategy for the Reuse of Construction Materials. Appl. Sci. 2021, 11, 939. [Google Scholar] [CrossRef]
- Ataei, A.; Chiniforush, A.A.; Bradford, M.; Valipour, H. Cyclic behaviour of bolt and screw shear connectors in steel-timber composite (STC) beams. J. Constr. Steel Res. 2019, 161, 328–340. [Google Scholar] [CrossRef]
- Bradford, M.A.; Hassanieh, A.; Valipour, H.R.; Foster, S.J. Sustainable Steel-timber Joints for Framed Structures. Procedia Eng. 2017, 172, 2–12. [Google Scholar] [CrossRef]
- Chiniforush, A.A.; Akbarnezhad, A.; Valipour, H.; Xiao, J. Energy implications of using steel-timber composite (STC) elements in buildings. Energy Build. 2018, 176, 203–215. [Google Scholar] [CrossRef]
- Romero, A.; Odenbreit, C. Experimental investigation on novel shear connections for demountable steel-timber composite (STC) beams and flooring systems. Eng. Struct. 2024, 304, 117620. [Google Scholar] [CrossRef]
- Song, X.; Zhao, L.; Liu, Y.; Gong, M. Experimental and nonlinear analytical of the flexural performance of timber-filled steel tubular composite beams. Eng. Struct. 2024, 301, 117312. [Google Scholar] [CrossRef]
- Tupenaite, L.; Kanapeckiene, L.; Naimaviciene, J.; Kaklauskas, A.; Gecys, T. Timber Construction as a Solution to Climate Change: A Systematic Literature Review. Buildings 2023, 13, 976. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Wu, P.; Li, Y. Experimental investigation on the flexural and shear behaviour of LVL I-beam strengthened with steel channels. Constr. Build. Mater. 2022, 341, 127719. [Google Scholar] [CrossRef]
- Wdowiak-Postulak, A.; Świt, G.; Dziedzic-Jagocka, I. Application of Composite Bars in Wooden, Full-Scale, Innovative Engineering Products—Experimental and Numerical Study. Materials 2024, 17, 730. [Google Scholar] [CrossRef]
- Romero, A.; Odenbreit, C. Experimental Investigation on Strength and Stiffness Properties of Laminated Veneer Lumber (LVL). Materials 2023, 16, 7194. [Google Scholar] [CrossRef]
- Environmental Product Declaration in Accordance with ISO 14025 and EN 15804:2012+A2:2019 for Kerto LVL Laminated Veneer Lumber; EPD International AB: Stockholm, Sweden, 2022.
- Environmental Product Declaration as per ISO 14025 and EN 15804 for STEICO LVL Laminated Veneer Lumber, Institut Bauen und Umwelt e.V. (IBU): Berlin, Germany, 2019.
- Li, M.; He, M.; Li, Z.; Yun, X. Flexural behavior of LVL made from Australian radiata pine. Structures 2024, 61, 106014. [Google Scholar] [CrossRef]
- Lu, H.R.; El Hanandeh, A.; Gilbert, B.; Bailleres, H. A comparative life cycle assessment (LCA) of alternative material for Australian building construction. MATEC Web Conf. 2017, 120, 02013. [Google Scholar] [CrossRef]
- Bakalarz, M.M.; Kossakowski, P.G. Numerical, Theoretical, and Experimental Analysis of LVL-CFRP Sandwich Structure. Materials 2024, 17, 61. [Google Scholar] [CrossRef]
- Asdrubali, F.; Ferracuti, B.; Lombardi, L.; Guattari, C.; Evangelisti, L.; Grazieschi, G. A review of structural, thermo-physical, acoustical, and environmental properties of wooden materials for building applications. Build. Environ. 2017, 114, 307–332. [Google Scholar] [CrossRef]
- Pasternack, R.; Wishnie, M.; Clarke, C.; Wang, Y.; Belair, E.; Marshall, S.; Gu, H.; Nepal, P.; Dolezal, F.; Lomax, G.; et al. What Is the Impact of Mass Timber Utilization on Climate and Forests? Sustainability 2022, 14, 758. [Google Scholar] [CrossRef]
- Wang, Z.; Gong, M.; Chui, Y.-H. Mechanical properties of laminated strand lumber and hybrid cross-laminated timber. Constr. Build. Mater. 2015, 101, 622–627. [Google Scholar] [CrossRef]
- Brandner, R.; Flatscher, G.; Ringhofer, A.; Schickhofer, G.; Thiel, A. Cross laminated timber (CLT): Overview and development. Eur. J. Wood Prod. 2016, 74, 331–351. [Google Scholar] [CrossRef]
- Burgan, B.A.; Sansom, M.R. Sustainable steel construction. J. Constr. Steel Res. 2006, 62, 1178–1183. [Google Scholar] [CrossRef]
- Colla, V.; Branca, T.A. Sustainable Steel Industry: Energy and Resource Efficiency. Low-Emissions and Carbon-Lean Production. Metals 2021, 11, 1469. [Google Scholar] [CrossRef]
- Aspila, A.; Heinisuo, M.; Mela, K.; Malaska, M.; Pajunen, S. Elastic design of steel-timber composite beams. Wood Mater. Sci. Eng. 2022, 17, 243–252. [Google Scholar] [CrossRef]
- Hassanieh, A.; Valipour, H.R.; Bradford, M.A. Load-slip behaviour of steel-cross laminated timber (CLT) composite connections. J. Constr. Steel Res. 2016, 122, 110–121. [Google Scholar] [CrossRef]
- Zhao, Y.; Yuan, Y.; Wang, C.-L.; Meng, S. Experimental and finite element analysis of flexural performance of steel-timber composite beams connected by hybrid-anchored screws. Eng. Struct. 2023, 292, 116503. [Google Scholar] [CrossRef]
- Kyvelou, P.; Gardner, L.; Nethercot, D.A. Design of composite cold-formed steel flooring systems. Structures 2017, 12, 242–252. [Google Scholar] [CrossRef]
- Kyvelou, P.; Gardner, L.; Nethercot, D.A. Finite element modelling of composite cold-formed steel flooring systems. Eng. Struct. 2018, 158, 28–42. [Google Scholar] [CrossRef]
- Chybiński, M.; Polus, Ł. Structural Behaviour of Aluminium–Timber Composite Beams with Partial Shear Connections. Appl. Sci. 2023, 13, 1603. [Google Scholar] [CrossRef]
- Gardner, L.; Baddoo, N.R. Fire testing and design of stainless steel structures. J. Constr. Steel Res. 2006, 62, 532–543. [Google Scholar] [CrossRef]
- Chiniforush, A.A.; Makki Alamdari, M.; Dackermann, U.; Valipour, H.R.; Akbarnezhad, A. Vibration behaviour of steel-timber composite floors. part (1): Experimental & numerical investigation. J. Constr. Steel Res. 2019, 161, 244–257. [Google Scholar] [CrossRef]
- Chocholaty, B.; Roozen, N.B.; Maeder, M.; Marburg, S. Vibroacoustic response of steel–timber composite elements. Eng. Struct. 2022, 271, 114911. [Google Scholar] [CrossRef]
- Hamm, P.; Richter, A.; Winter, S. Floor vibrations–new results. In Proceedings of the 11th World Conference on Timber Engineering 2010 (WCTE 2010), Trentino, Italy, 20–24 June 2010; Ceccotti, A., Ed.; Trees and Timber Institute, National Research Council: Sesto Fiorentino, Italy, 2010. [Google Scholar]
- Cheraghi-Shirazi, N.; Crews, K.; Malek, S. Review of Vibration Assessment Methods for Steel-Timber Composite Floors. Buildings 2022, 12, 2061. [Google Scholar] [CrossRef]
- Lenartowicz, A.; Przychodzki, M.; Guminiak, M.; Garbowski, T. Optimal Placement of Viscoelastic Vibration Dampers for Kirchhoff Plates Based on PSO Method. Materials 2021, 14, 6616. [Google Scholar] [CrossRef]
- Knitter-Piątkowska, A.; Guminiak, M. Application of 1-D and 2-D Discrete Wavelet Transform to Crack Identification in Statically and Dynamically Loaded Plates. Eng. Trans. 2020, 68, 137–157. [Google Scholar] [CrossRef]
- Hassanieh, A.; Chiniforush, A.A.; Valipour, H.R.; Bradford, M.A. Vibration behaviour of steel-timber composite floors. part (2): Evaluation of human-induced vibrations. J. Constr. Steel Res. 2019, 158, 156–170. [Google Scholar] [CrossRef]
- Odeh, D.J.; Kuehnel, P. The Hybrid CLT Steel Residence Hall. Structure 2019. Available online: https://www.structuremag.org/?p=14845 (accessed on 15 April 2024).
- Komorowski, M. Podręcznik Projektowania i Budowania w Systemie STEICO. Podstawy. Fizyka Budowli. Zalecenia Wykonawcze; Forestor Communication: Warsaw, Poland, 2020. (In Polish) [Google Scholar]
- Abramowicz, M.; Chybiński, M.; Polus, Ł.; Wróblewski, T. Free Vibrations of Sustainable Laminated Veneer Lumber Slabs. Sustainability 2024, 16, 166. [Google Scholar] [CrossRef]
- Inspection Certificate 3.1. IPE 140 in Grade S355J2; Celsa Huta Ostrowiec: Ostrowiec Świętokrzyski, Poland, 2021.
- Bogucki, W.; Żyburtowicz, M. Tablice do Projektowania Konstrukcji Metalowych; Arkady: Warsaw, Poland, 2006. (In Polish) [Google Scholar]
- EN 10034:1996; Structural Steel I and H Sections—Tolerances on Shape and Dimensions. European Committee for Standardization: Brussels, Belgium, 1996.
- Pełka-Sawenko, A.; Wróblewski, T.; Szumigała, M. Validation of Computational Models of Steel-Concrete Composite Beams. Eng. Trans. 2016, 64, 53–67. [Google Scholar] [CrossRef]
- Abramowicz, M.; Berczyński, S.; Wróblewski, T. Modelling and parameter identification of steel–concrete composite beams in 3D rigid finite element method. Arch. Civ. Mech. Eng. 2020, 20, 103. [Google Scholar] [CrossRef]
- Ewins, D.J. Modal Testing: Theory, Practice and Application, 2nd ed.; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Szewczyk, P.; Szumigała, M. Optimal Design of Steel–Concrete Composite Beams Strengthened under Load. Materials 2021, 14, 4715. [Google Scholar] [CrossRef]
- Hassanieh, A.; Valipour, H.R.; Bradford, M.A. Experimental and analytical behaviour of steel-timber composite connections. Constr. Build. Mater. 2016, 118, 63–75. [Google Scholar] [CrossRef]
- Romero, A.; Yang, J.; Hanus, F.; Odenbreit, C. Numerical Investigation of Steel-LVL Timber Composite Beams. ce/papers 2022, 5, 21–30. [Google Scholar] [CrossRef]
- Hassanieh, A.; Valipour, H.R.; Bradford, M.A. Experimental and numerical study of steel-timber composite (STC) beams. J. Constr. Steel Res. 2016, 122, 367–378. [Google Scholar] [CrossRef]
- Dorn, M.; Habrová, K.; Koubek, R.; Serrano, E. Determination of coefficients of friction for laminated veneer lumber on steel under high pressure loads. Friction 2020, 9, 367–379. [Google Scholar] [CrossRef]
- Jarosińska, M.; Berczyński, S. Changes in Frequency and Mode Shapes Due to Damage in Steel–Concrete Composite Beam. Materials 2021, 14, 6232. [Google Scholar] [CrossRef] [PubMed]
- Marwala, T. Finite-Element-Model Updating Using Computational Intelligence Techniques; Springer: London, UK, 2010. [Google Scholar]
- Shabani, A.; Feyzabadi, M.; Kioumarsi, M. Model updating of a masonry tower based on operational modal analysis: The role of soil-structure interaction. Case Stud. Constr. Mater. 2022, 16, e00957. [Google Scholar] [CrossRef]
- Pastor, M.; Binda, M.; Harčarik, T. Modal Assurance Criterion. Procedia Eng. 2012, 48, 543–548. [Google Scholar] [CrossRef]







| Elastic Modulus [MPa] | Poisson’s Ratio [–] | Shear Modulus [MPa] | Density [kg/m3] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| E1 | E2 | E3 | υ12 | υ13 | υ23 | G12 | G13 | G23 | ρ |
| 17,550 | 500 | 500 | 0.48 | 0.48 | 0.22 | 1000 | 1000 | 100 | 665.2 |
| C | Mn | Si | P | S | Cu | Cr | Ni |
|---|---|---|---|---|---|---|---|
| 0.10 | 1.32 | 0.19 | 0.018 | 0.026 | 0.28 | 0.11 | 0.08 |
| Mo | Ti | V | Al | N | Nb | Sb | Co |
| 0.01 | 0.001 | 0.070 | 0.0036 | 0.009 | 0.002 | 0.003 | 0.008 |
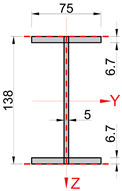
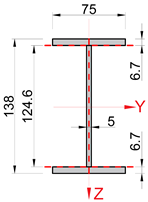
| Catalogue Dimensions [43] | Measured Dimensions | |
|---|---|---|
 | 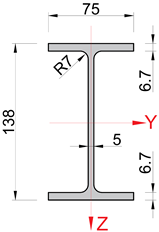 | |
| moment of inertia, Jx [cm4] | 2.48 | 2.49 |
| moment of inertia, Jy [cm4] | 541 | 529.6 |
| moment of inertia, Jz [cm2] | 44.9 | 47.3 |
| cross-sectional area, A [cm2] | 16.4 | 16.7 |
| Model A | Model B | Model C | Model D | |
|---|---|---|---|---|
 |  |  | 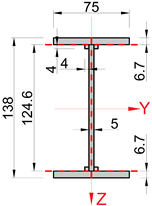 | |
| moment of inertia Jx [cm4] | 2.05 | 2.08 | 2.02 | 2.54 |
| moment of inertia Jy [cm4] | 527.8 | 543.0 | 514.1 | 537.4 |
| moment of inertia Jz [cm2] | 47.2 | 47.3 | 47.2 | 47.4 |
| cross-sectional area A [cm2] | 16.62 | 16.95 | 16.28 | 16.92 |
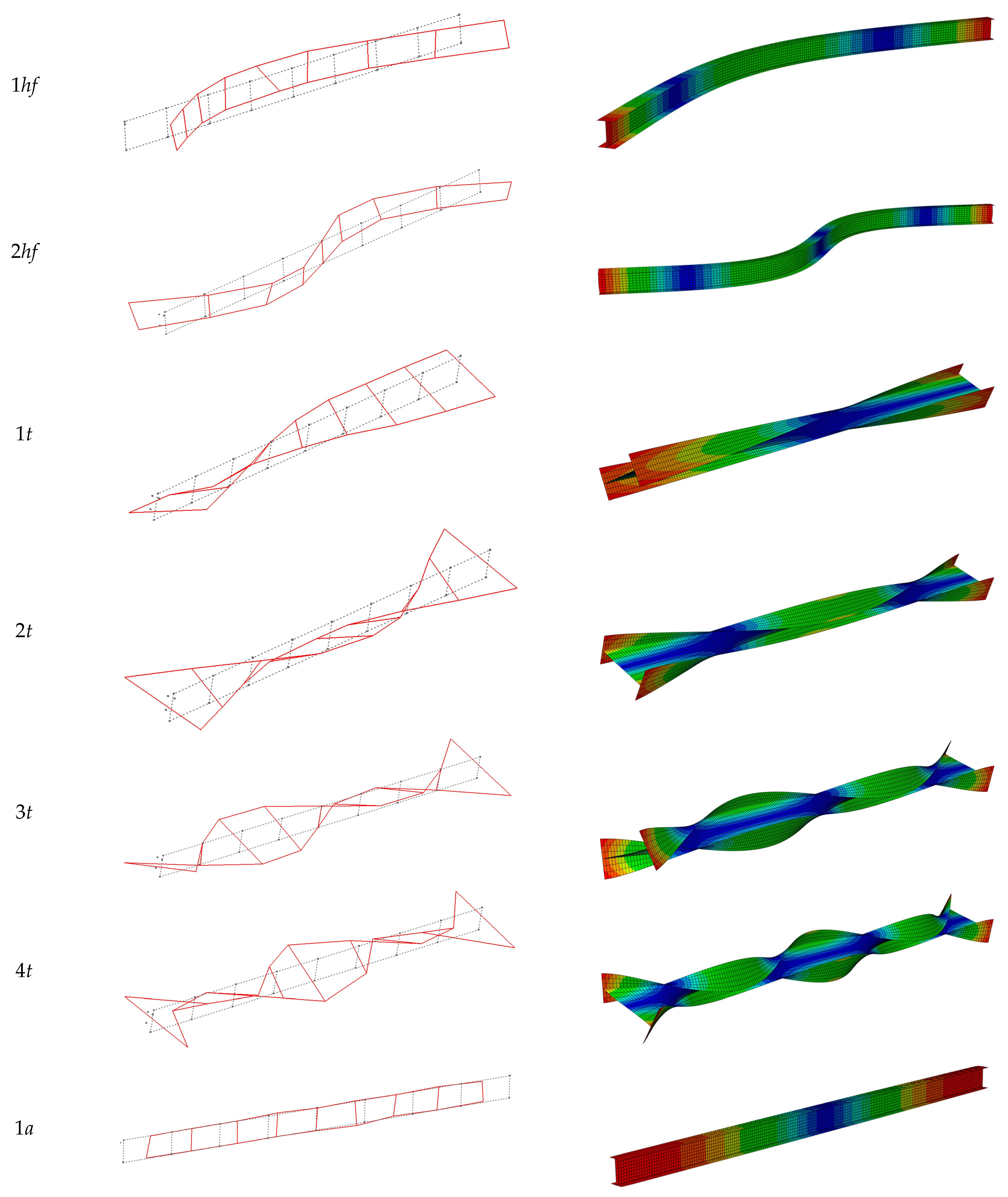
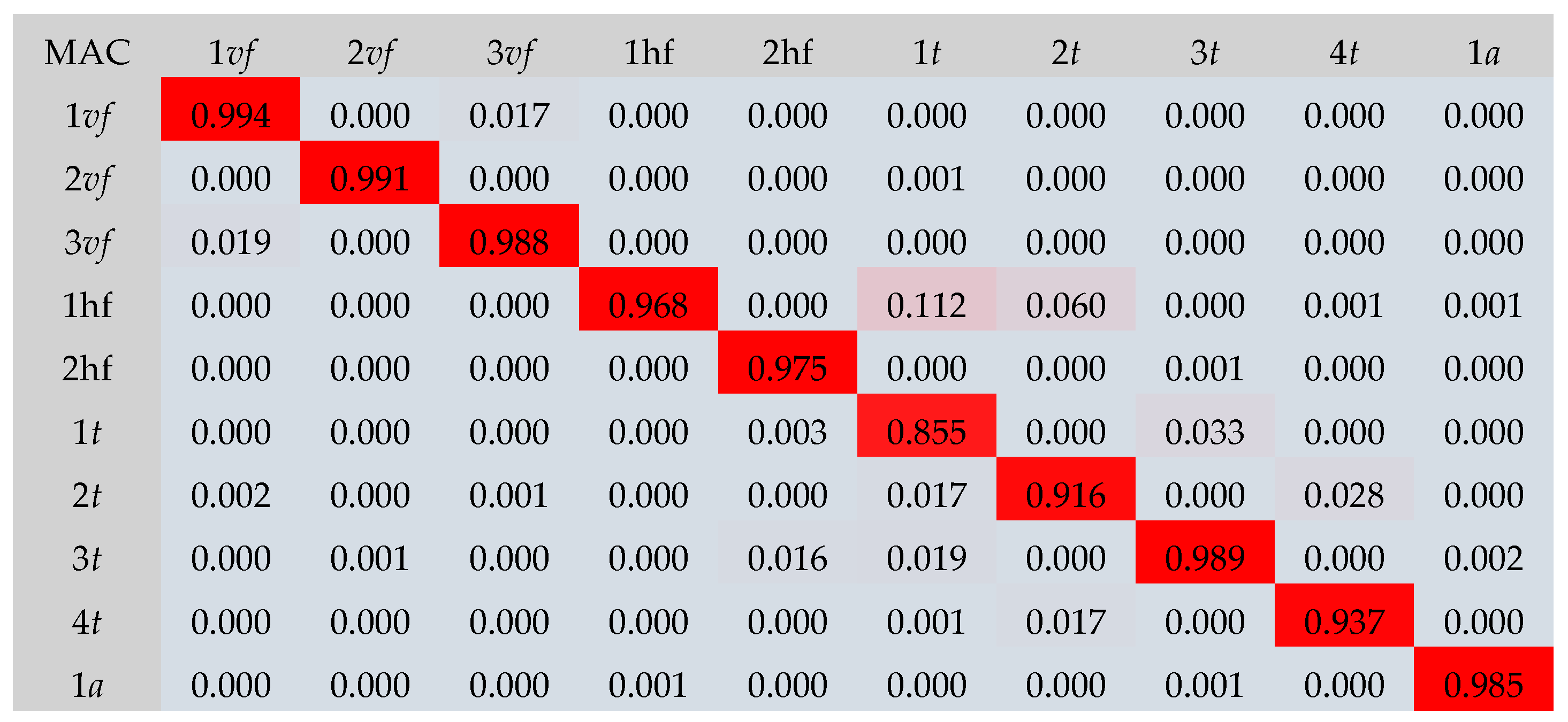
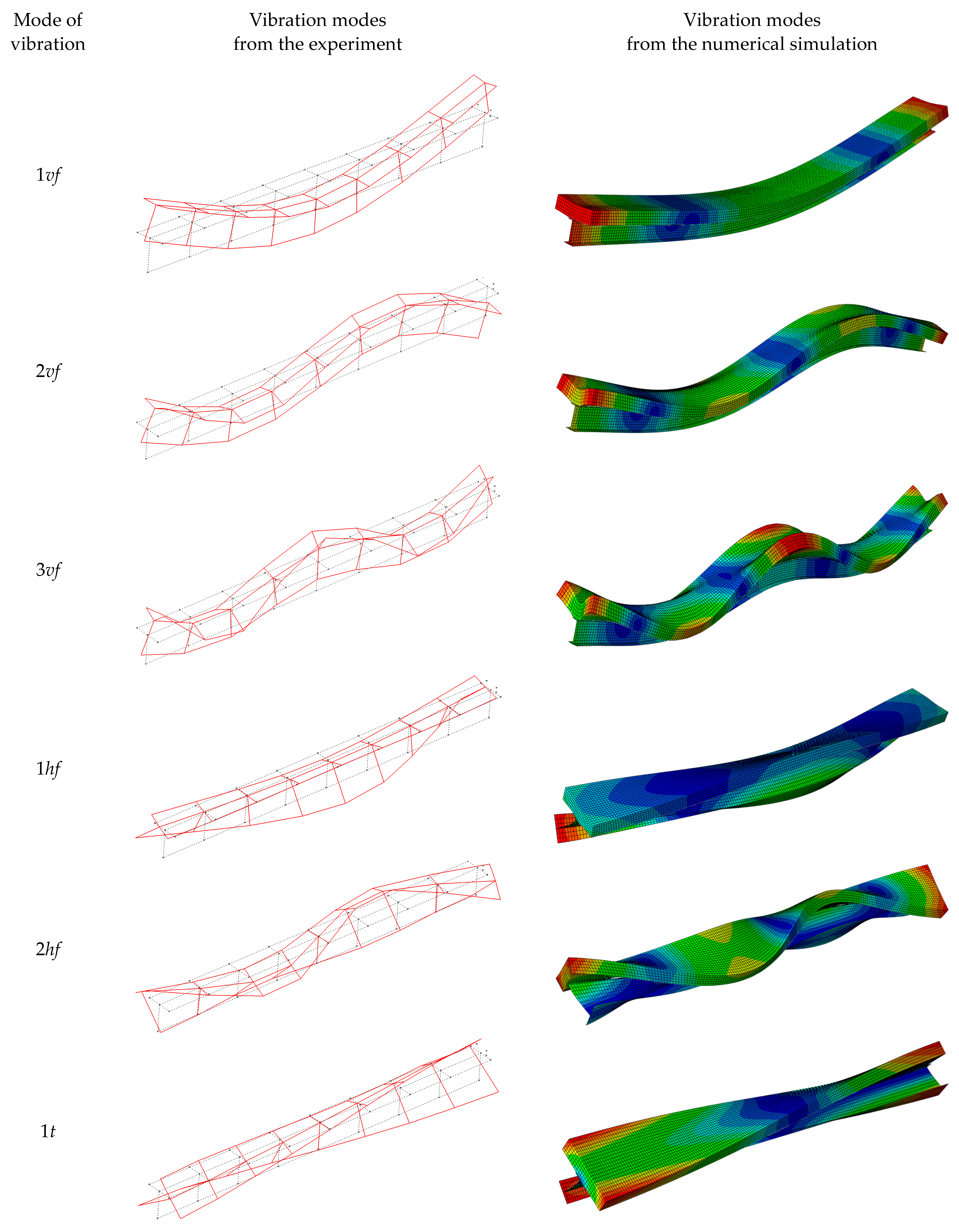
| Mode of Vibration | Experimental Frequency fexp [Hz] | Computational Frequency fcom | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Model A [Hz] | (∆) [%] | Model B [Hz] | (∆) [%] | Model C [Hz] | (∆) [%] | Model D [Hz] | (∆) [%] | ||
| 1vf | 113.10 | 112.03 | (0.95) | 112.30 | (0.71) | 111.82 | (1.13) | 112.13 | (0.86) |
| 2vf | 293.93 | 294.87 | (−0.32) | 294.70 | (−0.26) | 294.88 | (−0.32) | 295.55 | (−0.55) |
| 3vf | 540.26 | 542.87 | (−0.48) | 540.70 | (−0.08) | 544.12 | (−0.71) | 545.04 | (−0.88) |
| 1hf | 33.80 | 33.81 | (−0.05) | 33.48 | (0.93) | 34.15 | (−1.05) | 33.58 | (0.64) |
| 2hf | 91.72 | 92.76 | (−1.14) | 91.91 | (−0.21) | 93.62 | (−2.07) | 92.07 | (−0.38) |
| 1t | 37.95 | 32.68 | (13.89) | 31.24 | (17.67) | 34.37 | (9.42) | 34.82 | (8.98) |
| 2t | 82.81 | 76.31 | (7.85) | 72.85 | (12.03) | 80.28 | (3.06) | 80.71 | (2.60) |
| 3t | 147.20 | 142.94 | (2.89) | 136.38 | (7.35) | 150.22 | (−2.05) | 149.66 | (−1.64) |
| 4t | 233.49 | 239.57 | (2.60) | 228.66 | (2.07) | 251.38 | (−7.66) | 248.80 | (−6.15) |
| 1a | 857.48 | 857.37 | (0.01) | 857.38 | (0.01) | 857.33 | (0.02) | 857.33 | (0.02) |
| S ∙ 10−2 [−] | 2.72 | 5.17 | 1.68 | 1.30 | |||||
| Mode of Vibration | Computational Frequency fcom [Hz] | Experimental Frequency fexp | |||||
|---|---|---|---|---|---|---|---|
| Beam S30 [Hz] | (∆) [%] | Beam S60 [Hz] | (∆) [%] | Beam S90 [Hz] | (∆) [%] | ||
| 1vf | 128.54 | 126.25 | (−1.82) | 127.73 | (−0.64) | 126.65 | (−1.49) |
| 2vf | 305.68 | 293.78 | (−4.05) | 298.30 | (−2.48) | 297.59 | (−2.72) |
| 3vf | 488.49 | 463.74 | (−5.34) | 475.01 | (−2.84) | 469.90 | (−3.96) |
| 1hf | 100.65 | 96.79 | (−3.98) | 97.67 | (−3.06) | 96.07 | (−4.77) |
| 2hf | 320.17 | 310.32 | (−3.17) | 313.75 | (−2.05) | 309.60 | (−3.41) |
| 1t | 76.09 | 71.97 | (−5.72) | 72.84 | (−4.46) | 71.88 | (−5.86) |
| 2t | 266.70 | 251.58 | (−6.01) | 254.65 | (−4.73) | 253.06 | (−5.39) |
| 3t | 368.38 | 338.46 | (−8.84) | 342.96 | (−7.41) | 341.00 | (−8.03) |
| 4t | 471.27 | 440.15 | (−7.07) | 448.35 | (−5.11) | 441.75 | (−6.68) |
| 1a | 855.95 | 837.82 | (−2.16) | 854.51 | (−0.17) | 842.68 | (−1.57) |
| S ∙ 10−2 [−] | 1.40 | 1.51 | 2.35 | ||||
| Mode of Vibration | Beam S30 | Beam S60 | Beam S90 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| fexp [Hz] | fcom [Hz] | (∆) [%] | fexp [Hz] | fcom [Hz] | (∆) [%] | fexp [Hz] | fcom [Hz] | (∆) [%] | |
| 1vf | 126.25 | 126.74 | (−0.39) | 127.73 | 127.24 | (0.38) | 126.65 | 127.39 | (−0.58) |
| 2vf | 293.78 | 299.09 | (−1.81) | 298.30 | 300.76 | (−0.83) | 297.59 | 301.22 | (−1.22) |
| 3vf | 463.74 | 479.81 | (−3.47) | 475.01 | 481.00 | (−1.26) | 469.90 | 481.09 | (−2.38) |
| 1hf | 96.79 | 98.61 | (−1.87) | 97.67 | 98.59 | (−0.95) | 96.07 | 98.563 | (−2.59) |
| 2hf | 310.32 | 313.75 | (−1.11) | 313.75 | 316.58 | (−0.90) | 309.60 | 317.45 | (−2.54) |
| 1t | 71.97 | 73.00 | (−1.43) | 72.84 | 73.11 | (−0.36) | 71.88 | 73.131 | (−1.74) |
| 2t | 251.58 | 260.85 | (−3.68) | 254.65 | 260.64 | (−2.35) | 253.06 | 260.5 | (−2.94) |
| 3t | 338.46 | 350.63 | (−3.60) | 342.96 | 350.60 | (−2.23) | 341.00 | 350.52 | (−2.79) |
| 4t | 440.15 | 461.68 | (−4.89) | 448.35 | 461.71 | (−2.98) | 441.75 | 461.6 | (−4.49) |
| 1a | 837.82 | 845.96 | (−0.97) | 854.51 | 857.18 | (−0.31) | 842.68 | 858.51 | (−1.88) |
| S ∙ 10−2 [−] | 0.74 | 0.24 | 0.64 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abramowicz, M.; Chybiński, M.; Polus, Ł.; Szewczyk, P.; Wróblewski, T. Dynamic Response of Steel–Timber Composite Beams with Varying Screw Spacing. Sustainability 2024, 16, 3654. https://doi.org/10.3390/su16093654
Abramowicz M, Chybiński M, Polus Ł, Szewczyk P, Wróblewski T. Dynamic Response of Steel–Timber Composite Beams with Varying Screw Spacing. Sustainability. 2024; 16(9):3654. https://doi.org/10.3390/su16093654
Chicago/Turabian StyleAbramowicz, Małgorzata, Marcin Chybiński, Łukasz Polus, Piotr Szewczyk, and Tomasz Wróblewski. 2024. "Dynamic Response of Steel–Timber Composite Beams with Varying Screw Spacing" Sustainability 16, no. 9: 3654. https://doi.org/10.3390/su16093654







