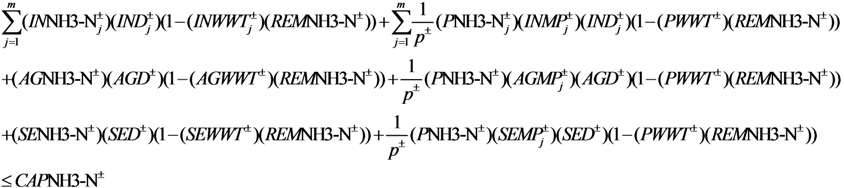Optimizing the Regional Industrial Structure Based on the Environmental Carrying Capacity: An Inexact Fuzzy Multi-Objective Programming Model
Abstract
:1. Introduction
- The industrial structure optimization model was established at the environment carrying capacity level.
- The fuzzy linear programming (FLP) and inexact linear programming (ILP) methods are introduced into the optimization model to reflect the complexity and uncertainty.
- The whole industrial structure optimization was considered in the research, including the primary, secondary and tertiary sectors.
2. Environmental Carrying Capacity
3. Model
3.1. Methodology




3.1.1. Fuzzy Linear Programming (FLP) Transformation and Fuzzy Goals














3.1.2. Inexact Linear Programming (ILP) Transformation







3.1.3. IFMOP Sub-Models















3.2. The Objective Function

- INDj± (endogenous variable): the added value of industry j of the secondary sector (10 thousand RMB Yuan/a);
- AGD± (endogenous variable): the added value of the primary sector (10 thousand RMB Yuan/a);
- SED± (endogenous variable): the added value of the tertiary sector (10 thousand RMB Yuan/a);
- WWC±: unit cost of wastewater treatment (10 thousand RMB Yuan/ton);
- INWWTj±: wastewater treatment rate of industry j (%);
- AGWWT±: wastewater treatment rate of the primary sector (%);
- SEWWT±: wastewater treatment rate of the tertiary sector (%);
- PWWT±: domestic wastewater treatment rate (%);
- INWWDj±: wastewater emission per unit output value of industry j (ton/10 thousand RMB Yuan);
- AGWWD±: wastewater emission per unit output value of the primary sector (ton/10 thousand RMB Yuan);
- SEWWD±: wastewater emission per unit output value of the tertiary sector (ton/10 thousand RMB Yuan);
- PWWD±: annual sewage discharge per capita (ton/person);
- INWSDj±: solid waste emission per unit output value of industry j (ton/10 thousand RMB Yuan);
- AGWSD±: solid waste emission per unit output value of the primary sector (ton/10 thousand RMB Yuan);
- SEWSD±: solid waste emission per unit output value of the tertiary sector (ton/10 thousand RMB Yuan);
- PWSD±: annual solid waste emission per capita (ton/person);
- INWSTj±: solid waste treatment rate of industry j (%);
- AGWST±: solid waste treatment rate of the primary sector (%);
- SEWST±: solid waste treatment rate of the tertiary sector (%);
- PWST±: garbage disposal rate (%);
- WSC±: unit cost of solid waste treatment (10 thousand RMB Yuan/ton);
- INMPj±: the number of employees per unit output value of industry j (person/10 thousand RMB Yuan);
- AGMP±: the number of employees per unit output value of the primary sector (person/10 thousand RMB Yuan);
- SEMP±: the number of employees per unit output value of the tertiary sector (person/10 thousand RMB Yuan);
- p±: the ratio of employment (%).
3.3. Constraints
3.3.1. Water Environmental Capacity Constraint
- (1)
- COD emission constraint: The COD emissions from production and living should be within the limits of the environmental capacity of COD. The production COD emissions consist of primary, secondary and tertiary sector COD emissions.
- (2)
- NH3-N emission constraint: The NH3-N emissions from production and living should be within the limits of the environmental capacity of NH3-N. The production NH3-N emissions consist of primary, secondary and tertiary sector NH3-N emissions.
3.3.2. Water Resource Constraint

3.3.3. Atmospheric Environmental Capacity Constraints

3.3.4. Energy Constraint

3.3.5. Economic Constraints
3.3.6. Non-Negative Constraints

- AGCOD±: COD emission per unit output value of the primary sector (ton/10 thousand RMB Yuan);
- AGNH3-N±: NH3-N emission per unit output value of the primary sector (ton/10 thousand RMB Yuan);
- AGSO2±: SO2 emission per unit output value of the primary sector (ton/10 thousand RMB Yuan);
- INCODj±: COD emission per unit output value of industry j (ton/10 thousand RMB Yuan);
- INNH3-Nj±: NH3-N emission per unit output value of industry j (ton/10 thousand RMB Yuan);
- INSO2j±: SO2 emission per unit output value of industry j (ton/10 thousand RMB Yuan);
- SECOD±: COD emission per unit output value of the tertiary sector (ton/10 thousand RMB Yuan);
- SENH3-N±: NH3-N emission per unit output value of the tertiary sector (ton/10 thousand RMB Yuan);
- SESO2±: SO2 emission per unit output value of the tertiary sector (ton/10 thousand RMB Yuan);
- PCOD±: annual COD discharge per capita (ton/person);
- PNH3-N±: annual NH3-N discharge per capita (ton/person);
- PSO2±: annual SO2 discharge per capita (ton/person);
- REMCOD±: COD removal rate of sewage treatment plant (%);
- REMNH3-N±: NH3-N removal rate of sewage treatment plant (%);
- CAPCOD±: environmental capacity of COD (ton/a);
- CAPNH3-N±: environmental capacity of NH3-N (ton/a);
- CAPSO2±: environmental capacity of SO2 (ton/a);
- INWDj±: water demand per unit output value of industry j (ton/10 thousand RMB Yuan);
- AGWD±: water demand per unit output value of the primary sector (ton/10 thousand RMB Yuan);
- SEWD±: water demand per unit output value of the tertiary sector (ton/10 thousand RMB Yuan);
- PWD±: water demand per capita (ton/person);
- MAXW±: water supply (ton/a);
- INGD±: energy demand per unit output value of industry j (tce/10 thousand RMB Yuan);
- PGD±: energy demand per capita (tce/person);
- AGGD±: energy demand per unit output value of the primary sector (tce/10 thousand RMB Yuan);
- SEGD±: energy demand per unit output value of the tertiary sector (tce/10 thousand RMB Yuan);
- MAXG ± energy supply (tce/a);
- UGDPJ: the added value upper limit of industry j of the secondary sector (10 thousand RMB Yuan);
- LGDPJ: the added value lower limit of industry j of the secondary sector (10 thousand RMB Yuan);
- UGDP1: the added value upper limit of the primary sector (10 thousand RMB Yuan);
- LGDP1: the added value lower limit of the primary sector (10 thousand RMB Yuan);
- UGDP3: the added value upper limit of the tertiary sector (10 thousand RMB Yuan);
- LGDP3: the added value lower limit of the tertiary sector (10 thousand RMB Yuan);
4. Study Area and Data Sources
4.1. Site Description
4.2. Data Sources
5. Scenario Establishment
| Items | 2015 | 2020 | ||
|---|---|---|---|---|
| Lower limits | Upper limits | Lower limits | Upper limits | |
| CAPCOD± (tons) | 3558.06 | 3558.06 | 3558.06 | 3558.06 |
| CAPSO2± (tons) | 34,520 | 41,311 | 34,520 | 41,311 |
| CAPNH3-N± (tons) | 351 | 429 | 315 | 385 |
| MAXW± (10,000 tons) | 45,057.2 | 60,960.0 | 48,587.7 | 65,736.3 |
| MAXG ± (10,000 tce) | 407.4 | 456.8 | 576.2 | 640.2 |
6. Results and Discussion
6.1. Industry Scale and Structure
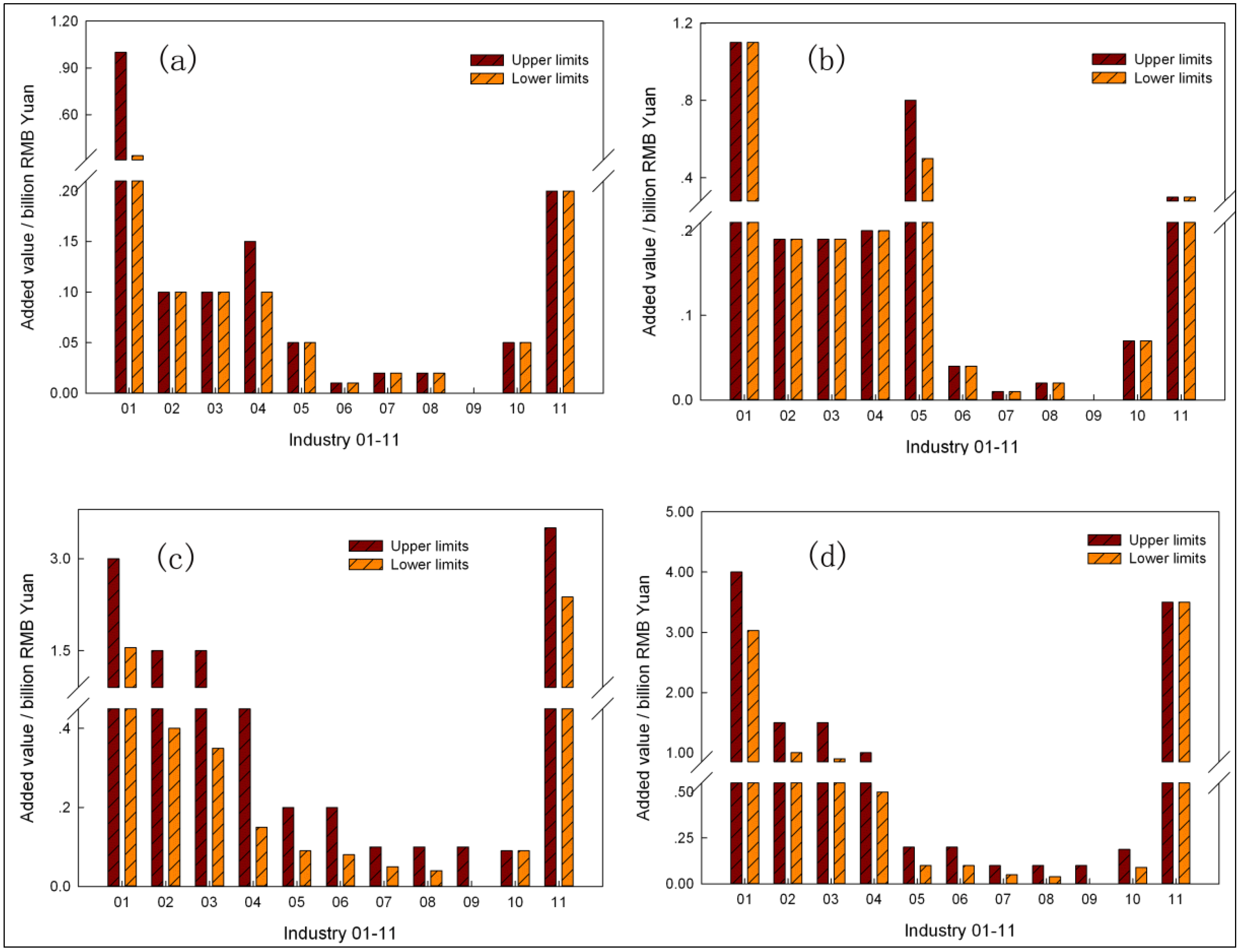
6.2. Economic Development Scale
| 2015 | 2020 | |||||
|---|---|---|---|---|---|---|
| Upper limits (billion RMB Yuan) | Lower limits (billion RMB Yuan) | Percentage (%) | Upper limits (billion RMB Yuan) | Lower limits (billion RMB Yuan) | Percentage (%) | |
| Primary sector | 0.20 | 0.20 | 5–11 | 0.20 | 0.20 | 3–6 |
| Secondary sector | 1.70 | 0.99 | 46–55 | 2.92 | 2.62 | 41–76 |
| Tertiary sector | 1.82 | 0.60 | 34–49 | 4.03 | 0.61 | 18–56 |
| Tongzhou’s GDP | 3.72 | 1.79 | 7.15 | 3.43 | ||
| 2015 | 2020 | |||||
|---|---|---|---|---|---|---|
| Upper limits (billion RMB Yuan) | Lower limits (billion RMB Yuan) | Percentage (%) | Upper limits (billion RMB Yuan) | Lower limits (billion RMB Yuan) | Percentage (%) | |
| Primary sector | 0.40 | 0.40 | 2–5 | 0.70 | 0.70 | 1–4 |
| Secondary sector | 10.79 | 5.17 | 56–60 | 12.39 | 9.31 | 26–58 |
| Tertiary sector | 8.20 | 3.00 | 35–42 | 34.74 | 6.10 | 38–73 |
| Tongzhou’s GDP | 19.39 | 8.57 | 47.82 | 16.11 | ||
6.3. Population Size
| 2015 | 2020 | |||||
|---|---|---|---|---|---|---|
| Upper limits (thousand persons) | Lower limits (thousand persons) | Percentage (%) | Upper limits (thousand persons) | Lower limits (thousand persons) | Percentage (%) | |
| Primary sector | 29.45 | 27.15 | 15–27 | 23.15 | 22.17 | 8–17 |
| Secondary sector | 89.84 | 50.78 | 46–50 | 126.29 | 91.40 | 44–69 |
| Tertiary sector | 77.16 | 22.78 | 23–39 | 134.18 | 18.28 | 14–47 |
| Total working population | 196.46 | 100.71 | 283.63 | 131.85 | ||
| 2015 | 2020 | |||||
|---|---|---|---|---|---|---|
| Upper limits (thousand persons) | Lower limits (thousand persons) | Percentage (%) | Upper limits (thousand persons) | Lower limits (thousand persons) | Percentage (%) | |
| Primary sector | 50.91 | 42.31 | 7–14 | 74.04 | 68.27 | 5–18 |
| Secondary sector | 383.55 | 167.72 | 53–57 | 238.23 | 143.42 | 17–38 |
| Tertiary sector | 288.91 | 86.55 | 29–40 | 1068.90 | 166.39 | 44–78 |
| Total working population | 723.37 | 296.58 | 1381.17 | 378.08 | ||

| Scenario 1 (thousand RMB Yuan/person) | Scenario 2 (thousand RMB Yuan/person) | |||||||
|---|---|---|---|---|---|---|---|---|
| 2015 | 2020 | 2015 | 2020 | |||||
| Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | |
| Primary sector | 7.37 | 6.79 | 9.02 | 8.64 | 9.45 | 7.86 | 10.25 | 9.45 |
| Secondary sector | 19.50 | 18.92 | 28.67 | 23.12 | 30.83 | 28.13 | 64.91 | 52.01 |
| Tertiary sector | 26.34 | 23.59 | 33.37 | 30.03 | 34.66 | 28.38 | 36.66 | 32.50 |
| Total | 18.94 | 17.77 | 26.01 | 25.21 | 28.90 | 26.81 | 42.61 | 34.62 |
7. Conclusions
Acknowledgments
Conflicts of interests
References
- Figuières, C.; Guyomard, H.; Rotillon, G. Sustainable development: Between moral injunctions and natural constraints. Sustainability 2010, 2, 3608–3622. [Google Scholar] [CrossRef]
- Bishop, A.B. Carrying Capacity in Regional Environmental Management; United States Environmental Protection Agency: Washington, DC, USA, 1974. [Google Scholar]
- Arrow, K.; Bolin, B.; Costanza, R.; Dasgupta, P.; Folke, C.; Holling, C.S.; Jansson, B.O.; Levin, S.; Mäler, K.G.; Perrings, C. Economic growth, carrying capacity, and the environment. Ecol. Econ. 1995, 15, 91–95. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Xia, J.; Wang, Z.G. Integrated water resources carrying capacity in Tongzhou district, Beijing city. J. Res. Ecol. 2010, 1, 253–258. [Google Scholar]
- Ahmadi, P.; Dincer, I.; Rosen, M.A. Thermodynamic modeling and multi-objective evolutionary-based optimization of a new multigeneration energy system. Energ. Convers. Manag. 2013, 76, 282–300. [Google Scholar] [CrossRef]
- Kaviri, A.G.; Jaafar, M.N.M.; Lazim, T.M.; Barzegaravval, H. Exergoenvironmental optimization of heat recovery steam generators in combined cycle power plant through energy and exergy analysis. Energ. Convers. Manag. 2013, 67, 27–33. [Google Scholar] [CrossRef]
- Ahmadi, P.; Dincer, I.; Rosen, M.A. Performance assessment and optimization of a novel integrated multigeneration system for residential buildings. Energ. Build. 2013, 67, 568–578. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, J. Predicting and optimization of energy consumption using system dynamics-fuzzy multiple objective programming in world heritage areas. Energy 2013, 49, 19–31. [Google Scholar] [CrossRef]
- Giannoccaro, I.; Pontrandolfo, P.; Scozzi, B. A fuzzy echelon approach for inventory management in supply chains. Eur. J. Oper. Res. 2003, 149, 185–196. [Google Scholar] [CrossRef]
- Rong, A.; Lahdelma, R. Fuzzy chance constrained linear programming model for optimizing the scrap charge in steel production. Eur. J. Oper. Res. 2008, 186, 953–964. [Google Scholar] [CrossRef]
- Petrovic, D.; Roy, R.; Petrovic, R. Supply chain modelling using fuzzy sets. Int. J. Prod. Econ. 1999, 59, 443–453. [Google Scholar] [CrossRef]
- Salema, M.I.G.; Barbosa-Povoa, A.P.; Novais, A.Q. An optimization model for the design of a capacitated multi-product reverse logistics network with uncertainty. Eur. J. Oper. Res. 2007, 179, 1063–1077. [Google Scholar] [CrossRef]
- Shahnazari-Shahrezaei, P.; Tavakkoli-Moghaddam, R.; Kazemipoor, H. Solving a multi-objective multi-skilled manpower scheduling model by a fuzzy goal programming approach. Appl. Math. Model. 2013, 37, 5424–5443. [Google Scholar] [CrossRef]
- Qin, X.S.; Xu, Y. Analyzing urban water supply through an acceptability-index-based interval approach. Adv. Water. Resour. 2011, 34, 873–886. [Google Scholar] [CrossRef]
- Simic, V.; Dimitrijevic, B. Risk explicit interval linear programming model for long-term planning of vehicle recycling in the EU legislative context under uncertainty. Resour. Conserv. Recy. 2013, 73, 197–210. [Google Scholar] [CrossRef]
- Dong, C.; Huang, G.; Cai, Y.; Xu, Y. An interval-parameter minimax regret programming approach for power management systems planning under uncertainty. Appl. Energ. 2011, 88, 2835–2845. [Google Scholar] [CrossRef]
- Sabri, E.H.; Beamon, B.M. A multi-objective approach to simultaneous strategic and operational planning in supply chain design. Omega 2000, 28, 581–598. [Google Scholar] [CrossRef]
- Shastri, Y.; Diwekar, U. Sensor placement in water networks: A stochastic programming approach. J. Water Resour. Plann. Manag. 2006, 132, 192–203. [Google Scholar] [CrossRef]
- Guan, Z.; Philpott, A.B. A multistage stochastic programming model for the New Zealand dairy industry. Int. J. Prod. Econ. 2011, 134, 289–299. [Google Scholar] [CrossRef]
- Ahmed, S.; King, A.J.; Parija, G. A multi-stage stochastic integer programming approach for capacity expansion under uncertainty. J. Global. Optim. 2003, 26, 3–24. [Google Scholar] [CrossRef]
- Kouwenberg, R. Scenario generation and stochastic programming models for asset liability management. Eur. J. Oper. Res. 2001, 134, 279–292. [Google Scholar] [CrossRef]
- Gu, J.; Guo, P.; Huang, G.; Shen, N. Optimization of the industrial structure facing sustainable development in resource-based city subjected to water resources under uncertainty. Stoch. Environ. Res. Risk Assess. 2013, 27, 659–673. [Google Scholar] [CrossRef]
- Li, H.; Zhang, K. Development of a fuzzy-stochastic nonlinear model to incorporate aleatoric and epistemic uncertainty. J. Contam. Hydrol. 2010, 111, 1–12. [Google Scholar] [CrossRef]
- Lacagnina, V.; Pecorella, A. A stochastic soft constraints fuzzy model for a portfolio selection problem. Fuzzy Set. Syst. 2006, 157, 1317–1327. [Google Scholar] [CrossRef]
- Li, P.; Chen, B. Fsilp: Fuzzy-stochastic-interval linear programming for supporting municipal solid waste management. J. Environ. Manag. 2011, 92, 1198–1209. [Google Scholar] [CrossRef]
- Li, X.M. Study on urban environmental carrying capacity based on an inexact fuzzy multiobjective programming model. Adv. Mater. Res. 2012, 518, 1226–1232. [Google Scholar]
- Wu, S.; Huang, G.; Guo, H. An interactive inexact-fuzzy approach for multiobjective planning of water resource systems. Water Sci. Technol. 1997, 36, 235–242. [Google Scholar]
- Huang, G.H. IPWM: An interval parameter water quality management model. Eng. Optimiz. 1996, 26, 79–103. [Google Scholar] [CrossRef]
- Wang, L.; Meng, W.; Guo, H.; Zhang, Z.; Liu, Y.; Fan, Y. An interval fuzzy multiobjective watershed management model for the lake Qionghai watershed, China. Water Resour. Manag. 2006, 20, 701–721. [Google Scholar] [CrossRef]
- Zou, R.; Guo, H.; Chen, B. A multiobjective approach for integrated environmental economic planning under uncertainty. Civ. Eng. Environ. Syst. 2000, 17, 267–291. [Google Scholar] [CrossRef]
- Li, Y.F.; Li, Y.P.; Huang, G.H.; Zhou, M.; Xie, Y.L. Modeling for environmental-economic management systems under uncertainty. Procedia Environ. Sci. 2010, 2, 192–198. [Google Scholar] [CrossRef]
- Dvarioniene, J.; Stasiskiene, Z. Integrated water resource management model for process industry in lithuania. J. Clean. Prod. 2007, 15, 950–957. [Google Scholar] [CrossRef]
- Shadiya, O.O.; Satish, V.; High, K.A. Process enhancement through waste minimization and multiobjective optimization. J. Clean. Prod. 2012, 31, 137–149. [Google Scholar] [CrossRef]
- O’Regan, B.; Moles, R. Using system dynamics to model the interaction between environmental and economic factors in the mining industry. J. Clean. Prod. 2006, 14, 689–707. [Google Scholar] [CrossRef]
- Zhou, M.; Chen, Q.; Cai, Y. Optimizing the industrial structure of a watershed in association with economic-environmental consideration: An inexact fuzzy multi-objective programming model. J. Clean. Prod. 2012, 42, 116–131. [Google Scholar] [CrossRef]
- Swart, R.J.; Raskin, P.; Robinson, J. The problem of the future: Sustainability science and scenario analysis. Global. Environ. Change 2004, 14, 137–146. [Google Scholar] [CrossRef]
- Huang, G.; Baetz, B.; Patry, G. Grey fuzzy integer programming: An application to regional waste management planning under uncertainty. Socioecon. Plann. Sci. 1995, 29, 17–38. [Google Scholar] [CrossRef]
- Guo, H.C. Environmental Planning Methods and Applications; Chemical Industry Press: Beijing, China, 2006. [Google Scholar]
Appendix
| Items | Scenario 1 | Scenario 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| 2015 | 2020 | 2015 | 2020 | |||||
| Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | |
| REMCOD± (%) | 0.86 | 0.90 | 0.90 | 0.95 | 0.86 | 0.90 | 0.90 | 0.95 |
| PCOD± (kg/people) | 77.20 | 79.20 | 79.20 | 81.20 | 26.00 | 27.00 | 27.00 | 28.00 |
| PWWT± (%) | 0.64 | 0.67 | 0.67 | 0.70 | 0.90 | 0.95 | 0.95 | 1.00 |
| REMNH3-N± (%) | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 0.93 |
| PNH3-N± (kg/people) | 7.20 | 7.30 | 7.30 | 7.50 | 2.10 | 2.20 | 2.20 | 2.30 |
| PSO2± (kg/people) | 0.03 | 0.06 | 0.01 | 0.03 | 0.001 | 0.006 | 0.001 | 0.003 |
| PWD± (ton/people) | 41.45 | 42.50 | 40.42 | 41.45 | 28.16 | 29.93 | 26.95 | 28.16 |
| PGD± (ton/people) | 0.53 | 0.56 | 0.56 | 0.59 | 0.46 | 0.50 | 0.50 | 0.53 |
| 2015 | INWWTj± (I01–I11), AGWWT± (I12) and SEWWT± (I13) (%) | INWWDj± (I01–I11), AGWWD± (I12) and SEWWD± (I13) (ton/10 thousand RMB Yuan) | INCODj± (I01–I11), AGCOD± (I12) and SECOD± (I13)(kg/million RMB Yuan) | INNH3-Nj± (I01–I11), AGNH3-N± (I12) and SENH3-N± (I13) (kg/million RMB Yuan) | INSO2j± (I01–I11), AGSO2± (I12) and SESO2± (I13) (kg/million RMB Yuan) | INWDj± (I01–I11), AGWD± (I12) and SEWD± (I13) (ton/10 thousand RMB Yuan) | INGDj± (I01–I11), AGGD± (I12) and SEGD± (I13) (ton/10 thousand RMB Yuan) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | |
| I01 | 0.60 | 0.69 | 1.68 | 2.73 | 49.76 | 81.80 | 8.29 | 13.63 | 23.51 | 48.41 | 7.12 | 10.06 | 0.55 | 0.58 |
| I02 | 0.64 | 0.78 | 15.50 | 18.53 | 468.64 | 580.40 | 52.88 | 63.29 | 58.18 | 146.29 | 27.76 | 33.50 | 0.86 | 0.90 |
| I03 | 0.60 | 0.69 | 11.73 | 13.63 | 629.95 | 1024.63 | 51.12 | 66.76 | 46.25 | 80.90 | 23.75 | 29.27 | 1.02 | 1.03 |
| I04 | 0.60 | 0.69 | 8.24 | 10.62 | 173.82 | 230.78 | 28.97 | 38.46 | 52.8979 | 128.41 | 15.11 | 19.81 | 0.72 | 0.75 |
| I05 | 0.60 | 0.69 | 7.91 | 9.32 | 179.75 | 229.27 | 24.22 | 30.64 | 30.53 | 60.99 | 12.20 | 15.41 | 0.36 | 0.38 |
| I06 | 0.60 | 0.70 | 1.61 | 3.06 | 24.20 | 45.98 | 42.25 | 58.00 | 54.91 | 85.77 | 3.06 | 4.94 | 0.77 | 0.86 |
| I07 | 0.60 | 0.69 | 12.95 | 15.41 | 558.70 | 707.18 | 99.39 | 124.62 | 415.74 | 676.32 | 30.61 | 40.01 | 0.80 | 0.84 |
| I08 | 0.60 | 0.69 | 3.30 | 4.50 | 50.21 | 63.77 | 20.92 | 26.58 | 1136.47 | 1585.98 | 13.81 | 19.07 | 2.37 | 2.76 |
| I09 | 0.60 | 0.69 | 71.29 | 81.33 | 4555.86 | 5185.48 | 253.19 | 288.21 | 204.36 | 426.77 | 136.35 | 158.21 | 1.45 | 1.69 |
| I10 | 0.50 | 0.60 | 35.66 | 40.75 | 265.00 | 280.00 | 25.01 | 34.27 | 68.00 | 266.00 | 41.95 | 48.40 | 0.81 | 0.92 |
| I11 | 0 | 0 | 4.12 | 4.86 | 0.00 | 0.00 | 0.00 | 0.00 | 3.92 | 11.85 | 13.51 | 16.15 | 0.23 | 0.26 |
| I12 | 0 | 0 | 482.18 | 596.64 | 960.00 | 1020.00 | 103.00 | 107.00 | 110.33 | 177.11 | 1178.00 | 1356.00 | 1.69 | 1.73 |
| I13 | 0.90 | 0.95 | 9.28 | 10.37 | 470.33 | 482.25 | 56.12 | 57.88 | 6.83 | 26.04 | 12.33 | 15.94 | 0.28 | 0.32 |
| 2020 | INWWTj± (I01–I11), AGWWT± (I12) and SEWWT± (I13) (%) | INWWDj± (I01–I11), AGWWD± (I12) and SEWWD± (I13) (ton/10 thousand RMB Yuan) | INCODj± (I01–I11), AGCOD± (I12) and SECOD± (I13) (kg/million RMB Yuan) | INNH3-Nj± (I01–I11), AGNH3-N± (I12) and SENH3-N± (I13) (kg/million RMB Yuan) | INSO2j± (I01–I11), AGSO2± (I12) and SESO2± (I13) (kg/million RMB Yuan) | INWDj± (I01–I11), AGWD± (I12) and SEWD± (I13) (ton/10 thousand RMB Yuan) | INGDj± (I01–I11), AGGD± (I12) and SEGD± (I13) (ton/10 thousand RMB Yuan) | |||||||
| Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | |
| I01 | 0.69 | 0.8 | 0.63 | 1.68 | 18.96 | 49.76 | 3.16 | 8.29 | 11.41 | 23.51 | 4.40 | 7.12 | 0.54 | 0.55 |
| I02 | 0.78 | 0.95 | 12.47 | 15.5 | 357.27 | 468.64 | 42.46 | 52.88 | 14.53 | 58.19 | 22.39 | 27.76 | 0.84 | 0.86 |
| I03 | 0.69 | 0.8 | 9.83 | 11.73 | 224.72 | 629.95 | 36.90 | 51.12 | 25.33 | 46.25 | 19.73 | 23.75 | 1.00 | 1.02 |
| I04 | 0.69 | 0.8 | 5.86 | 8.24 | 123.71 | 173.82 | 20.62 | 28.97 | 15.04 | 52.90 | 11.13 | 15.11 | 0.70 | 0.72 |
| I05 | 0.69 | 0.8 | 6.5 | 7.91 | 130.91 | 179.75 | 17.89 | 24.22 | 10.12 | 30.53 | 9.20 | 12.20 | 0.35 | 0.36 |
| I06 | 0.7 | 0.8 | 0.16 | 1.61 | 2.43 | 24.20 | 26.50 | 42.25 | 24.05 | 54.91 | 1.17 | 3.06 | 0.69 | 0.78 |
| I07 | 0.69 | 0.8 | 10.49 | 12.95 | 446.10 | 558.70 | 80.11 | 99.39 | 201.59 | 415.75 | 23.75 | 30.61 | 0.78 | 0.80 |
| I08 | 0.69 | 0.8 | 2.11 | 3.3 | 29.84 | 50.21 | 12.43 | 20.92 | 691.06 | 1136.47 | 9.22 | 13.81 | 2.15 | 2.37 |
| I09 | 0.69 | 0.8 | 61.24 | 71.29 | 3970.14 | 4555.86 | 220.63 | 253.19 | 66.50 | 204.36 | 116.90 | 136.35 | 1.31 | 1.45 |
| I10 | 0.65 | 0.66 | 30.57 | 35.66 | 250.00 | 265.00 | 15.75 | 25.01 | 167.00 | 68.00 | 35.51 | 41.95 | 0.70 | 0.81 |
| I11 | 0 | 0 | 3.39 | 4.12 | 0.00 | 0.00 | 0.00 | 0.00 | 1.07 | 3.92 | 11.31 | 13.51 | 0.21 | 0.23 |
| I12 | 0 | 0 | 420.00 | 482.18 | 930.00 | 960.00 | 99.00 | 103.00 | 11.41 | 23.51 | 1000.00 | 1178.00 | 1.66 | 1.69 |
| I13 | 0.95 | 1 | 8.19 | 9.28 | 461.04 | 470.33 | 54.49 | 56.12 | 1.48 | 6.83 | 11.15 | 12.33 | 0.25 | 0.28 |
| 2015 | INWWTj± (I01–I11), AGWWT± (I12) and SEWWT± (I13) (%) | INWWDj± (I01–I11), AGWWD± (I12) and SEWWD± (I13) (ton/10 thousand RMB Yuan) | INCODj± (I01–I11), AGCOD± (I12) and SECOD± (I13) (kg/million RMB Yuan) | INNH3-Nj± (I01–I11), AGNH3-N± (I12) and SENH3-N± (I13) (kg/million RMB Yuan) | INSO2j± (I01–I11), AGSO2± (I12) and SESO2± (I13) (kg/million RMB Yuan) | INWDj± (I01–I11), AGWD± (I12) and SEWD± (I13) (ton/10 thousand RMB Yuan) | INGDj± (I01–I11), AGGD± (I12) and SEGD± (I13) (ton/10 thousand RMB Yuan) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | |
| I01 | 0.60 | 0.69 | 2.71 | 4.82 | 41.00 | 72.00 | 6.80 | 12.00 | 20.00 | 40.00 | 5.83 | 8.92 | 0.41 | 0.48 |
| I02 | 0.64 | 0.78 | 6.63 | 15.49 | 100.00 | 350.00 | 17.00 | 42.00 | 44.00 | 120.00 | 12.49 | 23.80 | 0.64 | 0.75 |
| I03 | 0.60 | 0.69 | 9.26 | 16.37 | 140.00 | 250.00 | 20.00 | 40.00 | 33.00 | 67.00 | 15.60 | 24.70 | 0.73 | 0.85 |
| I04 | 0.60 | 0.69 | 6.70 | 12.09 | 100.00 | 180.00 | 17.00 | 30.00 | 40.00 | 110.00 | 10.22 | 16.53 | 0.54 | 0.62 |
| I05 | 0.60 | 0.69 | 4.82 | 9.36 | 70.00 | 170.00 | 12.00 | 25.00 | 23.00 | 51.00 | 5.84 | 11.61 | 0.27 | 0.32 |
| I06 | 0.50 | 0.70 | 1.54 | 3.06 | 13.00 | 83.00 | 42.00 | 58.00 | 0.00 | 0.00 | 3.06 | 4.94 | 0.76 | 0.89 |
| I07 | 0.60 | 0.69 | 6.30 | 11.80 | 190.00 | 350.00 | 31.00 | 59.00 | 390.00 | 640.00 | 20.79 | 30.74 | 0.6 | 0.69 |
| I08 | 0.60 | 0.69 | 2.15 | 3.91 | 26.00 | 47.00 | 11.00 | 20.00 | 1000.00 | 1500.00 | 10.02 | 16.07 | 2.37 | 2.76 |
| I09 | 0.60 | 0.69 | 18.64 | 63.27 | 840.00 | 2800.00 | 47.00 | 160.00 | 200.00 | 430.00 | 41.48 | 96.82 | 1.45 | 1.69 |
| I10 | 0.50 | 0.65 | 21.23 | 30.89 | 120.00 | 190.00 | 26.00 | 34.00 | 170.00 | 270.00 | 26.90 | 37.98 | 0.67 | 0.78 |
| I11 | 0.50 | 0.65 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.20 | 14.00 | 13.10 | 15.65 | 0.3 | 0.32 |
| I12 | 0.00 | 0.00 | 450.37 | 526.24 | 1020.00 | 1070.00 | 103.00 | 107.00 | 80.00 | 160.00 | 1164.00 | 1355.00 | 1.51 | 1.59 |
| I13 | 0.60 | 0.80 | 7.53 | 12.76 | 470.00 | 480.00 | 56.00 | 58.00 | 8.70 | 30.00 | 9.41 | 15.94 | 0.35 | 0.37 |
| 2020 | INWWTj± (I01–I11), AGWWT± (I12) and SEWWT± (I13) (%) | INWWDj± (I01–I11), AGWWD± (I12) and SEWWD± (I13) (ton/10 thousand RMB Yuan) | INCODj± (I01–I11), AGCOD± (I12) and SECOD± (I13) (kg/million RMB Yuan) | INNH3-Nj± (I01–I11), AGNH3-N± (I12) and SENH3-N± (I13) (kg/million RMB Yuan) | INSO2j± (I01–I11), AGSO2± (I12) and SESO2± (I13) (kg/million RMB Yuan) | INWDj± (I01–I11), AGWD± (I12) and SEWD± (I13) (ton/10 thousand RMB Yuan) | INGDj± (I01–I11), AGGD± (I12) and SEGD± (I13) (ton/10 thousand RMB Yuan) | |||||||
| Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | Lower limits | Upper limits | |
| I01 | 0.69 | 0.80 | 0.98 | 2.71 | 15.00 | 41.00 | 2.50 | 6.80 | 7.30 | 20.00 | 3.42 | 5.83 | 0.34 | 0.41 |
| I02 | 0.78 | 0.95 | 0.61 | 6.63 | 9.00 | 100.00 | 1.50 | 17.00 | 9.00 | 44.00 | 5.20 | 12.49 | 0.53 | 0.64 |
| I03 | 0.69 | 0.80 | 2.89 | 9.26 | 40.00 | 140.00 | 7.00 | 20.00 | 15.00 | 170.00 | 7.90 | 15.60 | 0.61 | 0.73 |
| I04 | 0.69 | 0.80 | 2.08 | 6.70 | 31.00 | 100.00 | 5.20 | 17.00 | 9.60 | 40.00 | 4.97 | 10.22 | 0.45 | 0.54 |
| I05 | 0.69 | 0.80 | 0.33 | 4.82 | 4.90 | 70.00 | 0.80 | 12.00 | 6.50 | 23.00 | 0.91 | 5.84 | 0.22 | 0.27 |
| I06 | 0.70 | 0.90 | 0.16 | 1.54 | 4.50 | 13.00 | 26.00 | 42.00 | 0.00 | 0.00 | 1.17 | 3.06 | 0.63 | 0.76 |
| I07 | 0.69 | 0.80 | 1.30 | 6.30 | 39.00 | 190.00 | 6.50 | 31.00 | 180.00 | 390.00 | 12.65 | 20.79 | 0.5 | 0.60 |
| I08 | 0.69 | 0.80 | 0.25 | 2.15 | 3.00 | 26.00 | 1.27 | 11.00 | 580.00 | 1000.00 | 5.48 | 10.02 | 1.98 | 2.37 |
| I09 | 0.69 | 0.80 | 3.32 | 18.64 | 150.00 | 840.00 | 8.30 | 47.00 | 61.00 | 200.00 | 19.34 | 41.48 | 1.21 | 1.45 |
| I10 | 0.65 | 0.80 | 11.73 | 21.23 | 50.00 | 120.00 | 15.00 | 26.00 | 70.00 | 170.00 | 15.91 | 26.90 | 0.56 | 0.67 |
| I11 | 0.65 | 0.80 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.50 | 5.20 | 11.25 | 13.10 | 0.29 | 0.30 |
| I12 | 0.00 | 0.00 | 390.18 | 450.37 | 900.00 | 1020.00 | 99.00 | 103.00 | 40.00 | 80.00 | 1000.00 | 1164.00 | 1.48 | 1.51 |
| I13 | 0.80 | 1.00 | 4.45 | 7.53 | 450.00 | 470.00 | 50.00 | 56.00 | 2.00 | 8.70 | 5.56 | 9.41 | 0.34 | 0.35 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, W.; Zeng, W. Optimizing the Regional Industrial Structure Based on the Environmental Carrying Capacity: An Inexact Fuzzy Multi-Objective Programming Model. Sustainability 2013, 5, 5391-5415. https://doi.org/10.3390/su5125391
Wang W, Zeng W. Optimizing the Regional Industrial Structure Based on the Environmental Carrying Capacity: An Inexact Fuzzy Multi-Objective Programming Model. Sustainability. 2013; 5(12):5391-5415. https://doi.org/10.3390/su5125391
Chicago/Turabian StyleWang, Wenyi, and Weihua Zeng. 2013. "Optimizing the Regional Industrial Structure Based on the Environmental Carrying Capacity: An Inexact Fuzzy Multi-Objective Programming Model" Sustainability 5, no. 12: 5391-5415. https://doi.org/10.3390/su5125391
APA StyleWang, W., & Zeng, W. (2013). Optimizing the Regional Industrial Structure Based on the Environmental Carrying Capacity: An Inexact Fuzzy Multi-Objective Programming Model. Sustainability, 5(12), 5391-5415. https://doi.org/10.3390/su5125391