Meeting the Electrical Energy Needs of a Residential Building with a Wind-Photovoltaic Hybrid System
Abstract
:1. Introduction
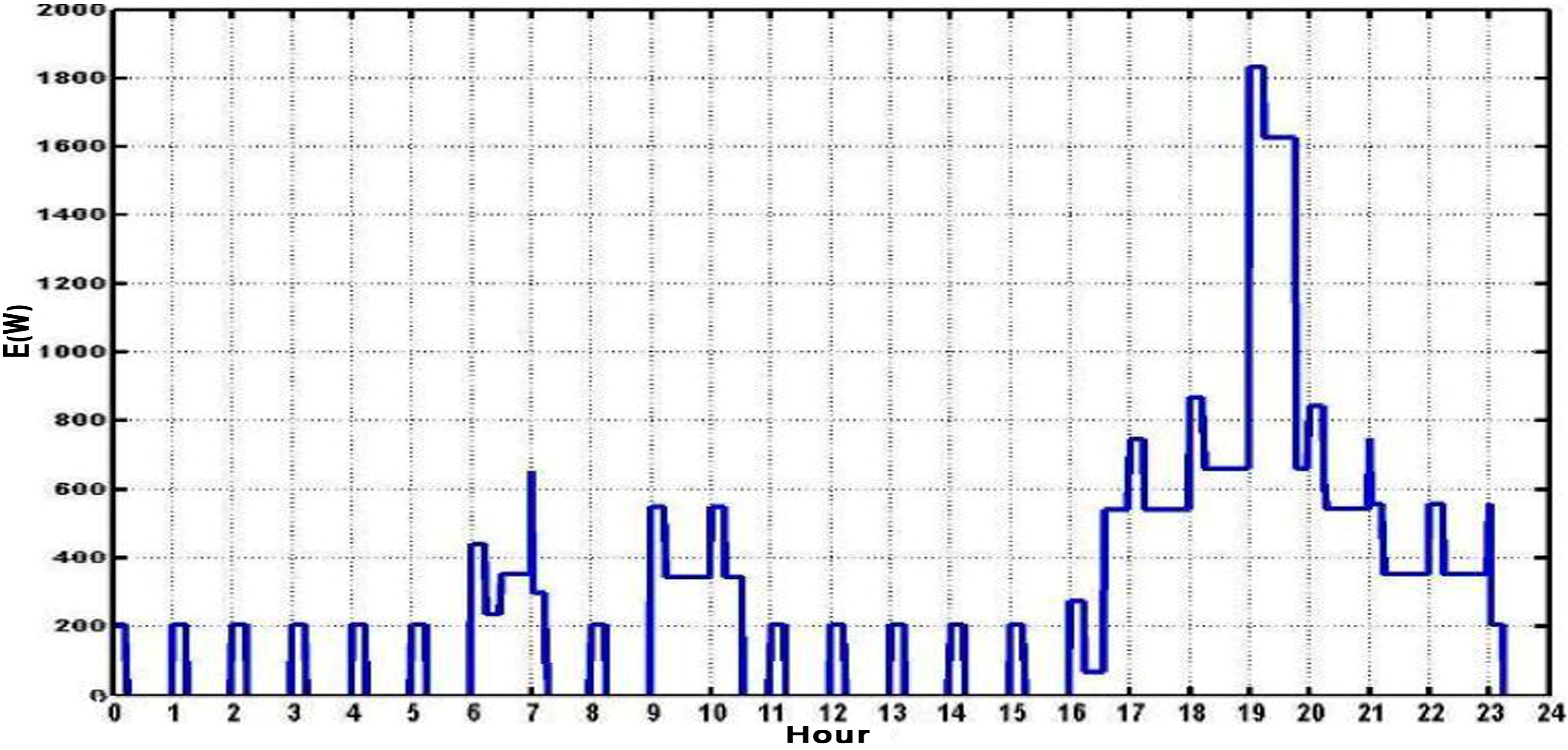
2. Description of Building

| Hour | Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.051 | 0.051 | 0.055 | 0.055 | 0.064 | 0.068 | 0.07 | 0.07 | 0.067 | 0.0615 | 0.056 | 0.067 |
| 2 | 0.051 | 0.051 | 0.055 | 0.055 | 0.064 | 0.068 | 0.07 | 0.07 | 0.067 | 0.0615 | 0.056 | 0.067 |
| 3 | 0.051 | 0.051 | 0.055 | 0.055 | 0.064 | 0.068 | 0.07 | 0.07 | 0.067 | 0.0615 | 0.056 | 0.067 |
| 4 | 0.051 | 0.051 | 0.055 | 0.055 | 0.064 | 0.068 | 0.07 | 0.07 | 0.067 | 0.0615 | 0.056 | 0.067 |
| 5 | 0.051 | 0.051 | 0.055 | 0.055 | 0.064 | 0.068 | 0.07 | 0.07 | 0.067 | 0.0615 | 0.056 | 0.067 |
| 6 | 0.051 | 0.051 | 0.055 | 0.055 | 0.064 | 0.068 | 0.07 | 0.07 | 0.067 | 0.0615 | 0.056 | 0.067 |
| 7 | 0.41 | 0,41 | 0.055 | 0.055 | 0.064 | 0.068 | 0.07 | 0.07 | 0.067 | 0.0615 | 0.056 | 0.067 |
| 8 | 0.21 | 0.21 | 0.21 | 0.21 | 0.217 | 0.221 | 0.217 | 0.223 | 0.22 | 0.215 | 0.21 | 0.204 |
| 9 | 0.21 | 0.21 | 0.21 | 0.21 | 0.217 | 0.221 | 0.217 | 0.223 | 0.22 | 0.215 | 0.21 | 0.204 |
| 10 | 0.18 | 0.18 | 0.189 | 0.189 | 0.193 | 0.197 | 0.2 | 0.199 | 0.196 | 0.191 | 0.185 | 0.181 |
| 11 | 0.18 | 0.18 | 0.189 | 0.189 | 0.193 | 0.197 | 0.2 | 0.199 | 0.196 | 0.191 | 0.185 | 0.181 |
| 12 | 0.18 | 0.18 | 0.189 | 0.189 | 0.193 | 0.197 | 0.2 | 0.199 | 0.196 | 0.191 | 0.185 | 0.181 |
| 13 | 0.05 | 0.05 | 0.06 | 0.06 | 0.064 | 0.068 | 0.07 | 0.07 | 0.067 | 0.0615 | 0.056 | 0.067 |
| 14 | 0.05 | 0.05 | 0.06 | 0.06 | 0.064 | 0.068 | 0.07 | 0.07 | 0.067 | 0.0615 | 0.056 | 0.067 |
| 15 | 0.05 | 0.05 | 0.06 | 0.06 | 0.064 | 0.068 | 0.07 | 0.07 | 0.067 | 0.0615 | 0.056 | 0.067 |
| 16 | 0.051 | 0.051 | 0.055 | 0.055 | 0.064 | 0.068 | 0.071 | 0.07 | 0.067 | 0.061 | 0.056 | 0.067 |
| 17 | 0.714 | 0.242 | 0.246 | 0.25 | 0.254 | 0.258 | 0.261 | 0.26 | 0.257 | 0.252 | 0.718 | 0.714 |
| 18 | 0.714 | 0.714 | 0.718 | 0.723 | 0.254 | 0.258 | 0.261 | 0.732 | 0.729 | 0.724 | 0.718 | 0.714 |
| 19 | 0.805 | 0.806 | 0.807 | 0.814 | 0.817 | 0.822 | 0.817 | 0.823 | 0.82 | 0.815 | 0.809 | 0.805 |
| 20 | 0.805 | 0.806 | 0.807 | 0.814 | 0.817 | 0.822 | 0.817 | 0.823 | 0.82 | 0.815 | 0.809 | 0.805 |
| 21 | 0.71 | 0.71 | 0.714 | 0.719 | 0.723 | 0.727 | 0.73 | 0.729 | 0.726 | 0.721 | 0.715 | 0.711 |
| 22 | 0.52 | 0.52 | 0.524 | 0.53 | 0.533 | 0.538 | 0.54 | 0.539 | 0.536 | 0.53 | 0.524 | 0.52 |
| 23 | 0.405 | 0.405 | 0.409 | 0.414 | 0.814 | 0.422 | 0.424 | 0.417 | 0.421 | 0.416 | 0.41 | 0.406 |
| 24 | 0.051 | 0.051 | 0.055 | 0.06 | 0.064 | 0.058 | 0.071 | 0.07 | 0.067 | 0.062 | 0.056 | 0.052 |
3. Mathematical Models of the Systems

3.1. Basic Mathematical Model of PV Modules
| PV Module Type | ηr (%) | NOCT (°C) | ρp (1/°C) |
|---|---|---|---|
| Mono-Si | 13 | 45 | 0.4 |
| Poly-Si | 11 | 45 | 0.4 |
| a-Si | 5 | 50 | 0.11 |
| CdTe | 7 | 46 | 0.24 |
| CIS | 7.5 | 47 | 0.46 |
3.2. Basic Mathematical Model of Wind Generator
| Wind turbine charateritics | Values |
|---|---|
| Cut-in wind speed (m/s) | 3.1 |
| Rate wind speed (m/s) | 13.8 |
| Rated power (kW) | 10 |
| Furling wind speed (m/s) | 15.6 |
| Type | 3 blade up wind |
| Swept area (m2) | 38.47 |
| Gear box | Non-direct drive |
| Temperature range (°C) | −40 to 60 |
| Generator | Parameters magnet alternator |
| Tower height (m) | 24 |
| ui (m/s) | Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. | Annual |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1–3 | 59 | 62 | 82 | 79 | 71 | 76 | 98 | 106 | 119 | 96 | 64 | 60 | 752 |
| 4–6 | 25 | 36 | 65 | 61 | 53 | 67 | 73 | 51 | 42 | 37 | 31 | 8 | 437 |
| 7–10 | 15 | 22 | 20 | 32 | 27 | 27 | 7 | 5 | 6 | 10 | 14 | 2 | 161 |
| 11–16 | 0 | 2 | 2 | 7 | 12 | 3 | 2 | 1 | 0 | 2 | 2 | 2 | 29 |
| >16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
4. Optimization Procedure




| Option | PV Model | PV Area (m2) | Wind Turbine Model | Wind Turbine Units | Battery Capacity (kWh) | Electrical Cost (US$/kWh) |
|---|---|---|---|---|---|---|
| PV + Battery | Mono-Si | 32 | - | - | 12.9 | 0.83 |
| Wind turbine + Battery | - | - | Bergey Excel-S | 12 | 8.1 | 1.11 |
| PV + Wind turbine + Battery | Mono-Si | 26.6 | Bergey Excel-S | 1 | 8.9 | 0.62 |

5. Conclusions
Author Contributions
Nomenclature
| Ppv | Photovoltaic output power (kW) |
| A | Surface area of PV panel (m2) |
| H | Electrical conversion efficiency |
| Gt | Global radiation (W/m2) |
| B | Mean anomaly (degree) |
| δ | Sun declination (degree) |
| w | Hour angle(degree) |
| θ | Angle of incidence (degree) |
| β | Slope angle (degree) |
| Goh | Horizontal extraterrestrial radiation (W/m2) |
| Gon | Normal extraterrestrial radiation (W/m2) |
Global radiation on horizontal panel (W/m2) | |
| K | Clearness index factor |
| Gbt | Beam radiation on tilted surface (W/m2) |
| F | Correction factor |
| Ta | Environment temperature (°C) |
| TC | Cell temperature (°C) |
| Uc | Cut-in wind turbine speed (m/s) |
| Ur | Rated wind turbine speed (m/s) |
| Per | Rated power (kW) |
| Pe,ave | Average wind turbine electrical power output (kW) |
| C | Unit electricity cost (US$/kWh) |
| Cp | Unit electricity cost for photovoltaic system (US$/kWh) |
| CI | Unit installation cost (US$/kWh) |
| Co | Unit maintenance cost (US$/kWh) |
| Cf | Average annual electrical use (kWh/day) |
Conflicts of Interest
References
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 3rd Ed. ed; John Wiely: New York, NY, USA, 2006. [Google Scholar]
- Hocaoglu, F.O.; Gerek, O.N. A novel hybrid (wind-photovoltaic) system sizing procedure. Sol. Energy 2009, 83, 2019–2028. [Google Scholar] [CrossRef]
- Calderon, M.; Calderon, A.J. Weather data and energy balance of a hybrid photovoltaic-wind system with hydrogen storage. Int. J. Hydrog. Energy 2010, 35, 7706–7715. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, W. Optimal sizing method for stand-alone hybrid solar-wind system with LPSP technology using genetic algorithm. Sol. Energy 2008, 82, 354–367. [Google Scholar] [CrossRef]
- Yang, H.X.; Lu, L.; Burnett, J. Weather data and probability analysis of hybrid photovoltaic-wind power generation systems in Hong Kong. Renew. Energy 2003, 28, 1813–1824. [Google Scholar] [CrossRef]
- Calderon, M.; Calderon, A.J.; Ramiro, A.; Gonzalez, J.F.; Gonzalez, I. Evaluation of a hybrid photovoltaic-wind system with hydrogen storage performance using exergy analysis. Int. J. Hydrog. Energy 2011, 36, 5751–5762. [Google Scholar] [CrossRef]
- Maatallah, T.; Alimi, S.E. Performance modeling and investigation of fixed, single and dual-axis tracking photovoltaic panel in Monastir city, Tunisia. Renew. Sustain. Energy Rev. 2011, 15, 4053–4066. [Google Scholar] [CrossRef]
- Brunelli, D.; Dondi, D. Photovoltaic scavenging systems: Modeling and optimization. Microelectron. J. 2009, 40, 1337–1344. [Google Scholar] [CrossRef]
- Wang, F.; Bai, L. The methodology for aerodynamic study on a small domestic wind turbine with scoop. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Ahmadi, A.; Ehyaei, M.A. Exergy analysis of wind turbine. Int. J. Exergy 2009, 6, 1–16. [Google Scholar] [CrossRef]
- Bojic, M.; Nikolic, N. Toward a positive-net-energy residential building in Serbian conditions. Appl. Energy 2011, 88, 2407–2419. [Google Scholar] [CrossRef]
- Mavromatakis, F.; Makrides, G. Modeling the photovoltaic potential of a site. Renew. Energy 2010, 35, 1387–1390. [Google Scholar] [CrossRef]
- Lopez, R.D.; Agustin, J.L.B. Design and economical analysis of hybrid PV-wind system connected to the grid for the intermittent production of hydrogen. Energy Policy 2009, 37, 3082–3095. [Google Scholar] [CrossRef]
- Park, K.E.; Kang, G.H. Analysis of thermal and electrical performance of semi-transparent photovoltaic (PV) module. Energy 2010, 35, 2681–2687. [Google Scholar] [CrossRef]
- Abdollahpour, A.; Ahmadi, M.H.; Mohammadi, A.H. Thermodynamic model to study a solar collector for its application to Stirling engines. Energy Convers. Manag. 2014, 79, 666–673. [Google Scholar] [CrossRef]
- Eltawil, M.A.; Zhao, Z. Grid-connected photovoltaic power system: Technical and potential problems: A review. Renew. Sustain. Energy Rev. 2010, 14, 112–129. [Google Scholar] [CrossRef]
- Li, Y.; Lence, B.J. An integrated model for estimating energy cost of a tidal current turbine farm. Energy Convers. Manag. 2011, 52, 1677–1687. [Google Scholar] [CrossRef]
- Kaldellis, J.K.; Zafirakis, D. The wind energy revolution: A short review of a long history. Renew. Energy 2011, 36, 1887–1901. [Google Scholar] [CrossRef]
- Li, Z.; Boyle, F. Domestic application of micro wind turbines in Ireland: Investigation of their economic viability. Renew. Energy 2011, 124, 1–11. [Google Scholar]
- Chong, W.T.; Naghavi, M.S. Techno-economic analysis of a wind-solar hybrid renewable energy system with rainwater collection feature for urban high-rise application. Appl. Energy 2011, 88, 4067–4077. [Google Scholar] [CrossRef]
- Martinez, J.; Medina, A. A state space model for the dynamic operation representation of small-scale wind-photovoltaic hybrid system. Renew. Energy 2010, 35, 1159–1168. [Google Scholar] [CrossRef]
- Shakya, B.D.; Aye, L. Technical feasibility and financial analysis of hybrid wind-photovoltaic system with hydrogen storage for Cooma. Int. J. Hydrog. Energy 2004, 30, 9–20. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammadnezami, M.H.; Ehyaei, M.A.; Rosen, M.A.; Ahmadi, M.H. Meeting the Electrical Energy Needs of a Residential Building with a Wind-Photovoltaic Hybrid System. Sustainability 2015, 7, 2554-2569. https://doi.org/10.3390/su7032554
Mohammadnezami MH, Ehyaei MA, Rosen MA, Ahmadi MH. Meeting the Electrical Energy Needs of a Residential Building with a Wind-Photovoltaic Hybrid System. Sustainability. 2015; 7(3):2554-2569. https://doi.org/10.3390/su7032554
Chicago/Turabian StyleMohammadnezami, Mohammad Hosein, Mehdi Ali Ehyaei, Marc A. Rosen, and Mohammad Hossein Ahmadi. 2015. "Meeting the Electrical Energy Needs of a Residential Building with a Wind-Photovoltaic Hybrid System" Sustainability 7, no. 3: 2554-2569. https://doi.org/10.3390/su7032554
APA StyleMohammadnezami, M. H., Ehyaei, M. A., Rosen, M. A., & Ahmadi, M. H. (2015). Meeting the Electrical Energy Needs of a Residential Building with a Wind-Photovoltaic Hybrid System. Sustainability, 7(3), 2554-2569. https://doi.org/10.3390/su7032554








