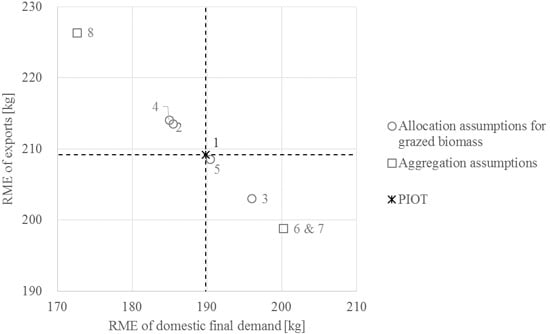
As a political goal, sustainability is commonly operationalized by means of targets, identified based on perceived thresholds of sustainability and by indicators reflecting the progress towards these targets [
1]. The research in industrial and social ecology has advanced the indicator of domestic material consumption (DMC = domestic extraction + imports − exports) to track the scale, composition, and dynamics of material use. Material use is related to many of the most pressing sustainability challenges including anthropogenic climate change (through the use of fossil energy carriers and the extraction of biomass), biodiversity and livelihood loss (through the expansion of resource use frontiers), and groundwater pollution (through mining of metals). A challenge for material flow accounting in particular and environmental accounting in general is presented by the rising volume of international trade and the global fragmentation of supply and use chains [
2,
3]. The DMC indicator reflects so-called apparent consumption and allocates materials used in the production of traded goods and services to the country where production occurs. Exported goods are accounted for in the material use of the importing country with their mass upon crossing the administrative boundary [
4]. The increasingly common spatial disconnect between production and consumption creates the need for robust information on the amount and composition of upstream material requirements (and the associated environmental impacts) associated with a given level of final demand, no matter where they occur. The
raw material consumption (RMC) indicator (also referred to as
material footprint) currently under development is designed to provide this information. It expresses material consumption in its raw material equivalents (RME),
i.e., it considers trade flows including the upstream material requirements that were associated with their production. RMC is equal to domestic extraction plus the RME of imports minus the RME of exports. The RMC indicator allocates material use that occurs in the production of traded goods and services to the material use of the country that ultimately imports these goods to meet final demand.
In order to calculate upstream material requirements associated with traded goods, it is necessary to open the “black box” as which material flow accounting commonly treats the socioeconomic system. Not only inputs into and outputs from but also patterns of transformation within the system must be considered. Material flow accounting currently does not consider which economic sectors supply or use materials. Instead, it collects and reports data on 45 types of extracted material, of which biomass, fossil energy carriers, metals and non-metallic minerals are the main four [
4]. In the most common approach to calculating RMC, monetary input-output tables (MIOTs) are used to provide the required information on the structure of an economy. The material use that occurs directly and indirectly for the production of traded goods and services is determined by extending this monetary input-output framework with data on material inputs in physical units. Because the material flow data is not available in sectoral resolution, assumptions as to the allocation of material flows to economic sectors must be made in constructing the environmental extension. This method, referred to as environmentally extended input-output analysis (EEIOA) and essentially based on Leontief’s framework [
5,
6], is constantly advanced and applied to RMC or material footprints [
7,
8,
9] as well as to other RMC-type indicators on energy [
10,
11], carbon and greenhouse gas emissions [
12,
13,
14], land (reviewed in [
15] and [
16]), the Ecological Footprint [
17,
18], water (reviewed in [
19]), changes in biodiversity [
20], and labor requirements [
21,
22] and inequality [
23] associated with traded goods and services.
In combining physical and monetary accounting, the EEIOA approach faces constraints related to this integration of different types of data: (i) Physical and monetary accounting apply system boundaries which do not perfectly overlap (see
Section 2) and (ii) the level of aggregation at which the monetary input-output data are reported entails economically and physically inhomogeneous flows being grouped together. As will be discussed and illustrated in this article, decisions must be and are commonly made in addressing these constraints in the calculation of RMC. These decisions have an impact on results and must be considered in interpreting the EEIOA-based indicators. RME indicators calculated via MIOTs with material extensions must not be interpreted as though they had been calculated via
physical input-output tables (PIOTs). In this article, the differences between a physical and a monetary accounting system are demonstrated using a PIOT and a MIOT of a small hypothetical economy. Different variations of RME calculation are performed based on assumptions commonly made in EEIOA. These assumptions were formulated based on a review of the relevant literature, which is summarized in the following two sub-sections of this article. The interpretability of the RMC indicator on which this article focuses is especially relevant in the face of the policy interest this indicator has already sparked: Analyses of global resource use induced by final demand are increasingly required, as is exemplified by the call to account for “the EU’s global consumption” in the European Union’s Roadmap to a Resource Efficient Europe [
24] and by the consensus recently reached in the European Commission in identifying “GDP relative to Raw Material Consumption (RMC) […] as the most suitable indicator for a possible resource efficiency target” [
25].
1.1. How the Use of a Method Entails ex ante Assumptions about Responsibility
With DMC and RMC, two material use indicators are available which allocate material use to socio-economic systems in an inherently distinct manner. DMC is defined as the sum of all material extracted and used by a socioeconomic system (domestic extraction) plus its physical imports minus its exports. Domestic extraction is defined as the material flow that crosses the boundary between the environment and the socioeconomic system and is used by humans, their livestock, or artifacts (also see [
4]). Trade (imports and exports) is accounted for as the mass of the material flows that cross the boundary between two socioeconomic systems (most commonly two countries). The DMC indicator provides a measure of the net use of material within a country in a given year. It can additionally serve as an indicator of domestic waste potential [
26]: All material used eventually turns into waste, almost immediately in the case of through-flow materials such as agricultural biomass or fossil fuels or with a considerable time lag in the case of materials integrated into stocks or durable consumer products. In its specific allocation of material flows to countries, the DMC indicator implicitly assigns responsibility: Countries are responsible for the material use occurring on their territory but they are neither responsible for the impacts their exported products may have elsewhere nor for the impact associated with the production of goods they import. Countries can reduce their DMC and thus improve their environmental performance as it is reflected by this indicator by importing comparatively “light” (
i.e., highly processed) goods and exporting “heavy” goods such as raw materials or primary commodities [
27]. The DMC indicator cannot reflect how much of the production and associated material use within one country is dedicated to the production of goods for export. Chile, for example, extracts very large amounts of copper ore out of which it exports comparatively small quantities of concentrated copper, leading to a very high value for the DMC indicator, which, in contrast to that of other countries, is not directly driven by domestic consumption [
28].
With the RMC indicator, the “Chilean problem” is solved by using monetary data on the structure of production and consumption contained in MIOTs in order to determine how much of the material extracted domestically is used for the production of goods for export. RMC allocates to any one country all material extraction, no matter where it occurs globally, which is directly and indirectly required to meet its final demand. For example, in the RMC, the waste rock extracted alongside the metal, which adds to Chile’s DMC, would be allocated to those countries where final consumption of Chilean copper exports (and of all products containing this copper) occurs. In this way, material use as measured by RMC is a reflection of the purpose for which material is extracted (i.e., for domestic or for foreign final demand).
While the DMC assigns responsibility for the material use that occurs during production almost exclusively to the producer (or producing country), the RMC shifts the burden to the consumer (or consuming country). Making their argument for CO
2 emissions that occur in production, Jakob and Marschinski [
29] have pointed out that either form of allocation (to the producer or to the consumer) could be contested. The conclusions these authors draw on emissions can also be applied to material use. Production for export not only entails the environmental burden associated with final demand elsewhere (which the RMC indicator aims to capture) but also socioeconomic benefits. Responsibility for the associated material use might most appropriately be shared between the producer and the consumer. In the past, some comparative assessments of producer and consumer responsibility have been conducted [
14,
30] that have discussed the possibilities of allocating responsibility by (economic) benefits (such as value added) or by (ecological) benefits (such as avoided pollution or obtained resources) [
31]. However, even if the decision is made to allow producers and consumers to share responsibility, different options exist as to how this would be expressed mathematically [
29,
32,
33,
34] and such an approach has therefore not yet been widely applied to the DMC or the RMC indicator.
As RMC-type indicators were being developed, one of the hopes was that they would be able to reflect “outsourcing” of resource-intensive production steps by which countries might improve their own sustainability record while not actually curbing their impact on global sustainability. The RMC indicator cannot directly prove or disprove this hypothesis. If countries are able to specifically relocate resource-intensive production steps to other countries, the latter countries must have, to some degree, specialized in resource-intensive production for export.
The data currently available for the EEIOA approach do not allow for the distinction of production for exports from production for domestic final demand [
29]. EEIOA precision could therefore be improved by the use of more highly disaggregated sectoral data, the generation of which, if possible given existing data constraints, entails a major additional effort [
35,
36,
37]. Given the limitations in the available data, it must commonly be assumed that each sector uses the same production technology in outputs to domestic and foreign final demand. For example, if a country were to devote its high-yielding agricultural areas to production of maize for export and simultaneously produce maize in lower yielding production systems for domestic demand, common practice in the EEIOA approach, given data availability, is to assume the same production structures for both [
15].
1.2. The Role of Assumptions in the EEIOA Approach under Data Constraints
As the EEIOA approach is further developed and more widely applied, comparisons have revealed differences in results [
15,
38,
39,
40] and given rise to the need to understand where these differences stem from. This sub-section provides an overview of the scientific appraisals of assumptions made in the EEIOA approach and how these relate to the aforementioned data constraints. Important themes in current research with regard to the RMC indicator are the allocation of material flows to economic sectors in the construction of the environmental extension and the assumption of product homogeneity, both of which are closely related to the level of sectoral aggregation. Improving the validity of the assumption of price homogeneity and the treatment of capital investments are further topics currently being dealt with in EEIOA applications.
The material flow data is introduced into EEIOA models as an extension. Since material flow data (like many other types of data in the environmental accounts) are not compiled by sectors but by material categories, a material extension is not readily available but must be compiled by the researchers creating the EEIOA model. Even though energy and CO
2 emissions data are more frequently compiled by economic activities, decisions on the allocation of environmental factors to the sectors as they are reported in the input-output tables have to be made for these environmental extensions as well [
41]. How to allocate material flows to economic sectors is not always straight-forward: Sand, for example, is used for various industrial purposes, fossil energy carriers are used by almost all sectors, and grazed biomass is used in both meat and dairy production. The more detailed both the monetary and the material data are, the more unambiguous the allocation of environmental factors to sectors usually is. Given the high level of sectoral aggregation in most existing MIOTs, the choices in the construction of the material extension affect how material flows are distributed through the economic system and thus impact the RMC results.
Once allocated in the environmental extension, physical flows are distributed through the economy and to final demand as though they would flow proportionally to monetary flows. For energy and emissions, it has been shown that this assumed proportionality could lead to uncertainties in the results on the order of 10%–50% [
42]. Hubacek and Giljum [
43] argued that for the analysis of upstream land requirements associated with the production of traded goods, results based on physical accounts are more appropriate since material flows are a better proxy for land requirements than monetary flows. Under which conditions monetary relations can be used to distribute physical flows and what the consequences of this choice in method could be are issues that have since been raised by other scholars [
17,
44].
In theory, MIOTs should be equivalent to PIOTs based on a transformation via prices—this was illustrated by Leontief in his exposition of the fundamental calculations on which EEIOA is still based today [
5,
6]. The reason for differences in results yielded by calculations based on monetary and physical input-output tables that persisted in practice [
45,
46] was found to lie in violations of the assumptions of homogenous products and prices that would have to be fulfilled in order for an MIOT-based EEIOA approach to yield the same results as a PIOT-based approach [
38]. The assumption of homogenous products is that each economic activity delivers one homogenous product to the other activities and to final demand. The assumption of homogenous products has a greater tendency to be true the more highly disaggregated the input-output tables are. In practice, economic sectors at the level of detail at which they are included in MIOTs produce more than one type of output. The violation of the product homogeneity assumption is therefore closely related to the level of sectoral and spatial aggregation that is known to lead to substantial differences in results for EEIOA models [
47,
48,
49], an issue most widely explored for carbon footprints [
48,
50,
51]. While disaggregated data may improve the validity of the homogeneity assumption, they cannot solve the problem entirely: In reality, different types of co-production will commonly exist. In developing an approach to calculating the RME of Europe’s trade, Schoer and colleagues [
7] have pointed out the lack of detail that results from the high aggregation of primary and secondary sectors in many countries’ input-output tables.
The allocation of material use to economic sectors raises issues that have been the subject of a long-standing debate on the allocation of environmental burdens to products and processes in the life cycle assessment (LCA) community [
52]: Where one production process yields more than one product, environmental burdens may either be allocated to the dominant product (characteristic production in input-output terminology) (see [
53]) or to all of the co-products according to their share in monetary value of production (e.g., [
54]) or according to their share in the total mass, energy, or exergy content of production. Although seldom feasible due to data constraints, it has also been suggested that multi-product production processes could be broken down into single-product processes [
55,
56], conceptually comparable to the development towards greater sectoral detail in input-output applications [
8,
47,
57]. The LCA community has further debated the possibility of expanding the system boundaries of analysis by allocating to each product of a multi-product process that environmental burden that would occur in the corresponding single-product process [
55,
58]. In light of this allocation challenge being shared by LCA and EEIOA applications, an effort is currently being made to learn from the possibilities and limits in both approaches in order to identify best-practice examples [
59].
The assumption of homogenous prices is that products have the same price throughout the economic system,
i.e., whether they are bought by primary, secondary, or tertiary sectors or delivered to final demand. In early energy analyses, it was already noted that energy is not sold at the same price to all users, making it preferable to use data in physical units,
i.e., in Joules [
60]. As a result of price inhomogeneity, prices, assumed to be a vector with one entry per activity, can more realistically be represented as a matrix with one entry for the output of each activity to each other activity [
61]. The differences in price of equivalent products impact the estimation of the associated RME. Whether a loaf of bread costs 1 Euro or 5 Euros, the amount of crops required in the production of each will be roughly the same and not differ by the factor 5 [
38]. This distinction may be especially relevant in calculating the RMC of those economies that account for money spent in the country by tourists as exports, such as China [
62]: If tourists were to, on average, pay more for the same commodities than locals (e.g., by eating in more expensive restaurants), a relative increase in the RME of exports would result.
Most recently, Merciai and Heijungs [
63] showed that when prices differ per purchaser and the homogenous price assumption is violated, the calculated demand in physical units may be unequal to the calculated supply, causing a violation of the mass balance of the environmentally extended input-output model. In moving towards a solution to this problem, accounts focusing on household consumption commonly use mixed prices, allowing households to pay other prices than industry does [
64,
65].
Capital investments have long been identified as an area in which currently applied assumptions impact the results of EEIOA. In MIOTs, investment is currently treated as a category of final demand [
66]. However, capital, such as buildings, infrastructure, or machines, also constitutes an input into production both in the monetary sense and in terms of the physical capital stocks that are used and worn down during production. National capital accounts can be used to close the IO model for investments and capital depreciation as part of the intermediate use of sectors [
67,
68,
69]. When investments are endogenized in such a manner, the results for RMC-type indicators differ significantly from those of accounts in which investments are treated as final demand, especially for services [
7,
70].
This also becomes important when comparing RME indicators of different countries: Mature industrial economies use large infrastructure and building stocks accumulated over the past decades, while emerging economies are currently just expanding them [
71,
72]. For example, in-use stocks of steel in mature industrial economies are up to 5–10 times larger than in emerging and developing economies [
73]. An economy currently building up or growing its infrastructure may have much higher material inputs, especially of construction minerals (which would be included in the material extension in an EEIOA-based approach and partly wind up in the RME of exports) than an economy with established infrastructure. The size of in-use stocks and of accumulated physical capital influences the size of material flows [
74] and therefore impacts the RME associated with traded products.
Due to the assumptions made in calculating RMC in an EEIOA-based approach given existing data constraints, the resulting indicator cannot be interpreted in the same manner as other material flow indicators that are calculated based purely on physical data. In this article, a simple hypothetical input-output model with material extensions is used to illustrate the impact of some of the most common assumptions in EEIOA on RMC results.
Section 2 contains the description of the model and its extension and
Section 3 presents results for different sets of assumptions in the calculation. The aim is to render the method and the data on which the RMC indicator is based comprehensible and its results interpretable for sustainability researchers and practitioners. The (political) interpretability of the RMC indicator is discussed in depth in
Section 4, leading to the conclusion that RMC must be understood not as an extension or a replacement of DMC but as an entirely new indicator with its own potential messages for sustainability.