Analysis of the Influence of the Stability Factors of PV/T-SAHP on the Performance of the System

Abstract

The integrated photovoltaic/thermal collector (PV/T) with solar assisted heat pump (SAHP) often operates under an undesigned condition. Against the backdrop of heat pump system oscillation resulting from the mismatching between collectors area and compressor capacity, this work explores the dynamic performance of heat pump system at a fixed compressor frequency when the condensing water temperature and electronic expansion valve (EEV) opening are variable or invariable. We also consider why the system is unstable and propose the theory of SAHP system stability. Also, a preliminary performance analysis is made on SAHP system that is respectively influenced by an inverter compressor and EEV. The MSS(Minimum Stable Signal) line theory is proposed to account for system unstabilty in the research of the match between EEV and evaporators, that is to say, the critical problem of keep the system stability is to find out how evaporators superheat under the circumstance of specified loads and its corresponding EEV opening, in other words, to find the MSS line.

1. Introduction

The SAHP system combines a solar collector and a heat pump for the purpose of improving the coefficient of the performance (COP) of a heat pump and the efficiency of its thermal collectors. Therefore, the main purpose of the SAHP system operation control is to balance the system COP and collector efficiency. With a compressor of a rated capacity, a heat pump assists an evaporator in extracting thermal energy primarily from solar energy that varies over different seasons or even different times of a day. As the variation of solar radiation becomes intensified, it is hardly possible for a constant-frequency compressor to meet the demand of a SAHP system under a dynamic condition. However, an inverter compressor is able to make an SAHP system operate under a better condition by changing the frequency of the system as the solar radiation differs. Through a full-year forecast of SAHP system that applied an inverter compressor, researchers like Chaturvedi suggest that not only the COP of a heat pump and thermal efficiency of its collectors, but also the system premium operating performance can be guaranteed by converting the frequency of the compressor to an optimal performance according to weather status in different seasons throughout the whole year [1]. Targeting better heat pump performance and collector efficiencies, temperature of collectors should be 5~10 °C higher than environment temperature [2]. Chaturvedi, also further studies the influence of the frequency of the compressor on the system performance, and put forward the frequency conversion range (40~70 Hz) of the compressor at different temperatures (25 °C, 20 °C, 12 °C) and the solar radiation intensity (400~1100 W/m²), in order to guarantee the system COP greater than 2 or 2.5 [3]. Also, Hawlader introduces an inverter compressor into their SAHP water heating system and studies the influence of frequency conversion on system COP and collector’s thermal efficiency [4]. Likewise, to get SAHP to operate in a perfect condition, an EEV with a controller could be used to regulate the flow of system refrigerating fluid for a premium COP [5].

For further study of the performance of the SAHP, some novel design and control strategy suggestions for the analysis of gas-burner supplemented DX-SAHP are proposed to minimize the use of primary energy [6]. A model without any information about the refrigerant fluid properties of independent Carnot inverse cycle which applied both to a household refrigerator and to a DX-SAHP is considered to be quite effective [7]. On retrofitting water cooled solar hybrid panels, a cheap and “easy to implement” solution is to fix the thermal plate on the rear of the panel by means of wood ribs [8].

This paper represents an analysis of a SAHP system in which installing EEV and an inverter compressor. The present work is an attempt to examine the influences of the stability factors of SAHP on the performance of the system and how to solve the problem of the matching of the system evaporator area and the capacity of the compressor in the non design condition through experiment and simulation.

2. System Design

This work explores further the mismatching under an undesigned operating condition based on the PV/T-SAHP system [9,10,11,12,13,14,15,16,17]. The system is designed according to the frequency conversion compressor and EEV (as seen in Figure 1 and Figure 2).

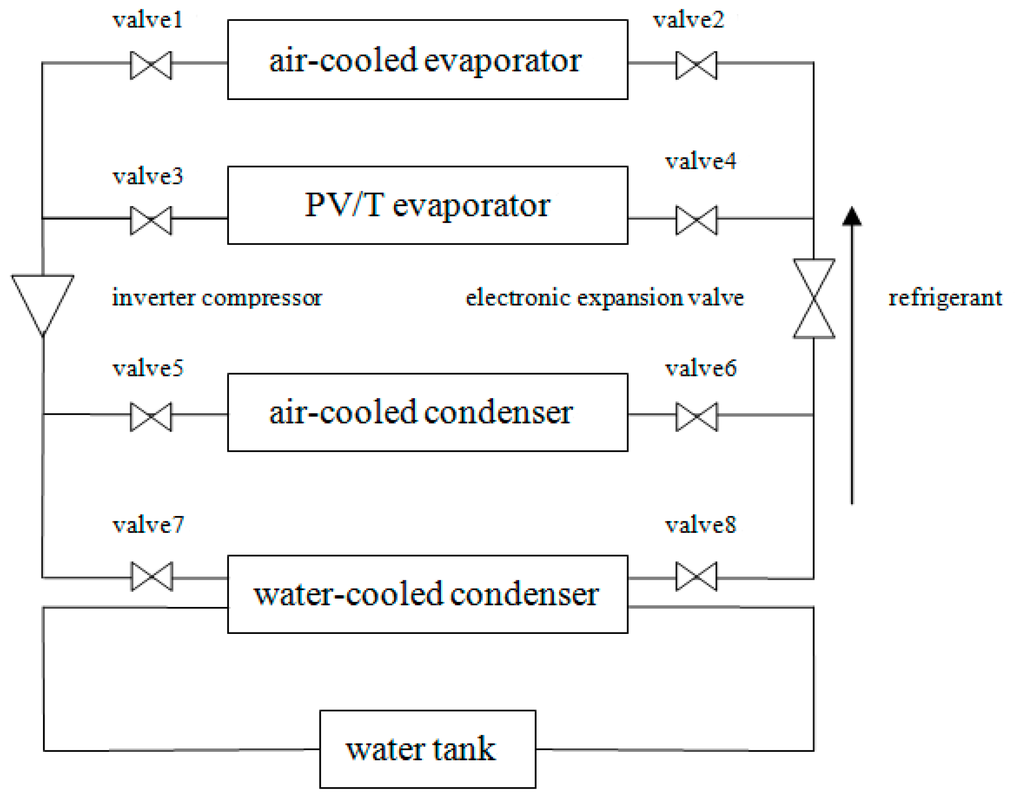
Figure 1. Schematic diagram of photovoltaic/thermal collector (PV/T)-solar assisted heat pump (SAHP) system.

Figure 1. Schematic diagram of photovoltaic/thermal collector (PV/T)-solar assisted heat pump (SAHP) system.

Figure 2. The prototype of PV/T-SAHP.

Figure 2. The prototype of PV/T-SAHP.

The photovoltaic part is composed of crystalline silicon battery, inverter, controller, battery, electric cabinet, wire, load, and so on. Each PV module independently completes the photoelectric conversion, generates the 48 V DC current, and the nine modules of PV current are connected in parallel to charge the battery through the inverter controller. The battery or photovoltaic cell 48 V DC inverter converted to 220 V AC, for load use.

The characteristics of the system using single crystal silicon photovoltaic cells are as follows: open circuit voltage 0.63 V, short circuit current 5.12 A ,maximum power 2.40 W, maximum power point voltage 0.53 V, maximum power point current 4.58 A, single cell efficiency 15.4%, fill factor 74.8%, test intensity 1000 w/m², test environment temperature 25 °C, battery factory I-V test curve as shown in Figure 3.

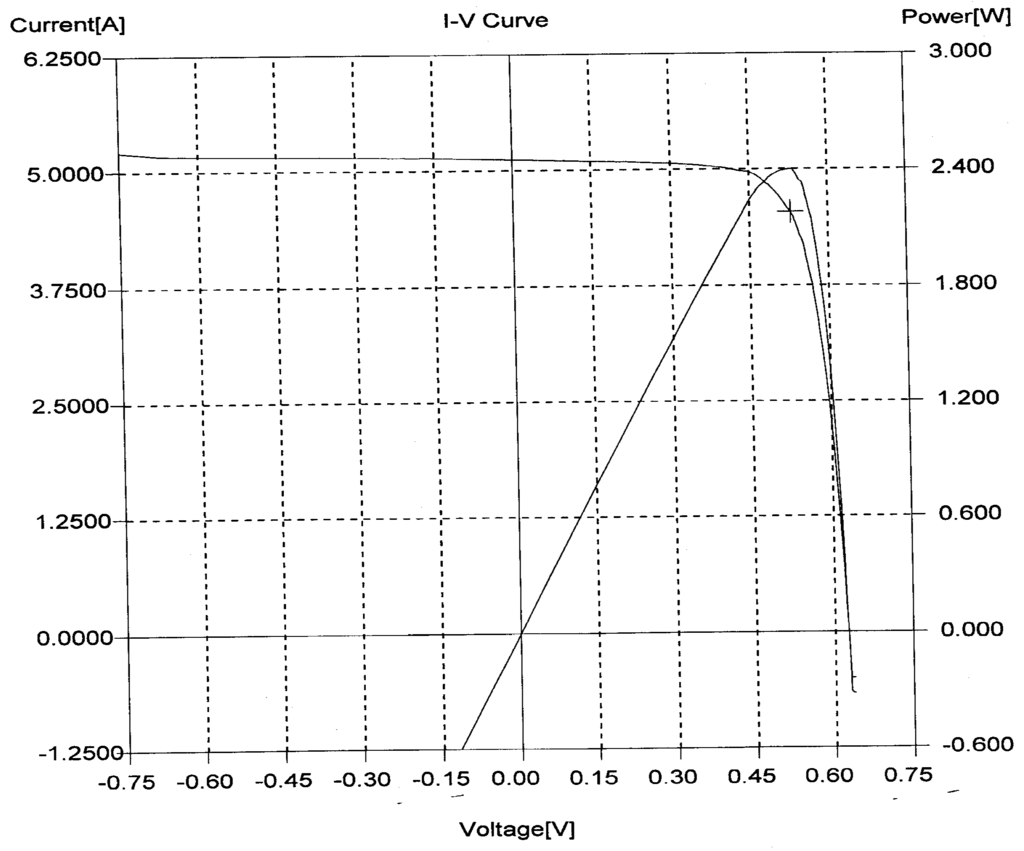
Figure 3. I-V performance curve of photovoltaic cells.

Figure 3. I-V performance curve of photovoltaic cells.

The copper tube (diameter, 6 mm), with pipe spacing 130 mm, is a working coil, packed in a special adhesive aluminum plate (thickness, 0.5 mm) in the groove. Then, the adhesive aluminum plate and the substrate surface are sealed together. The working coil is sealed in the middle of the two to ensure the heat conduction between the coil and the two layer plate. The whole PV evaporator module is fixed in an aluminum frame.

As is shown in Figure 1, there are different apparatus within a SAHP system as a PV/T evaporator, an air-cooled evaporator, an inverter compressor, a air-cooled condenser, a water-cooled condenser, an EEV, among which the inverter compressor and the EEV are most variable. The change of the frequency of the compressor can change the speed of the compressor, the input power, the compression ratio, and then change the evaporation pressure, condensation pressure, thermal efficiency, photoelectric efficiency, output power and other performance parameters of SAHP system. The PV/T evaporator will convert part of the energy from solar radiation into electricity current as output and the rest into heat as an evaporating heat source in a heat-pump circle. The air-cooled heat exchanger acts as an auxiliary heat source.

3. Matching Relations between the EEV and the Evaporator

As it is known, there should be an optimal matching between the EEV and the evaporator which means that the expansion valve and evaporators can work together in a stable manner while providing maximal energy. Likewise, there always exists a Minimum Stable Signal line (MMS line for short) within each evaporator [18]. Figure 4 shows different refrigerants with their own critical degree of superheat in the MSS line of evaporators: When it is on the left of the MSS line, the refrigerating system will show a unstable performance; when it is on the right of the MSS line, the refrigerating system operates in a stable but inefficient way due to too high superheat temperature; Point A on the curve that acts as the static line of the expansion valve should be the best matching time when evaporators’ temperature is in a critical but stable condition with a maximum heat production.

Figure 4. Matching relations between the electronic expansion valve (EEV) and evaporators (OPS is evaporators’ operating degree of superheat).

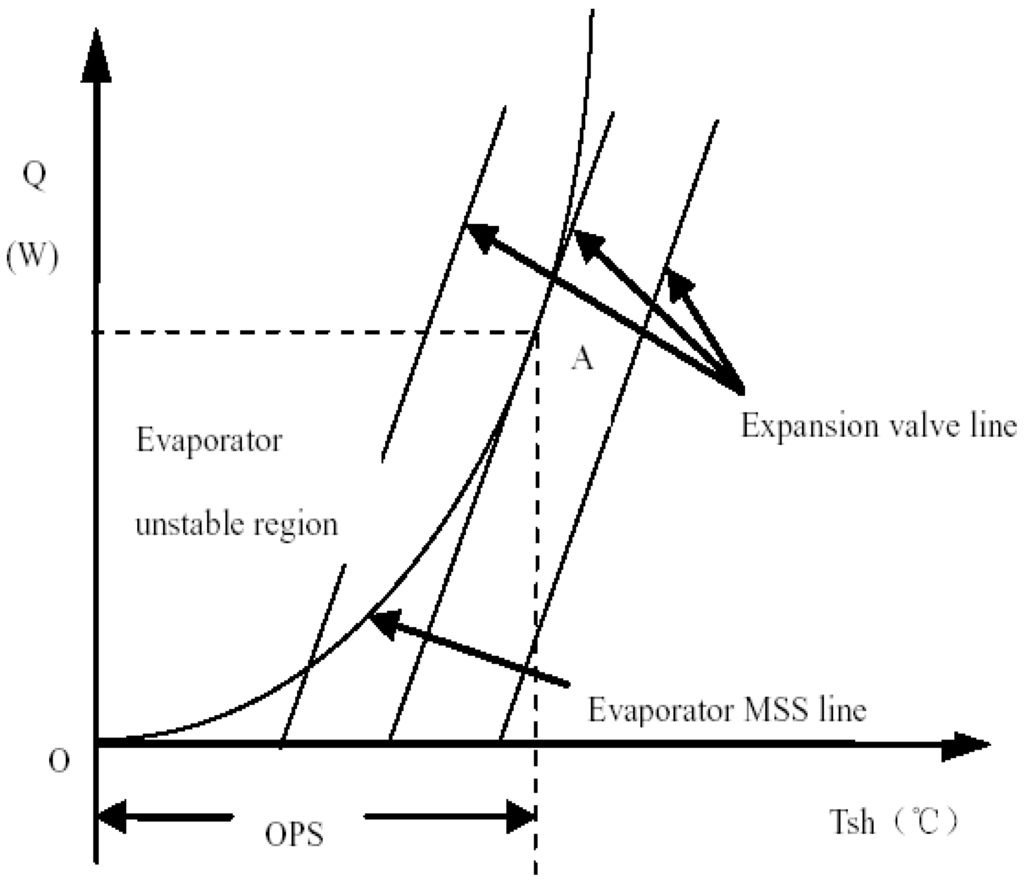
Figure 4. Matching relations between the electronic expansion valve (EEV) and evaporators (OPS is evaporators’ operating degree of superheat).

4. System Simulation

4.1. Mathematical Models for System Apparatus

4.1.1. Mathematical Models for Compressor

As the time constant of the compressor is much smaller than the evaporator and the condenser, a steady lumped-parameters compressor model has been adopted in our simulation model [19]:

For compressor motor power N_th

$$N_{th}={\mathsf{\eta }}_{v}nV{P}_s\frac{k}{k-1}[{(\frac{P_d}{P_s})}^{\frac{k-1}{k}}-1]$$

(1)

$$m_r=Vn\mathsf{\rho }/60$$

(2)

$$n=60f/p$$

(3)

where ${\mathsf{\eta }}_v$ is the volumetric efficiency, $n$ is Motor’s revolving speed, V is Compressor’s gas displacement, $P_d$ and $P_s$ are the discharge and suction ends of the compressor pressure respectively, $k$ is the adiabatic compression index, $\mathsf{\rho }$ is Compressor’s medium inlet density, $f$ is Voltage frequency, $P$ is Motor’s pole number, $m_r$ is Refrigerant’s mass flow.

4.1.2. Mathematic Model for Photovoltaic Evaporator

$$m=\sqrt{\frac{U_{loss}}{k_{abs}{\mathsf{\delta }}_{abs}+k_{lam}{\mathsf{\delta }}_{lam}}}$$

$$F=\frac{\tanh [m(w-d)/2]}{m(w-d)/2}$$

$$F_t={[1/F_t+U_{loss}w/\mathrm{\pi }d{h}_{tube}]}^{-1}$$

$$Q_u=A_c{F}_t[(\mathsf{\tau }\mathsf{\alpha }-\mathsf{\tau }{\mathsf{\eta }}_{el})G-U_{loss}(T_{fm}-T_a)]$$

$$T_p=T_{fm}+\frac{Q_u}{2m_r{c}_p}$$

$$U_{loss}={\left\{\frac{N}{\frac{C}{T_p}{\left[\frac{(T_p-T_a)}{(N+f)}\right]}^e}+\frac{1}{h_{wind}}\right\}}^{-1}+\frac{\mathsf{\sigma }(T_p+T_a)({T_p}^2+{T_a}^2)}{{({\mathsf{\epsilon }}_p+0.00591N{h}_{wind})}^{-1}+\frac{(2N+f-1+0.133{\mathsf{\epsilon }}_p)}{{\mathsf{\epsilon }}_g}-N}$$

$$f=(1+0.089h_{wind}-0.1166h_{wind}{\mathsf{\epsilon }}_p)(1+0.07866N)$$

$$e=0.43(1-\frac{100}{T_p})$$

$$c=520(1-0.000051{\mathsf{\beta }}^2)$$

$$h_{tube}=0.023{\mathrm{Re}}^{0.8}{\mathrm{Pr}}^{0.4}\frac{k}{d}$$

$$h_{wind}=2.8+3.0V_{wind}$$

Among calculations above [20]:

$U_{loss}$ 

is the heat loss of collector’s top ($W/(m^2\cdot °\text{C})$)

$K_{abs}$ 

is the thermal conductivity of heat insulating layer at the bottom of the collector (W/m·K)

${\mathsf{\delta }}_{abs}$ 

is the thickness of heat insulating layer at the bottom of the collector (mm)

$K_{lam}$ 

is the thermal conductivity of lamination layer at the bottom of the collector (W/m·K)

${\mathsf{\delta }}_{lam}$ 

is the thickness of lamination layer at the bottom of the collector (mm)

$w$ 

is the space between heat-absorbing tubes (mm)

$d$ 

is the diameter of heat-absorbing tubes (mm)

$F$ 

is the collector’s efficiency factor

$F_t$ 

is the collector’s heat transfer factor

$h_{tube}$ 

is the coefficient of heat convection between refrigerant within the tube and the tube wall (W/m²·K)

$Q_u$ 

is collector’s effective yield (W)

$A_c$ 

is the solar panel area (m²)

$\mathsf{\tau }\mathsf{\alpha }$ 

is the product of penetration rate and absorption rate of solar perpendicular incidence and diffuse radiation against the solar panel

${\mathsf{\eta }}_{el}$ 

is the photoelectric conversion efficiency

$G$ 

is solar irradiation intensity

$T_{fm}$ 

is the average temperature of refrigerants within tubes of the collector (°C)

$T_a$ 

is the environment temperature (°C)

$m_r$ 

is refrigerants’ mass flow (kg/s)

$c_p$ 

is the specific heat capacity under a constant pressure (kJ/(kg·k))

$N$ 

is the number of overlying layers

$T_p$ 

is the temperature of heat-collection plates (°C)

$h_{wind}$ 

is the coefficient of heat convection caused by wind (W/m²·K)

${\mathsf{\epsilon }}_p$ 

is the emissivity of heat-collection plates

${\mathsf{\epsilon }}_g$ 

is the emissivity of the glass layer

$\mathsf{\beta }$ 

is collector’s inclination angle

$V_{wind}$ 

is the wind speed (m/s)

4.1.3. Mathematical Model for EEV

As is shown in Figure 5, if the high degree of the valve is h, the hole diameter of valve is d and the valve angle is β, then the passage area A_EEV can be calculated by:

$$A_{EEV}=\mathrm{\pi }h\sin \frac{\mathsf{\beta }}{2}[d-\frac{1}{2}h\sin \mathsf{\beta }]$$

(4)

Supposing $A_{EEV\max }=\frac{1}{4}\mathrm{\pi }{d}^2$, $\mathsf{\beta }=36°$, then

$$\frac{A_{EEV}}{A_{EEV\max }}=\frac{2.568-\frac{h}{h_{\max }}}{1.568}.\frac{h}{h_{\max }}$$

(5)

Simplify equation above:

$$A_{EEV}=-0.15h^2+1.135h$$

(6)

$$h=\frac{n}{172}$$

(7)

$$\text{So}\hspace{1em}{A}_{EEV}=-5.07\times {10}^{-6}{n}^2+0.0066n$$

(8)

Among calculations above, where n is the opening pulse of EEV, $A_{EEV}$ is the passage area of EEV ($m{m}^2$)

$$h_{in}=h_{out}$$

(9)

$$m_r=C_D{A}_{EEV}\sqrt{2\rho (p_1-p_2)}$$

(10)

$$C_D=0.02005\sqrt{\rho }+0.634\mathsf{\upsilon }$$

(11)

Among calculations above, where $C_D$ is Flow coefficient of expansion valve, $A_{EEV}$ is Passage area of expansion valve, $\mathsf{\rho }$ is Refrigerant inlet density of expansion valve, $h_{in}$ is Refrigerant inlet enthalpy of expansion valve, $h_{out}$ is Refrigerant outlet enthalpy of expansion valve, $p_1$ and $p_2$ are respectively the pressure on the front and the back of expansion valve, $\mathsf{\upsilon }$ is refrigerant outlet specific volume of expansion valve [21].

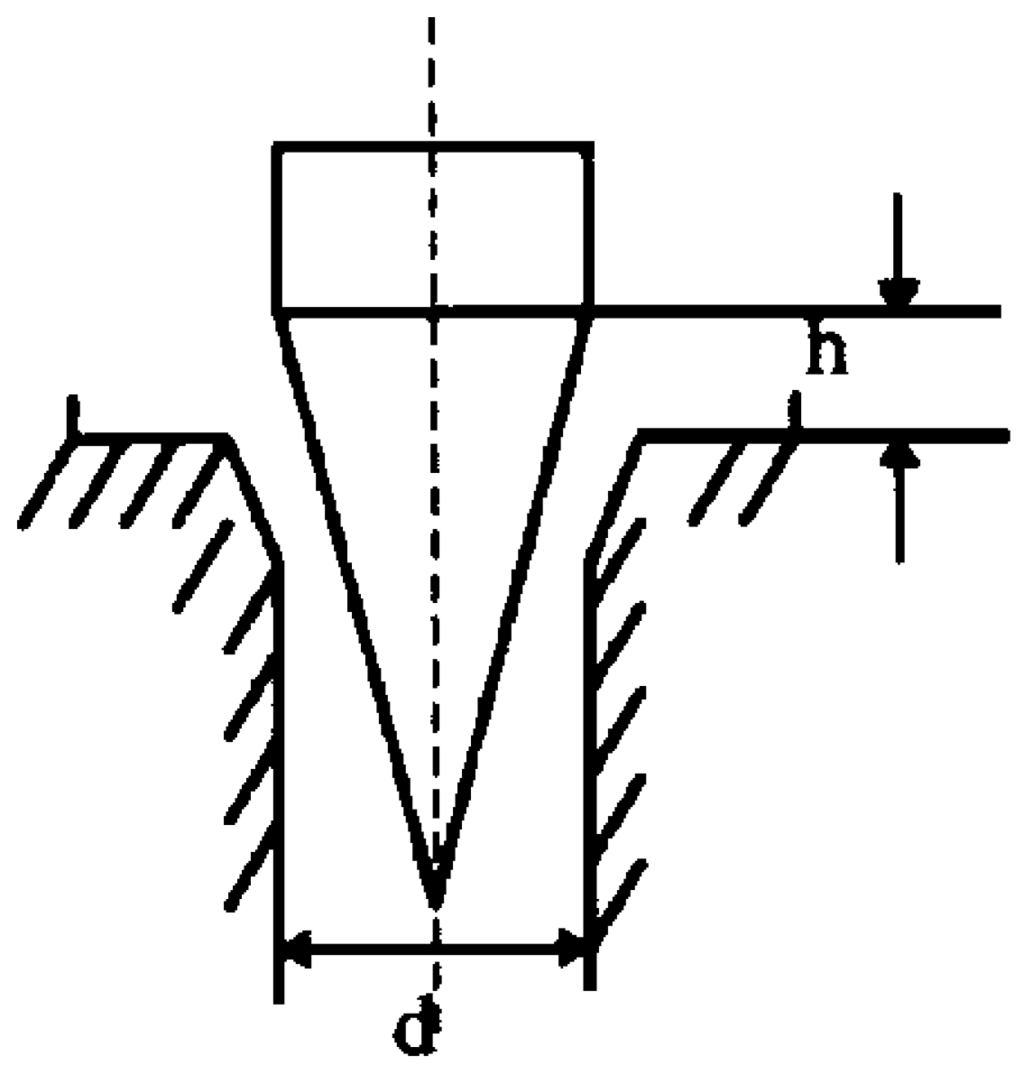
Figure 5. Structure diagram of EEV.

Figure 5. Structure diagram of EEV.

4.1.4. Mathematical Model for Heat Exchanger in Water Tank

Total coefficient of heat transfer of panel heat exchanger (U) can be calculated by $U=Q/(A_{EX}\cdot \Delta t_m)$, among which Q is heat absorbed by water, A_EX is total heat transfer area of panel heat exchanger, and $\Delta t_m$ is log-mean temperature difference.

If $h_c$ as the coefficient of water heat convection can be calculated by

$$Nu=a_1{\mathrm{Re}}^{a_2}f(\mathrm{Pr}){(\frac{\mathsf{\mu }}{{\mathsf{\mu }}_w})}^{a_3}$$

(12)

which is the panel thermal performance formula proposed by Alfa Laval Thermal company [20].

Among Equation (12) Nu is the Nusselt number of water condensation and $Nu=h_{c}d/K$ where K is tube wall’s coefficient of heat conductivity, $\frac{\mathsf{\mu }}{{\mathsf{\mu }}_w}$ is the modification of heat convection coefficient in the case of considering a tube wall temperature, where $\mathsf{\mu }$ and ${\mathsf{\mu }}_w$ are respectively liquid viscosity coefficients of water temperature and water side wall temperature, $a_1$, $a_2$ and $a_3$ correspond to different constant values as Re varies, $\mathrm{Pr}$ is water Prandtl number.

If $h_v$ is the coefficient of vapor condensation heat transfer, then

$$Nu=0.0143{({\mathrm{Re}}_l/H)}^{0.864}{{\mathrm{Pr}}_l}^{0.33}{({\mathsf{\rho }}_l/{\mathsf{\rho }}_v)}^{0.055}$$

(13)

$Nu$ is the Nusselt Number of vapor condensation, so $Nu=h_{v}d/K_l$, where $K_l$ is the coefficient of heat conductivity of liquid film, ${\mathrm{Re}}_l$ is the Reynolds Number of liquid film condensation, so ${\mathrm{Re}}_l=G_v(1-x_0)d/{\mathsf{\mu }}_l$, where $G_v$ is the vapor flow rate, $x_0$ is the dryness of refrigerant at the time of going out, and $d$ is the qualitative size, $H$ is the dimensionless parameter in the case that film condensation might influence the coefficient of condensation heat transfer, so $H=c_p\Delta T/\mathsf{\gamma }$, where $\Delta T$ is the temperature difference between saturated vapor and its side wall and $\mathsf{\gamma }$ is the latent heat of refrigerants’ vaporization, ${\mathsf{\rho }}_l$ is the density of condensing film, ${\mathsf{\rho }}_v$ is the density of refrigerants’ saturated vapor at the condensing temperature [22].

4.1.5. Thermophysical Model for Refrigerating Medium within the Heat Hump

Heat pump system simulation is based on the calculation of refrigerants’ thermal physical property. The coupling of apparatus such as compressor, a throttle, condensers, evaporators into one single heat pump system can be linked to refrigerants energy and quality conservation. Moreover, the calculating subroutine of refrigerants’ thermophysical property is a fundamental part of the whole system simulation.

Calculations of refrigerants’ thermo physical property consists of vapor space state equation, saturated vapor pressure equation, saturated liquid density equation, and specific heat, enthalpy and entropy equation of ideal gas at a constant volume [23]:

(1)

Vapor space state equation:

$$Z=1+{\displaystyle \sum _{i=1}^r({\displaystyle \sum _{j=0}^s{b}_{ij}/T_r^j){\mathsf{\rho }}^i}}$$

Among this equation, Z is the compressibility factor, T_r is the reduced temperature, ρ is the density (kg/m³) and b_ij is a constant.

(2)

Saturated vapor pressure equation:

$$p_s=p_c\exp [Ri\ln T_r+(R_i-4+P_{\mathsf{\alpha }})\mathsf{\psi }(T_r)]$$

$$\mathsf{\psi }(T_r)=4[(T_r-1)/T_r]+S(T_r)-5.3\ln T_r$$

$$S(T_r)=(T_r-1)[0.2{(T_r+1)}^2+0.5]$$

Among this equation, p_c is the critical pressure (MPa), p_s is the saturation pressure (MPa), and R_i, P_a is the criterion number.

(3)

Saturated liquid density equation:

$${\mathsf{\rho }}^{\prime }={\mathsf{\rho }}_c\exp [a_1{(1-T_r)}^{1/3}+a_{2}S(T_r)]$$

Among this equation, ${\mathsf{\rho }}^{\prime }$ is the saturated liquid density (kg/m³), and a₁ and a₂ is the materials constant.

(4)

Specific heat equation of ideal gas at a constant volume: $c_{v0}={\displaystyle \sum _{i=0}^4{d}_i{T}_r^i}$

Among this equation, c_v0 is the specific heat at a constant volume (kJ/(kg·K)) and d_i is the materials constant.

(5)

Specific enthalpy equation of ideal gas at a constant volume:

$$\begin{array}{l}h=-{\displaystyle \int [T_r{(\frac{\partial P}{\partial T_r})}_{\mathsf{\rho }}-P]{\mathsf{\rho }}^{-2}d\mathsf{\rho }+\frac{P}{\mathsf{\rho }}+u_0+h_c}\\ =R{T}_c{T}_r(1+l_1+l_3)+u_0+h_c\end{array}{u}_0={\displaystyle \int c_{v0}dT=T_c{\displaystyle \sum _{i=0}^4\frac{d_i}{i+1}{T}_r^{i+1}}}$$

Among this equation, u₀ is the specific energy at a constant volume (kJ/kg) and h_c is the benchmark enthalpy constant (kJ/kg)

(6)

Specific entropy equation of ideal gas at a constant volume:

$$s=-T_c^{-1}{\displaystyle \int {(\frac{\partial P}{\partial T_r})}_{\mathsf{\rho }}{\mathsf{\rho }}^{-2}d\mathsf{\rho }+s_0+s_c}=R(l_3-l_2-\ln \mathsf{\rho })+s_0+s_c$$

$$s_0={\displaystyle \int \frac{c_{v0}}{T}dT=d_0}\ln T_r+{\displaystyle \sum _{i=1}^4\frac{d_i}{i}{T}_r^i}$$

Among this equation, s₀ is the specific entropy at a constant volume (kJ/kg) and s_c is the benchmark entropy constant (kJ/kg).

(7)

Enthalpy equation of saturated liquid:

$$h^{\prime }=h^{″}-\frac{1}{10}{T}_r{T}_c(\frac{1}{{\mathsf{\rho }}^{″}}-\frac{1}{{\mathsf{\rho }}^{\prime }})\frac{d{P}_s}{dT}$$

Among this equation, $h^{″}$ is the enthalpy of saturated vapor (kJ/kg), ${\mathsf{\rho }}^{″}$ is the saturated vapor density (kg/m³), ${\mathsf{\rho }}^{\prime }$ is the saturated liquid density (kg/m³) and P_s is the saturated vapor pressure (MPa).

(8)

Entropy equation of saturated liquid:

$$s^{\prime }=s^{″}-\frac{1}{10}(\frac{1}{{\mathsf{\rho }}^{″}}-\frac{1}{{\mathsf{\rho }}^{\prime }})\frac{d{P}_s}{dT}$$

Among this equation, $s^{″}$ is the saturated vapor entropy (kJ/kg·k).

(9)

Enthalpy and entropy equation of wet vapor:

$$\begin{array}{l}{h}_x=x{h}^{″}+(1-x)h^{\prime }\\ s_x=x{s}^{″}+(1-x)s^{\prime }\end{array}$$

Among this equation, h_x is the wet vapor enthalpy (kJ/kg), s_x is the wet vapor entropy (kJ/kg·k) and x is the wet vapor dryness.

4.2. Simulation Results and Discussion

Relations between compressor frequency, solar radiation and COP when EEV opening pulse is 400.

It is difficult to clarify complicated relations between compressor frequency, solar radiation and COP of the heat pump through a number of tests. The relationships between them can be obtained only by mathematical simulation.

From Figure 6, it is evident that at a constant opening pulse, the COP of the heat pump is extremely high at a low frequency. For example, at a frequency of 20 Hz, the COP increases as solar radiation does. At such a low frequency, when solar radiation is 937 W/m², the COP will rapidly reach 9.0, which can be explained by high vaporization pressure resulting from an increased radiation and a low compressor rotated speed. However, this COP number (9.0) only exists in the simulation but not in the reality, because diminished outlet refrigerants superheat that draws gradually near zero will lead to a low collectors’ thermal efficiency due to an incomplete refrigerants’ vaporization (see in Figure 7), as well as a violent system vibration in an unstable condition according to MSS theory (see in Figure 4). That will also be illuminated by data later.

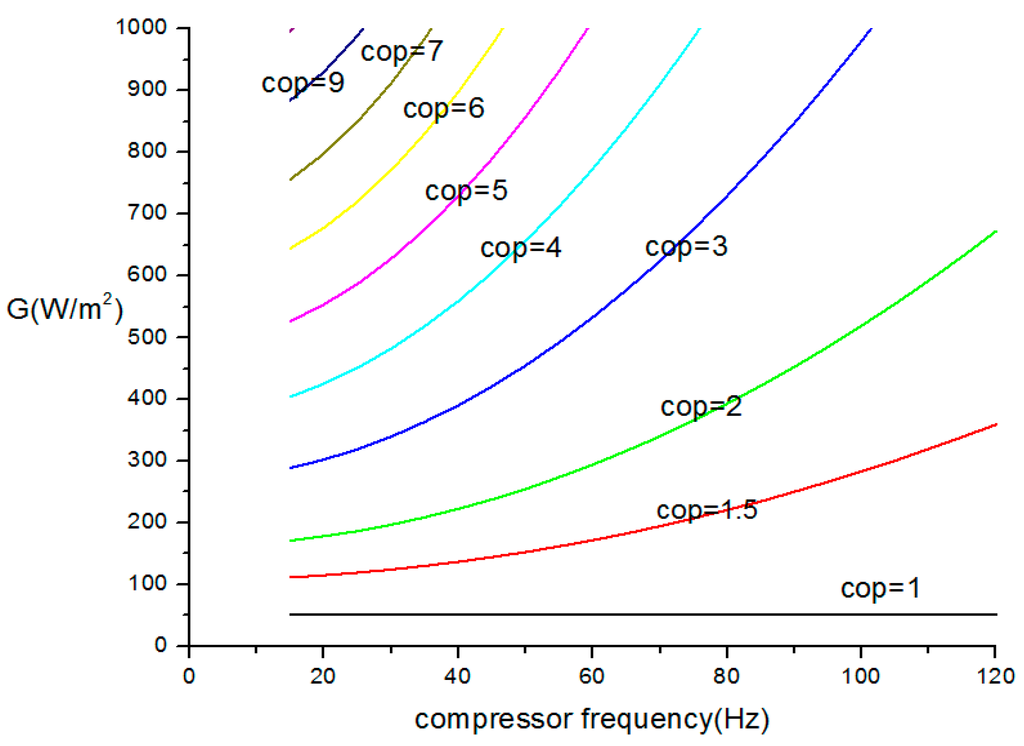
Figure 6. Relations between compressor frequency, solar radiation (G) and COP.

Figure 6. Relations between compressor frequency, solar radiation (G) and COP.

As solar radiation remains constant and the compressor frequency rises, its rotating speed also rises but the system vaporization pressure falls, which will makes the evaporator’s superheat higher and the system COP lower. For instance, supposing that the solar irradiation is 600 W/m² , the COP is expected to arrive at 7.0 at 30 Hz, and will be only 1.87 at 120 Hz at which the system operation becomes less available and economic. Supposing that solar radiation is 950 W/m², COP is expected to get 8.5 at a frequency of 50 Hz, which corresponds well to below data.

From above analysis, if compressor rotating speed is too high, there will be an unsatisfactory heat transfer, and low system COP and operation availability; if compressor rotating speed is too low, there will be an incomplete refrigerants vaporization within the evaporators, even a compressor liquid hammer. Therefore, a compressor rotating speed that is neither too high nor too low is allowed in a practical operation to prevent a toll on the heat pump system.

Figure 7 shows relations between system COP and collector’ thermal efficiency at different compressor frequencies with solar radiation of 900 W/m² and the opening pulse of 400. At a low frequency, there will be a high system COP but a low collector’ thermal efficiency, which can be analyzed in the same way as above. As frequency and evaporator outlet superheat increases, the system COP reduces but the collector’s thermal efficiency continues to ascend. In this sense, system COP is reversely related to the collector’s thermal efficiency as the compressor’s frequency increases. As seen in Figure 7, the frequency at the crossing point of two lines is 28 Hz. That point indicates system COP is 13.4 and collectors’ thermal efficiency is 30% at 28 Hz and the valve opening pulse of 400 with solar irradiation of 900 W/m², but this does not mean that this is the best time for system operation.

It is clear from Figure 7 that, as compressor frequency increases, the SAHP system collector’s thermal efficiency climbs and the system COP goes the opposite way. If use solar radiation and environment temperature are considered to be the controlling parameters of SAHP system, there is little possibility of system COP and collector thermal efficiency being optimal together. However, the influence of evaporator outlet superheat on system COP and collector thermal efficiency are almost the same. As it is known, superheat is not conducive to enhancing system performance, so the refrigerants’ liquid supply can be controlled by tuning the superheat as long as the minimum temperature corresponding to the evaporator heat load (Q) is found.

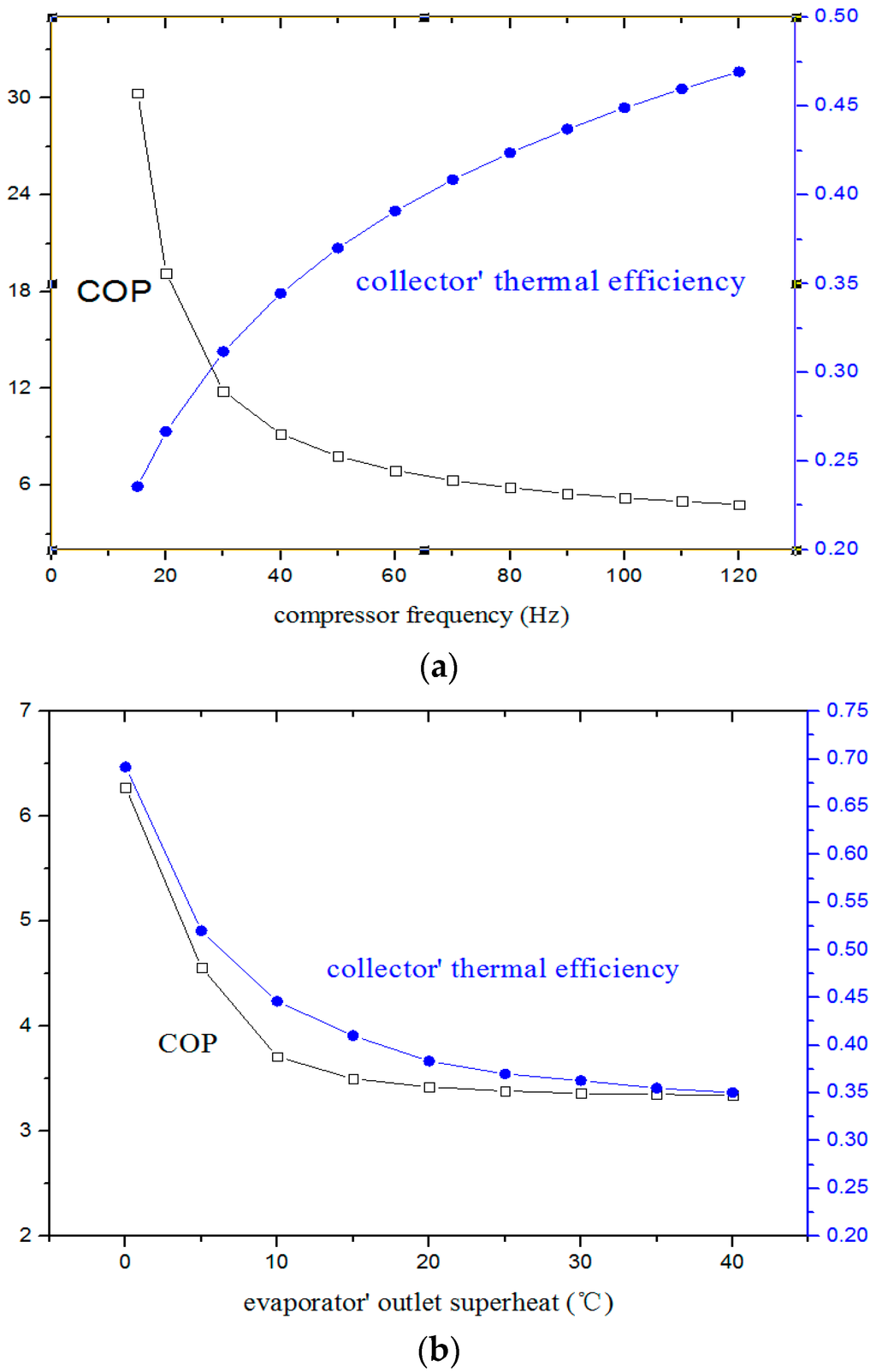
Figure 7. Relations between system COP (a) and collector thermal efficiency (b) influenced respectively by compressor frequency and evaporator’ outlet superheat.

Figure 7. Relations between system COP (a) and collector thermal efficiency (b) influenced respectively by compressor frequency and evaporator’ outlet superheat.

Based on the above analysis, a method of controlling SAHP system is introduced in this paper, namely the EEV-degree of superheat of the compressor inlet refrigerant vapor temperature control (shown in Figure 8). The vapor suction superheat control system is made up of an EEV, a pressure sensor, a temperature sensor and a controller. Now let us see its work flow: evaporators outlet refrigerant pressure (p) and compressor inlet refrigerant temperature ($T$) is transmitted by the pressure sensor to the controller, and $p$ is translated by controller into corresponding saturated refrigerants temperature ($T_e$), so the system superheat degree is $T-T_e$. Then, the controller orders a stepper motor of EEV to set a required opening so as to meet the demand of evaporator’s liquid supply that can make a real-time match with the evaporator heat load (Q). In other words, the opening of EEV can be altered via the controller to effectively control the superheat. Besides, it takes only a few seconds for EEV to switch its opening from fully closed to fully open, and the opening and the switch speed can be configured with a fine tuning of 10%–100% based on products’ features. If EEV-inlet vapor temperature control is used, the compressor is capable of maintaining optimal system COP and collectors’ thermal efficiency ${\mathsf{\eta }}_{coll}$ either under a standard or variable condition or at full load or variable load.

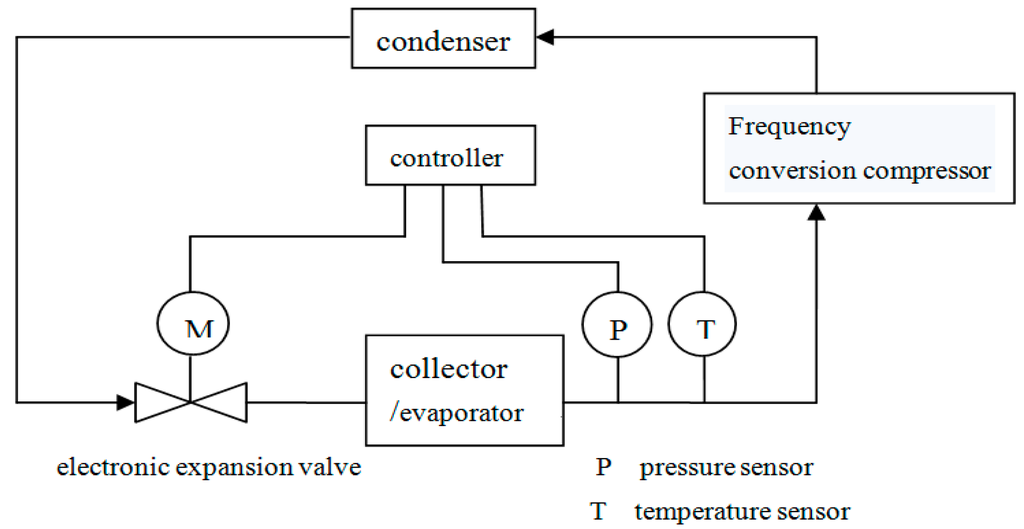
Figure 8. Schematic chart of SAHP system control.

Figure 8. Schematic chart of SAHP system control.

5. Test on System

5.1. Test with Increasing Condensing Water Temperature and Varying EEV Opening Pulse

5.1.1. Test Conditions

Provided that the opening of EEV is different and the water temperature is about 20 °C–55 °C, a test on SAHP system performance was made in Hefei city (31°53’ N and 117°15’ E) from 23 October to 2 November of 2014. The test condition is shown in Table 1, Figure 9. This test assumed that valves 1, 2, 5, 6 were closed while valves 3, 4, 7, 8 were open. The compressor operated at 50 Hz and was powered by the public grid; PV output current was consumed by external load after being inverted by the inverter. The water tank stocked 80 kg water and the flow rate of water-cooling panel heat exchanger was 0.217 kg/s.

Table 1. Test conditions.

EEV Opening Pulse	Inlet Water Temperature (°C)	Time for Test	Sign as
100	20 ± 0.2 °C	2 November 2014	A
200	20 ± 0.2 °C	31 October 2014	B
300	20 ± 0.2 °C	1 November 2014	C
400	20 ± 0.2 °C	23 October 2014	D

Table 1. Test conditions.

EEV Opening Pulse	Inlet Water Temperature (°C)	Time for Test	Sign as
100	20 ± 0.2 °C	2 November 2014	A
200	20 ± 0.2 °C	31 October 2014	B
300	20 ± 0.2 °C	1 November 2014	C
400	20 ± 0.2 °C	23 October 2014	D

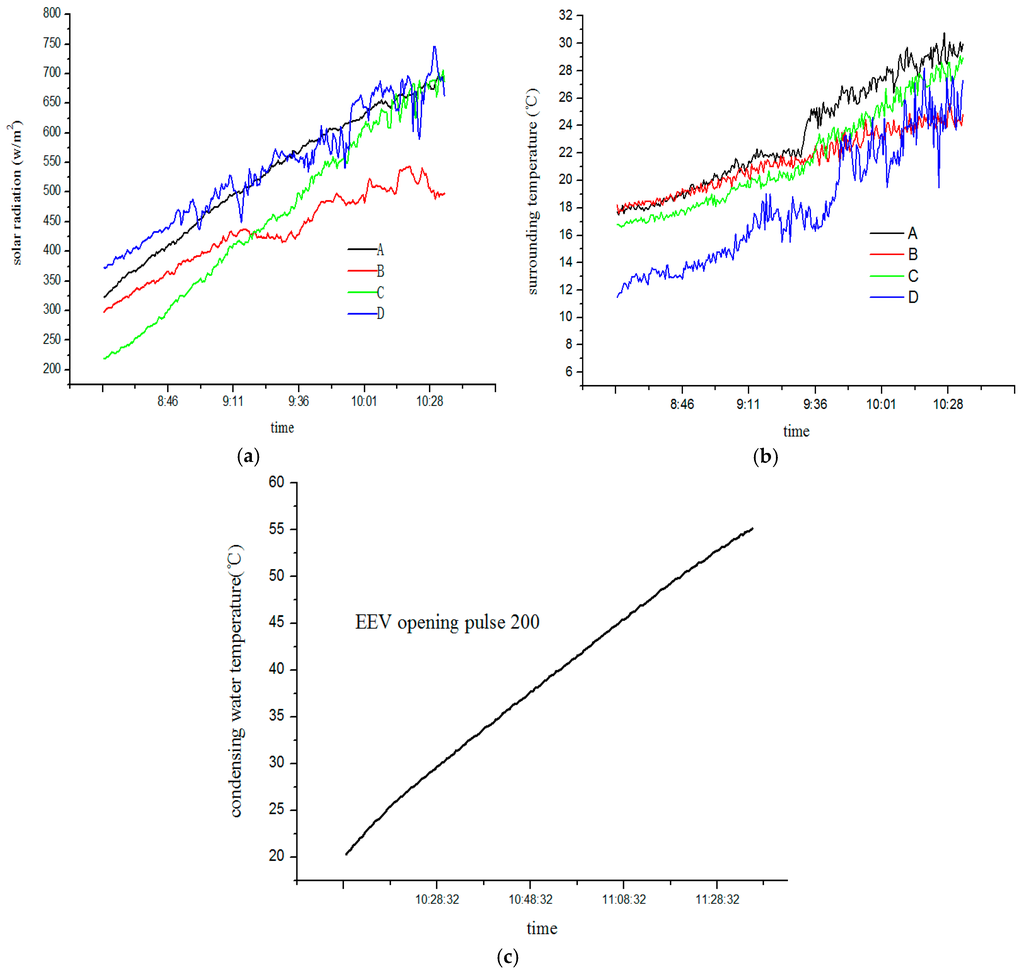
Figure 9. The solar radiation (a), surrounding temperature (b) and condensing water temperature (c) during test.

Figure 9. The solar radiation (a), surrounding temperature (b) and condensing water temperature (c) during test.

5.1.2. Test Results and Discussion

(1)

At an opening pulse of 100, 200, 300 or 400

Figure 10 shows the variation tendency of system COP and collectors’ thermal efficiency (${\mathsf{\eta }}_{coll}$) at different valve opening pulses during the test period. During this test, condensing heat was conveyed through the panel condensing heat exchanger to the water tank, with the water temperature went up from 20 (±0.2 °C) to 55.0 °C. System COP, which was the highest at a low water temperature, drops and tends to be stable as water temperature and compressor power increased. It is a fact that System COP and collectors’ thermal efficiency at the opening pulse of 200 was appreciably higher than that at any other opening pulse. As the temperature increased, the average COP was 6.1, with 10.4 as its peak.

Figure 10. COP (a)and collectors’ thermal efficiency (b) with different openings.

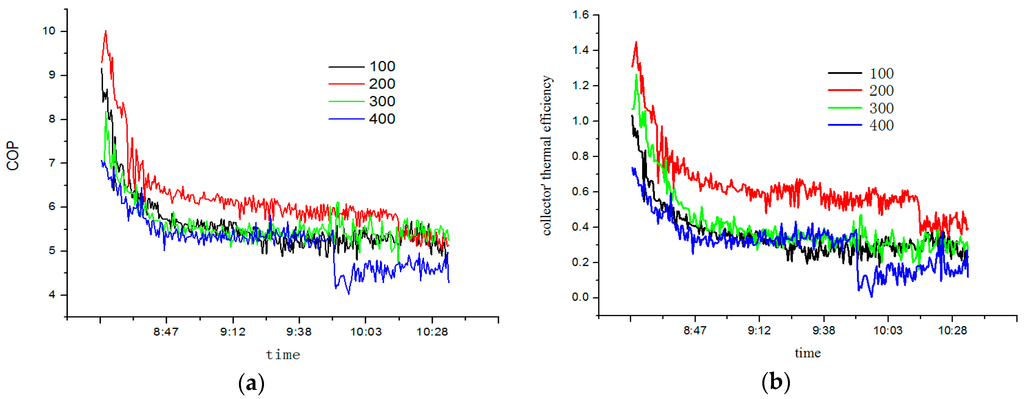
Figure 10. COP (a)and collectors’ thermal efficiency (b) with different openings.

At opening pulses of 100 or 200, evaporators outlet superheat of refrigerant can effectively match its corresponding openings, and compressor power rises with the condensing temperature. In this moment, the SAHP system operates stably (see Figure 11). As the opening pulse continued to increase to 300 or 400, the evaporator’s outlet superheat of refrigerant is lower than that at any other opening pulse.

Figure 11. Compressor power with different openings.

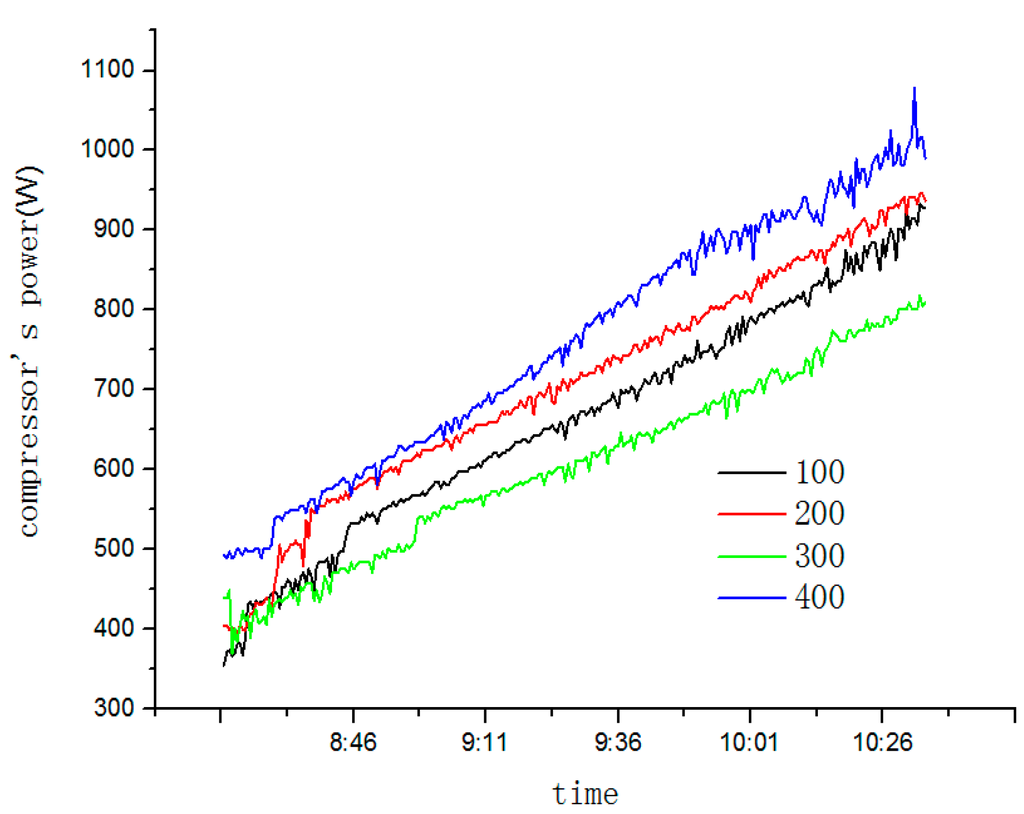
Figure 11. Compressor power with different openings.

In this moment, system evaporators operate unstably and compressor power begins to fluctuate (see Figure 11) based on the MSS theory (see Figure 4). It can be seen from Figure 7 that as solar radiation intensified, evaporators’ load (Q) becomes larger and its outlet refrigerants’ superheat rises. In that case, the valve opening and refrigerants’ flow rate should be reduced to maintain optimal system COP.

The photovoltaic efficiency (${\mathsf{\eta }}_{pv}$) boosts with the intensification of solar radiation. The reason for this is the cooling of photovoltaic modules by refrigerant vaporization outperforming the heating of evaporators by air and solar radiation. Based on the fact that ${\mathsf{\eta }}_{pv}$ rises with the fall of temperature, it can be inferred that ${\mathsf{\eta }}_{pv}$ will record a rapid growth during this time period because refrigerants vaporization takes away large amounts of heat of the photovoltaic battery surface. At the opening pulse of 400, ${\mathsf{\eta }}_{pv}$ will go up to 13.27%, with an average efficiency of 12.06% higher than that of any other openings due to the larger refrigerants flow rate at this time. However, as solar radiation intensifies and system evaporating temperature increases, ${\mathsf{\eta }}_{pv}$ will plunge due to a smaller cooling effect on photovoltaic modules by evaporization at a higher evaporating temperature. Meanwhile, the largest photovoltaic power is 426.7 W, with a average of 340.5 W since photovoltaic power changes in step with photovoltaic efficiency as time proceeds. The peak value of photovoltaic power appeared at the equilibrium point of refrigerants evaporization cooling and solar radiation and air heating but not at the top of solar radiation (see Figure 12).

The condensing and evaporating pressure of different openings at different times are given in Figure 13. At the opening pulse of 400, condensing and evaporating pressure fluctuates a lot as condensing temperature goes up to a certain value, which makes system operate in a stable manner. On the basis of MSS theory, the opening should be reduced while evaporators’ outlet superheat should be heated up at that moment.

Figure 14 indicates condensing power and evaporator power of different valve openings at different times. The condensing power at a opening pulse of 200 is higher than that at any other openings pulse before 10:12. However, after that, system begines to fluctuate. However, if the opening pulse is reduced to 100, evaporators outlet refrigerants superheat rises and the system operates stably again. The evaporator power has the same trend as the condensing power.

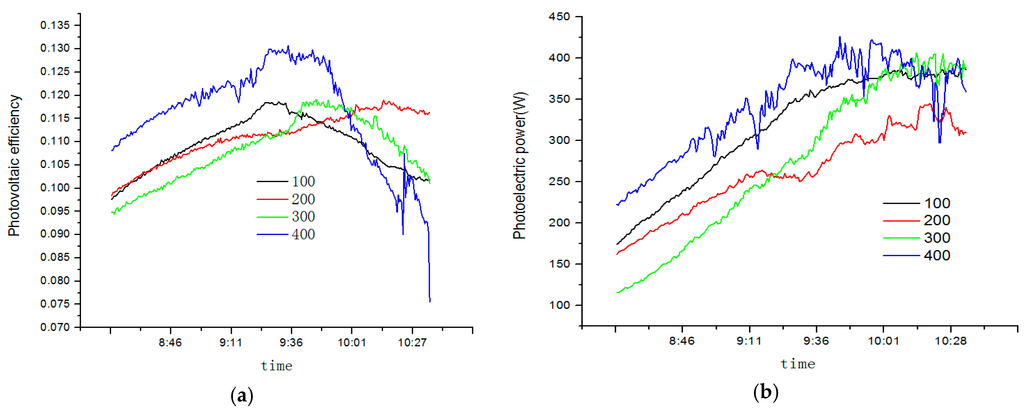
Figure 12. Photoelectric efficiency (a) and photoeletric power (b) with different openings.

Figure 12. Photoelectric efficiency (a) and photoeletric power (b) with different openings.

Figure 13. Condensing pressure (a) and evaporating pressure (b) with different openings.

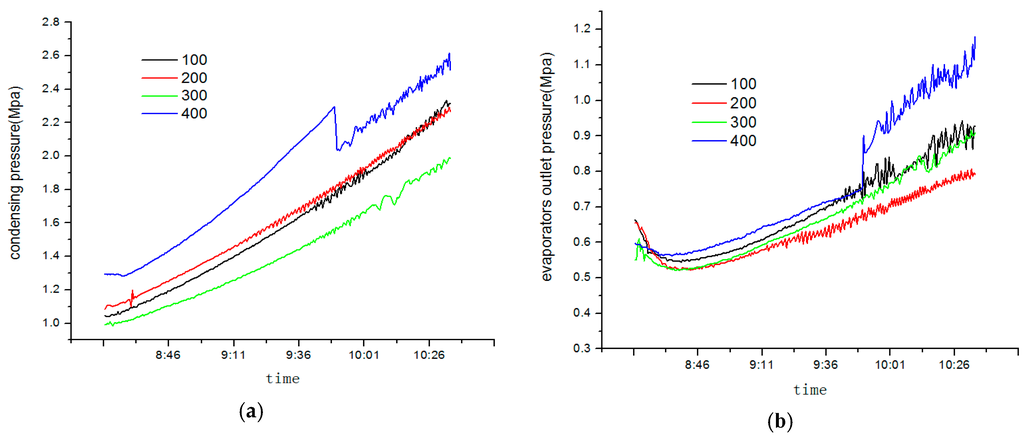
Figure 13. Condensing pressure (a) and evaporating pressure (b) with different openings.

Figure 14. Condensing power (a) and evaporator power (b) with different openings.

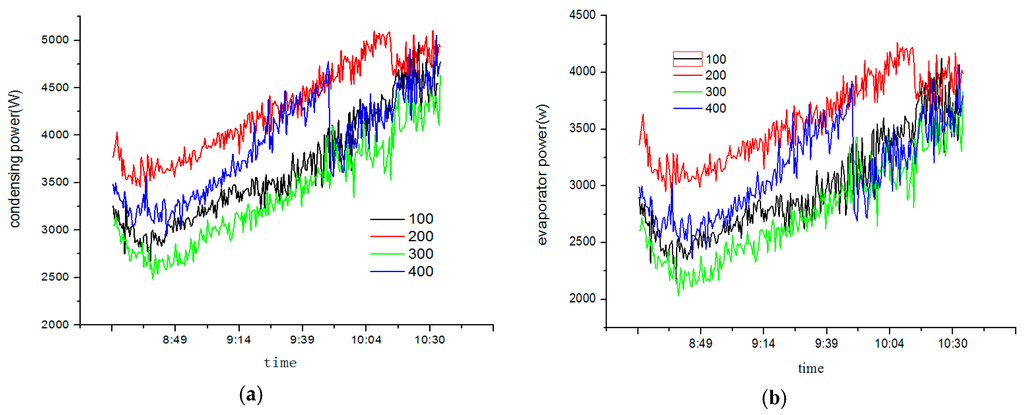
Figure 14. Condensing power (a) and evaporator power (b) with different openings.

(2)

At a EEV opening pulse is 500

At the opening pulse of 500, i.e., a full opening of the valve, relevant instant meteorological parameters during the test are shown in Figure 15.

Figure 15. Meteorological parameters when opening pulse is 500.

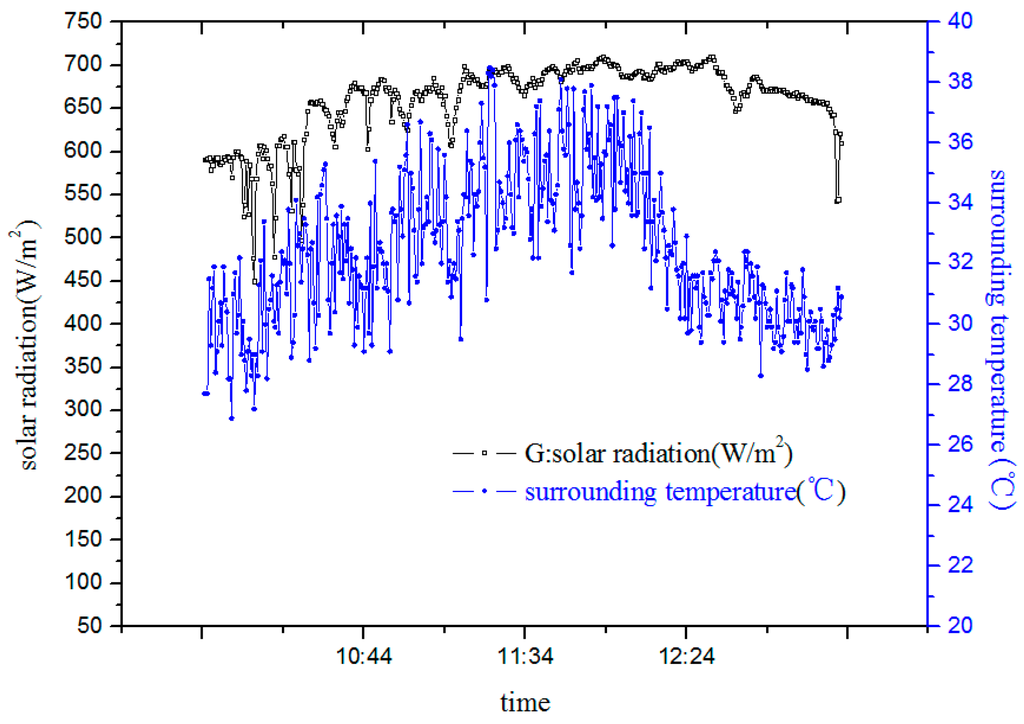
Figure 15. Meteorological parameters when opening pulse is 500.

Figure 16 demonstrates that, as system begines to operate, there will be a large refrigerant flow rate and a low evaporator outlet superheat due to the largest valve opening. Based on the MSS theory, the system is under an unstable condition at that time and compressor power oscillates periodically and rapidly at a high amplitude. As solar radiation intensified, evaporators’ refrigerants outlet superheat goes up and the compressor operating condition alternates between stable and unstable with the former being longer, which illustrates that the system operation condition undergoes a transition from unstable to stable with the rise of the superheat. In that case, as solar radiation intensified, the valve opening has to be reduced to make the system operate stably, preventing system performance from being affected by a long-time unstable compressor operation.

Figure 16. Compressor power when opening pulse is 500.

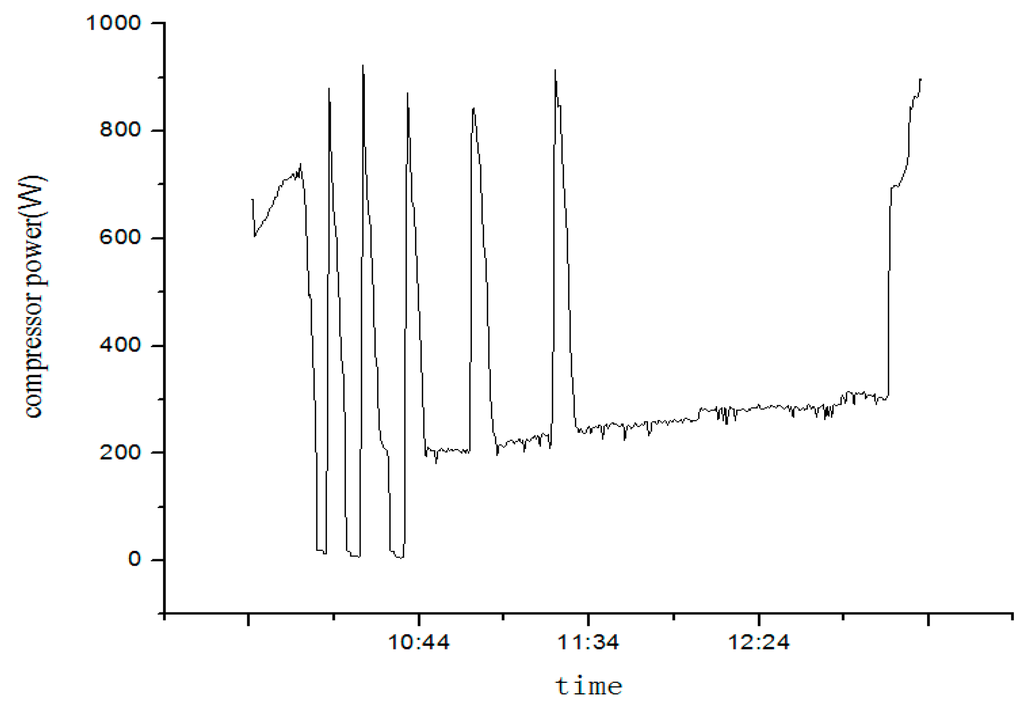
Figure 16. Compressor power when opening pulse is 500.

5.2. At a Constant Condensing Water Temperature and EEV Opening Pulse

5.2.1. Test Conditions

More than 10 tests on the SAHP system performance were made under different environment conditions for comparison over three months of from October to December in 2014. The test condition is shown in Table 2 and Figure 17. As a result, test data of three tests out of 10 are picked up as samples for analysis.

Table 2. Test conditions.

EEV Opening Pulse	Condensing Water Temperature (°C)	Time for Test	Sign as
400	30 ± 0.2 °C	14 October 2014	E
400	30 ± 0.2 °C	6 November 2014	F
400	30 ± 0.2 °C	2 December 2014	G

Table 2. Test conditions.

EEV Opening Pulse	Condensing Water Temperature (°C)	Time for Test	Sign as
400	30 ± 0.2 °C	14 October 2014	E
400	30 ± 0.2 °C	6 November 2014	F
400	30 ± 0.2 °C	2 December 2014	G

Figure 17. The solar radiation (a), surrounding temperature (b) and condensing water temperature (c) during test.

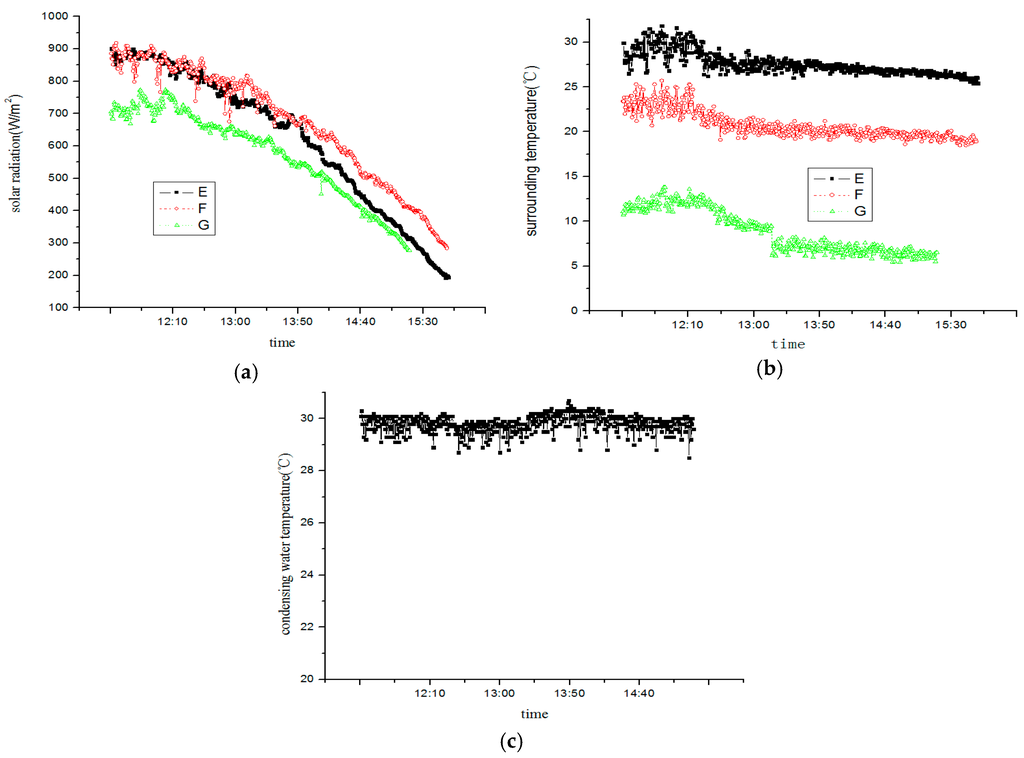
Figure 17. The solar radiation (a), surrounding temperature (b) and condensing water temperature (c) during test.

At the valve opening pulse of 400 and the condensing water temperature of 30 ± 0.2 °C, tests on SAHP system performance were launched in Hefei city (31°53’ N and 117°15’ E) respectively on 14 October (sign as E), 6 November (sign as F) and 2 December (sign as G) of 2014. This test assumed that valve 1, 2, 5, 6 was closed while valve 3, 4, 7, 8 was open. The instant meteorological parameteres and condensing water temperature during the test period can be seen in Figure 17. The compressor operated at 50 Hz and was powered by the public grid.

5.2.2. Test Results and Analysis

Given much cloudy weather in autumn, test data was recorded from 11:21 for better observation and comparison before water temperature was heated up to 30 °C and maintained at this temperature. As seen in Figure 17, it is evident that solar radiation on afternoons of those three days are different, which is conducive to our analysis.

Evaporator outlet pressure varies in step with environment temperature, which seems to suffer a subtle influence by solar radiation. Solar radiation after 13:00 on October 14, 2014 is less intensified than that on 6 November 2014. It is clear from Figure 18 that evaporating pressure increases as solar radiation becomes weaker and the influence of environment temperature on evaporating pressure is stronger than that of solar radiation. The 14 October 2014 saw a mild change of evaporating pressure with an average temperature of 28.2 °C. The evaporators outlet superheat, according to MSS theory (see Figure 4), is on the right of MSS line, which means system operates in a stable manner. When the average temperature declined to 22.1 °C on 6 November 2014, the evaporator outlet superheat becomes low, especially after 12:00, failing to stay above the minimum superheat corresponding to the evaporator load. Based on MSS theory, the system at this time operates unstably and the evaporator outlet pressure begines to fluctuate. As solar radiation becomes weaker, the minimum superheat corresponding to the evaporator load gradually dropped, which makes the system operation and evaporator outlet pressure stable. When the average environment temperature continued to fall to 7.4 °C on 2 December 2014, the evaporating temperature is lower and evaporator outlet pressure fluctuates in a more violent way. The oscillating range of the condensation pressure is small because of a constant condensing temperature. The reasons for the oscillation of the condensation pressure at low temperature is the same as the reason for oscillating evaporating pressure. All of the above phenomena can also be explained from Figure 14 (pulse 400).

Figure 18. Evaporator outlet pressure (a) and condensing pressure (b) under different surrounding conditions.

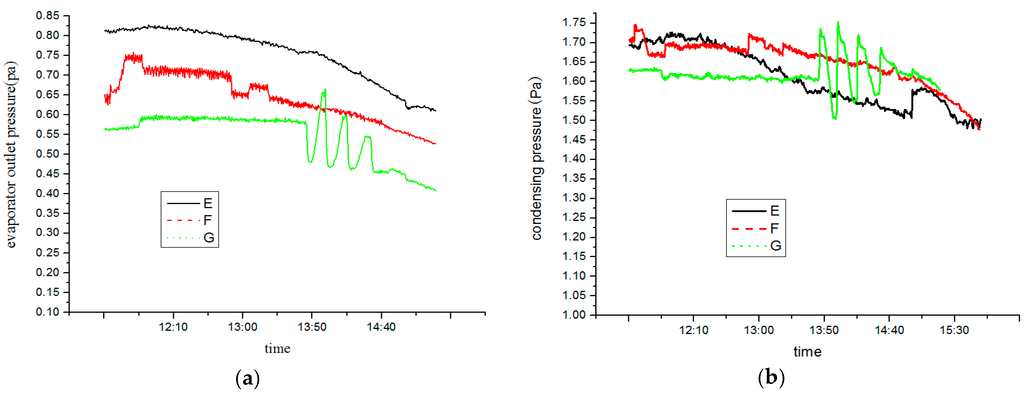
Figure 18. Evaporator outlet pressure (a) and condensing pressure (b) under different surrounding conditions.

Figure 19 describes system photovoltaic efficiency and photovoltaic power under different environment conditions. It is clear from Figure 19 that, as environment temperature falls, photovoltaic efficiency rose to a highest value of 13.4% at a low average environment temperature of 7.4 °C on 2 December 2014, which is clearly higher than 12% of normal photovoltaic modules. Such a high efficiency is mainly due to the cooling effect of the evaporation of the photovoltaic module. This enables the PV/T-SAHP system to be maintained at a low operating temperature even under high irradiation conditions, which can ensure the high photoelectric conversion efficiency. Moreover, the photovoltaic power keep changes in step with solar radiation, so photovoltaic power reaches its highest value when solar radiation becomes most intense.

Figure 19. Photovoltaic efficiency (a) and photovoltaic power (b) under different surrounding conditions.

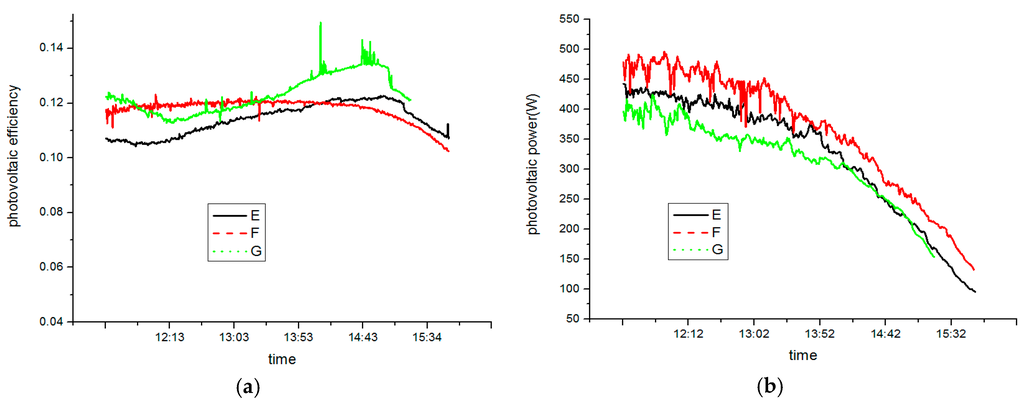
Figure 19. Photovoltaic efficiency (a) and photovoltaic power (b) under different surrounding conditions.

COP is a critical indicator for system performance and the quotient of condensing efficiency being multiplied by compressor power consumption. Therefore, it is well able to distinguish the performance difference between various heat pump systems. The system COP varies as solar radiation and environment temperature differed, ss illustrated in Figure 20. As the system continues to operate, the system COP clearly drops. This is because, as the temperature difference between the inlet and outlet of the condenser at 12:00 increased, the power of the condensation increased. However, the compressor power consumption changes slightly when the compressor frequency (50 Hz) and electronic expansion valve are opened (pulse 400) or fixed (see Figure 21). Therefore, at 12:00, the COP is the highest (those are respectively 7.7, 6.9 and 5.1).

Figure 20. COP under different surrounding conditions.

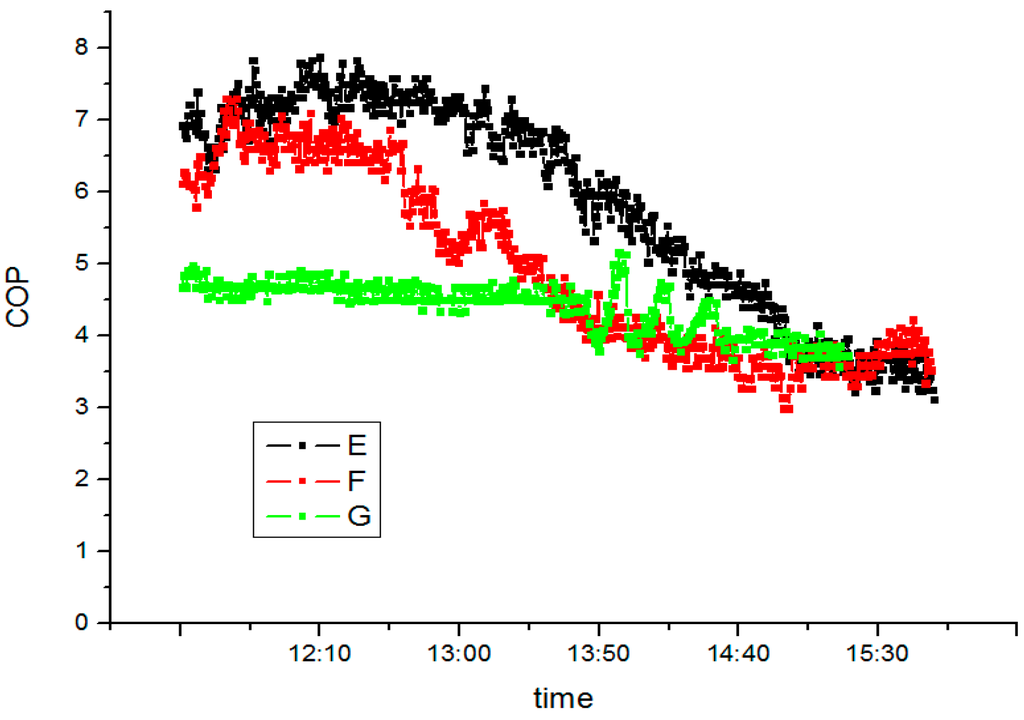
Figure 20. COP under different surrounding conditions.

According to MSS theory, it is easy to understand above phenomenon. When the environment temperature is high (E), the evaporator outlet refrigerants superheat is also high and on the right of MSS line, making the system operate steadily. When the environment temperature is low (G), the evaporator outlet superheat is also low and on the left of MSS line, making the system operate unsteadily and the compressor oscillate strongly.

Figure 21. Compressor power under different surrounding conditions.

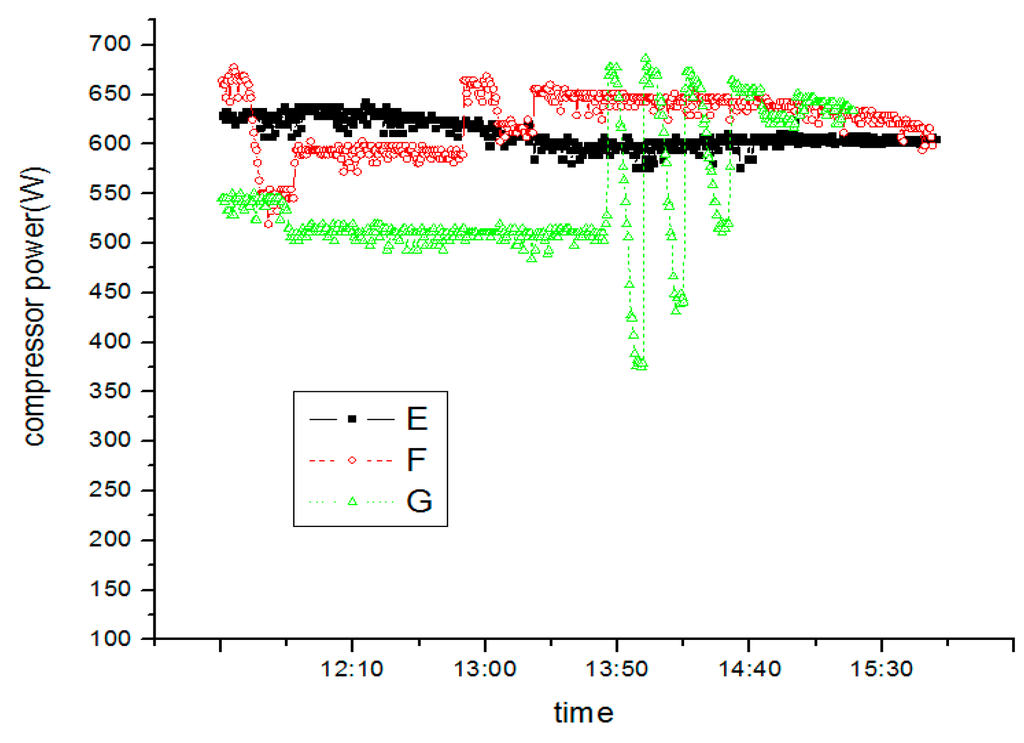
Figure 21. Compressor power under different surrounding conditions.

5.3. Test on SAHP System at Different Frequencies

To investigate better system frequency conversion performance, tests were made respectively at frequencies of 30 Hz, 50 Hz and 70 Hz.

5.3.1. Test condition

Over 10 tests on the SAHP system performance were made at different frequencies for comparison in December 2014. As a result, test data of three tests out of 10 were picked up as samples for analysis.

At a valve opening pulse of 400 and a water temperature of 25 °C, tests on SAHP system performance were launched in Hefei city (31°53’ N and 117°15’ E) respectively on 14, 15 and 19 December 2014. This test assumed that valves 1, 2, 5, 6 was closed while valves 3, 4, 7, 8 was open. The instant meteorological parameteres during the test period can be seen in Figure 22. The compressor operated at frequencies of 30 Hz, 50 Hz and 70 Hz, and was powered by the public grid.

Figure 22. Solar radiation (a) and surrounding temperature (b) during test.

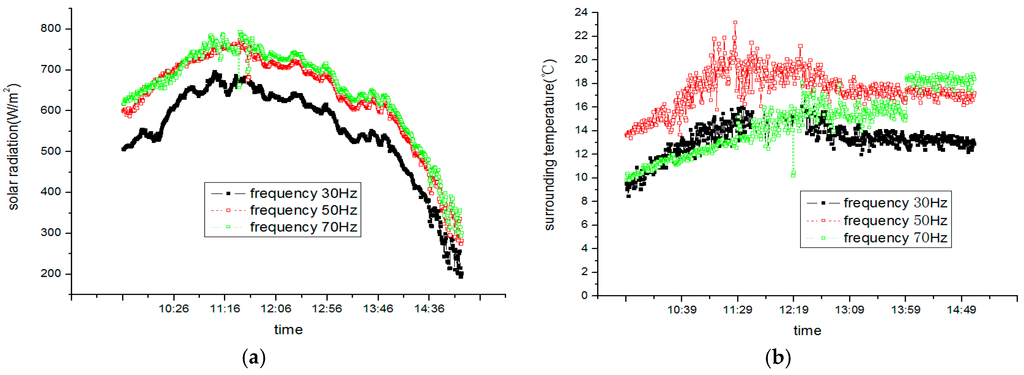
Figure 22. Solar radiation (a) and surrounding temperature (b) during test.

5.3.2. Test Results and Analysis

Figure 23 demonstrates the SAHP system compressor power at different frequencies. At 30 Hz, compressor power is stable, with an average power of 315 W. At 50 Hz, it remaines stable , with an average power of 522 W;.At 70 Hz, however, compressor power fluctuates at around 12:00 and levels off after 12:30. All of this could be explained according to MSS theory.

Figure 23. Compressor power with different compressor frequency.

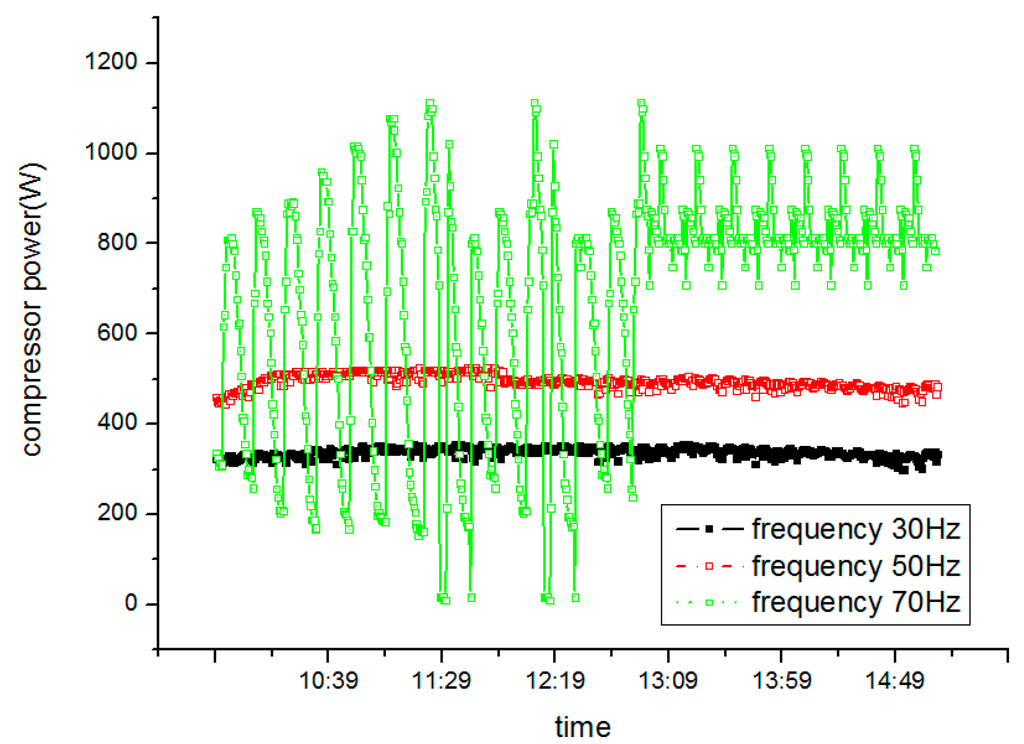
Figure 23. Compressor power with different compressor frequency.

Figure 24 shows the system COP at different frequencies. As compressor frequency rises from 30 Hz to 50 Hz, PV/T-SAHP system COP falls. At 50 Hz, the average COP of SAHP system reaches 4.36, which is much higher than that of a normal heat pump of 3.25 (at an environment temperature of 25 °C), COP increases by 43.0% under similar conditions. However, strong oscillation occurs after system transitions into an unsteady operation at 70 Hz.

Figure 24. System COP with different compressor frequency.

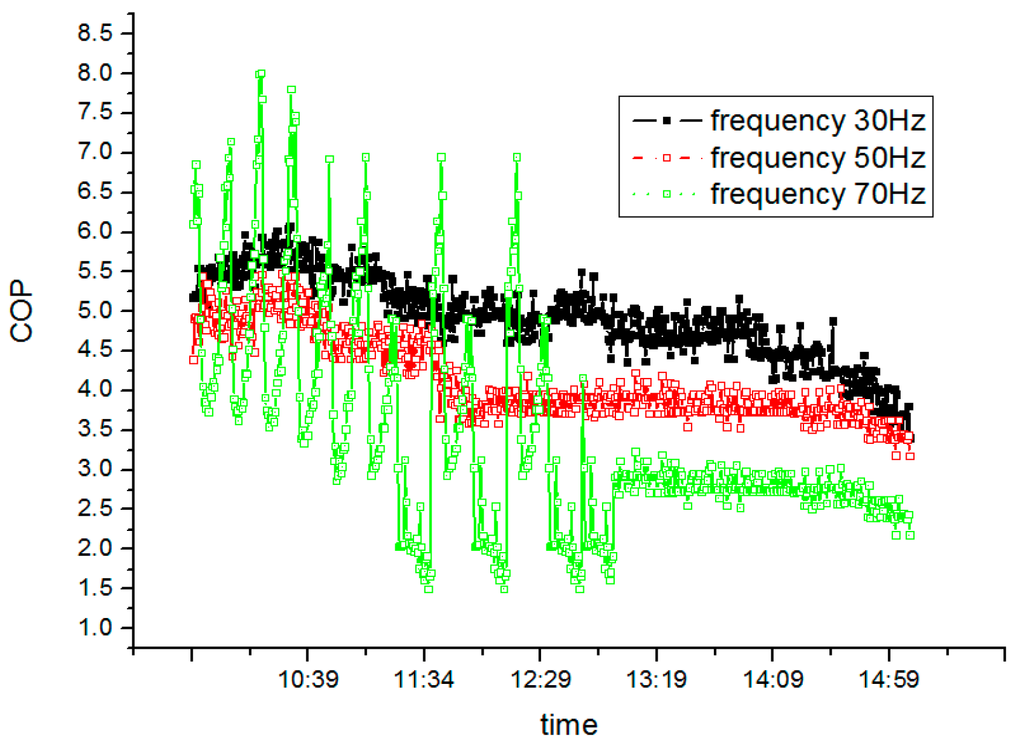
Figure 24. System COP with different compressor frequency.

Figure 25 shows photovoltaic efficiency at different frequencies. Based on the fact that system average photovoltaic efficiencies are respectively 8.15% at 30 Hz, 10.27% at 50 Hz and 12.74% at 70 Hz, it can be seen that photovoltaic efficiency increases dramatically as frequency increases. The main factor behind this efficiency growth is that the temperature of the photovoltaic cells after being combined with evaporators is much lower than that of normal photovoltaic cells because of the heat absorption caused by refrigerants vaporization. In other words, as frequency goes up, evaporators makes better use of solar radiation, resulting in a lower evaporator surface temperature and a higher system photovoltaic efficiency. The temperature of the photovoltaic cells is influenced by both solar radiation and heat pump refrigerants vaporization. In this sense, heat pump refrigerants vaporization playes a major role when solar radiation changes a little. At high frequency, the speed of the compressor is accelerated, the heat from the evaporator is increased, and the surface temperature of the evaporator is reduced. On the other hand, the compression ratio becomes bigger and the evaporating pressure clearly drops; the evaporation temperature of the working fluid becomes lower. So the cooling effect of photovoltaic cells becomes more obvious. Therefore, photovoltaic efficiency at a high compressor frequency is higher than that at a low compressor frequency.

Figure 25. Photovoltaic efficiency under different frequencies.

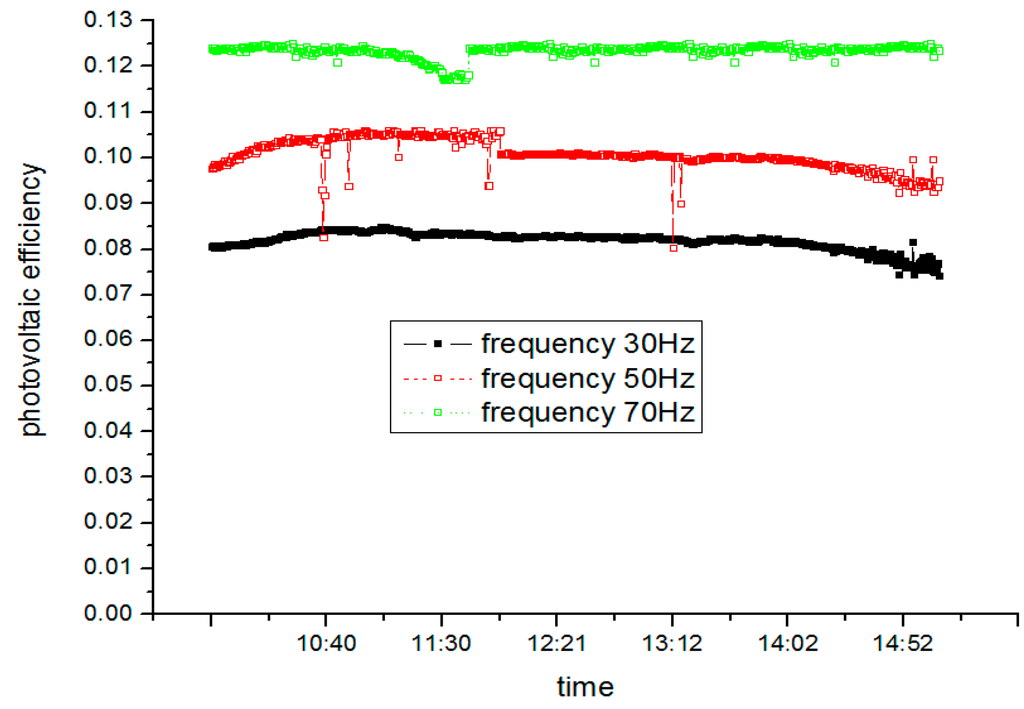
Figure 25. Photovoltaic efficiency under different frequencies.

Through the analysis of 30 Hz, 50 Hz and 70 Hz, the high frequency operation can improve the system’s cooling power, shorten the operating time, reduce the evaporation temperature and pressure, and can improve the photoelectric conversion efficiency, but the system COP is low. The low frequency operation has a higher energy efficiency ratio, especially in the high water temperature operation, the system can maintain good performance.

6. Theory of SAHP System Stability

Based on test results and analysis, it can be summarized that the SAHP system will exhibit uneconomic and unsafe system oscillation under a certain condition. Previously, in order to keep system stability, due to the lack of theoretical and quantitative research on the stability of the system, we tended to increase evaporators superheat. This greatly reduces the utilization of the evaporator because the heat release coefficient of refrigerant in the heat zone is less than 20 percent of the maximum heat release coefficient of the two phase regions [24]. Appropriate to reduce the superheat temperature of the evaporator can obtain a certain energy-saving benefits, but can not blindly reduce the superheat to the pursuit of economic performance.The pursuit of economic performance will lead to system oscillation. Only by quantitative analysis made on the dynamic characteristics of the evaporator and the expansion valve itself, can we determine the critical stability region (MSS line) and the factors that affect the stability of the SAHP system, and the quantitative relationships between them, which deliver the maximum utilization of the effective heat transfer area of the evaporator. The appropriate choice of electronic expansion valve—suction heat control—is the best way to achieve the stability and to get the highest economic results from an SAHP system.

7. Conclusions

By way of analysis of SAHP system stability, some conclusions can be drawn as follows:

If the SAHP system is designed according to the traditional heat pump design, there will be an appreciable conflict between its quantitative operating medium and dynamic operating conditions, which influences system stability. In that case, we can apply the theory of SAHP system stability as a solution to the conflict that plays an important role in the research of an SAHP system.

(1)

MSS theory is able to account for system instabilty in the research of the match between EEV and evaporators.

(2)

As system load varies, compressor rotating speed should be accordingly tuned to meet the demand of evaporator load; and then the opening of EEV should also be changed to make sure that evaporator outlet refrigerants superheat is optimal.

(3)

The crux of optimizing SAHP system is to determine the evaporator superheat under the circumstance of specified loads and its corresponding EEV opening, which means establishing the MSS line.