Simulation and Assessment of Whole Life-Cycle Carbon Emission Flows from Different Residential Structures
Abstract
:1. Introduction
2. Literature Review
2.1. Whole Life-Cycle Carbon Emissions from Residences
2.2. Social Carbon Cost
2.3. Social Discount Rate of Carbon Emissions
3. Methodology
3.1. Matrix Normalization
3.2. Construction of the Model for Residential Carbon Emission Flows
4. Results
4.1. Simulation of Whole Life-Cycle Carbon Emission Flow Diagrams for Different Residential Structures
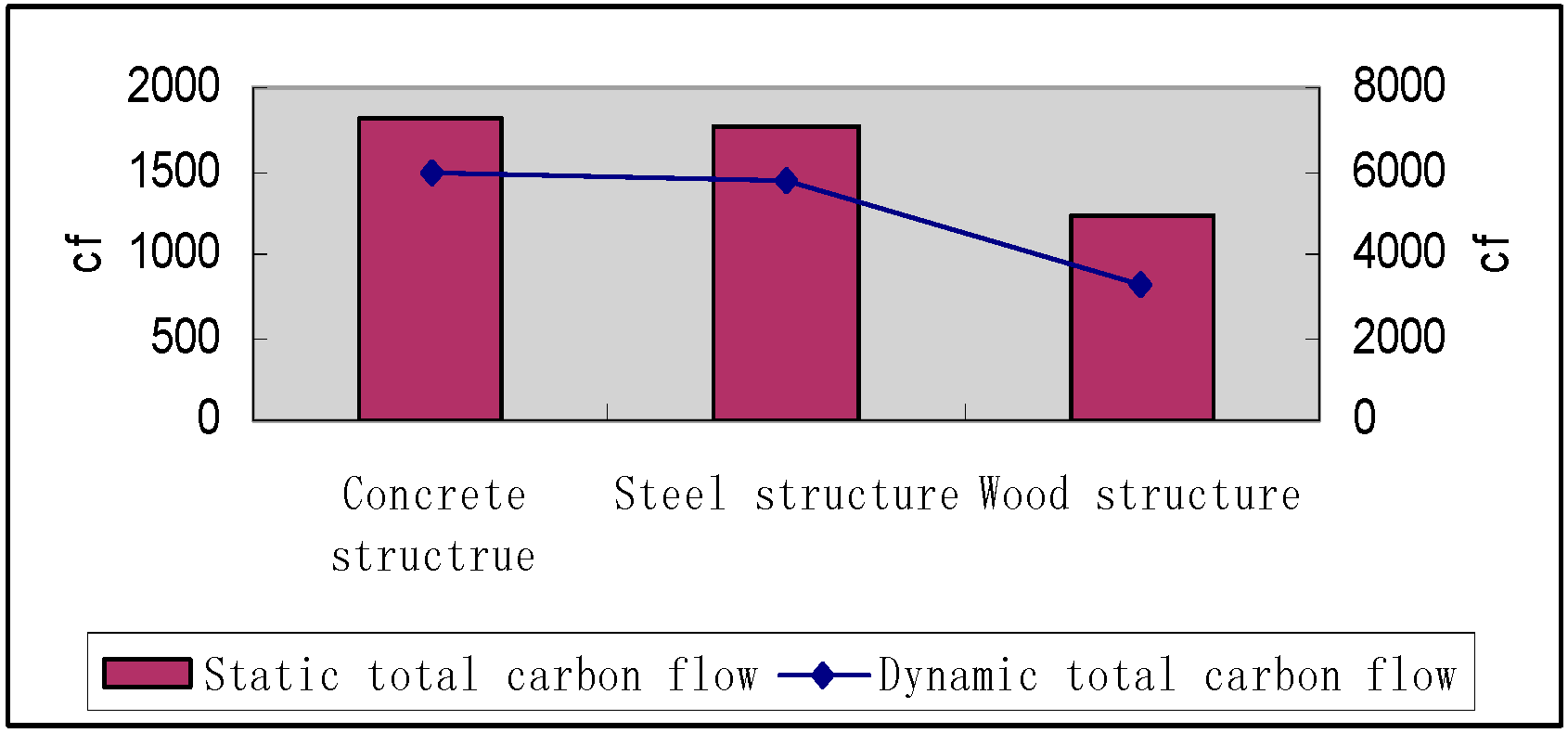
4.2. Assessment of Total Carbon Emission Flows and Absolute Carbon Emissions of Different Residential Structures over Their Whole Life-Cycle
4.3. Assessment of Whole Life-Cycle Building Carbon Cost of Various Structures
5. Discussion
6. Conclusions
- 1)
- In the embodied carbon stage, concrete structures have the highest carbon flow, followed by steel, while wood structures have net negative carbon flow.
- 2)
- In the operations stage, there are no significant differences in carbon emission flows among the structures.
- 3)
- In the demolition and reclamation stage, due to the recyclability of steel and use of wood as a substitute fuel source, both structures have large negative carbon emissions, whereas due to difficulties in materials recovery and thus a low recovery rate, concrete structures have negligible negative carbon emissions.
- 1)
- Concrete structures have the highest total carbon flow, absolute carbon emissions, and dynamic building carbon cost. Concrete has a higher risk in low-carbon residential construction.
- 2)
- Wood structures have the lowest values in all indicators. Wood structures are the best option for low-carbon residential construction.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Brinnel, V.; munstermann, S.; Bleck, W.; Foldmenn, M.; Reese, S. Structural requirements and material solutions for sustainable buildings. Rev. Metall. 2013, 110, 37–46. [Google Scholar] [CrossRef]
- Alcorn, J.A.; Baird, G. Use of a hybrid energy analysis method for evaluating the embodied energy of building materials. Renew. Energy 1996, 8, 319–322. [Google Scholar] [CrossRef]
- Buchanan, A.H.; Honey, B.G. Energy and carbon dioxide implications of building construction. Energy Build. 1994, 20, 205–217. [Google Scholar] [CrossRef]
- Björklund, T.; Jönsson, Å.; Tillman, A.M. LCA of building frame structures: Environmental impact over the life cycle of concrete and steel frames. Int. J. Life Cycle Assess. 1998, 3, 216–224. [Google Scholar]
- Canadian Wood Council (CWC). IBS4—Sustainability and Life Cycle Analysis for Residential Buildings [EB/OL]. Available online: http://cwc.ca/publications/technical/fact-sheets/ (accessed on 6 August 2016).
- Guggemos, A.A.; Horvath, A. Comparison of environmental effects of steel- and concrete-framed buildings. J. Infrastruct. Syst. 2005, 11, 93–101. [Google Scholar] [CrossRef]
- Arima, T. Wood construction as “Urban Forest Reserves”. In Proceedings of the 11th World Conference on Timber Engineering, Trentino, Italy, 20–24 June 2010.
- Shang, C.J.; Chu, C.L.; Zhang, Z.H. Comparison of different structures carbon emissions in building lifecycle. Build. Sci. 2011, 27, 66–70. [Google Scholar]
- Li, S.H. Embodied Environmental burdens of wood structure in Taiwan compared with reinforced concrete and steel structures with various recovery rates. Appl. Mech. Mater. 2012, 174, 202–210. [Google Scholar] [CrossRef]
- Rossi, B.; Marique, A.F.; Reiter, S. Life-cycle assessment of residential building in three different European locations, case study. Build. Environ. 2012, 51, 402–407. [Google Scholar] [CrossRef]
- Griffin, C.T.; Donville, E.; Thompson, B.; Hoffman, M. A multi-performance comparison of long-span structural systems. In Proceedings of the 2nd International Conference on Structures and Architecture, Guimaraes, Portugal, 24–26 July 2013.
- Kim, S.; Moon, J.H.; Shin, Y.; Kim, G.H.; Seo, D.S. Life comparative analysis of energy consumption and CO2 emissions of different building structural frame types. Sci. World J. 2013, 2013, 175702. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Cui, S.H.; Gao, L.J. Comparative study on the carbon footprint of brick and concrete shear wall building structures. Environ. Sci. Technol. 2012, 35, 18–22. [Google Scholar]
- Tol, R.S.J. The marginal costs of carbon dioxide emissions: An assessment of the uncertainties. Energy Policy 2005, 33, 2064–2074. [Google Scholar] [CrossRef]
- Stern, N. The stern review on the economic effects of climate change. Popul. Dev. Rev. 2006, 32, 793–798. [Google Scholar]
- Hope, C. Critical issues for the calculation of the social cost of CO2: Why the estimates from PAGE09 are higher than those from PAGE2002. Clim. Chang. 2013, 117, 531–543. [Google Scholar] [CrossRef]
- Klaassen, R.E.; Patel, M.K. District heating in the Netherlands today: A techno-economic assessment for NGCC-CHP (Natural Gas Combined Cycle combined heat and power). Energy 2013, 54, 63–73. [Google Scholar] [CrossRef]
- Oliva, H.S.; MacGill, I.; Passey, R. Estimating the net societal value of distributed household PV systems. Sol. Energy 2014, 100, 9–22. [Google Scholar] [CrossRef]
- Ackerman, F.; Stanton, E.A. Climate Risks and Carbon Prices: Revising the Social Cost of Carbon. Economics 2012, 6, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Gustavsson, L.; Sathre, R. Variability in energy and carbon dioxide balances of wood and concrete building materials. Build. Environ. 2006, 41, 940–951. [Google Scholar] [CrossRef]
- Adalberth, K. Energy Use and Environmental Impact of New Residential Buildings; Lund University: Lund, Sweden, 2000. [Google Scholar]
- Cole, R.J. Energy and greenhouse gas emissions associated with the construction of alternative structural systems. Build. Environ. 1998, 34, 335–348. [Google Scholar] [CrossRef]
- Glover, J.; White, D.O.; Langrish, T.A.G. Wood versus concrete and steel in house construction—A life cycle assessment. J. For. 2002, 100, 34–41. [Google Scholar]
- Gerilla, G.P.; Teknomo, K.; Hokao, K. An environmental assessment of wood and steel reinforced concrete housing construction. Build. Environ. 2007, 42, 2778–2784. [Google Scholar] [CrossRef]
- Pongiglione, M.; Calderini, C. Material savings through structural steel reuse: A case study in Genoa. Resour. Conserv. Recycl. 2014, 86, 87–92. [Google Scholar] [CrossRef]
- Luo, Z.X. Study on the computation method of CO2 emission from building materials and the strategies for emission reduction. Constr. Sci. 2011, 27, 1–7. [Google Scholar]
- Lin, B.R.; Liu, N.X.; Peng, B.; Zhu, Y.X. Comparative study on international building life-cycle energy consumption and CO2 emission. Constr. Sci. 2013, 29, 22–27. [Google Scholar]
- Ju, Y.; Chen, Y. Study on the computation method of building carbon emission under the whole life-cycle theory—Statistical analyses based on 1997–2013 publications on CNKI. Resid. Technol. 2014, 5, 32–37. [Google Scholar]
- She, J.Q.; Zhang, Y.B.; Qi, S.J. Whole life-cycle carbon emission characteristics and emission reduction strategy of public building in subtropical region—Case study on Xiamen. Constr. Sci. 2014, 2, 13–18. [Google Scholar]
- Watkiss, P.; Downing, T.; Handley, C.; Butterfield, R. The Impacts and Costs of Climate Change, AEA Technology Environment, Stockholm Environment Institute; Commissioned by European Commission DG Environment: Oxford, UK, 2005. [Google Scholar]
- Cox, M.; Brown, M.A.; Sun, X. Energy benchmarking of commercial buildings: A low-cost pathway toward urban sustainability. Environ. Res. Lett. 2013, 8, 035018. [Google Scholar] [CrossRef]
- Mizrach, B. Integration of the global carbon markets. Energy Econ. 2012, 34, 335–349. [Google Scholar] [CrossRef]
- Boersen, A.; Scholtens, B. The relationship between European electricity markets and emission allowance futures prices in phase II of the EU (European Union) emission trading scheme. Energy 2014, 74, 585–594. [Google Scholar] [CrossRef]
- McKibbin, W.J.; Morris, A.C.; Wilcoxen, P.J. Pricing carbon in the U.S.: A model-based analysis of power-sector-only approaches. Resour. Energy Econ. 2014, 36, 130–150. [Google Scholar]
- Sousa, R.; Aguiar-Conraria, L.; Soares, M.J. Carbon financial markets: A time-frequency analysis of CO2 prices. Available online: http://repositorium.sdum.uminho.pt/handle/1822/27957 (accessed on 6 August 2016).
- Creti, A.; Jouvet, P.A.; Mignon, V. Carbon price drivers: Phase I versus Phase II equilibrium. Energy Econ. 2012, 34, 327–334. [Google Scholar] [CrossRef]
- Chen, X.H. Selling 27K Tons of “Carbon” in 11 Months. Shenzhen Economic Daily, 11 June 2014; A04. [Google Scholar]
- Yu, M.K.W. The social discount rate on climate change: A case study of Part L of Schedule 1 of the UK Building Regulations—Conservation of fuel and power. Prop. Manag. 2006, 24, 144–161. [Google Scholar]
- Borenstein, S. The private and public economics of renewable electricity generation. J. Econ. Perspect. 2012, 26, 67–92. [Google Scholar] [CrossRef]
- Dorbian, C.S.; Wolfe, P.J.; Waitz, I.A. Estimating the climate and air quality benefits of aviation fuel and emissions reductions. Atmos. Environ. 2011, 45, 2750–2759. [Google Scholar] [CrossRef]
- IPCC. Fourth Assessment Report of the Intergovernmental Panel in Climate Change; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Fib. Model Code for Service Life Design; Bulletin 34; Fib: Lausanne, Switzerland, 2006. [Google Scholar]
- Stewart, M.G.; Wang, X.; Nguyen, M.N. Climate change impact and risks of concrete infrastructure deterioration. Eng. Struct. 2011, 33, 1326–1337. [Google Scholar] [CrossRef]
- Wei, C.P. The optimization basis and properties of the sum-product method in AHP. Syst. Eng. Theory Pract. 1999, 9, 113–115. [Google Scholar]
- He, B.; Chen, C. Theoretical derivation of ranking results in analytic hierarchy process. J. Yunnan Norm. Univ. 2002, 4, 11–14. [Google Scholar]






| Type | Embodied Carbon (kg CO2/m2) | |||
|---|---|---|---|---|
| CWC | Arima | Shang et al. | Li | |
| Concrete | 433 | 407 | 338 | 332 |
| Steel | 354 | 513 | 278 | 241 |
| Wood | 288 | 266 | 172 | 108 |
| Type | Total Carbon Flow (cf) | Absolute Carbon Emissions (kg CO2/m2) | ||
|---|---|---|---|---|
| Static | Dynamic | Static | Dynamic | |
| Concrete | 1815.7 | 5991 | 1652 | 5452 |
| Steel | 1765 | 5797 | 1659 | 5449 |
| Wood | 1226 | 3236 | 1177 | 3107 |
| Social Carbon Cost ($/kg CO2) | ||
|---|---|---|
| Embodied Carbon Phase | Operations Phase | Demolition and Reclamation Phase |
| 0.025 | 0.035 | 0.058 |
| Building Carbon Cost ($/m2) | ||
|---|---|---|
| Type | Static Building Carbon Cost | Dynamic Building Carbon Cost |
| Concrete | 54 | 175 |
| Steel | 53 | 170 |
| Wood | 40 | 109 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, R.; Qi, S.; Jrade, A. Simulation and Assessment of Whole Life-Cycle Carbon Emission Flows from Different Residential Structures. Sustainability 2016, 8, 807. https://doi.org/10.3390/su8080807
Wen R, Qi S, Jrade A. Simulation and Assessment of Whole Life-Cycle Carbon Emission Flows from Different Residential Structures. Sustainability. 2016; 8(8):807. https://doi.org/10.3390/su8080807
Chicago/Turabian StyleWen, Rikun, Shenjun Qi, and Ahmad Jrade. 2016. "Simulation and Assessment of Whole Life-Cycle Carbon Emission Flows from Different Residential Structures" Sustainability 8, no. 8: 807. https://doi.org/10.3390/su8080807
APA StyleWen, R., Qi, S., & Jrade, A. (2016). Simulation and Assessment of Whole Life-Cycle Carbon Emission Flows from Different Residential Structures. Sustainability, 8(8), 807. https://doi.org/10.3390/su8080807







