Hyperspectral Shallow-Water Remote Sensing with an Enhanced Benthic Classifier
Abstract
1. Introduction
2. Materials and Methods
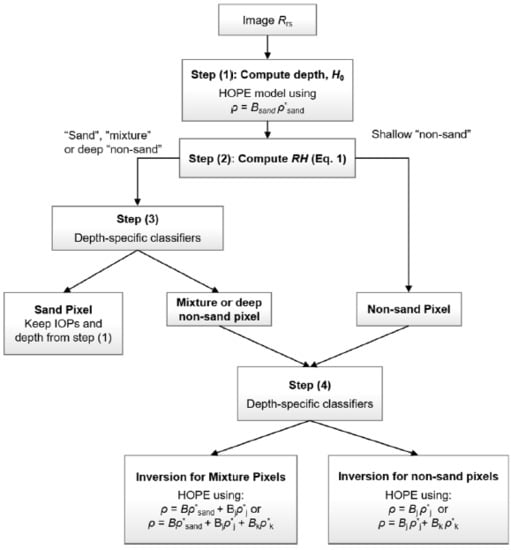
2.1. Workflow
2.2. Depth-Specific Classifiers
2.2.1. LUT Generation
0.001 ≤ adg(440) ≤ 0.6 m−1
0.001 ≤ bbp(440) ≤ 0.01 m−1
2.2.2. Classifiers aided by Binary Space Partitioning Trees
- A principal component analysis (PCA) is performed on the initial LUT of ;
- The LUT is subdivided into a left and right child node using a dividing plane in spectral space. This dividing plane is perpendicular to the first principal component and passes through the spectral mean of the LUT;
- The left and right child nodes are then subdivided into two nodes with same procedure, with PCA performed on the given node, thus computing the dividing plane.
- Terminal nodes are formed when a child node contains from one benthic class or when a benthic class has a lower limit of 50 spectra. This lower limit is necessary in order to have enough spectra per class to generate a classifier (i.e., a non-singular covariance matrix).
- At each terminal node a classifier is trained from the spectra present in that node. Additionally, for the classifiers in step (3) of the workflow, 70% of the of each class present in the node were randomly selected and used to generate the classifier. The remaining 30% were used to assess the misclassification rates. The reasoning behind this is described below.
2.3. Retrievals of IOPs and Depth
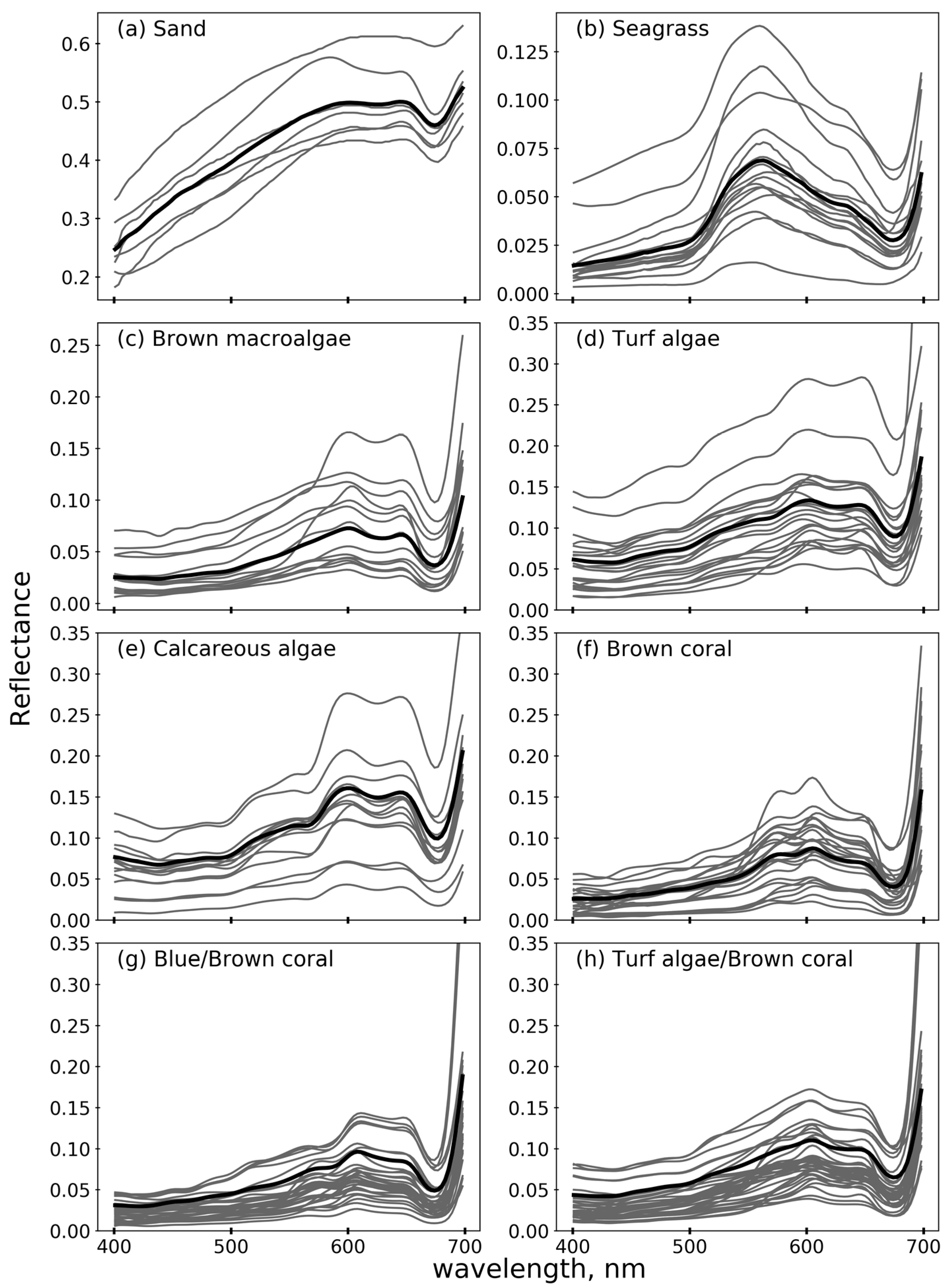
2.3.1. Parameterization of Bottom Reflectance
2.3.2. Optimization and Constraints
2.4. Evaluation with Simulated Data
2.5. Evaluation with PRISM Imagery
2.5.1. PRISM Imagery and Preprocessing
2.5.2. Validation Data
- The PRISM-derived for the validation point was < 10% (i.e., very weak bottom signal), or;
- The validation point was deemed to be optically deep (see Section 2.5.1).
3. Results
3.1. Evaluation with Simulated Data
3.2. Evaluation with PRISM Imagery
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bellwood, D.R.; Hughes, T.P.; Folke, C.; Nyström, M. Confronting the coral reef crisis. Nature 2004, 429, 827–833. [Google Scholar] [CrossRef] [PubMed]
- Burke, L.; Reytar, K.; Spalding, M.; Perry, A. Reefs at Risk Revisited; World Resources Institute: Washington, DC, USA, 2011. [Google Scholar]
- Pandolfi, J.M.; Connolly, S.R.; Marshall, D.J.; Cohen, A.L. Projecting coral reef futures under global warming and ocean acidification. Science 2011, 333, 418–422. [Google Scholar] [CrossRef] [PubMed]
- Mumby, P.; Green, E.P.; Edwards, A.J.; Clark, C.D. The cost-effectiveness of remote sensing for tropical coastal resources assessment and management. J. Environ. Manag. 1999, 55, 157–166. [Google Scholar] [CrossRef]
- Selgrath, J.C.; Roelfsema, C.; Gergel, S.E.; Vincent, A.C.J. Mapping for coral reef conservation: Comparing the value of participatory and remote sensing approaches. Ecosphere 2016, 7, e01325. [Google Scholar] [CrossRef]
- Phinn, S.R.; Roelfsema, C.M.; Mumby, P.J. Multi-scale, object-based image analysis for mapping geomorphic and ecological zones on coral reefs. Int. J. Remote Sens. 2012, 33, 3768–3797. [Google Scholar] [CrossRef]
- Tulloch, V.J.; Possingham, H.P.; Jupiter, S.D.; Roelfsema, C.; Tulloch, A.I.T.; Klein, C.J. Incorporating uncertainty associated with habitat data in marine reserve design. Biol. Conserv. 2013, 162, 41–51. [Google Scholar] [CrossRef]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: San Diego, CA, USA, 1994. [Google Scholar]
- Andréfouët, S.; Kramer, P.; Torres-Pulliza, D.; Joyce, K.E.; Hochberg, E.J.; Garza-Pérez, R.; Mumby, P.J.; Riegl, B.; Yamano, H.; White, W.H.; et al. Multi-site evaluation of IKONOS data for classification of tropical coral reef environments. Remote Sens. Environ. 2003, 88, 128–143. [Google Scholar] [CrossRef]
- Mumby, P.J.; Clark, C.D.; Green, E.P.; Edwards, A.J. Benefits of water column correction and contextual editing for mapping coral reefs. Int. J. Remote Sens. 1998, 19, 203–210. [Google Scholar] [CrossRef]
- Dekker, A.G.; Phinn, S.R.; Anstee, J.; Bissett, P.; Brando, V.E.; Casey, B.; Fearns, P.F.; Hedley, J.; Klonowski, W.; Lee, Z.P.; et al. Intercomparison of shallow water bathymetry, hydro-optics, and benthos mapping techniques in Australian and Caribbean coastal environments. Limnol. Oceanogr. Methods 2011, 9, 396–425. [Google Scholar] [CrossRef]
- Philpot, W.; Davis, C.O.; Bisset, P.W.; Mobley, C.D.; Kohler, D.D.R.; Lee, Z.P.; Bowles, J.; Steward, R.G.; Agrawal, Y.; Trowbridge, J.; et al. Bottom Characterization from Hyperspectral Image Data. Oceanography 2003, 17, 76–85. [Google Scholar] [CrossRef]
- Defoin-Platel, M.; Chami, M. How ambiguous is the inverse problem of ocean color in coastal waters? J. Geophys. Res. Oceans 2007, 112, C03004. [Google Scholar] [CrossRef]
- Mobley, C.D.; Sundman, L.K.; Davis, C.O.; Bowles, J.H.; Downes, T.V.; Leathers, R.A.; Montes, M.J.; Bissett, W.P.; Kohler, D.D.R.; Reid, R.P.; et al. Interpretation of hyperspectral remote-sensing imagery by spectrum matching and look-up tables. Appl. Opt. 2005, 44, 3576–3592. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.P.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. 2. Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar] [CrossRef] [PubMed]
- Klonowski, W.M.; Fearns, P.R.; Lynch, M.J. Retrieving key benthic cover types and bathymetry from hyperspectral imagery. J. Appl. Remote Sens. 2007, 1, 011505. [Google Scholar] [CrossRef]
- Brando, V.E.; Anstee, J.M.; Wettle, M.; Dekker, A.G.; Phinn, S.R.; Roelfsema, C. A physics-based retrieval and quality assessment of bathymetry from suboptimal hyperspectral data. Remote Sens. Environ. 2009, 113, 755–770. [Google Scholar] [CrossRef]
- Giardino, C.; Candiani, G.; Bresciani, M.; Lee, Z.; Gagliano, S.; Pepe, M. BOMBER: A tool for estimating water quality and bottom properties from remote sensing images. Comput. Geosci. 2012, 45, 313–318. [Google Scholar] [CrossRef]
- Jay, S.; Guillaume, M.; Minghelli, A.; Deville, Y.; Chami, M.; Lafrance, B.; Serfaty, V. Hyperspectral remote sensing of shallow waters: Considering environmental noise and bottom intra-class variability for modeling and inversion of water reflectance. Remote Sens. Environ. 2017, 200, 352–367. [Google Scholar] [CrossRef]
- Petit, T.; Bajjouk, T.; Mouquet, P.; Rochette, S.; Vozel, B.; Delacourt, C. Hyperspectral remote sensing of coral reefs by semi-analytical model inversion—Comparison of different inversion setups. Remote Sens. Environ. 2017, 190, 348–365. [Google Scholar] [CrossRef]
- Hedley, J.D.; Roelfsema, C.; Phinn, S.R. Efficient radiative transfer model inversion for remote sensing applications. Remote Sens. Environ. 2009, 113, 2527–2532. [Google Scholar] [CrossRef]
- Lee, Z.P.; Carder, K.L.; Chen, R.F.; Peacock, T.G. Properties of the water column and bottom derived from airborne visible infrared imaging spectrometer (AVIRIS) data. J. Geophys. Res. Oceans 2001, 106, 639–651. [Google Scholar] [CrossRef]
- Phinn, S.R.; Roelfsema, C.M.; Mumby, P.J. Benthic cover map of Heron Reef derived from a high-spatial-resolution multi-spectral satellite image using object-based image analysis. PANGAEA 2012. [Google Scholar] [CrossRef]
- Gower, J.F.R.; King, S.; Borstad, G.A.; Brown, L. Detection of intense plankton blooms using the 709 nm band of the MERIS imaging spectrometer. Int. J. Remote Sens. 2005, 26, 2005–2012. [Google Scholar] [CrossRef]
- Hu, C. A novel ocean color index to detect floating algae in the global oceans. Remote Sens. Environ. 2009, 113, 2118–2129. [Google Scholar] [CrossRef]
- Hedley, J.D.; Roelfsema, C.M.; Phinn, S.R.; Mumby, P.J. Environmental and sensor limitations in optical remote sensing of coral reefs: Implications for monitoring and sensor design. Remote Sens. 2012, 4, 271–302. [Google Scholar] [CrossRef]
- Garcia, R.A.; Hedley, J.; Tin, H.; Fearns, P. A Method to Analyze the Potential of Optical Remote Sensing for Benthic Habitat Mapping. Remote Sens. 2015, 7, 13157–13189. [Google Scholar] [CrossRef]
- Hochberg, E.J.; Atkinson, M.J.; Andréfouët, S. Spectral reflectance of coral reef bottom-types worldwide and implications for coral reef remote sensing. Remote Sens. Environ. 2003, 85, 159–173. [Google Scholar] [CrossRef]
- Jones, C.G.; Lawton, J.H.; Shachak, M. Organisms as ecosystem engineers. Oikos 1994, 69, 373–386. [Google Scholar] [CrossRef]
- Cole, A.J.; Pratchett, M.; Jones, G.P. Diversity and functional importance of coral-feeding fishes on tropical coral reefs. Fish Fish. 2008, 9, 1–22. [Google Scholar] [CrossRef]
- Hochberg, E.J.; Atkinson, M.J.; Apprill, A.; Andrefouet, S. Spectral reflectance of coral. Coral Reefs 2004, 23, 84–95. [Google Scholar] [CrossRef]
- Wanders, J.B.W. The role of benthic algae in the shallow reef of Curacao (Netherlands Antilles). I. Primary productive in the coral reef. Aquat. Bot. 1976, 2, 235–270. [Google Scholar] [CrossRef]
- Klumpp, D.W.D.; Mckinnon, D.; Daniel, P. Damselfish territories: Zones of high productivity on coral reefs. Mar. Ecol. Prog. Ser. 1987, 40, 41–51. [Google Scholar] [CrossRef]
- Klumpp, D.W.D.; McKinnon, A.D. Temporal and spatial patterns in primary production of a coral-reef epilithic algal community. J. Exp. Mar. Biol. Ecol. 1989, 131, 1–22. [Google Scholar] [CrossRef]
- Ogden, J.C.; Lobel, P.S. The role of herbivorous fishes and urchins in coral reef communities. Environ. Biol. Fish. 1978, 3, 49–63. [Google Scholar] [CrossRef]
- Klumpp, D.W.; Polunin, N.V.C. Partitioning of food resources between grazers within damselfish territories on a coral reef. J. Exp. Mar. Biol. Ecol. 1989, 125, 145–169. [Google Scholar] [CrossRef]
- Stearn, C.W.; Scoffin, T.P.; Martindale, W. Calcium carbonate budget of a fringing reef on the west coast of Barbados. Part I- zonation and productivity. Bull. Mar. Sci. 1977, 27, 479–510. [Google Scholar]
- Barnes, D.J.; Chalker, B.E. Calcification and photosynthesis in reef-building corals and algae. In Ecosystems of the World: Coral Reefs; Dubinsky, Z., Ed.; Elsevier: Amsterdam, The Netherlands, 1990; pp. 109–131. [Google Scholar]
- Borowitzka, M.A. Calcium carbonate deposition by reef algae: Morphological and physiological aspects. In Perspectives on Coral Reef; Barnes, D.J., Ed.; Brian Clouston: Australian Capital Territory, Australian, 1983; pp. 16–28. [Google Scholar]
- Morse, D.E.; Hooker, N.; More, A.N.C.; Jensen, R.A. Control of larval metamorphosis and recruitment in sympatric agariciid corals. J. Exp. Mar. Biol. Ecol. 1988, 116, 193–217. [Google Scholar] [CrossRef]
- McCook, L.J.; Jompa, J.; Diaz-Pulido, G. Competition between corals and algae on coral reefs: A review of evidence and mechanisms. Coral Reefs 2001, 19, 400–417. [Google Scholar] [CrossRef]
- Valentine, J.F.; Heck, K.L., Jr. Seagrass herbivory: Evidence for the continued grazing of marine grasses. Mar. Ecol. Prog. Ser. 1999, 176, 291–302. [Google Scholar] [CrossRef]
- Prieur, L.; Sathyendranath, S. An optical classification of coastal and oceanic waters based on the specific spectral absorption curves of phytoplankton pigments, dissolved organic matter, and other particulate materials. Limonol. Oceanogr. 1981, 2, 671–689. [Google Scholar] [CrossRef]
- Winter, M.E. N-FINDR: An algorithm for fast autonomous spectral end-member determination in hyperspectral data. In Imaging Spectrometry V; Descour, M.R., Shen, S.S., Eds.; Proceedings of SPIE; International Society for Optics and Photonics: Bellingham, WA, USA, 1999; Volume 3753, pp. 266–275. [Google Scholar]
- Rencher, A.C.; Christensen, W.F. Methods of Multivariate Analysis. International Statistical Review, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Leiper, I.; Phinn, S.; Dekker, A.G. Spectral reflectance of coral reef benthos and substrate assemblages on Heron Reef, Australia. Int. J. Remote Sens. 2012, 33, 3946–3965. [Google Scholar] [CrossRef]
- Garcia, R.A.; McKinna, L.I.W.; Hedley, J.D.; Fearns, P.R.C.S. Improving the optimization solution for a semi-analytical shallow water inversion model in the presence of spectrally correlated noise. Limnol. Oceanogr. Methods 2014, 12, 651–669. [Google Scholar] [CrossRef]
- Lee, Z.P.; Casey, B.; Arnone, R.; Weidemann, A.; Parsons, R.; Montes, M.J.; Gao, B.-C.; Goode, W.; Davis, C.O.; Dye, J. Water and bottom properties of a coastal environment derived from Hyperion data measured from the EO-1 spacecraft platform. J. Appl. Remote Sens. 2007, 1, 011502. [Google Scholar] [CrossRef]
- Klonowski, W. Hyperspectral Remote Sensing Applied to Shallow Coastal Waters. Ph.D. Thesis, Curtin University, Bentley, Australia, 2015. [Google Scholar]
- Mouroulis, P.; Van Gorp, B.; Green, R.O.; Dierssen, H.; Wilson, D.W.; Eastwood, M.; Boardman, J.; Gao, B.-C.; Cohen, D.; Franklin, B.; et al. Portable Remote Imaging Spectrometer coastal ocean sensor: Design, characteristics, and first flight results. Appl. Opt. 2014, 53, 1363–1380. [Google Scholar] [CrossRef] [PubMed]
- Gao, B.C.; Heidebrecht, K.B.; Goetz, A.F. Derivation of scaled surface reflectances from AVIRIS data. Remote Sens. Environ. 1993, 44, 165–178. [Google Scholar] [CrossRef]
- Thompson, D.R.; Gao, B.C.; Green, R.O.; Roberts, D.A.; Dennison, R.E.; Lundeen, S.R. Atmospheric correction for global mapping spectroscopy: ATREM advances for HyspIRI preparatory campaign. Remote Sens. Environ. 2015, 167, 64–77. [Google Scholar] [CrossRef]
- Thompson, D.R.; Seidel, F.C.; Gao, B.C.; Gierach, M.M.; Green, R.O.; Kudela, R.M.; Mouroulis, P. Optimizing irradiance estimates for coastal and inland water imaging spectroscopy. Geophys. Res. Lett. 2015, 42, 4116–4123. [Google Scholar] [CrossRef]
- Felzenszwalb, P.; Huttenlocher, D. Efficient Graph-Based Image Segmentation. Int. J. Comput. Vis. 2004, 59, 167–181. [Google Scholar] [CrossRef]
- Salmond, J.; Loder, J.; Roelfsema, C.; Host, R.; Passenger, J. Reef Check Australia: 2015 Heron Reef Health Report; Reef Check Foundation Ltd.: Australia, 2016. [Google Scholar]
- Roelfsema, C.M.; Phinn, S.R.; Dennison, W.C. Spatial distribution of benthic microalgae on coral reefs determined by remote sensing. Coral Reefs 2002, 21, 264–274. [Google Scholar] [CrossRef]
- Leiper, I.A.; Phinn, S.R.; Roelfsema, C.M.; Joyce, K.E.; Dekker, A.G. Mapping coral reef benthos, substrates, and bathymetry, using compact airborne spectrographic imager (CASI) data. Remote Sens. 2014, 6, 6423–6445. [Google Scholar] [CrossRef]
- Botha, E.J.; Brando, V.E.; Anstee, J.M.; Dekker, A.G. Increased spectral resolution enhances coral detection under varying water conditions. Remote Sens. Environ. 2013, 131, 247–261. [Google Scholar] [CrossRef]
- Garcia, R.A.; Fearns, P.R.C.S.; McKinna, L.I.W. Detecting trend and seasonal changes in bathymetry derived from HICO imagery: A case study of Shark Bay, Western Australia. Remote Sens. Environ. 2014, 147, 186–205. [Google Scholar] [CrossRef]
- Moses, W.J.; Gitelson, A.A.; Berdnikov, S.; Bowles, J.H.; Povazhnyi, V.; Saprygin, V.; Wagner, E.J.; Patterson, K.W. HICO-based NIR-red models for estimating chlorophyll-a concentration in productive coastal waters. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1111–1115. [Google Scholar] [CrossRef]
- Moses, W.J.; Bowles, J.H.; Corson, M.R. Expected improvements in the quantitative remote sensing of optically complex waters with the use of an optically fast hyperspectral spectrometer—A modeling study. Sensors 2015, 15, 6152–6173. [Google Scholar] [CrossRef] [PubMed]
- Kobryn, H.T.; Wouters, K.; Beckley, L.E.; Heege, T. Ningaloo reef: Shallow marine habitats mapped using a hyperspectral sensor. PLoS ONE 2013, 8, e70105. [Google Scholar] [CrossRef] [PubMed]
- Joyce, K.E.; Phinn, S.R.; Roelfsema, C.M. Live coral index testing and application with hyperspectral airborne image data. Remote Sens. 2013, 5, 6116–6137. [Google Scholar] [CrossRef]



| Acronym | Units | Definition |
|---|---|---|
| IOPs | Inherent Optical Properties | |
| SA | Semianalytical model | |
| LUT | Look up table | |
| BSP | Binary Space Partitioning | |
| PCA | Principal Component Analysis | |
| HOPE | Hyperspectral Optimization Process Exemplar | |
| BRUCE | Bottom Reflectance Un-mixing Computation of the Environment | |
| PRISM | Portable Remote Imaging Spectrometer | |
| rrs | sr−1 | Subsurface remote sensing reflectance |
| Rrs | sr−1 | Above-water remote sensing reflectnace |
| sr−1 | Forward modeled Rrs | |
| sr−1 | Sensor-derived Rrs | |
| ρi(λ) | dimensionlesss | Bottom reflectance of class i |
| (λ) | dimensionlesss | ρi(λ) normalized to a value of 1.0 at 550 nm |
| dimensionless | Percentage contribution of the bottom signal to rrs | |
| Λ | nanometers | Wavelength |
| θs | radians | Solar zenith angle |
| aw(λ) | m−1 | Absorption coefficient of pure water |
| aphy(λ) | m−1 | Absorption coefficient of phytoplankton |
| adg(λ) | m−1 | Absorption coefficient of detritus and gelbstoff |
| bbw(λ) | m−1 | Backscattering coefficient fo pure water |
| bbp(λ) | m−1 | Backscattering coefficient of suspended particles |
| P | m−1 | aphy(440) |
| G | m−1 | adg(440) |
| X | m−1 | bbp(440) |
| H | m | Geometric depth of the water column |
| τ | m | Optical depth of the water column |
| Bi | dimensionless | ρi(550) |
| RH | sr−1 | The relative height of the Rrs peak between 685 and 740 nm |
| Combination Number | ρ1 | ρ2 | ρ3 |
|---|---|---|---|
| 1 | Sand | Seagrass | Brown Algae |
| 2 | Sand | Calcareous Algae | Brown Algae |
| 3 | Sand | Calcareous Algae | Brown Coral |
| 4 | Sand | Calcareous Algae | Blue Coral |
| 5 | Sand | Turf Algae | Brown Algae |
| 6 | Sand | Turf Algae | Brown Coral |
| 7 | Sand | Turf Algae | Blue Coral |
| 8 | Sand | Brown Coral | Blue Coral |
| 9 | Calcareous Algae | Brown Coral | Blue Coral |
| 10 | Turf Algae | Brown Coral | Blue Coral |
| 11 | Brown Algae | Brown Coral | Blue Coral |
| Parameter | Lower Bound | Upper Bound |
|---|---|---|
| aphy(440), P [m−1] | 0.003 | 0.5 |
| adg(440), G [m−1] | 0.0 | 0.6 |
| bbp(440), X [m−1] | 0.0 | 0.5 |
| Depth, H [m] | 0.0 | 60 |
| BSeagrass | 0.0 | 0.16 |
| BBrown Algae | 0.0 | 0.12 |
| BTurf Algae | 0.0 | 0.22 |
| BCalcareous Algae | 0.0 | 0.26 |
| BBrown Coral | 0.0 | 0.15 |
| BBlue Coral | 0.0 | 0.15 |
| BSand | 0.0 | 0.60 |
| Parameter | Overall Classification Accuracy (%) | ||
|---|---|---|---|
| 0 to 2 m | 4 to 6 m | 8 to 10 m | |
| θs, solar zenith (°) | |||
| 10 | 98.4 † | 90.3 | 71.6 |
| 30 * | 98.5 | 89.7 | 69.6 |
| 50 | 98.6 | 88.2 | 63.7 |
| 60 | 98.7 | 86.8 † | 59.3 |
| Y (slope of bbp) | |||
| 0.0 | 98.5 | 83.8 | 47.0 |
| 0.5 * | 98.5 | 89.7 | 69.6 |
| 1.0 | 98.4 | 86.2 | 56.6 |
| 1.5 | 98.3 † | 80.7 † | 44.4 † |
| Sdg (slope of adg) | |||
| 0.012 | 95.5 † | 56.6 † | 34.4 † |
| 0.015 | 98.6 | 83.6 | 46.0 |
| 0.018 * | 98.5 | 89.7 | 69.6 |
| 0.020 | 97.6 | 83.8 | 55.2 |
| Sand | Algae | Coral | Coral/Algae | Sand/Algae | Sd/Al/Cr 1 | Other | User Accuracy, % | |
|---|---|---|---|---|---|---|---|---|
| Sand | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Algae | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Coral | 0 | 2 ‡ | 0 | 1 | 0 | 0 | 0 | 0 |
| Coral/Algae | 0 | 1 | 0 | 9 | 0 | 0 | 3 | 69 |
| Sand/Algae | 0 | 0 | 0 | 0 | 4 | 0 | 0 | 100 |
| Sd/Al/Cr 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| Other | 0 | 0 | 0 | 0 | 0 | 0 | 0 | N/A |
| Producer Accuracy, % | 0 | 0 | 0 | 82 | 83 | 0 | N/A |
| Sand | Algae | Coral | Coral/Algae | Sand/Algae | Sd/Al/Cr 1 | User Accuracy, % | |
|---|---|---|---|---|---|---|---|
| Sand | 1 | 0 | 0 | 0 | 0 | 0 | 100 |
| Algae | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Coral | 0 | 0 | 0 | 2 | 1 ‡ | 0 | 0 |
| Coral/Algae | 0 | 0 | 0 | 12 | 0 | 1 | 92 |
| Sand/Algae | 0 | 0 | 0 | 0 | 4 | 0 | 100 |
| Sd/Al/Cr 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Producer Accuracy, % | 100 | 0 | 0 | 75 | 80 | 0 |
| Parameter | BRUCE | HOPE-LUT | BRUCE vs. HOPE-LUT Relative Difference (%) |
|---|---|---|---|
| aphy(440), m−1 | 0.0166 | 0.0116 | 36 |
| adg(440), m−1 | 0.0532 | 0.0330 | 47 |
| bbp(550), m−1 | 0.0603 | 0.0279 | 74 |
| Depth, m | 2.56 | 2.36 | 8 |
| BSand | 0.451 (74%) | 0.529 | |
| BBrown Algae | 0.006 (1%) | - | |
| BCalcareous Algae | 0.150 (25%) | - | |
| BC(max. λ), % | 63.61 | 86.03 | |
| Relative Error, % | 0.91 | 1.53 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcia, R.A.; Lee, Z.; Hochberg, E.J. Hyperspectral Shallow-Water Remote Sensing with an Enhanced Benthic Classifier. Remote Sens. 2018, 10, 147. https://doi.org/10.3390/rs10010147
Garcia RA, Lee Z, Hochberg EJ. Hyperspectral Shallow-Water Remote Sensing with an Enhanced Benthic Classifier. Remote Sensing. 2018; 10(1):147. https://doi.org/10.3390/rs10010147
Chicago/Turabian StyleGarcia, Rodrigo A., Zhongping Lee, and Eric J. Hochberg. 2018. "Hyperspectral Shallow-Water Remote Sensing with an Enhanced Benthic Classifier" Remote Sensing 10, no. 1: 147. https://doi.org/10.3390/rs10010147
APA StyleGarcia, R. A., Lee, Z., & Hochberg, E. J. (2018). Hyperspectral Shallow-Water Remote Sensing with an Enhanced Benthic Classifier. Remote Sensing, 10(1), 147. https://doi.org/10.3390/rs10010147