Identifying Generalizable Image Segmentation Parameters for Urban Land Cover Mapping through Meta-Analysis and Regression Tree Modeling
Abstract
:1. Introduction
1.1. High-Resolution Remote Sensing and GEOBIA
1.2. Multiresolution Segmentation (MRS) Algorithm
- If f < S2, then merge the two image segments
- If f ≥ S2, then do not merge the two image segments
1.3. Segmentation Parameter Selection
1.4. Objective of This Study
2. Related Work
3. Methodology
3.1. Literature Survey
3.2. Extracting Image/Segmentation Parameter Information from Past Studies
- Image-based information
- MRS parameter information
- Land cover information
3.3. Regression Analysis to Estimate Appropriate SP Values
3.4. Evaluating the Performance of the RT Models for Each Land Cover Type
4. Results and Discussion
4.1. Regression Modeling
4.2. Evaluation of Image Segmentation Results
4.2.1. Applying the RT Model Results
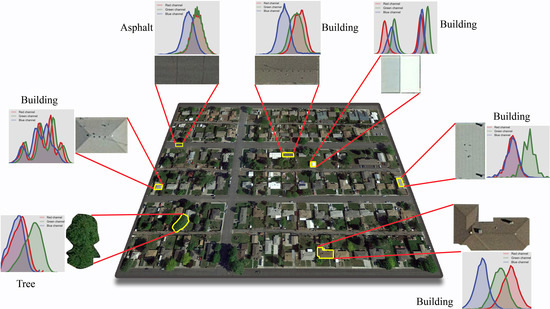
4.2.2. Visual Evaluation Results for the Test Images
4.2.3. Quantitative Evaluation Results for the Test Images
4.3. General Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix B


Appendix C





References
- Cetin, M. Using GIS analysis to assess urban green space in terms of accessibility: Case study in Kutahya. Int. J. Sustain. Dev. World Ecol. 2015, 22, 420–424. [Google Scholar] [CrossRef]
- Tang, Z.; Engel, B.A.; Lim, K.J.; Pijanowski, B.C.; Harbor, J. Minimizing the impact of urbanization on long term runoff. J. Am. Water Resour. Assoc. 2005, 41, 1347–1359. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Wang, L.; Sousa, W.P.; Gong, P. Integration of object-based and pixel-based classification for mapping mangroves with IKONOS imagery. Int. J. Remote Sens. 2004, 25, 5655–5668. [Google Scholar] [CrossRef]
- Jebur, M.N.; Mohd Shafri, H.Z.; Pradhan, B.; Tehrany, M.S. Per-pixel and object-oriented classification methods for mapping urban land cover extraction using spot 5 imagery. Geocarto Int. 2014, 29, 792–806. [Google Scholar] [CrossRef]
- Platt, R.V.; Rapoza, L. An evaluation of an object-oriented paradigm for land use/land cover classification. Prof. Geogr. 2008, 60, 87–100. [Google Scholar] [CrossRef]
- Tenenbaum, D.E.; Yang, Y.; Zhou, W. A comparison of object-oriented image classification and transect sampling methods for obtaining land cover information from digital orthophotography. GISci. Remote Sens. 2011, 48, 112–129. [Google Scholar] [CrossRef]
- Jabari, S.; Zhang, Y. Very high resolution satellite image classification using fuzzy rule-based systems. Algorithms 2013, 6, 762–781. [Google Scholar] [CrossRef]
- Li, X.; Meng, Q.; Gu, X.; Jancso, T.; Yu, T.; Wang, K.; Mavromatis, S. A hybrid method combining pixel-based and object-oriented methods and its application in hungary using Chinese HJ-1 satellite images. Int. J. Remote Sens. 2013, 34, 4655–4668. [Google Scholar] [CrossRef]
- Estoque, R.C.; Murayama, Y.; Akiyama, C.M. Pixel-based and object-based classifications using high- and medium-spatial-resolution imageries in the urban and suburban landscapes. Geocarto Int. 2015, 30, 1113–1129. [Google Scholar] [CrossRef]
- Acharya, T.; Ray, A.K. Image Processing: Principles and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2005; p. 428. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2007; pp. 711–800. [Google Scholar]
- Tian, J.; Chen, D.M. Optimization in multi-scale segmentation of high-resolution satellite images for artificial feature recognition. Int. J. Remote Sens. 2007, 28, 4625–4644. [Google Scholar] [CrossRef]
- Baatz, M.; Schäpe, A. Multiresolution segmentation: An optimization approach for high quality multi-scale image segmentation. In Angewandte Geographische Informationsverarbeitung XII. Beiträge zum AGIT-Symposium Salzburg 2000; Herbert Wichmann Verlag: Karlsruhe, Germany, 2000; pp. 12–23. [Google Scholar]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. Remote Sens. 2004, 58, 239–258. [Google Scholar] [CrossRef]
- Witharana, C.; Civco, D.L. Optimizing multi-resolution segmentation scale using empirical methods: Exploring the sensitivity of the supervised discrepancy measure Euclidean distance 2 (ED2). ISPRS J. Photogramm. Remote Sens. 2014, 87, 108–121. [Google Scholar] [CrossRef]
- Drăguţ, L.; Csillik, O.; Eisank, C.; Tiede, D. Automated parameterisation for multi-scale image segmentation on multiple layers. ISPRS J. Photogramm. Remote Sens. 2014, 88, 119–127. [Google Scholar] [CrossRef] [PubMed]
- Johnson, B.A. Scale issues related to the accuracy assessment of land use/land cover maps produced using multi-resolution data: Comments on “the improvement of land cover classification by thermal remote sensing”. Remote Sens. 2015, 7, 8368–8390. Remote Sens. 2015, 7, 13436–13439. [Google Scholar] [CrossRef]
- Grybas, H.; Melendy, L.; Congalton, R.G. A comparison of unsupervised segmentation parameter optimization approaches using moderate- and high-resolution imagery. GISci. Remote Sens. 2017, 54, 515–533. [Google Scholar] [CrossRef]
- Jozdani, S.E.; Momeni, M.; Johnson, B.A.; Sattari, M. A regression modelling approach for optimizing segmentation scale parameters to extract buildings of different sizes. Int. J. Remote Sens. 2018, 39, 684–703. [Google Scholar] [CrossRef]
- Smith, A. Image segmentation scale parameter optimization and land cover classification using the random forest algorithm. J. Spat. Sci. 2010, 55, 69–79. [Google Scholar] [CrossRef]
- Johnson, B.; Bragais, M.; Endo, I.; Magcale-Macandog, D.; Macandog, P. Image segmentation parameter optimization considering within- and between-segment heterogeneity at multiple scale levels: Test case for mapping residential areas using landsat imagery. ISPRS Int. J. Geo-Inf. 2015, 4, 2292–2305. [Google Scholar] [CrossRef]
- Ma, L.; Cheng, L.; Li, M.; Liu, Y.; Ma, X. Training set size, scale, and features in geographic object-based image analysis of very high resolution unmanned aerial vehicle imagery. ISPRS J. Photogramm. Remote Sens. 2015, 102, 14–27. [Google Scholar] [CrossRef]
- Li, M.; Ma, L.; Blaschke, T.; Cheng, L.; Tiede, D. A systematic comparison of different object-based classification techniques using high spatial resolution imagery in agricultural environments. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 87–98. [Google Scholar] [CrossRef]
- Myint, S.W.; Galletti, C.S.; Kaplan, S.; Kim, W.K. Object vs. Pixel: A systematic evaluation in urban environments. Geocarto Int. 2013, 28, 657–678. [Google Scholar] [CrossRef]
- Li, X.; Myint, S.W.; Zhang, Y.; Galletti, C.; Zhang, X.; Turner, B.L. Object-based land-cover classification for metropolitan Phoenix, Arizona, using aerial photography. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 321–330. [Google Scholar] [CrossRef]
- Alahmadi, M.; Atkinson, P.; Martin, D. Fine spatial resolution residential land-use data for small-area population mapping: A case study in Riyadh, Saudi Arabia. Int. J. Remote Sens. 2015, 36, 4315–4331. [Google Scholar] [CrossRef]
- Drǎguţ, L.; Tiede, D.; Levick, S.R. ESP: A tool to estimate scale parameter for multiresolution image segmentation of remotely sensed data. Int. J. Geogr. Inf. Sci. 2010, 24, 859–871. [Google Scholar] [CrossRef]
- Johnson, B.; Xie, Z. Unsupervised image segmentation evaluation and refinement using a multi-scale approach. ISPRS J. Photogramm. Remote Sens. 2011, 66, 473–483. [Google Scholar] [CrossRef]
- Tong, H.; Maxwell, T.; Zhang, Y.; Dey, V. A supervised and fuzzy-based approach to determine optimal multi-resolution image segmentation parameters. Photogramm. Eng. Remote Sens. 2012, 78, 1029–1044. [Google Scholar] [CrossRef]
- Witharana, C.; Lynch, H. An object-based image analysis approach for detecting penguin guano in very high spatial resolution satellite images. Remote Sens. 2016, 8, 375. [Google Scholar] [CrossRef]
- Liu, J.; Du, M.; Mao, Z. Scale computation on high spatial resolution remotely sensed imagery multi-scale segmentation. Int. J. Remote Sens. 2017, 38, 5186–5214. [Google Scholar]
- Arvor, D.; Durieux, L.; Andrés, S.; Laporte, M.-A. Advances in geographic object-based image analysis with ontologies: A review of main contributions and limitations from a remote sensing perspective. ISPRS J. Photogramm. Remote Sens. 2013, 82, 125–137. [Google Scholar] [CrossRef]
- Belgiu, M.; Drǎguţ, L. Comparing supervised and unsupervised multiresolution segmentation approaches for extracting buildings from very high resolution imagery. ISPRS J. Photogramm. Remote Sens. 2014, 96, 67–75. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Li, M.; Ma, X.; Cheng, L.; Du, P.; Liu, Y. A review of supervised object-based land-cover image classification. ISPRS J. Photogramm. Remote Sens. 2017, 130, 277–293. [Google Scholar] [CrossRef]
- Johnson, B.A. High-resolution urban land-cover classification using a competitive multi-scale object-based approach. Remote Sens. Lett. 2013, 4, 131–140. [Google Scholar] [CrossRef]
- Myint, S.W.; Gober, P.; Brazel, A.; Grossman-Clarke, S.; Weng, Q. Per-pixel vs. Object-based classification of urban land cover extraction using high spatial resolution imagery. Remote Sens. Environ. 2011, 115, 1145–1161. [Google Scholar] [CrossRef]
- Berger, C.; Voltersen, M.; Hese, O.; Walde, I.; Schmullius, C. Robust extraction of urban land cover information from HSR multi-spectral and LIDAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1–16. [Google Scholar] [CrossRef]
- Cowen, D.J.; Jensen, J.R.; Bresnahan, P.J.; Ehler, G.B.; Graves, D.; Huang, X.; Wiesner, C.; Mackey, H.E. The design and implementation of an integrated geographic information system for environmental applications. Photogramm. Eng. Remote Sens. 1995, 61, 1393–1404. [Google Scholar]
- Liu, Y.; Bian, L.; Meng, Y.; Wang, H.; Zhang, S.; Yang, Y.; Shao, X.; Wang, B. Discrepancy measures for selecting optimal combination of parameter values in object-based image analysis. ISPRS J. Photogramm. Remote Sens. 2012, 68, 144–156. [Google Scholar] [CrossRef]
- Clinton, N.; Holt, A.; Scarborough, J.; Yan, L.; Gong, P. Accuracy assessment measures for object-based image segmentation goodness. Photogramm. Eng. Remote Sens. 2010, 76, 289–299. [Google Scholar] [CrossRef]
- Zhang, X.; Feng, X.; Xiao, P.; He, G.; Zhu, L. Segmentation quality evaluation using region-based precision and recall measures for remote sensing images. ISPRS J. Photogramm. Remote Sens. 2015, 102, 73–84. [Google Scholar] [CrossRef]
- Woodcock, C.E.; Strahler, A.H. The factor of scale in remote sensing. Remote Sens. Environ. 1987, 21, 311–332. [Google Scholar] [CrossRef]
- Kim, M.; Madden, M.; Warner, T. Estimation of optimal image object size for the segmentation of forest stands with multispectral IKONOS imagery. In Object-Based Image Analysis: Spatial Concepts for Knowledge-Driven Remote Sensing Applications; Blaschke, T., Lang, S., Hay, G.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 291–307. [Google Scholar]
- Espindola, G.M.; Camara, G.; Reis, I.A.; Bins, L.S.; Monteiro, A.M. Parameter selection for region-growing image segmentation algorithms using spatial autocorrelation. Int. J. Remote Sens. 2006, 27, 3035–3040. [Google Scholar] [CrossRef]
- Gao, Y.; Mas, J.F.; Kerle, N.; Pacheco, J.A.N. Optimal region growing segmentation and its effect on classification accuracy. Int. J. Remote Sens. 2011, 32, 3747–3763. [Google Scholar] [CrossRef]
- Martha, T.R.; Kerle, N.; Westen, C.J.V.; Jetten, V.; Kumar, K.V. Segment optimization and data-driven thresholding for knowledge-based landslide detection by object-based image analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4928–4943. [Google Scholar] [CrossRef]
- Cánovas-García, F.; Alonso-Sarría, F. A local approach to optimize the scale parameter in multiresolution segmentation for multispectral imagery. Geocarto Int. 2015, 30, 937–961. [Google Scholar] [CrossRef]
- Yang, J.; Li, P.; He, Y. A multi-band approach to unsupervised scale parameter selection for multi-scale image segmentation. ISPRS J. Photogramm. Remote Sens. 2014, 94, 13–24. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image processing system (SIPS)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Martha, T.R.; Kerle, N.; Jetten, V.; van Westen, C.J.; Kumar, K.V. Characterising spectral, spatial and morphometric properties of landslides for semi-automatic detection using object-oriented methods. Geomorphology 2010, 116, 24–36. [Google Scholar] [CrossRef]
- Stumpf, A.; Kerle, N. Object-oriented mapping of landslides using random forests. Remote Sens. Environ. 2011, 115, 2564–2577. [Google Scholar] [CrossRef]
- R Core Team, R. R: A Language and Environment for Statistical Computing; The R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Kim, M.; Warner, T.A.; Madden, M.; Atkinson, D.S. Multi-scale geobia with very high spatial resolution digital aerial imagery: Scale, texture and image objects. Int. J. Remote Sens. 2011, 32, 2825–2850. [Google Scholar] [CrossRef]
- Belgiu, M.; Drǎguţ, L.; Strobl, J. Quantitative evaluation of variations in rule-based classifications of land cover in urban neighbourhoods using worldview-2 imagery. ISPRS J. Photogramm. Remote Sens. 2014, 87, 205–215. [Google Scholar] [CrossRef] [PubMed]
- Haque, M.E.; Al-Ramadan, B.; Johnson, B.A. Rule-based land cover classification from very high-resolution satellite image with multiresolution segmentation. J. Appl. Remote Sens. 2016, 10. [Google Scholar] [CrossRef]








| Sensor | Radiometric Resolution | Spatial Resolution | Bands Used for Segmentation | Location | Tested Classes |
|---|---|---|---|---|---|
| Airborne | 8 bit | 25 cm | RGB | Cache, Utah, USA | Building, vegetation, water |
| Airborne | 8 bit | 30 cm | RGB | Calhoun, Illinois, USA | Building, vegetation, water, road |
| World-View-2 | 11 bit | 50 cm | RGB | Washington DC, USA | Buildings, road, water |
| Airborne | 8 bit | 65 cm | RGB | Riverside, California, USA | Building, vegetation, water |
| Airborne | 8 bit | 75 cm | RGB | Dakota, Minnesota, USA | Buildings, vegetation, water |
| IKONOS | 11 bit | 1 m | RGB | Hobart, Tasmania, Australia | Buildings, vegetation, road, bare soil water |
| Total Number of Papers Reviewed | Number of Papers Data Extracted from | Total Number of Data | Extracted Parameters | Last Search Date |
|---|---|---|---|---|
| 215 | 39 | 114 | SP, Compactness/Smoothness, Shape/Color | 21 June 2017 |
| Step of Reviewing | Number of Papers Considered | Reason for Not Considering |
|---|---|---|
| 1 | 215 | Not related to urban mapping |
| 2 | 151 | MRS not applied |
| 3 | 124 | Optical/VHR imagery not applied |
| 4 | 88 | No classification applied |
| 5 | 39 | MRS parameters not reported |
| Class | Shape | Compactness |
|---|---|---|
| Building | 0.38 | 0.61 |
| Vegetation | 0.31 | 0.56 |
| Road | 0.44 | 0.54 |
| Bare soil | 0.36 | 0.55 |
| Water | 0.38 | 0.59 |
| Satellite/Airborne Sensor | Building | Vegetation | Road | Bare Soil | Water |
|---|---|---|---|---|---|
| IKONOS (1 m, 11 bits) | 110 | 85 | 80 | 40 | 40 |
| Quickbird (60 cm, 11 bits) | 110 | 85 | 40 | 85 | 40 |
| GeoEye-1 (41 cm, 11 bits) | 110 | 10 | 10 | 50 | 30 |
| GeoEye-2 (31 cm, 11 bits) | 110 | 20 | 10 | 50 | 30 |
| WorldView-1 and 2 (46 cm, 11 bits) | 110 | 85 | 40 | 50 | 30 |
| WorldView-3 and 4 (31 cm, 11 bits) | 110 | 20 | 10 | 50 | 30 |
| Pléiades (50 cm, 12 bits) | 110 | 85 | 120 | 120 | 120 |
| Airborne (25 cm, 8 bits) | 110 | 185 | 115 | 115 | 115 |
| Airborne (30 cm, 8 bits) | 110 | 185 | 115 | 115 | 115 |
| Airborne (65 cm, 8 bits) | 110 | 185 | 115 | 100 | 40 |
| Airborne (75 cm, 8 bits) | 110 | 185 | 115 | 100 | 40 |
| Building | Vegetation | Water | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scale | OSeg | USeg | D | F | OSeg | USeg | D | F | OSeg | USeg | D | F |
| 10 | 0.95 | 0.18 | 0.71 | 0.09 | 0.98 | 0.10 | 0.71 | 0.04 | 1.00 | 0.04 | 0.71 | 0.01 |
| 20 | 0.83 | 0.16 | 0.62 | 0.24 | 0.91 | 0.11 | 0.66 | 0.13 | 0.99 | 0.07 | 0.71 | 0.02 |
| 30 | 0.70 | 0.17 | 0.53 | 0.38 | 0.83 | 0.18 | 0.63 | 0.21 | 0.97 | 0.10 | 0.70 | 0.04 |
| 40 | 0.58 | 0.22 | 0.48 | 0.46 | 0.73 | 0.26 | 0.60 | 0.27 | 0.95 | 0.10 | 0.69 | 0.07 |
| 50 | 0.49 | 0.27 | 0.45 | 0.51 | 0.63 | 0.33 | 0.56 | 0.33 | 0.93 | 0.12 | 0.68 | 0.10 |
| 60 | 0.42 | 0.31 | 0.43 | 0.53 | 0.56 | 0.37 | 0.55 | 0.35 | 0.92 | 0.13 | 0.67 | 0.12 |
| 70 | 0.34 | 0.35 | 0.41 | 0.55 | 0.46 | 0.45 | 0.52 | 0.38 | 0.90 | 0.16 | 0.66 | 0.14 |
| 80 | 0.24 | 0.44 | 0.41 | 0.54 | 0.36 | 0.49 | 0.50 | 0.40 | 0.86 | 0.16 | 0.64 | 0.17 |
| 90 | 0.18 | 0.49 | 0.42 | 0.51 | 0.34 | 0.51 | 0.51 | 0.39 | 0.84 | 0.16 | 0.62 | 0.20 |
| 100 | 0.13 | 0.55 | 0.43 | 0.49 | 0.25 | 0.53 | 0.48 | 0.41 | 0.82 | 0.17 | 0.62 | 0.21 |
| 110 | 0.12 | 0.59 | 0.45 | 0.46 | 0.16 | 0.60 | 0.48 | 0.41 | 0.80 | 0.17 | 0.60 | 0.24 |
| 120 | 0.11 | 0.65 | 0.49 | 0.41 | 0.14 | 0.66 | 0.51 | 0.36 | 0.75 | 0.17 | 0.57 | 0.28 |
| 130 | 0.10 | 0.68 | 0.50 | 0.38 | 0.12 | 0.67 | 0.50 | 0.36 | 0.73 | 0.18 | 0.55 | 0.31 |
| 140 | 0.09 | 0.71 | 0.52 | 0.35 | 0.10 | 0.71 | 0.53 | 0.32 | 0.70 | 0.18 | 0.54 | 0.32 |
| 150 | 0.09 | 0.73 | 0.54 | 0.32 | 0.10 | 0.71 | 0.53 | 0.32 | 0.66 | 0.19 | 0.52 | 0.36 |
| 160 | 0.07 | 0.76 | 0.55 | 0.30 | 0.09 | 0.72 | 0.53 | 0.31 | 0.64 | 0.19 | 0.50 | 0.38 |
| 170 | 0.07 | 0.79 | 0.57 | 0.27 | 0.07 | 0.74 | 0.53 | 0.31 | 0.53 | 0.21 | 0.44 | 0.48 |
| 180 | 0.07 | 0.79 | 0.57 | 0.26 | 0.07 | 0.74 | 0.54 | 0.30 | 0.51 | 0.22 | 0.42 | 0.50 |
| 190 | 0.06 | 0.82 | 0.59 | 0.23 | 0.07 | 0.77 | 0.55 | 0.28 | 0.51 | 0.23 | 0.44 | 0.48 |
| 200 | 0.05 | 0.83 | 0.60 | 0.22 | 0.07 | 0.78 | 0.56 | 0.26 | 0.48 | 0.24 | 0.43 | 0.49 |
| ESP tool | 0.03 | 0.88 | 0.63 | 0.16 | 0.07 | 0.81 | 0.59 | 0.23 | 0.30 | 0.33 | 0.39 | 0.53 |
| RT models | 0.12 | 0.58 | 0.44 | 0.47 | 0.17 | 0.69 | 0.53 | 0.34 | 0.92 | 0.15 | 0.67 | 0.12 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Johnson, B.A.; Jozdani, S.E. Identifying Generalizable Image Segmentation Parameters for Urban Land Cover Mapping through Meta-Analysis and Regression Tree Modeling. Remote Sens. 2018, 10, 73. https://doi.org/10.3390/rs10010073
Johnson BA, Jozdani SE. Identifying Generalizable Image Segmentation Parameters for Urban Land Cover Mapping through Meta-Analysis and Regression Tree Modeling. Remote Sensing. 2018; 10(1):73. https://doi.org/10.3390/rs10010073
Chicago/Turabian StyleJohnson, Brian A., and Shahab E. Jozdani. 2018. "Identifying Generalizable Image Segmentation Parameters for Urban Land Cover Mapping through Meta-Analysis and Regression Tree Modeling" Remote Sensing 10, no. 1: 73. https://doi.org/10.3390/rs10010073
APA StyleJohnson, B. A., & Jozdani, S. E. (2018). Identifying Generalizable Image Segmentation Parameters for Urban Land Cover Mapping through Meta-Analysis and Regression Tree Modeling. Remote Sensing, 10(1), 73. https://doi.org/10.3390/rs10010073