Analysis of Permafrost Region Coherence Variation in the Qinghai–Tibet Plateau with a High-Resolution TerraSAR-X Image
Abstract
1. Introduction
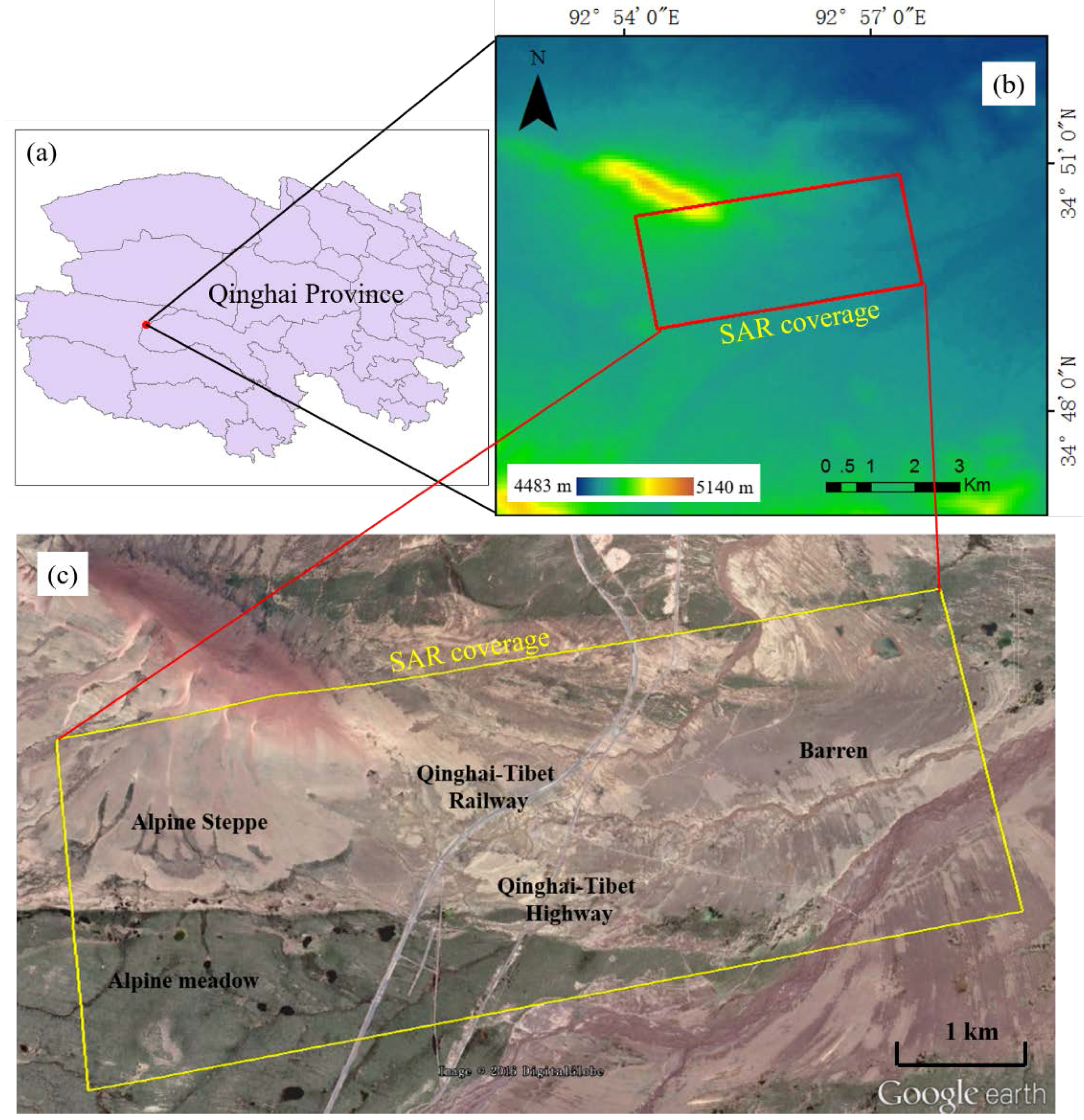
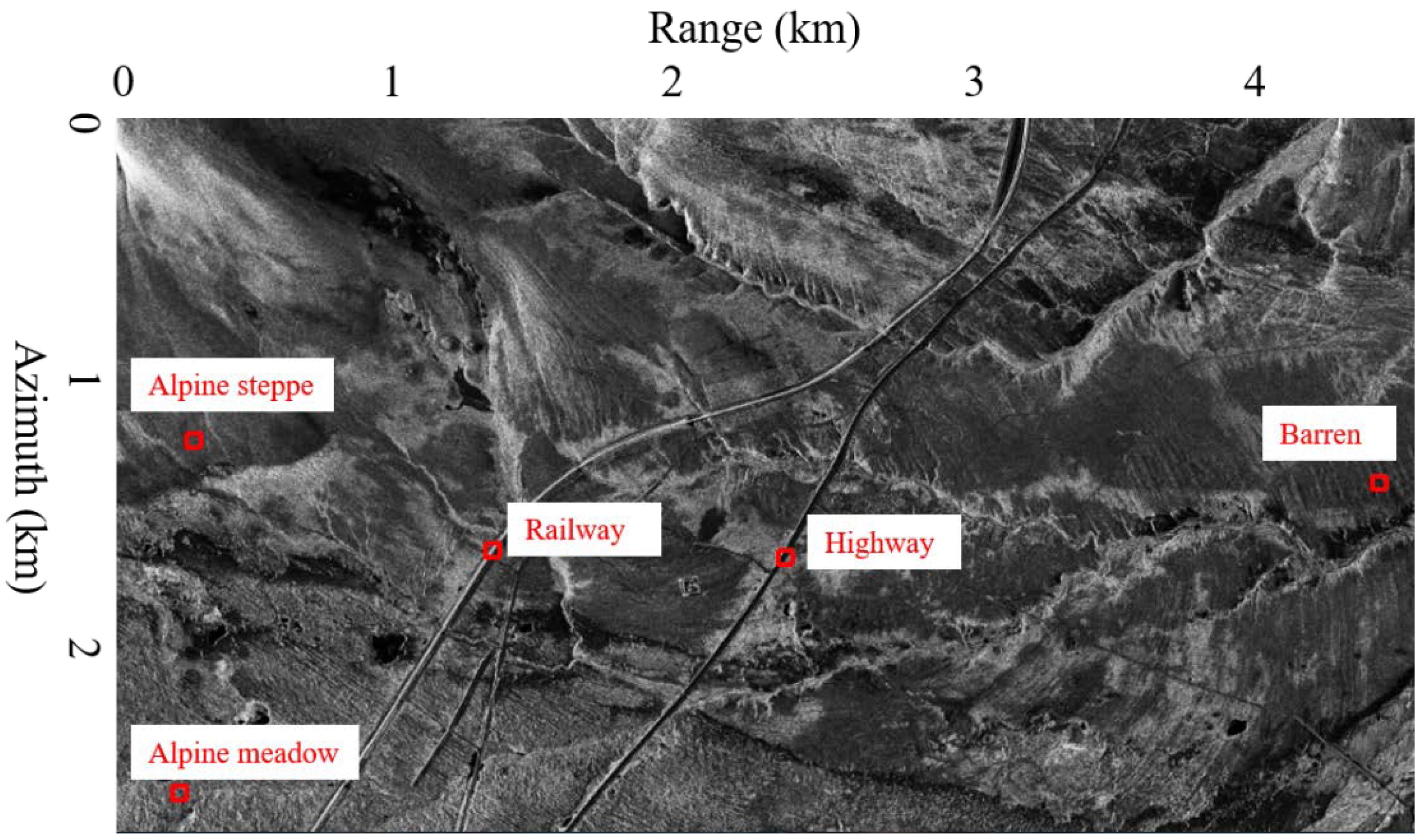
2. Study Area and Dataset
3. Method
3.1. Coherence
3.2. Modelling of Temporal Decorrelation
3.3. Time-Series Coherence Analysis
4. Experimental Results
4.1. Time-Series Interferometric Coherence
4.2. Modelling of Temporal Decorrelation
5. Discussion
5.1. Effect of Vegetation
5.2. Effect of Soil Moisture
5.3. Effect of Active Layer (AL) Freezing and Thawing
5.4. Effect of Human Activity
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Harris, S.; French, H.; Heginbottom, J.; Johnston, G.; Ladanyi, B.; Sego, D.; van Everdingen, R. Glossary of Permafrost and Related Ground-Ice Terms; Technical Memorandum 142; National Research Council of Canada: Ottawa, ON, Canada, 1988. [Google Scholar]
- Wu, Q.B.; Hou, Y.D.; Yun, H.B.; Liu, Y.Z. Changes in active-layer thickness and near-surface permafrost between 2002 and 2012 in alpine ecosystems, Qinghai–Xizang (Tibet) Plateau, China. Glob. Planet. Chang. 2015, 124, 149–155. [Google Scholar] [CrossRef]
- Zhao, L.; Wu, Q.B.; Marchenko, S.S.; Sharkhuu, N. Thermal state of permafrost and active layer incentral Asia during the International Polar Year. Permafr. Periglac. 2010, 21, 198–207. [Google Scholar] [CrossRef]
- Subcommittee, Permafrost. Glossary of Permafrost and Related Ground-Ice Terms; Technical Memorandum; National Research Council of Canada: Ottawa, ON, Canada, 1988. [Google Scholar]
- Chen, F.L.; Lin, H.; Zhou, W.; Hong, T.H.; Wang, G. Surface deformation detected by ALOS PALSAR small baseline SAR interferometry over permafrost environment of Beiluhe section, Tibet Plateau, China. Remote Sens. Environ. 2013, 138, 10–18. [Google Scholar] [CrossRef]
- Cheng, G.; Wu, T. Responses of permafrost to climate change and their environmental significance, Qinghai-Tibet Plateau. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Guo, D.; Wang, H. Simulation of permafrost and seasonally frozen ground conditions on the Tibetan Plateau, 1981–2010. J. Geophys. Res. 2013, 118, 5216–5230. [Google Scholar] [CrossRef]
- Lin, Z.J.; Niu, F.J.; Luo, J.; Lu, J.H.; Liu, H. Changes in permafrost environments caused by construction and maintenance of Qinghai-Tibet Highway. J. Cent. South Univ. Technol. 2011, 18, 1454–1464. [Google Scholar] [CrossRef]
- Pang, Q.; Cheng, G.; Li, S.X.; Zhang, W.G. Active layer thickness calculation over the Qinghai–Tibet Plateau. Cold Reg. Sci. Technol. 2009, 57, 23–28. [Google Scholar] [CrossRef]
- Wu, Q.B.; Niu, F.J. Permafrost changes and engineering stability in Qinghai-Xizang Plateau. Chin. Sci. Bull. 2013, 58, 1079–1094. [Google Scholar] [CrossRef]
- Ma, W.; Mu, Y.; Wu, Q.B.; Sun, Z.Z.; Liu, Y.Z. Characteristics and mechanisms of embankment deformation along the Qinghai–Tibet Railway in permafrost regions. Cold Reg. Sci. Technol. 2011, 67, 178–186. [Google Scholar] [CrossRef]
- Niu, F.J.; Lin, Z.; Lu, J.H.; Liu, H.; Xu, Z.Y. Characteristics of roadbed settlement in embankment–bridge transition section along the Qinghai-Tibet Railway in permafrost regions. Cold Reg. Sci. Technol. 2011, 65, 437–445. [Google Scholar] [CrossRef]
- Li, S.Y.; Lai, Y.M.; Zhang, M.Y.; Dong, Y.H. Study on long-term stability of Qinghai–Tibet Railway embankment. Cold Reg. Sci. Technol. 2009, 57, 139–147. [Google Scholar] [CrossRef]
- Li, Z.; Tang, P.; Zhou, J.; Tian, B.; Chen, Q.; Fu, S. Permafrost environment monitoring on the Qinghai-Tibet Plateau using time series ASAR images. Int. J. Digit. Earth 2014, 8, 1–21. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Z.J.; Zhang, H.; Wu, Q.B.; Zhang, B.; Tang, Y.X. Seasonal deformation features on Qinghai-Tibet railway observed using time-series InSAR technique with high-resolution TerraSAR-X images. Remote Sens. Lett. 2017, 1, 1–10. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, R. Monitoring surface deformation over permafrost with an improved SBAS-InSAR algorithm: With emphasis on climatic factors modeling. Remote Sens. Environ. 2016, 184, 276–287. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Lanari, R.; Mora, O.; Manunta, M.; MallorquíJ, J.; Berardino, P.; Sansosti, E. A small-baseline approach for investigating deformations on full-resolution differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Chen, F.; Guo, H.; Ishwaran, N.; Zhou, W.; Yang, R.; Jing, L.; Zeng, H. Synthetic aperture radar (SAR) interferometry for assessing Wenchuan earthquake (2008) deforestation in the Sichuan giant panda site. Remote Sens. 2014, 6, 6283–6299. [Google Scholar] [CrossRef]
- Wickramanayake, A.; Henschel, M.D.; Hobbs, S.; Buehler, S.A.; Ekman, J.; Lehrbass, B. Seasonal variation of coherence in SAR interferograms in Kiruna, Northern Sweden. Int. J. Remote Sens. 2016, 2, 370–387. [Google Scholar]
- Antonova, S.; Kääb, A.; Heim, B.; Langer, M.; Boike, J. Spatio-temporal variability of X-band radar backscatter and coherence over the Lena River Delta, Siberia. Remote Sens. Environ. 2016, 182, 169–191. [Google Scholar] [CrossRef]
- Jung, H.C.; Alsdorf, D. Repeat-Pass Multi-Temporal Interferometric SAR Coherence Variations with Amazon Floodplain and Lake Habitats. Int. J. Remote Sens. 2010, 31, 881–901. [Google Scholar] [CrossRef]
- Weydahl, D. Analysis of ERS Tandem SAR Coherence from Glaciers, Valleys, and Fjord Ice on Svalbard. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2029–2039. [Google Scholar] [CrossRef]
- Zebker, H.A.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Wei, M.; Sandwell, D.T. Decorrelation of L-band and C-band interferometry over vegetated areas in California. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2942–2952. [Google Scholar]
- Wang, T.; Liao, M.; Perissin, D. InSAR coherence-decomposition analysis. IEEE Geosci. Remote Sens. Lett. 2010, 7, 156–160. [Google Scholar] [CrossRef]
- Hoen, E.W.; Zebker, H.A. Penetration depths inferred from interferometric volume decorrelation observed over the Greenland ice sheet. IEEE Trans. Geosci. Remote Sens. 2010, 38, 2571–2583. [Google Scholar]
- Guarnieri, A.M.; Tebaldini, S. Hybrid Cramér–Rao bounds for crustal displacement field estimators in SAR interferometry. IEEE Signal Proc. Lett. 2007, 14, 1012–1015. [Google Scholar] [CrossRef]
- Rossi, C.; Minet, C.; Fritz, T.; Eineder, M.; Bamler, R. Temporal monitoring of subglacial volcanoes with TanDEM-X—Application to the 2014–2015 eruption within the Bárðarbunga volcanic system, Iceland. Remote Sens. Environ. 2016, 181, 186–197. [Google Scholar] [CrossRef]
- Tang, P.; Zhou, W.; Tian, B.; Chen, F.; Li, Z.; Li, G. Quantification of temporal decorrelation in x-, c-, and l-band interferometry for the permafrost region of the qinghai-tibet plateau. IEEE Geosci. Remote Sens. Lett. 2017, 99, 1–5. [Google Scholar] [CrossRef]
- Tang, P.P.; Li, Z.; Zhou, J.M.; Tian, B.S.; Xu, J. Coherence based analysis of distributed scatterers in the Qinghai-Tibet Plateau. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, Australia, 21–26 July 2013; pp. 1356–1359. [Google Scholar]
- Kubanek, J.; Westerhaus, M.; Schenk, A.; Aisyah, N.; Brotopuspito, K.S.; Heck, B. Volumetric change quantification of the 2010 Merapi eruption using TanDEM-X InSAR. Remote Sens. Environ. 2015, 164, 16–25. [Google Scholar] [CrossRef]
- Gabriel, A.; Goldstein, R.; Zebker, H. Mapping small elevation changes over large areas: Differential radar interferometry. J. Geophys. Res. 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- De Zan, F.; Parizzi, A.; Prats-Iraola, P.; López-Dekker, P. A SAR interferometric model for soil moisture. IEEE Trans. Geosci. Remote Sens. 2014, 52, 418–425. [Google Scholar] [CrossRef]
- Zwieback, S.; Hensley, S.; Hajnsek, I. Assessment of soil moisture effects on L-band radar interferometry. Remote Sens. Environ. 2015, 164, 77–89. [Google Scholar] [CrossRef]
- Zwieback, S.; Hensley, S.; Hajnsek, I. Soil Moisture Estimation Using Differential Radar Interferometry: Toward Separating Soil Moisture and Displacements. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5069–5083. [Google Scholar] [CrossRef]




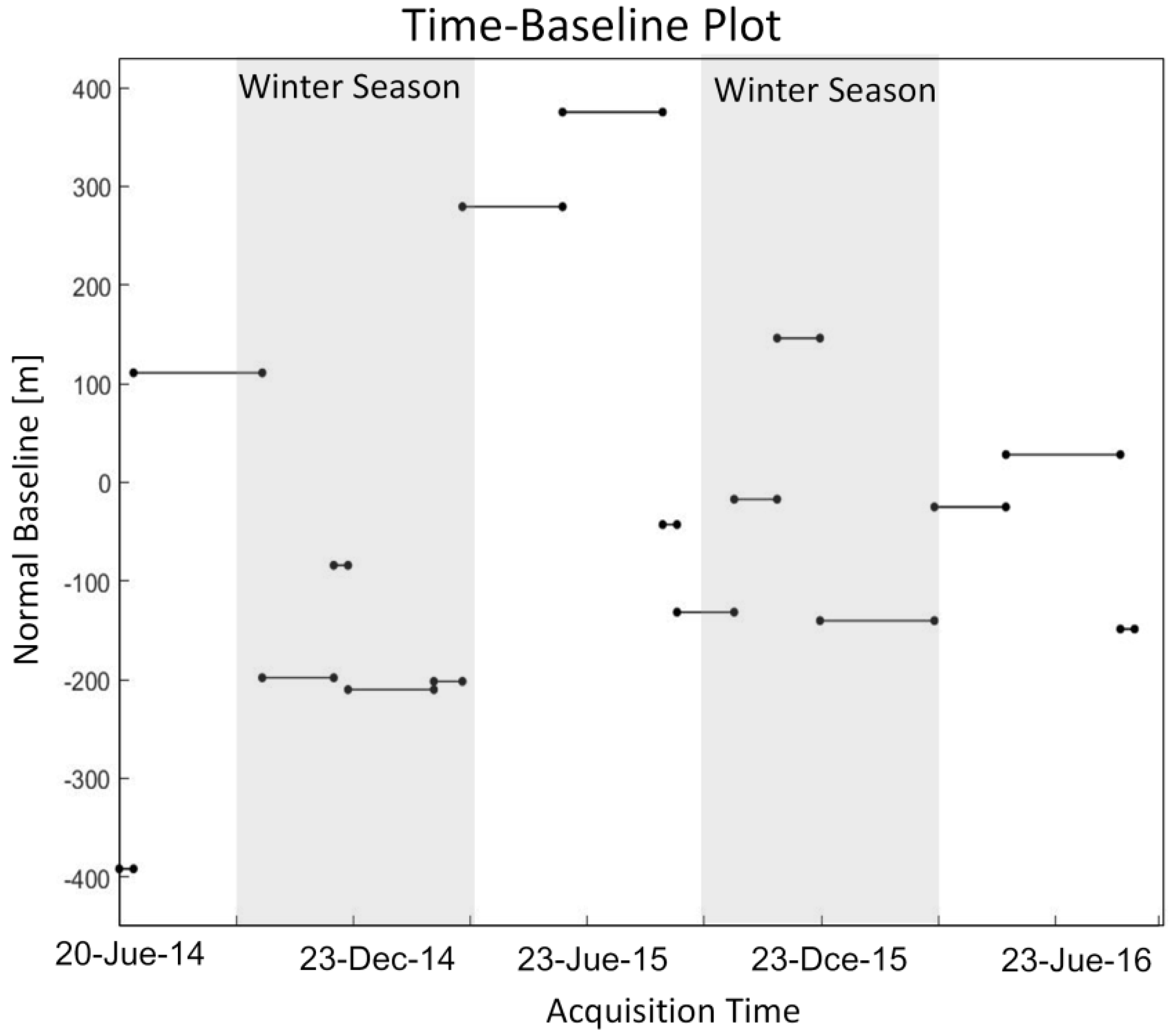





| Image Number | Acquisition Date | Normal Baseline (m) | Temporal Baseline (Day) | Thawing (T)/Freezing (F) Season |
|---|---|---|---|---|
| 1 | 20 June 2014 | 0 | 0 | T |
| 2 | 1 July 2014 | 391 | 11 | T |
| 3 | 8 October 2014 | 280 | 110 | F |
| 4 | 2 December 2014 | 478 | 165 | F |
| 5 | 13 December 2014 | 562 | 176 | F |
| 6 | 17 February 2015 | 772 | 242 | F |
| 7 | 11 March 2015 | 974 | 264 | F |
| 8 | 27 May 2015 | 695 | 341 | T |
| 9 | 12 August 2015 | 320 | 418 | T |
| 10 | 23 August 2015 | 362 | 429 | T |
| 11 | 6 October 2015 | 494 | 473 | F |
| 12 | 8 November 2015 | 511 | 506 | F |
| 13 | 11 December 2015 | 365 | 539 | F |
| 14 | 8 March 2016 | 505 | 627 | F |
| 15 | 2 May 2016 | 530 | 682 | T |
| 16 | 29 July 2016 | 502 | 770 | T |
| 17 | 9 October 2016 | 651 | 781 | T |
| Int a No | Master Image | Slave Image | Normal Baseline (m) | Temporal Baseline (Day) | Acquisition Season b | Acquisition Season c |
|---|---|---|---|---|---|---|
| 1 | 2 December 2014 | 20 June 2014 | 478 | −165 | Winter | Summer |
| 2 | 2 December 2014 | 1 July 2014 | 87 | −147 | Winter | Summer |
| 3 | 2 December 2014 | 8 October 2014 | 198 | −55 | Winter | Summer |
| 4 | 2 December 2014 | 13 December 2014 | 84 | 11 | Winter | Winter |
| 5 | 2 December 2014 | 17 February 2015 | 294 | 77 | Winter | Winter |
| 6 | 2 December 2014 | 11 March 2015 | 495 | 99 | Winter | Winter |
| 7 | 2 December 2014 | 27 May 2015 | 216 | 176 | Winter | Summer |
| 8 | 2 December 2014 | 12 August 2015 | 158 | 253 | Winter | Summer |
| 9 | 2 December 2014 | 23 August 2015 | 115 | 264 | Winter | Summer |
| 10 | 2 December 2014 | 6 October 2015 | 15 | 308 | Winter | Summer |
| 11 | 2 December 2014 | 8 November 2015 | 32 | 341 | Winter | Winter |
| 12 | 2 December 2014 | 11 December 2015 | 113 | 374 | Winter | Winter |
| 13 | 2 December 2014 | 8 March 2016 | 27 | 462 | Winter | Winter |
| 14 | 2 December 2014 | 2 May 2016 | 52 | 517 | Winter | Summer |
| 15 | 2 December 2014 | 29 July 2016 | 23 | 605 | Winter | Summer |
| 16 | 2 December 2014 | 9 October 2016 | 172 | 616 | Winter | Summer |
| Int a No | Master Image | Slave Image | Normal Baseline (m) | Temporal Baseline (Day) | Acquisition Season b | Acquisition Season c |
|---|---|---|---|---|---|---|
| 1 | 20 June 2014 | 1 July 2014 | 391 | 11 | Summer | Summer |
| 2 | 1 July 2014 | 8 October 2014 | 110 | 99 | Summer | Summer |
| 3 | 8 October 2014 | 2 December 2014 | 198 | 55 | Summer | Winter |
| 4 | 2 December 2014 | 13 December 2014 | 84 | 11 | Winter | Winter |
| 5 | 13 December 2014 | 17 February 2015 | 209 | 66 | Winter | Winter |
| 6 | 17 February 2015 | 11 March 2015 | 201 | 22 | Winter | Winter |
| 7 | 11 March 2015 | 27 May 2015 | 279 | 77 | Winter | Summer |
| 8 | 27 May 2015 | 12 August 2015 | 375 | 77 | Summer | Summer |
| 9 | 12 August 2015 | 23 August 2015 | 42 | 11 | Summer | Summer |
| 10 | 23 August 2015 | 6 October 2015 | 131 | 44 | Summer | Summer |
| 11 | 6 October 2015 | 8 November 2015 | 17 | 33 | Summer | Winter |
| 12 | 8 November 2015 | 11 December 2015 | 146 | 33 | Winter | Winter |
| 13 | 11 December 2015 | 8 March 2016 | 140 | 88 | Winter | Winter |
| 14 | 8 March 2016 | 2 May 2016 | 24 | 55 | Winter | Summer |
| 15 | 2 May 2016 | 29 July 2016 | 28 | 88 | Summer | Summer |
| 16 | 29 July 2016 | 9 October 2016 | 148 | 11 | Summer | Summer |
| Land Cover Type | a | b | c | R2 | RMSE |
|---|---|---|---|---|---|
| Railway | −1.11 × 10−4 | 0.033 | 0.917 | 0.66 | 0.0224 |
| Highway | −2.08 × 10−4 | 0.028 | 0.899 | 0.62 | 0.0345 |
| Mountain slope | −9.002 × 10−4 | 0.091 | 0.74 | 0.52 | 0.176 |
| Barren | −8.82 × 10−4 | 0.111 | 0.7714 | 0.54 | 0.1716 |
| Alpine meadow | −9.68 × 10−4 | 2.43 × 10−4 | 0.223 | 0.14 | 0.086 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wang, C.; Zhang, H.; Tang, Y.; Liu, X. Analysis of Permafrost Region Coherence Variation in the Qinghai–Tibet Plateau with a High-Resolution TerraSAR-X Image. Remote Sens. 2018, 10, 298. https://doi.org/10.3390/rs10020298
Zhang Z, Wang C, Zhang H, Tang Y, Liu X. Analysis of Permafrost Region Coherence Variation in the Qinghai–Tibet Plateau with a High-Resolution TerraSAR-X Image. Remote Sensing. 2018; 10(2):298. https://doi.org/10.3390/rs10020298
Chicago/Turabian StyleZhang, Zhengjia, Chao Wang, Hong Zhang, Yixian Tang, and Xiuguo Liu. 2018. "Analysis of Permafrost Region Coherence Variation in the Qinghai–Tibet Plateau with a High-Resolution TerraSAR-X Image" Remote Sensing 10, no. 2: 298. https://doi.org/10.3390/rs10020298
APA StyleZhang, Z., Wang, C., Zhang, H., Tang, Y., & Liu, X. (2018). Analysis of Permafrost Region Coherence Variation in the Qinghai–Tibet Plateau with a High-Resolution TerraSAR-X Image. Remote Sensing, 10(2), 298. https://doi.org/10.3390/rs10020298






