Estimation of AOD Under Uncertainty: An Approach for Hyperspectral Airborne Data
Abstract
:1. Introduction
2. Theoretical Background
2.1. Basic Atmospheric Effect Modeling
- the total radiance as measured by the sensor, ,
- the total path radiance that consists of the light scattered in the path,
- the total ground radiance that consists of all the light reflected by the surface and traveling directly towards the sensor, ,
- the direct ground reflectance, as a fraction of resulting from direct illumination of the ground surface.
2.2. Aerosol Optical Depth
3. Datasets
3.1. The Process to Generate the Synthetic Datasets
- Spectra of materials are extracted from an existing library. The choice of materials depends on the type of surface required for an experiment. We extract the materials from the database of Jasper Ridge, spectral library [39] available in ENVI software [40] and the database of the Johns Hopkins University Spectral Library [41].
- To generate a sensor specific image, the library is resampled using the sensor response curve. For our experiments, we use response curve of the Hyperspectral Mapper (HyMap) airborne hyperspectral sensor [42].
- Depending on the number of materials, a fraction image comprising abundance of materials is required. We used, MATLAB Hyperspectral Imagery Synthesis tools, available online [43] to generate the abundance images. A convolution of a library of materials with an abundance image generates a synthetic reflectance cube.
- To transform synthetic reflectance to at-sensor radiance, the forward radiative transfer modeling is performed. Details of this modeling are given in Section 4.
- In a real dataset, sensor noise and processing noise are major sources of distortion. Sensor noise refers to the random electronic noise like dark current, processing noise occurs due to the final pre-processing steps on the reflectance datacube, e.g., spectral smoothing. We added the two types of noise to the datasets at two stages: sensor noise to the radiance cube and processing noise to the estimated reflectance cube. To observe the effect of the different noise levels we considered three levels of the correlated processing noise, with signal-to-noise ratios (SNR): 30, 40, and 50 dB, respectively. All correlated noise levels were generated from independent, normally distributed noise by low-pass filtering with a normalized cut-off frequency of for each SNR with B being the number of channels. Figure 1 shows four pixelwise estimates of reflectance at 2200 nm (band 100) when SNR of at-sensor radiance was limited to: 30, 40, 50, and 60 dB with random (white) noise. To estimate the four pixelwise reflectance, true AC parameters were employed and no correlated noise was added. When SNR of the at-sensor radiance was limited to 30 dB, 40 dB, and 50 dB the reflectance estimates were severely distorted. Further, [42] suggests that HyMap sensor is highly optimized for mineral exploration tasks which demanded high SNR. From the experiments with the noise levels and following the SNR values given in the literature, we found that sensor noise with SNR = 60 dB was a realistic choice for HyMap sensor.
3.2. Case Study: A Vegetation Surface with Usual Scattering Conditions
3.3. Case Studies: High Scattering Conditions
3.3.1. Surfaces with Spectrally Close and Spectrally Distinct Materials
3.3.2. Surfaces with Dark and Bright Materials
3.4. Real Data
4. The Forward Modeling and the Performance Discriminator
4.1. Profile of the Condition Parameters for the Usual Scattering Conditions
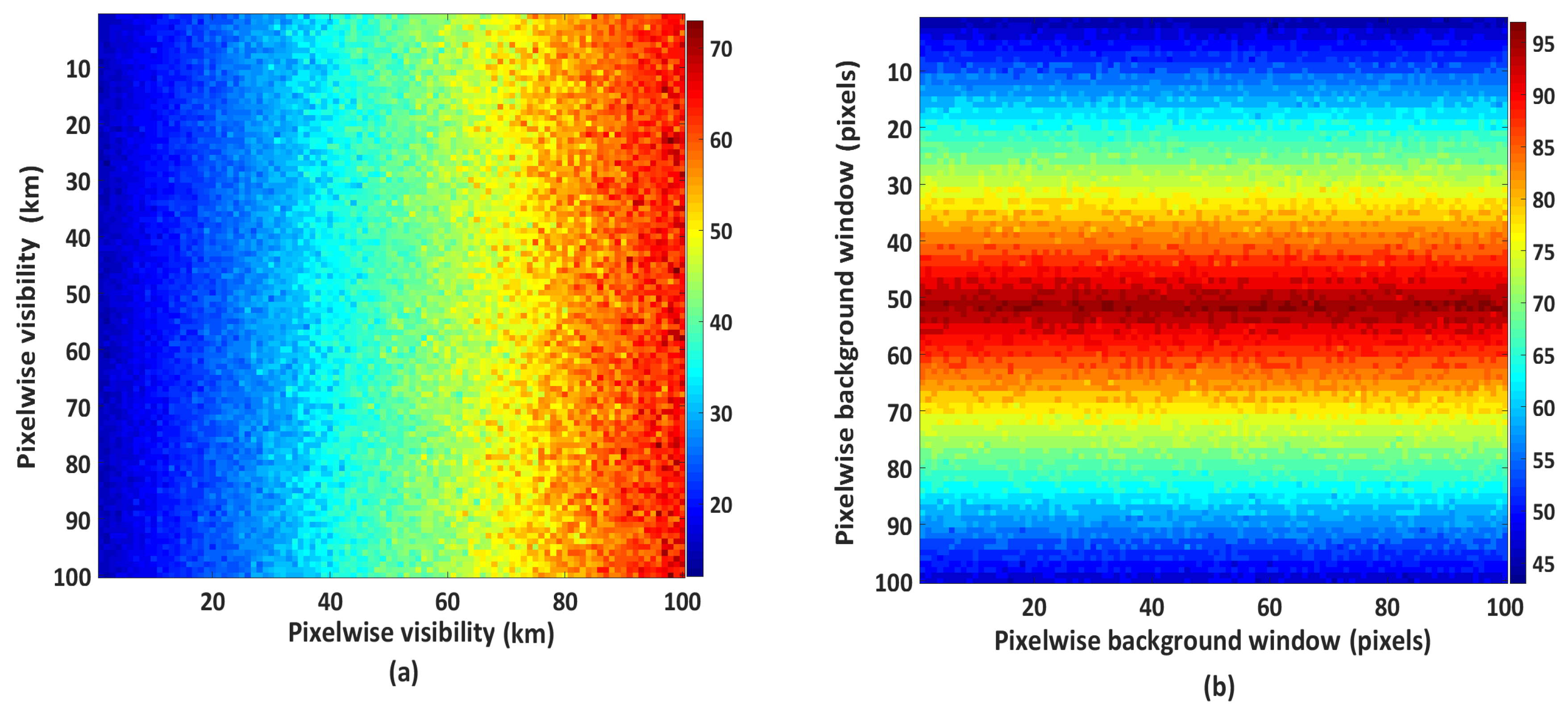
4.2. Pixelwise Parameter Configuration for the Usual Scattering Conditions
4.3. Profile of the Parameters for the High Scattering Conditions
4.4. Performance Discriminators
5. Estimation
5.1. Linear Model for Calibration
5.2. Searching for Reference Library Spectra
5.3. Generating the First Visibility Estimate
5.4. Iterations
5.5. Interpolation of Visibility
- Case 1: No overlapping of the neighborhood. This case accounts for the scenario when within the neighborhood of the target reference pixel , no other reference pixel fall.
- Case 2: Overlapping of the neighborhood. This case accounts for scenarios when the neighborhood of two or more reference pixels overlaps with . This occurs when two or more pixels falls within .
- Case 3: No reference pixel is available for spatial estimation. This case account for the scenario when to estimate visibility at the unsampled location, no reference pixel can be spatially linked using .
- Step 1, find the spatial variation of visibility using values estimated for Case 1 and Case 2. We distinguished three types of spatial variation in visibility: (a) vertical; (b) horizontal; and (c) diagonal. The specific variation is obtained by evaluating histograms of visibility values from line transects in vertical, horizontal, and diagonal directions. A bimodality or multimodality of the histogram from a specific line transect shows a strong variation of the visibility. For instance, if visibility is vertically varying (column wise) then the histogram obtained from the horizontal line transect shows bimodality or multimodality,
- Step 2, the histogram that shows unimodality, that is direction of non-variation of visibility, is used to generate the distribution . For instance, if visibility is vertically varying then histogram generated from the values from vertical line transect are used to generate the ,
- Step 3, for vertical and horizontal variation, a randomly sampled value from is assigned to a spatially unrelated pixel. If visibility is diagonally varying then nearest neighborhood method [57] is used to interpolate the missing value.
6. Results of Experiments with Usual Scattering and with Real Data
6.1. Specific Choices of Methods and Values
6.2. Visibility Estimation for the Simulated Dataset
6.3. Visibility Estimation for the Real Dataset
- From the real at sensor radiance cube, a set of endmembers is manually selected, whereas the corresponding pixels are called reference pixels.
- Reflectance are estimated by performing AC using various pre-selected combinations of the atmospheric condition parameters.
- From the estimated reflectance cubes spectra of the reference pixels are evaluated to check distortion in terms of shape (Section 5.3).
- The reflectance cube that corresponds to the optimal combination serves as the reference cube.
- The reference cube is transformed to obtain a pseudo at sensor radiance cube using the MODTRAN 4 forward modelling simulations with the same atmospheric conditions as used in the forward modelling of the simulated dataset.
- To the pseudo reference dataset we added 60 dB white Gaussian noise at sensor level and 30 dB correlated noise to the estimated reflectance cube, as we did for the simulated dataset.
6.4. Experiment with Spatial Variability
7. Results of Experiments with High Scattering Conditions
Specific Choices of Methods and Values
8. Discussion
9. Conclusions and Outlooks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jarocinska, A.M.; Kacprzyk, M.; Marcinkowska, A.; Ochtyra, A.; Zagajewski, B.; Meuleman, K. The application of APEX images in the assessment of the state of non-forest vegetation in the Karkonosze Mountains. Misc. Geogr. 2016, 20, 21–27. [Google Scholar] [CrossRef] [Green Version]
- Tagliabue, G.; Panigada, C.; Colombo, R.; Fava, F.; Cilia, C.; Baret, F.; Vreys, K.E.A. Forest species mapping using airborne hyperspectral APEX data. Misc. Geogr. 2016, 20, 28–33. [Google Scholar] [CrossRef] [Green Version]
- Mierczyk, M.; Zagajewski, B.; Jarocińska, A.; Knapik, R. Assessment of Imaging Spectroscopy for rock identification in the Karkonosze Mountains, Poland. Misc. Geogr. 2016, 20, 34–40. [Google Scholar] [CrossRef] [Green Version]
- Krówczyńska, M.; Wilk, E.; Pabjanek, P.; Zagajewski, B.; Meuleman, K. Mapping asbestos-cement roofing with the use of APEX hyperspectral airborne imagery: Karpacz area, Poland—A case study. Misc. Geogr. 2016, 20, 41–46. [Google Scholar] [CrossRef]
- Demarchi, L.; Canters, F.; Cariou, C.; Licciardi, G.; Chan, J. Assessing the performance of two unsupervised dimensionality reduction techniques on hyperspectral APEX data for high resolution urban land-cover mapping. ISPRS J. Photogramm. Remote Sens. 2014, 87, 166–179. [Google Scholar] [CrossRef]
- Seidel, F.C.; Kokhanovsky, A.A.; Schaepman, M.E. Fast retrieval of aerosol optical depth and its sensitivity to surface albedo using remote sensing data. Atmos. Res. 2012, 116, 22–32. [Google Scholar] [CrossRef]
- Bhatia, N.; Stein, A.; Reusen, I.; Tolpekin, V.A. An optimization approach to estimate and calibrate column water vapour for hyperspectral airborne data. Int. J. Remote Sens. 2018, 39, 2480–2505. [Google Scholar] [CrossRef]
- Popp, C.; Brunner, D.; Damm, A.; Roozendael, M.V.; Fayt, C.; Buchmann, B. High-resolution NO2 remote sensing from the Airborne Prism EXperiment (APEX) imaging spectrometer. Atmos. Meas. Tech. 2012, 5, 2211–2225. [Google Scholar] [CrossRef]
- Gao, B.C.; Davis, C.; Goetz, A. A Review of Atmospheric Correction Techniques for Hyperspectral Remote Sensing of Land Surfaces and Ocean Color. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 1979–1981. [Google Scholar]
- Gao, B.C.; Montes, M.J.; Davis, C.O.; Goetz, A.F. Atmospheric correction algorithms for hyperspectral remote sensing data of land and ocean. Remote Sens. Environ. 2009, 113, S17–S24. [Google Scholar]
- Richter, R.; Schlapfer, D. Atmospheric/Topographic Correction for Airborne Imagery (ATCOR-4 User Guide); User Guide; DLR-German Aerospace Center: Köln, Germany, 2007. [Google Scholar]
- Biesemans, J.; Sterckx, S.; Knaeps, E.; Vreys, K.; Adriaensen, S.; Hooyberghs, J.; Meuleman, K.; Kempeneers, P.; Deronde, B.; Everaerts, J.; et al. Image processing work flows for airborne remote sensing. In Proceedings of the 5th EARSeL Workshop on Imaging Spectroscopy. European Association of Remote Sensing Laboratories (EARSeL), Bruges, Belgium, 23–25 April 2007. [Google Scholar]
- Sterckx, S.; Vreys, K.; Biesemans, J.; Iordache, M.; Bertels, L.; Meuleman, K. Atmospheric correction of APEX hyperspectral data. Misc. Geogr. 2016, 20, 16–20. [Google Scholar] [CrossRef]
- Diner, D.J.; Martonchik, J.V.; Kahn, R.A.; Pinty, B.; Gobron, N.; Nelson, D.L.; Holben, B.N. Using angular and spectral shape similarity constraints to improve MISR aerosol and surface retrievals over land. Remote Sens. Environ. 2005, 94, 155–171. [Google Scholar] [CrossRef]
- North, P.R.J. Estimation of aerosol opacity and land surface bidirectional reflectance from ATSR-2 dual-angle imagery: Operational method and validation. J. Geophys. Res. Atmos. 2002, 107. [Google Scholar] [CrossRef] [Green Version]
- Deuz, J.L.; Breon, F.M.; Devaux, C.; Goloub, P.; Herman, M.; Lafrance, B.; Maignan, F.; Marchand, A.; Nadal, F.; Perry, G.; Tanre, D. Remote sensing of aerosols over land surfaces from POLDER-ADEOS-1 polarized measurements. J. Geophys. Res. Atmos. 2001, 106, 4913–4926. [Google Scholar] [CrossRef] [Green Version]
- Kaufman, Y.J.; Tanre, D.; Remer, L.A.; Vermote, E.F.; Chu, A.; Holben, B.N. Operational remote sensing of tropospheric aerosol over land from EOS moderate resolution imaging spectroradiometer. J. Geophys. Res. Atmos. 1997, 102, 17051–17067. [Google Scholar] [CrossRef] [Green Version]
- Liang, S.; Fang, H. An improved atmospheric correction algorithm for hyperspectral remotely sensed imagery. IEEE Geosci. Remote Sens. Lett. 2004, 1, 112–117. [Google Scholar] [CrossRef]
- Teillet, P.M.; Fedosejevs, G. An improved atmospheric correction algorithm for hyperspectral remotely sensed imagery. Can. J. Remote Sens. 1995, 21, 374–387. [Google Scholar] [CrossRef]
- Christopher, S.A.; Zhang, J.; Holben, B.N.; Yang, S.K. GOES-8 and NOAA-14 AVHRR retrieval of smoke aerosol optical thickness during SCAR-B. Int. J. Remote Sens. 2002, 23, 4931–4944. [Google Scholar] [CrossRef]
- Hauser, A.; Oesch, D.; Foppa, N.; Wunderle, S. NOAA AVHRR derived aerosol optical depth over land. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef] [Green Version]
- Kaufman, Y.J.; Tanre, D.; Gordon, H.R.; Nakajima, T.; Lenoble, J.; Frouins, R.; Grassl, H.; Herman, B.M.; King, M.D.; Teillet, P.M. Passive remote sensing of tropospheric aerosol and atmospheric correction for the aerosol effect. J. Geophys. Res. Atmos. 1997, 102, 16815–16830. [Google Scholar] [CrossRef] [Green Version]
- Remer, L.A.; Kaufman, Y.J.; Tanre, D.; Mattoo, S.; Chu, D.A.; Martins, J.V.; Li, R.R.; Ichoku, C.; Levy, R.C.; Kleidman, R.G.; et al. The MODIS Aerosol Algorithm, Products, and Validation. J. Atmos. Sci. 2005, 62, 947–973. [Google Scholar] [CrossRef] [Green Version]
- Rahman, M.S.; Di, L.; Shrestha, R.; Yu, E.G.; Lin, L.; Kang, L.; Deng, M. Comparison of selected noise reduction techniques for MODIS daily NDVI: An empirical analysis on corn and soybean. In Proceedings of the 2016 Fifth International Conference on Agro-Geoinformatics, Tianjin, China, 18–20 July 2016; pp. 1–5. [Google Scholar]
- Richter, R.; Schlapfer, D.; Muller, A. An automatic atmospheric correction algorithm for visible/NIR imagery. Int. J. Remote Sens. 2006, 27, 2077–2085. [Google Scholar] [CrossRef]
- Bhatia, N.; Tolpekin, V.A.; Reusen, I.; Sterckx, S.; Biesemans, J.; Stein, A. Sensitivity of Reflectance to Water Vapor and Aerosol Optical Thickness. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3199–3208. [Google Scholar] [CrossRef]
- Bhatia, N.; Iordache, M.D.; Stein, A.; Reusen, I.; Tolpekin, V.A. Propagation of uncertainty in atmospheric parameters to hyperspectral unmixing. Remote Sens. Environ. 2018, 204, 472–484. [Google Scholar] [CrossRef]
- Haan, J.F.; Kokke, J.M.M. Remote Sensing Algorithm Development Toolkit I: Operationalization of Atmospheric Correction Methods for Tidal and Inland Waters; Development Toolkit NRSP-2 96-16; Netherlands Remote Sensing Board: Delft, The Netherlands, 1996. [Google Scholar]
- Verhoef, W. Theory of Radiative Transfer Models Applied in Optical Remote Sensing of Vegetation Canopies. Ph.D. Thesis, University of Wageningen, Wageningen, The Netherlands, 1998. [Google Scholar]
- Schlapfer, D. Differential Absorption Methodology for Imaging Spectroscopy of Atmospheric Water Vapor. Ph.D. Thesis, Remote Sensing Laboratories, Department of Geography, Universiy of Zurich, Zurich, Switzerland, 1998. [Google Scholar]
- Verhoef, W.; Bach, H. Simulation of hyperspectral and directional radiance images using coupled biophysical and atmospheric radiative transfer models. Remote Sens. Environ. 2003, 87, 23–41. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Chetwynd, J.H.; Bernstein, L.S.; Shettle, E.P.; Matthew, M.W.; Adler-Golden, S.M. MODTRAN 4 User’s Manual; Technical Report; Air Force Research Laboratory: Hanscom AFB, MA, USA; Naval Research Laboratory: Washington, DC, USA; Spectral Sciences: Burlington, MA, USA, 2000. [Google Scholar]
- Staenz, K.; Secker, J.; Gao, B.C.; Davis, C.; Nadeau, C. Radiative transfer codes applied to hyperspectral data for the retrieval of surface reflectance. ISPRS J. Photogramm. Remote Sens. 2002, 57, 194–203. [Google Scholar] [CrossRef]
- Stamnes, K.; Tsay, S.C.; Wiscombe, W.; Jayaweera, K. Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media. Appl. Opt. 1988, 27, 2502–2509. [Google Scholar] [CrossRef] [PubMed]
- Boucher, O. General Introduction. In Atmospheric Aerosols; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Kaufman, Y.; Tanre, D.; Boucher, O. A satellite view of aerosols in the climate system. Nature 2002, 419, 215–223. [Google Scholar] [CrossRef] [PubMed]
- Kaskaoutis, D.G.; Kambezidis, H.D. Investigation into the wavelength dependence of the aerosol optical depth in the Athens area. R. Meteorol. Soc. (Q.) 2006, 132, 2217–2234. [Google Scholar] [CrossRef] [Green Version]
- Lenoble, J. Atmopsheric Radiative Transfer; A. Deepak Publishing: Hampton, VA, USA, 1998. [Google Scholar]
- ENVI-Team. ENVI Classic Tutorial: Vegetation Hyperspectral Analysis; Technical Report; Exelis Visual Information Solutions, Inc.: Boulder, CO, USA, 2014. [Google Scholar]
- ENVI-Guide. ENVI EX User’s Guide; Technical Report; ITT Visual Information Solutions: Boulder, CO, USA, 2009. [Google Scholar]
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Cocks, T.; Jenssen, T.; Stewart, A.; Wilson, I.; Shields, T. The HYMAPTM Airborne Hyperspectral Sensor: The System, Calibration and Performance. In Proceedings of the 1st EARSeL Workshop on Imaging Spectroscopy, Zurich. European Association of Remote Sensing Laboratories (EARSeL), Zurich, Switzerland, 6–8 October 1998; pp. 37–42. [Google Scholar]
- Matlab-Toolbox. Hyperspectral Imagery Synthesis (EIAs) Toolbox; Technical Report; Grupo de Inteligencia Computacional, Universidad del Pa’s Vasco/Euskal Herriko Unibertsitatea (UPV/EHU): Vizcaya, Spain; The MathWorks, Inc.: Natick, MA, USA, 2012. [Google Scholar]
- Kokaly, R.F.; Clark, R.N.; Swayze, G.A.; Livo, K.E.; Hoefen, T.M.; Pearson, N.C.; Wise, R.A.; Benzel, W.M.; Lowers, H.A.; et al. USGS Spectral Library Version 7; Technical Report; U.S. Geological Survey Data Series 1035: Reston, VA, USA, 2017. [Google Scholar]
- Schaepman, M.E.; Jehle, M.; Hueni, A.; D’Odorico, P.; Damm, A.; Weyermann, J.; Schneider, F.D.; Laurent, V.; Popp, C.; Seidel, F.C.; et al. Advanced radiometry measurements and Earth science applications with the Airborne Prism Experiment (APEX). Remote Sens. Environ. 2015, 158, 207–219. [Google Scholar] [CrossRef] [Green Version]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman and Hall/CRC: London, UK, 1986. [Google Scholar]
- Duong, T. ks: Kernel Smoothing, 2016, R package version 1.10.3. In Kernel Smoothing; Wand, M.P., Jones, M.C., Eds.; Chapman and Hall/CRC: London, UK, 2016. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2008. [Google Scholar]
- Silverman, B.W. Using Kernel Density Estimates to investigate multimodality. J. R. Stat. Soc. 1981, 43, 97–99. [Google Scholar]
- Hall, P.; York, M. On the calibration of Silvermans test for multimodality. Stat. Sin. 2001, 11, 515–536. [Google Scholar]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Sparse Unmixing of Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2014–2039. [Google Scholar] [CrossRef] [Green Version]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Total Variation Spatial Regularization for Sparse Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 484–4502. [Google Scholar] [CrossRef]
- Chambolle, A. An algorithm for total variation minimization and applications. J. Math. Imaging Vis. 2004, 20, 89–97. [Google Scholar]
- Jonathan, E.; Bertsekas, D.P. On the Douglas—Rachford splitting method and the proximal point algorithm for maximal monotone operators. Math. Programm. 1992, 55, 293–318. [Google Scholar] [Green Version]
- Heinz, D.C.; Chang, C.I. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 529–545. [Google Scholar] [CrossRef]
- Bateson, C.A.; Asner, G.P.; Wessman, C.A. Endmember bundles: A new approach to incorporating endmember variability into spectral mixture analysis. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1083–1094. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. Spatial interpolation methods applied in the environmental sciences: A review. Environ. Model. Softw. 2014, 53, 173–189. [Google Scholar] [CrossRef]
- Babak, O.; Deutsch, C.V. Statistical approach to inverse distance interpolation. Stoch. Environ. Res. Risk Assess. 2009, 23, 543–553. [Google Scholar] [CrossRef]
- Davies, W.H.; North, P.R.J.; Grey, W.M.F.; Barnsley, M.J. Improvements in Aerosol Optical Depth Estimation Using Multiangle CHRIS/PROBA Images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 18–24. [Google Scholar] [CrossRef]
- Hadjimitsis, D.G.; Clayton, C. Determination of aerosol optical thickness through the derivation of an atmospheric correction for short-wavelength Landsat TM and ASTER image data: An application to areas located in the vicinity of airports at UK and Cyprus. Appl. Geomat. 2009, 1, 31–40. [Google Scholar] [CrossRef]
- Tan, F.; Lim, H.S.; Abdullah, K.; Holben, B. Estimation of aerosol optical depth at different wavelengths by multiple regression method. Environ. Sci. Pollut. Res. 2016, 23, 2735–2748. [Google Scholar] [CrossRef]
- Gupta, P.; Levy, R.C.; Mattoo, S.; Remer, L.A.; Munchak, L.A. A surface reflectance scheme for retrieving aerosol optical depth over urban surfaces in MODIS dark target retrieval algorithm. Atmos. Meas. Tech. 2016, 9, 3293–3308. [Google Scholar] [CrossRef]
- Guang, J.; Xue, Y.; Wang, Y.; Li, Y.; Mei, L.; Xu, H.; Liang, S.; Wang, J.; Bai, L. Simultaneous determination of aerosol optical thickness and surface reflectance using ASTER visible to near-infrared data over land. Int. J. Remote Sens. 2011, 32, 6961–6974. [Google Scholar] [CrossRef]
- Kassianov, E.; Ovchinnikov, M.; Berg, L.K.; McFarlane, S.A.; Flynn, C. Retrieval of aerosol optical depth in vicinity of broken clouds from reflectance ratios: Sensitivity study. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 1677–1689. [Google Scholar] [CrossRef]
- Wilson, R.T.; Milton, R.J.; Nield, J.M. Are visibility-derived AOT estimates suitable for parameterizing satellite data atmospheric correction algorithms? Int. J. Remote Sens. 2015, 36, 1675–1688. [Google Scholar] [CrossRef] [Green Version]
- Lindstrot, R.; Preusker, R.; Diedrich, H.; Doppler, L.; Bennartz, R.; Fischer, J. 1D-Var retrieval of daytime total columnar water vapour from MERIS measurements. Atmos. Meas. Tech. 2012, 5, 631–646. [Google Scholar] [CrossRef] [Green Version]
- Fraser, R.S.; Kaufman, Y.J. The Relative Importance of Aerosol Scattering and Absorption in Remote Sensing. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 625–633. [Google Scholar] [CrossRef]



















| True Visibility (km) | True AOD |
|---|---|
| 1 | 4.94 |
| 4 | 1.42 |
| 7 | 0.89 |
| 10 | 0.68 |
| 15 | 0.48 |
| True Visibility (km) | Set Visibility (km) | True AOD | Set AOD |
|---|---|---|---|
| 01 | 05 | 4.94 | 1.17 |
| 04 | 01 | 1.42 | 4.94 |
| 04 | 10 | 1.42 | 0.68 |
| 07 | 02 | 0.89 | 2.60 |
| 07 | 12 | 0.89 | 0.57 |
| 10 | 05 | 0.68 | 1.17 |
| 10 | 15 | 0.68 | 0.48 |
| 15 | 10 | 0.48 | 0.68 |
| 15 | 20 | 0.48 | 0.37 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhatia, N.; Tolpekin, V.A.; Stein, A.; Reusen, I. Estimation of AOD Under Uncertainty: An Approach for Hyperspectral Airborne Data. Remote Sens. 2018, 10, 947. https://doi.org/10.3390/rs10060947
Bhatia N, Tolpekin VA, Stein A, Reusen I. Estimation of AOD Under Uncertainty: An Approach for Hyperspectral Airborne Data. Remote Sensing. 2018; 10(6):947. https://doi.org/10.3390/rs10060947
Chicago/Turabian StyleBhatia, Nitin, Valentyn A. Tolpekin, Alfred Stein, and Ils Reusen. 2018. "Estimation of AOD Under Uncertainty: An Approach for Hyperspectral Airborne Data" Remote Sensing 10, no. 6: 947. https://doi.org/10.3390/rs10060947
APA StyleBhatia, N., Tolpekin, V. A., Stein, A., & Reusen, I. (2018). Estimation of AOD Under Uncertainty: An Approach for Hyperspectral Airborne Data. Remote Sensing, 10(6), 947. https://doi.org/10.3390/rs10060947






