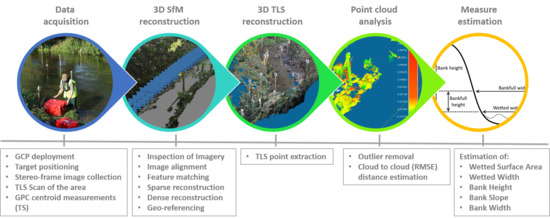
1. Introduction
Legislative approaches have been introduced across the world with the intent of improving the quality of rivers since the second half of the 19th century [
1]. Some examples include the Australian and New Zealand guidelines for fresh and marine water quality under the National Water Quality Management Strategy [
2] and the U.S. Clean Water Act [
3]. The most recent example of a pan-continental approach is perhaps the Water Framework Directive (WFD) [
4], which aims at achieving good chemical and ecological status of both surface and groundwater bodies. An important component of WFD implementation is the development and implementation of monitoring programmes to characterise water bodies in terms of chemical, biological and morphological parameters. This includes protocols such as the River Habitat Survey (RHS) [
5] for the morphological assessment of reaches, the River Invertebrate Prediction and Classification System [
6] for the characterisation of water quality, and the Multimeric Macroinvertebrate Index Flanders [
7] for the identification of macroinvertebrates.
The increased need for monitoring has resulted in the rapid development of autonomous and wide-area monitoring techniques and technologies. This is particularly evident with hydromorphological characterisation where both hydrology (i.e., the quantity and dynamics of water flow and connection to groundwater bodies) and morphology (i.e., reach depth, structure and substrate of the river, structure of the riparian zone and river continuity) are measured [
4]. Some of the approaches developed include, amongst others, the use of Unmanned Aerial Vehicles (UAVs) for continuous river habitat mapping [
8,
9], radio controlled boats with embedded sensors for hydromorphological characterisation [
10,
11,
12,
13] and the development of novel statistical methods for automated river environment data analysis [
9,
14].
Recent developments in photogrammetry and Structure from Motion (SfM) based methodologies show particular promise in the context of hydromorphological characterisation. SfM is an automated method capable of creating 3D river environment models using imagery from cameras [
15]. The low cost and flexibility of SfM based methods enable them to be used at different scales and in varying environments [
16]. In general, SfM methods use imagery gathered from a single camera either mounted on an aerial platform or on a stand at ground level. For example, SfM methods applied to aerial imagery have been used for the large-scale high resolution elevation mapping of the Waimakariri River in New Zealand [
17], for the quantification of topographical changes (i.e., erosion and deposition patterns) over time along a 1 km reach along the River Daan (Taiwan) [
18], to model the submerged fluvial topography of shallow rivers for the River Arrow (Warwickshire, UK) and the Coledale Beck (Braithwaite, UK) [
8] and to evaluate temporal changes of river bar morphology along the Browns Canyon (Arkansas River, Colorado, USA). Examples of SfM applied to ground based imagery include: the use of low oblique imagery to monitor changes in stream channel morphology at cross-section level along the Souhegan River (New Hampshire, USA) [
19] and the use of stereoscopic imagery to characterise bank erosion [
20] along a 60 m reach in the River Yarty (Devon, UK).
However, there are multiple limitations associated with SfM approaches used in the ways above described that curtail the implementation of wide-area fully autonomous systems for hydromorphological river characterisation. Solutions for automated wide-area hydromorphological characterisation based on aircraft imagery are generally associated with low resolution hydromorphological assessments [
14] due to the compromised detail of the raw imagery captured; there is always a trade-off between image scale, spatial coverage and theoretical precision [
17]. Similarly, methods based on (high/low resolution) aerial imagery (e.g., based on imagery from unmanned aerial vehicles or aircraft) may fail to capture side views of the river environment and do not enable a full hydromorphological characterisation of all relevant attributes [
9] (e.g., water depth, flow velocity or bank morphometry). Photogrammetric approaches implemented with aerial imagery obtain the elevation from the vegetation top rather than the ground surface [
17] and therefore provide low resolution in areas with thick vegetation [
19]. Methods relying on imagery collected at ground level (i.e., from the bank) also fail to provide a full overview of the river environment and are not cost-effective; they are generally based on oblique imagery collected from the bank and require multiple camera set ups on both banks to enable a full characterisation of a selected reach. The need to set up multiple stations for data collection does not enable time-efficient wide-area applications of the proposed approaches.
A plausible solution to overcome some of the limitations described above is the use of a camera mounted on an on-water platform capable of navigating autonomously along the river. This, combined with adequate battery endurance, tailored processing algorithms and sensors, would enable the continuous wide-area characterisation of key features (e.g., river width, hydraulic units, habitat units, and water depth) along the river [
21] from different angles. Previous studies [
10] have successfully explored the use of stereo-cameras for autonomous vessel navigation in riverine environments via image processing analysis. The stereo-camera collects in-channel imagery for navigation purposes, and also offers the opportunity to characterise hydromorphology from multiple angles through the analysis of the imagery already captured. The use of stereo-cameras has also been recognised as a means of improving the performance of an SfM model by: (i) enabling image capture from different spatial positions; and (ii) the generation of more robust 3D models than that obtained from a single camera [
22]. However, to the authors’ knowledge, the characterisation of river hydromorphology from in-channel stereo-camera imagery is unexplored. The works by Pyle et al. [
23] and Chandler et al. [
24] are the only documented studies where stereo-cameras have been used to monitor river hydromorphology. In [
23], bank erosion was characterised along the proglacial stream of the Haut Glacier d’Arolla (Valais, Switzerland) using oblique terrestrial photogrammetry. The accuracy of the DEM was estimated to be 8 mm. In [
24], close-range oblique photogrammetry was used to quantify the dynamic topographic water surface along the Blackwater river (Farnham, UK). The stereoscopic coverage of the river reach was achieved via two synchronised cameras mounted on two standard camera tripods on the bank. This study reported accuracies of 3 mm.
In this paper, we contribute to address this gap in knowledge by presenting a SfM based framework for the semi-automatic quantification of hydromorphological measures from 3D models of river environments using in-channel based oblique imagery captured from a stereo-camera. This was achieved through three sequential objectives: (1) to determine the optimal stereo-camera height setting for in-channel imagery collection; (2) to estimate key hydromorphological measures from the 3D model for a range of river environments; and (3) to assess the accuracy of the SfM framework developed in Objectives (1) and (2). Results obtained are used to inform plausible configurations of stereo-camera settings for on-water platforms that enable autonomous hydromorphological characterisation.
4. Discussion
This paper aimed to develop a SfM based framework for the semi-automatic quantification of hydromorphological measures from 3D models of river environments using in-channel based imagery. This was achieved through three sequential objectives: (1) to determine the optimal stereo-camera height setting for in-channel imagery collection; (2) to estimate key hydromorphological measures from a 3D model for a range of river environments; and (3) to assess the accuracy of the framework developed in Objectives (1) and (2).
With respect to Objective (1), the stereo-camera height setting had an effect on the SfM-3D models produced of the river environment. This is due to the configuration of the point cloud obtained for each camera height setting and how this transferred to the estimation of the hydromorphological measures. Overall, the RMSE of distance measurements between the SfM and the TLS point clouds were less than 24.2 cm for stereo-camera height settings along the two reaches considered (i.e., Chicheley Brook and River Ouzel), with the RMSE for the rigid structures (i.e., bridge) along the River Ouzel presenting RMSEs below 7 cm. The RMSE values were greater than the 6 mm over 50 m reported in [
43] for the comparison of two point clouds obtained with a repeated TLS survey along a rapidly meandering eroding bedrock river (Rangitikei river canyon, New Zealand). In [
43], the reach under study was 50–70 m wide and the reported RMSE of distance measurements insignificant within the context of the river scale, whereas the RMSE reported in our study is larger and more significant when compared to the scale of the reaches sampled. However, as opposed to [
43], the values in our study are the result of comparing two very distinct methods (SfM and TLS) to obtain dense point clouds. Within this context, the performance here obtained exceeds that reported by [
35] for the 3D SfM modelling of two contiguous reaches (1.6 km and 1.7 km, with a braiding width of 500–800 m) (Ahuriri River, New Zealand) using SfM and a 10,622 RTK-GPS GCP ground truth derived point clouds.
The RMSE results obtained for the Chicheley Brook and the River Ouzel are encouraging. In [
35], RMSE of 17 cm for bare ground and 78 cm for vegetated areas were reported, with an overall RMSE of 23 cm for all the areas combined. In our study, unlike in [
35], additional sources of bias were present, namely: (i) data were collected when the vegetation was growing and present; (ii) oblique imagery was used as opposed to near vertical aerial photography; and (ii) the SfM point cloud was neither decimated nor corrected for vegetation presence. Without the data pre-processing methodology proposed by [
35], the reported RMSE of distance measurements between clouds in their study were 2.41 m. Removal of the vegetated and undesirable mapped areas from the point cloud in [
35] resulted in RMSEs of 20 cm. These values were similar to the maximum RMSE registered in our study. Without removing any vegetation linked artefacts.
It has to be noted that the RMSE of distance measurements registered also depends upon the number and location of GCPs used for the georegistration process. For example, in [
45], the effect of the location of GCPs has in georeferencing within the photogrammetric process was investigated, with results showing that best performance was achieved when the GCPs were evenly distributed within the study area. The effect of GCPs on georeferencing was also investigated by [
46,
47] with results recommending stratified distribution of GCPs. The effect that the number of GCPs has on the implementation of SfM on aerial photography was investigated in [
48] for an area of 420 m × 420 m, with improvements in accuracy considered to be minimal when more than 15 GCPs were used. In [
45], the accuracy in the photogrammetric process was found to systematically increase with the number of GCPs up to a maximum of 27 GCPs. The framework presented in this paper has used a stratified random approach to GCPs distribution for a pre-determined number of GCPs, with a total of six GCPs placed along every 10 m of the selected reaches. Further work should be carried out to assess the effect that differing number and location of GCPs has on the overall RMSE.
The impact of the RMSE on the hydromorphological measures depended on the measure selected and the characteristics of the reach. For example, the stereo-camera setting was of particular importance for the estimation of WS and WW; on the River Ouzel, the measured WS increased from 36.6 m
2 to 75.88 m
2 (39.2 m
2) when using the minimum stereo-camera setting of 0.5 m compared with the maximum setting of 1.6 m, whereas, for the Chicheley Brook, the WS decreased from 15.01 m
2 to 10.86 m
2 (4.15 m
2). Similarly, the mapped WS became more discontinuous and asymmetric as the stereo-camera height increased. Increasing the stereo-camera height resulted in an additional 49 cm (from 32 cm to 81 cm) of error in WW estimation on the Chicheley Brook and a decrease of 2.08 m (from 3.42 m to 1.34 m) in error on the River Ouzel. For both sites, stereo-camera settings of approximately 1 m provided the best compromise for the estimation of the various hydromorphological measures whilst providing an angle of view slightly above that of existing river boat prototypes [
49]. The hydromorphological configuration of the River Ouzel, with a wider mean WW (≈8 m) and more gently sloping banks than the Chicheley Brook (≈2 m), was better captured with stereo-camera settings of greater than 1 m whereas the Chicheley Brook was better characterised with camera at or below 1 m. These findings indicate that ideally, the stereo-camera height should be optimised on-site based on the characteristics of the reach. However, it has to be noted that the practicality of using camera heights greater than 1 m may be challenging on a boat. The effect of platform yaw, pitch and roll could impact the quality of the imagery, the field of view could be easily obstructed by overarching branches and greater likelihood of the cameras getting tangled with vegetation. However, with low height stereo-camera settings (e.g., 0.5 m), the lenses are more likely to be affected by water splash and lens obstruction arising from the boat navigation equipment. Potential solutions to overcome these problems could include the use of highly stable gimbals and the development of algorithms for obstacle avoidance during autonomous navigation.
With respect to Objectived (2) and (3), the configuration of the river also had an impact on the estimation of the hydromorphological variables. Significant differences were observed in the estimation of the variables at all three sites. The largest (absolute) errors were observed at the River Ouzel site. On the River Ouzel, densely vegetated banks, overhanging vegetation, meandering morphology and debris on occasions obstructed the camera field of view (
Figure 9 and
Figure 10). On the Chicheley Brook and the River Great Ouse, differences were observed depending upon the hydromorphological measure. The steep banks of the Chicheley Brook enabled a more robust estimation of WW and BW whilst the sparse vegetation along the banks of the River Great Ouse provided better estimates of BH and overall BS.
The magnitude of the mean error should be interpreted based on the objective for which the measures are calculated and the dimensions of the overall reach. For example, the proposed framework provides estimates of WW with mean errors not exceeding 1.81 m in any of the study sites. However, on average, the errors represent 67% of the reach width at the Chicheley Brook and less than 6% at the River Great Ouse. Similarly, the mean error for BW estimation did not exceed 3.6 m for the Chicheley Brook (20% of the cross-section bank width) and River Great Ouse (16% of the cross-section bank width), although on the River Ouzel it was 11.15 m (27%) due to site configuration (presence of debris and overhanging vegetation which created additional imagery artefacts). The magnitude of these errors may not be significant for large scale hydrological or flood modelling but may have a substantial impact if the resulting measures are used for the assessment of localised interventions (e.g., river restoration appraisal). Note that in this study, the TLS point cloud and associated hydromorphological measures have been assumed to be the ground truthed through the use of reference points. However, some distortion of the TLS point cloud may occur due to the movement of scene features (e.g., leaves, water, and floating debris) and changes in light conditions during the day which would then have a consequent impact on the estimation of TLS derived hydromorphological measures. The mean error values for each of the estimated measures need to be interpreted with regards to this limitation. Similarly, the movement of scene features and changing light conditions would also have affected the structure of the SfM derived point cloud [
35].
For all SfM analysis here presented, the co-registration errors were comparatively small with respect of the overall hydromorphological measures presented. For the calibration study, the error did not exceed 29 cm in any direction, whereas, for the main study, the error was always below 8.6 cm for any of the three 40 m reaches surveyed. It is therefore envisaged that translation, rotation and scaling within the SfM process does not result in significant errors in hydromorphological measure estimation. However, further work should focus on propagation the co-registration error, and additional sources of error such as the number and location of GCPs, through the overall processing work flow to assess the overall impact in performance.
The results presented here are only representative of rivers with similar characteristic to those described. How the proposed framework will perform in other river settings is as yet unknown. Further research should expand the stereo-camera calibration exercise and testing of the proposed framework to other river settings that capture a wider range of river ecosystems. There is also a need to assess the performance of the proposed framework in rivers larger (i.e., wider) to those here considered and determine whether there is a river size operational limit. The quality of long-range reconstruction is dependent on many factors like camera resolution, positions and scene layout. Some authors implemented long-range SfM reconstructions within other research areas such as extraction of terrain information (up to several kilometres). Other authors highlighted that an increase of the distance to matching features (i.e., discrete objects in the scene) had a detrimental effect in the implementation of SfM techniques [
50]. It is envisaged that, for large rivers where all matching features are located along the distant banks, the accuracy of the estimated metrics will be lower than that presented in our study. Further work should also investigate the effect that yaw, pitch and roll of boat based systems has on image quality. It is envisaged that imagery captured with stereo-cameras on boats will result in more artefacts (or poorer image quality) than those encountered in this study. The work by Kriechbaumer et al. [
49] showed that none of these artefacts affected the implementation of Simultaneous Localisation And Mapping (SLAM) algorithms for autonomous navigation. Similar results are therefore expected in the use of the algorithms tested in this paper.
In our study, the baseline of the stereo-cameras was determined to be 24 cm based on previous work by other authors that reported the advantages and limitations of different camera settings. For example, in [
51] the author recommended stereo-cameras of at least 20 cm baseline between the lenses to maximise underwater mapping. In [
52], a 12 cm baseline stereo-camera embedded in a rotorcraft is used to map the river environment and determine river width and canopy height; the authors argued that the small stereo-camera baseline was the cause of poor performance of the proposed visual odometry approach. In [
10], the author identified that larger stereo-camera baselines could reduce the uncertainty in the 3D position of objects derived from stereo-matching. This uncertainty is inversely proportional to the stereo-baseline [
53,
54]; for distances of 20 m, a baseline increase from 12–50 cm reduced the standard deviation of the object’s displacement error from 0.23 m to 0.06 m [
10,
54]. The proposed 24 cm stereo-camera baseline addressed some of the limitations identified above, with the added advantage of being comparable to existing commercial products (e.g., Bumblebee XB3-FLIR [
55]). In addition, the reaches sampled in this study were less than 15 m wide and, as a result, the features used in the photogrammetric process were not expected to be more than 10 m away from the camera lenses. Features located further away became closer to the lenses as the cameras moved through the environment, thus improving their localisation for stereo-imagery matching via the photogrammetric process. Based on [
56], the accuracy obtained in depth accuracy for baselines larger than 20 cm is 0.1 m for features located at 10 m distance. These values were considered sufficiently accurate for the purpose of the study. However, further work should look into quantifying the performance of the proposed SfM based framework for different stereo-camera baselines to inform a wider range of users with different stereo-camera settings and requirements. Comparative studies considering other existing cameras and methodologies will also highlight the advantages and limitations of the proposed approach.
The proposed framework would also benefit from real-time implementation with global georeferencing of processed outcomes. This will enable the integration of the framework with autonomous navigation solutions [
49] for the rapid characterisation of water courses. At present, the overall data analysis as presented in this paper is time consuming and CPU demanding. For example, the generation of the point cloud from SfM requires between 304 h and 405 h for a 40 m long reach (
Table 1), followed by another 8 h of data processing for semi-autonomous measure estimation. The reduction of such times will require the development of fast algorithms specifically tailored for this purpose. This should include the automatic detection of low quality images, development of real-time SfM solutions, exclusion of redundant points in the cloud, detection and elimination of outliers in the point cloud and the integration of these solutions with tools for real-time visualisation. Current advances in algorithm performance and technology are already available. For example, within the context of blurred image detection, Ribeiro-Gomes [
57] successfully developed fast algorithms to detect blurred images from UAV data collected along a 40 ha case study area, with a reduction of up to 69% of the time required for image selection. Similarly, in [
58], a filtering algorithm was developed for the automatic detection of blurred images in UAV image sets. Other authors have successfully developed alternative methodologies based on wavelet transforms and linear Gaussian theory [
59,
60,
61]. The ZED stereo-camera (StereoLabs, San Francisco, CA) and associated algorithms already provide a feasible solution for real-time SfM implementation. The SfM processing is fast enough to make real-time river environment scanning feasible on reach lengths up to 10 m. The RANSAC algorithm [
62] in real-time could be used to delete extreme/outlier cross sections that have to be deleted manually in this current version of the framework. Previous work [
63] has shown positive results in the robust and effective identification of points within a cloud for ground versus vegetation identification. Similarly, tools for real-time visualisation in 3D have already been developed for other purposes [
64,
65]. The challenge now is to integrate all these solutions together with the SfM framework for the estimation of hydromorphological measures presented here.
The work presented here is another step forward towards an autonomous vessel for real-time hydromorphological river characterisation. In [
49], we developed, tested and validated a solution for autonomous vessel navigation in riverine environments. In [
9,
14], we developed and tested the algorithms for hydromorphological feature identification. In this study we highlighted the potential of SfM to estimate basic and more complex hydromorphological features such as habitat or hydraulic units, automatically. The novel application of SfM-based techniques to river environments has provided the opportunity to generate detailed and spatially continuous models of river reaches. However, the image processing techniques used requires high volumes of data collection and high processing times. The next challenge is to work towards the integration of these scientific advances and developing technological solutions to enable the collection and processing of the vast amounts of imagery that will be collected over reaches up to 2000 m.