Initial Assessment of Precise Point Positioning with LEO Enhanced Global Navigation Satellite Systems (LeGNSS)

Abstract

The main challenge of precise point positioning (PPP) applications is the long convergence time of typically a half hour, or even more, to achieve centimeter accuracy. Even when the multi-constellation is involved and ambiguity resolution is implemented, it still requires about ten minutes. It is becoming a hot spot to incorporate the low Earth orbit (LEO) satellite constellation for enhancing the Global Navigation Satellite System (GNSS), named here as LEO-enhanced GNSS (LeGNSS). In this system, the LEO satellites cannot only receive GNSS signals, but also serve as GNSS satellites by transmitting similar navigation signals to the ground users, but with higher signal strength and much faster geometric change due to their low altitude. As a result, the convergence time of PPP is expected to be shortened to a few minutes, or even seconds. Simulation software is developed to simulate GNSS and LEO observations for ground stations taking into account tropospheric delay, satellite clock errors, observation noises, as well as other error sources. Then the number of visible satellites, the geometry dilution of precision (GDOP), and the convergence time of the kinematic mode of PPP are evaluated on a global scale compared to those of GNSS systems. The simulation results show that LeGNSS can decrease the PPP convergence to 5 min. If there are more LEO satellites included in the LeGNSS, it is expected that the initialization of PPP can be further shortened.

1. Introduction

The long convergence time of precise point positioning [1] is a troublesome factor limiting its wider adoption, especially in real-time applications [2]. Thus, many efforts have been made to improve the PPP performance, such as improving the GNSS orbit and clock products [3], speeding up the ambiguity resolution (AR) [4,5,6,7,8], using multi-frequency GNSS signals [9,10,11], and combining multi-constellation GNSS systems [12,13,14].

With the rapid development of multi-GNSS constellations, multi-GNSS PPP has been of interest because of its potential to significantly improve the positioning performance in terms of accuracy and convergence time. The multi-GNSS PPP can be traced back to 2007 [12] when only GPS and the GLONASS systems were available. Since then the positioning accuracy and convergence time have been confirmed to be improved [13,15,16]. China’s BeiDou Navigation Satellite System (BDS) has been providing the positioning, navigation, and timing (PNT) service to the whole Asia-Pacific region with the constellation of five geostationary Earth orbit (GEO) satellites, five inclined geosynchronous satellite orbit (IGSO) satellites, and four medium Earth orbit (MEO) satellites since the end of 2012 [17]. The European Galileo satellite navigation constellation has announced the start of initial service [18], which will consist of thirty satellites in three orbital planes. With this progress, multi-GNSS PPP has attracted increasing interest in the GNSS community, and many types of research have been conducted to show the performance of multi-GNSS [19,20,21,22]. Though the convergence time can be indeed improved compared to single-system PPP, it still takes several tens of minutes for multi-GNSS PPP initialization since the satellite geometry change with respect to a ground station is slow, taking satellites hours to pass overhead.

Recently, some commercial companies, such as SpaceX and OneWeb, have proposed to build global LEO constellations, which would consist of hundreds of LEO satellites to provide access to the Internet worldwide [23]. This sheer number of LEO satellites gives rise to great opportunities not only for broadband communication, but also as a platform for navigation services. Compared to the GNSS satellites, the LEO satellites have the advantage of being closer to the Earth, thus delivering potentially stronger signals. Moreover, LEO satellites move faster relative to ground stations, passing them in minutes instead of hours for MEO satellites. This brings great geometry changes and, consequently, results in a shorter convergence time for precise positioning. However, many LEO satellites are needed to cover the Earth because of their small footprint compared to GPS satellites. Scientists from Stanford University [24] made a thorough investigation of the user geometry, signal-in-space ranging error (SISRE), and how these LEO constellations can be piggybacked to deliver navigation services.

In this study, we propose an extended GNSS system with a LEO constellation transmitting navigation signals, which is called a LEO-enhanced Global Navigation Satellite System (LeGNSS), for precise positioning service. Since there is no LEO GNSS-like data at ground stations so far, we developed simulation software to simulate all the observations, including GNSS observations and LEO observations for ground stations. Even though we can simulate all the GNSS observations, it is not necessary since the convergence time of multi-PPP still needs about 10 min. We employ 24 GPS satellites as initially designed, 14 BDS satellites serving the Asia-Pacific region currently, and the Iridium satellite constellation consisting of 66 LEO satellites for our LeGNSS system. The reasons we chose these three systems are as follows: Firstly, the products of GPS have the best consistency and the performance of GPS can be used as the reference in our data simulation. Secondly, BDS, as the regional navigation satellite system, has its own characteristics with three different types of orbits. The differences of PPP performance within and without its service area can be investigated. The Iridium satellite constellation, as the largest LEO constellation so far, is the best choice to simulate to study the PPP performance.

The LeGNSS and its space segment are presented in the next section, followed by describing the simulation configuration. Then, the global positioning availability is evaluated in terms of the number of visible satellites. Furthermore, the convergence time on a global scale is presented along with the comprehensive analysis of four specific stations. Finally, the conclusions are summarized.

2. The LeGNSS Constellation

The constellation configuration of the LeGNSS is presented as follows: GPS satellites are operating in six orbital planes with a 55° inclination angle at 20,200 km in altitude, while BDS has three types of satellites. The GEO satellites, with a period of revolution of 23 h 56 min at 35,786 km in altitude, are positioned along the equator at 58.75°E, 80°E, 110.5°E, 140°E, and 160°E, respectively. The IGSO satellites have an inclination of 55°, and their orbital periods are the same as those of GEO satellites. The MEO satellites are distributed in three orbital planes with an inclination of 55° at 21,528 km in altitude. The orbital period of MEO satellites is 12 h 53 min. The Iridium constellation has six orbital planes spaced 30° apart with 11 satellites in each plane. The orbital plane is inclined at 86.4° and approximately 780 km in altitude. Iridium has the most latitude coverage due to the near-polar circular orbits. Figure 1 shows the whole constellation of LeGNSS, which clearly displays the different altitudes of all types of satellite.

Although the major part of the LeGNSS is similar to the current GNSS, the important component of the LeGNSS is the LEO constellation that can transmit GNSS-like signals to the ground receivers. The whole system will be operated as follows: All satellites in LeGNSS will transmit navigation signals, onboard LEO receivers receive signals from GNSS satellites in view, while ground receivers receive signals from all satellites. Data at ground stations will be streamed to a computation center in real-time for generating precise orbit and clock products. Onboard LEO data can also be streamed to the computation center for centralized processing or processed directly onboard with precise orbit and clock products of GNSS satellites held fixed. With these LeGNSS products, precise point positioning can be conducted.

3. Simulation Configuration

In this section, the observation simulation software developed by us will be introduced in detail. Then, the adaption of the Positioning and Navigation Data Analyst (PANDA) software originally developed by Liu and Ge [25] for the LeGNSS PPP is briefly described. Finally, we present the setup of the experiments conducted in the next sections.

3.1. The Simulation Software

Until now, there is no GNSS-like observation data from LEO satellites to ground tracking stations available. In this study, simulation software is developed to simulate the GNSS and LEO observations for ground stations. We include the Iridium satellite constellation into our LeGNSS and assume that the frequencies of LEO constellation are the same as of GPS for the sake of convenience to simulate the observations. Thus, most of the correction models of GPS can be directly used for the LEO constellation. All the relevant data are simulated strictly according to the observation model to make the simulation data as close as possible to reality.

The simulation configuration is introduced as follows. The observation equations for the undifferenced (UD) code P and phase L read:

$$P_{r,j_s,k}^s={\rho }_{r,k}^s+\Delta t_{r,k}-\Delta t_k^s+T_{r,k}^s+I_{r,j_s,k}^s+b_{r,j_s}-b_{j_s}^s+{\epsilon }_{P_{r,j_s,k}^{,s}}$$

(1)

$$L_{r,j_s,k}^s={\rho }_{r,k}^s+\Delta t_{r,k}-\Delta t_k^s+T_{r,k}^s-I_{r,j_s,k}^s+{\lambda }_{j_s}{N}_{r,j_s}^s+{\delta }_{r,j_s}-{\delta }_{j_s}^s+{\epsilon }_{L_{r,j_s,k}^s}$$

(2)

where the super- and subscripts s, r, j_s, and k denote the satellite, receiver, carrier frequency, and epoch, respectively. ${\rho }_{r,k}^s$ denotes the geometric distance between the phase centers of satellite and receiver antenna at the signal transmitting and receiving time. $\Delta t_{r,k}$ and $\Delta t_k^s$ are the clock biases of receiver and satellite; $T_{r,k}^s$ is the tropospheric delay; $I_{r,j_s,k}^s$ is the ionospheric delay at frequency j_s; $b_{r,j_s}$ and $b_{j_s}^s$ are code biases of receiver and satellite, respectively; ${\delta }_{r,j_s}$ and ${\delta }_{j_s}^s$ are the receiver- and satellite-dependent uncalibrated phase delay (UPD) [5]; $N_{r,j_s}^s$ is the integer ambiguity with the wavelength ${\lambda }_{j_s}$; and ${\epsilon }_{P_{r,j_s,k}^s}$ and ${\epsilon }_{L_{r,j_s,k}^s}$ denote the measurement noises of code and phase.

The primary task of the simulator is to calculate all the components on the right side of observation equations. Some important issues should be clarified here. The satellite-to-receiver distance is computed with the receiver positions and precise satellite orbits. Especially, this distance is associated with the center of mass of the satellite and the receiver, which should be corrected by the phase center offset (PCO) and phase center variation (PCV) of the receiver and the satellite. For the PCO and PCV corrections of GNSS satellites, igs08.atx is used, while for those of LEO satellites, we set the PCO and PCV values to zero. For BDS and LEO satellites, the PCO and PCV corrections of tracking stations are assumed to be the same as the corrections of GPS frequencies. The receiver and satellite clocks can be simulated as white noise. The satellites clock biases can also be extracted from the precise clock file, except for the LEO satellites. Regarding the tropospheric delay, we use the Saastamoinen model [26] together with the Global Mapping Function (GMF) [27] for the ground tracking stations. We do not simulate the ionospheric delay since the ionospheric-free (IF) combination will be used in the PPP model and higher-order ionospheric delays will be neglected in this study. Moreover, the relativistic correction, phase wind-up correction, and tidal displacements are all taken into consideration in the simulation, though they are not included in the equations. The observation noises are simulated as a zero-mean normal distribution with a standard deviation of 1.0 m and 5 mm for code and phase observations, respectively. In summary, the simulation configurations are listed in

Table 1. Simulation configurations of the LeGNSS observation data.

	GNSS		LEO
Satellite part	BDS	GPS	LEO
Angular range	GEO/IGSO: 10°	14.3°	65°
	MEO: 15°
PCO	YES	YES	NO
PCV	NO	YES	NO
Clock	YES	YES	YES
Receiver part
Cut off elev.	1°		1°
PCO	YES		YES
PCV	YES		YES
Clock	YES		YES
Solid/Pole/Ocean tidal	YES		YES
Propagation path
Troposphere	YES		YES
Ionosphere	NO		NO
Phase windup	YES		YES
General relativity	YES		YES
STD of noise
Code	1.0 m		1.0 m
Phase	5 mm		5 mm

.

It should be pointed out that the angular range in Table 1 is an essential issue in data simulation since it is one of the most important factors for the number of observations recorded by ground stations. Due to the different orbit altitude of different types of satellites, each type of orbits has its own angular range. Usually, the angular range $\theta$ is calculated by $\theta ={\sin }^{-1}\left(r/\left(r+l\right)\right)$, with $r$ and l denoting the radius of the Earth and the altitude of the satellites, respectively. We set the angular range to 65° for LEO satellites [24], 10° for BDS GEO and IGSO satellites, 15° for BDS MEO satellites [17], and 14.3° for GPS satellites [28], respectively.

3.2. The Adaption of PANDA Software

The PANDA [25] software has been developed as a multi-functional data processing software package for various applications, such as precise positioning services and POD of GNSS and LEO satellites. We implemented our LeGNSS PPP on the PANDA platform in this study. The LeGNSS PPP model and its processing strategies are presented as follows.

Usually, the IF combination is used in PPP to eliminate the first-order ionospheric delays. For the tropospheric delay, its dry component is precisely corrected via an a priori model, while the residual (wet) part is captured in data processing by setting up a zenith wet delay (ZTD). Then the linearization of Equations (1) and (2) read as:

$$p_{r,IF,k}^s=-{\mathit{u}}_r^s\mathit{r}+\Delta t_{r,k}+b_{r,IF}+m_r{z}_{r,k}+{\epsilon }_{P_{r,IF,k}^s}$$

(3)

$$l_{r,IF,k}^s=-{\mathit{u}}_r^s\mathit{r}+\Delta t_{r,k}+{\delta }_{r,IF}+m_r{z}_{r,k}+{\lambda }_{IF}{\tilde{N}}_{r,IF}^s+{\epsilon }_{L_{r,IF,k}^s}$$

(4)

where $p_{r,IF,k}^s$ and $l_{r,IF,k}^s$ denote the observed-minus-computed code and phase observations from satellite s to receiver r at epoch k. ${\mathit{u}}_r^s$ is the unit vector of the direction from receiver to satellite. $\mathit{r}$ denotes the vector of receiver position increments relative to an a priori position. $z_{r,i}$ is the ZTD parameter with the mapping function $m_r$, ${\tilde{N}}_{r,IF}^s=N_{r,IF}^s+\left(b_{IF}^s-{\delta }_{IF}^s\right)/{\lambda }_{IF}$. The remaining symbols have the same meanings as in Equations (1) and (2). For the LeGNSS case with combined GPS, BDS, and LEO systems, the PPP model reads:

$$p_{r,IF,k}^G=-{\mathit{u}}_r^G\mathit{r}+\Delta {\overline{t}}_{r,k}+m_r{z}_{r,k}+{\epsilon }_{P_{r,IF,k}^G}$$

(5)

$$p_{r,IF,k}^C=-{\mathit{u}}_r^C\mathit{r}+\Delta {\overline{t}}_{r,k}+IS{B}_{GC}+m_r{z}_{r,k}+{\epsilon }_{P_{r,IF,k}^C}$$

(6)

$$p_{r,IF,k}^L=-{\mathit{u}}_r^L\mathit{r}+\Delta {\overline{t}}_{r,k}+IS{B}_{GL}+m_r{z}_{r,k}+{\epsilon }_{P_{r,IF,k}^L}$$

(7)

$$l_{r,IF,k}^G=-{\mathit{u}}_r^G\mathit{r}+\Delta {\overline{t}}_{r,k}+m_r{z}_{r,k}+{\lambda }_{IF,G}{\overline{N}}_{r,IF}^G+{\epsilon }_{L_{r,IF,k}^G}$$

(8)

$$l_{r,IF,k}^C=-{\mathit{u}}_r^C\mathit{r}+\Delta {\overline{t}}_{r,k}+IS{B}_{GC}+m_r{z}_{r,k}+{\lambda }_{IF,C}{\overline{N}}_{r,IF}^C+{\epsilon }_{L_{r,IF,k}^C}$$

(9)

$$l_{r,IF,k}^L=-{\mathit{u}}_r^L\mathit{r}+\Delta {\overline{t}}_{r,k}+IS{B}_{GL}+m_r{z}_{r,k}+{\lambda }_{IF,L}{\overline{N}}_{r,IF}^L+{\epsilon }_{L_{r,IF,k}^L}$$

(10)

where the superscripts G, C, and L refer to GPS, BDS, and LEO satellites. $\Delta {\overline{t}}_{r,k}=\Delta t_{r,k}+b_{rG,IF}$ is the lumped (estimable) receiver clock biases. $IS{B}_{GC}=b_{rC,IF}-b_{rG,IF}$ and $IS{B}_{GL}=b_{rL,IF}-b_{rG,IF}$ are the receiver inter-system biases (ISB) parameters between GPS and BDS, as well as between GPS and LEO systems. $b_{rG,IF}$, $b_{rC,IF}$, and $b_{rL,IF}$ are the IF receiver code biases for GPS, BDS, and LEO satellites, respectively. The reparametrized ambiguity is ${\overline{N}}_{r,IF}^G={\tilde{N}}_{r,IF}^G+\left({\delta }_{rG,IF}-b_{rG,IF}\right)/{\lambda }_{IF,G}$ for GPS and they are completely analogously for BDS and LEO.

Then the unknown parameter vector is:

$$\mathit{X}={\left[{\mathit{r}}^T,\Delta {\overline{t}}_{r,k},IS{B}_{GC},IS{B}_{GL},z_{r,k},{\left({\overline{\mathit{N}}}_{r,IF}^s\right)}^T\right]}^T$$

(11)

In the PPP model, the observations from all satellites are processed simultaneously in a single adjustment. The receiver positions are estimated in kinematic mode, while the ZTD is estimated as a random walk process with noise of $1 \mathrm{cm}/\sqrt{1 \mathrm{hour}}$. The receiver clock is estimated epoch-wise as white noise. The ambiguities are estimated as constant for each arc, and the ISB is estimated as constant over time.

3.3. Setup

With the aforementioned simulation software, we simulated GNSS and LEO observations for ground stations on a global scale (they are grid points assumed to be distributed globally with the space resolution 5° by 5°) from 1 June 2014 to 7 June 2014. Then the adapted PANDA software is used to conduct the LeGNSS PPP in order to evaluate the performance of LeGNSS. In particular, four stations located at P1 (80°S, 30°W), P2 (0°S, 30°W), P3 (30°N, 120°E), and P4 (75°N, 120°E) are adopted for the kinematic mode of PPP tests in order to show the PPP performance more clearly.

4. Assessment and Analysis of LeGNSS Precise Positioning

In this section, the satellite visibility of LeGNSS are assessed with different system combinations. We elaborate the LeGNSS PPP performance, including the time span of each satellite, the sky plot, and the convergence time with four stations. Finally, the convergence time and its influence factor of the sampling rate are statistically analyzed for all system combinations on a global scale (they are grid points assumed distributed globally with the space resolution of 5° by 5°), followed by the discussion.

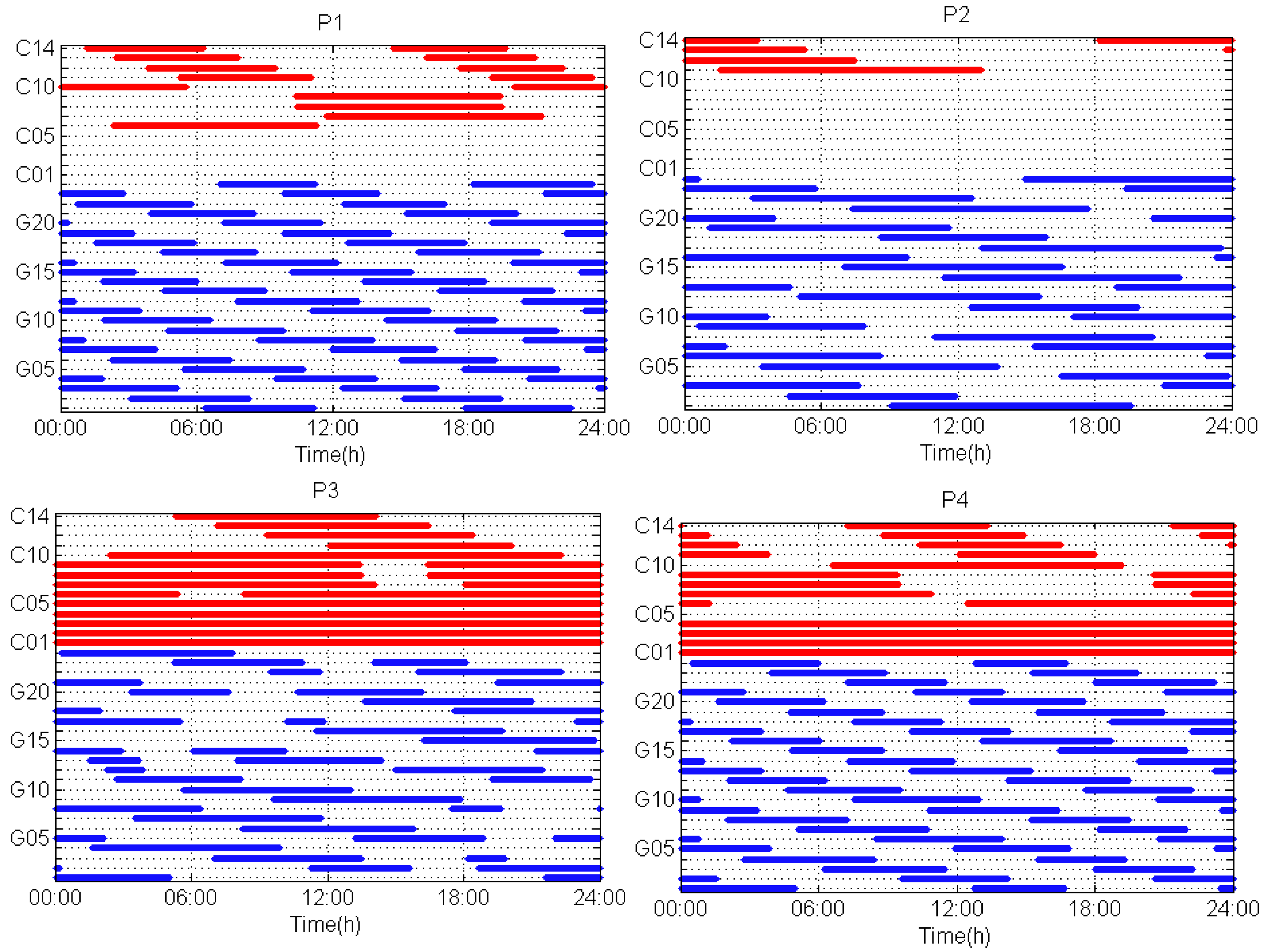
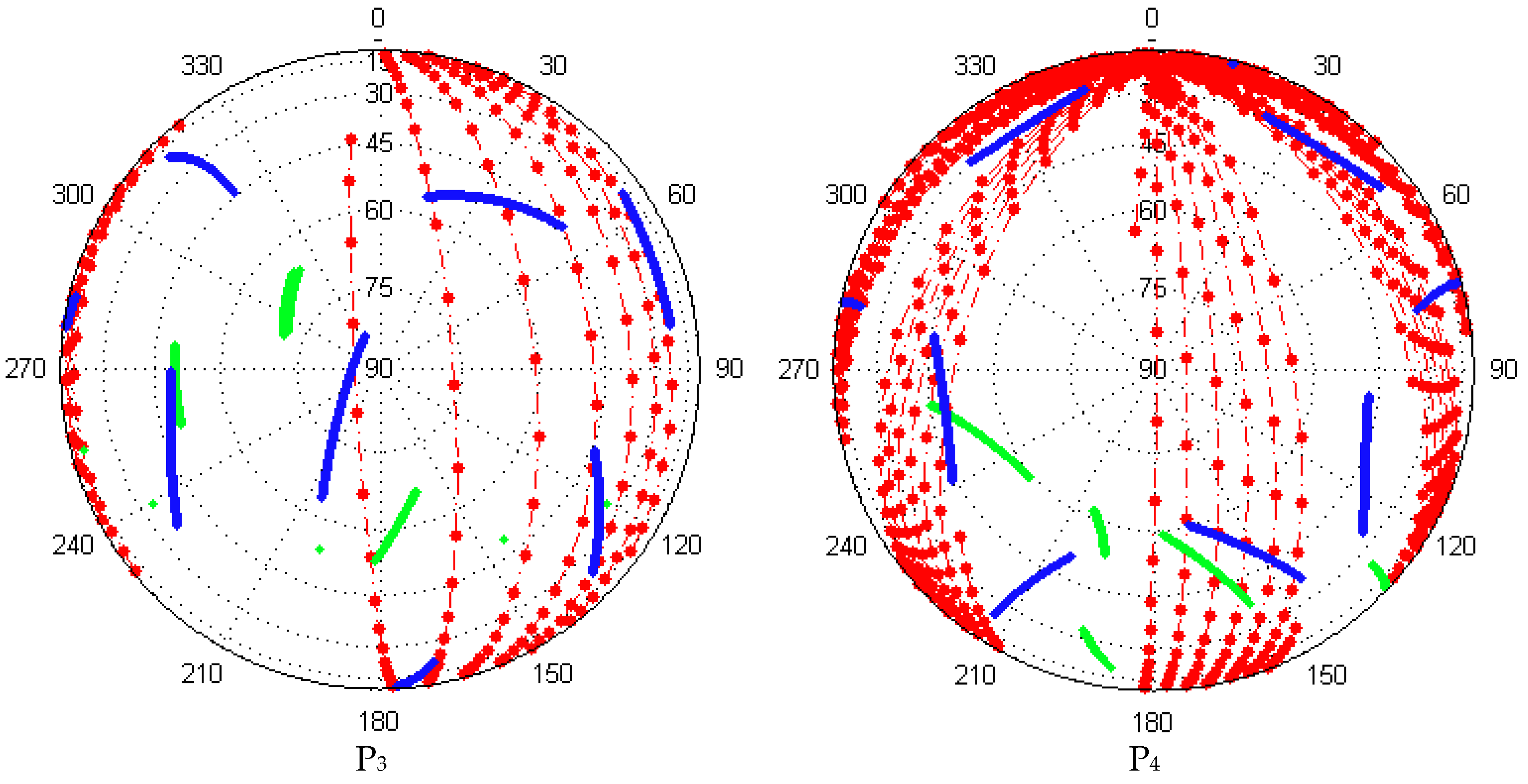
4.1. Satellite Visibility

In order to make a comprehensive comparison, the datasets are processed in six different constellation combinations, i.e., GPS-only, BDS-only, LEO-only, GPS/BDS, GPS/LEO, and GPS/BDS/LEO. The satellite elevation mask angle is set to 7°. The coverage of the calculation is global, and the space resolution is 5° by 5°. The sampling interval is 5 min. Figure 2 shows the average number of visible satellites over the entire analysis period for six constellation combinations.

As shown in Figure 2, GPS, BDS, and LEO satellites provide different coverage. There are always more than four visible GPS satellites everywhere in the world. For the BDS-only case, the number of visible satellites in the Asia-Pacific area creates a large elliptical zone, since the BDS GEO, and IGSO satellites operate in this area so far. Users can observe nine to fourteen BDS satellites in BeiDou service areas while only about one to three BDS satellites in other areas. It is interesting to see the number of visible LEO satellites on a global scale, for which one can observe nearly eight to ten LEO satellites in polar areas and only five or even fewer satellites in other areas. This is easy to understand since the LEO satellites have near-polar circular orbits. However, due to their low Earth orbit, the footprint of LEO satellite is much smaller than that of other GNSS satellites. The diameter of the footprint is around 3000 km for Iridium satellites, while being about 12,000 km for GPS satellites [29]. As a result, much fewer visible LEO satellites can be observed in medium and low latitude regions. It is clear to see that the different constellation combination provides coverage improvement. The LeGNSS (GPS + BDS + LEO) exhibits the best coverage of satellite visibility on a global scale, and the number of visible satellites is thirteen to twenty-five.

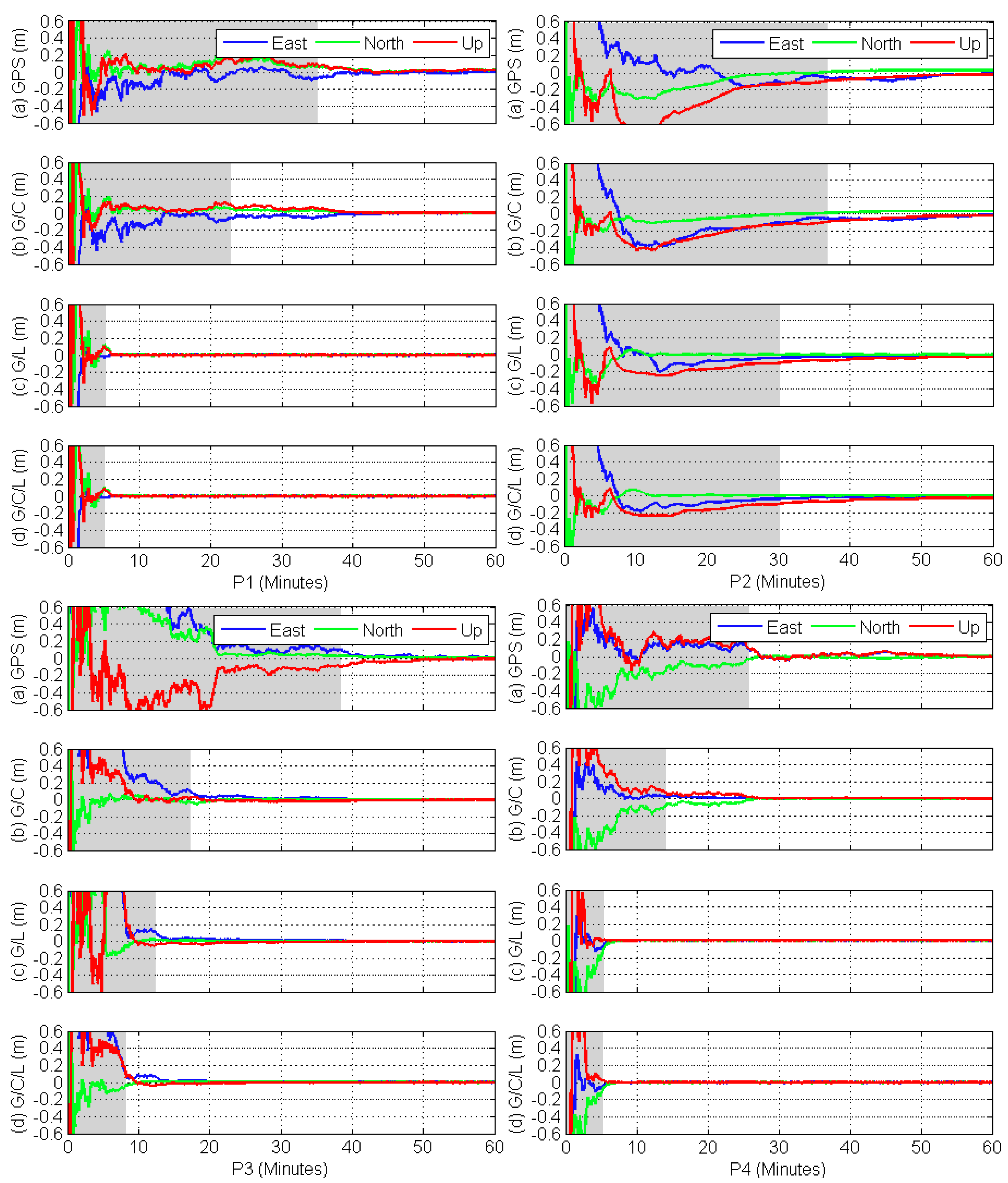
4.2. Assessment and Analysis of LeGNSS PPP Performance

In order to fully demonstrate the contribution of the LeGNSS system to PPP solutions, four stations located at P1 (80°S, 30°W), P2 (0°S, 30°W), P3 (30°N, 120°E), and P4 (75°N, 120°E) are adopted for the kinematic mode of PPP tests with GPS-only, GPS/BDS (G/C), GPS/LEO (G/L), and GPS/BDS/LEO (G/C/L) (i.e., the LeGNSS system). The locations of the stations are shown in Figure 3. In this study, the convergence time of the positioning solution is defined as the time when the positioning errors for each component reaches ±10 cm and stays within that value.

As clearly shown in Figure 4, the time span of each GPS satellite differs from locations. For higher latitude location, e.g., P1, the GPS time span of every pass is shorter than that at lower latitude location, such as P2 where the time span is almost 8–10 h. The visibility is very different for the various orbital types, especially for the regional satellite system. At station P2, some BDS MEO satellites are tracked while most of the BDS satellites are tracked at stations P3 and P4 because they are located within the current BDS service region. For P1, BDS GEO cannot be observed, while all the IGSO and MEO can be tracked. The time span is also different depending on the orbital types. The BDS GEO satellites have the longest tracking periods. The BDS IGSO satellites are tracked relatively shorter than those of GEO satellites with data gaps of about 5 h at low latitude for one day. The tracking periods of BDS MEO satellites are the shortest compared to GEO and IGSO satellites.

The tracking period of LEO satellites is shown in Figure 5. We can easily see the very short time span of LEO satellites with respect to the ground station. It is only about 5–10 min and much shorter than that of GNSS satellites. This is mainly because of the low Earth orbit of LEO satellites, causing the fast motion with respect to the ground stations. Such fast motion gives an opportunity to shorten the convergence time. On the other hand, since the LEO satellites are usually polar satellites with the orbital period of about 1.5 h, every LEO satellite in one orbit plane would be tracked by polar stations for every 1.5 h, e.g., P1 and P4. Thus, stations at high latitude can track one specific LEO satellite by more than ten times a day, e.g., P1 and P4, while only four to five times for stations in low and medium latitude, e.g., P2 and P3 because of the polar orbit and small footprint of LEO satellites, which were already mentioned in the section of satellite visibility and availability.

To clearly show the convergence process for different situations, one hour of data of these four stations is calculated as an example. Figure 6 shows the sky plots (azimuth (0–360°) vs. elevation (0–90°)) of GPS, BDS, and LEO, respectively. The elevation variations of GNSS satellites are generally from 0° to 30° over one hour, while those of LEO satellites are quite large and from 1 to 90°. In particular, the sampling interval between adjacent dots are 30 s. As we can see, the elevation change of a LEO satellite can reach up to 5°, or even 20° over 30 s.

This fast motion can also be observed from the quick variation of GDOP values. Figure 7 shows the number of satellites and their corresponding GDOP values for different combinations of four stations. These four stations can generally observe seven to ten GPS satellites and the GDOP of GPS-only is generally from 2 to 4. The number of tracked BDS satellites mainly depend on the location of stations since BDS provides service only in Asia-Pacific areas currently. The GDOP values of G/C are much smaller than those of GPS-only, except for stations P1 and P2. As shown in Figure 6, though there are three to four BDS satellites tracked by station P1, the low elevation and short arc of BDS satellites make the geometric distribution of G/C almost the same as GPS-only. For station P2, since it is out of the BDS service region, the GDOP values of G/C are unchanged compared to GPS-only. For stations P1 and P4, 5–8 LEO satellites can be tracked while only 1–2 can be tracked for stations P2 and P3 since the higher latitude of P1 and P4. The GDOP values of G/C/L are smaller than those of G/C for stations P1 and P4, which attribute to the increased number of LEO satellites.

With the aforementioned characteristics of the LeGNSS, including the time span, sky plot, and GDOP values, Figure 8 presents the kinematic PPP results for GPS-only, G/C, G/L, and G/C/L, respectively. Here we show the hourly results just in order to clearly see the convergence time. The convergence times of different combinations for all stations are listed in

Table 2. Convergence time of different combinations for all stations. Unit: min.

	GPS-Only	GPS/BDS	GPS/LEO	GPS/BDS/LEO
P1	34.9	22.8	5.2	5.2
P2	36.8	36.8	30.0	30.0
P3	38.3	17.1	12.3	8.2
P4	26.0	14.0	5.3	5.0

. As we can see, the GPS-only PPP needs nearly 30 min to converge when the positioning errors of three components are all smaller than 0.1 m. Except for station P2, the G/C PPP significantly shortens the convergence time against the GPS-only case. Station P2 is not within the BDS service region and only one BDS MEO satellite is tracked, as shown in Figure 7, which has nearly no contribution to the convergence time. For the other stations, the convergence time is 10 min faster than the GPS-only case, where the G/C GDOP values become smaller.

The convergence time of the G/L combination can be dramatically decreased to around 5 min at stations P1 and P4, although their GDOP values are not as small as those of the G/C combination. With P4, for example, the G/C convergence time is about 15 min, while for G/L it is only 5 min. However, the G/C GDOP is about 2 while G/L GDOP is between 2 and 4. This much shorter convergence time of G/L is attributed mainly to the fast motion of LEO satellites with respect to the ground stations, which is observed from the quick variation of GDOP values. For stations P2 and P3, there are not as many LEO satellites observed as at stations P1 and P4, which generates the relative larger G/L convergence time for about 30 and 12 min. However, for the P3 case, though, there are only 2 to 3 LEO satellites in G/L combination, the G/L convergence time is shorter than that of G/C convergence time, which has nine BDS satellites in G/C combination. This reassures the contribution of fast geometric change of LEO to the PPP. For the G/C/L PPP, the convergence time is further shortened to several minutes, which is much shorter compared to that of multi-GNSS PPP. Actually, with the same simulated situation, the convergence time of combined GPS, GLONASS, BDS, and Galileo PPP is also about ten minutes which is close to that of the real situation. This, again, verifies the fact that the fast geometric change of LEO with respect to the ground stations can indeed greatly shorten the convergence time. Such a result is very promising, which means that the convergence time would be shortened to a few seconds if more LEO satellites are incorporated in the navigation service.

4.3. Statistical Analysis of Convergence Time on a Global Scale

To fully reflect the PPP performance of the LeGNSS, we conduct the PPP computations for simulated stations with the space resolution 5° by 5° on a global scale. For each station, the data is calculated every two hours for one week in total. Thus, there are 84 computations for each station in one week. Afterwards, the averaged convergence time for each component of each station is calculated. Here, we repeat our definition of convergence time as the number of epochs from the first epoch to the epoch when the positioning errors for each component reach, and afterward remain within, ±10 cm.

In terms of the numerical analysis, both BDS-only and LEO-only cannot provide standalone positioning service in some specific areas. In this statistic analysis, we choose four system combinations of GPS-only, G/C, G/L, and G/C/L to investigate their convergence time in each component on a global scale. The distributions of the convergence time are shown in Figure 9 in units of minutes.

As shown in Figure 9, the averaged convergence time of GPS-only is 33.0, 24.9, and 32.7 min for east, north, and up components, respectively. The maximum convergence time is over 100 min for all three components. For 95% of the world’s area, it takes about one hour to converge. For the G/C case, the averaged convergence time is reduced by 52.1%, 57.0%, and 57.5% for east, north, and up components, respectively. Most regions in the world need about 32 min to converge for three components. With the integration of GPS and LEO satellites, the results are very astonishing with the averaged convergence time of only 8.2, 5.5, and 7.3 min for east, north, and up components, respectively. It should be pointed out that the contribution of LEO to the convergence time is much greater than that of BDS, though there are a very limited number of LEO satellites in medium and low latitude regions. For G/C/L case, the averaged convergence time is 6.1, 4.2, and 5.1 min for east, north, and up directions, respectively. The improvement is not significant compared to G/L combination. This is mainly because of the slow motion and regional availability of BDS satellites with respect to the ground stations. The convergence time of more than 10 min is mostly in regions where the visible LEO satellites are rather few. It is prospective that the convergence time can be shortened to several minutes, even seconds, if there are enough LEO satellites in the sky.

As aforementioned, the fast motion of LEO satellites can indeed make a significant contribution to the convergence time of PPP. Since the geometric change of LEO satellites is much faster than that of GNSS, which can be seen from the sky plot, the sampling interval of the observation data may be another factor to the convergence time. Hence we investigate the effect of the sampling rate of observation data to the combined G/C/L PPP convergence time.

The distributions of convergence time for sampling intervals of 30, 10, 5, and 1 s G/C/L PPP are shown in Figure 10. The averaged convergence time is generally 10.0 min for all the components at all sampling intervals. With higher sampling interval, the convergence time is shorter. This reason is that the LEO satellites are moving fast, every second can already achieve great geometric change with respect to the ground stations. It takes 7.9, 5.3, and 6.9 min for east, north, and up components to converge with 30 s sampling interval while 6.9, 4.9, and 5.8 min with 10 s sampling interval, respectively. Further increasing the sampling interval does not shorten the convergence time significantly anymore, which means that the satellites’ geometric change with respect to the ground stations are not great enough to improve the PPP convergence time. The convergence time of 5 s sampling interval is almost the same as that of 10 s. The averaged convergence time of 1 s sampling interval is the shortest, which are all smaller than 5.0 min, with the improvement of 44.3%, 41.5%, and 46.4% compared to those of the 30 s sampling rate for east, north, and up components, respectively.

5. Discussion

As aforementioned, 66 LEO satellites, which can transmit GNSS-like signals, have been recruited to shorten the PPP convergence time. For the satellite visibility, eight to ten LEO satellites can be observed in polar areas while only one to three can be tracked in low and medium latitude regions because of the small footprint of LEO satellites and their polar orbits. Compared to those in hours flying overhead of GNSS satellites, LEO satellites fly overhead just in five to ten minutes, which offers the fast-geometric change with respect to the ground stations, resulting in the short convergence time. The experimental results for four stations show that the convergence time can reach to five minutes in polar areas where enough LEO satellites can be observed. Even though a few LEO satellites can be tracked in low and medium latitude regions, the improvement of the convergence time is greater than that of multi-GNSS. The global kinematic PPP results show that in most part of the world, one can achieve cm-level precise positioning just in five minutes.

There are still some issues to be investigated, such as the bounds of the convergence time of the LeGNSS as a function of the number of LEOs. Moreover, since the world population is between latitudes 35° N and 35° S, the short convergence time in this area is much more expected than that in polar areas. As a result, not only the number of LEO satellites, but also the constellation configuration of LEO satellites, should be taken into consideration in our future studies. If it comes true, the precise pointing technique will see a great change since there is no need for dense reference stations anymore. One can achieve the cm-level positioning results immediately without any additional augmentations.

6. Conclusions

In order to shorten the convergence time of PPP, we put forward the idea of the LEO-enhanced GNSS system, which is called LeGNSS. The LEO constellation can transmit GNSS signals to enhance GNSS service. We investigated the benefits of LeGNSS compared with the current GPS, BDS, and Iridium constellation itself. The conclusions are summarized as follows:

(1)

The LEO constellation can improve the availability of the current GNSS system, especially in the polar areas, since LEO are usually polar satellites. With 66 Iridium satellites, it is difficult to provide LEO-only positioning service since there are not enough satellites at medium and low latitudes.

(2)

LEO satellites are moving quite fast, flying overhead in minutes compared to the GNSS satellites in hours, which gives rise to improving the geometric condition of ground stations, resulting in the fast convergence time of PPP.

(3)

The convergence time of combined G/C/L can be shortened to 5 min in most of the areas of the world with 5 s data while, as far as we are concerned, it is impossible with GNSS to achieve such quick convergence even with 1 s data.

We emphasize that the achievements of this LeGNSS results are with just 66 LEO satellites. It is very promising that the performance will be much better if more LEO satellites, especially in inclined orbits, are involved in the LeGNSS system.