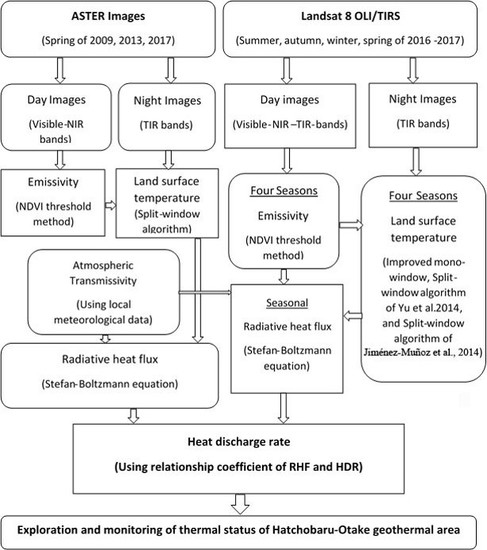
1. Introduction
The Hatchobaru–Otake (HO) geothermal area is situated 5–6 km west of the Kuju volcano, within the Hohi graben system (the Beppu-Shimabara Graben) of central Kyushu, Japan (
Figure 1) [
1,
2,
3]. It is about 900 to 1000 m above sea level and forms a basin-like topography, surrounded by volcanic domes [
4]. The extent of the HO geothermal area is about 1 km from east to west and about 3 km from north to south [
5]. The Kusu River runs towards the north, through the central part of the geothermal area, and active fumaroles and hot springs are found on the eastern side of the river [
4,
5]. The HO geothermal area is a typical water-dominated geothermal system, which supplies steam to two geothermal power plants, Otake and Hatchobaru, installed in 1967 and 1977, respectively [
6]. The Otake power plant in the Otake hot spring region has generated about 12.5 MW of peak power since 1967. Two power plants were installed in the Hatchobaru geothermal field, Unit 1 has generated about 55 MW of peak power since 1977, while Unit 2 has generated about 55 MW since 1990 [
7]. The geothermal reservoirs lie about 500–1000 m below ground, along faults. The fluid temperatures are about 220–260 °C and 250–290 °C in Otake and Hatchobaru geothermal reservoirs, respectively [
7,
8].
Geothermal energy is one of the most important clean and renewable energies in the world. Geothermal resources are related to volcanoes or hot springs. Given their geological setting, continuous monitoring is required in order to evaluate the sustainability of the geothermal system. Typically, there are many ground-based geophysical and geochemical monitoring systems in and around geothermal power plants. Such monitoring is expensive, time-consuming, and sometimes difficult to carry out, because these areas may be within national parks and may be restricted because of fumaroles or unstable regions. Remote sensing could be used effectively for monitoring developed geothermal systems, such as the HO geothermal area in Japan; this would involve less time and money. Because the HO geothermal region is monitored using ground-based geophysical and geochemical methods, there has been no monitoring of the thermal activity of the HO area using satellite remote sensing thermal infrared data to date.
Satellite remote sensing has already been used for monitoring heat loss from active volcanoes and other geothermal areas [
9,
10,
11,
12,
13,
14,
15]. It is very important to quantify surface heat loss from geothermal areas, in order to protect them as resources and to protect their surrounding environments. Such data can be used as an input for reservoir simulation modeling and to improve the sustainability of geothermal fluid use [
16,
17]. Multi-spectral satellite images, such as Landsat 8 and ASTER, have thermal bands that are used to estimate thermal anomalies, as well the heat loss from volcanic and geothermal systems. There are some limitations to using satellite images, including their coarse resolution (i.e., 30–90 m), difficulty in obtaining good-quality cloud-free images, and limited ground validation. An ASTER image has five multispectral thermal bands with a 90 m resolution (30 m resampled resolution), reflecting an electromagnetic (EM) range from 8.125 to 11.65 μm. Of these, band 13 (EM = 10.25–10.95 μm) and band 14 (EM = 10.95–11.65 μm) are used in split-window (SW) algorithms for determining the land surface temperature (LST) [
18]. Subsequently, these LST estimates are used for heat loss or thermal anomaly mapping of volcanic or geothermal areas. Similarly, the Landsat 8 thermal infrared sensor (TIRS) has two thermal bands with a 100 m resolution (30 m resampled resolution). Band 10 (EM = 10.60–11.19 μm) and band 11 (EM = 11.50–12.51 μm) are used for the LST measurement of thermal anomalies using both mono-window (MW) and SW algorithms [
19,
20,
21]. The sensor variation is distinct in the case of ASTER and Landsat 8 TIRS, as are their EM ranges of the thermal infrared data. Although there are various methods of LST measurement, no study has yet investigated the variation related to using various LST estimation methods in volcanic or geothermal regions.
Many factors affect the measurement of LST. Of them, seasonal variation could be an important factor affecting the monitoring of LST and the heat loss from thermally active areas using satellite thermal infrared (TIR) data. There are some man-made features, including buildings, roads, and cultivated fields, that will have an effect on the total geothermal RHL measurements if these features may radiate above background RHL. Another important factor to consider is meteorology. We used various meteorological data, such as the daytime versus nighttime ambient temperature and the relative humidity, so as to estimate the atmospheric transmissivity of the geothermal area during the satellite image acquisition. Solar effects are an important drawback of evaluating geothermal heat loss in daytime satellite thermal infrared data. We evaluated whether nighttime satellite thermal images could be used to avoid solar effects.
There are three pathways of heat transfer from a geothermal system, convection, conduction, and radiation. Of them, only the radiative part of heat loss can be estimated using remote sensing TIR data. The total heat loss or heat discharge rate (HDR) is the sum of the radiative, convective, and conductive heat loss from any volcanic or geothermal field. There is a relationship coefficient based on the field as well as TIR data, between the radiative heat flux (RHF) and HDR, in the literature [
15,
22]. We proposed, based on the total heat loss or HDR from the study area, using this relationship in the discussion. Our motivation was to evaluate the limitations and to refine the techniques of estimating heat loss using the satellite images of the HO geothermal area.
In this study, we explored and monitored the thermal status of the HO geothermal area for the first time, using satellite thermal infrared data. Our main objective was to explore its thermal anomaly using LST and to monitor its RHL from 2009 to 2017, using three sets of nighttime ASTER TIR data. A thermal anomaly means that there is a higher range of LST values in the geothermal area than in the surrounding area (i.e., LST is above ambient). The RHF anomaly indicates the RHF value above zero. Our secondary objective was to evaluate the solar and seasonal effects of heat loss using both day- and night-time Landsat 8 operational land imager (OLI)/TIRS satellite data for the study area. Lastly, there are three well-established methods for LST measurement using Landsat 8 TIR data, namely, an improved MW algorithm (IMW), the SW algorithm of Yu et al. [
19], and the SW algorithm of Jiménez-Muñoz et al. [
20]. We estimated the LSTs, using all of these methods to compare their variation in the heat loss estimates for the study area.
5. Discussion
A lack of availability of the same sensor satellite data for the entire period is one of the limitations of the whole research work, for effectively monitoring the thermal activity of the HO geothermal area. Both the day- and night-time thermal infrared data of every year could be used for the thermal anomaly for the entire period of the research, but the drawback of the daytime image is the solar insolation. There are various types of algorithms that are used to retrieve the LST nowadays, such as single channel, multichannel, multi-angle, and multi-time methods [
36]. Among them, the temperature and emissivity separation (TES) and split-window (SW) algorithm are widely used for LST measurement, using the ASTER thermal infrared image. The TES algorithm is designed for the ASTER image, to estimate the LST and emissivity, with a maximum–minimum difference (MMD) module. The MMD is an empirical relationship between the minimum emissivity and the difference between the maximum and minimum emissivity, used to make the number of observe equations equal to that of the unknown variables [
37]. This technique can estimate the LST and emissivity at a 90 m resolution, only with the atmospheric-corrected data of the TIR, without any prior knowledge of emissivity [
37]. The accuracy of the atmospheric correction is the key factor for the efficiency of the TES method, and sometimes, the results of this algorithm are inaccurate for low emissivity land cover, such as dense vegetation, water, and snow [
37,
38]. On the other hand, the SW algorithm can calculate the LST (30 m in resolution) by removing the atmospheric effect from the linear or nonlinear combination of the brightness temperature of the adjacent bands (i.e., such as 11 and 12 μm in the wavelength) [
37]. This SW method reduces the requirements of the detail atmospheric data [
37]. The SW method is used widely from a variety of thermal infrared sensors, such as ASTER, and Landsat, among others, because of its simplicity, efficiency, and insensitivity to atmospheric uncertainty. The only prior requirement of the SW algorithm is the emissivity of the land cover of the study area. For this reason, the SW algorithm was used in the current study to calculate the LST from the ASTER thermal infrared data. There are various approaches to predicting land surface emissivity from normalized differential vegetation index (NDVI) values [
28,
29]. The NDVI based emissivity method is very popular and is used to retrieve emissivity at a 15 m resolution for soil, vegetation, and water bodies efficiently, contrasting the TES method used to retrieve the emissivity of a 90 m resolution. In the case of the Landsat 8 images, it is well known and documented that the TIRS has suffered from a stray light problem since the launch of this satellite [
39]. Although an algorithm was applied to correct the stray light problem, and the corrected TIRS data was supplied from February 2017, it was still not recommended to apply the TIRS band 11 for the split-window algorithm [
39].
The heat losses monitored using the ASTER TIR data from 2009 to 2017 show that the highest total heat losses occurred in 2013 and lowest ones occurred in 2009, although the highest pixel value of the RHF was recorded in 2017, and the lowest one in 2009. Based on previous studies regarding the relationship between the RHF and HDR (15% ± 10%), we proposed HDR for the study area, after multiplying the total RHL by the coefficient of the relationship (15% or 6.49) [
15,
22]. The total heat losses or HDRs could be about 2.3 (±10%) MW, 257 (±10%) MW, and 191 (±10%) MW for 2009, 2013, and 2017, respectively, from our study area (
Table 4 and
Figure 7B). We compared the observed LST and RHF with the ASTER standard products based LST and RHF. The maximum LST and RHF was found to have a similar trend, but was lesser in value compared with the standard products observed, because of the resolution of the pixel (i.e., observed LST and RHF thematic map resolution of 15 m and the standard products resolution of 90 m). There is an inverse relationship between the pixel size and the retrieved maximum LST with a heterogeneous surface, which resulted in an inverse temperature radiance [
40]. Hence, in the case of total RHL, we obtained a higher heat loss in 2017 than 2013 with ASTER standard products, opposite to that of the observed heat loss. This may be due to the emissivity value variations (high range for standards than observed) and resolutions (90 m for standard and 15 m for observed).
There is another source of uncertainty with the absorbed atmospheric temperature of land cover within the thermal ground in the case of the heat loss estimation, even with the nighttime thermal infrared data [
40]. The background heat loss could be subtracted from the estimated heat loss of the study area, in order to derive the actual geothermal heat loss, but there were uncertainties or difficulties in selecting a similar topographic, altitude, land cover, and non-volcanic area as the background in and around the study area [
40]. Moreover, our approach to evaluate the relative proportion of the RHL by pixels of background LST (average) on total RHL, may overestimate the geothermal RHL from total retrieved RHL. Based on the background LSTs (average), the contribution of the background was not so high on total the RHL, as the average background LSTs were less than expected (
Figure 8 and
Figure 21). Actually, if the background LST of any pixel is less than or equal to ambient, then the RHF value will be negative or zero, according to the Stefan–Boltzmann equation of RHF used in this study. As we added only the positive RHF, most of the background RHFs (mostly negative or zero) were not counted on the total RHL. Of course, some of the background pixels close to the geothermal area showed a higher LST than ambient, and resulted in RHL values more than the expected from the HO geothermal region. It seems that geothermal RHL still has some influence on the background, as we used the background average LST, which is much less than what is was originally in some of the pixels close to the HO geothermal area.
The variation of the thermal activity may be related to some of the reasons in this study area from 2009 to 2017, such as (1) the natural perturbation of geothermal system, (2) the impossibility of removing all of the background heat flux, and (3) the variation of heated water withdrawn from subsurface of the two geothermal power plants (i.e., Hatchobaru and Otake). It may possible to validate these results using the power plants information, such as the reservoir heated water temperature at well head, the water withdrawn volume, and the rate of electricity production during the period of the study, however, these data are not available to be used publicly from the authority of the power plants operating company.
The day- and night-time LST results showed that much higher thermal anomalies or LSTs were established in the daytime than during the nighttime, reflecting the effect of solar insolation during the image acquisition. The autumn LST maps had high thermal anomalies related to cloud cover during the daytime. This result coincided with a recent study of cloud effects on air temperature using MODIS TIR data, that is, clouds mainly influence the LST (max) estimation on the daytime image by affecting the relationship between the LST (max) and daytime LST, and hence, the error result of the LST (max) is larger in the daytime than in the nighttime [
41]. The nighttime image analysis showed that higher thermal anomalies were associated with the HO geothermal system, with maximum LSTs recorded in the summer and the lowest ones recorded in the winter for all three conventional methods of the LST estimation using Landsat 8 TIRS data (
Figure 13). The daytime maximum LSTs were about three, six to eight, two to seven, and two times that of the nighttime maximum LST, for the spring, winter, autumn, and summer seasons, respectively, with all three of the LST methods. All of the three methods showed a similar range of variations for the maximum LST during the day- and night-time in all of the seasons, except autumn (
Table 5). The RGB combinations of LST values for all three of the methods showed high anomalies associated with the Hatchobaru, Otake, and Yutsubo hot spring areas. Although white pixels indicate the same LST for all three of the LST methods, different shades of color (R/G/B) indicate where one LST method is over- or under-estimated by the other LST methods, which might be due to the sensitivity of LST measurement of these methods (
Figure 13). The IWM method shows a possible average error of about −0.05 K and a root mean square error (RMSE) of about 0.84 K, which is less than the single channel method (average error −2.86 K and RMSE 1.05 K) [
21]. The possible source of the error in the case of a single channel or IWM method is the water vapor content in the atmospheric profile [
21]. On the other hand, the RMSE of SW-Yu et al. is about 1.025 K, as the LST retrieval from band 11 has more uncertainty than band 10 [
19]. In the case of SW
, Jiménez-Muñoz et al., the average error is about 1.5–2.1 K, while the RMSE is below 1.5 K [
20].
The daytime RHFs had high values in all seasons around the Hatchobaru and Otake hot spring areas, except in autumn, when the highest RHF values were related to cloud cover, especially in the LSTs derived from the SW algorithms. The nighttime radiative heat loss anomalies were linked to the OH geothermal area in all of the seasons. The daytime RHFs were much higher in all of the seasons because of the solar effects. The daytime maximum RHFs were about 10–11, 2–4, 1–17, and 5–7 times that of the nighttime maximum RHF, for the spring, winter, autumn, and summer seasons, respectively, with all three of the LST methods based the RHF. These three methods showed a close range of variations of the maximum RHF during day- and night-time in all seasons, except autumn (
Table 5). A comparison of all three of the LST estimation methods showed that the IMW algorithm derived maximum LSTs in all seasons, except summer. This may be due to the differences in the day- and night-time acquisition time, which are higher in summer (about two months) than in the other seasons (less than a month), resulting in the variation in emissivity. The result of IMW is quite different than the SW algorithm, as the SW method used band 10 as well as band 11, which is not recommended for LST, because of the light stray problem of the TIRS sensor of Landsat 8. Similar intra-seasonal trends were observed for all of the methods based on the 101-random point sampling of the nighttime LSTs of the study area. After using both the day- and night-time LSTs for estimating the total RHLs, we observed that the total RHLs derived using the SW-based LSTs were higher than those for the IMW-based LSTs in all seasons, except for summer (in daytime images). In the nighttime images, the IMW-based LSTs yielded total RHLs that were higher in all seasons, except for summer. The seasonal variations were significant in each season, with little variations in the applied three LST methods (
Figure 18). Winter and autumn had higher RHFs, while summer and spring had lower RHFs in the nighttime TIR data, related to lower ambient temperatures. The RHFs were more or less similar in all three of the methods for the seasons of spring and summer. Exploring the relationships between RHF and LST against NDVI (or landcover) showed that the NDVI values of less than 0.5 (mixed or bare ground) were associated with higher LST and RHF values within the HO geothermal area.
The average heat flux of the continental crust is about 0.065 W/m
2 [
40]. The heat flux is reported as about 21 W/m
2 (average) and about 37 W/m
2 (maximum) from an active thermal area of the Yellowstone national park, which is more than 300 times that of the continental heat flux [
40]. In this study, we obtained a maximum heat flux of about 31 W/m
2, using nighttime ASTER TIR data, and about 29 W/m
2, using Landsat 8 TIRS data from the active HO geothermal area (
Table 4 and
Table 6).
We would like to suggest the IWM method for estimating LST using Landsat 8 TIRS data, considering the error of thermal band 11 as a result of the stray light problem of Landsat 8 TIRS sensor, the LST estimations accuracy (based on the source articles [
19,
20]), and the consistency of the LST results in three out of four seasons in this study. A significant limitation of this research is the lack of ground validation information due to the inaccessible fumaroles, and unavailable data of previous heat loss and power plants. However, we validated our retrieved RHL with ASTER standard products (AST_05, emissivity and AST_08, temperature), based on the results of total RHL in this study, with strong Pearson correlation coefficients. As a first study for thermal status monitoring with comparison of method, and solar and seasonal effects, continuous nighttime satellite thermal infrared data of same month or seasons could be worth it for the long-term monitoring of thermal activity at the HO geothermal area, so as to help with the sustainability of the geothermal resource.
6. Conclusions
To address the issue of spatial heat loss from the HO geothermal area, we used ASTER and Landsat 8 images to monitor the geothermal heat loss from 2009 to 2017, compared with the solar effects, seasonal variation, and LST measurement methods in this study. Our study of the nighttime ASTER TIR data indicates that the thermal activity has undergone both an increase and decrease within the HO geothermal area from 2009 to 2017, keeping an uncertainty of the limited numbers of data. The RHLs were more in the Otake than Hatchobaru thermal area in the year of 2013 (~31%) and 2017 (~78%). The daytime heat losses were much higher than nighttime ones, because of solar effects on daytime Landsat 8 satellite images. The heat losses in all four seasons were distinct in both the daytime and nighttime Landsat images. The highest heat losses were in winter and autumn, while the lowest losses were in spring and summer in the nighttime satellite images. The heat losses calculated using the IMW-based LSTs were slightly higher than those of the SW algorithms. The HO geothermal area had higher LSTs as well RHLs in all of the seasons, compared with its surrounding non-thermal areas. The total RHLs ranged from 10 to 451 MW (after removing RHL by pixels with background LST-average on total RHL) in the daytime over all four seasons, with the highest values in spring and the lowest ones in autumn. In contrast, at night, the RHLs ranged from 1 to 67 MW (after removing RHL by pixels with background LST-average on total RHL), with the highest values in autumn and the lowest ones in spring, based on the Landsat 8 TIRS images. Individually, during the day, the RHLs ranged from 1–42 MW and 0.19–25 MW over all four seasons, from the Hatchobaru and Otake thermal area, respectively, with the highest values in spring and the lowest in autumn. At night, the RHLs ranged from 0.23–7 MW and 0.19–5 MW over all four seasons, from the Hatchobaru and Otake thermal area, respectively, with the highest in winter and the lowest in summer. In this study, we applied limited numbers of ASTER TIR data to monitor the geothermal activity of the study area from 2009 to 2017, because of the unavailability of the data, while the Landsat 8 OLI/TIRS seasonal data were used to evaluate the solar, seasonal, and methodological effects on the LST and RHF estimations.