Crustal Deformation on the Northeastern Margin of the Tibetan Plateau from Continuous GPS Observations
Abstract
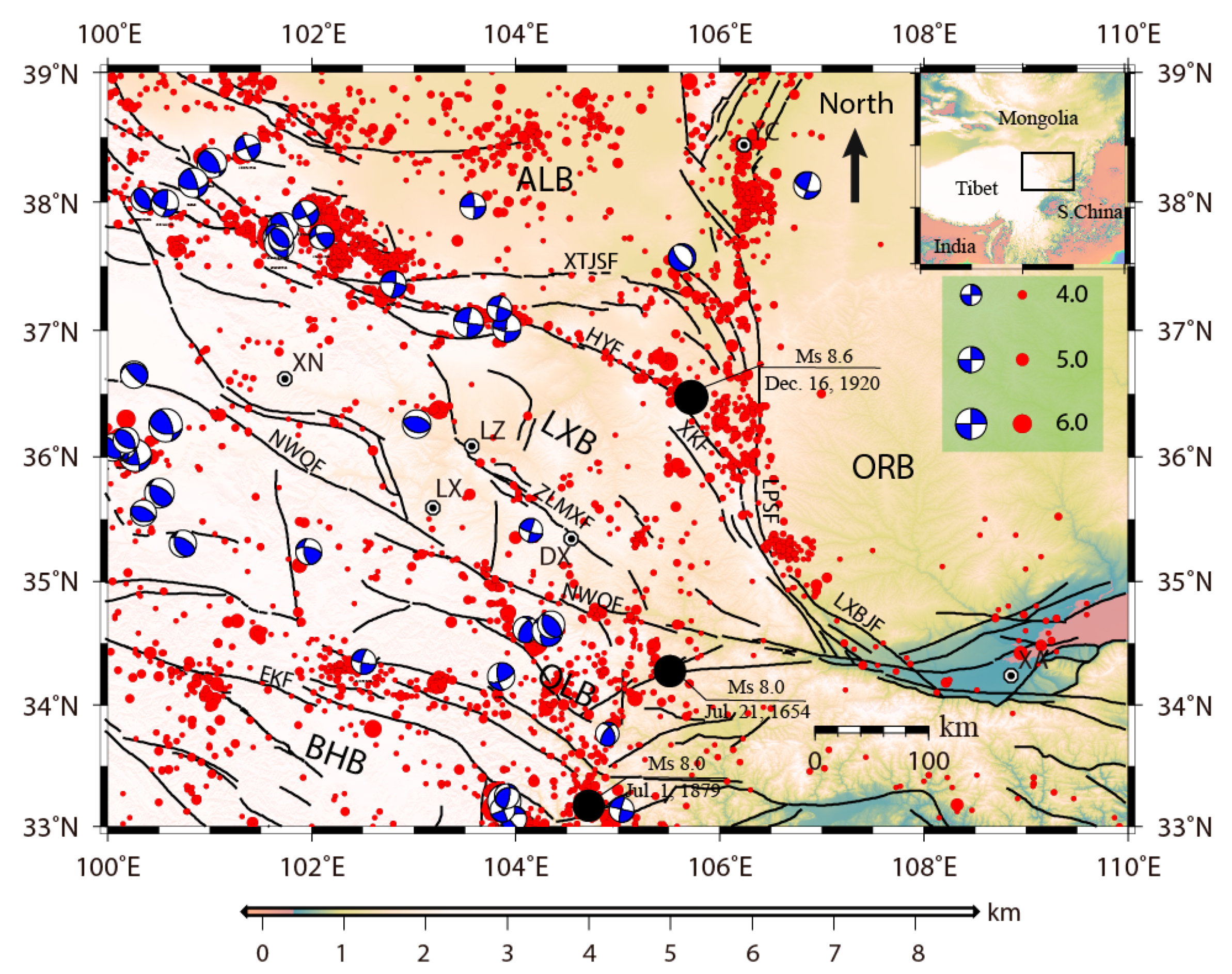
:1. Introduction
2. GPS Data and Data Processing
2.1. GPS Observations
2.2. GPS Data Processing
2.3. Time Series Analysis
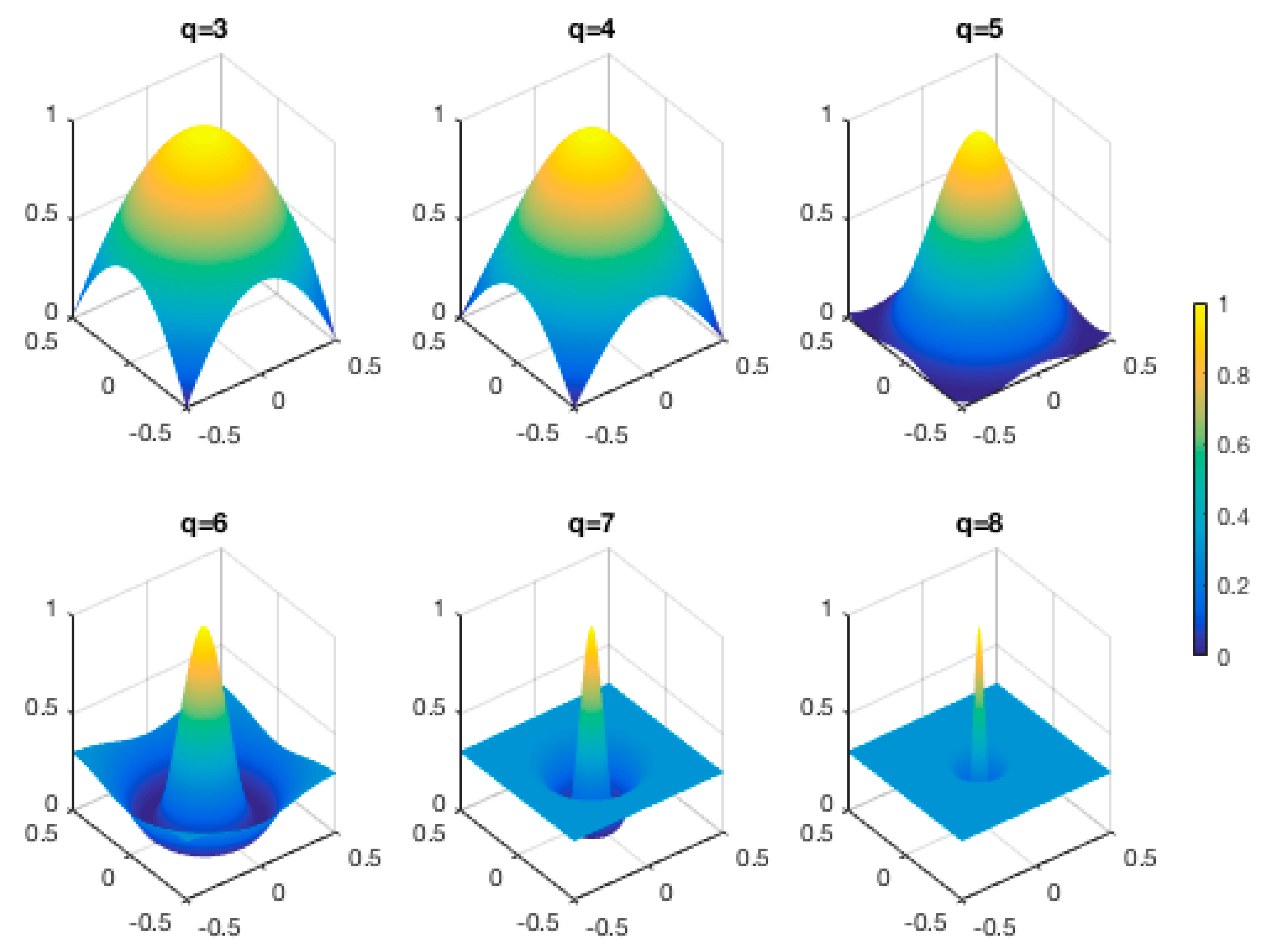
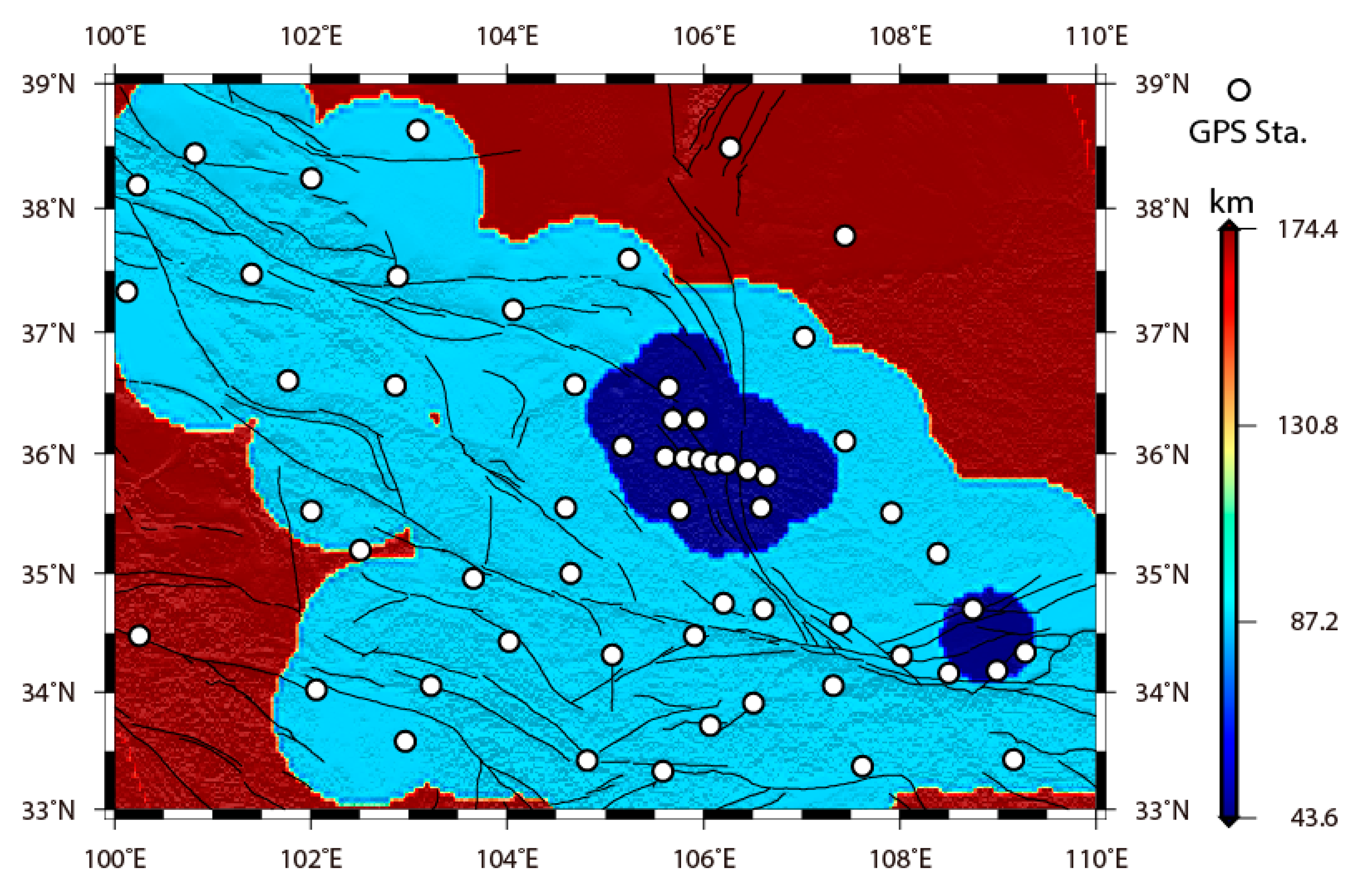
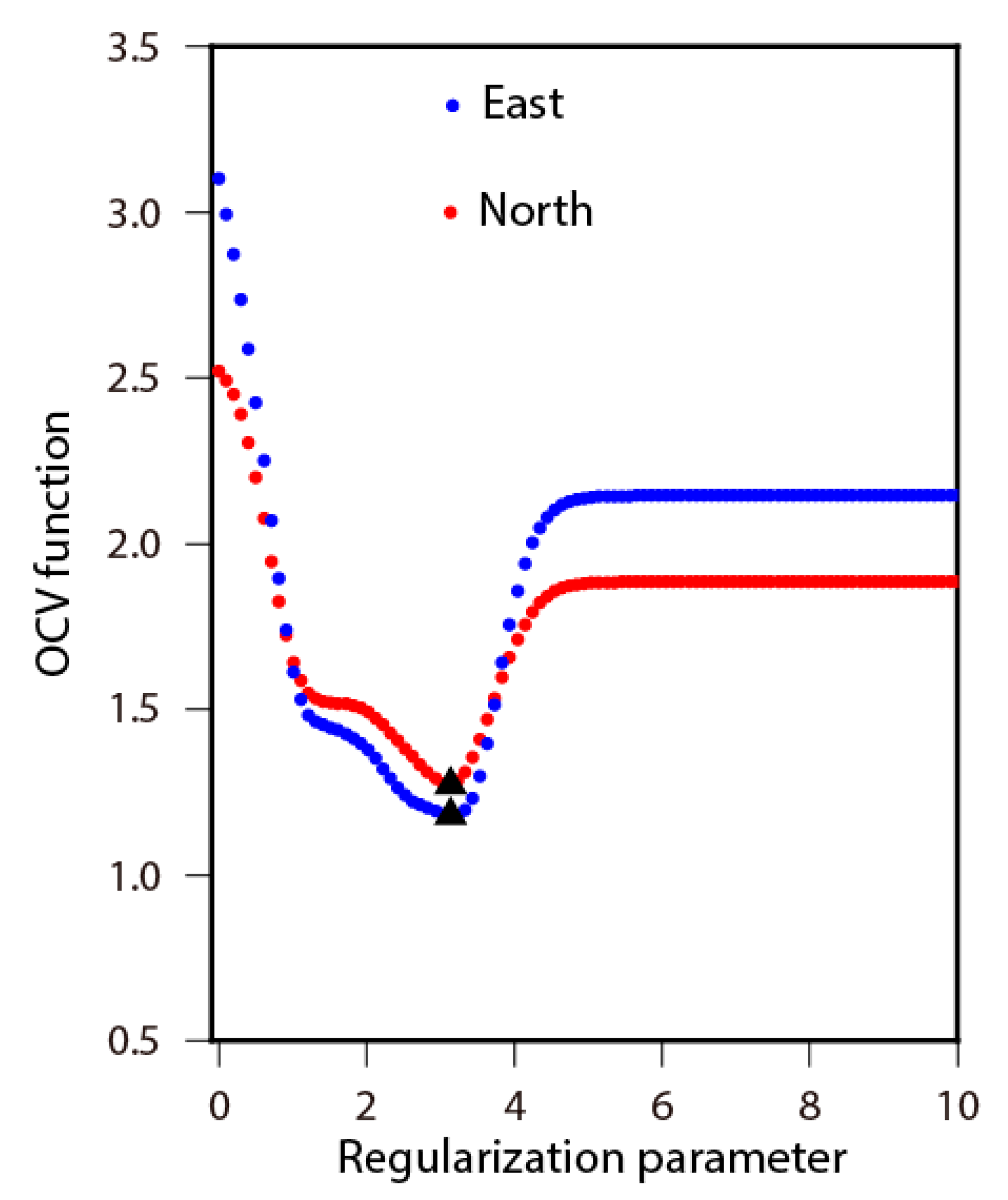
3. Strain Rate Calculation
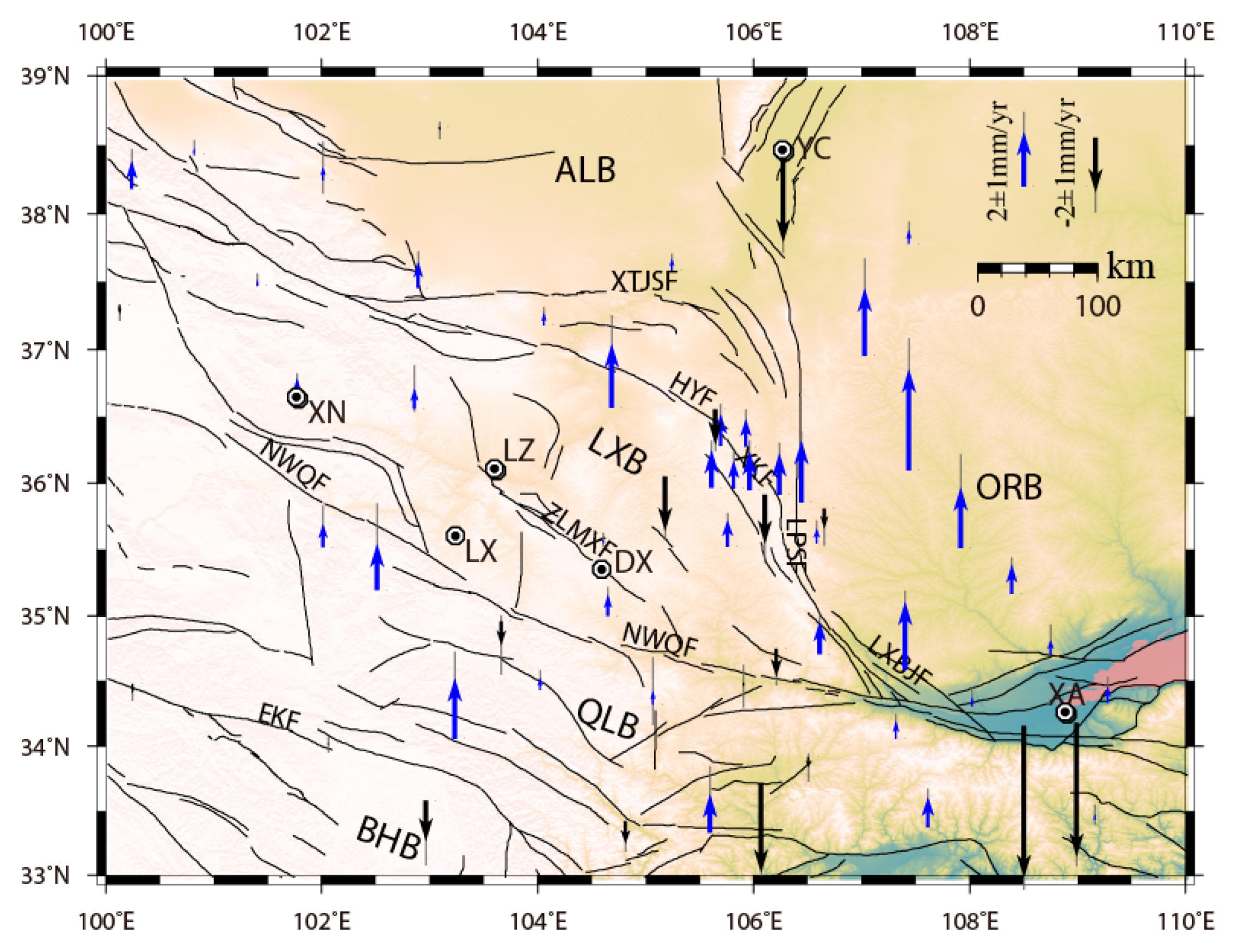
4. GPS-Derived Three-Dimensional Velocities
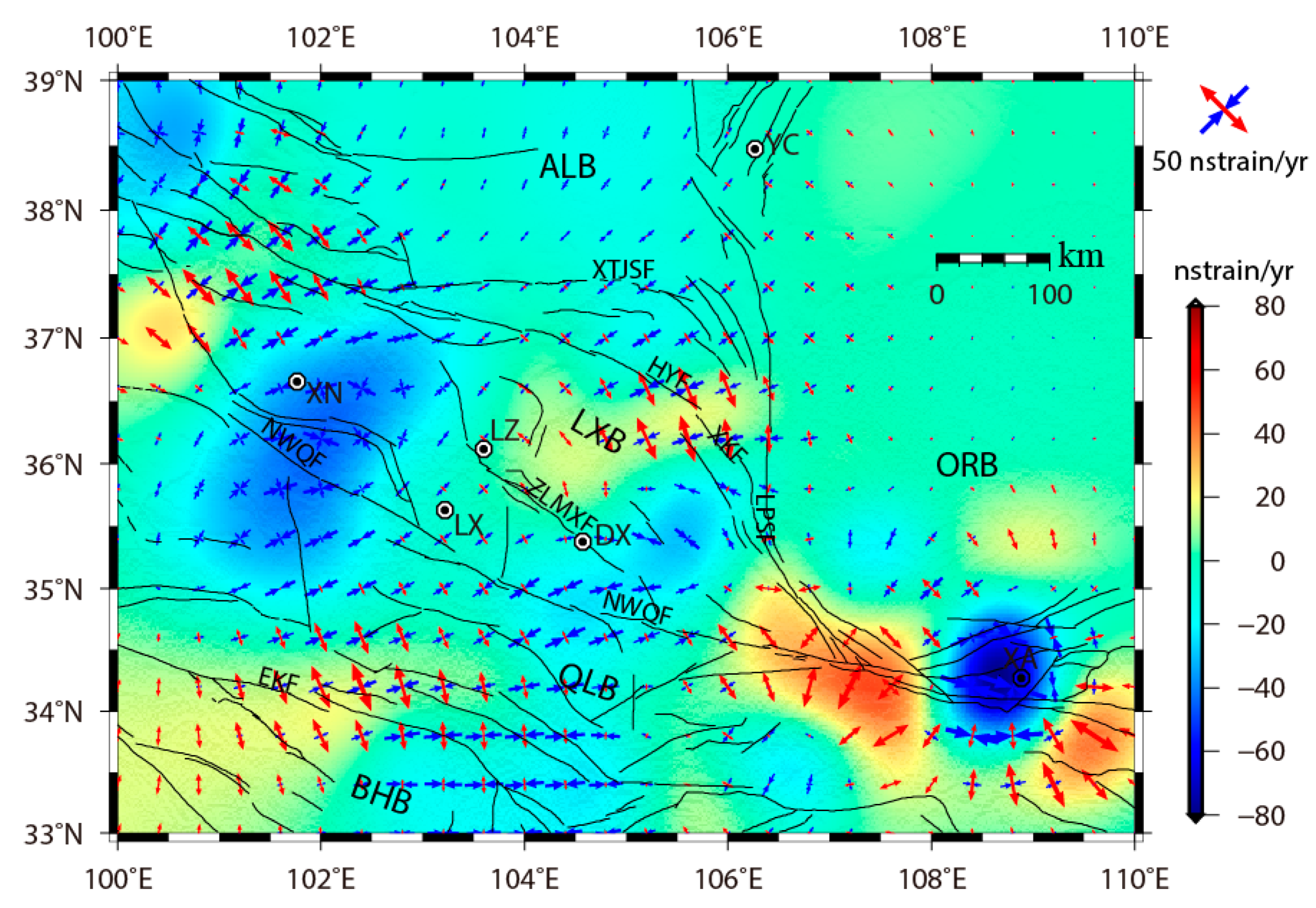
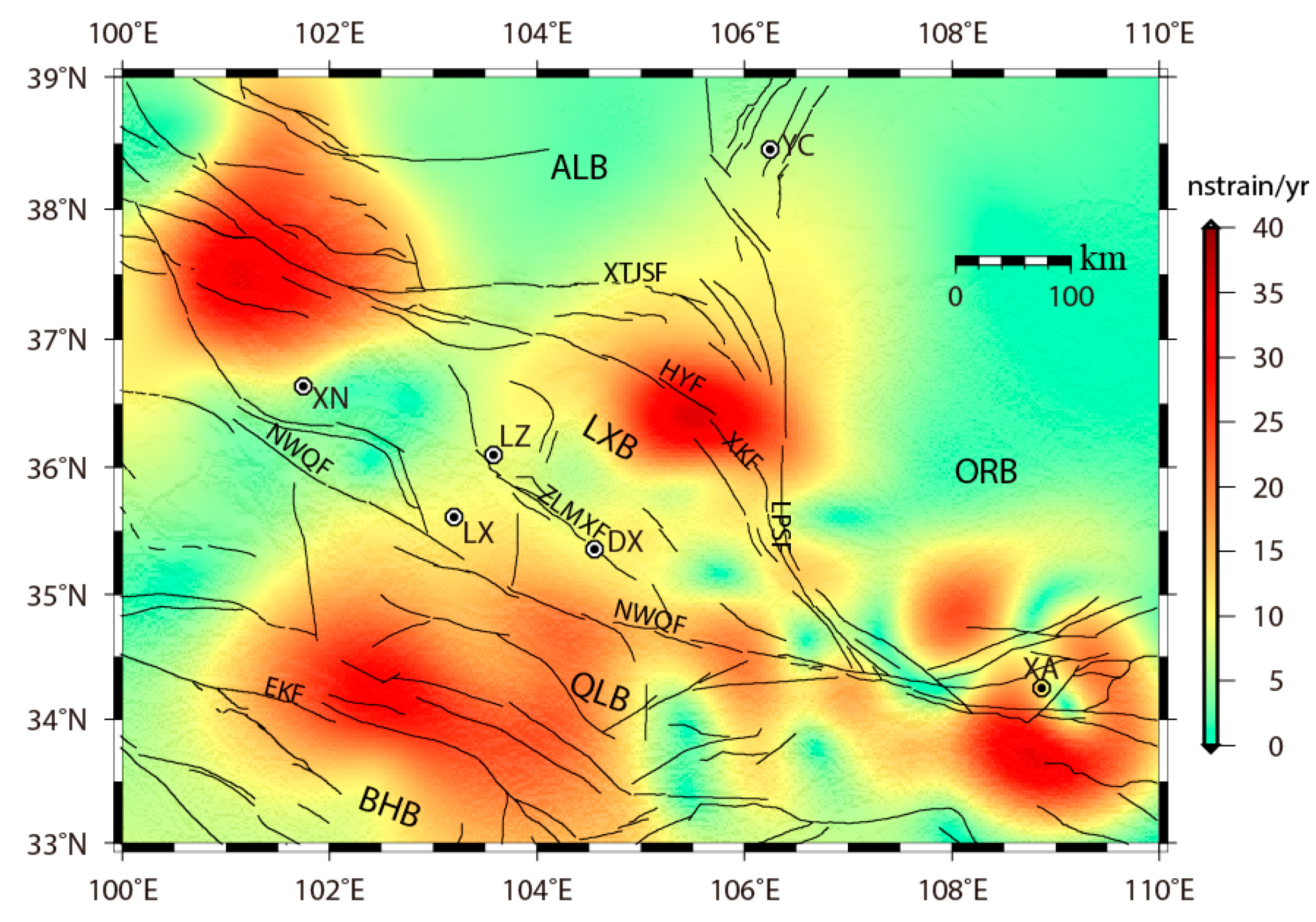
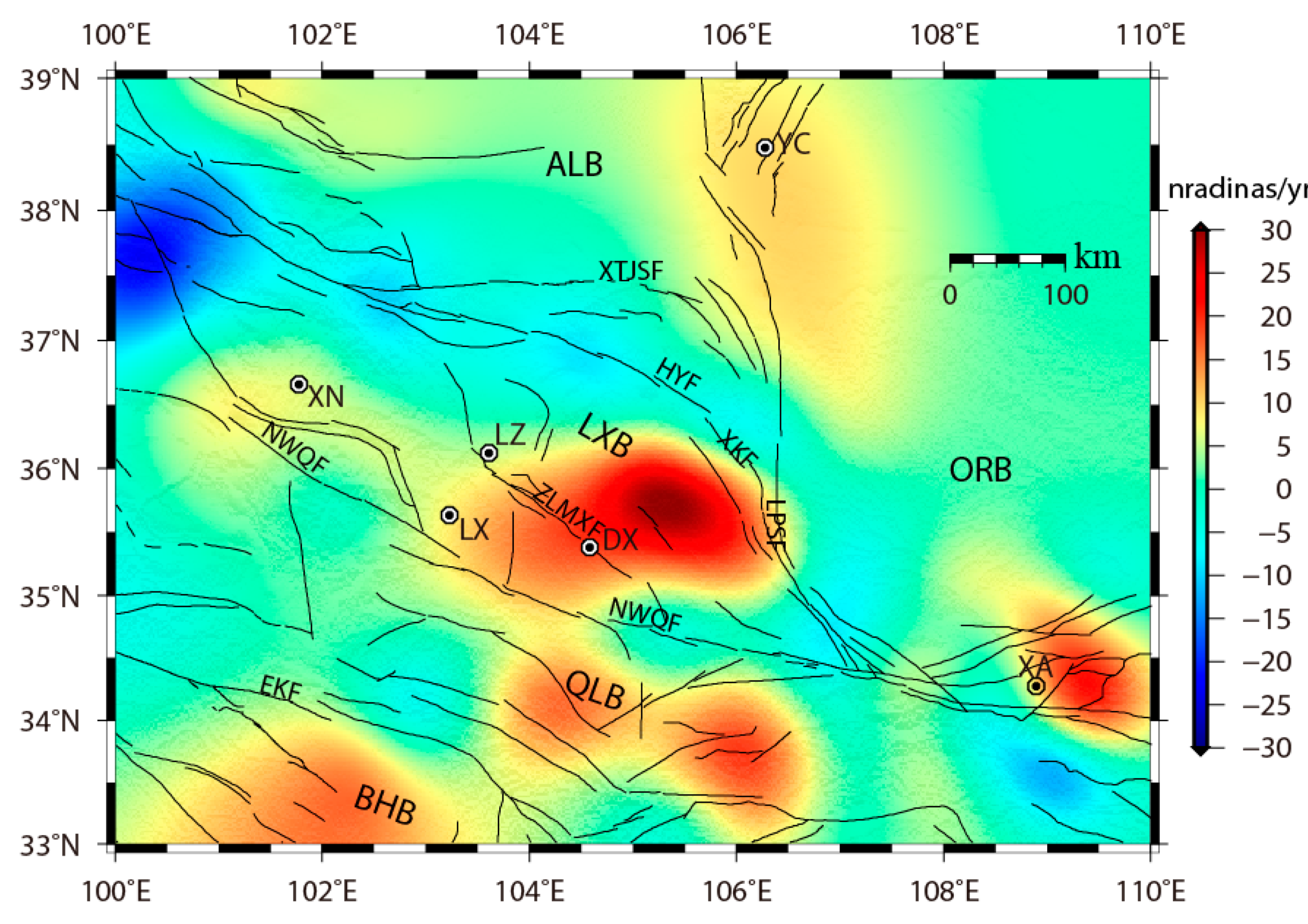
5. GPS-Derived Strain Rates
6. Discussion
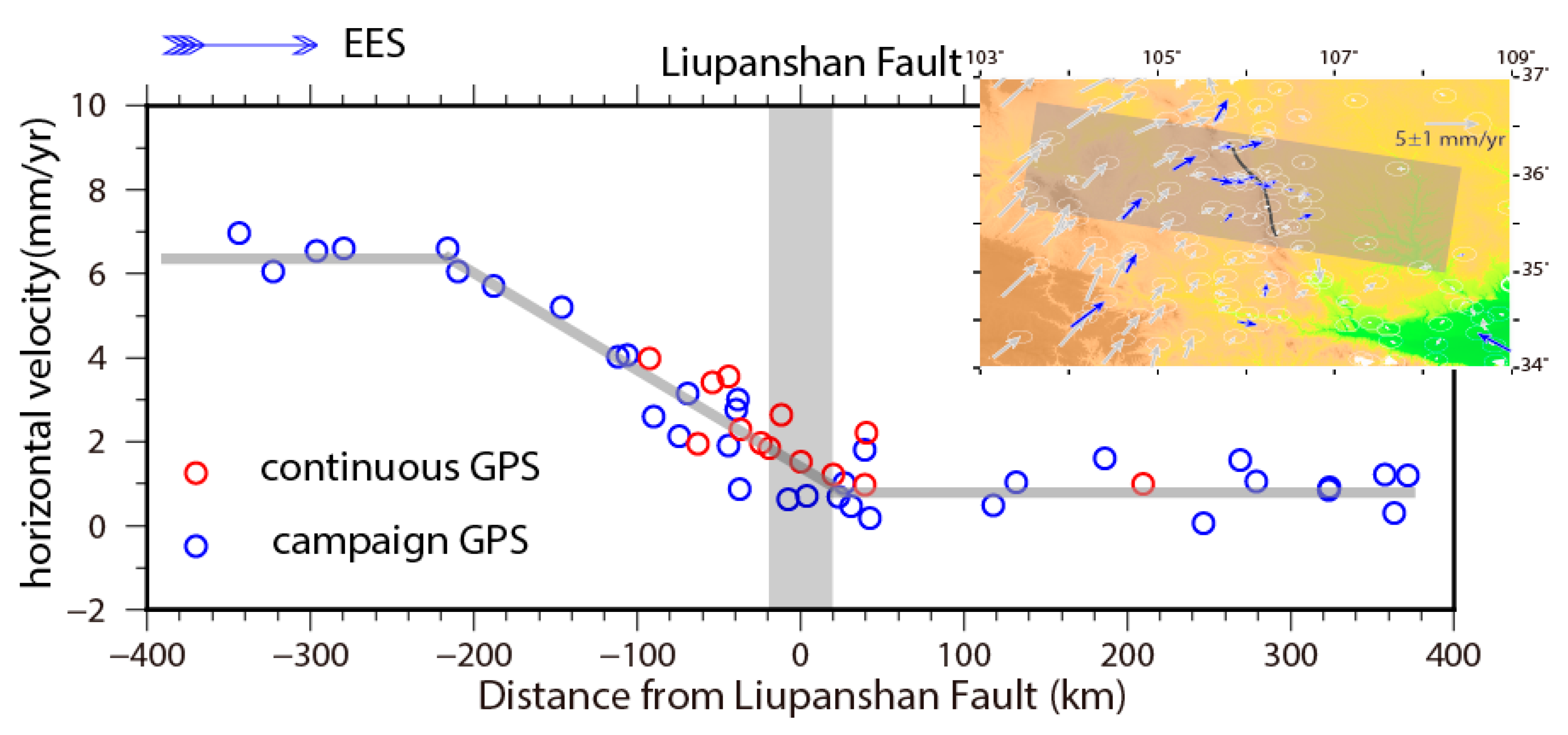
6.1. Strain Buildup at Various Spatial Scales
6.2. Strain Partitioning at Different Fault Activity Styles
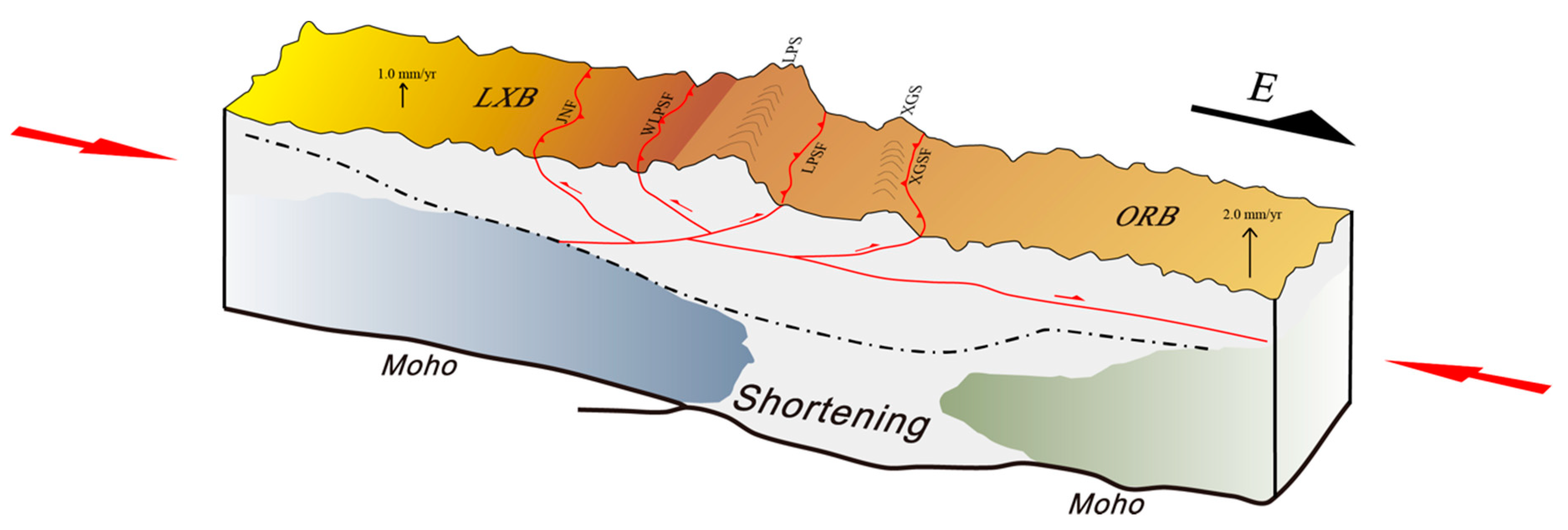
6.3. Decoupling between Uplift of the Ordos Block and Horizontal Extrusion on the Northeastern Tibetan Plateau
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tapponnier, P.; Xu, Z.; Francoise, R.; Bertrand, M.; Nicolas, A.; Gérard, W.; Yang, J.S. Oblique Stepwise Rise and Growth of the Tibet Plateau. Science 2001, 294, 1671–1677. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Shen, Z.; Wang, M.; Gan, W.; Bürgmann, R.; Molnar, P.; Wang, Q.; Niu, Z.; Sun, J.; Wu, J.; et al. Continuous deformation of the Tibetan Plateau from global positioning system data. Geology 2004, 32, 809–812. [Google Scholar] [CrossRef]
- Ding, G.; Chen, J.; Tian, Q.; Shen, X.; Xing, C.; Wei, K. Active faults and magnitudes of left-lateral displacement along the northern margin of the Tibetan Plateau. Tectonophysics 2004, 380, 243–260. [Google Scholar] [CrossRef]
- Dayem, K.E.; Molnar, P.; Clark, M.K.; Houseman, G.A. Far-field lithospheric deformation in Tibet during continental collision. Tectonics 2009, 28. [Google Scholar] [CrossRef] [Green Version]
- Lease, R.O.; Burbank, D.W.; Zhang, H.; Liu, J.; Yuan, D. Cenozoic shortening budget for the northeastern edge of the Tibetan Plateau: Is lower crustal flow necessary? Tectonics 2012, 31. [Google Scholar] [CrossRef] [Green Version]
- Yuan, D.; Ge, W.; Chen, Z.; Li, C.; Wang, Z.; Zhang, H.; Zhang, P.; Zheng, D.; Zheng, W.; Craddock, W.H.; et al. The growth of northeastern Tibet and its relevance to large-scale continental geodynamics: A review of recent studies. Tectonics 2013, 32, 1358–1370. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Kirby, E.; Zhang, P.; Zheng, D.; Zhang, G.; Zhang, H.; Zheng, W.; Cai, C. Tertiary basin evolution along the northeastern margin of the Tibetan Plateau: Evidence for basin formation during Oligocene transtension. Geol. Soc. Am. Bull. 2012, 125, 377–400. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Gao, R.; Li, S.; Xu, X.; Huang, X.; Wang, H.; Li, W.; Zhao, S.; Li, X. Lithospheric architecture and deformation of NE Tibet: New insights on the interplay of regional tectonic processes. Earth Planet. Sci. Lett. 2016, 449, 89–95. [Google Scholar] [CrossRef]
- Zheng, R.; Wu, T.; Zhang, W.; Xu, C.; Meng, Q.; Zhang, Z. Late Paleozoic subduction system in the northern margin of the Alxa block, Altaids: Geochronological and geochemical evidences from ophiolites. Gondwana Res. 2014, 25, 842–858. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Burchfiel, B.C.; Molnar, P.; Zhang, W.; Jiao, D.; Deng, Q.; Wang, Y.; Royden, L.; Song, F. Amount and style of Late Cenozoic Deformation in the Liupan Shan Area, Ningxia Autonomous Region, China. Tectonics 1991, 10, 1111–1129. [Google Scholar] [CrossRef]
- Li, C.; Zhang, P.; Yin, J.; Min, W. Late Quaternary left-lateral slip rate of the Haiyuan fault, northeastern margin of the Tibetan Plateau. Tectonics 2009, 28. [Google Scholar] [CrossRef] [Green Version]
- Bao, X.; Xu, M.; Wang, L.; Mi, N.; Yu, D.; Li, H. Lithospheric structure of the Ordos Block and its boundary areas inferred from Rayleigh wave dispersion. Tectonophysics 2011, 499, 132–141. [Google Scholar] [CrossRef]
- Darby, B.J.; Gehrels, G. Detrital zircon reference for the North China block. J. Asian Earth Sci. 2006, 26, 637–648. [Google Scholar] [CrossRef]
- Guo, X.; Gao, R.; Wang, H.; Li, W.; Keller, G.R.; Xu, X.; Li, H.; Encarnacion, J. Crustal architecture beneath the Tibet-Ordos transition zone, NE Tibet, and the implications for plateau expansion. Geophys. Res. Lett. 2015, 42, 10631–10639. [Google Scholar] [CrossRef]
- Burchfiel, B.C.; Zhang, P.; Wang, Y.; Zhang, W.; Song, F.; Deng, Q.; Molnar, P.; Royden, L. Geology of the Haiyuan Fault Zone, Ningxia-Hui Autonomous Region, China, and its relation to the evolution of the Northeastern Margin of the Tibetan Plateau. Tectonics 1991, 10, 1091–1110. [Google Scholar] [CrossRef]
- Zhang, P.; Burchfiel, B.C.; Molnar, P.; Zhang, W.; Jiao, D.; Deng, Q.; Wang, Y.; Royden, L.; Song, F. Late Cenozoic tectonic evolution of the Ningxia-Hui Autonomous Region, China. Geol. Soc. Am. Bull. 1990, 192, 1484–1498. [Google Scholar] [CrossRef]
- Li, X.; Zhang, P.; Zheng, W.; Feng, X.; Pierce, L.K.D.; Xu, H.; Li, X.; Ai, M.; Chen, G.; Dong, J.; et al. Kinematics of Late Quaternary slip along the Qishan-Mazhao fault: Implications for tectonic deformation on the southwestern Ordos, China. Tectonics 2018, 37, 2983–3000. [Google Scholar] [CrossRef]
- Li, Y.; Liu, M.; Wang, Q.; Cui, D. Present-day crustal deformation and strain transfer in northeastern Tibetan Plateau. Earth Planet. Sci. Lett. 2018, 487, 179–189. [Google Scholar] [CrossRef]
- Li, Y.; Shan, X.; Qu, C.; Wang, Z. Fault locking and slip rate deficit of the Haiyuan-Liupanshan fault zone in the northeastern margin of the Tibetan Plateau. J. Geodyn. 2016, 102, 47–57. [Google Scholar] [CrossRef]
- Li, Y.; Shan, X.; Qu, C.; Zhang, Y.; Song, X.; Jiang, Y.; Zhang, G.; Nocquet, J.M.; Gong, W.; Gan, W.; et al. Elastic block and strain modeling of GPS data around the Haiyuan-Liupanshan fault, northeastern Tibetan Plateau. J. Asian Earth Sci. 2017, 150, 87–97. [Google Scholar] [CrossRef]
- Liang, S.; Gan, W.; Shen, C.; Xiao, G.; Liu, J.; Chen, W.; Ding, X.; Zhou, D. Three-dimensional velocity field of present-day crustal motion of the Tibetan Plateau derived from GPS measurements. J. Geophys. Res. 2013, 118, 5722–5732. [Google Scholar] [CrossRef] [Green Version]
- Qu, W.; Lu, Z.; Zhang, Q.; Hao, M.; Wang, Q.; Qu, F.; Zhu, W. Present-day crustal deformation characteristics of the southeastern Tibetan Plateau and surrounding areas by using GPS analysis. J. Asian Earth Sci. 2018, 163, 22–31. [Google Scholar] [CrossRef]
- Zheng, W.; Liu, X.; Yu, J.; Yuan, D.; Zhang, P.; Ge, W.; Pang, J.; Liu, B. Geometry and late Pleistocene slip rates of the Liangdang-Jiangluo fault in the western Qinling mountains, NW China. Tectonophysics 2016, 687, 1–13. [Google Scholar] [CrossRef]
- Chen, J.; Yang, S.; Yan, W.; Wang, J.; Chen, Q.; Zhang, Y. Recent results of the Chinese CMONOC GNSS network. In Proceedings of the ION Pacific PNT 2017 Conference (ION PNT 2017), Honolulu, HI, USA, 1–4 May 2017; pp. 539–546. [Google Scholar]
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. GAMIT Reference Manual (Version 10.6); Massachusetts Institute of Technology: Cambridge, MA, USA, 2015; Available online: http://geoweb.mit.edu/gg/GAMIT_Ref.pdf (accessed on 16 June 2015).
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. GLOBK Reference Manual (Version 10.6); Massachusetts Institute of Technology: Cambridge, MA, USA, 2015; Available online: http://geoweb.mit.edu/gg/GLOBK_Ref.pdf (accessed on 16 June 2015).
- Chousianitis, K.; Ganas, A.; Evangelidis, C.P. Strain and rotation rate patterns of mainland Greece from continuous GPS data and comparison between seismic and geodetic moment release. J. Geophys. Res. 2015, 120, 3909–3931. [Google Scholar] [CrossRef] [Green Version]
- Chousianitis, K.; Ganas, A.; Gianniou, M. Kinematic interpretation of present-day crustal deformation in central Greece from continuous GPS measurements. J. Geodyn. 2013, 71, 1–13. [Google Scholar] [CrossRef]
- Petrie, E.J. Modelling Higher-Order Ionospheric Effects on Global GPS Solutions. Ph.D. Thesis, University of Newcastle upon Tyne, Newcastle, UK, December 2010. [Google Scholar]
- Thébault, E.; Finlay, C.C.; Alken, P.; Beggan, C.D.; Canet, E.; Chulliat, A.; Langlais, B.; Lesur, V.; Lowes, F.J.; Manoj, C.; et al. Evaluation of candidate geomagnetic field models for IGRF-12. Earth Planets Space 2015, 67, 112. [Google Scholar] [CrossRef]
- Thébault, E.; Finlay, C.C.; Beggan, C.D.; Alken, P.; Aubert, J.; Barrois, O.; Bertrand, F.; Bondar, T.; Boness, A.; Brocco, L.; et al. International Geomagnetic Reference Field: The 12th generation. Earth Planets Space 2015, 67, 79. [Google Scholar] [CrossRef]
- Beutler, G.; Moore, A.W.; Mueller, I.I. The international global navigation satellite systems service (IGS): Development and achievements. J. Geodesy 2009, 83, 297–307. [Google Scholar] [CrossRef]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Zus, F.; Dick, G.; Dousa, J.; Wickert, J. Systematic errors of mapping functions which are based on the VMF1 concept. GPS Solut. 2014, 19, 277–286. [Google Scholar] [CrossRef]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dynam. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions; IERS Technical Note No. 32; International Earth Rotation and Reference Systems Service: Frankfurt, Germany, 2004. [Google Scholar]
- Beutler, G.; Brockmann, E.; Gurtner, W.; Hugentobler, U.; Mervart, L.; Rothacher, M.; Verdun, A. Extended orbit modeling techniques at the CODE Processing Center of the International GPS Service for Geodynamics (IGS): Theory and initial results. Manuscripta Geodaetica 1994, 19, 367–386. [Google Scholar]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. 2016, 121, 6109–6131. [Google Scholar] [CrossRef] [Green Version]
- Langbein, J. Noise in two-color electronic distance meter measurements revisited. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Nikolaidis, R. Observation of Geodetic and Seismic Deformation with the Global Positioning System. Ph.D. Thesis, University of California, San Diego, CA, USA, January 2002. [Google Scholar]
- Su, X.; Meng, G.; Sun, H.; Wu, W. Positioning Performance of BDS Observation of the Crustal Movement Observation Network of China and Its Potential Application on Crustal Deformation. Sensors 2018, 18, 3353. [Google Scholar] [CrossRef] [PubMed]
- Williams, S.D.P. Error analysis of continuous GPS position time series. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Bos, M.S.; Fernandes, R.M.S.; Williams, S.D.P.; Bastos, L. Fast Error Analysis of Continuous GNSS Observations with Missing Data. J. Geodesy 2013, 87, 351–360. [Google Scholar] [CrossRef]
- Tape, C.; Musé, P.; Simons, M.; Dong, D.; Webb, F. Multiscale estimation of GPS velocity fields. Geophys. Int. 2009, 179, 945–971. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.; Su, X.; Meng, G.; Li, C. Crustal deformation prior to the 2017 Jiuzhaigou, Northeastern Tibetan Plateau(China), Ms 7.0 earthquake derived from GPS observations. Remote Sens. 2018, 10, 2028. [Google Scholar] [CrossRef]
- Allmendinger, R.W.; Reilinger, R.; Loveless, J. Strain and rotation rate from GPS in Tibet, Anatolia, and the Altiplano. Tectonics 2007, 26. [Google Scholar] [CrossRef] [Green Version]
- Ye, M.; Meng, G.; Su, X. Locking characteristics and slip deficits of the main faults in the Northeast margin of Tibetan Plateau. Earthquake 2018, 38, 1–12. [Google Scholar]
- Wu, Y.; Jiang, Z.; Zhao, J.; Liu, X.; Wei, W.; Liu, Q.; Zou, Z.; Zhang, L. Crustal deformation before the 2008 Wenchuan Ms 8.0 earthquake studied using GPS data. J. Geodyn. 2015, 85, 11–23. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, Z.; Liang, H.; Pang, Y.; Zhu, S.; Chang, L.; Chen, C.; Li, J. Deformation Response of Seismogenic Faults to the Wenchuan MS 8.0 Earthquake: A Case Study for the Southern Segment of the Longmenshan Fault Zone. Remote Sens. 2018, 10, 894. [Google Scholar] [CrossRef]
- Zhou, D.; Can, W.; Ren, J. Inversion of slip rates of the Zhuanglanghe Faults and the northern marginal fault of Maxianshan based on GPS measurements. Dizhen Dizhi (Seismol. Geol.) 2005, 27, 706–714. [Google Scholar]
- Sun, Z.; Yang, Z.; Yang, T.; Lin, A. Early Cretaceous Paleomagnetic Results From The Haiyuan Area And Their Tectonic Implications. Chin. J. Geophys. 2001, 44, 675–683. [Google Scholar] [CrossRef]
- Du, F.; Wen, X.; Feng, J.; Liang, M.; Long, F.; Wu, J. Seismo-tectonics and seismic potential of the Liupanshan fault zone (LPSFZ), China. Chin. J. Geophys. 2018, 41, 545–559. [Google Scholar] [CrossRef]
- Zheng, W.; Zhang, P.; He, W.; Yuan, D.; Shao, Y.; Zheng, D.; Ge, W.; Min, W. Transformation of displacement between strike-slip and crustal shortening in the northern margin of the Tibetan Plateau: Evidence from decadal GPS measurements and late Quaternary slip rates on faults. Tectonophysics 2013, 584, 267–280. [Google Scholar] [CrossRef]
- Gao, R.; Wang, H.; Yin, A.; Dong, S.; Kuang, Z.; Zuza, A.V.; Li, W.; Xiong, X. Tectonic development of the northeastern Tibetan Plateau as constrained by high-resolution deep seismic-reflection data. Lithosphere 2013, 5, 555–574. [Google Scholar] [CrossRef]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, X.; Yao, L.; Wu, W.; Meng, G.; Su, L.; Xiong, R.; Hong, S. Crustal Deformation on the Northeastern Margin of the Tibetan Plateau from Continuous GPS Observations. Remote Sens. 2019, 11, 34. https://doi.org/10.3390/rs11010034
Su X, Yao L, Wu W, Meng G, Su L, Xiong R, Hong S. Crustal Deformation on the Northeastern Margin of the Tibetan Plateau from Continuous GPS Observations. Remote Sensing. 2019; 11(1):34. https://doi.org/10.3390/rs11010034
Chicago/Turabian StyleSu, Xiaoning, Lianbi Yao, Weiwei Wu, Guojie Meng, Lina Su, Renwei Xiong, and Shunying Hong. 2019. "Crustal Deformation on the Northeastern Margin of the Tibetan Plateau from Continuous GPS Observations" Remote Sensing 11, no. 1: 34. https://doi.org/10.3390/rs11010034
APA StyleSu, X., Yao, L., Wu, W., Meng, G., Su, L., Xiong, R., & Hong, S. (2019). Crustal Deformation on the Northeastern Margin of the Tibetan Plateau from Continuous GPS Observations. Remote Sensing, 11(1), 34. https://doi.org/10.3390/rs11010034





