Variational Assimilation of Radio Occultation Observations into Numerical Weather Prediction Models: Equations, Strategies, and Algorithms
Abstract
:1. Introduction
2. Basic Equations
2.1. Ray Equations
2.2. Bending Angle
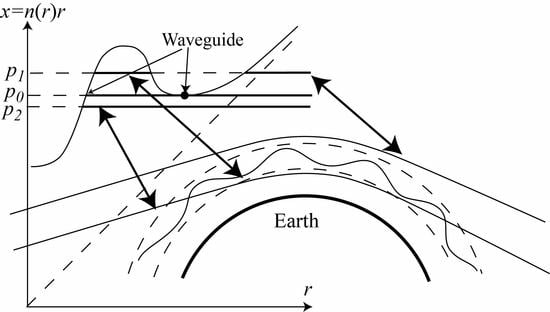
2.3. Influence of Waveguides
3. Observation Operators
3.1. 3-D Assimilation of Bending Angles
3.1.1. The Physical Model of RO Observations
3.1.2. Model of the 3-D Refractivity Field and Its Derivatives
3.1.3. Variations of Refractivity
3.1.4. Variations of Ray Geometry
3.1.5. Variations of Refraction Angle
3.1.6. Error Covariances
3.2. 1-D Assimilation of Bending Angles
3.2.1. Operators Based on the Abel Integral
3.2.2. 1-D Ray-Tracing Operators
3.3. Assimilation of Refractivity
3.3.1. 1-D Assimilation of Refractivity
3.3.2. Refractivity-Mapping Operators
4. Numerical Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| RO | Radio Occultation |
| NWP | Numerical Weather Prediction |
| GO | Geometrical Optics |
| 1-D | One-dimensional |
| 2-D | Two-dimensional |
| 3-D | Three-dimensional |
| NCEP | National Centers for Environmental Prediction |
| METOP | Meteorological Operational satellite |
| COSMIC | Constellation Observing System for Meteorology, Ionosphere, and Climate |
| GFS | Global Forecast System at NCEP |
References
- Gorbunov, M.E.; Sokolovskiy, S.V. Remote Sensing of Refractivity from Space for Global Observations of Atmospheric Parameters; Report 119; Max-Planck Institute for Meteorology: Hamburg, Germany, 1993. [Google Scholar]
- Ware, R.; Exner, M.; Feng, D.; Gorbunov, M.; Hardy, K.; Herman, B.; Kuo, Y.H.; Meehan, T.; Melbourne, W.; Rocken, C.; et al. GPS Sounding of the Atmosphere from Low Earth Orbit: Preliminary Results. Bull. Am. Meteorol. Soc. 1996, 77, 19–40. [Google Scholar] [CrossRef] [Green Version]
- Rocken, C.; Anthes, R.; Exner, M.; Hunt, D.; Sokolovsky, S.; Ware, R.; Gorbunov, M.; Schreiner, W.; Feng, D.; Herman, B.; et al. Analysis and validation of GPS/MET data in the neutral atmosphere. J. Geophys. Res. 1997, 102, 29849–29866. [Google Scholar] [CrossRef]
- Anthes, R.; Exner, M.; Rocken, C.; Ware, R. Results from the GPS/MET Experiment and Potential Applications to GEWEX. GEWEX News 1997, 7, 3–6. [Google Scholar]
- Rocken, C.; Kuo, Y.H.; Schreiner, W.S.; Hunt, D.; Sokolovskiy, S.; McCormick, C. COSMIC System Description. Terr. Atmos. Ocean. Sci. 2000, 11, 21–52. [Google Scholar] [CrossRef] [Green Version]
- Le Dimet, F.X.; Talagrand, O. Variational algorithms for analysis and assimilation of meteorological observation: Theoretical aspects. Tellus A 1986, 38, 97–110. [Google Scholar] [CrossRef]
- Eyre, J.R. Assimilation of Radio Occultation Measurements into a Numerical Weather Prediction System; Technical Memorandum No. 199; European Center for Medium-Range Weather Forecast: Reading, UK, 1994. [Google Scholar]
- Zou, X.; Kuo, Y.H.; Guo, Y.R. Assimilation of Atmospheric Radio Refractivity Using a Nonhydrostatic Adjoint Model. Mon. Weather Rev. 1995, 123, 2229–2249. [Google Scholar] [CrossRef] [Green Version]
- Zou, X.; Vandenberghe, F.; Wang, B.; Gorbunov, M.E.; Kuo, Y.H.; Sokolovskiy, S.; Chang, J.C.; Sela, J.G.; Anthes, R. A ray-tracing operator and its adjoint for the use of GPS/MET refraction angle measurements. J. Geophys. Res. 1999, 104, 22301–22318. [Google Scholar] [CrossRef] [Green Version]
- Zou, X.; Wang, B.; Liu, H.; Aathes, R.A.; Matsumura, T.; Zhu, Y.J. Use of GPS/MET refraction angles in three-dimensional variational analysis. Q. J. R. Meteorol. Soc. 2000, 126, 3013–3040. [Google Scholar] [CrossRef]
- Liu, H.; Zou, X.; Shao, H.; Anthes, R.A.; Chang, J.C.; Tseng, J.H.; Wang, B. Impact of 837 GPS/MET bending angle profiles on assimilation and forecasts for the period June 20–30, 1995. J. Geophys. Res. 2001, 106, 31771–31786. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Zou, X. Improvements to a GPS radio occultation ray-tracing model and their impacts on assimilation of bending angle. J. Geophys. Res. 2003, 108, 4548. [Google Scholar] [CrossRef]
- Kuo, Y.H.; Sokolovskiy, S.V.; Anthes, R.A.; Vandenberghe, F. Assimilation of GPS Radio Occultation Data for Numerical Weather Prediction. Terr. Atmos. Ocean. Sci. 2000, 11, 157–186. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.E.; Kornblueh, L. Principles of Variational Assimilation of GNSS Radio Occultation Data; Report No. 350; Max Planck Institute for Meteorology: Hamburg, Germany, 2003. [Google Scholar]
- Pingel, D.; Rhodin, A. Assimilation of Radio Occultation Data in the Global Meteorological Model GME of the German Weather Service. In New Horizons in Occultation Research; Steiner, A., Pirscher, B., Foelsche, U., Kirchengast, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 109–128. [Google Scholar] [CrossRef]
- Anlauf, H.; Pingel, D.; Rhodin, A. Assimilation of GPS radio occultation data at DWD. Atmos. Meas. Tech. 2011, 4, 1105–1113. [Google Scholar] [CrossRef] [Green Version]
- Kursinski, E.R.; Hajj, G.A. A comparison of water vapor derived from GPS occultations and global weather analyses. J. Geophys. Res. 2001, 106, 1113–1138. [Google Scholar] [CrossRef]
- Healy, S.B.; Jupp, A.M.; Marquardt, C. Forecast impact experiment with GPS radio occultation measurements. Geophys. Res. Lett. 2005, 32, L03804. [Google Scholar] [CrossRef] [Green Version]
- Von Engeln, A.; Nedoluha, G.; Kirchengast, G.; Bühler, S. One-dimensional variational (1-D Var) retrieval of temperature, water vapor, and a reference pressure from radio occultation measurements: A sensitivity analysis. J. Geophys. Res. 2003, 108, 4337. [Google Scholar] [CrossRef]
- Healy, S.B.; Thépaut, J.N. Assimilation experiments with CHAMP GPS radio occultation measurements. Q. J. R. Meteorol. Soc. 2006, 132, 605–623. [Google Scholar] [CrossRef]
- Cucurull, L.; Derber, J.C.; Treadon, R.; Purser, R.J. Assimilation of Global Positioning System Radio Occultation Observations Into NCEP’s Global Data Assimilation System. Mon. Weather Rev. 2007, 135, 3174–3193. [Google Scholar] [CrossRef] [Green Version]
- Cucurull, L.; Derber, J.C.; Treadon, R.; Purser, R.J. Preliminary Impact Studies Using Global Positioning System Radio Occultation Profiles at NCEP. Mon. Weather Rev. 2008, 136, 1865–1877. [Google Scholar] [CrossRef] [Green Version]
- Cucurull, L.; Derber, J.C.; Purser, R.J. A bending angle forward operator for global positioning system radio occultation measurements. J. Geophys. Res. 2013, 118, 14–28. [Google Scholar] [CrossRef]
- Burrows, C.P.; Healy, S.B.; Culverwell, I.D. Improving the bias characteristics of the ROPP refractivity and bending angle operators. Atmos. Meas. Tech. 2014, 7, 3445–3458. [Google Scholar] [CrossRef] [Green Version]
- Syndergaard, S.; Kursinski, E.R.; Herman, B.M.; Lane, E.M.; Flittner, D.E. A Refractive Index Mapping Operator for Assimilation of Occultation Data. Mon. Weather Rev. 2005, 133, 2650–2668. [Google Scholar] [CrossRef]
- Sokolovskiy, S.; Kuo, Y.H.; Wang, W. Assessing the Accuracy of a Linearized Observation Operator for Assimilation of Radio Occultation Data: Case Simulations with a High-Resolution Weather Model. Mon. Weather Rev. 2005, 133, 2200–2212. [Google Scholar] [CrossRef] [Green Version]
- Sokolovskiy, S.; Kuo, Y.H.; Wang, W. Evaluation of a Linear Phase Observation Operator with CHAMP Radio Occultation Data and High-Resolution Regional Analysis. Mon. Weather Rev. 2005, 133, 3053–3059. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Kuo, Y.H.; Wang, B.; Wu, W.S.; Sokolovskiy, S. Comparison of Local and Nonlocal Observation Operators for the Assimilation of GPS RO Data with the NCEP GSI System: An OSSE Study. Mon. Weather Rev. 2009, 137, 3575–3587. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Anderson, J.; Kuo, Y.H.; Snyder, C.; Caya, A. Evaluation of a Nonlocal Quasi-Phase Observation Operator in Assimilation of CHAMP Radio Occultation Refractivity with WRF. Mon. Weather Rev. 2008, 136, 242–256. [Google Scholar] [CrossRef]
- Aparicio, J. A framework for a 3D operator to assimilate radio occultations without assuming spherical symmetry. In Proceedings of the Joint OPAC-6 & IROWG-5, International Workshop on Occultations for Probing Atmosphere and Climate, Graz, Austria, 8–14 September 2016. [Google Scholar]
- Healy, S.B.; Eyre, J.R.; Hamrud, M.; Thépaut, J.N. Assimilating GPS radio occultation measurements with two-dimensional bending angle observation operators. Q. J. R. Meteorol. Soc. 2007, 133, 1213–1227. [Google Scholar] [CrossRef]
- Tatarskii, V.I. The Effects of the Turbulent Atmosphere on Wave Propagation; Translated from the Russian; Israel Program for Scientific Translations: Jerusalem, Israel, 1971. [Google Scholar]
- Mishchenko, A.S.; Shatalov, V.E.; Sternin, B.Y. Lagrangian Manifolds and the Maslov Operator; Springer: Berlin, Germany; New York, NY, USA, 1990. [Google Scholar]
- Arnold, V.I. Mathematical Methods of Classical Mechanics; Springer: New York, NY, USA, 1978. [Google Scholar]
- Zou, X.; Liu, H.; Anthes, R.A. A Statistical Estimate of Errors in the Calculation of Radio-Occultation Bending Angles Caused by a 2D Approximation of Ray Tracing and the Assumption of Spherical Symmetry of the Atmosphere. J. Atmos. Ocean. Technol. 2002, 19, 51–64. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Sokolovskiy, S.V.; Bengtsson, L. Space Refractive Tomography of the Atmosphere: Modeling of Direct and Inverse Problems; Report No. 210; Max-Planck Institute for Meteorology: Hamburg, Germany, 1996. [Google Scholar]
- Gorbunov, M.E.; Kornblueh, L. Analysis and validation of GPS/MET radio occultation data. J. Geophys. Res. 2001, 106, 17161–17169. [Google Scholar] [CrossRef]
- Healy, S.B. Radio occultation bending angle and impact parameter errors caused by horizontal refractive index gradients in the troposphere: A simulation study. J. Geophys. Res. 2001, 106, 11875–11890. [Google Scholar] [CrossRef]
- Sokolovskiy, S.V. Effect of super refraction on inversions of radio occultation signals in the lower troposphere. Radio Sci. 2003, 38, 1058. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.E. Canonical transform method for processing radio occultation data in the lower troposphere. Radio Sci. 2002, 37, 9-1–9-10. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Lauritsen, K.B. Canonical Transform Methods for Radio Occultation Data; Scientific Report 02-10; Danish Meteorological Institute: Copenhagen, Denmark, 2002; Available online: https://www.dmi.dk/fileadmin/Rapporter/SR/sr02-10.pdf (accessed on 3 December 2019).
- Jensen, A.S.; Benzon, H.H.; Lohmann, M.S. A New High Resolution Method for Processing Radio Occultation Data; Scientific Report 02-06; Danish Meteorological Institute: Copenhagen, Denmark, 2002. [Google Scholar]
- Jensen, A.S.; Lohmann, M.S.; Benzon, H.H.; Nielsen, A.S. Full spectrum inversion of radio occultation signals. Radio Sci. 2003, 38, 6-1–6-15. [Google Scholar] [CrossRef]
- Jensen, A.S.; Lohmann, M.S.; Nielsen, A.S.; Benzon, H.H. Geometrical optics phase matching of radio occultation signals. Radio Sci. 2004, 39, RS3009. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.E.; Lauritsen, K.B. Analysis of wave fields by Fourier integral operators and its application for radio occultations. Radio Sci. 2004, 39, RS4010. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Lauritsen, K.B. Canonical Transform Methods for Radio Occultation Data. In Occultations for Probing Atmosphere and Climate; Kirchengast, G., Foelsche, U., Steiner, A.K., Eds.; Institute for Geophysics, Astrophysics, and Meteorology, University of Graz: Graz, Austria; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2004; pp. 61–68. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Benzon, H.H.; Jensen, A.S.; Lohmann, M.S.; Nielsen, A.S. Comparative analysis of radio occultation processing approaches based on Fourier integral operators. Radio Sci. 2004, 39, RS6004. [Google Scholar] [CrossRef] [Green Version]
- Vorob’ev, V.V.; Krasil’nikova, T.G. Estimation of the Accuracy of the Atmospheric Refractive Index Recovery from Doppler Shift Measurements at Frequencies Used in the NAVSTAR System. Izv. Atm. Ocean. Phys. 1994, 29, 602–609. [Google Scholar]
- Sokolovskiy, S.; Hunt, D. Statistical optimization approach for GPS/MET data inversions. In URSI GPS/MET Workshop; Allen Institute for AI: Seattle, WA, USA, 1996. [Google Scholar]
- Gorbunov, M.E.; Gurvich, A.S.; Bengtsson, L. Advanced Algorithms of Inversion of GPS/MET Satellite Data and their Application to Reconstruction of Temperature and Humidity; Report No. 211; Max-Planck Institute for Meteorology: Hamburg, Germany, 1996. [Google Scholar]
- Gorbunov, M.E. Ionospheric correction and statistical optimization of radio occultation data. Radio Sci. 2002, 37, 17-1–17-19. [Google Scholar] [CrossRef] [Green Version]
- Sokolovskiy, S.; Schreiner, W.; Rocken, C.; Hunt, D. Optimal Noise Filtering for the Ionospheric Correction of GPS Radio Occultation Signals. J. Atmos. Ocean. Technol. 2009, 26, 1398–1403. [Google Scholar] [CrossRef]
- Li, Y.; Kirchengast, G.; Scherllin-Pirscher, B.; Wu, S.; Schwärz, M.; Fritzer, J.; Zhang, S.; Carter, B.A.; Zhang, K. A new dynamic approach for statistical optimization of GNSS radio occultation bending angles for optimal climate monitoring utility. J. Geophys. Res. 2013, 118, 13022–13040. [Google Scholar] [CrossRef]
- Li, Y.; Kirchengast, G.; Scherllin-Pirscher, B.; Norman, R.; Yuan, Y.; Fritzer, J.; Schwärz, M.; Zhang, K. Dynamic statistical optimization of GNSS radio occultation bending angles: Advanced algorithm and performance analysis. Atmos. Meas. Tech. 2015, 8, 3447–3465. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Z.; Sokolovskiy, S.; Schreiner, W.; Hunt, D.; Lin, J.; Kuo, Y.H. Ionospheric correction of GPS radio occultation data in the troposphere. Atmos. Meas. Tech. 2016, 9, 335–346. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.E.; Gurvich, A.S. Microlab-1 experiment: Multipath effects in the lower troposphere. J. Geophys. Res. 1998, 103, 13819–13826. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Gurvich, A.S. Algorithms of inversion of Microlab-1 satellite data including effects of multipath propagation. Int. J. Remote Sens. 1998, 19, 2283–2300. [Google Scholar] [CrossRef]
- Syndergaard, S. Modeling the impact of the Earth’s oblateness on the retrieval of temperature and pressure profiles from limb sounding. J. Atmos. Sol. Terr. Phys. 1998, 60, 171–180. [Google Scholar] [CrossRef]
- Xu, X.; Li, Z.; Luo, J. Correction on effect of Earth’s oblateness in inversion of GPS occultation data. Geo-Spat. Inf. Sci. 2005, 8, 247–250. [Google Scholar] [CrossRef] [Green Version]
- Yeh, W.H.; Huang, C.Y.; Chiu, T.C.; Chen, M.Q.; Liu, J.Y.; Liou, Y.A. Ray Tracing Simulation in Nonspherically Symmetric Atmosphere for GPS Radio Occultation. Terr. Atmos. Ocean. Sci. 2014, 25, 801. [Google Scholar] [CrossRef] [Green Version]
- DKRZ. The ECHAM3 Atmospheric General Circulation Model; Techreport 6; Deutsches Klimarechenzentrum, Modellberatungsgruppe: Hamburg, Germany, 1993. [Google Scholar]
- Satoh, M. Atmospheric Circulation Dynamics and General Circulation Models; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Kuo, Y.H.; Wee, T.K.; Sokolovskiy, S.; Rocken, C.; Schreiner, W.; Hunt, D.; Anthes, R.A. Inversion and Error Estimation of GPS Radio Occultation Data. J. Meteorol. Soc. Jpn. 2004, 82, 507–531. [Google Scholar] [CrossRef] [Green Version]
- Lohmann, M.S. Application of dynamical error estimation for statistical optimization of radio occultation bending angles. Radio Sci. 2005, 40, RS3011. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.E.; Lauritsen, K.B.; Rhodin, A.; Tomassini, M.; Kornblueh, L. Radio holographic filtering, error estimation, and quality control of radio occultation data. J. Geophys. Res. 2006, 111, D10105. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Kuo, Y.H.; Sokolovskiy, S.; Zou, X.; Zeng, Z.; Hsiao, L.F.; Ruston, B.C. A quality control procedure based on bending angle measurement uncertainty for radio occultation data assimilation in the tropical lower troposphere. J. Atmos. Ocean. Technol. 2018, 35, 2117–2131. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Kirchengast, G. Uncertainty propagation through wave optics retrieval of bending angles from GPS radio occultation: Theory and simulation results. Radio Sci. 2015, 50, 1086–1096. [Google Scholar] [CrossRef] [Green Version]
- Schwarz, J.; Kirchengast, G.; Schwaerz, M. Integrating uncertainty propagation in GNSS radio occultation retrieval: From excess phase to atmospheric bending angle profiles. Atmos. Meas. Tech. 2018, 11, 2601–2631. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.E.; Kirchengast, G. Wave-optics uncertainty propagation and regression-based bias model in GNSS radio occultation bending angle retrievals. Atmos. Meas. Tech. 2018, 11, 111–125. [Google Scholar] [CrossRef] [Green Version]
- Schwarz, J.; Kirchengast, G.; Schwärz, M. Integrating uncertainty propagation in GNSS radio occultation retrieval: From bending angle to dry-air atmospheric profiles. Earth Space Sci. 2017, 4, 200–228. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, B.; Tyler, G.L. The two-dimensional resolution kernel associated with retrieval of ionospheric and atmospheric refractivity profiles by abelian inversion of radio occultation phase data. Radio Sci. 1998, 33, 129–142. [Google Scholar] [CrossRef]
- Gorbunov, M.E. Solution of the inverse problems of remote atmospheric refractometry on limb paths. Izv. Atmos. Ocean. Phys. 1990, 26, 86–91. [Google Scholar]
- Gurevich, G.S.; Khattatov, V.U. Retrieval of Atmospheric Gas Concentrations from Limb Sounding Data. Izv. Atm. Ocean. Phys. 1988, 24, 436–440. [Google Scholar]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gorbunov, M.; Stefanescu, R.; Irisov, V.; Zupanski, D. Variational Assimilation of Radio Occultation Observations into Numerical Weather Prediction Models: Equations, Strategies, and Algorithms. Remote Sens. 2019, 11, 2886. https://doi.org/10.3390/rs11242886
Gorbunov M, Stefanescu R, Irisov V, Zupanski D. Variational Assimilation of Radio Occultation Observations into Numerical Weather Prediction Models: Equations, Strategies, and Algorithms. Remote Sensing. 2019; 11(24):2886. https://doi.org/10.3390/rs11242886
Chicago/Turabian StyleGorbunov, Michael, Razvan Stefanescu, Vladimir Irisov, and Dusanka Zupanski. 2019. "Variational Assimilation of Radio Occultation Observations into Numerical Weather Prediction Models: Equations, Strategies, and Algorithms" Remote Sensing 11, no. 24: 2886. https://doi.org/10.3390/rs11242886