Next Article in Journal
Optimal Segmentation Scale Parameter, Feature Subset and Classification Algorithm for Geographic Object-Based Crop Recognition Using Multisource Satellite Imagery
Previous Article in Journal
Weakly Supervised Segmentation of SAR Imagery Using Superpixel and Hierarchically Adversarial CRF
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 11
Issue 5
10.3390/rs11050513
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Remote Sensing Based Method to Detect Soil Erosion in Forests

by
Hanqiu Xu
1,*,
Xiujuan Hu
1,
Huade Guan
2,
Bobo Zhang
1,
Meiya Wang
1,
Shanmu Chen
3 and
Minghua Chen
3
1
College of Environment and Resources, Institute of Remote Sensing Information Engineering, Key Laboratory of Spatial Data Mining & Information Sharing of Ministry of Education, Fujian Provincial Key Laboratory of Remote Sensing of Soil Erosion, Fuzhou University, Fuzhou 350116, China
2
National Centre for Groundwater Research and Training, College of Science and Engineering, Flinders University, Adelaide, SA 5001, Australia
3
Fujian Monitoring Station of Water and Soil Reservation, Fuzhou 350001, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2019, 11(5), 513; https://doi.org/10.3390/rs11050513
Submission received: 30 January 2019 / Revised: 23 February 2019 / Accepted: 26 February 2019 / Published: 2 March 2019
(This article belongs to the Section Forest Remote Sensing)
Browse Figures
Versions Notes

Abstract

:
Rainwater-induced soil erosion occurring in the forest is a special phenomenon of soil erosion in many red soil areas. Detection of such soil erosion is essential for developing land management to reduce soil loss in areas including southern China and other red soil regions of the world. Remotely sensed canopy cover is often used to determine the potential of soil erosion over a large spatial scale, which, however, becomes less useful in forest areas. This study proposes a new remote sensing method to detect soil erosion under forest canopy and presents a case study in a forest area in southern China. Five factors that are closely related to soil erosion in forest were used as discriminators to develop the model. These factors include fractional vegetation coverage, nitrogen reflectance index, yellow leaf index, bare soil index and slope. They quantitatively represent vegetation density, vegetation health status, soil exposure intensity and terrain steepness that are considered relevant to forest soil erosion. These five factors can all be derived from remote sensing imagery based on related thematic indices or algorithms. The five factors were integrated to create the soil erosion under forest model (SEUFM) through Principal Components Analysis (PCA) or a multiplication method. The case study in the forest area in Changting County of southern China with a Landsat 8 image shows that the first principal component-based SEUFM achieves an overall accuracy close to 90%, while the multiplication-based model reaches 81%. The detected locations of soil erosion in forest provide the target areas to be managed from further soil loss. The proposed method provides a tool to understand more about soil erosion in forested areas where soil erosion is usually not considered an issue. Therefore, the method is useful for soil conservation in forest.

Graphical Abstract

1. Introduction

Soil erosion is a serious problem common in many areas of the world. It causes severe land degradation and affects soil fertility, agriculture productivity, water quality and regional ecosystems and environments [1]. Among various types of soil erosion, rainwater-induced soil erosion under forest canopy is a special phenomenon of soil erosion [2,3]. Such soil erosion occurs in areas with moderate to high forest coverage, where soil erosion is often not considered an issue.
However, severe soil loss in forest areas is common in many red soil regions of southern China [2,3,4,5]. This issue has attracted considerable attention and has been an active research topic for the last decade. Liao et al. [6] investigated soil erosion in forests based on 9-year monitoring data of seven sub-catchments in Zhejiang Province, southern China and summarized the processes of soil erosion under forest canopy. Through both artificial rainfall simulation experiments and laboratory experiments, Xu [7] examined the soil-loss process of Masson pine forest and its dynamics in Fujian Province. Zhu et al. [4] investigated soil erosion occurring in the forest of the Taihu watershed in Jiangsu Province and attributed the cause of the erosion to low soil fertility. Lei [3] studied soil loss in forests in a granite region of Xingguo County, Jiangxi Province and provided suggestions to control soil erosion in the forest. He et al. [2] discussed the status and causes of soil erosion in Pinus massoniana woodlands in hilly red soil regions of southern China and found that the lack of vegetation mulch under trees and human disturbance were the main factors causing the erosion. Zhang et al. [5] assessed soil erosion from remote sensing data in rehabilitated high-density forests of Hetian, a typical red soil region in southern China and found that the eroded areas were primarily distributed in locations with elevations between 300 to 500 m.
To date, a wide range of methods has been developed to monitor and estimate soil loss at multiple scales. Among them, Revised/Universal Soil Loss Equation (R/USLE) [8,9] is most commonly used. Other models include Aerial Nonpoint Source Watershed Environment Response Simulation (ANSWERS) [10], Water Erosion Prediction Project (WEPP) [11], Soil and Water Assessment Tool (SWAT) model [12], Unit Stream Power-based Erosion Deposition (USPED) [13], European Soil Erosion Model (EUROSEM) [14], Limburg Soil Erosion Model (LISEM) [15,16] and Hillslope Erosion Model (HEM) [17]. These models are different in the number and type of input factors, complexity, processes considered and amount of data required [18]. Estimation of soil erosion using the models is still a challenge due largely to data availability [1].
Remote sensing techniques have been increasingly used to detect the areas at the risk of extensive soil erosion [5,8,9]. The remote sensing based methods provide a cost-effective way to investigate soil erosion whereas the terrains are not accessible or direct field methods are expensive [19,20]. Various remote sensing based methods have been developed and applied to detect features related to soil erosion. Satellite-based spectral indices, for example, Normalized Difference Vegetation Index (NDVI), Normalized Difference Soil Index (NDSI), Tasselled Cap Transformation (TCT), along with Linear Spectral Unmixing Analysis (LSMA) have been frequently employed to estimate soil erosion process [21,22], investigate soil exposure intensity [23], measure soil reflectance [24,25], evaluate soil erosion status [5,26] and assess soil properties and bare soil fractions [27]. In addition, object-oriented analysis has been used to aid image classification and gully erosion identification [28,29]. Recently, machine-learning approaches have been applied to reveal statistical relationships between gully erosion and its controlling factors [30] and to retrieve key factors for soil erosion risk detection [31].
As for the remote sensing data sources used in soil erosion detection, optical multispectral imagery is most frequently used. Nevertheless, Synthetic Aperture Radar (SAR) data can provide an auxiliary source and the fusion of microwave and optical data can help soil erosion monitoring [32,33]. Recently, data from Unmanned Aerial Vehicle (UAV) imagery have also been used for small-scale monitoring of soil erosion, which provided very-high spatial resolution images for the monitoring [34,35,36].
There are a number of factors that influence soil erosion and are therefore involved in model construction for soil erosion detection. Of them, rainfall is one of the frequently-considered factors as rainfall-induced soil erosion occurs commonly in various environments. Long-term rainfall data are useful to identify the period of strong soil erosion, when used as the rainfall erosivity factor (R-factor) of RUSLE for investigating rainfall erosivity variability [37]. Rainfall influences land surfaces by its duration, intensity and cumulative amount per event. A recent study in a clayey coastal hilly area in Italy showed that soil erosion was correlated more with cumulative rainfall than with peak rainfall intensity [38]. Rainfall can have interactions with land covers and therefore, the coupling of rainfall and vegetation helped a quick identification of the month that had the highest soil erosion risk [39].
Soil erodibility is also an important factor used in modelling soil erosion. It works as a key factor in the models such as RUSLE (K-factor) and Chinese Soil Loss Equation (CSLE) [40] and is useful for estimating soil erosion rate [41]. Work in Ecuadorian Andes indicated that soil erodibility was the most important factor in the dry season for agricultural areas [42]. A study carried out in Shaanxi province, one of the most serious soil erosion regions in China, showed that soil erodibility played the second most important role among the four factors (rainfall erosivity, slope steepness and slope length being the other three) [40].
Remote sensing derivable factors also play critical roles in soil erosion detection. Fractional vegetation coverage (FVC) is among the most frequently-used factors. It can even be used alone to effectively detect the surfaces prone to soil erosion [43]. Many studies employed FVC to estimate the cover-management factor (C-factor) of the RUSLE model [44,45,46,47]. FVC has been shown to explain 57% of the sediment yield variance in a soil erosion modelling [43] and is a useful indicator to assess sediment connectivity between adjacent catchments [48]. Slope is another remote sensing data derivable factor that has been commonly-used in soil erosion monitoring as many of deriving forces to soil erosion have been associated with slope [9,11,15,49,50]. Slope is an important basic input of many soil erosion models currently in operation in the world, such as those of [9,11,14,15,17]. The factor can be represented by slope steepness and slope length [9,11,17], while the latter is not as popular as the former. A recent study in the karst regions of southwestern China found that slope degree influenced soil loss more than slope length [51].
Although various models have been successfully applied for soil erosion detection around the world, there is no suitable model for all soil erosion applications. In particular, the application of the existing models to estimate soil erosion under forest canopy becomes even more challenging because the relevant surface features are hidden under the canopy [5]. To date, few studies have focused on this special soil-erosion phenomenon in forest. Therefore, this study aims to develop a method to quickly detect soil erosion spots occurring under forest canopy solely using remote sensing techniques. A model, referred to as the Soil Erosion Under Forest Model (SEUFM), is proposed and tested. The model incorporates remotely sensed erosion-related cause and/or effect variables, including fractional vegetation cover, tree health status, soil exposure degree and slope. It provides a relatively easy-to-use method to identify the areas in forest that are at risk of soil erosion. The model was applied in a subtropical forest in Changting County of Fujian Province in southern China.

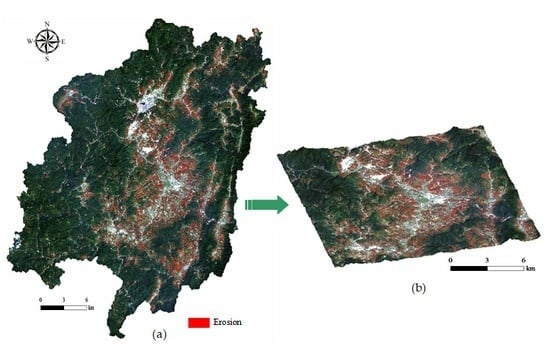
2. Study Area

Changting County is located in western Fujian Province of south-eastern China between 116°00′–116°40′E and 25°18′–26°02′N. The county has long been a severe red soil loss area in southern China. After the treatments to reduce soil erosion over 30 years, the soil loss has been dramatically reduced. The mountainous and hilly areas have been gradually covered with forests [23]. Nevertheless, soil loss is still occurring in many forested areas due to the exposure of topsoil under forest canopy (Figure 1).
Changting covers an area of 3099 km2. It has a subtropical monsoon climate with an annual average temperature of 18.3 °C and annual rainfall ranging from 1500 to 1700 mm (http://www.changting.gov.cn/xxgk/tjxx). Topographically, the county sinks at the central part around Hetian town, which is thus called the Hetian Basin in the region. The elevations of the county range from 210 to 1459 m above mean sea level. Changting has a forested area of 2487 km2 (http://www.changting.gov.cn/xxgk/tjxx). Based on the 2014 Landsat 8 image (Figure 2), most of the county’s area is covered by green forests, except for the area surrounding the Hetian basin, where greyish colour in the image suggests the exposure of surface soil.

3. Materials and Methods

3.1. Remote Sensing Data and Image Pre-processing

The data source used in this study is mainly from Landsat 8 satellite imagery and ASTER DEM. The satellite image is a Landsat 8 Operational Land Imager (OLI) image of Changting (path 121, Row 42), acquired on October 8, 2014. The Level 1T image was downloaded from the EarthExplorer of U.S. Geological Survey (https://earthexplorer.usgs.gov). The image was radiometrically corrected using the algorithms and coefficients from the official Landsat 8 Data Users Handbook with the addition of the atmospheric correction model of Chavez [52,53]. The main equations are given below:
Lλ = MLQcal + AL
where Lλ is the spectral radiance of band λ (W/(m2 sr μm)), ML is the radiance multiplicative scaling factor for band λ, AL is the radiance additive scaling factor for band λ and Qcal is the pixel value in DN of band λ.
ρλ = (MρQcal + Aρ)/cosθZ
where ρλ is the top of atmosphere (TOA) reflectance of band λ, Mρ is the reflectance multiplicative scaling factor for band λ, Aρ is the reflectance additive scaling factor for band λ and θ is the solar elevation angle. The parameters for the calculation with the equations can be found in the metadata of the image.

3.2. Selection of Predictor Factors

This study aims to provide a method solely based on relatively easier obtained remote sensing data in order to make the model more applicable. Accordingly, the factors were selected mainly from those that can be directly derived from remote sensing imagery. In addition, soil erosion under forest canopy is a special phenomenon of soil erosion that is related closely to plant status. Therefore, the selection of predictor factors focuses more on those that are closely related to vegetation.
Studies show that soil erodibility in forest can be closely related to the agents including fractional vegetation coverage, vegetation health status, soil exposure degree and slope steepness of terrain [23,54,55,56]. According to the Standards for Classification and Gradation of Soil Erosion [57], the soil erosion rate in planar surfaces is measured with two factors: FVC and slope. Accordingly, vegetation coverage and slope are the two important factors for the identification of soil loss. Nevertheless, these two factors are only applicable to common types of soil erosion. Information included in these two factors may not be sufficient to detect soil erosion under forest canopy. Therefore, in addition to the two factors, the health status of vegetation and soil exposure degree are also introduced to the model. The reasons to include these additional two factors are:
(1) Healthy trees reduce raindrop-induced soil erosion by forming a dense and multi-storey canopy with plenty of branches and leaves and, therefore, can greatly dissipate the kinetic energy of raindrops before reaching the ground surface. In addition, healthy trees often have more developed root zones, which reduce soil erosion potential. In contrast, poor healthy trees with sparse branches and leaves cannot effectively obstruct the strike of raindrops and hence are unable to reduce the rainfall erosivity and fails to protect the soil from the direct impact of raindrops and throughfall [58]. Yan et al. [59] and Zhu et al. [4] reported that the areas covered with unhealthy trees tended to be more likely to develop soil erosion. On the other hand, a surface with soil erosion does not retain good water and nutrient condition, which may lead to a poor tree health condition. Thus, tree health status can be a good indicator for soil erosion.
(2) Our field surveys found that soil erosion in forest usually took place in the areas with highly exposed topsoil due to the absence of sub-storey grass mulch covers (Figure 1). The work of Zhou et al. [60] has shown that the on- and near-ground vegetation layer in forest is the key to preventing soil erosion. He et al. [2] pointed out that soil erosion in forest mostly occurred in the areas that were devoid of understory grass covers and stated that a high degree of soil exposure under tree canopy was the most important cause for soil erosion in forest. Zhang et al. [5] reported that many soil erosion sites in Changting County had almost no vegetation under the forest canopy and exhibited various degrees of soil exposure. Sun [61] found that a combined vegetation cover of trees and grass reduced surface runoff by 25% and sediment by 90% in comparison with a forest without ground vegetation cover.
Accordingly, the major factors that influence soil erosion in forest are FVC, vegetation health status, soil exposure degree and slope. The vegetation health status can be determined by two factors, yellow leaf index and nitrogen index. The selected factors are essential to identify the spots in forest that are particularly prone to erosion and thus were considered in the SEUFM model development. All five factors, detailed in the next section, can be derived directly from remote sensing data. This provides a quick and easy way to detect soil erosion potential in forest.

3.3. Retrieval of the Selected Factors

3.3.1. FVC

Regional FVC is usually computed using remote sensing based models [62]. Two commonly used models are those proposed by Carlson and Ripley [63] and Gutman and Ignatov [64], expressed as:
Carlson and Ripley:
FVC = [(NDVI −NDVI0)/(NDVI∞ − NDVI0)]2
Gutman and Ignatov:
FVC = (NDVI − NDVI0)/(NDVI∞ − NDVI0)
where NDVI is the NDVI value of a pixel, NDVI0 is the NDVI value for bare soil selected from entirely bare soil and NDVI∞ corresponds to the NDVI value of a surface with an FVC of 100%, selected from extremely dense forest.
The difference between Equations (3) and (4) lies in whether the relationship between FVC and NDVI is quadratic or linear. The quadratic FVC (hereafter referred to as “FVCquadratic”) has a lower value than the linear FVC (hereafter referred to as “FVClinear”). As a result, FVCquadratic could avoid the overestimation of FVC in medium- to low-vegetation cover areas but may underestimate FVC in high-vegetation cover areas. The FVClinear performs inversely. Therefore, the selection of an appropriate FVC model is highly dependent on the status of vegetation coverage in the area to be studied [56,65].
In order to select an appropriate model, both FVCquadratic and FVClinear were tested with the Landsat 8 OLI image of Changting. The retrieved FVC results of the two models were then verified with the Google Earth (GE) high spatial resolution image of 20 December 2014, using the subpixel accuracy assessment method suggested by Wu and Murray [66]. For every sampled FVC pixel, the corresponding high-resolution GE image was digitized and the FVC was calculated. In this way, each sampled FVC pixel was related to the actual percentage of vegetation coverage of the GE high-resolution image within that pixel.

3.3.2. Nitrogen Reflectance Index (NRI)

Nitrogen is one of the most important nutritional elements for plant growth. It plays an important role in the process of the formation of cell, tissue and organs of plants. Soil sampling for nitrogen availability is well documented but requires considerable effort for sample collection and processing. The nitrogen index developed using remote sensing techniques provides a rapid assessment of plant nitrogen status on a frequent basis [67] and thus was adopted in this study to characterize the vegetation health status. The Nitrogen Reflectance Index (NRI) of Bausch and Duke [67] is expressed as:
NRI = NIR/Green
where Green and NIR are the reflectance of green and near-infrared bands.

3.3.3. Yellow Leaf Index (YLI)

Stress from soil moisture and nutrient can lead to yellow leaves. In the plant growing season, the occurrence of a great number of yellow leaves is an important indicator of unhealthy vegetation [68]. A yellow band of remote sensing image (e.g. WorldView 2 imagery) would be of value in detecting the yellow appearance of vegetation. However, Landsat 8 OLI imagery does not have a yellow band and, therefore, cannot directly observe the status of plant yellow leaves. Nevertheless, a yellow band can be simulated by the addition of green and red bands according to the principle of three primary colours [69] and is computed as:
Yellow = (Green + Red)/2
The validation of such simulated yellow band derived from the green and red bands of Landsat 8 imagery was performed by comparison with a WorldView 2 image. The WorldView-2 image has eight bands, including coastal, blue, green, yellow, red, red edge, near-infrared 1 and near-infrared 2 bands. Among them, the real yellow band can be used for the validation of the simulated yellow band based on Landsat 8.

3.3.4. Soil Exposure Index

Soil erosion in forest often occurs in the areas where topsoil is left bare and exposed to raindrop impact and surface runoff due to the absence of understory grass and shrub cover. Information of exposed soils under forest canopy is useful to detect the area prone to erosion. Remote sensing based models could effectively detect bare or exposed soil surface owing to its advances in enhancing soil features from background information [70]. In this study, the Normalized Difference Soil Index (NDSI) of Kearney et al. [71] was adopted to identify exposed soils in forest. The index is expressed as:
NDSI = (MIR1 − NIR)/(MIR1 + NIR)
where MIR1 is the reflectance of the mid-infrared band covering a wavelength between 1570 to 1650 nm.

3.3.5. Slope

The slope factor is represented by slope angle that can be derived from a digital elevation model (DEM) [55]. Current commercial remote sensing software usually has a tool to convert DEM to slope. A 30 m resolution ASTER DEM of Changting was downloaded from the USGS website (https://earthexplorer.usgs.gov) and then converted to a slope angle map.

3.4. Model Development

The soil erosion under forest model (SEUFM) was developed with the factors including FVC, NRI, YLI, NDSI and slope. Due to the difference in unit and data ranges, the five factors have to be normalized within [0, 1] before they can be integrated. The formula used for the normalization is as follows:
NIi = (Ii − Imin)/(Imax − Imin)
where NIi is the normalized value of pixel i of a factor, Ii is the value of pixel i of the factor, Imin and Imax are the minimum and maximum values of the factor, respectively.
The five normalized factors were integrated to form SEUFM using two methods, that is, principal components analysis (PCA) and the multiplication approach.
PCA is a statistical technique that converts a set of measurements into a set of values of uncorrelated principal components (PCs) using an orthogonal transformation. PCA automatically weighs the contribution of each variable into each principal component based on the variable’s loading [69]. The integration of the selected five factors in a model involves an evaluation of the contribution of each factor to soil erosion, which is very likely to be different. This suggests that a weight may have to be assigned to each factor. If the soil erosion can be associated with one or more PCs, PCA can be a good method to integrate the selected factors for SEUFM because PCA can automatically quantify the contribution of each factor into each PC according to factor loadings. This can avoid the trouble and uncertainty caused by the prescribed weights [69].
Figure 3 summarizes the main techniques and procedures for the development of SEUFM algorithms addressed above.

4. Results

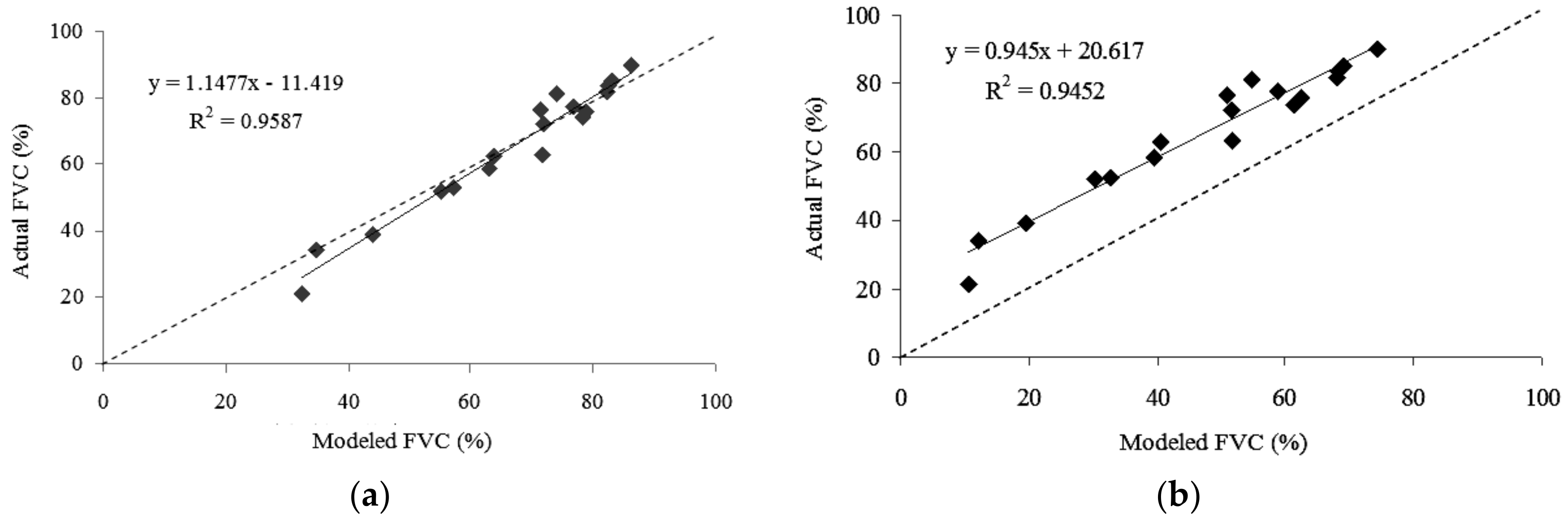
4.1. Validation of Two FVC Models and Yellow Leaf Index (YLI)

Figure 4 is the validation result of the two FVC models using the method described in 3.3.1. It shows that FVClinear has higher accuracy than FVCquadratic as its scatters spread closer to 1:1 line (dotted line in Figure 4) than those of FVCquadratic and its RMSE (4.63) is much lower than that of FVCquadratic (18.42). The scatters of FVCquadratic lie far above 1:1 line, indicating a significant underestimation of FVCquadratic. This result is consistent with Zhou et al [60] in which the FVClinear is reported out-performing the quadratic FVCquadratic for a pinon-juniper woodland. Thus, FVClinear is chosen to retrieve FVC for the study area.
The validity of the simulated yellow band using YLI (Equation (6)) was assisted with a WorldView 2 image of Changting, acquired on 13 December 2011. The green and red bands of the WorldView 2 image were mixed to produce a yellow band using Equation (6) and then compared with the real yellow band of the image. Table 1 shows that the simulated yellow band is highly correlated with the real yellow band (R2 = 0.984, p < 0.001) with a nearly identical mean value. This suggests that the yellow band generated using Equation (6) effectively simulates a real yellow band and can be served as a YLI.
The actual yellow band of the WorldView 2 image was further compared with the Equation (6)-derived yellow band of the Landsat 8 image. Due to the time difference (three years apart) and seasonal difference (October vs. December) between the two images, only invariant vegetation patches were chosen from both images for the comparison. The comparison yielded an R2 of 0.928 (Table 1 and Figure 5, p < 0.001), suggesting that the simulated Landsat 8 yellow band is reliable. The lower agreement than the comparison result of WorldView 2 image (0.984) is probably due to the difference both in season and spatial resolution between the two images though invariant vegetation patches were applied. The seasonal difference between the two images also contributes to a higher mean of the simulated Landsat 8 yellow band, compared with the mean of the real yellow band of the WorldView 2 image, as the Landsat 8 image was acquired in early October while the WorldView 2 image was in December.

4.2. Model Construction

4.2.1. PCA-based Model

The first principal component (PC1) measures the highest variation within the five-factor dataset and each succeeding component has the highest variance in the data which is not already accounted for by previous PCs. Table 2 is a PCA of the five factors, represented by an eigenvector of the covariance matrix in which the contribution of each factor to PCs is given in its loading. Of the five PCs, PC1 has the largest possible variance as its eigenvalue accounts for 80.12% of the variability in the whole data of the study area. PC2 describes the second largest amount of variance in the data that is not already described by PC1 and makes up 13.04% of data variance.
In PC1 and PC2, the loadings of NDSI and YLI have the same positive sign and thus can be classified in one category. FVC and NRI have the same negative sign for their loadings in both PC1 and PC2 and hence can be assigned to the other group. Based on our understanding, these two groups of factors happen to have contrasting relation with soil erosion. However, the loading of Slope has a negative sign in PC1 but a positive sign in PC2. This may reflect two different mechanisms of the slope condition for soil erosion—(1) a steeper slope reduces human activity and thus decreases the erosion potential and (2) a steeper slope enhances erosion due to water and landslide potential. Thus, it is likely that PC1 and/or PC2 can be used to quantify soil erosion.
The succeeding components from PC3 to PC5 are neglected as they account only for a very small amount of data variance and the sign of the loading of each factor is not interpretable in terms of their possible relationship with soil erosion.
Given that PC1 accounts for 80% variance of the five factors, the first SEUFM option (SEUFM1) is based on PC1:
SEUFM1 = PC1(FVC, NRI, YLI, NDSI, Slope)
The second SEUFM option (SEUFM1&2) is based on the sum of PC1 and PC2 in order to consider the positive sign of the slope factor. We did not use PC2 alone as it accounts only for 13% of variance within the whole data.
SEUFM1&2 = (PC1 + PC2) (FVC, NRI, YLI, NDSI, Slope)
To calculate the SEUFM1 and SEUFM1&2, the images of five factors were used as five bands to form a new image. The PCA was then performed on the new five-band image using statistic/remote sensing software. The calculated results were normalized to have a value ranging from 0 to 1. The greater the value, the more likely the occurrence of soil erosion under tree canopy.

4.4.2. Multiplication-based Model

The model was developed by the integration of the five factors through multiplication. As indicated by PCA, the sign of FVC and NRI is negative, whereas the sign of Slope is either negative or positive. Accordingly, the model can be developed in the following two forms:
SEUFMm-slope = (1 − FVC)·(1 − NRI)·(1 − Slope)·YLI·NDSI
SEUFMm+slope = (1 − FVC)·(1 − NRI)·Slope·YLI·NDSI
The calculated results of SEUFMm-slope and SEUFMm+slope also need to be normalized within [0, 1]. A greater value indicates a more likelihood of the occurrence of soil erosion in forest.

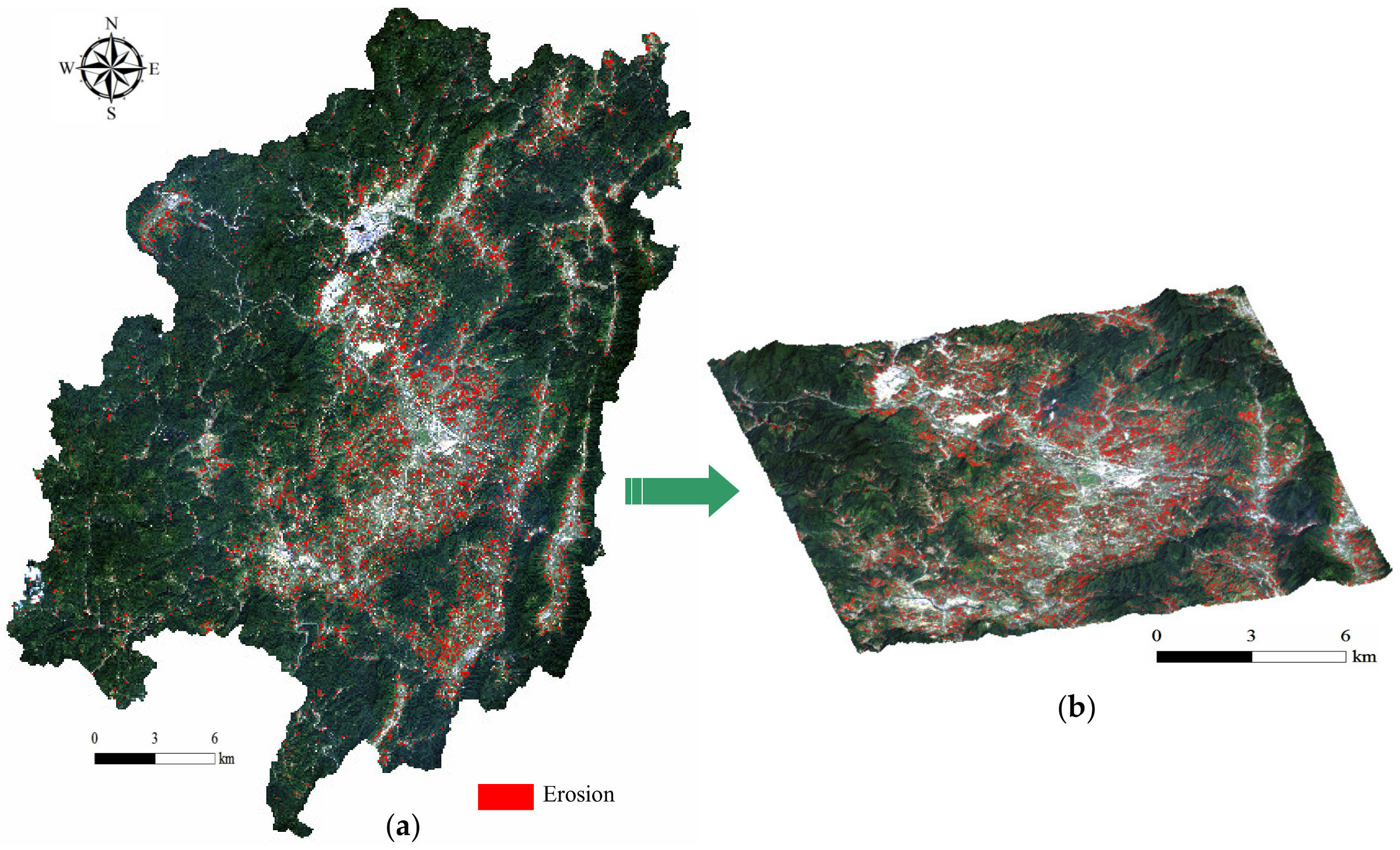
4.3. Detecting Soil Erosion Potential in Forest

Four thematic images corresponding to the factors of FVC, NRI, YLI and NDSI were then retrieved from the Landsat 8 image of Changting and shown in Figure 6. The croplands were masked out from the thematic images since this study focuses on forest areas. The four thematic factor images coupled with DEM-derived Slope factor image were then used as input data to calculate the SEUFMs using the Equations of (9) to (12).
Independent field investigations, led by the staff members from the Fujian Monitoring Station for Water and Soil Conservation, were carried out in Changting during the rainy seasons of 2014 and 2015 to validate the extracted results. The staff members of the station well know the locations where soil erosion in forest occurs based on the historical monitoring data of the station mentioned above and their local knowledge and experience. A total of 77 accessible sites in forest were hence chosen (Figure 2), which includes 57 sites of soil erosion and 20 sites of non-erosion. Statistics show that the differences in the five factors between the erosion and non-erosion sites are substantial (Table 3).
The validation results show that for the two PCA-based models, the highest accuracy was achieved when the threshold value was adjusted to ~1.045 times of the mean. While for the two multiplication-based models, the optimum threshold was roughly the mean ±10%, respectively (Table 4). Values greater or smaller than the thresholds all resulted in a decrease in accuracy.
Among the four SEUFM models, SEUFM1, the model based on PC1, achieves the highest accuracy close to 90% and SEUFMm-slope, the multiplication-based model, has the second highest accuracy of 81% (Table 5). Thus, SEUFM1 is chosen as the optimum model to identify soil erosion locations under forest in Changting. The result indicates a soil erosion area of 312.76 km2 in the forests of the county (Figure 7), which accounts for 12.58% forest in the county. The detected result (312.76 km2) is within the area (300~350 km2) estimated by the county’s Monitoring Station for Water and Soil Conservation. In addition, Zhang et al. [5] conducted a similar study to identify forest soil erosion in Changting but only concentrated their study area in Hetian town. Using a vegetation-restoration-degree (VRS) model, they found that the eroded forested area in Hetian was 67 km2 in 2009. This is comparable with our result of the same area (64.8 km2). A 2.2-km2 difference could be due to a 5-year time difference between the two studies.
Figure 7 clearly shows that the soil erosion in forests of Changting occurs mainly along the Hetian basin roughly in a north-south direction but is concentrated at the lower part of the hillside with little density of forest and therefore, where the protective effect of canopy is low (Figure 7b). The mapped erosion areas are consistent with our understanding of soil erosion development in relation to the characteristic of the pedospheric condition, vegetation cover and human activities in the study area.

5. Discussion

This study has revealed that the Hetian basin is the main area susceptible to forest soil erosion in Changting. The basin has long been the most severe soil loss areas in the county due to intensive disturbance by human activities [5,23]. In order to control soil erosion, a three-decade reforestation program has been carried out through restoration of vegetation in the previously deforested lands. Since the early 1980s, the local residents have been planting a great number of Pinus massoniana trees in the areas. However, the red soils developed from parent granitic rocks in the region are acidic and often low in nutrients. The iron oxide-rich soils inhibit the growth of shrub and grass [5]. Due to low soil fertility, a lack of shrub/grass sub-storey covers, as well as frequent human activities, the rehabilitated forests, particularly those developed in the hillslopes surrounding the Hetian basin (Figure 7b), are in poor health status and thus susceptible to soil erosion.
The study results show that the PC1-based model, SEUFM1, can detect soil erosion areas in forest with high accuracy. This suggests the effectiveness of the selected five factors in association with soil erosion. Figure 8 indicates the degree of separation of each factor between erosion and non-erosion sites of the 77 field validation locations.
Among the five factors, FVC, NRI, YLI and NDSI can be approximately separated between erosion and non-erosion sites within the range of the mean ±1 standard deviation. Table 3 indicates that compared with the non-erosion sites, the erosion sites have lower mean values in FVC and NRI by 19.0% and 24.8%, respectively and higher mean values in NDSI and YLN by 53.8% and 36.7%, respectively. These differences are tested significantly as their p-values are much less than the significance level of 1% (Table 3). However, the data ranges of Slope between erosion and non-erosion sites are overlapped. Table 3 shows that although the mean of Slope of the erosion sites is higher than that of the non-erosion sites by 6.31%, the very high p-value (0.821) suggests insignificance of the difference. This supports our previous discussion that the slope effect on soil loss in forest has two opposite mechanisms. Generally, high-angle slopes are conducive to high levels of erosion. However, this may not be always the case in forested areas where the slopes are covered with forests with various densities. Areas of low slope angles may suffer more erosion because lower slope inclinations are usually subject to more frequent human activities such as walking, weeding and firewood gathering and thus have no or poorly-developed sub-storey grass/shrub mulch. The study conducted by Zhang et al. [5] found that the soil erosion in forests in Hetian mainly occurred in areas with slope angles of 8° to 15° and became weaker when the slope was steeper than 15°.
The dual effects of the slope factor explain why the slope factor has a negative loading sign in PC1 but a positive loading sign in PC2. Initially, we considered excluding the slope factor for the SEUFM development due to its dual effects but our experiments showed that a four-factor model without Slope does not perform as well as the one with five factors. This suggests the importance of Slope for the SEUFM.
Two models that consider the erosion-enhancement effect of the slope factor are SEUFM1+2 and SEUFMm+slope. Neither of them performs as well as the ones without considering this erosion enhancement effect (Table 5). This suggests that the slope may play a role in reducing human activity more than in enhancing erosion in the studied forest areas.
In this study, the two multiplicative models, SEUFMm-slope and SEUFMm+slope, have lower accuracy than two PCA-based models, SEUFM1 and SEUFM1+2, correspondingly (Table 5). This is likely related to that the five factors are equally weighted in the models. The multiplicative method assumes that each factor reflects the erosion independently. Hence, they can be multiplied to obtain a lumped and enhanced association with the erosion. However, the correlation matrix (Table 6) indicates that the assumption of independence between the selected factors is not supported in the study area as the selected five factors are more or less related. Thus, there is a need to somehow weight the different information embedded in these erosion-associated but interdependent factors for erosion estimation. While, the PCA-based method provides such a weighing approach.
The threshold values listed in Table 4 and Table 5 for separating erosion and non-erosion sites in forest are around the mean values of SEUFM images (within ±10%). This suggests that the mean could be initially used as a threshold but is subject to a manual adjustment to achieve an optimum threshold. This method for selecting threshold is probably specific to the study area and may not be suitable for other areas. Nevertheless, the selected five factors for SEUFM are rooted in the concept of soil erosion conditions in forested areas. Therefore, the method is not area-dependent and can be used as a spatially-explicit tool to evaluate the soil erosion potential in forest.
SEUFM is the model especially designed for detecting soil erosion occurring in forested areas. Therefore, apart from the factors that are usually selected for soil erosion detection like slope and soil factors, SEUFM is enhanced with more vegetation-related factors such as yellow leaf index, nitrogen reflectance index, as well as FVC. This makes it different from other soil erosion related models that usually have only one vegetation-related factor, such as RUSLE, LISEM and WEPP. Zhang et al. [5] also detected soil erosion in forest in Changting. They developed a VRD model in which two vegetation-related factors (FVC and leaf area index) were involved. Their result is in general agreement with this study, in spite of the differences in model factors and model construction between the two methods. The other difference between SEUFM and other models is that SEUFM is derived completely from remote sensing data and is designed to detect sites prone to soil erosion in forest but not to quantitatively measure the amount/intensity of soil loss. Therefore, the result of SEUFM is a binary image. Each pixel of the image is represented by a value of 0 or 1 (indicating erosion or non-erosion state) rather than a value representing the amount of soil loss. Nevertheless, the model may be used to obtain qualitative values by classifying soil erosion into high, moderate and low levels, as the modelling result is represented by a value between 0 and 1. The greater the value, the more likely the occurrence of soil erosion.
Remote sensing has been served as a measurement surrogate of spatial distributions of soil-erosion status and provides accurate detection of soil erosion sites for decades. Nevertheless, remote sensing based mapping of soil erosion in forest remains a challenge because the methods specially developed for this have seldom been addressed in previous studies. This study has demonstrated an application of a full remote sensing based model (SEUFM) in soil erosion detection in forested areas. The five factors of the model are easily obtained as they are all derived from remote sensing data alone. This will overcome the difficulty in data availability [1]. The integration of the five factors using PCA also avoids the weight allocation that may cause errors in the results due to subjective selections of weights. The method proposed in this paper will facilitate quick and effective detection of soil erosion in forest over a very large area, which makes SEUFM a relatively simple soil erosion monitoring tool for forested lands.

6. Conclusions

Soil erosion in forests is closely related to, and can be reflected in, factors such as forest coverage, forest health status, soil exposure intensity and slope. These are the factors considered in this study for the development of the SEUFMs. Of the two types of SEUFM models developed in this study, the PCA-based method achieved higher accuracy than the multiplication-based method because it handles the five factors according to their contributions (loadings) to each PC. The lower accuracy of the multiplication-based models is due to its assumption of an equal independent association of the five factors with soil erosion. Among the four developed models, SEUFM1, the PC1-based model, mapped the areas of soil erosion in forest with the highest accuracy.
Whether a model is appropriate for a certain application depends on a number of factors, including data requirement and ease of use. The lack of data is usually the main drawback of model applications. The proposed method in this study is completely based on remote sensing techniques and is relatively easy to use. The required data of each factor for the model can be derived directly from remote sensing imagery. This advantage makes the model more applicable. SEUFM is intended for use as a spatially-explicit tool to detect areas with potential soil erosion in forest. The method-derived results would be useful for decision makers in the development of future soil conservation strategies to reduce soil loss in forest.

Author Contributions

H.X. conceived the idea and designed the experiments; H.X., X.H., B.Z. and M.W. performed the experiments; S.C. and M.C. led the ground truth; H.X. analysed the data and wrote the paper; H.G. reviewed and commented on the manuscript. All authors gave final approval for publication.

Funding

This research was funded by China’s National Science and Technology Supporting Project, grant number 2013BAC08B01-05 and Fujian Provincial Monitoring Station of Water and Soil Reservation, grant number MSK201704.

Acknowledgments

We appreciate the six anonymous reviewers for their helpful comments and suggestions on the manuscript.

Conflicts of Interest

The authors declare that they have no conflict of interest.

References

  1. Aiello, A.; Adamo, M.; Canora, F. Remote sensing and GIS to assess soil erosion with RUSLE3D and USPED at river basin scale in southern Italy. Catena 2015, 131, 174–185. [Google Scholar] [CrossRef]
  2. He, S.; Xie, J.; Yang, J. Status, causes and prevention of soil and water loss in Pinus massoniana woodland in hilly red soil region of southern China. Sci. Soil Water Conserv. 2011, 9, 65–70. [Google Scholar]
  3. Lei, H.Q. Soil and water loss of granite region under the trees in Xingguo County and its prevention and control. Soil Water Conserv China 2007, 3, 58–59. [Google Scholar]
  4. Zhu, S.Q.; Gong, J.; Lin, E.B. Discussion on characteristics of soil erosion under forest canopy in hilly area of southern China. Subtrop. Soil Water Conserv. 2013, 25, 24–30. [Google Scholar]
  5. Zhang, H.D.; Yu, D.S.; Dong, L.L.; Shi, X.Z.; Warner, E.; Gu, Z.J.; Sun, J.J. Regional soil erosion assessment from remote sensing data in rehabilitated high density canopy forests of southern China. Catena 2014, 123, 106–112. [Google Scholar] [CrossRef]
  6. Liao, C.; Wei, T. Characteristics of soil and water loss on red soil slope land under forest with different tree species. Bull. Soil Water Conserv. 2013, 33, 198–202. [Google Scholar]
  7. Xu, Y.B. Research on Process of Undergrowth Loss the Soil and Water in Red Soil Hilly Region of Southern China. Master’s Thesis, Fujian Normal University, Fuzhou, China, 2012. [Google Scholar]
  8. Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); U.S. Department of Agriculture: Washington, DC, USA, 1997.
  9. Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; U.S. Department of Agriculture: Washington, DC, USA, 1978.
  10. Beasley, D.B.; Huggins, L.F.; Monke, E.J. Answers: A model for watershed planning. Trans. ASAE 1980, 23, 938–944. [Google Scholar] [CrossRef]
  11. Nearing, M.A.; Foster, G.R.; Lane, L.J.; Finkner, S.C. A process-based soil-erosion model for USDA-water erosion prediction project technology. Trans. ASAE 1989, 32, 1587–1593. [Google Scholar] [CrossRef]
  12. Engel, B.A.; Srinivasan, R.; Arnold, J.; Rewerts, C.; Brown, S.J. Nonpoint-source (NPS) pollution modeling using models integrated with geographic information systems (GIS). Water Sci. Technol. 1993, 28, 685–690. [Google Scholar] [CrossRef]
  13. Mitas, L.; Mitasova, H. Distributed erosion modeling for effective erosion prevention. Water Resour. Res. 1998, 34, 505–516. [Google Scholar] [CrossRef]
  14. Morgan, R.P.C.; Quinton, J.N.; Smith, R.E.; Govers, G.; Poesen, J.W.A.; Auerswald, K.; Chisci, G.; Torri, D.; Styczen, M.E. The European soil erosion model (EUROSEM): A dynamic approach for predicting sediment transport from fields and small catchments. Earth Surf. Process. Landf. 1998, 23, 527–544. [Google Scholar] [CrossRef]
  15. Roo, A.P.J.D.; Jetten, V.G. Calibrating and validating the LISEM model for two data sets from the Netherlands and South Africa. Catena 1999, 37, 477–493. [Google Scholar] [CrossRef]
  16. Jetten, V.G.; de Roo, A.P.J. Spatial analysis of erosion conservation measures with LISEM. In Landscape Erosion and Evolution Modeling; Harmon, R.S., Doe, W.W., Eds.; Springer: Boston, MA, USA, 2001; pp. 429–445. [Google Scholar]
  17. Coogle, A.L.; Lane, L.J.; Basher, L. Testing the Hillslope Erosion Model for Application in India, New Zealand and Australia. Environ. Model. Softw. 2003, 18, 825–830. [Google Scholar] [CrossRef]
  18. Merritt, W.S.; Letcher, R.A.; Jakeman, A.J. A review of erosion and sediment transport models. Environ. Model. Softw. 2003, 18, 761–799. [Google Scholar] [CrossRef]
  19. Chappell, A.; Zobeck, T.M.; Brunner, G. Using bi-directional soil spectral reflectance to model soil surface changes induced by rainfall and wind-tunnel abrasion. Remote Sens. Environ. 2006, 102, 328–343. [Google Scholar] [CrossRef]
  20. Mwaniki, M.W.; Agutu, N.O.; Mbaka, J.G.; Ngigi, T.G.; Waithaka, E.H. Landslide scar/soil erodibility mapping using Landsat TM/ETM+ bands 7 and 3 normalised difference index: A case study of central region of Kenya. Appl. Geogr. 2015, 64, 108–120. [Google Scholar] [CrossRef]
  21. Singh, D.; Herlin, I.; Berroir, J.P.; Silva, E.F.; Meirelles, M.S. An approach to correlate NDVI with soil colour for erosion process using NOAA/AVHRR data. Adv. Space Res. 2004, 33, 328–332. [Google Scholar] [CrossRef]
  22. Vrieling, A. Satellite remote sensing for water erosion assessment: A review. Catena 2006, 65, 2–18. [Google Scholar] [CrossRef]
  23. Xu, H.Q. Dynamic of soil exposure intensity and its effect on thermal environment change. Int. J. Climatol. 2014, 34, 902–910. [Google Scholar] [CrossRef]
  24. Sayao, V.M.; Dematte, J.A.M.; Bedin, L.G.; Nanni, M.R.; Rizzo, R. Satellite land surface temperature and reflectance related with soil attributes. Geoderma 2018, 325, 125–140. [Google Scholar] [CrossRef]
  25. Lobser, S.E.; Cohen, W.B. MODIS tasselled cap: land cover characteristics expressed through transformed MODIS data. Int. J. Remote Sens. 2007, 28, 5079–5101. [Google Scholar] [CrossRef]
  26. Metternicht, G.I.; Fermont, A. Estimating erosion surface features by linear mixture modeling. Remote Sens. Environ. 1998, 64, 254–265. [Google Scholar] [CrossRef]
  27. Guerschman, J.P.; Scarth, P.F.; McVicar, T.R.; Renzullo, L.J.; Malthus, T.J.; Stewart, J.B.; Rickards, J.E.; Trevithick, R. Assessing the effects of site heterogeneity and soil properties when unmixing photosynthetic vegetation, non-photosynthetic vegetation and bare soil fractions from Landsat and MODIS Data. Remote Sens. Environ. 2015, 161, 12–26. [Google Scholar] [CrossRef]
  28. Shruthi, R.; Kerle, N.; Jetten, V.; Abdellah, L.; Machmach, I. Quantifying temporal changes in gully erosion areas with object oriented analysis. Catena 2015, 128, 262–277. [Google Scholar] [CrossRef]
  29. Rahmati, O.; Tahmasebipour, N.; Haghizadeh, A.; Pourghasemi, H.R.; Feizizadeh, B. Evaluating the influence of geo-environmental factors on gully erosion in a semi-arid region of Iran: An integrated framework. Sci. Total Environ. 2017, 579, 913–927. [Google Scholar] [CrossRef] [PubMed]
  30. Garosi, Y.; Sheklabadi, M.; Pourghasemi, H.R.; Besalatpour, A.A.; Conoscenti, C.; Van Oost, K. Comparison of differences in resolution and sources of controlling factors for gully erosion susceptibility mapping. Geoderma 2018, 330, 65–78. [Google Scholar] [CrossRef]
  31. Cheng, Z.L.; Lu, D.S.; Li, G.Y.; Huang, J.Q.; Sinha, N.; Zhi, J.J.; Li, S.J. A random forest-based approach to map soil erosion risk distribution in Hickory Plantations in western Zhejiang Province, China. Remote Sens. 2018, 10, 1899. [Google Scholar] [CrossRef]
  32. Leek, R.; Solberg, R. Using remote-sensing for monitoring of autumn tillage in Norway. Int. J. Remote Sens. 1995, 16, 447–466. [Google Scholar] [CrossRef]
  33. Khawlie, M.; Awad, M.; Shaban, A.; Kheir, R.B.; Abdallah, C. Remote sensing for environmental protection of the eastern Mediterranean rugged mountainous areas, Lebanon. ISPRS J. Photogramm. 2002, 57, 13–23. [Google Scholar] [CrossRef]
  34. d’Oleire-Oltmanns, S.; Marzolff, I.; Peter, K.D.; Ries, J.B. Unmanned Aerial Vehicle (UAV) for monitoring soil erosion in Morocco. Remote Sens. 2012, 4, 3390–3416. [Google Scholar] [CrossRef]
  35. Chen, J.J.; Yi, S.H.; Qin, Y.; Wang, X.Y. Improving estimates of fractional vegetation cover based on UAV in alpine grassland on the Qinghai-Tibetan Plateau. Int. J. Remote Sens. 2016, 37, 1922–1936. [Google Scholar] [CrossRef]
  36. Neugirg, F.; Stark, M.; Kaiser, A.; Vlacilova, M.; Seta, M.D.; Vergari, F.; Schmidt, J.; Becht, M.; Haas, F. Erosion processes in calanchi in the Upper Orcia Valley, Southern Tuscany, Italy based on multitemporal high-resolution terrestrial LiDAR and UAV surveys. Geomorphology 2016, 269, 8–22. [Google Scholar] [CrossRef]
  37. Verstraeten, G.; Poesen, J.; Demaree, G.; Salles, C. Long-term (105 years) variability in rain erosivity as derived from 10-min rainfall depth data for Ukkel (Brussels, Belgium): Implications for assessing soil erosion rates. J. Geophys. Res. Atmos. 2006, 111, D22109. [Google Scholar] [CrossRef]
  38. Piacentini, T.; Galli, A.; Marsala, V.; Miccadei, E. Analysis of Soil Erosion Induced by Heavy Rainfall: A Case Study from the NE Abruzzo Hills Area in Central Italy. Water 2018, 10, 1314. [Google Scholar] [CrossRef]
  39. Li, X.; Zhang, X.; Zhang, L.; Wu, B. Rainfall and Vegetation Coupling Index for soil erosion risk mapping. J. Soil Water Conserv. 2014, 69, 213–220. [Google Scholar] [CrossRef]
  40. Yin, S.; Zhu, Z.Y.; Wang, L.; Liu, B.Y.; Xie, Y.; Wang, G.N.; Li, Y.S. Regional soil erosion assessment based on a sample survey and geostatistics. Hydrol. Earth Syst. Sci. 2018, 22, 1695–1712. [Google Scholar] [CrossRef]
  41. Mateos, E.; Miguel, E.J.; Ormaetxea, L. Soil erosion and forests biomass as energy resource in the basin of the Oka River in Biscay, northern Spain. Forests 2017, 8, 258. [Google Scholar] [CrossRef]
  42. Ochoa, P.A.; Fries, A.; Mejia, D.; Burneo, J.I.; Ruiz-Sinoga, J.D.; Cerda, A. Effects of climate, land cover and topography on soil erosion risk in a semiarid basin of the Andes. Catena 2016, 140, 31–42. [Google Scholar] [CrossRef]
  43. Meusburger, K.; Baenninger, D.; Alewell, C. Estimating vegetation parameter for soil erosion assessment in an alpine catchment by means of QuickBird imagery. Int. J. Appl. Earth Obs. 2010, 12, 201–207. [Google Scholar] [CrossRef]
  44. Molina, A.; Govers, G.; Poesen, J.; Van Hemelryck, H.; De Bievre, B.; Vanacker, V. Environmental factors controlling spatial variation in sediment yield in a central Andean mountain area. Geomorphology 2008, 98, 176–186. [Google Scholar] [CrossRef]
  45. Panagos, P.; Borrelli, P.; Meusburger, K.; Alewell, C.; Lugato, E.; Montanarella, L. Estimating the soil erosion cover-management factor at the European scale. Land Use Policy 2015, 48, 38–50. [Google Scholar] [CrossRef] [Green Version]
  46. Schonbrodt, S.; Saumer, P.; Behrens, T.; Seeber, C.; Scholten, T. Assessing the USLE crop and management factor C for soil erosion modeling in a large mountainous watershed in Central China. J. Earth Sci. 2010, 21, 835–845. [Google Scholar] [CrossRef]
  47. Yang, X.H. Deriving RUSLE cover factor from time-series fractional vegetation cover for hillslope erosion modelling in New South Wales. Soil Res. 2014, 52, 253–261. [Google Scholar] [CrossRef]
  48. Foerster, S.; Wilczok, C.; Brosinsky, A.; Segl, K. Assessment of sediment connectivity from vegetation cover and topography using remotely sensed data in a dryland catchment in the Spanish Pyrenees. J. Soils Sediment. 2014, 14, 1982–2000. [Google Scholar] [CrossRef] [Green Version]
  49. Kinnell, P.I.A.; Wang, J.; Zheng, F. Comparison of the abilities of WEPP and the USLE-M to predict event soil loss on steep loessal slopes in China. Catena 2018, 171, 99–106. [Google Scholar] [CrossRef]
  50. Qin, C.Z.; Gao, H.R.; Zhu, L.J.; Zhu, A.X.; Liu, J.Z.; Wu, H. Spatial optimization of watershed best management practices based on slope position units. J. Soil Water Conserv. 2018, 73, 504–517. [Google Scholar] [CrossRef]
  51. Dai, Q.; Peng, X.; Wang, P.J.; Li, C.; Shao, H.B. Surface erosion and underground leakage of yellow soil on slopes in karst regions of southwest China. Land Degrad. Dev. 2018, 29, 2438–2448. [Google Scholar] [CrossRef]
  52. Chavez, P.S. Image-based atmospheric corrections revisited and improved. Photogramm. Eng. Remote Sens. 1996, 62, 1025–1036. [Google Scholar]
  53. Xu, H.Q. Retrieval of the reflectance and land surface temperature of the newly-launched Landsat 8 satellite. Chin. J. Geophys. China 2015, 58, 741–747. [Google Scholar]
  54. Hu, X.J.; Xu, H.Q.; Guo, Y.B.; Zhang, B.B. Remote sensing detection of vegetation health status after ecological restoration in soil and water loss region. Chin. J. Appl. Ecol. 2017, 38, 250–256. [Google Scholar]
  55. Schmitter, P.; Kibret, K.S.; Lefore, N.; Barron, J. Suitability mapping framework for solar photovoltaic pumps for smallholder farmers in Sub-Saharan Africa. Appl. Geogr. 2018, 94, 41–57. [Google Scholar] [CrossRef]
  56. Xu, H.Q.; He, H.; Huang, S.L. Analysis of fractional vegetation cover change and its impact on thermal environment in the Hetian basinal area of County Changting, Fujian Province, China. Acta Ecol. Sin. 2013, 33, 2954–2963. [Google Scholar]
  57. Ministry of Water Resources of China. Standards for Classification and Gradation of Soil Erosion; SL 190-2007; Ministry of Water Resources of China: Beijing, China, 2008.
  58. Blanco, H.; Lal, R. Principles of Soil Conservation and Management; Springer: Heidelberg, Germany, 2010. [Google Scholar]
  59. Yan, C.Y.; Liu, Q.; Niu, Z.; Wang, C.Y. Inversion of vegetation biochemicals by remote sensing. J. Remote Sens. 2004, 8, 300–308. [Google Scholar]
  60. Zhou, G.Y.; Morris, J.D.; Yan, J.H.; Yu, Z.Y.; Peng, S.L. Hydrological impacts of reafforestation with eucalypts and indigenous species: A case study in southern China. For. Ecol. Manag. 2002, 167, 209–222. [Google Scholar] [CrossRef]
  61. Sun, J. Using LAI Express the Effect of Vegetation in Preventing Soil Erosion and Vegetation Recovering Degree. Ph.D. Thesis, Institute of Soil Science, Chinese Academy of Sciences, Beijing, China, 2010. [Google Scholar]
  62. Franceschini, M.H.D.; Dematte, J.A.M.; Terra, F.D.; Vicente, L.E.; Bartholomeus, H.; de Souza, C.R. Prediction of soil properties using imaging spectroscopy: Considering fractional vegetation cover to improve accuracy. Int. J. Appl. Earth Obs. 2015, 38, 358–370. [Google Scholar] [CrossRef]
  63. Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
  64. Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens. 1998, 19, 1533–1543. [Google Scholar] [CrossRef]
  65. Zhou, X.; Guan, H.D.; Xie, H.; Wilson, J.L. Analysis and optimization of NDVI definitions and areal fraction models in remote sensing of vegetation. Int. J. Remote Sens. 2009, 30, 721–751. [Google Scholar] [CrossRef]
  66. Wu, C.S.; Murray, A.T. Estimating impervious surface distribution by spectral mixture analysis. Remote Sens. Environ. 2003, 84, 493–505. [Google Scholar] [CrossRef]
  67. Bausch, W.C.; Duke, H.R. Remote sensing of plant nitrogen status in corn. Trans. ASAE 1996, 39, 1869–1875. [Google Scholar] [CrossRef]
  68. Jensen, J.R. Remote Sensing of the Environment: An Earth Resource Perspective, 2nd ed.; Pearson Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
  69. Jensen, J.R. Introductory Digital Image Processing: A Remote Sensing Perspective, 4th ed.; Pearson Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 2015. [Google Scholar]
  70. Hill, J.; Schutt, B. Mapping complex patterns of erosion and stability in dry Mediterranean ecosystems. Remote Sens. Environ. 2000, 74, 557–569. [Google Scholar] [CrossRef]
  71. Kearney, M.S.; Rogers, A.S.; Townshend, J.R.G. Developing a model for determining coastal marsh “health”. In Proceedings of the Third Thematic Conference on Remote Sensing for Marine and Coastal Environments, Seattle, WA, USA, 18–20 September 1995; pp. 527–537. [Google Scholar]
Remotesensing 11 00513 g001 550
Figure 1. Photo showing a site in Changting that is vulnerable to soil erosion due to exposed top-soils under the forest canopy.
Figure 1. Photo showing a site in Changting that is vulnerable to soil erosion due to exposed top-soils under the forest canopy.
Remotesensing 11 00513 g001
Remotesensing 11 00513 g002 550
Figure 2. Landsat 8 image of Changting County (October 8, 2014) (Red, Green and Blue channel combination: Bands 4, 3 and 2). The rectangle marks the location of the Hetian basin and the field survey sites are shown as yellow dots.
Figure 2. Landsat 8 image of Changting County (October 8, 2014) (Red, Green and Blue channel combination: Bands 4, 3 and 2). The rectangle marks the location of the Hetian basin and the field survey sites are shown as yellow dots.
Remotesensing 11 00513 g002
Remotesensing 11 00513 g003 550
Figure 3. Flowchart of the technical procedures for the development of soil erosion under forest model (SEUFM).
Figure 3. Flowchart of the technical procedures for the development of soil erosion under forest model (SEUFM).
Remotesensing 11 00513 g003
Remotesensing 11 00513 g004 550
Figure 4. Regression between modelled fractional vegetation coverage (FVC) and actual FVC for the accuracy comparison of FVClinear (a) with FVCquadratic (b) models.
Figure 4. Regression between modelled fractional vegetation coverage (FVC) and actual FVC for the accuracy comparison of FVClinear (a) with FVCquadratic (b) models.
Remotesensing 11 00513 g004
Remotesensing 11 00513 g005 550
Figure 5. Regression of Landsat 8 simulated yellow band vs. WorldView 2 yellow band.
Figure 5. Regression of Landsat 8 simulated yellow band vs. WorldView 2 yellow band.
Remotesensing 11 00513 g005
Remotesensing 11 00513 g006 550
Figure 6. Thematic images of the five factors. (a) FVC, (b) NRI, (c) NDSI, (d) YLI and (e) Slope. White areas in (a) to (d) are the areas with a slope degree less than 5°.
Figure 6. Thematic images of the five factors. (a) FVC, (b) NRI, (c) NDSI, (d) YLI and (e) Slope. White areas in (a) to (d) are the areas with a slope degree less than 5°.
Remotesensing 11 00513 g006
Remotesensing 11 00513 g007 550
Figure 7. Detected soil erosion areas under forest canopy in Changting County (a) and a 3D perspective of soil erosion areas in forests in the central county (Hetian basin) area (b).
Figure 7. Detected soil erosion areas under forest canopy in Changting County (a) and a 3D perspective of soil erosion areas in forests in the central county (Hetian basin) area (b).
Remotesensing 11 00513 g007
Remotesensing 11 00513 g008 550
Figure 8. Separability of each factor between erosion and non-erosion sites (Y: Erosion, N: Non-Erosion).
Figure 8. Separability of each factor between erosion and non-erosion sites (Y: Erosion, N: Non-Erosion).
Remotesensing 11 00513 g008
Table
Table 1. Comparison between simulated and real yellow bands.
Table 1. Comparison between simulated and real yellow bands.
WorldView 2WorldView 2
Yellow Band
(Invariant Patches)		Landsat 8 Simulated Yellow Band
(Invariant Patches)
Yellow BandSimulated
Yellow Band
Mean0.0550.0540.0550.063
Std Dev0.0340.0320.0320.030
R20.9840.928
Table
Table 2. Eigenvector of covariance matrix and related eigenvalue of each principal component (PC).
Table 2. Eigenvector of covariance matrix and related eigenvalue of each principal component (PC).
PC1PC2PC3PC4PC5
FVC−0.621−0.219−0.0490.2230.717
NRI−0.466−0.1290.778−0.256−0.310
NDSI0.3610.1810.5530.7050.187
YLI0.4040.1050.293−0.6210.595
Slope−0.3220.944−0.043−0.0500.022
Eigenvalue0.129 0.021 0.006 0.004 0.001
Percent eigenvalue (%)80.12 13.04 3.73 2.48 0.62
Table
Table 3. Statistical characteristics of the five factors in soil erosion and non-soil erosion sites.
Table 3. Statistical characteristics of the five factors in soil erosion and non-soil erosion sites.
Soil ErosionNon-Soil ErosionPercent Difference (%)p-Value
MinMaxMeanStd DevMinMaxMeanStd Dev
Slope0.070 0.541 0.219 0.096 0.026 0.397 0.206 0.135 6.310.821
FVC0.454 0.785 0.651 0.074 0.721 0.897 0.804 0.064 −19.030.000
NRI0.283 0.467 0.358 0.040 0.375 0.594 0.476 0.065 −24.780.003
NDSI0.069 0.524 0.283 0.084 0.110 0.275 0.184 0.049 53.800.001
YLI0.214 0.433 0.309 0.049 0.172 0.292 0.226 0.048 36.730.004
Table
Table 4. Mean and threshold values of each SEUFMs.
Table 4. Mean and threshold values of each SEUFMs.
Mean/Initial ThresholdFinal ThresholdThreshold to Mean
SEUFM10.3550.3711.045
SEUFM1+20.3500.3661.046
SEUFMm-slope0.1530.1661.089
SEUFMm+slope0.0880.0790.898
Table
Table 5. Accuracy assessment of the four SEUFMs.
Table 5. Accuracy assessment of the four SEUFMs.
ErosionNon-ErosionTotalUser’s Accuracy %
SEUFM1 (threshold: 0.371)
Erosion5125396.23
Non-Erosion6202676.92
Total572279
Producer’s accuracy (%)89.4790.91
Overall accuracy (%)89.87 Kappa0.761
SEUFM1+2 (threshold: 0.366)
Erosion4465088.00
Non- Erosion13162955.17
Total572279
Producer’s accuracy (%)77.1972.73
Overall accuracy (%)75.95 Kappa0.455
SEUFMm-slope (threshold: 0.166)
Erosion4865488.89
Non-Erosion9162564.00
Total572279
Producer’s accuracy (%)84.2172.73
Overall accuracy (%)81.01 Kappa0.547
SEUFMm+slope (threshold: 0.079)
Erosion40105080.00
Non-Erosion17122941.38
Total572279
Producer’s accuracy (%)70.1854.55
Overall accuracy (%)65. 82 Kappa0.225
Table
Table 6. Correlation matrix of the selected factors.
Table 6. Correlation matrix of the selected factors.
SlopeFVCNRINDSIYLI
Slope1.000
FVC0.4141.000
NRI0.4060.8691.000
NDSI−0.324−0.829−0.7051.0000.767
YLI−0.421−0.897−0.7590.7671.000

Share and Cite

MDPI and ACS Style

Xu, H.; Hu, X.; Guan, H.; Zhang, B.; Wang, M.; Chen, S.; Chen, M. A Remote Sensing Based Method to Detect Soil Erosion in Forests. Remote Sens. 2019, 11, 513. https://doi.org/10.3390/rs11050513

AMA Style

Xu H, Hu X, Guan H, Zhang B, Wang M, Chen S, Chen M. A Remote Sensing Based Method to Detect Soil Erosion in Forests. Remote Sensing. 2019; 11(5):513. https://doi.org/10.3390/rs11050513

Chicago/Turabian Style

Xu, Hanqiu, Xiujuan Hu, Huade Guan, Bobo Zhang, Meiya Wang, Shanmu Chen, and Minghua Chen. 2019. "A Remote Sensing Based Method to Detect Soil Erosion in Forests" Remote Sensing 11, no. 5: 513. https://doi.org/10.3390/rs11050513

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop