Impact of the Revisit of Thermal Infrared Remote Sensing Observations on Evapotranspiration Uncertainty—A Sensitivity Study Using AmeriFlux Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Scaling ET from Instantaneous Observations to Daytime Averages
2.1.1. Four Scaling Methods Based on Self-Preservation of Evaporative Ratios
2.1.2. β Factors, a Metric to Evaluate the Self-Preservation of Evaporative Ratios
2.1.3. Metrics to Evaluate the Different Scaling Methods
2.2. Assessing the Impact of the Satellite Revisit Period on ET
2.2.1. Generation of Series of Observations with Different Revisit Periods
2.2.2. Interpolation between Clear-Sky Observations
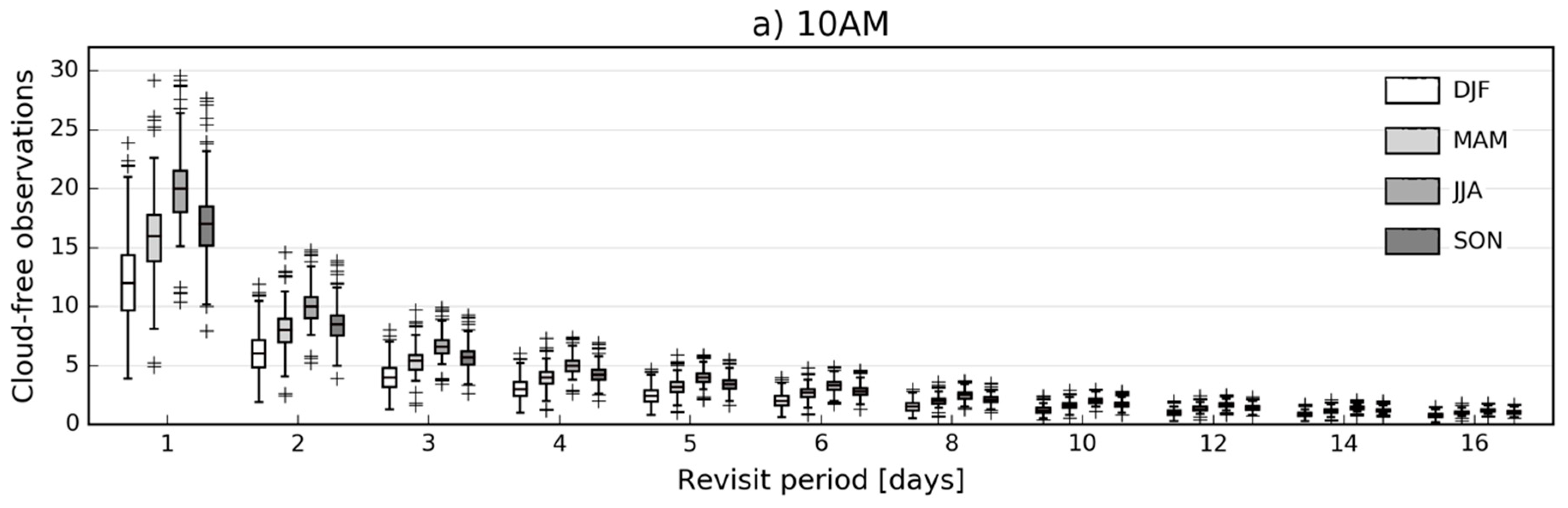
2.2.3. Clear Sky Identification
2.3. The AmeriFlux Network
3. Results
3.1. Clear Sky Identification
3.2. Scaling ET from Instantaneous Observations to Daytime Averages
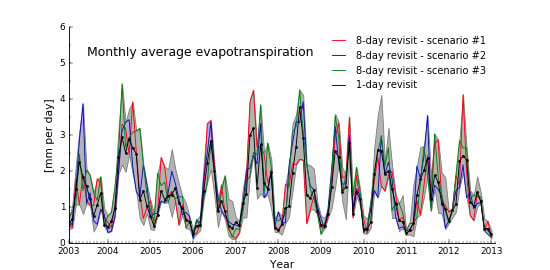
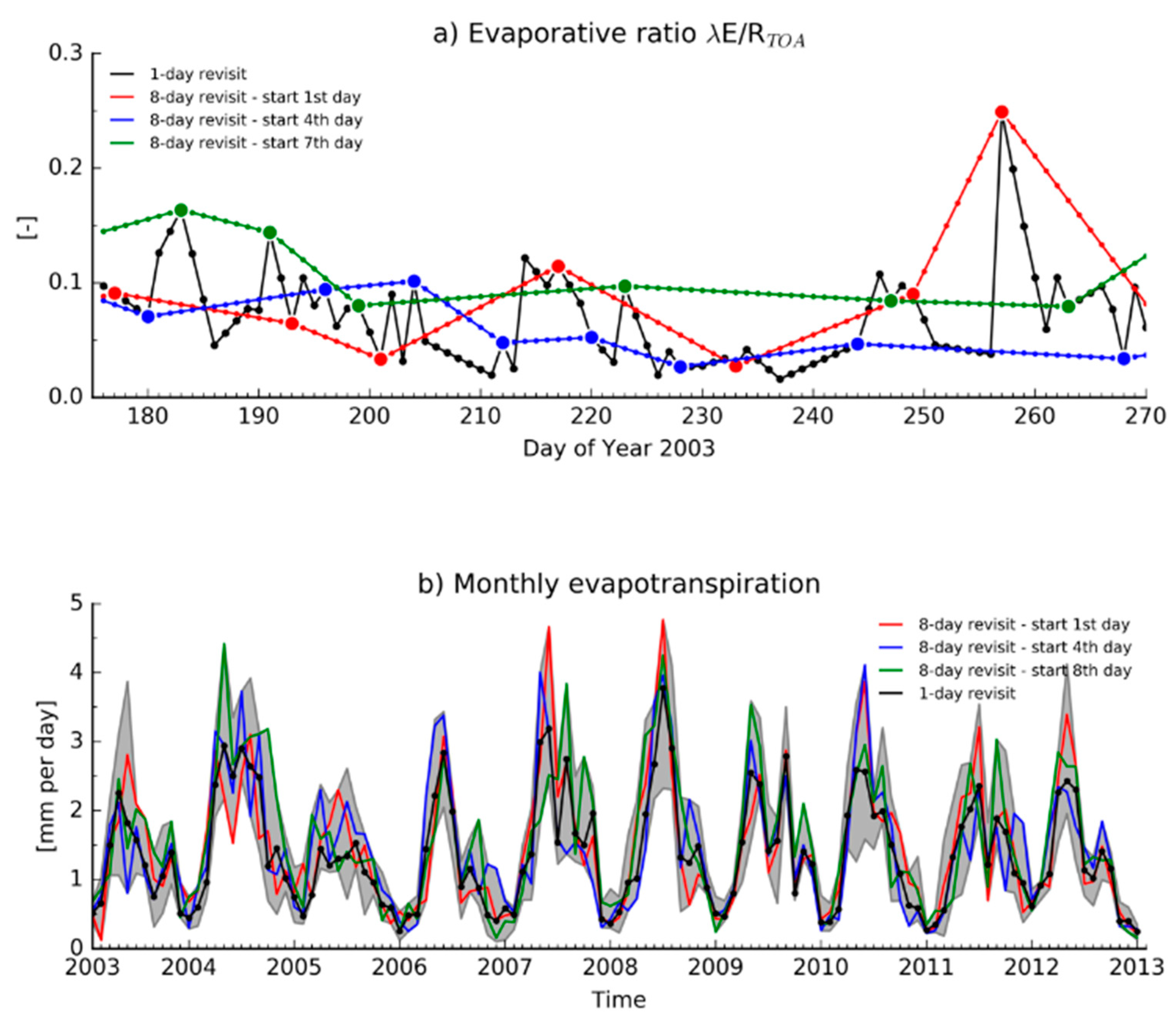
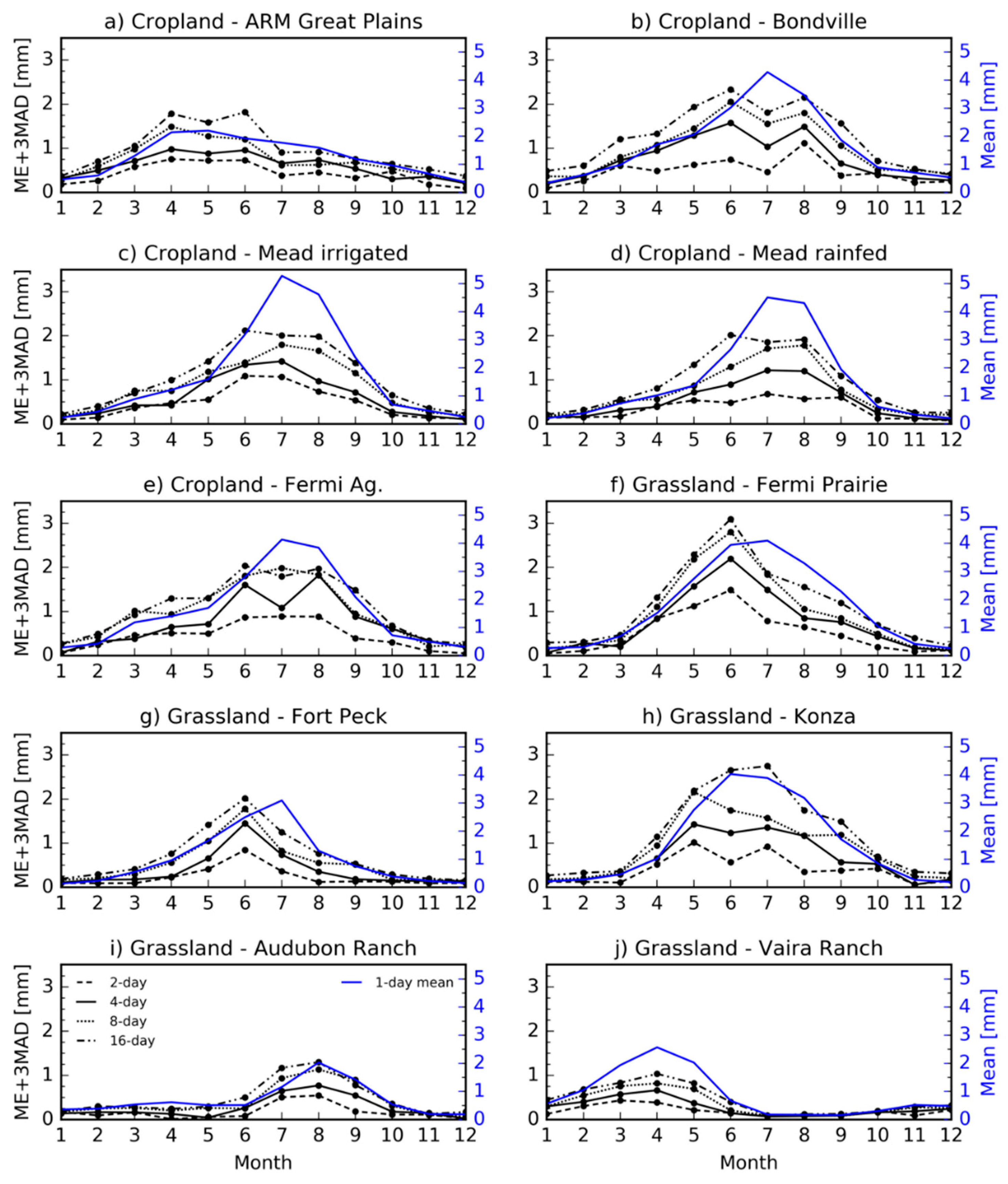
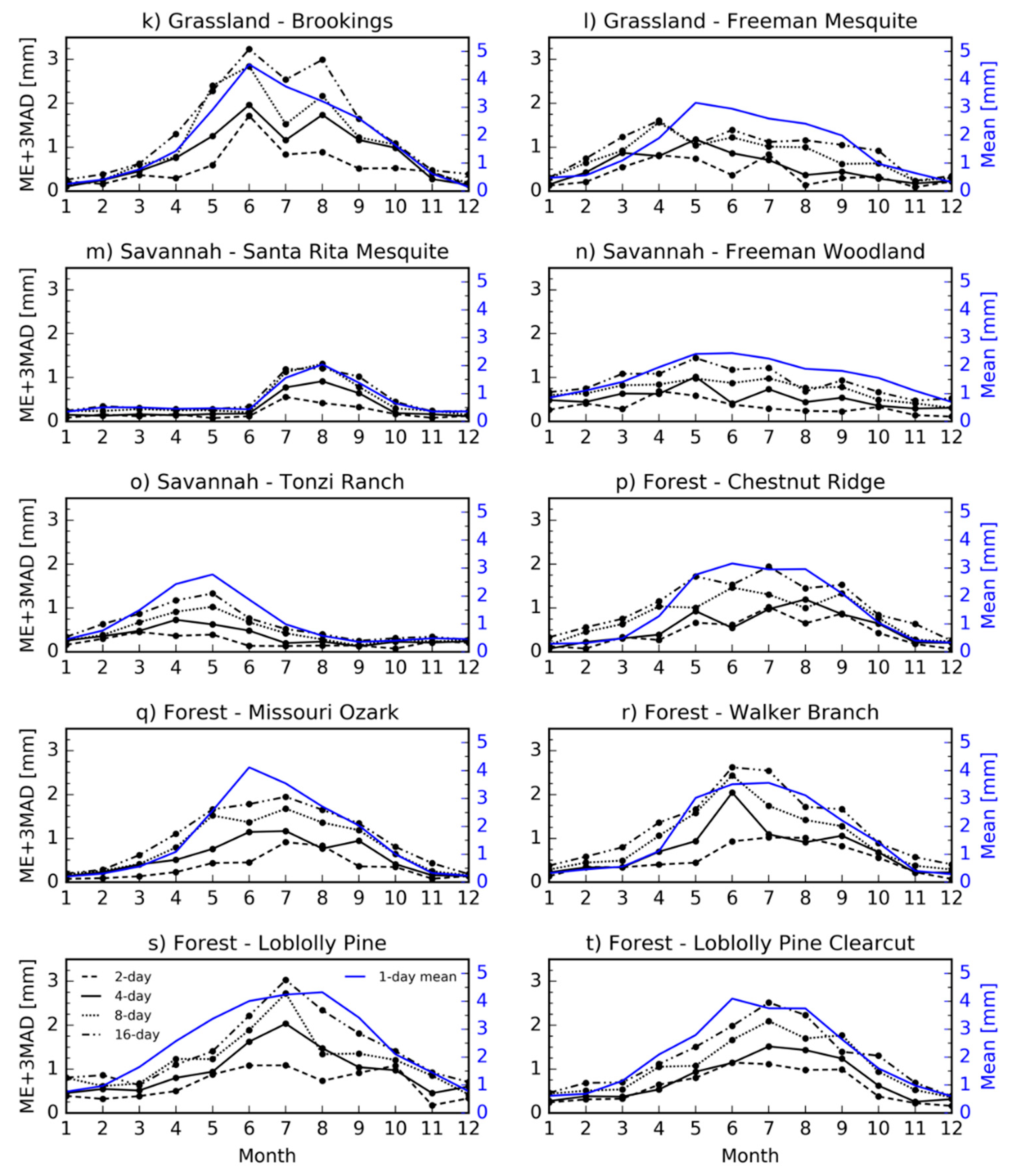
3.3. Impact of the Satellite Revisit Period on ET Estimates
4. Discussion
4.1. Scaling ET from Instantaneous Observations to Daytime Averages
4.2. Impact of the Satellite Revisit Period on ET Estimates
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Site ID | 10:00 Overpass | 13:00 Overpass | ||||||
|---|---|---|---|---|---|---|---|---|
| AE | RG | RTOA | PET | AE | RG | RTOA | PET | |
| ARM | 1.24 | 1.11 | 0.98 | 1.10 | 1.15 | 1.01 | 0.93 | 1.14 |
| Aud | 1.40 | 1.09 | 0.89 | 1.18 | 1.32 | 1.12 | 1.07 | 1.29 |
| Bo1 | 1.25 | 1.11 | 0.87 | 1.15 | 1.07 | 1.00 | 0.96 | 1.11 |
| Bkg | 1.28 | 1.14 | 0.98 | 1.15 | 1.14 | 1.02 | 0.94 | 1.17 |
| ChR | 1.22 | 1.13 | 1.00 | 1.12 | 1.12 | 1.03 | 0.91 | 1.14 |
| IB1 | 1.04 | 1.13 | 0.86 | 1.14 | 1.08 | 1.02 | 1.00 | 1.14 |
| IB2 | 1.14 | 1.09 | 0.84 | 1.11 | 1.08 | 1.02 | 0.98 | 1.13 |
| Fpe | 1.42 | 1.13 | 0.88 | 1.24 | 1.15 | 1.05 | 0.96 | 1.20 |
| FR2 | 1.10 | 1.10 | 0.94 | 1.09 | 1.20 | 1.12 | 1.01 | 1.17 |
| FR3 | 1.03 | 0.99 | 0.97 | 0.95 | 1.27 | 1.19 | 1.08 | 1.26 |
| Kon | 1.15 | 1.06 | 1.00 | 1.01 | 1.27 | 1.11 | 1.02 | 1.22 |
| NC2 | 1.20 | 1.11 | 0.90 | 1.14 | 1.13 | 1.02 | 0.96 | 1.14 |
| NC1 | 1.23 | 1.11 | 0.89 | 1.14 | 1.15 | 1.04 | 0.97 | 1.17 |
| Ne1 | 1.13 | 1.09 | 0.92 | 1.10 | 1.13 | 1.04 | 0.98 | 1.17 |
| Ne2 | 1.11 | 1.07 | 0.90 | 1.08 | 1.16 | 1.07 | 1.00 | 1.20 |
| Ne3 | 1.10 | 1.05 | 0.88 | 1.06 | 1.20 | 1.09 | 1.03 | 1.23 |
| MOz | 1.20 | 1.09 | 0.87 | 1.11 | 1.18 | 1.08 | 1.00 | 1.19 |
| SRM | 0.98 | 1.03 | 0.98 | 1.05 | 1.25 | 1.18 | 1.06 | 1.29 |
| Ton | 1.22 | 1.06 | 0.99 | 1.10 | 1.22 | 1.11 | 1.03 | 1.24 |
| Var | 1.30 | 1.12 | 1.03 | 1.17 | 1.25 | 1.08 | 1.00 | 1.25 |
| WBW | 1.24 | 1.17 | 1.04 | 1.18 | 1.10 | 1.03 | 0.91 | 1.12 |
| Season | 10:00 | 13:00 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| DJF | MAM | JJA | SON | DJF | MAM | JJA | SON | ||
| 2-day revisit | All sites | 0.132 | 0.270 | 0.373 | 0.196 | 0.103 | 0.250 | 0.371 | 0.189 |
| (29%) | (18%) | (13%) | (18%) | (24%) | (16%) | (13%) | (18%) | ||
| Cropland | 0.101 | 0.307 | 0.439 | 0.182 | 0.090 | 0.263 | 0.378 | 0.176 | |
| (25%) | (21%) | (12%) | (16%) | (24%) | (19%) | (11%) | (17%) | ||
| Grassland | 0.109 | 0.240 | 0.364 | 0.151 | 0.091 | 0.270 | 0.359 | 0.130 | |
| (25%) | (16%) | (16%) | (18%) | (26%) | (17%) | (16%) | (17%) | ||
| Broadleaf Forest | 0.142 | 0.256 | 0.373 | 0.219 | 0.100 | 0.226 | 0.445 | 0.253 | |
| (42%) | (17%) | (12%) | (18%) | (31%) | (15%) | (13%) | (20%) | ||
| Needleleaf Forest | 0.187 | 0.314 | 0.406 | 0.351 | 0.156 | 0.280 | 0.522 | 0.326 | |
| (24%) | (13%) | (9%) | (16%) | (21%) | (12%) | (13%) | (16%) | ||
| Woody Savannah | 0.182 | 0.228 | 0.178 | 0.184 | 0.121 | 0.189 | 0.170 | 0.147 | |
| (29%) | (16%) | (11%) | (20%) | (20%) | (12%) | (11%) | (17%) | ||
| 4-day revisit | All sites | 0.181 | 0.409 | 0.550 | 0.273 | 0.146 | 0.349 | 0.549 | 0.268 |
| (39%) | (27%) | (19%) | (25%) | (35%) | (23%) | (19%) | (26%) | ||
| Cropland | 0.149 | 0.447 | 0.626 | 0.252 | 0.146 | 0.379 | 0.571 | 0.250 | |
| (38%) | (30%) | (18%) | (22%) | (39%) | (27%) | (16%) | (24%) | ||
| Grassland | 0.162 | 0.362 | 0.524 | 0.220 | 0.117 | 0.340 | 0.510 | 0.206 | |
| (38%) | (25%) | (23%) | (26%) | (33%) | (22%) | (23%) | (27%) | ||
| Broadleaf Forest | 0.178 | 0.402 | 0.591 | 0.344 | 0.131 | 0.338 | 0.695 | 0.373 | |
| (53%) | (27%) | (19%) | (28%) | (41%) | (22%) | (21%) | (30%) | ||
| Needleleaf Forest | 0.268 | 0.461 | 0.592 | 0.441 | 0.213 | 0.352 | 0.673 | 0.371 | |
| (34%) | (20%) | (14%) | (21%) | (29%) | (15%) | (17%) | (18%) | ||
| Woody Savannah | 0.227 | 0.383 | 0.314 | 0.226 | 0.167 | 0.302 | 0.278 | 0.215 | |
| (36%) | (26%) | (19%) | (24%) | (28%) | (20%) | (19%) | (25%) | ||
| 8-day revisit | All sites | 0.228 | 0.549 | 0.728 | 0.362 | 0.189 | 0.492 | 0.735 | 0.347 |
| (50%) | (36%) | (26%) | (33%) | (45%) | (33%) | (26%) | (33%) | ||
| Cropland | 0.189 | 0.560 | 0.822 | 0.355 | 0.186 | 0.507 | 0.774 | 0.341 | |
| (48%) | (38%) | (23%) | (31%) | (50%) | (36%) | (22%) | (32%) | ||
| Grassland | 0.194 | 0.495 | 0.684 | 0.285 | 0.155 | 0.478 | 0.670 | 0.283 | |
| (45%) | (34%) | (31%) | (34%) | (43%) | (31%) | (30%) | (37%) | ||
| Broadleaf Forest | 0.234 | 0.636 | 0.799 | 0.423 | 0.169 | 0.558 | 0.906 | 0.438 | |
| (69%) | (42%) | (26%) | (35%) | (53%) | (37%) | (27%) | (35%) | ||
| Needleleaf Forest | 0.331 | 0.613 | 0.806 | 0.575 | 0.273 | 0.523 | 0.929 | 0.508 | |
| (42%) | (26%) | (19%) | (27%) | (37%) | (23%) | (23%) | (25%) | ||
| Woody Savannah | 0.290 | 0.489 | 0.418 | 0.318 | 0.224 | 0.389 | 0.414 | 0.268 | |
| (46%) | (34%) | (25%) | (34%) | (38%) | (25%) | (28%) | (32%) | ||
| 16-day revisit | All sites | 0.285 | 0.689 | 0.924 | 0.471 | 0.237 | 0.627 | 0.901 | 0.447 |
| (62%) | (45%) | (32%) | (43%) | (56%) | (41%) | (31%) | (43%) | ||
| Cropland | 0.261 | 0.719 | 1.017 | 0.498 | 0.230 | 0.659 | 0.967 | 0.472 | |
| (66%) | (49%) | (29%) | (43%) | (62%) | (47%) | (27%) | (45%) | ||
| Grassland | 0.239 | 0.642 | 0.880 | 0.376 | 0.202 | 0.613 | 0.833 | 0.341 | |
| (56%) | (44%) | (39%) | (44%) | (56%) | (39%) | (38%) | (45%) | ||
| Broadleaf Forest | 0.285 | 0.805 | 1.050 | 0.527 | 0.214 | 0.690 | 1.065 | 0.552 | |
| (84%) | (53%) | (34%) | (43%) | (68%) | (45%) | (32%) | (44%) | ||
| Needleleaf Forest | 0.408 | 0.694 | 1.007 | 0.713 | 0.331 | 0.645 | 1.083 | 0.619 | |
| (52%) | (29%) | (23%) | (33%) | (45%) | (28%) | (27%) | (30%) | ||
| Woody Savannah | 0.341 | 0.567 | 0.554 | 0.370 | 0.279 | 0.493 | 0.542 | 0.340 | |
| (54%) | (39%) | (34%) | (40%) | (47%) | (32%) | (36%) | (40%) | ||
References
- Chahine, M.T. The hydrological cycle and its influence on climate. Nature 1992, 359, 373–380. [Google Scholar] [CrossRef]
- Fisher, J.B.; Whittaker, R.; Malhi, Y. ET Come Home: Potential evapotranspiration in geographical ecology. Glob. Ecol. Biogeogr. 2011, 20, 1–18. [Google Scholar] [CrossRef]
- Fisher, J.B. Land-atmosphere interactions: Evapotranspiration. In Encyclopedia of Remote Sensing; Njoku, E., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–5. [Google Scholar]
- Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Mecikalski, J.R. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sens. Environ. 1997, 60, 195–216. [Google Scholar] [CrossRef]
- Olioso, A.; Chauki, H.; Courault, D.; Wigneron, J.-P. Estimation of evapotranspiration and photosynthesis by assimilation of remote sensing data into SVAT models. Remote Sens. Environ. 1999, 68, 341–356. [Google Scholar] [CrossRef]
- Merchant, C.J.; Matthiessen, S.; Rayner, N.A.; Remedios, J.J.; Jones, P.D.; Olesen, F.; Trewin, B.; Thorne, P.W.; Auchmann, R.; Corlett, G.K.; et al. The Surface Temperatures of the Earth: Steps towards Integrated Understanding of Variability and Change. Geosci. Instrum. Methods 2013, 2, 305–321. [Google Scholar] [CrossRef]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The Future of Evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Anderson, M.C.; Hain, C.; Wardlow, B.; Pimstein, A.; Mecikalski, J.R.; Kustas, W.P. Evaluation of Drought Indices Based on Thermal Remote Sensing of Evapotranspiration over the Continental United States. J. Clim. 2011, 24, 2025–2044. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land-atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Gallego-Elvira, B.; Olioso, A.; Mira, M.; Reyes-Castillo, S.; Boulet, G.; Marloie, O.; Garrigues, S.; Courault, D.; Weiss, M.; Chauvelon, P.; et al. EVASPA (EVApotranspiration Assessment from SPAce) tool: An overview. Procedia Environ. Sci. 2013, 19, 303–310. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Kimball, J.S.; McDowell, N.G.; Running, S.W. A Remotely Sensed Global Terrestrial Drought Severity Index. Bull. Am. Meteorol. Soc. 2013, 94, 83–98. [Google Scholar] [CrossRef]
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)-model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Noordman, E.J.M.; Pelgrum, H.; Davids, G.; Thoreson, B.P.; Allen, R.G. SEBAL Model with remotely sensed data to improve water resources management under actual field conditions. J. Irrig. Drain. Eng. 2005, 131, 85–93. [Google Scholar] [CrossRef]
- Gómez, M.; Olioso, A.; Sobrino, J.A.; Jacob, F. Retrieval of evapotranspiration over the Alpilles/ReSeDA experimental site using airborne POLDER sensor and a thermal camera. Remote Sens. Environ. 2005, 96, 399–408. [Google Scholar] [CrossRef]
- Lagouarde, J.-P.; Bach, M.; Sobrino, J.A.; Boulet, G.; Briottet, X.; Cherchali, S.; Coudert, B.; Dadou, I.; Dedieu, G.; Gamet, P.; et al. The MISTIGRI thermal infrared project: Scientific objectives and mission specifications. Int. J. Remote Sens. 2013, 34, 3437–3466. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef]
- Fisher, J.B.; Hook, S.; Allen, R.; Anderson, M.; French, A.; Hain, C.; Hulley, G.; Wood, E. The ECOsystem Spaceborne Thermal Radiometer Experiment on Space Station (ECOSTRESS): Science motivation. In Proceedings of the American Geophysical Union (AGU) Fall Meeting, San Francisco, CA, USA, 15–19 December 2014. [Google Scholar]
- Fisher, J.B.; Hook, S.; Allen, R.; Anderson, M.; French, A.; Hain, C.; Hulley, G.; Wood, E. ECOSTRESS: NASA’s next-generation mission to measure evapotranspiration from the International Space Station. In Proceedings of the American Geophysical Union (AGU) Fall Meeting, San Francisco, CA, USA, 14–18 December 2015. [Google Scholar]
- ECOSTRESS. Available online: http://ecostress.jpl.nasa.gov (accessed on 29 December 2018).
- Lee, C.M.; Cable, M.L.; Hook, S.J.; Green, R.O.; Ustin, S.L.; Mandl, D.J.; Middleton, E.M. An introduction to the NASA Hyperspectral Infrared Imager (HyspIRI) mission and preparatory activities. Remote Sens. Environ. 2015, 167, 6–19. [Google Scholar] [CrossRef]
- Koetz, B.; Bastiaanssen, W.; Berger, M.; Defourney, P.; Del Bello, U.; Drusch, M.; Drinkwater, M.; Duca, R.; Fernandez, V.; Ghent, D.; et al. High Spatio-Temporal Resolution Land Surface Temperature Mission—A Copernicus candidate mission in support of agricultural monitoring. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018. [Google Scholar] [CrossRef]
- Lagouarde, J.-P.; Bhattacharya, B.K.; Crébassol, P.; Gamet, P.; Babu, S.S.; Boulet, G.; Briottet, X.; Buddhiraju, K.M.; Cherchali, S.; Dadou, I.; et al. The Indian-French Trishna Mission: Earth Observation in the Thermal Infrared with High Spatio-Temporal Resolution. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018. [Google Scholar] [CrossRef]
- Mercury, M.; Green, R.; Hook, S.; Oaida, B.; Wu, W.; Gunderson, A.; Chodas, M. Global cloud cover for assessment of optical satellite observation opportunities: A HyspIRI case study. Remote Sens. Environ. 2012, 126, 62–71. [Google Scholar] [CrossRef]
- Lagouarde, J.-P.; Irvine, M.; Dupont, S. Atmospheric turbulence induced errors on measurements of surface temperature from space. Remote Sens. Environ. 2015, 68, 40–53. [Google Scholar] [CrossRef]
- Alfieri, J.G.; Anderson, M.C.; Kustas, W.P.; Cammalleri, C. Effect of the revisit interval and temporal upscaling methods on the accuracy of remotely sensed evapotranspiration estimates. Hydrol. Earth Syst. Sic. 2017, 21, 83–98. [Google Scholar] [CrossRef]
- Kustas, W.P.; Perry, E.M.; Doraiswamy, P.C.; Moran, M.S. Using satellite remote sensing to extrapolate evapotranspiration estimates in time and space over a semiarid rangeland basin. Remote Sens. Environ. 1994, 49, 275–286. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Molden, D.J.; Makin, I.W. Remote sensing for irrigated agriculture: Examples from research and possible applications. Agric. Water Manag. 2000, 46, 137–155. [Google Scholar] [CrossRef]
- Anderson, M.C.; Kustas, W.P.; Norman, J.M.; Hain, C.R.; Mecikalski, J.R.; Schultz, L.; Gonzalez-Dugo, M.P.; Cammalleri, C.; d’Urso, G.; Pimstein, A.; et al. Mapping daily evapotranspiration at field to continental scales using geostationary and polar orbiting satellite imagery. Hydrol. Earth Syst. Sci. 2011, 15, 223–239. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Gurney, R.J.; Hsu, A.Y.; Ormsby, J.P. FIFE, the variation on energy partition at surface flux sites. In Proceedings of the International Association of Hydrological Sciences (IAHS) Third Scientific Assembly, Baltimore, MD, USA, 10–19 May 1989; pp. 67–74. [Google Scholar]
- Shuttleworth, W.J. The Modellion concept. Rev. Geophys. 1991, 29, 585–606. [Google Scholar] [CrossRef]
- Jackson, R.D.; Hatfield, J.L.; Reginato, R.J.; Idso, S.B.; Pinter, P.J. Estimation of daily evapotranspiration from one time of day measurements. Agric. Water Manag. 1983, 7, 351–362. [Google Scholar] [CrossRef]
- Brutsaert, W.; Sugita, M. Application of self-preservation in the diurnal evolution of the surface energy budget to determine daily evaporation. J. Geophys. Res. 1992, 97, 18377–18382. [Google Scholar] [CrossRef]
- Zhang, L.; Lemeur, R. Evaluation of daily evaporation estimates from instantaneous measurements. Agric. For. Meteorol. 1995, 74, 139–154. [Google Scholar] [CrossRef]
- Delogu, E.; Boulet, G.; Olioso, A.; Coudert, B.; Chirouze, J.; Ceschia, E.; Le Dantec, V.; Marloie, O.; Chehbouni, G.; Lagouarde, J.-P. Reconstruction of temporal variations of evapotranspiration using instantaneous estimates at the time of satellite overpass. Hydrol. Earth Syst. Sci. 2012, 16, 2995–3010. [Google Scholar] [CrossRef]
- Van Niel, T.G.; McVicar, T.R.; Roderick, M.L.; van Djik, A.I.J.M.; Beringer, J.; Hutley, L.B.; van Gorsel, E. Upscaling latent heat flux for thermal remote sensing studies: Comparison of alternative approaches and correction of bias. J. Hydrol. 2012, 468–469, 35–46. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.-L.; Sun, X. Temporal upscaling of instantaneous evapotranspiration: An intercomparison of four methods using eddy covariance measurements and MODIS data. Remote Sens. Environ. 2013, 138, 102–118. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Kustas, W.P. Upscaling of evapotranspiration fluxes from instantaneous to daytime scales for thermal remote sensing applications. Hydrol. Earth Syst. Sci. 2014, 18, 1885–1894. [Google Scholar] [CrossRef]
- Ryu, Y.; Baldocchi, D.D.; Black, T.A.; Detto, M.; Law, B.E.; Leuning, R.; Miyata, A.; Reichstein, M.; Vargas, R.; Ammann, C.; et al. On the temporal upscaling of evapotranspiration from instantaneous remote sensing measurements to 8-day mean daily-sums. Agric. For. Meteorol. 2012, 152, 212–222. [Google Scholar] [CrossRef]
- Crago, R.D. Conservation and variability of the evaporative fraction during the daytime. J. Hydrol. 1996, 180, 173–194. [Google Scholar] [CrossRef]
- Sobrino, J.; Gomez, M.; Jimenez-Munoz, J.; Olioso, A. Application of a simple algorithm to estimate daily evapotranspiration from NOAA-AVHRR images for the Iberian Peninsula. Remote Sens. Environ. 2007, 110, 139–148. [Google Scholar] [CrossRef]
- Hoedjes, J.C.B.; Chehbouni, A.; Jacob, F.; Ezzahar, J.; Boulet, G. Deriving daily evapotranspiration from remotely sensed instantaneous evaporative fraction over olive orchard in semi-arid Morocco. J. Hydrol. 2008, 354, 53–64. [Google Scholar] [CrossRef]
- Crago, R.D.; Brutsaert, W. Daytime evaporation and the self-preservation of the evaporative fraction and the Bowen ratio. J. Hydrol. 1996, 178, 241–255. [Google Scholar] [CrossRef]
- Gentine, P.; Entekhabi, D.; Chehbouni, A.; Boulet, G.; Duchemin, B. Analysis of evaporative fraction diurnal behaviour. Agric. For. Meteorol. 2007, 143, 13–29. [Google Scholar] [CrossRef]
- Van Niel, T.G.; McVicar, T.R.; Roderick, M.L.; van Dijk, A.I.J.M.; Renzullo, L.J.; van Gorsel, E. Correcting for systematic error in satellite-derived latent heat flux due to assumptions in temporal scaling: Assessment from flux tower observations. J. Hydrol. 2011, 409, 140–148. [Google Scholar] [CrossRef]
- Sugita, M.; Brutsaert, W. Daily evaporation over a region from lower boundary layer profiles measured with radiosondes. Water Resour. Res. 1991, 27, 747–752. [Google Scholar] [CrossRef]
- Stannard, D.I.; Blanford, J.H.; Kustas, W.P.; Nichols, W.D.; Amer, S.A.; Schmugge, T.J.; Welt, M.A. Interpretation of surface-flux measurements in heterogeneous terrain during Monsoon ’90 experiment. Water Resour. Res. 1994, 30, 1227–1239. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. Fluxnet: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–3434. [Google Scholar] [CrossRef]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. 1948, 193, 120–145. [Google Scholar]
- Shuttleworth, W.J. Evaporation. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: Sydney, Australia, 1993; Chapter 4. [Google Scholar]
- McVicar, T.R.; Roderick, M.L.; Donohue, R.J.; Li, L.T.; Van Niel, T.G.; Thomas, A.; Grieser, J.; Jhajharia, D.; Himri, Y.; Mahowald, N.M.; et al. Global review and synthesis of trends in observed terrestrial near-surface wind speeds: Implications for evaporation. J. Hydrol. 2012, 416–417, 182–205. [Google Scholar] [CrossRef]
- Donohue, R.J.; McVicar, T.R.; Roderick, M.L. Assessing the ability of potential evaporation formulations to capture the dynamics in evaporative demand within a changing climate. J. Hydrol. 2010, 386, 186–197. [Google Scholar] [CrossRef]
- McVicar, T.R.; Roderick, M.L.; Donohue, R.J.; Van Niel, T.G. Less bluster ahead? Overlooked ecohydrological implications of global trends of terrestrial near-surface wind speeds. Ecohydrology 2012, 5, 381–388. [Google Scholar] [CrossRef]
- Delogu, E.; Boulet, G.; Olioso, A.; Garrigues, S.; Brut, A.; Tallec, T.; Demarty, J.; Soudani, K.; Lagouarde, J.-P. Evaluation of the SPARSE dual-source model for predicting water stress and evapotranspiration from thermal infra-red data over multiple crops and climates. Remote Sens. 2018, 10, 1806. [Google Scholar] [CrossRef]
- Lagouarde, J.-P.; Olioso, A.; Roujean, J.-L.; Boulet, G.; Coudert, B.; Dayau, S.; Castillo, S.; Weiss, M. Defining the revisit frequency for the MISTIGRI project of a satellite mission in the thermal infrared. In Proceedings of the 3rd International Symposium “Recent Advances in Quantitative Remote Sensing”, Valencia, Spain, 27 September–1 October 2010; pp. 824–829. [Google Scholar]
- Leys, C.; Ley, C.; Klein, O.; Bernard, P.; Licata, L. Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median. J. Exp. Soc. Psychol. 2013, 49, 764–766. [Google Scholar] [CrossRef]
- Billesbach, D.P.; Fischer, M.L.; Torn, M.S.; Berry, J.A. A Portable Eddy Covariance System for the Measurement of Ecosystem-Atmosphere Exchange of CO2, Water Vapor, and Energy. J. Atmos. Ocean. Technol. 2004, 21, 639–650. [Google Scholar] [CrossRef]
- Krishnan, P.; Meyers, T.P.; Scott, R.L.; Kennedy, L.; Heuer, M. Energy exchange and evapotranspiration over two temperate semi-arid grasslands in North America. Agric. For. Meteorol. 2012, 153, 31–44. [Google Scholar] [CrossRef]
- Meyers, T.P.; Hollinger, S.E. An assessment of storage terms in the surface energy balance of maize and soybean. Agric. For. Meteorol. 2004, 125, 105–115. [Google Scholar] [CrossRef]
- Hollinger, D.Y.; Ollinger, S.V.; Richardson, A.D.; Meyers, T.P.; Dail, D.B.; Martin, M.E.; Scott, N.A.; Arkebauer, D.; Baldocchi, D.; Clark, K.L.; et al. Albedo estimates for land surface models and support for a new paradigm based on foliage nitrogen concentration. Glob. Chang. Biol. 2010, 16, 696–710. [Google Scholar] [CrossRef]
- Matamala, R.; Jastrow, J.D.; Miller, R.M.; Garten, C.T. Temporal changes in C and N stocks of restored prairie: Implications for C sequestration strategies. Ecol. Appl. 2008, 18, 1470–1488. [Google Scholar] [CrossRef] [PubMed]
- Gilmanov, T.G.; Tieszen, L.L.; Wylie, B.K.; Flanagan, L.B.; Frank, A.B.; Haferkamp, M.R.; Meyers, T.P.; Morgan, J.A. Integration of CO2 flux and remotely-sensed data for primary production and ecosystem respiration analyses in the Northern Great Plains: Potential for quantitative spatial extrapolation. Glob. Ecol. Biogeogr. 2005, 14, 271–292. [Google Scholar] [CrossRef]
- Heinsch, F.A.; Heilman, J.L.; McInnes, K.J.; Cobos, D.R.; Zuberer, D.A.; Roelke, D.L. Carbon dioxide exchange in a high marsh on the Texas Gulf Coast: Effects of freshwater availability. Agric. For. Meteorol. 2004, 125, 159–172. [Google Scholar] [CrossRef]
- Brunsell, N.A.; Ham, J.M.; Owensby, C.E. Assessing the multi-resolution information content of remotely sensed variables and elevation for evapotranspiration in a tall-grass prairie environment. Remote Sens. Environ. 2008, 112, 2977–2987. [Google Scholar] [CrossRef]
- Noormets, A.; Gavazzi, M.J.; McNulty, S.G.; Domec, J.-C.; Sun, G.; King, J.S.; Chen, J. Response of carbon fluxes to drought in a coastal plain loblolly pine forest. Glob. Chang. Biol. 2010, 16, 272–287. [Google Scholar] [CrossRef]
- Verma, S.B.; Dobermann, A.; Cassman, K.G.; Walters, D.T.; Knops, J.M.; Arkebauer, T.J.; Suyker, A.E.; Burba, G.G.; Amos, B.; Yang, H.S.; et al. Annual carbon dioxide exchange in irrigated and rainfed maize-based agroecosystems. Agric. For. Meteorol. 2005, 131, 77–96. [Google Scholar] [CrossRef]
- Gu, L.H.; Meyers, T.; Pallardy, S.G.; Hanson, P.J.; Yang, B.; Heuer, M.; Hosman, K.P.; Liu, Q.; Riggs, J.S.; Sluss, D.; et al. Influences of biomass heat and biochemical energy storages on the land surface fluxes and radiative temperature. J. Geophys. Res. 2007, 112, D02107. [Google Scholar] [CrossRef]
- Scott, R.L.; Jenerette, G.D.; Potts, D.L.; Huxman, T.E. Effects of seasonal drought on net carbon dioxide exchange from a woody-plantencroached semiarid grassland. J. Geophys. Res. Biogeogr. 2009, 114, G04004. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Xu, L.K.; Kiang, N. How plant functional-type, weather, seasonal drought, and soil physical properties alter water and energy fluxes of an oak-grass savanna and an annual grassland. Agric. For. Meteorol. 2004, 123, 13–39. [Google Scholar] [CrossRef]
- Ryu, Y.; Baldocchi, D.D.; Ma, S.; Hehn, T. Interannual variability of evapotranspiration and energy exchanges over an annual grassland in California. J. Geophys. Res. 2008, 113, D09104. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Meyers, T.P. On using eco-physiological, micrometeorological and biogeochemical theory to evaluate carbon dioxide, water vapor and gaseous deposition fluxes over vegetation. Agric. For. Meteorol. 1998, 90, 1–25. [Google Scholar] [CrossRef]
- Chen, B.; Black, T.A.; Coops, N.C.; Hilker, T.; Trofymow, J.A.; Morgenstern, K. Assessing Tower Flux Footprint Climatology and Scaling Between Remotely Sensed and Eddy Covariance Measurements. Bound.-Lay. Meteorol. 2009, 130, 137–167. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulermans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–234. [Google Scholar] [CrossRef]
- Chehbouni, A.; Hoedjes, J.C.B.; Rodriguez, J.-C.; Watts, C.J.; Garatuza, J.; Jacob, F.; Kerr, Y. Using remotely sensed data to estimate area-averaged daily surface fluxes over a semi-arid mixed agricultural land. Agric. For. Meteorol. 2008, 148, 330–342. [Google Scholar]
- Baldocchi, D.D.; Ma, S. How will land use affect air temperature in the surface boundary layer? Lessons learned from a comparison study on the energy balance of an oak savanna and annual grassland in California, USA. Tellus 2013, 65, 19994. [Google Scholar] [CrossRef]
- Foken, T. The energy balance closure problem: An overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef]
- Leuning, R.; Van Gorsel, E.; Massman, W.J.; Isaac, P.R. Reflections on the surface energy imbalance problem. Agric. For. Meteorol. 2012, 156, 65–74. [Google Scholar] [CrossRef]
- Garrigues, S.; Olioso, A.; Calvet, J.-C.; Martin, E.; Lafont, S.; Moulin, S.; Chanzy, A.; Marloie, O.; Buis, S.; Desfonds, V.; et al. Evaluation of land surface model simulations of evapotranspiration over a 12-year crop succession: Impact of soil hydraulic and vegetation properties. Hydrol. Earth Syst. Sci. 2015, 19, 3109–3131. [Google Scholar] [CrossRef]
- AmeriFlux. Available online: http://ameriflux.ornl.gov (accessed on 29 December 2018).
- Boulet, G.; Mougenot, B.; Lhomme, J.-P.; Fanise, P.; Lili-Chabaane, Z.; Olioso, A.; Bahir, M.; Rivalland, V.; Jarlan, L.; Merlin, O.; et al. The SPARSE model for the prediction of water stress and evapotranspiration components from thermal infra-red data and its evaluation over irrigated and rainfed wheat. Hydrol. Earth Syst. Sci. 2015, 19, 4653–4672. Available online: www.hydrol-earth-syst-sci.net/19/4653/2015/ (accessed on 7 March 2019). [CrossRef]
- Ghilain, N.; Arboleda, A.; Gellens-Meulenberghs, F. Evapotranspiration modelling at large scale using near-real time MSG SEVIRI derived data. Hydrol. Earth Syst. Sci. 2011, 15, 771–786. [Google Scholar] [CrossRef]
- Roerink, G.J.; Su, Z.; Menenti, M. S-SEBI: A simple remote sensing algorithm to estimate the surface energy balance. Phys. Chem. Earth. Pt B 2000, 25, 147–157. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Guillevic, P.C.; Göttsche, F.; Nickeson, J.; Hulley, G.; Ghent, D.; Yu, Y.; Trigo, I.; Hook, S.; Sobrino, J.A.; Remedios, J.; et al. Land Surface Temperature Product Validation Best Practice Protocol. Version 1.1. In Best Practice for Satellite-Derived Land Product Validation; Guillevic, P., Göttsche, F., Nickeson, J., Román, M., Eds.; Land Product Validation Subgroup (WGCV/CEOS), NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2018; p. 58. [Google Scholar]
- Guillevic, P.C.; Bork-Unkelbach, A.; Goettsche, F.M.; Hulley, G.; Gastellu-Etchegorry, J.P.; Olesen, F.; Privette, J.L. Directional viewing effects on Satellite Land Surface Temperature products over sparse vegetation canopies—A multi-sensor analysis. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1464–1468. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating Land Surface Evaporation: A Review of Methods Using Remotely Sensed Surface Temperature Data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Petropoulos, G.; Carlson, T.N.; Wooster, M.J.; Islam, S. A review of Ts/VI remote sensing based methods for the retrieval of land surface energy fluxes and soil surface moisture. Prog. Phys. Geogr. 2009, 33, 224–250. [Google Scholar] [CrossRef]
- Karimi, P.; Bastiaanssen, W.G.M. Spatial evapotranspiration, rainfall and land use data in water accounting—Part 1: Review of the accuracy of the remote sensing data. Hydrol. Earth Syst. Sci. 2015, 19, 507–532. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating subpixel surface temperatures and energy fluxes from the vegetation index-radiometric temperature relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
- Eswar, R.; Sekhar, M.; Bhattacharya, B.K.; Bandyopadhyay, S. Spatial Disaggregation of Latent Heat Flux Using Contextual Models over India. Remote Sens. 2017, 9, 949. [Google Scholar] [CrossRef]
- Eswar, R.; Sekhar, M.; Bhattacharya, B.K. A simple model for spatial disaggregation of evaporative fraction: Comparative study with thermal sharpened land surface temperature data over India. J. Geophys. Res. Atmos. 2013, 118, 12029–12044. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Gao, F.; Hain, C.R.; Kustas, W.P. Mapping daily evapotranspiration at field scales over rainfed and irrigated agricultural areas using remote sensing data fusion. Agric. For. Meteorol. 2014, 186, 1–11. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F.G. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Bindhu, V.M.; Narasimhan, B.; Sudheer, K.P. Development and verification of a non-linear disaggregation method (NL-DisTrad) to downscale MODIS land surface temperature to the spatial scale of Landsat thermal data to estimate evapotranspiration. Remote Sens. Environ. 2013, 135, 118–129. [Google Scholar] [CrossRef]
- Guillevic, P.C.; Privette, J.L.; Coudert, B.; Palecki, M.A.; Demarty, J.; Ottlé, C.; Augustine, J.A. Land Surface Temperature product validation using NOAA’s surface climate observation networks—Scaling methodology for the Visible Infrared Imager Radiometer Suite (VIIRS). Remote Sens. Environ. 2012, 124, 282–298. [Google Scholar] [CrossRef]
- Guillevic, P.C.; Biard, J.; Hulley, G.C.; Privette, J.L.; Hook, S.J.; Olioso, A.; Göttsche, F.-M.; Radocinski, R.; Román, M.O.; Yu, Y.; et al. Validation of Land Surface Temperature products derived from the Visible Infrared Imager Radiometer Suite (VIIRS) using ground-based and heritage satellite measurements. Remote Sens. Environ. 2014, 154, 19–37. [Google Scholar] [CrossRef]









| Study/Reference | Scaling Quantities (1) | Data/Location/Experiment | Relevant Particularities | Key Findings |
|---|---|---|---|---|
| Jackson et al. [32] | Simulated RG | Crop sites in CA, NE, MN, ID | Daytime scale; impact of cloudiness | Good performance for cloud free days |
| Brutsaert and Sugita [33] | AE, RG, Rn | FIFE (2) | Daytime scale; impact of cloudiness | Good performance of the models based on AE, Rn, Rg |
| Crago [40] | AE | FIFE (2) | Daytime scale; impact of cloudiness | Variability of EF depends on cloudiness and advection of moisture |
| Zhang and Lemeur [34] | AE, Simulated RG | HAPEX-MOBILHY (3) experiment | Daytime scale; impact of cloudiness | Constant EF is valid under cloud-free conditions only |
| Anderson et al. [4] | AE | Large-area implementation | Daytime scale; Used a surface energy balance model | Found systematic error of 10%; Defined correction factor of 1.1 |
| Hoedjes et al. [42] | AE | Olive orchard in Morocco | Daytime scale; Applied correction factor under dry conditions | EF was well preserved under dry conditions only |
| Van Niel et al. [45] | AE | Two long-term (2001–2008) flux tower sites in Australia | Daily scale; account for observed biases and nighttime fluxes | β-correction functions significantly reduce observed bias |
| Delogu et al. [35] | RG, PET | Five agricultural fields; three-year datasets | Daytime scale; Interpolation between cloud free conditions | Best performance of the model based on RG for sites with water stress |
| Ryu et al. [39] | AE, RTOA | 34 flux towers from FLUXNET; one-year datasets | Daily scale; No correction factor; Comparison with satellite-based ET | Best performance of the model based on RTOA; up to 13% bias using AE |
| Van Niel et al. [36] | AE, RG (measured and modelled), RTOA | Two long-term (2001–2011) flux tower sites in Australia | Daytime scale; β-correction factors for each reference scaling flux | Best performance of the model based on RG |
| Tang et al. [37] | AE, RG, RTOA, PET | Yucheng, China | Daily scale; All sky conditions | Scaling based on PET had the best performance |
| Cammalleri et al. [38] | AE, RG, RTOA, PET | 14 Ameriflux sites; two-year datasets | Daytime scale; Applied β-correction factor of 1.1 to AE | RG is the most robust scaling variables; no seasonal variability was found |
| Site | ID | Lat | Lon | Surface Type | Period | Regional Climate | Reference |
|---|---|---|---|---|---|---|---|
| Southern Great Plains, OK | ARM | 36.606 | −97.489 | Cropland | 2003–2012 | Temperate | Billesbach et al. [57] |
| Audubon Ranch, AZ | Aud | 31.591 | −110.509 | Grassland | 2004–2008 | Semi-arid | Krishnan et al. [58] |
| Bondville, IL | Bo1 | 40.006 | −88.290 | Cropland | 1997–2007 | Temperate | Meyers and Hollinger [59] |
| Brookings, SD | Bkg | 44.345 | −96.836 | Grassland | 2005–2009 | Temperate | Hollinger et al. [60] |
| Chestnut Ridge, TN | ChR | 35.931 | −84.332 | Deciduous broadleaf | 2006–2013 | Temperate | Hollinger et al. [60] |
| Fermi, IL—Agricultural | IB1 | 41.859 | −88.223 | Cropland | 2006–2011 | Temperate | Matamala et al. [61] |
| Fermi, IL—Prairie | IB2 | 41.841 | −88.241 | Grassland | 2005–2011 | Temperate | Matamala et al. [61] |
| Fort Peck, MT | Fpe | 48.308 | −105.102 | Grassland | 2000–2008 | Temperate | Gilmanov et al. [62] |
| Freeman Ranch, TX—Mesquite | FR2 | 29.950 | −97.996 | Grassland | 2005–2008 | Semi-arid | Heinsch et al. [63] |
| Freeman Ranch, TX—Woodland | FR3 | 29.940 | −97.990 | Woody savannah | 2005–2012 | Semi-arid | Heinsch et al. [63] |
| Konza, KS | Kon | 39.082 | −96.560 | Grassland | 2007–2012 | Temperate | Brunsell et al. [64] |
| Loblolly Pine, NC | NC2 | 35.803 | −76.668 | Evergreen needleleaf | 2005–2010 | Sub-tropical | Noormets et al. [65] |
| Loblolly Pine Clearcut, NC | NC1 | 35.812 | −76.712 | Evergreen needleleaf | 2005–2009 | Sub-tropical | Noormets et al. [65] |
| Mead, NE—Irrigated maize | Ne1 | 41.165 | −96.477 | Irrigated cropland | 2002–2012 | Temperate | Verma et al. [66] |
| Mead, NE—Irrigated maize-soybean | Ne2 | 41.165 | −96.470 | Irrigated cropland | 2002–2012 | Temperate | Verma et al. [66] |
| Mead, NE—Rainfed maize-soybean | Ne3 | 41.180 | −96.440 | Rainfed cropland | 2002–2012 | Temperate | Verma et al. [66] |
| Missouri Ozark, MO | MOz | 38.744 | −92.200 | Deciduous broadleaf | 2005–2013 | Temperate | Gu et al. [67] |
| Santa Rita Mesquite, AZ | SRM | 31.821 | −110.866 | Woody savannah | 2004–2013 | Semi-arid | Scott et al. [68] |
| Tonzi Ranch, CA | Ton | 38.432 | −120.966 | Woody savannah | 2002–2012 | Semi-arid | Baldocchi et al. [69] |
| Vaira Ranch, CA | Var | 38.413 | −120.951 | Grassland | 2001–2012 | Semi-arid | Ryu et al. [70] |
| Walker Branch, TN | WBW | 35.959 | −84.287 | Deciduous broadleaf | 1995–2006 | Temperate | Baldocchi and Meyers [71] |
| Sky Condition before and after Clear Overpass | Scaling Flux | 10:00 Overpass | 13:00 Overpass | ||||
|---|---|---|---|---|---|---|---|
| β-Factor | ME | MAD | β-Factor | ME | MAD | ||
| All conditions (Clear or cloudy) | AE | 1.18 | −0.12 | 0.17 | 1.17 | −0.11 | 0.12 |
| RG | 1.09 | −0.06 | 0.16 | 1.07 | −0.04 | 0.13 | |
| RTOA | 0.93 | 0.06 | 0.17 | 0.99 | 0.01 | 0.13 | |
| PET | 1.11 | −0.08 | 0.16 | 1.19 | −0.13 | 0.12 | |
| Mostly clear sky | AE | 1.18 | −0.12 | 0.17 | 1.16 | −0.1 | 0.13 |
| RG | 1.07 | −0.05 | 0.15 | 1.04 | −0.03 | 0.13 | |
| RTOA | 0.98 | 0.02 | 0.17 | 1.00 | −0.01 | 0.13 | |
| PET | 1.09 | −0.06 | 0.16 | 1.18 | −0.12 | 0.12 | |
| Cloudy sky | AE | 1.18 | −0.12 | 0.17 | 1.18 | −0.11 | 0.13 |
| RG | 1.09 | −0.07 | 0.16 | 1.07 | −0.05 | 0.13 | |
| RTOA | 0.92 | 0.07 | 0.18 | 0.98 | 0.01 | 0.15 | |
| PET | 1.11 | −0.09 | 0.16 | 1.20 | −0.13 | 0.13 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guillevic, P.C.; Olioso, A.; Hook, S.J.; Fisher, J.B.; Lagouarde, J.-P.; Vermote, E.F. Impact of the Revisit of Thermal Infrared Remote Sensing Observations on Evapotranspiration Uncertainty—A Sensitivity Study Using AmeriFlux Data. Remote Sens. 2019, 11, 573. https://doi.org/10.3390/rs11050573
Guillevic PC, Olioso A, Hook SJ, Fisher JB, Lagouarde J-P, Vermote EF. Impact of the Revisit of Thermal Infrared Remote Sensing Observations on Evapotranspiration Uncertainty—A Sensitivity Study Using AmeriFlux Data. Remote Sensing. 2019; 11(5):573. https://doi.org/10.3390/rs11050573
Chicago/Turabian StyleGuillevic, Pierre C., Albert Olioso, Simon J. Hook, Joshua B. Fisher, Jean-Pierre Lagouarde, and Eric F. Vermote. 2019. "Impact of the Revisit of Thermal Infrared Remote Sensing Observations on Evapotranspiration Uncertainty—A Sensitivity Study Using AmeriFlux Data" Remote Sensing 11, no. 5: 573. https://doi.org/10.3390/rs11050573
APA StyleGuillevic, P. C., Olioso, A., Hook, S. J., Fisher, J. B., Lagouarde, J.-P., & Vermote, E. F. (2019). Impact of the Revisit of Thermal Infrared Remote Sensing Observations on Evapotranspiration Uncertainty—A Sensitivity Study Using AmeriFlux Data. Remote Sensing, 11(5), 573. https://doi.org/10.3390/rs11050573