A Two-Stage Aerial Target Localization Method Using Time-Difference-of-Arrival Measurements with the Minimum Number of Radars
Abstract
:1. Introduction
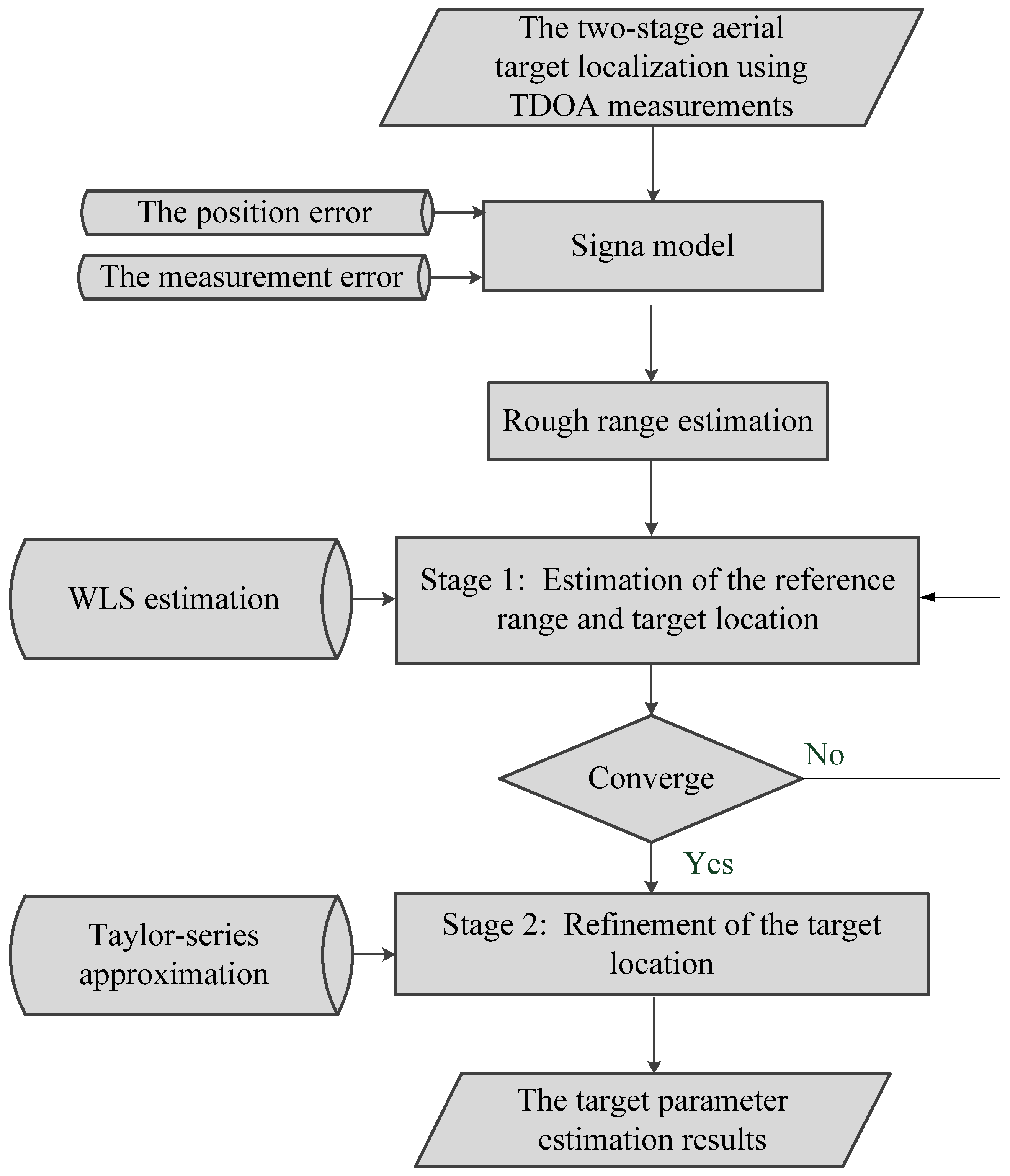
2. Materials and Methods
2.1. Basic Signal Model
2.2. Stage 1: Estimation of the Reference Range and the Target Location in an Iterative Way
2.3. Stage 2: Refinement of the Target Location Using Taylor Series Approximations
2.4. Cramer–Rao Lower Bound (CRLB)
3. Results
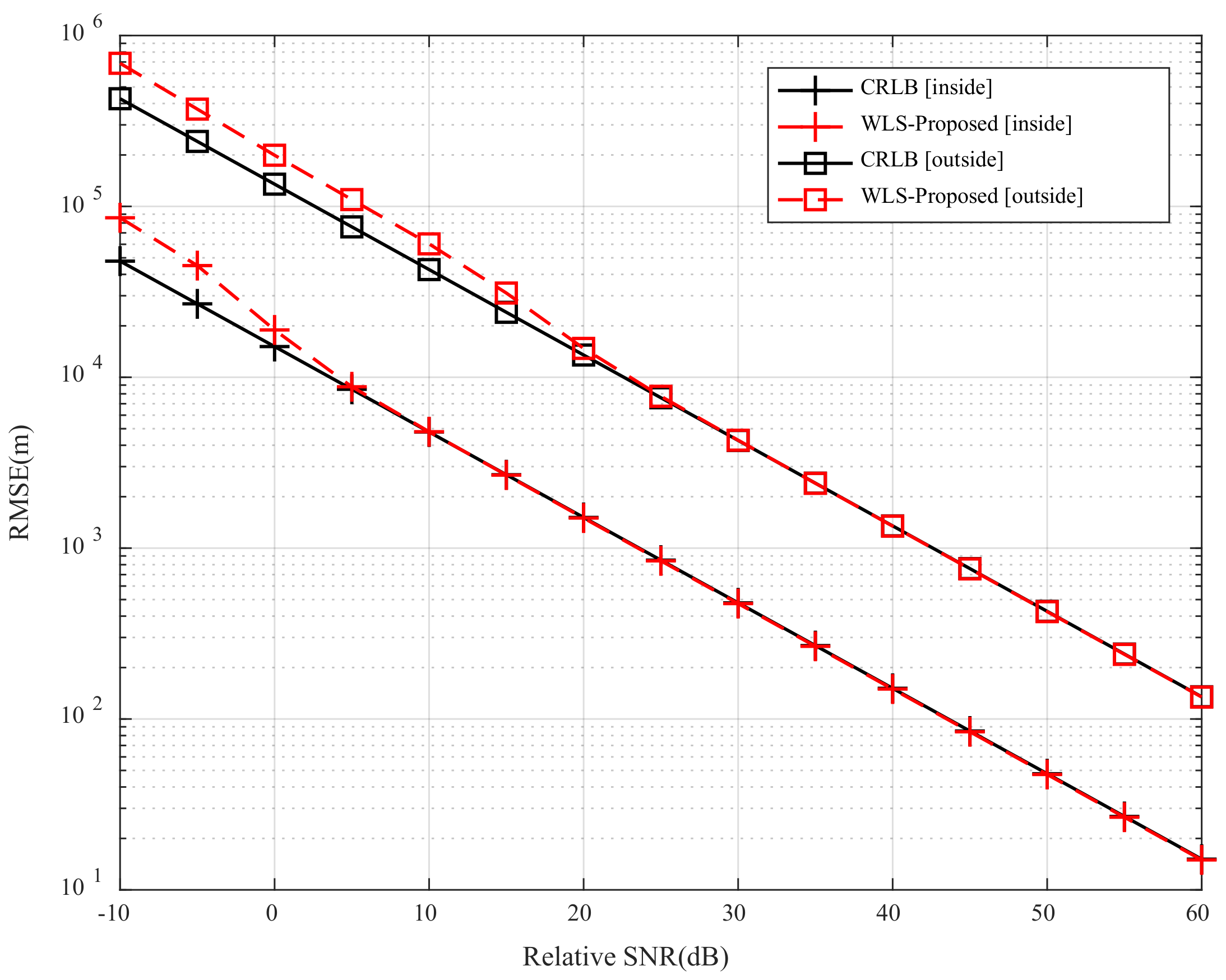
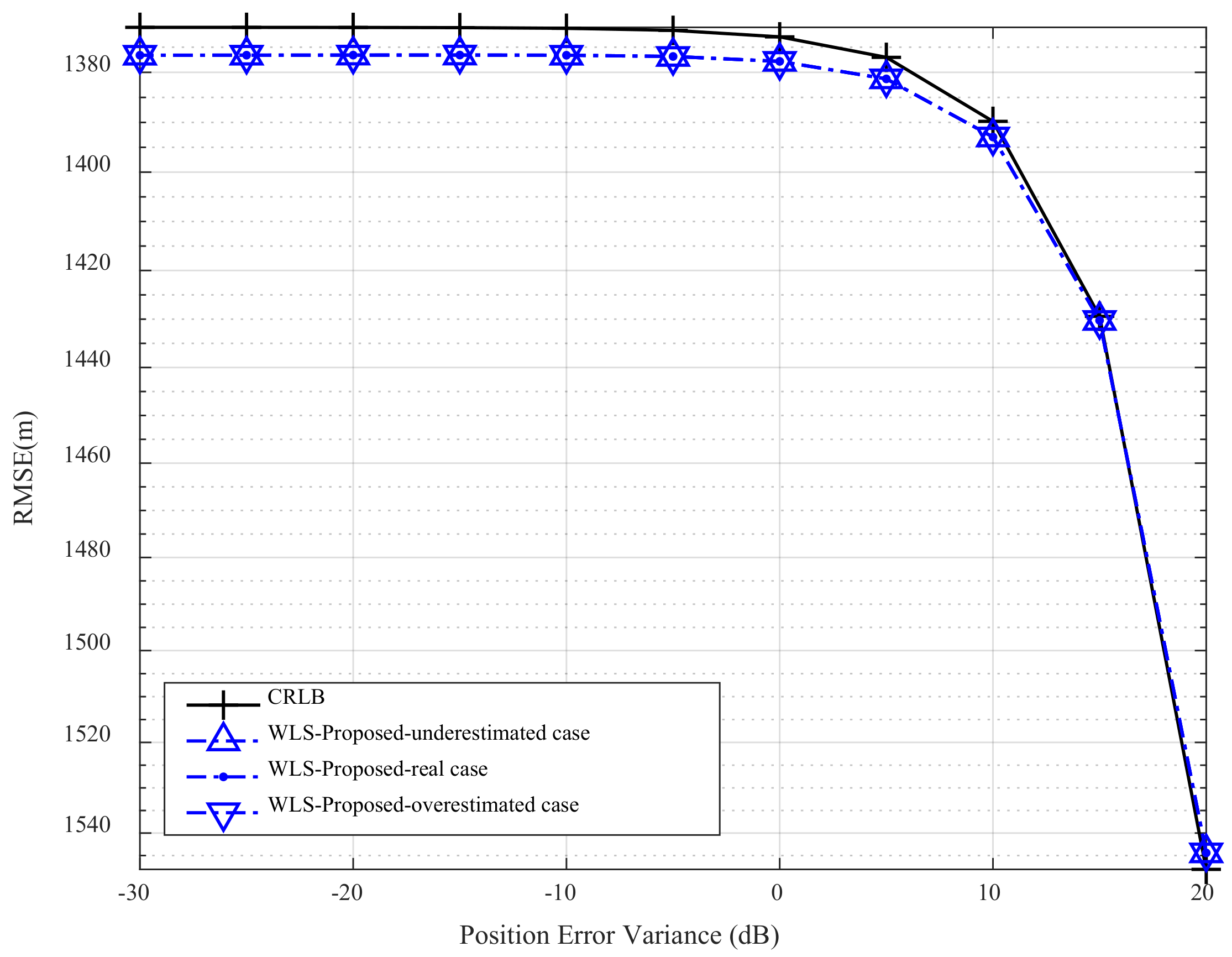
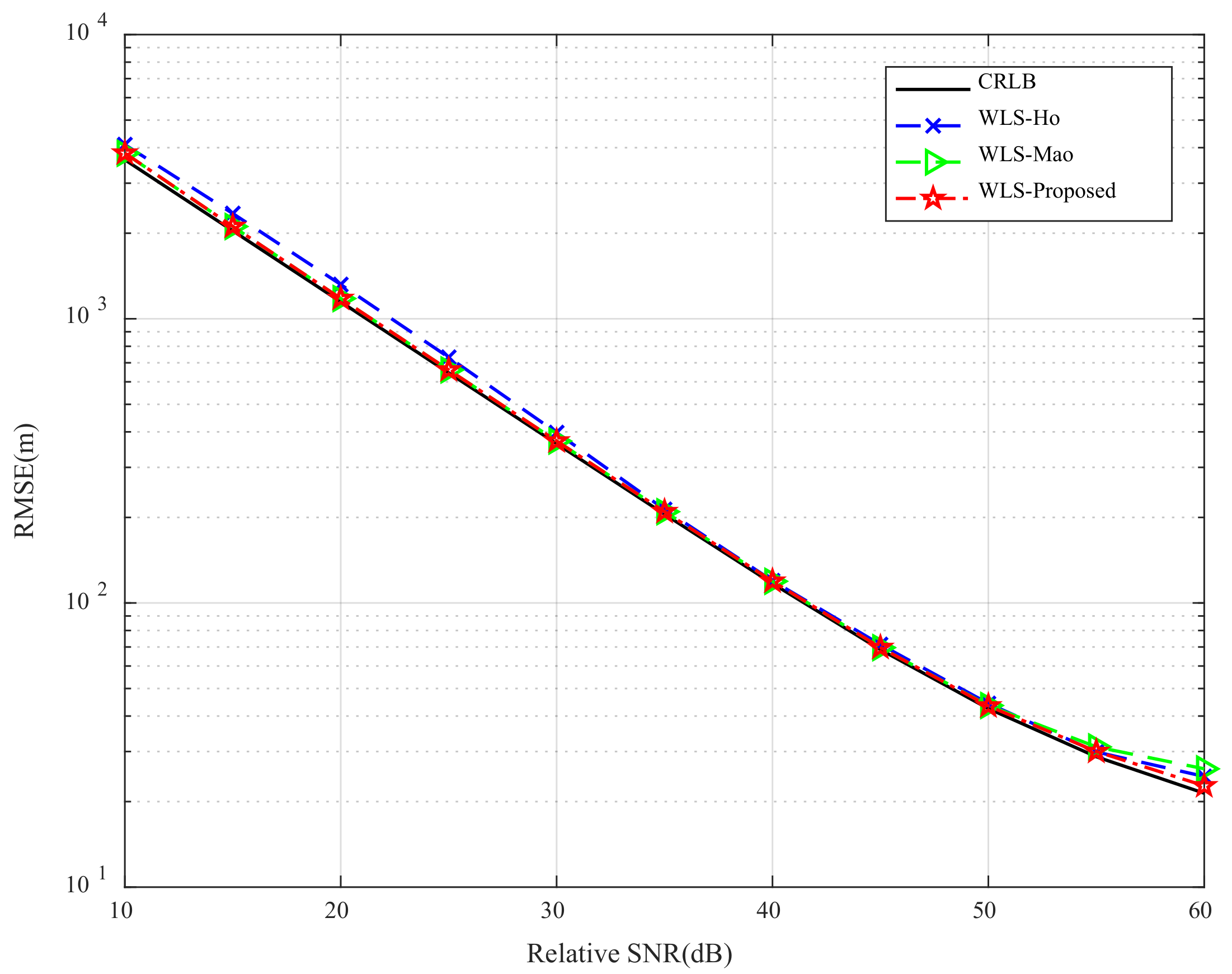
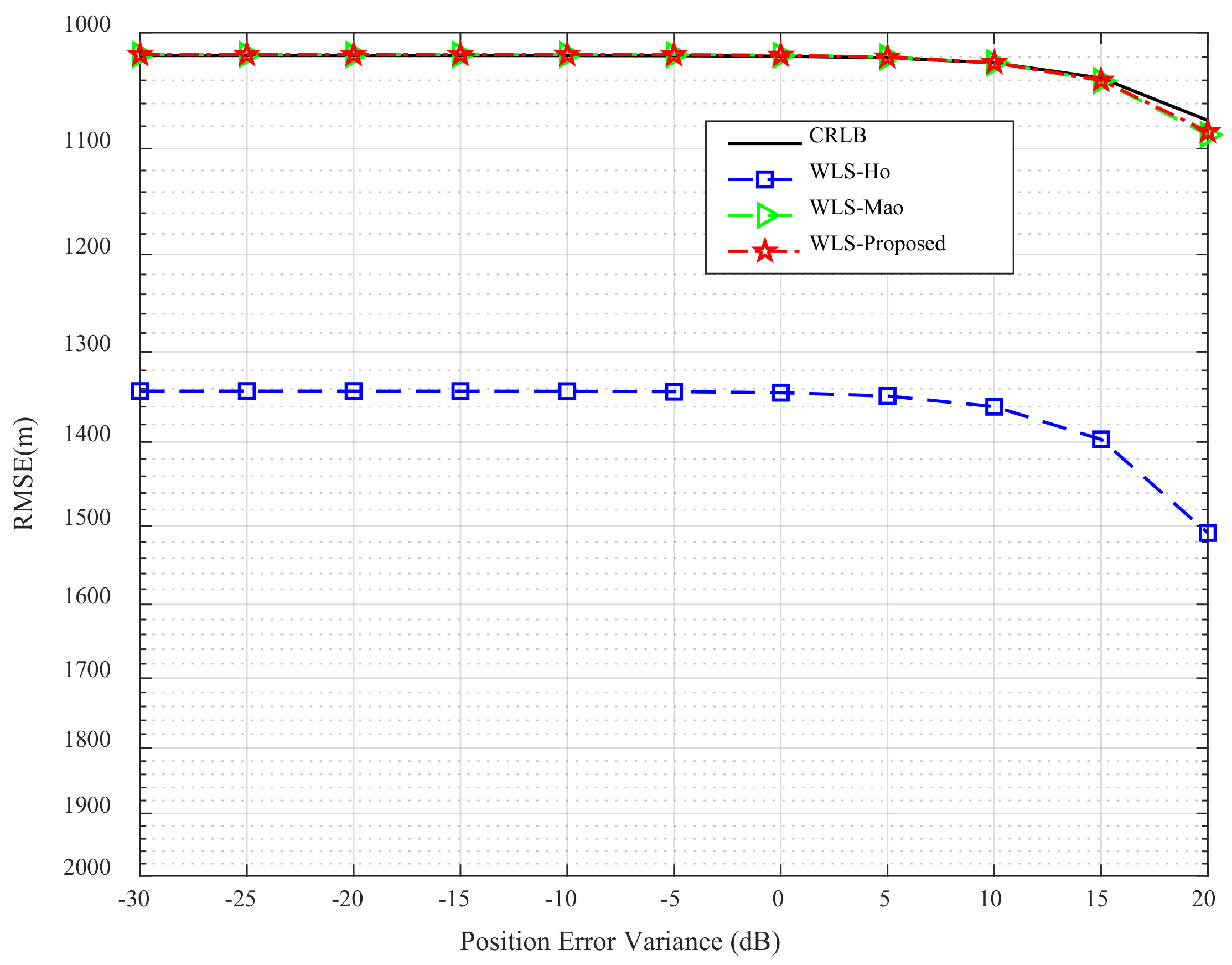
3.1. TDOA Target Localization with the Minimum Number of Radars
3.2. TDOA Target Localization with more Receiving Radars
4. Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Richard, A.P. Information Warfare and Electronic Warfare Systems, 1st ed.; Artech House: Norwood, MA, USA, 2013. [Google Scholar]
- Reza, A.; Buehrer, R.M. Handbook of Position Location: Theory, Practice and Advances, 1st ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2019. [Google Scholar]
- Malanowski, M. Signal Processing for Passive Bistatic Radar, 1st ed.; Artech House: Norwood, MA, USA, 2019. [Google Scholar]
- Weiss, A.J. Direct position determination of narrow band radio frequency transmitters. IEEE Signal Process. Lett. 2004, 11, 513–516. [Google Scholar] [CrossRef]
- Bar-Shalom, O.; Weiss, A.J. Direct positioning of stationary targets using MIMO radar. Signal Process. 2011, 91, 2345–2358. [Google Scholar] [CrossRef]
- Tzore, E.; Weiss, A.J. Expectation-maximization algorithm for direct position determination. Signal Process. 2017, 133, 32–39. [Google Scholar] [CrossRef]
- Smith, J.O.; Abel, J.S. Closed-form least-squares source location estimation from range difference measurements. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 1661–1669. [Google Scholar] [CrossRef]
- Hyuksso, S.; Wonzoo, C. Target localization using double-sided range measurements in distributed MMO systems. Sensors 2019, 19, 2524. [Google Scholar]
- Zhang, Y.; Ho, K.C. Multistatic localization in the absence of transmitter position. IEEE Trans. Signal Process. 2019, 67, 4745–4760. [Google Scholar] [CrossRef]
- Mellen, G., II; Pachter, M.; Raquet, J. Closed-form solution for determining emitter location using time difference of arrival measurements. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1056–1058. [Google Scholar] [CrossRef]
- Bhatta, B. Global Navigation Satellite Systems: New Technologies and Applications, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Xie, G. Principles of GPS, GLONASS, and Galileo, 1st ed.; Publishing Housing of Electronics Industry: Beijing, China, 2015. [Google Scholar]
- Kenneth, W.; So, H.C. A study of two-dimensional sensor placement using time difference-of-arrival-measurements. Digit. Signal Process. 2009, 19, 650–659. [Google Scholar]
- Nguyen, N.H.; Dogancay, K. Optimal geometry analysis for multistatic TOA localization. IEEE Trans. Signal Process. 2016, 64, 4180–4193. [Google Scholar] [CrossRef]
- Sadeghi, M.; Behnia, F.; Amiri, R. Optimal sensor placement for 2-D range-only target localization in constrained sensor geometry. IEEE Trans. Signal Process. 2020, 68, 2316–2327. [Google Scholar] [CrossRef]
- Fang, B.T. Simple solutions for hyperbolic and related position fixes. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 748–753. [Google Scholar] [CrossRef]
- Friedlander, B. A passive localization algorithm and its accuracy analysis. IEEE J. Ocean. Eng. 1987, 12, 234–245. [Google Scholar] [CrossRef]
- Schay, H.C.; Robinson, A.Z. Passive source localization employing intersecting spherical surfaces from time-of-arrival differences. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 1223–1225. [Google Scholar] [CrossRef]
- Foy, W.H. Position-location solutions by-Taylor-series estimation. IEEE Trans. Aerosp. Electron. Syst. 1976, 12, 187–194. [Google Scholar] [CrossRef]
- Koyaisaruch, L.; Ho, K.C.; So, H.C. Modified Taylor-series method for source and receiver localization using TDOA measurements with erroneous receiver positions. In Proceedings of the 2005 IEEE International Symposium on Circuits and Systems (ISCAS), Kobe, Japan, 23–26 May 2005; IEEE: Piscataway, NJ, USA, 2005. [Google Scholar]
- Chan, Y.T.; Ho, K.C. A simple and efficient estimator for hyperbolic location. IEEE Trans. Signal Process. 1994, 42, 1905–1915. [Google Scholar] [CrossRef]
- Ho, K.C.; Kovavisaruch, L.; Parikh, H. Source localization using TDOA with erroneous receiver positions. In Proceedings of the 2004 IEEE International Symposium on Circuits and Systems (ISCAS), Vancouver, BC, Canada, 23–26 May 2004; IEEE: Piscataway, NJ, USA, 2004. [Google Scholar]
- Ho, K.C.; Lu, X.N. Source localization using TDOA and FDOA measurements in the presence of receiver location errors: Analysis and solution. IEEE Trans. Signal Process. 2007, 55, 684–696. [Google Scholar] [CrossRef]
- Zhang, F.R.; Sun, Y.M.; Zou, J.F.; Zhang, D.; Wan, Q. Closed-form localization method for moving target in passive multistatic radar network. IEEE Sens. J. 2020, 20, 980–990. [Google Scholar] [CrossRef]
- Mao, Z.; Su, H.T.; He, B.; Jing, X. Moving source localization in passive sensor network with location uncertainty. IEEE Signal Process. Lett. 2021, 28, 823–827. [Google Scholar] [CrossRef]
- Ma, H.; Antoniou, M.; Stove, A.G.; Winkel, J.; Cherniakov, M. Maritime moving target localization using passive GNSS-based multistatic radar. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4808–4819. [Google Scholar] [CrossRef]
- Yang, L.; Ho, K.C. An approximately efficient TDOA localization algorithm in closed-form for locating multiple disjoint sources with erroneous sensor positions. IEEE Trans. Signal Process. 2009, 57, 4598–4615. [Google Scholar] [CrossRef]
- Sun, M.; Ho, K.C. An asymptotically efficient estimator for TDOA and FDOA positioning of multiple disjoint-sources in the presence of sensor location uncertainties. IEEE Trans. Signal Process. 2011, 59, 3434–3440. [Google Scholar]
- Liu, Y.; Guo, F.C.; Yang, L.; Jiang, W. An improved algebraic solution for TDOA localization with sensor position errors. IEEE Commun. Lett. 2015, 19, 2218–2221. [Google Scholar] [CrossRef]
- Cheung, K.W.; Ma, W.K.; So, H.C. Accurate approximation algorithm for TOA-based maximum likelihood mobile location using semidefinite programming. In Proceedings of the 2004 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Montreal, QC, Canada, 17–21 May 2004; IEEE: Piscataway, NJ, USA, 2004. [Google Scholar]
- Yang, K.; Wang, G.; Luo, Z.Q. Efficient convex relaxation methods for robust target localization by a sensor network using time differences of arrivals. IEEE Trans. Signal Process. 2009, 57, 2775–2784. [Google Scholar] [CrossRef]
- Zhao, R.C.; Wang, G.; Ho, K.C. Accurate semidefinite relaxation method for elliptic localization with unknown transmitter position. IEEE Trans. Wirel. Commun. 2021, 20, 2746–2760. [Google Scholar]
- Amiri, R.; Behnia, F.; Zamani, F. Asymptotically efficient target localization from bistatic range measurements in distributed MIMO radars. IEEE Signal Process. Lett. 2017, 20, 299–303. [Google Scholar] [CrossRef]
- Amiri, R.; Behnia, F.; Mohammad, A.M.S. Efficient positioning in MMO radars with widely separated antennas. IEEE Commun. Lett. 2017, 21, 1569–1572. [Google Scholar] [CrossRef]
- Amiri, R.; Behnia, F.; Sadr, M. Exact solution for elliptic localization in distributed MIMO radar systems. IEEE Trans. Veh. Technol. 2018, 67, 1075–1086. [Google Scholar] [CrossRef]
- Amiri, R.; Behnia, F.; Noroozi, A. Efficient joint moving target and antenna localization in distributed MIMO radars. IEEE Trans. Wirel. Commun. 2019, 18, 4425–4435. [Google Scholar] [CrossRef]
- Amiri, R.; Kazemi, R.; Behnia, F.; Noroozi, A. Efficient elliptic localization in the presence of antenna position uncertainties and clock parameter imperfections. IEEE Trans. Veh. Technol. 2019, 68, 9797–9805. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory, 1st ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Godrich, H.; Haimovich, A.M.; Blum, R.S. Target localization accuracy gain in MIMO radar-based systems IEEE Transactions on Information Theory. IEEE Trans. Inf. Theory 2010, 56, 2783–2803. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Li, Y.; Yang, X.; Li, Q.; Liu, F.; Wang, W.; Li, C.; Duan, C. A Two-Stage Aerial Target Localization Method Using Time-Difference-of-Arrival Measurements with the Minimum Number of Radars. Remote Sens. 2023, 15, 2829. https://doi.org/10.3390/rs15112829
Chen J, Li Y, Yang X, Li Q, Liu F, Wang W, Li C, Duan C. A Two-Stage Aerial Target Localization Method Using Time-Difference-of-Arrival Measurements with the Minimum Number of Radars. Remote Sensing. 2023; 15(11):2829. https://doi.org/10.3390/rs15112829
Chicago/Turabian StyleChen, Jinming, Yu Li, Xiaochao Yang, Qi Li, Fei Liu, Weiwei Wang, Caipin Li, and Chongdi Duan. 2023. "A Two-Stage Aerial Target Localization Method Using Time-Difference-of-Arrival Measurements with the Minimum Number of Radars" Remote Sensing 15, no. 11: 2829. https://doi.org/10.3390/rs15112829



