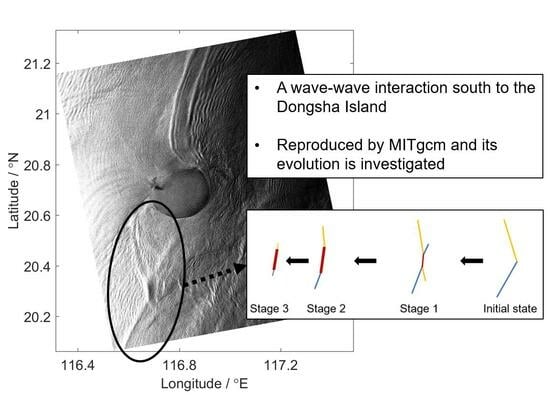
A Case Study of Wave–Wave Interaction South to Dongsha Island in the South China Sea
Abstract
:1. Introduction
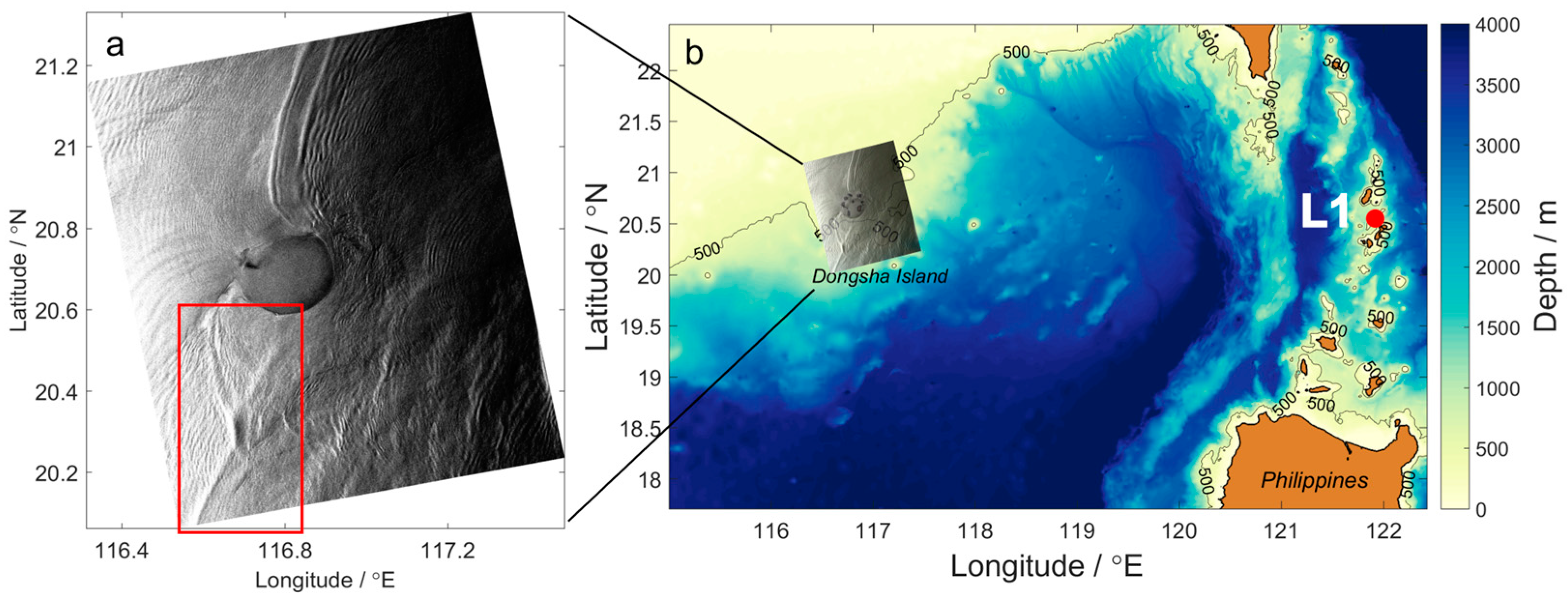
2. Model Setup and Validation
2.1. Model Setup
2.2. Model Validation
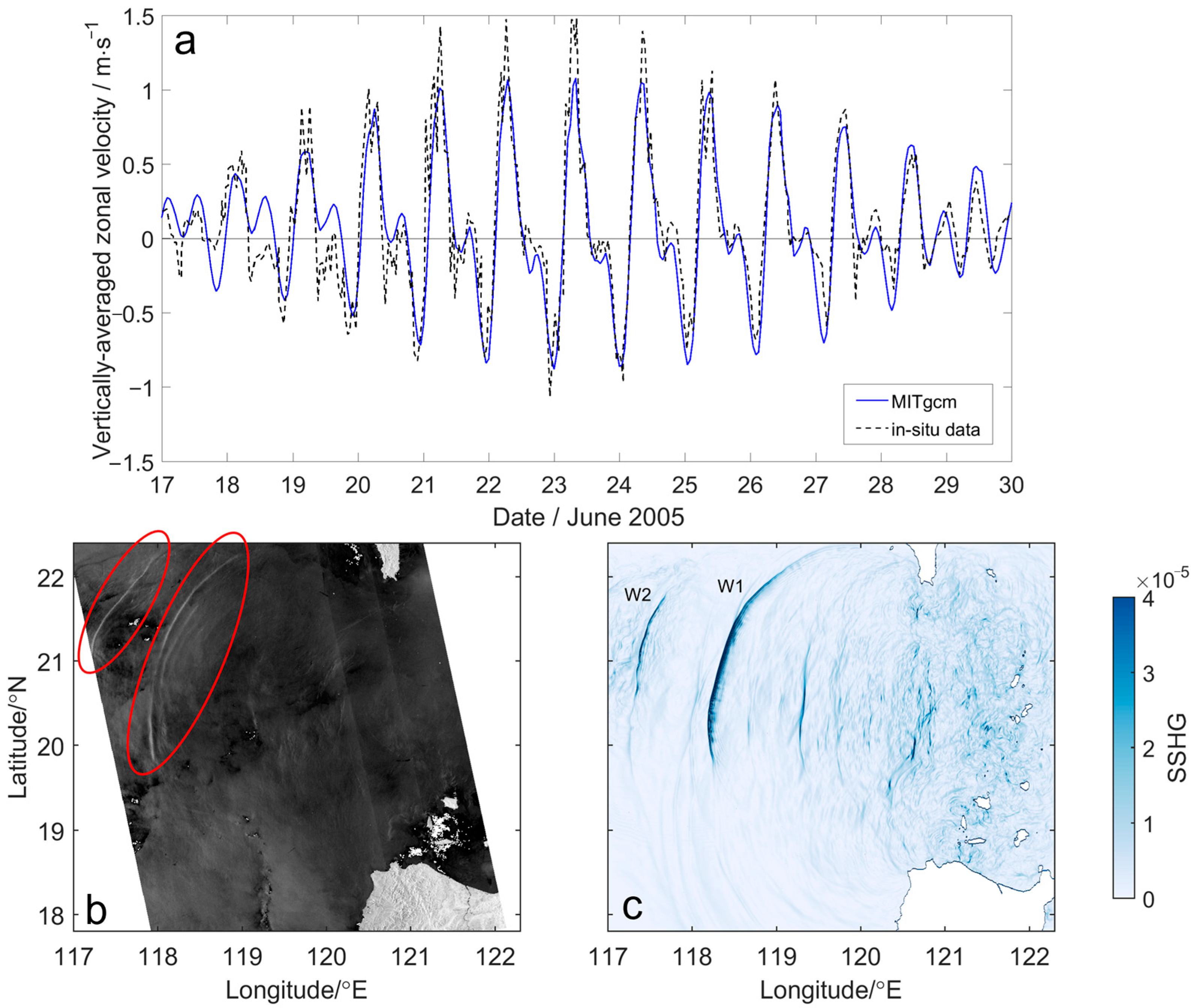
2.2.1. Comparison with In-Situ Measurements
2.2.2. Comparison with SAR Image
3. Results
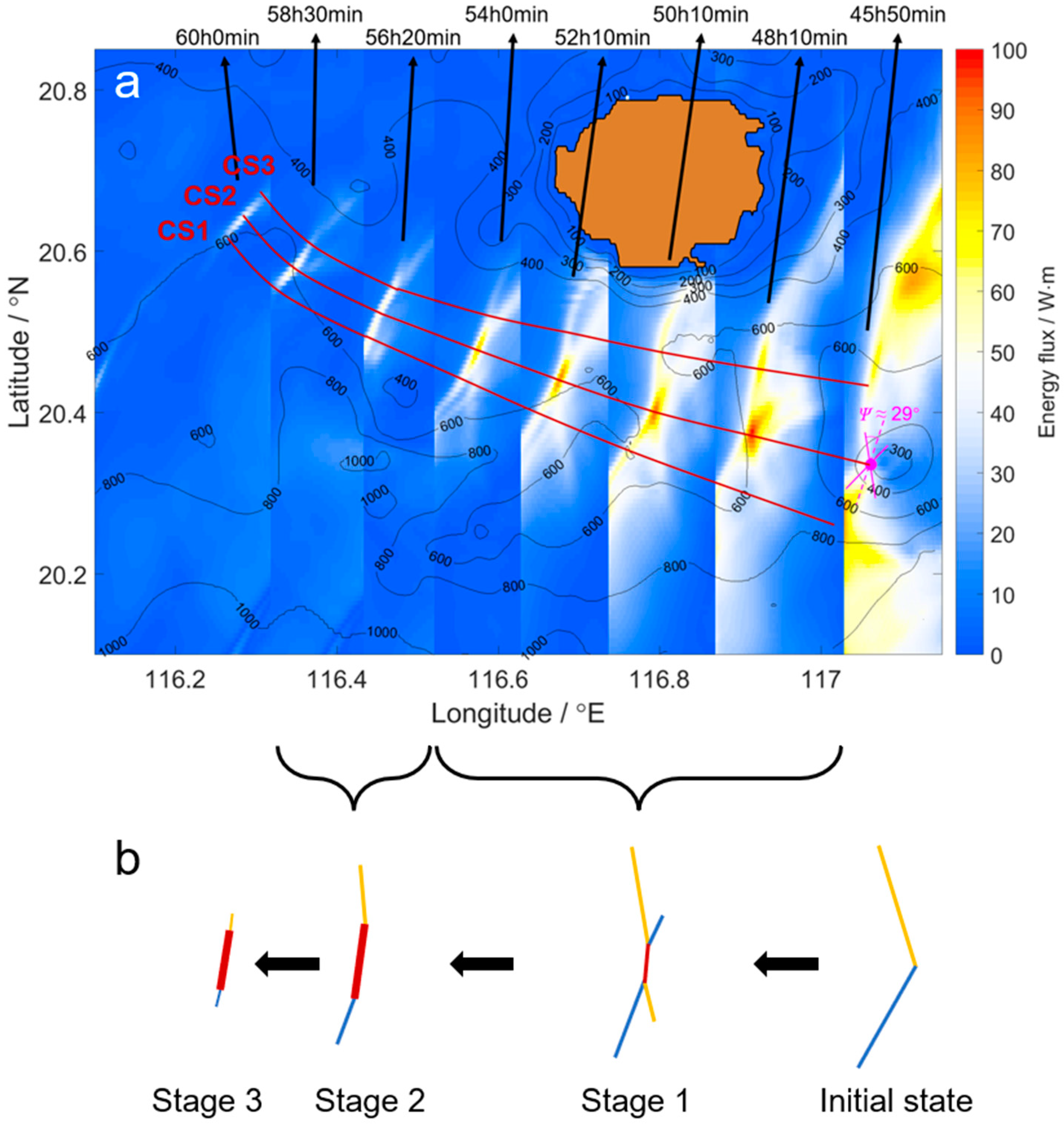
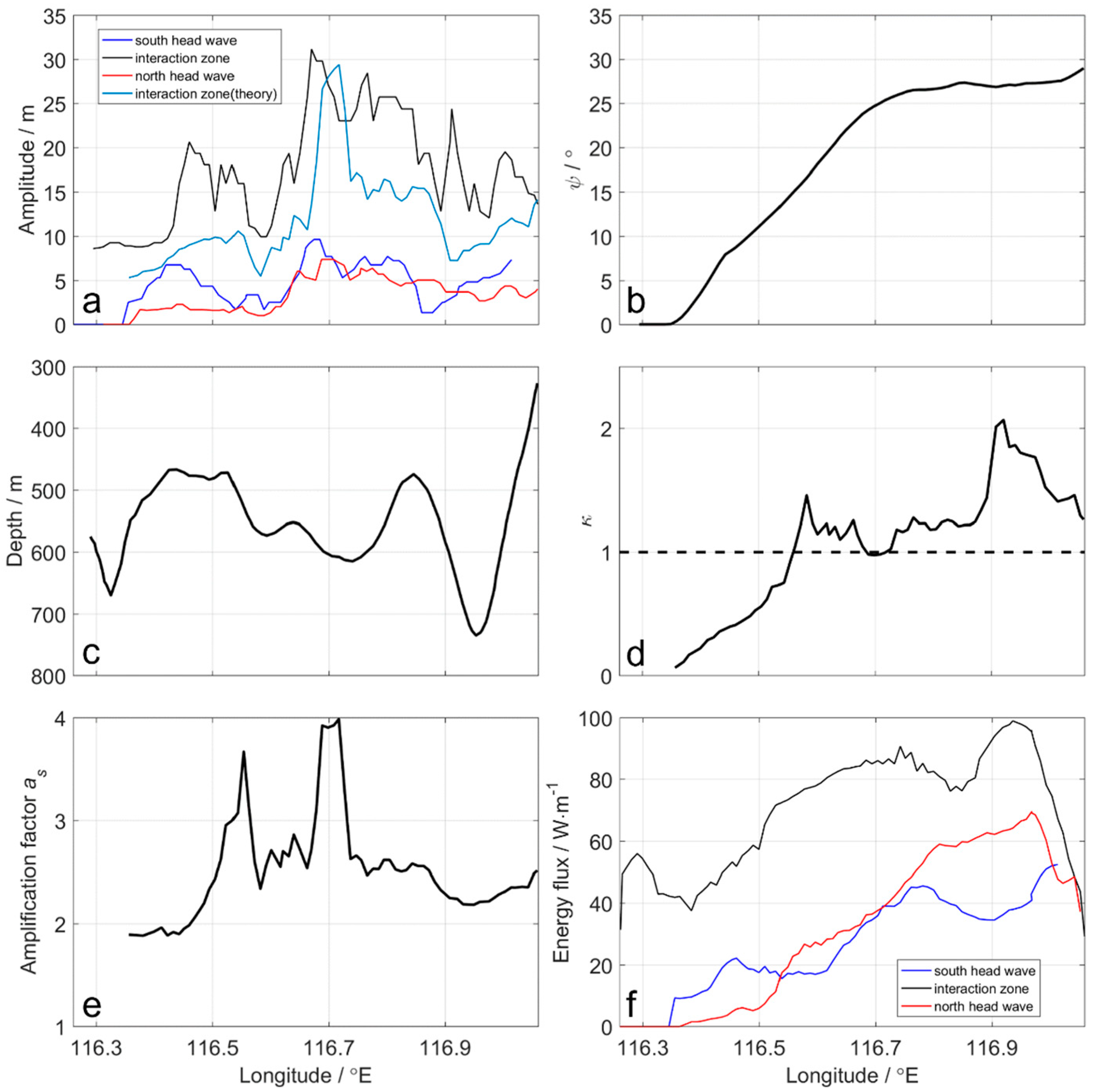
3.1. Model-Produced Amplitudes of the Internal Waves
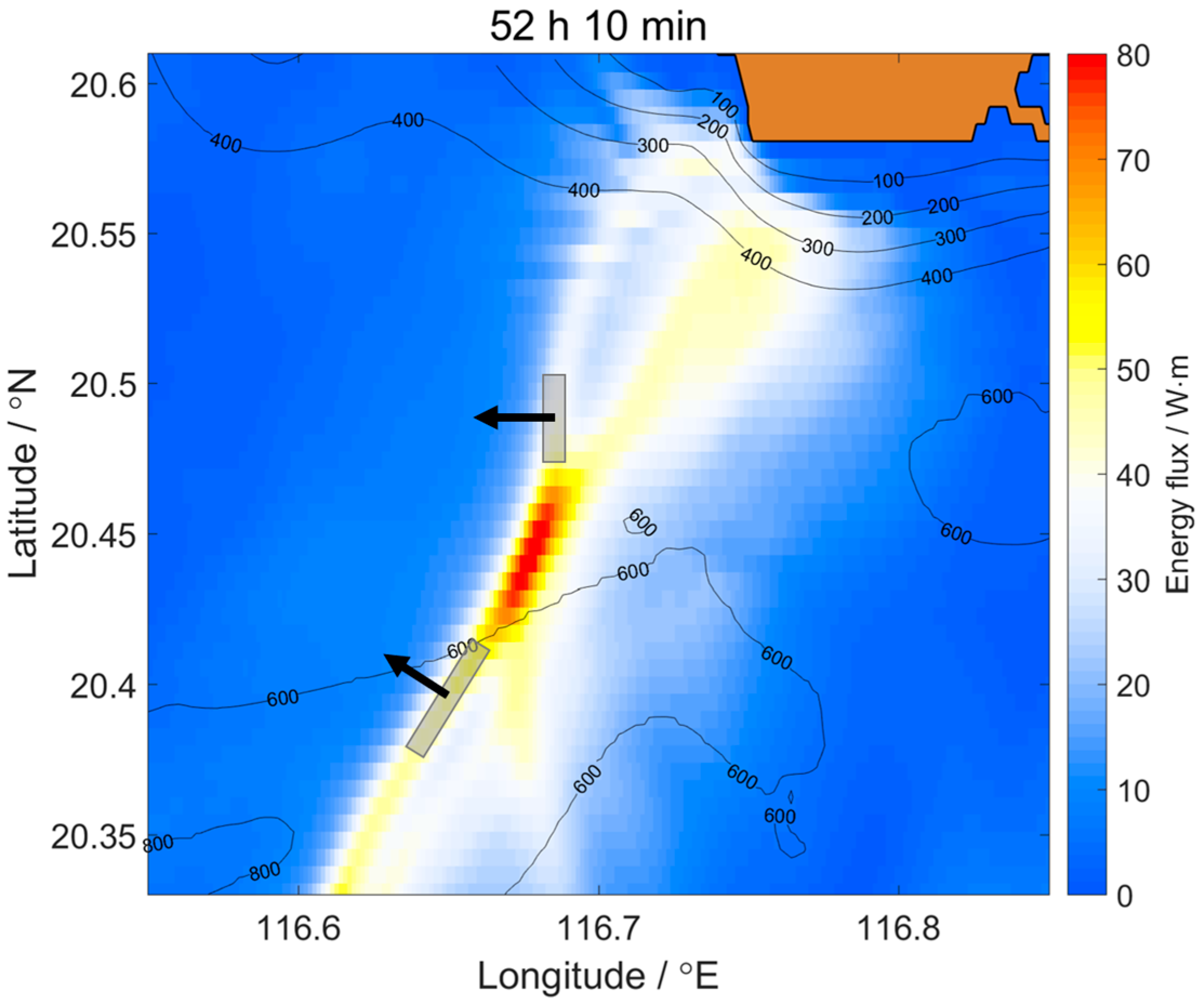
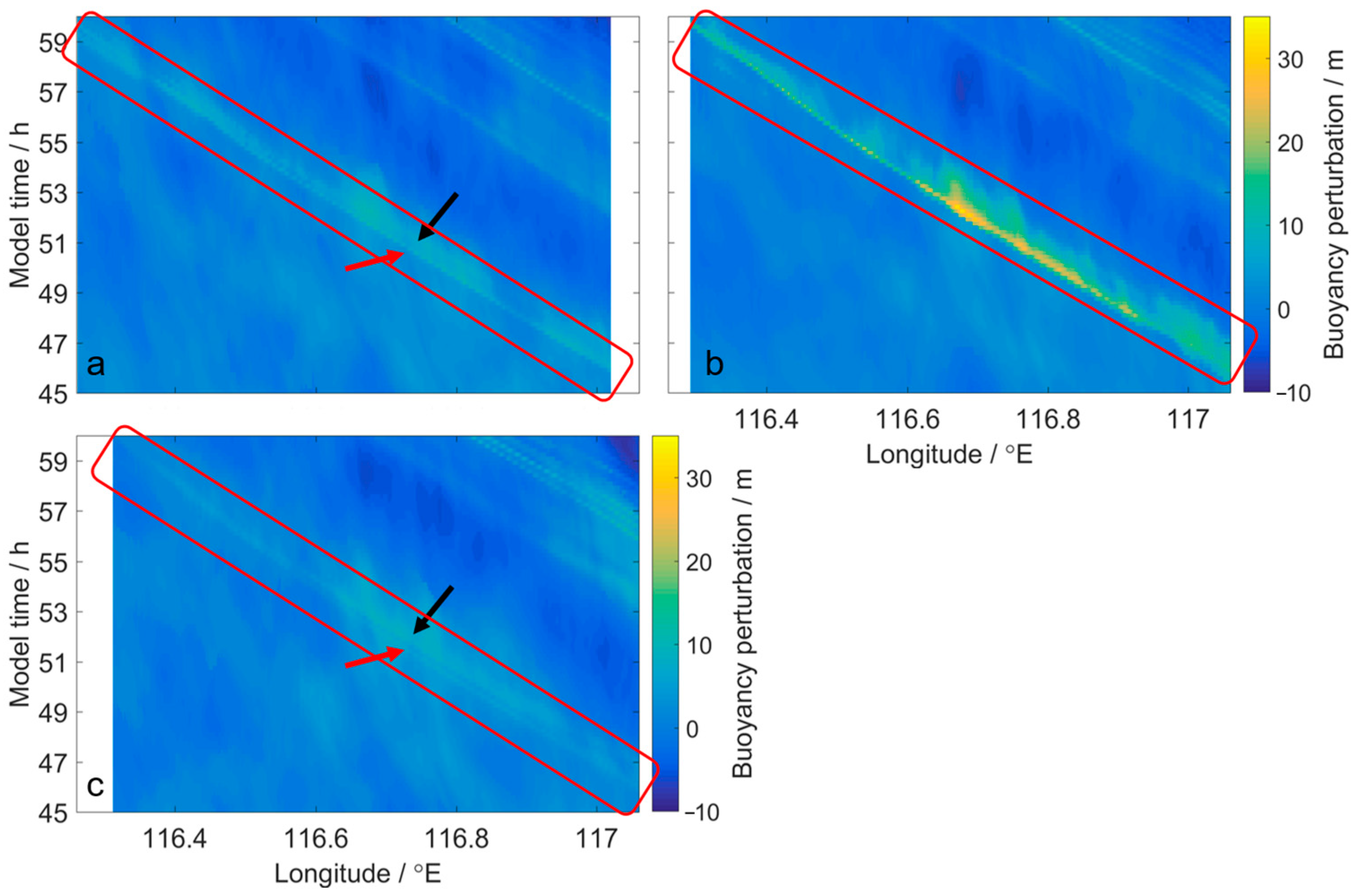
3.2. Spatial and Temporal Variation of the Wave–Wave Interaction
3.3. The Theoretical Amplitudes at the Initial State
4. Discussions and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Modal Harmonic Decomposition for Calculating Amplitudes of Internal Waves
Appendix B. Theory for the Oblique Interaction of Internal Waves
References
- Brandt, P.; Alory, G.; Awo, F.M.; Dengler, M.; Djakouré, S.; Imbol Koungue, R.A.; Jouanno, J.; Körner, M.; Roch, M.; Rouault, M. Physical processes and biological productivity in the upwelling regions of the tropical Atlantic. Ocean Sci. 2023, 19, 581–601. [Google Scholar] [CrossRef]
- Gill, A.E. On the Behavior of Internal Waves in the Wakes of Storms. J. Phys. Oceanogr. 1984, 14, 1129–1151. [Google Scholar] [CrossRef]
- Miles, J.W. Obliquely Interacting Solitary Waves. J. Fluid Mech. 1977, 79, 157–169. [Google Scholar] [CrossRef]
- Miles, J.W. Resonantly interacting solitary waves. J. Fluid Mech. 1977, 79, 171–179. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Zang, J.; Dong, G.; Zhou, L. Numerical investigation of harbor oscillations induced by focused transient wave groups. Coast. Eng. 2020, 158, 103670. [Google Scholar] [CrossRef]
- Zhang, M. Research Advancement on the Degradation Mechanism and Ecological Restoration Technology of Coastal Salt-marsh: A Review. J. Dalian Ocean Univ. 2022, 37, 539–549. [Google Scholar] [CrossRef]
- Shao, W.; Hu, Y.; Jiang, X.; Zhang, Y. Wave retrieval from quad-polarized Chinese Gaofen-3 SAR image using an improved tilt modulation transfer function. Geo-Spat. Inf. Sci. 2023. [Google Scholar] [CrossRef]
- Shao, W.; Yu, W.; Jiang, X.; Shi, J.; Wei, Y.; Ji, Q. Analysis of Wave Distributions Using the WAVEWATCH-Ⅲ Model in the Arctic Ocean. J. Ocean Univ. China 2022, 21, 15–27. [Google Scholar] [CrossRef]
- Shao, W.; Jiang, X.; Sun, Z.; Hu, Y.; Marino, A.; Zhang, Y. Evaluation of wave retrieval for Chinese Gaofen-3 synthetic aperture radar. Geo-Spat. Inf. Sci. 2022, 25, 15. [Google Scholar] [CrossRef]
- Korteweg, D.J.; De Vries, G. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Chen, H.; Zang, J.; Dong, G. On hydrodynamic characteristics of transient harbor resonance excited by double solitary waves. Ocean Eng. 2021, 219, 108345. [Google Scholar] [CrossRef]
- Melville, W.K. On the Mach reflexion of a solitary wave. J. Fluid Mech. 1980, 98, 285–297. [Google Scholar] [CrossRef]
- Funakoshi, M. Reflection of Obliquely Incident Solitary Waves. J. Phys. Soc. Jpn. 1980, 49, 2371–2379. [Google Scholar] [CrossRef]
- Johnson, R.S. On the oblique interaction of a large and a small solitary wave. J. Fluid Mech. 2006, 120, 49–70. [Google Scholar] [CrossRef]
- Kodama, Y. KP solitons in shallow water. J. Phys. A Math. Theor. 2010, 43, 434004. [Google Scholar] [CrossRef]
- Kadomtsev, B.B.; Petviashvili, V.I. On the stability of solitary waves in weakly dispersive media. In Doklady Akademii Nauk; Russian Academy of Sciences: Moscow, Russia, 1970; pp. 753–756. [Google Scholar]
- Wenwen, L.I.; Harry, Y.; Yuji, K. On the Mach reflection of a solitary wave: Revisited. J. Fluid Mech. 2011, 672, 326–357. [Google Scholar]
- Xue, J.; Graber, H.C.; Romeiser, R.; Lund, B. Understanding Internal Wave–Wave Interaction Patterns Observed in Satellite Images of the Mid-Atlantic Bight. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3211–3219. [Google Scholar] [CrossRef]
- Yeh, H.; Kodama, Y. The KP theory and Mach reflection. J. Fluid Mech. 2016, 800, 766–786. [Google Scholar]
- Oikawa, M.; Tsuji, H. Oblique interactions of weakly nonlinear long waves in dispersive systems. Fluid Dyn. Res. 2006, 38, 868–898. [Google Scholar] [CrossRef]
- Grimshaw, R.; Guo, C.; Helfrich, K.; Vlasenko, V. Combined Effect of Rotation and Topography on Shoaling Oceanic Internal Solitary Waves. J. Phys. Oceanogr. 2014, 44, 1116–1132. [Google Scholar] [CrossRef]
- Shimizu, K.; Nakayama, K. Effects of topography and Earth’s rotation on the oblique interaction of internal solitary-like waves in the Andaman Sea. J. Geophys. Res. Ocean. 2017, 122, 7449–7465. [Google Scholar] [CrossRef]
- Wang, C.; Pawlowicz, R. Oblique wave-wave interactions of nonlinear near-surface internal waves in the Strait of Georgia. J. Geophys. Res. 2012, 117, C06031. [Google Scholar] [CrossRef]
- Alford, M.H.; Peacock, T.; MacKinnon, J.A.; Nash, J.D.; Buijsman, M.C.; Centurioni, L.R.; Chao, S.-Y.; Chang, M.-H.; Farmer, D.M.; Fringer, O.B. The formation and fate of internal waves in the South China Sea. Nature 2015, 521, 65–69. [Google Scholar] [CrossRef] [PubMed]
- Buijsman, M.C.; Legg, S.; Klymak, J. Double-Ridge Internal Tide Interference and Its Effect on Dissipation in Luzon Strait. Am. Meteorol. Soc. 2012, 42, 1337–1356. [Google Scholar] [CrossRef]
- Farmer, D.; Li, Q.; Park, J.H. Internal wave observations in the South China Sea: The role of rotation and non-linearity. Atmos. Ocean 2009, 47, 267–280. [Google Scholar] [CrossRef]
- Ramp, S.R.; Tang, T.Y.; Duda, T.F.; Lynch, J.F.; Liu, A.K.; Chiu, C.S.; Bahr, F.L.; Kim, H.R.; Yang, Y.J. Internal solitons in the northeastern south China Sea. Part I: Sources and deep water propagation. IEEE J. Ocean. Eng. 2004, 29, 1157–1181. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, K.; Yin, B.; Zhao, Z.; Wang, Y.; Li, Q. Long-range propagation and associated variability of internal tides in the South China Sea. J. Geophys. Res. Ocean. 2016, 121, 8268–8286. [Google Scholar] [CrossRef]
- Gao, J.; Shi, H.; Zang, J.; Liu, Y. Mechanism analysis on the mitigation of harbor resonance by periodic undulating topography. Ocean Eng. 2023, 281, 114923. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Dong, G.; Chen, H.; Zang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Hsu, M.-K.; Liu, A.K.; Liu, C. A study of internal waves in the China Seas and Yellow Sea using SAR. Cont. Shelf Res. 2000, 20, 389–410. [Google Scholar] [CrossRef]
- Alpers, W. Theory of radar imaging of internal waves. Nature 1985, 314, 245–247. [Google Scholar] [CrossRef]
- Cai, S.; Xie, J. A propagation model for the internal solitary waves in the northern South China Sea. J. Geophys. Res. 2010, 115, C12074. [Google Scholar] [CrossRef]
- Chen, G.Y.; Liu, C.T.; Wang, Y.H.; Hsu, M.K. Interaction and generation of long-crested internal solitary waves in the South China Sea. J. Geophys. Res. Ocean. 2011, 116, C06013. [Google Scholar] [CrossRef]
- Jia, T.; Liang, J.; Li, Q.; Sha, J.; Li, X. Generation of shoreward nonlinear internal waves south of the Hainan Island: SAR observations and numerical simulations. J. Geophys. Res. Ocean. 2021, 126, e2021JC017334. [Google Scholar] [CrossRef]
- Ramp, S.R.; Yang, Y.J.; Bahr, F.L. Characterizing the nonlinear internal wave climate in the northeastern South China Sea. Nonlinear Process. Geophys. 2010, 17, 481–498. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient Inverse Modeling of Barotropic Ocean Tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Zhang, Z.; Fringer, O.B.; Ramp, S.R. Three-dimensional, nonhydrostatic numerical simulation of nonlinear internal wave generation and propagation in the South China Sea. J. Geophys. Res. Ocean. 2011, 116, C05022. [Google Scholar] [CrossRef]
- Leith, C. Stochastic models of chaotic systems. Phys. D Nonlinear Phenom. 1996, 98, 481–491. [Google Scholar] [CrossRef]
- Buijsman, M.C.; Kanarska, Y.; McWilliams, J.C. On the generation and evolution of nonlinear internal waves in the South China Sea. J. Geophys. Res. 2010, 115, C02012. [Google Scholar] [CrossRef]
- Miles, J.W. Internal waves generated by a horizontally moving source. Geophys. Fluid Dyn. 1971, 2, 63–87. [Google Scholar] [CrossRef]
- Gerkema, T.; Zimmerman, J. An introduction to internal waves. Lect. Notes R. NIOZ Texel 2008, 207, 207. [Google Scholar]
- Buijsman, M.C.; Klymak, J.M.; Legg, S.; Alford, M.H.; Farmer, D.; MacKinnon, J.A.; Nash, J.D.; Park, J.-H.; Pickering, A.; Simmons, H. Three-dimensional double-ridge internal tide resonance in Luzon Strait. J. Phys. Oceanogr. 2014, 44, 850–869. [Google Scholar] [CrossRef]
- Kang, D.; Fringer, O. Energetics of Barotropic and Baroclinic Tides in the Monterey Bay Area. J. Phys. Oceanogr. 2012, 42, 272–290. [Google Scholar] [CrossRef]
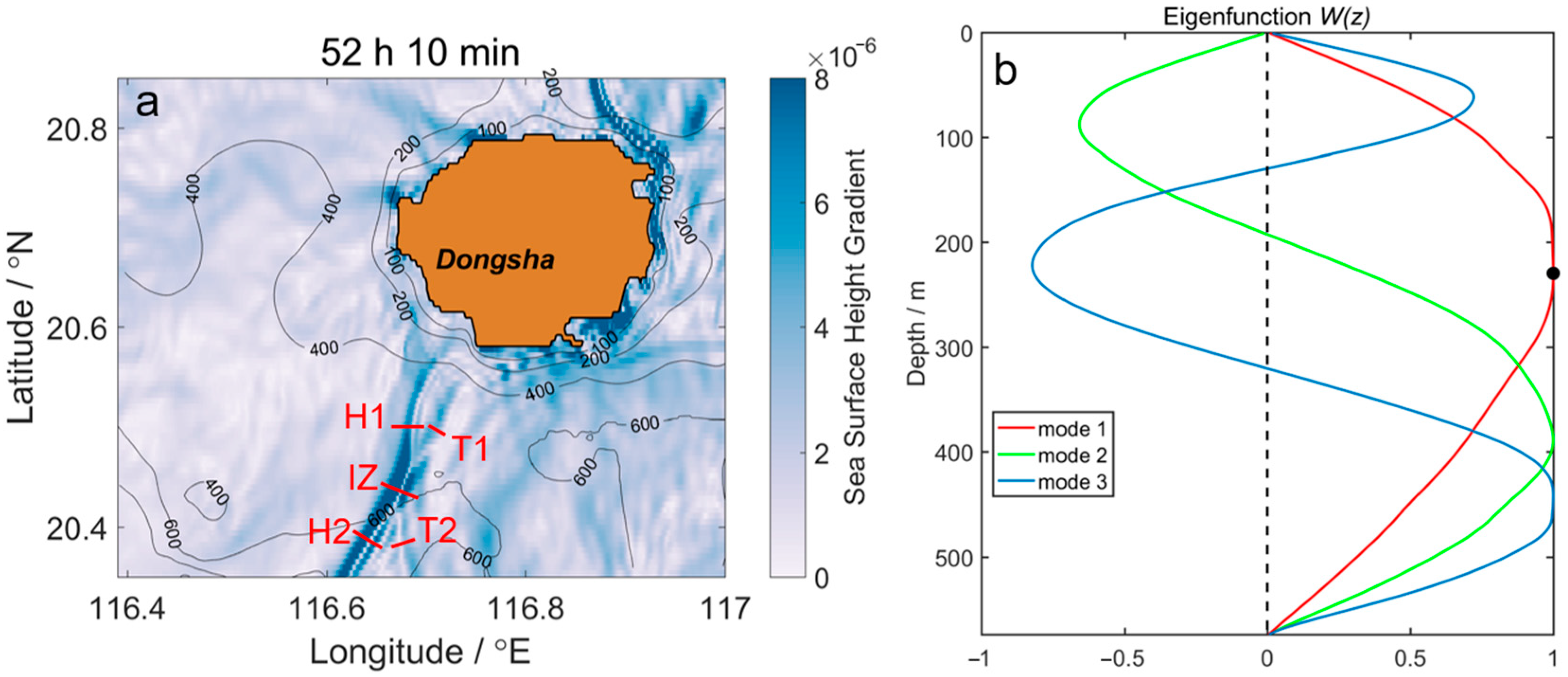

| Section | Water Depth/m | Depth of the Maximum Value of the First Mode/m | Isopycnal Displacement/m |
|---|---|---|---|
| H1 | 492.1 | 208 | 6 |
| H2 | 661.2 | 249 | 9 |
| T1 | 489.4 | 208 | 4 |
| T2 | 633.5 | 244 | 4 |
| IZ | 574.2 | 229 | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Z.; Chen, X.; Yuan, C.; Song, J. A Case Study of Wave–Wave Interaction South to Dongsha Island in the South China Sea. Remote Sens. 2024, 16, 337. https://doi.org/10.3390/rs16020337
Zeng Z, Chen X, Yuan C, Song J. A Case Study of Wave–Wave Interaction South to Dongsha Island in the South China Sea. Remote Sensing. 2024; 16(2):337. https://doi.org/10.3390/rs16020337
Chicago/Turabian StyleZeng, Zhi, Xueen Chen, Chunxin Yuan, and Jun Song. 2024. "A Case Study of Wave–Wave Interaction South to Dongsha Island in the South China Sea" Remote Sensing 16, no. 2: 337. https://doi.org/10.3390/rs16020337