1. Introduction
As one of the most frequently occurring natural hazards, landslides pose great threats to public safety in the world. It is generally acknowledged that monitoring of the slope instability is the key to looking into the landslide kinematics, as well as to protecting people from the related geological hazards. Earth-based systems, such as leveling, total stations, tiltmeter, optical fiber and the Global Positioning System (GPS), are being widely used for recording the surface and subsurface displacements associated with landslides [
1]. Despite their high accuracy, these conventional monitoring techniques have great limits in providing large-scale and high spatial resolution measurements, due to the prohibitive costs [
2]. For landslide-prone areas, where the exact locations of unstable slopes are still unknown, it is very difficult and even impossible to deploy these Earth-based systems.
In recent decades, spaceborne interferometric synthetic aperture radar (InSAR) technology has shown its great potential in the investigation of landslides. As an imaging radar system, InSAR is independent of sunlight and weather and can provide spatially-dense ground deformation measurements at a relatively large scale, without the need to carry out an
in situ survey [
3,
4]. These characteristics are of great importance for monitoring those landslides in mountainous areas, where there is a lack of public concern. The first applications of InSAR to investigate landslides emerged in the mid-1990s [
5,
6,
7], where the traditional differential InSAR (DInSAR) algorithm was employed to record single landslide events with generally centimeter or less accuracy. With the presence of abundant archived synthetic aperture radar (SAR) images, many multi-temporal InSAR (MTInSAR) algorithms have been developed since the early 2000s [
8,
9,
10,
11,
12]. By exploiting time series SAR images acquired over the same area during a certain period, these MTInSAR techniques can overcome the limitations associated with DInSAR and, therefore, improve the deformation measurement accuracy, as well as generate the deformation time series. These advancements have made MTInSAR widely employed for landslide investigation [
13,
14,
15,
16,
17,
18].
In this paper, we focus on studying the capability of the MTInSAR algorithms in the investigation of slow-moving landslides. In particular, with a time series of ALOS/PALSAR images acquired during September 2007, and March 2011, the temporarily-coherent point InSAR (TCPInSAR) technique [
12] is exploited to monitor the slope instability in Oso, Washington, United States, where a devastating mudslide occurred in the region 6.4 km east of Oso on 22 March 2014. A large quantity of mud and debris has been released by the mudslide, which dammed the North Fork of the Stillaguamish River and inundated an area larger than 2 km
2 [
19,
20]. At least 43 deaths and 49 destroyed structures were caused by this geological hazard. As a single landslide event that was not associated with an earthquake, volcanic eruption or dam collapse, the Oso mudslide caused the most casualties in the history of the United States [
21]. Actually, Oso has been suffering from landslide hazards for over half a century [
22]. However, the locations and distributions of the unstable slopes in this area are almost unknown to the public. This study can help us to have comprehensive information about the active landslides in the Oso area.
3. Results and Analysis
A total of 15 interferograms are generated from 13 ALOS PALSAR images with a maximum perpendicular baseline of nearly 900 m and a time interval shorter than 1000 days (
Figure 2). The selected criteria for the spatial-temporal baselines can guarantee that all of the 13 PALSAR images are involved without introducing a low-quality interferogram. The standard two-pass DInSAR algorithm is adopted to produce the differential interferogram with the SRTM DEM. In order to suppress the relative large phase noises related to mountainous environments, all of the interferograms were processed with a multilook operation (six looks in the range and 14 looks in the azimuth direction), followed by a modified Goldstein filter [
32]. It is worth noting that the conventional unwrapping methods are not required for the interferograms, since the TCPInSAR technique can isolate the arcs without phase ambiguities as observations by examining the least squares residuals. This is mainly based on the fact that ambiguities in arc observations can introduce abnormally large residuals during the parameter estimation [
25].
Figure 3a–d shows four interferograms of the pairs of 10.20.2007–04.27.2010, 06.06.2008–01.28.2011, 07.28.2010–10.28.2010 and 01.28.2011–03.15.2011, respectively, with the perpendicular and temporal baselines marked in the right top corner of each subplot. For the interferograms with medium perpendicular baselines and long temporal intervals (
Figure 3a,b), we observe several phase variations in the areas outlined by the real rectangles. This could be the surface displacement signals induced by slow-moving landslides, since they are not detected in the interferograms with short temporal intervals (
Figure 3c,d). The phase variations in these two interferograms, as outlined by the dashed circles, could be interpreted as the topographic residuals, since they are highly related to the perpendicular baselines. It is clear that these two kinds of phase variations are visually similar and quite difficult to distinguish based on one single DInSAR image. Besides the local phase variations, the orbital errors can be easily observed in most of the interferograms, which behave as long wavelength phase ramps.
Considering the fact that distributed scatterers are overwhelmingly available in mountainous environments, we preferred the coherence method to identify the TCPs in this case. A total of 220,889 TCPs were identified in the study area, from which 769,781 arcs were constructed at a spatial resolution of about 600 m.
Figure 4a exhibits the network constructed by the local Delaunay triangulation over the study area, where the black dots and green lines represent the TCPs and arcs, respectively. For simultaneously estimating the deformation rates, topographic residuals and orbital errors, a large sparse design matrix with a size of 11,546,715 × 441,836 was constructed. The value of 11,546,715 corresponds to the number of observations, including the phase differences at 769,781 arcs of 15 interferograms (
i.e., 769,781 × 15 = 11,546,715). The value of 441,836 corresponds to the number of unknowns, which are constituted by the deformation rates and topographic residuals at 220,888 TCPs and five polynomial coefficients for the orbital errors at 12 SAR images, with one TCP and one SAR image being the references (
i.e., 220,888 × 2 + 12 × 5 = 441,836). We used sparse least squares to resolve these parameters. After the phase ambiguity detector was applied, 190,940 arcs with phase ambiguities were removed in total, leaving 210,087 TCPs in the final results (
Figure 4b).
Figure 2.
Temporal and perpendicular baselines of the generated 15 interferograms. The lengths and colors of the horizontal lines indicate the variations of time intervals (i.e., temporal baselines) and perpendicular baselines, respectively.
Figure 2.
Temporal and perpendicular baselines of the generated 15 interferograms. The lengths and colors of the horizontal lines indicate the variations of time intervals (i.e., temporal baselines) and perpendicular baselines, respectively.
Figure 5a,b shows the deformation rates in the radar line-of-sight (LOS) direction and the topographic residuals of the TCPs estimated by the TCPInSAR algorithm, respectively, which were geocoded in the WGS 84 coordinate system and superimposed on the shaded relief map of the study area. In the LOS deformation rate results (
Figure 5a), local displacements in several slopes can be clearly found, with a maximum velocity of more than 2 cm/yr. Topographic residual results (
Figure 5b) reveal that the differences between the SRTM data derived from DEM and the real terrain range from −25 m to 25 m, resulting in a standard deviation (SD) of 4.3 m for the whole investigated area. This is a typical relative vertical accuracy for the SRTM data [
33]. No evident orbital ramps can be found in the LOS deformation rate or topographic residual maps. In order to further verify the capability of TCPInSAR to correct orbital errors, the LOS deformation rates were also estimated without including the orbital error polynomials in the joint model. As shown in
Figure 5c, the long wavelength orbital ramp remains in the deformation rate map.
Figure 5d exhibits the differences between the deformation rates shown in
Figure 5a,c. Up to 1.5 cm of the planar ramp indicates that the orbital errors can potentially hamper the accurate retrieval of deformation if they are not carefully mitigated with respect to the interferograms.
Figure 3.
Interferograms of the pairs 10.20.2007–04.27.2010 (a), 06.06.2008–01.28.2011 (b), 07.28.2010–10.28.2010 (c) and 01.28.2011–03.15.2011 (d). Rectangles and dashed circles indicate the areas affected by the surface displacements and the topographic residuals, respectively.
Figure 3.
Interferograms of the pairs 10.20.2007–04.27.2010 (a), 06.06.2008–01.28.2011 (b), 07.28.2010–10.28.2010 (c) and 01.28.2011–03.15.2011 (d). Rectangles and dashed circles indicate the areas affected by the surface displacements and the topographic residuals, respectively.
Figure 4.
(a) Local Delaunay triangulation network of the identified TCPs. (b) The network after removing arcs with phase ambiguities. The black dots and green lines represent the temporarily-coherent points (TCPs) and arcs, respectively. Both maps are in radar coordinates.
Figure 4.
(a) Local Delaunay triangulation network of the identified TCPs. (b) The network after removing arcs with phase ambiguities. The black dots and green lines represent the temporarily-coherent points (TCPs) and arcs, respectively. Both maps are in radar coordinates.
Figure 5.
(
a) TCPInSAR-derived LOS deformation rates for the Oso area; (
b) TCPInSAR-derived topographic residuals for the Oso area; (
c) LOS deformation rates derived by TCPInSAR without including the orbital error polynomial coefficients in the joint model; (
d) differences between the LOS deformation rates in (a,c). All of the maps are in the WGS 84 coordinate system. The pentagram indicates the location of the Oso mudslide that occurred in 2014. The square indicates the location of the precipitation station used in the study. Boxes A, B and C outline the areas exhibited in
Figure 6,
Figure 7 and
Figure 8, respectively.
Figure 5.
(
a) TCPInSAR-derived LOS deformation rates for the Oso area; (
b) TCPInSAR-derived topographic residuals for the Oso area; (
c) LOS deformation rates derived by TCPInSAR without including the orbital error polynomial coefficients in the joint model; (
d) differences between the LOS deformation rates in (a,c). All of the maps are in the WGS 84 coordinate system. The pentagram indicates the location of the Oso mudslide that occurred in 2014. The square indicates the location of the precipitation station used in the study. Boxes A, B and C outline the areas exhibited in
Figure 6,
Figure 7 and
Figure 8, respectively.
Since
in situ observation is unavailable for the investigated area, we cannot carry out ground-truth validation in this study. It is acknowledged that the accuracy of the LOS deformation rate mainly depends on the suppression of the InSAR inherent errors. We have mentioned that the TCPInSAR technique can handle the unwrapping errors, topographic residuals and orbital errors well. Regarding the decorrelation noises, they are quite sensitive to the heavy vegetation in the study area, but have been greatly minimized in the deformation rates as the result of a complex of multi-look operations, modified Goldstein filter and least squares adjustment used in the TCPInSAR. However, atmospheric artifacts can be introduced into the TCPInSAR measurements due to Oso’s mountainous environment. In this study, a linear polynomial model has been applied to correct the atmospheric effects, since they are dominated by the stratified disturbances in mountainous areas [
31]. Therefore, the LOS deformation rates obtained by the TCPInSAR technique are basically reliable to detect and monitor slow-moving landslides in Oso.
Figure 6.
Detected LOS deformation rate map for the A region. White lines show the locations of the profiles. The red polygon outlines the approximate area of deposits from the 2014 mudslide [
19]. In the graphs, the blue and green dots represent the displacement and topography extracted along the profiles, respectively.
Figure 6.
Detected LOS deformation rate map for the A region. White lines show the locations of the profiles. The red polygon outlines the approximate area of deposits from the 2014 mudslide [
19]. In the graphs, the blue and green dots represent the displacement and topography extracted along the profiles, respectively.
Slope deformations in three regions as outlined by the boxes in
Figure 5a are selected in this study for detailed analysis. It is worth noting that only the A region corresponds to the 2014 Oso mudslide, but the obvious deformations in the B and C regions indicate that these two areas also surfer from a landslide hazard. The A region covers an area of approximately 36 km
2, across the North Fork of the Stillaguamish River. Besides the 2014 large mudslide, this area has a long history of slope instabilities, which date back to at least the early 1950s, known as the Hazel Landslide [
34].
Figure 6 shows the slope deformation rates along the radar LOS direction in this region draped on the Google Earth map. Positive values indicate that the targets moved toward the satellite, and
vice versa. The moist soil and heavy vegetation here lead to relatively few TCPs and large noises in the deformation rate results. According to the slope orientation and the history record, the landslides in this region mainly occurred along the north-south direction, toward the North Fork of the Stillaguamish River. It is however acknowledged that the InSAR measurements are quite insensitive to the north-south deformations due to the polar orbits of the SAR satellite [
35]. As a result, only a few creeps are detected on the slopes around the North Fork of the Stillaguamish River. Nevertheless, the locations of these creeps agree well with that of the ancient landslides [
22], indicating that the slopes were in a potentially unstable state during the investigated period. Close inspections have been conducted of two profiles, where the displacement and topography are both measured. The AA’ profile, 2.6 km in length across the Stillaguamish River, shows a distinct variation in the deformation rate. The positive displacement, although across the river, could be the landslide deposit formed by the underground material mobilized by the deep-seated Hazel Landslide, while few TCPs were obtained on the slope due to its inappropriate orientation and inclination. The BB’ profile, 1.1 km in length along an active landslide, reveals clear downslope movements in the upper part of the slope.
Figure 7.
Detected LOS deformation rate map for the B region. White lines show the locations of the profiles. In the graphs, the blue and green dots represent the displacement and topography extracted along the profiles, respectively.
Figure 7.
Detected LOS deformation rate map for the B region. White lines show the locations of the profiles. In the graphs, the blue and green dots represent the displacement and topography extracted along the profiles, respectively.
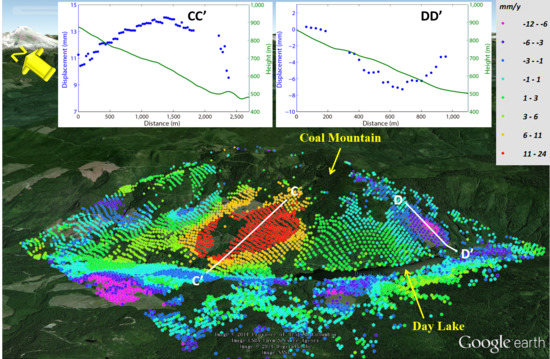
The B region is situated on Coal Mountain, north of Day Lake. The LOS deformation rates of the TCPs in this region are shown in
Figure 7, superimposed on the Google Earth map. It is found that the west slope of Coal Mountain experienced a significant slow-moving landslide, the boundary of which can be accurately defined. This landslide is quite favorable for the InSAR measurements, since the slope deformations were dominated by the west-wards and downslope movements. The positive deformation values, ranging from 6 to 24 mm/y, indicate that the west-wards movements were much larger than the downslope movements, as a natural result of the gentle incline. The CC’ profile, 2.7 km in length along the maximum slope direction, is examined for the displacement and topography. It is clear that the deformation rates of the landslide increase in the upper part, but then turn to deceleration in the lower part. Another distinct unstable slope is found in the southeast side of Coal Mountain. Although characterized by negative deformation values due to the east-wards and downslope movements, this landslide behaves similarly to the larger one on the west slope. This is also demonstrated by the displacement rates exacted along the DD’ profile, which is 1.1 km in length and along the southeast slope.
Figure 8.
Detected LOS deformation rate map for the C region. White lines show the locations of the profiles. In the graphs, the blue and green dots represent the displacement and topography extracted along the profiles, respectively.
Figure 8.
Detected LOS deformation rate map for the C region. White lines show the locations of the profiles. In the graphs, the blue and green dots represent the displacement and topography extracted along the profiles, respectively.
Obvious landslides are also detected in the C region, which is located in the north of the Granite Lake Potholes. As shown in
Figure 8, although with smaller scales and amplitudes, the slope deformations are more complex compared to those in the B region. The EE’ profile, 3 km in length across the active landslides on the northeast slope, reveals a gradient on the slope movement rates and some distinct variations in the landslide deposit, while for the FF’ profile, 1.6 km in length and along the slope facing northwest, irregular variations in the displacement rates are found on this gradual slope. The ground surface texture structure could be responsible for these displacement variations. However, the downward trend of this slow-moving landslide poses a threat of a landslide dam in the Deer Creek River, which is located in the foot of the slope.
Like other MTInSAR techniques, the TCPInSAR algorithm allows us to derive the time series of surface deformations from the multi-master interferograms, in which the topographic residuals have been corrected. However, the deformation evolution results are less accurate than the deformation rate results. This is expected, since the unknowns in the model increase, but the observations remain the same. Besides, the deformation evolutions are more susceptible to the atmospheric artifacts compared to the deformation rates. In
Figure 9, we exhibit six typical deformation evolutions derived by the TCPInSAR technique for the landslides on Coal Mountain (
i.e., the B region). The accumulated deformation fields in the subplots are relative to the earliest PALSAR acquisition date,
i.e., 4 September 2007. The accumulated days since the reference date are labeled in the right top corners. A sustainable growth can be easily identified for the landslide deformations during the investigated period, which had reached 8 cm after about three and a half years.
Figure 9.
TCPInSAR-derived LOS deformation evolution maps for the B region. The reference date is 4 September 2007, and the accumulated day since the reference image is labeled in the right top corner of each subplot.
Figure 9.
TCPInSAR-derived LOS deformation evolution maps for the B region. The reference date is 4 September 2007, and the accumulated day since the reference image is labeled in the right top corner of each subplot.
Precipitation, timber harvest, earthquakes and volcanic eruptions are typical factors that can trigger slope movements. With respect to the Oso landslide, the slope stabilities are mainly affected by the local groundwater variations, which respond directly to the timber harvest, as well as the precipitation [
35]. It had been reported that the timber harvest in Oso aggravated the activities of landslides as a result of the increased recharge of groundwater, with time lags of up to 20 years between timber removal and slope deformation [
37]. Precipitation also leads to the landslide movements by changing the pore-water pressure [
38]. In order to analyze the temporal correlation between the landslide movements and the precipitations, we conduct a comparison between the TCPInSAR-derived time series displacements and the time series precipitations. The total amount of the displacement evolutions at all of the TCPs in the three investigated regions is calculated and normalized to the smallest time unit,
i.e., 46 days [
39]. We then collected the precipitation data at Darrington Station in Washington to assess the results, which is also averaged to 46 days. The location of the station can be found in
Figure 5a. As shown in
Figure 10, the average rainfalls in the study area show a periodicity in the investigated four yearly cycles, which is very rainy in winter, while quite dry in summer, as a result of the Mediterranean climate. Furthermore, a dramatic increase of the precipitation can be found in the last two yearly cycles. On the other side, the general trend of the total deformations is quite similar to that of the precipitation. It is observed that the 46-day deformations behave as seasonal oscillations with a distinct increase in the last two yearly cycles. This is expected, since the low precipitations before 2010 provide favorable conditions for rainfall entrance and landslide movements in the following two years. Although it is difficult to calculate the exact time lags between the precipitation and the deformations, due to the poor temporal sampling of the PALSAR data used and the disturbances from other factors affecting them, the results clearly demonstrate that the slope deformation in Oso closely responds to the rainfall-induced groundwater variation.
Figure 10.
Comparison between the total deformation and the precipitation in 46 days.
Figure 10.
Comparison between the total deformation and the precipitation in 46 days.
4. Conclusions
Although InSAR has been proven to be a powerful tool for monitoring slow-moving landslides, this is not an easy task, since the inherent InSAR errors, such as decorrelation noise and topographic residuals, become more troublesome in the areas where landslide hazards frequently occur, which are usually dominated by mountains and hills with steep slopes. In addition, orbital errors will critically mix with landslide signals when the ALOS PALSAR data are employed in the application for their good capability of maintaining coherence. In this study, an alternative MTInSAR technique, termed TCPInSAR, has been examined in the investigation of slow-moving landslides in Oso, U.S., with 13 ALOS PALSAR images acquired during 2007 and 2011. Compared to the other MTInSAR techniques, TCPInSAR can identify the coherent pixels based on a small amount of SAR images and jointly estimate the deformation rates, topographic residuals and orbital errors without the error-prone phase unwrapping procedure. The following conclusions can be summarized from this work:
(1) The results have demonstrated that the TCPInSAR method can effectively detect and monitor active landslides. There were 210,087 TCPs identified for the investigated area, characterized by hilly terrain and heavy vegetation, resulting in an average density of ~170 TCPs/km2. The topographic residuals with an SD of 4.3 m have been estimated for the identified TCPs, which can be used to refine the local SRTM data. More importantly, up to 1.5 cm of the planar ramp induced by the orbital errors had been successfully separated from the deformation signals associated with the landslides.
(2) LOS deformation rates for the Oso landslides are the main outcome of this study. We had found evident and continuous landslide deformations on the slopes of Coal Mountain, with a rate of up to 24 mm/y. Other slope instabilities (−11~15 mm/y) were distinguished in the north of the Granite Lake Potholes, which were smaller in size, but more complicated in behavior, posing a potential threat to the adjacent Deer Creek River. With respect to the area that was affected by the major mudslide in March, 2014, only some small creeps (<10 mm/y) had been detected on the slopes around the North Fork of the Stillaguamish River, since the ascending ALOS PALSAR images are nearly blind to most of the slope deformations here; while a distinct displacement had been found across the river, which was expected to be caused by the deposit associated with the deep-seated Hazel Landslide.
(3) The deformation evolution results for the Oso landslides had also been provided by the TCPInSAR algorithm. For the most active slope on Coal Mountain, the LOS deformations were observed with a steady development during the investigated 3.5 years, reaching a peak of 8 cm. Furthermore, it was found that the normalized deformations and the average precipitations in 46 days exhibited seasonal oscillations with increased amplitudes in the last two yearly cycles. A good correlation between the deformations and precipitations indicates that the Oso landslides are highly sensitive to the variations of groundwater.
In the future, the following issues can be addressed to further enhance the applicability of InSAR for monitoring landslides in Oso and other areas. First, although the deformation evolution can be provided by TCPInSAR techniques, there is a lot of room to improve its accuracy by suppressing the atmospheric artifacts. Second, high-resolution TerraSAR-X and COSMO-SkyMed data should be utilized in the investigation of the Oso landslides in order to reduce the blind areas and to monitor the smaller-scale landslides. It has been demonstrated that the worse capability for penetrating the vegetation of the X-band data can be partly compensated for by their shorter revisit periods compared to those of the medium-resolution SAR data [
40]. Third, since no
in situ measurements are available in this area, quantitative assessment cannot be conducted for the TCPInSAR results. This is quite common for most of the landslide monitoring in mountainous areas, while some approaches should be developed to provide a precision report based on the InSAR measurements themselves.