Dynamic River Masks from Multi-Temporal Satellite Imagery: An Automatic Algorithm Using Graph Cuts Optimization
Abstract
:1. Introduction
- Introduce a flexible framework to consider spectral, spatial, and temporal information in the image for defining the water masks;
- Solve the optimization using graph cuts technique;
- Measure the uncertainty associated with the graph cuts solution;
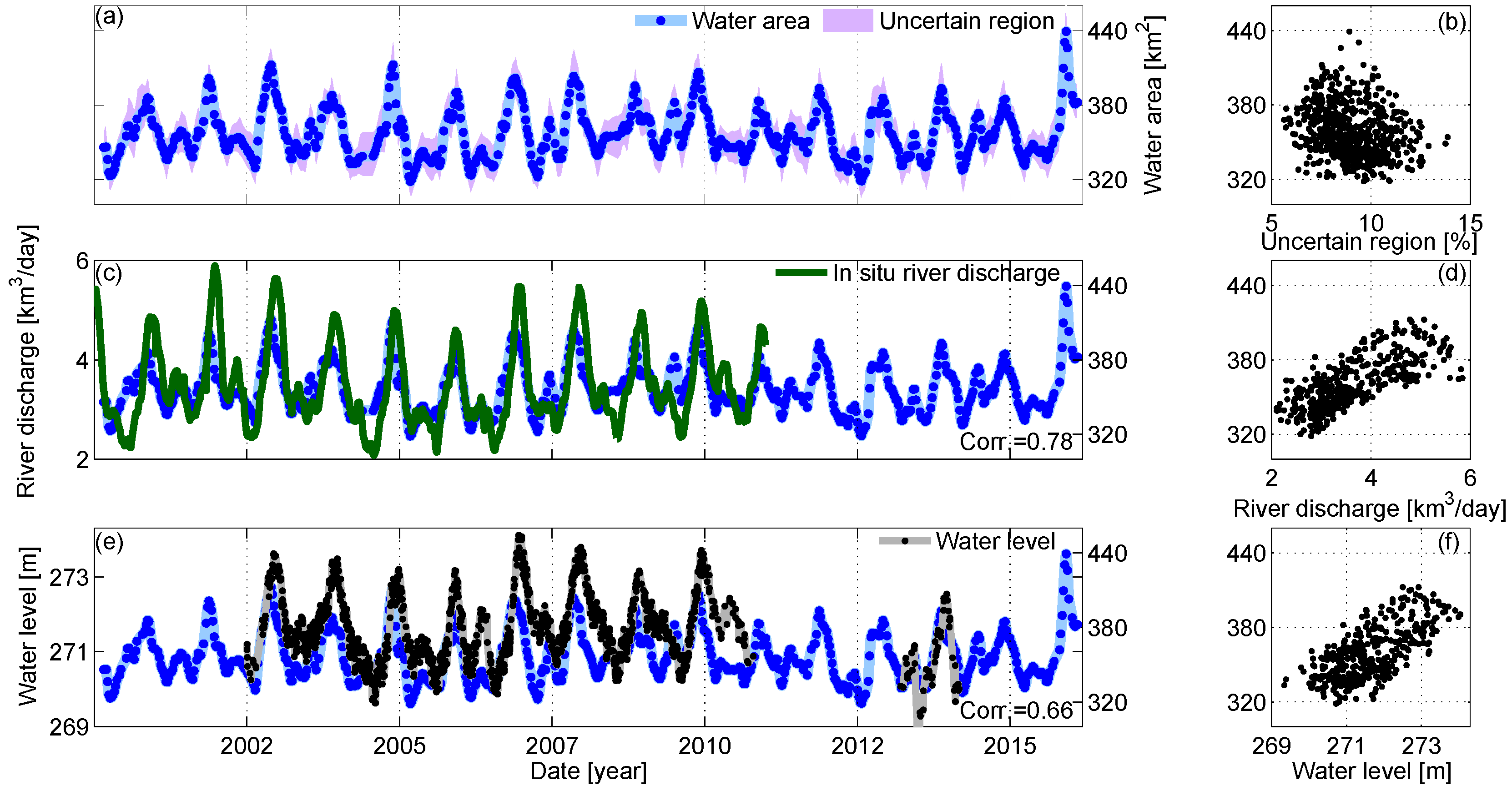
- Validate the measured water area time series indirectly through in situ river discharge and altimetric water level measurements.
2. Case Studies and Datasets
2.1. Case Study
2.2. Datasets
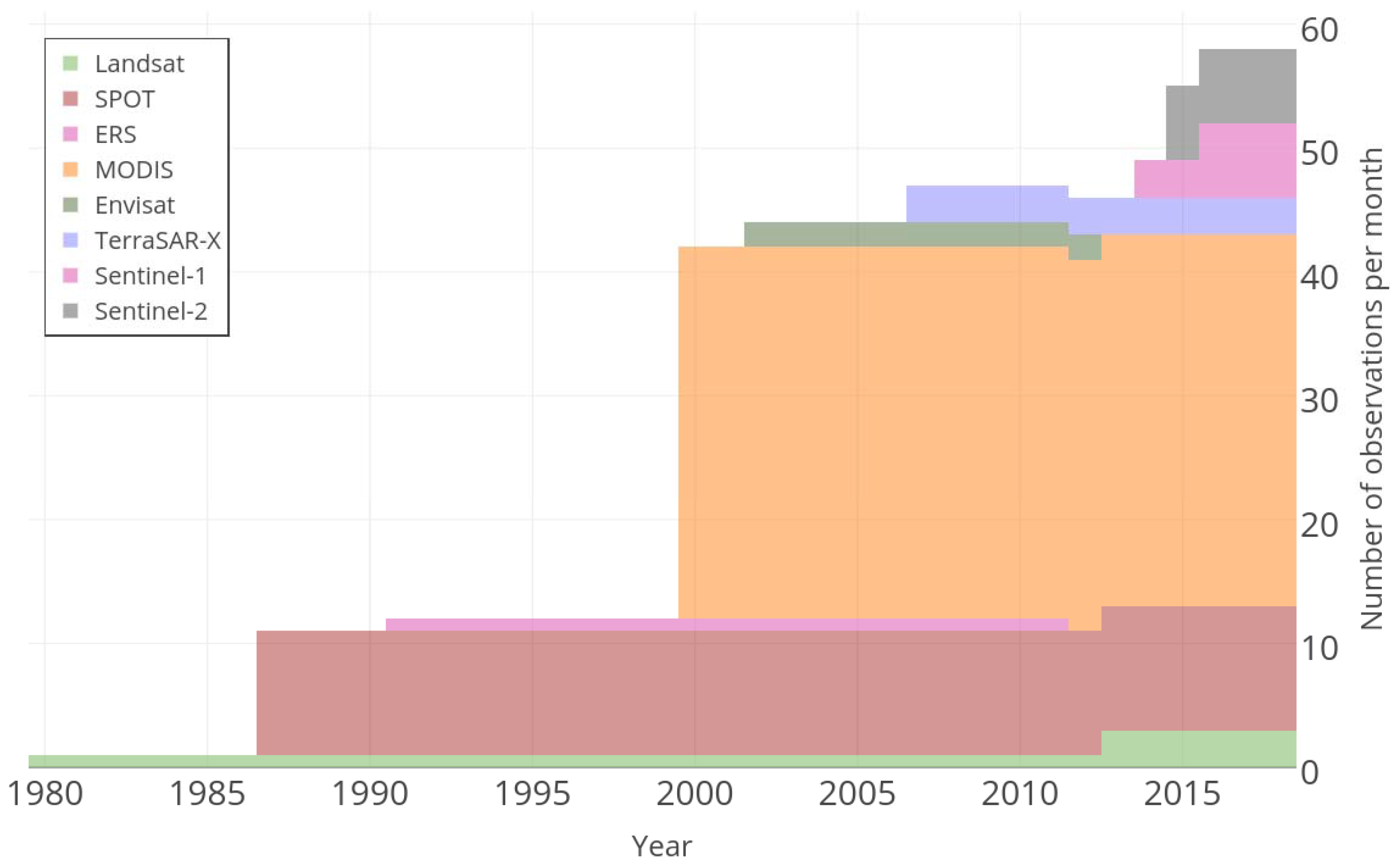
2.2.1. Imagery
2.2.2. In Situ Data
2.2.3. Satellite Altimetry
3. Methodology
3.1. An Overview of the Mathematical Concept
| : | a set of sites p (pixels). |
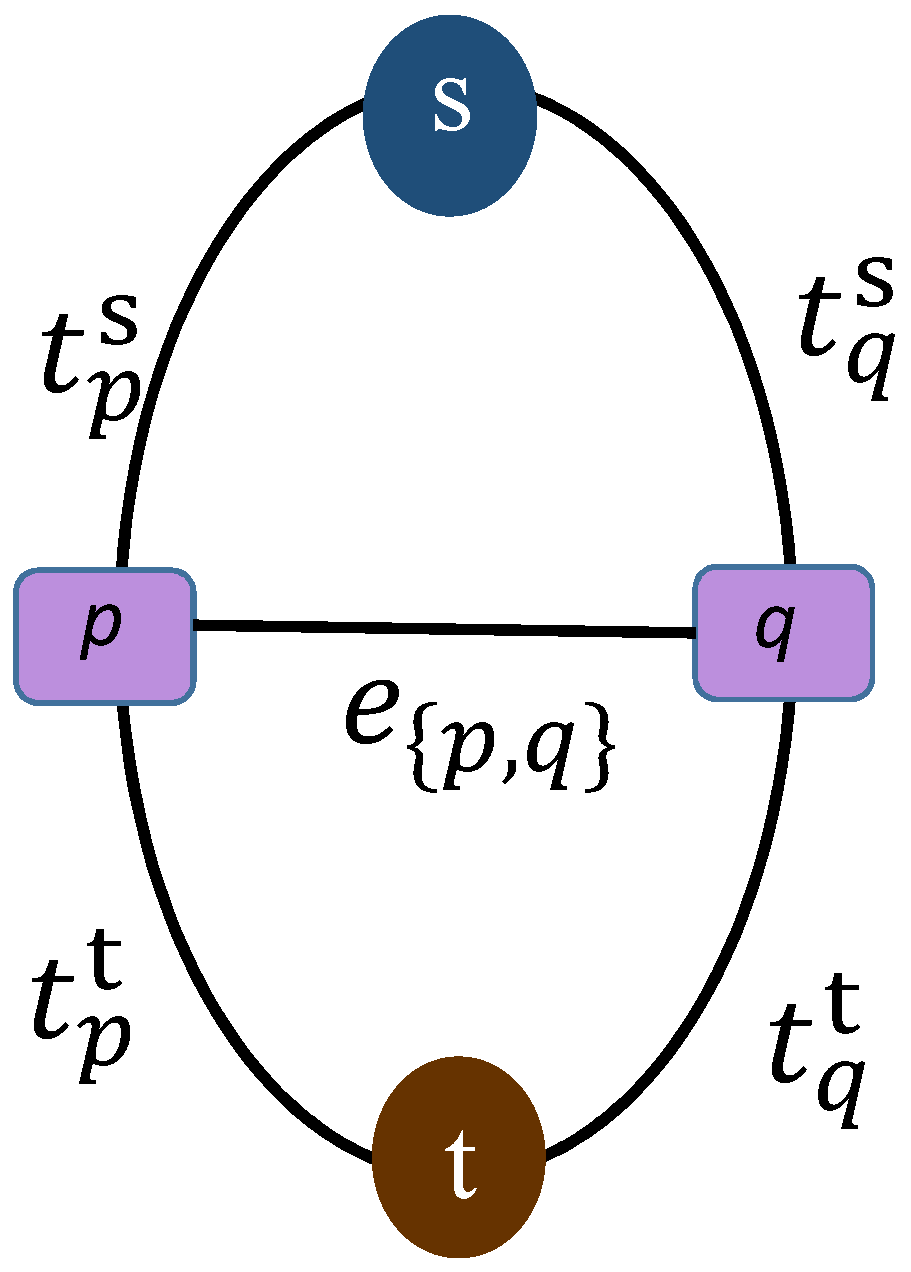
| : | a neighborhood system where is a subset of the pixels in located adjacent to the pixel p (Figure 3 is an example of a four-neighbor structure for pixel p). To provide a smoother result, one can think of a bigger neighborhood system. |
| : | the set of possible labels that can be assigned to a pixel (water or land). |
| : | a field of the random variables which takes a value regarding the possible label l. |
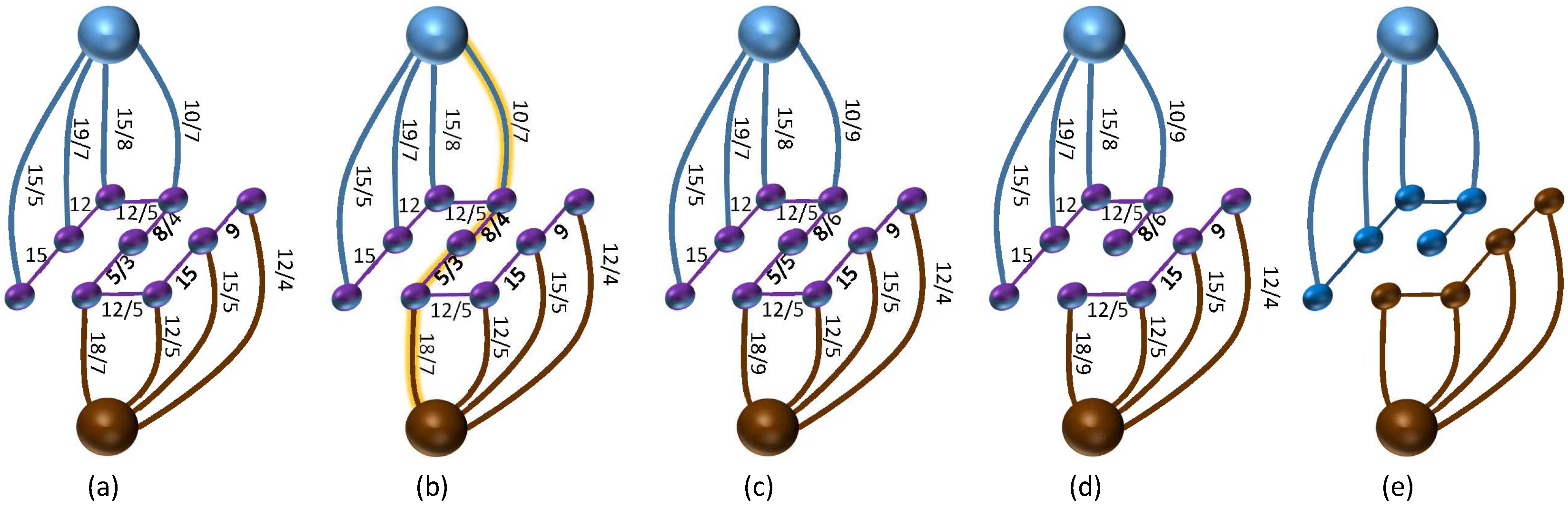
3.2. Basics of Graphs, Graph Cuts Techniques, and Max-Flow Algorithms
- Find a valid route between source and sink.
- Push the maximum flow equal to the capacity of the pass to the graph. This flow saturates an edge in the pass.
- Decrease the capacity of the path edges in the residual graph and increase the maximum flow regarding the previous step.
- Find all paths from source to sink with length k in the residual graph applying BFS
- Augment the detected paths, update the residual graph, increasing the total flow
- Replace k with k+1
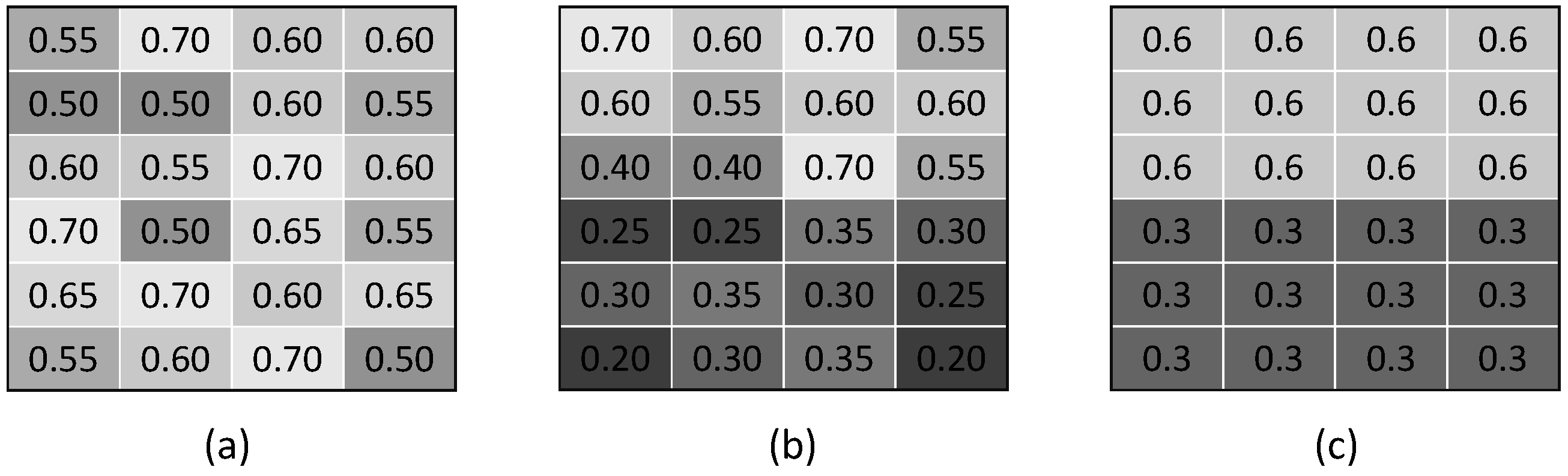
3.3. Measuring Uncertainty in the Graph Cuts Solution
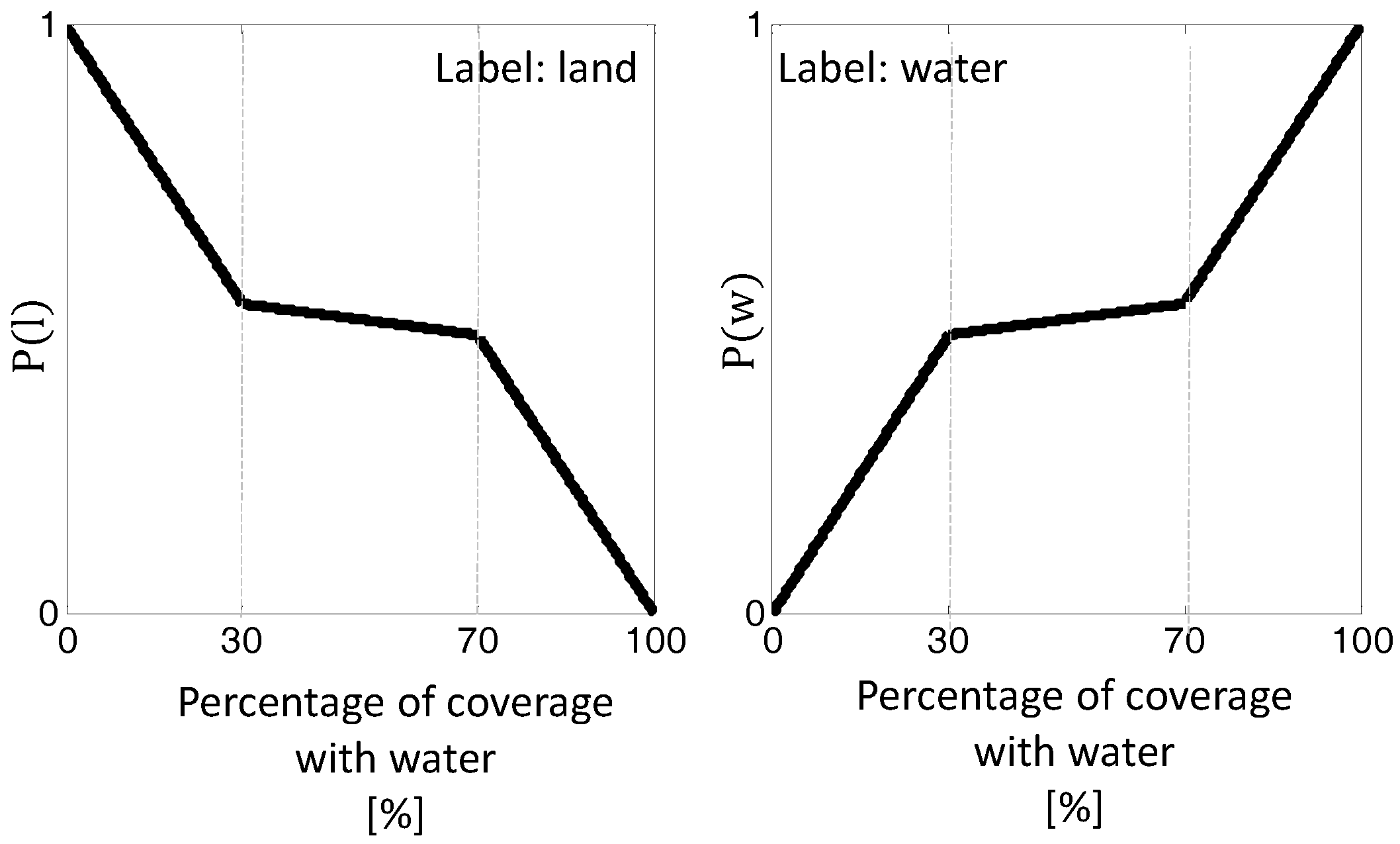
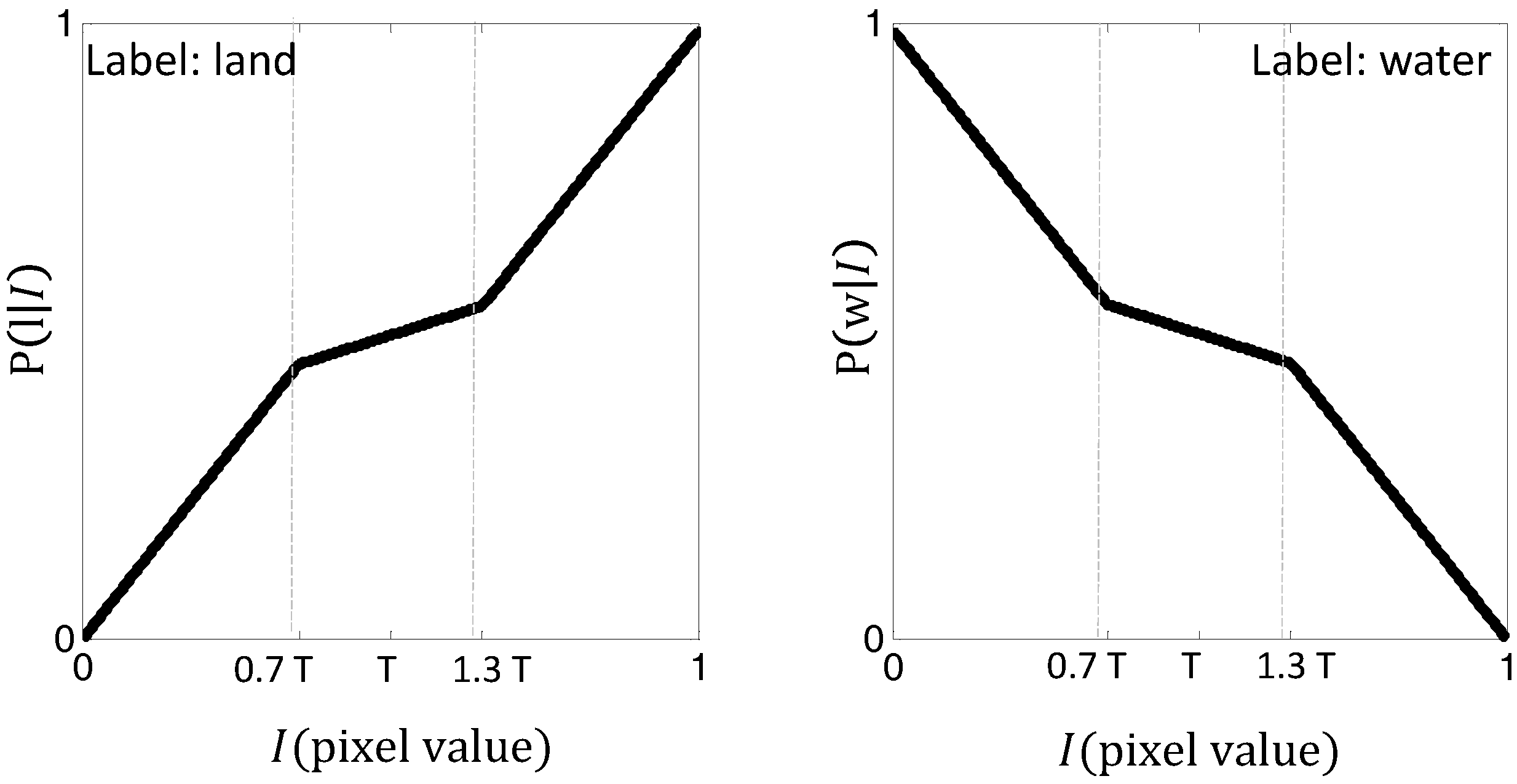
3.4. Implementation of Energy Functions
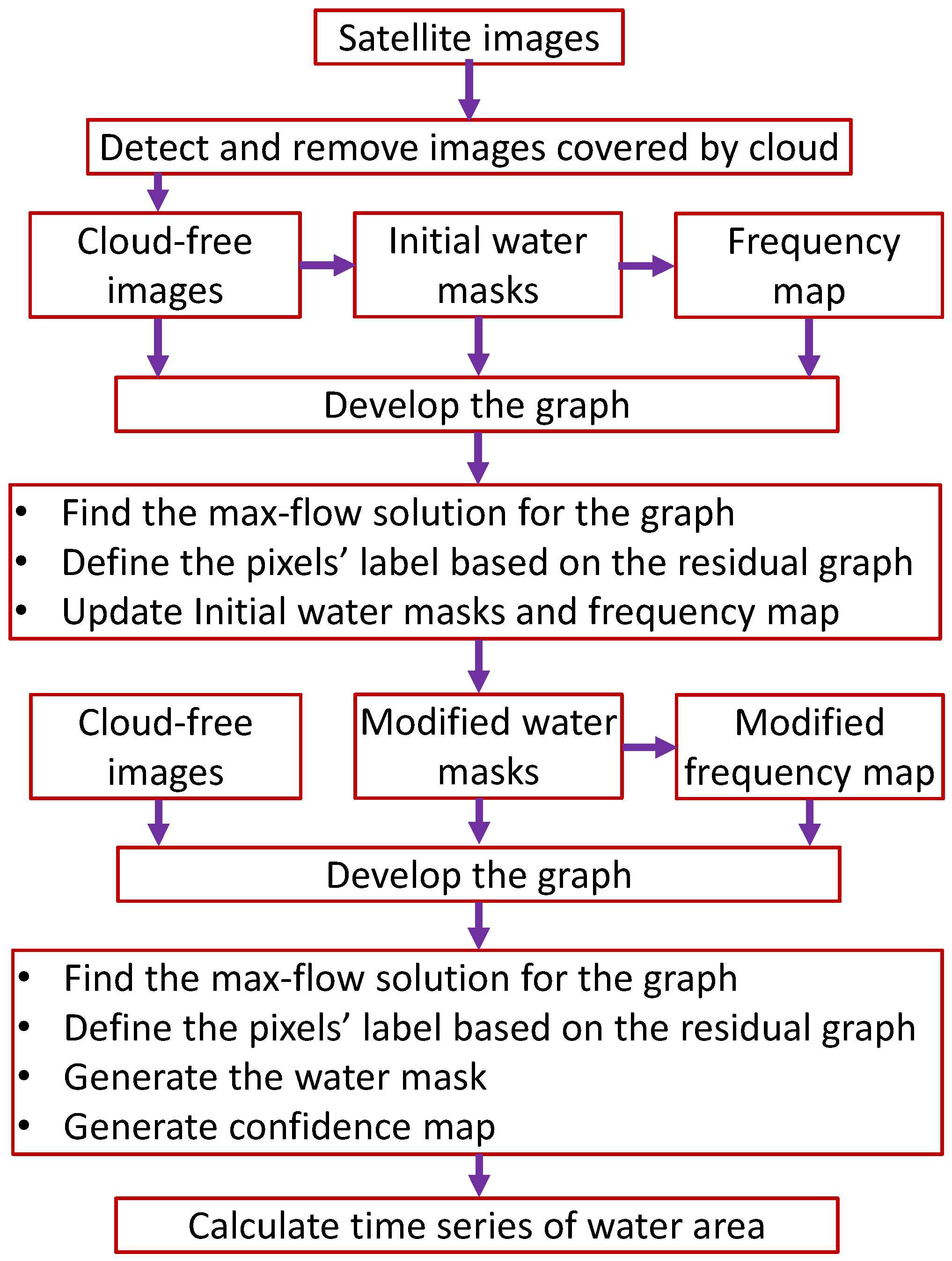
3.5. Review of the Proposed Method
4. Results and Validation
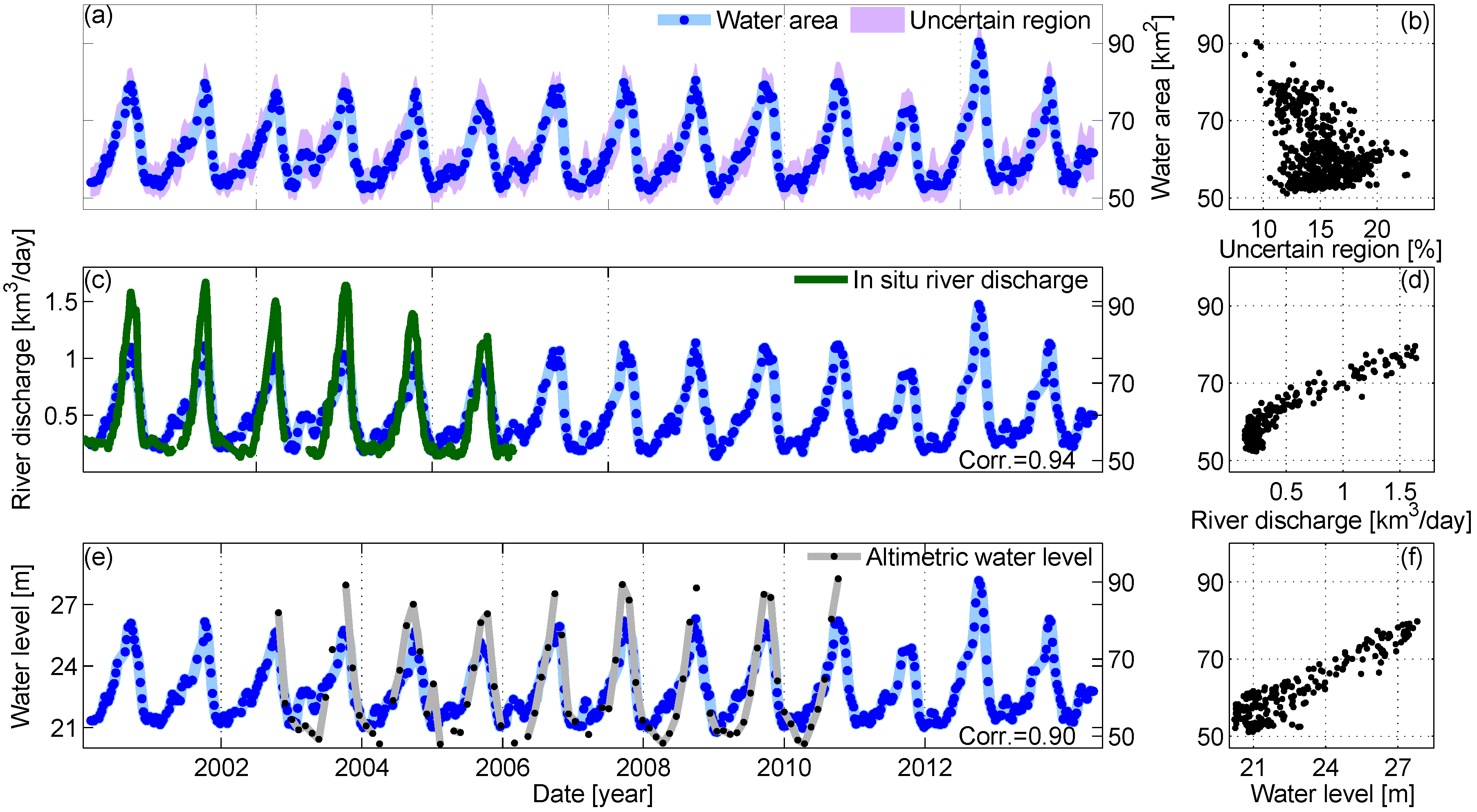
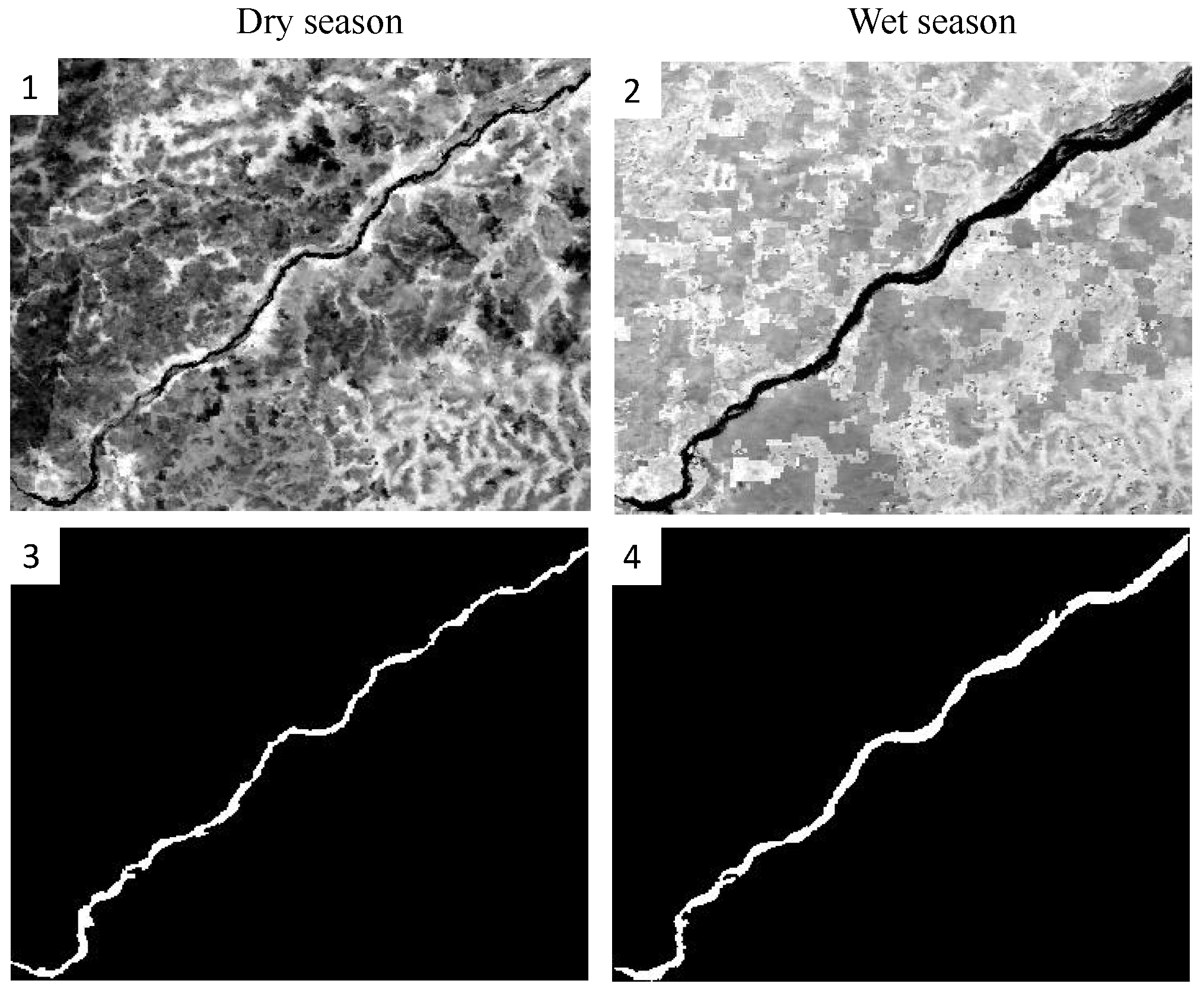
4.1. Niger River, Lokaja Station
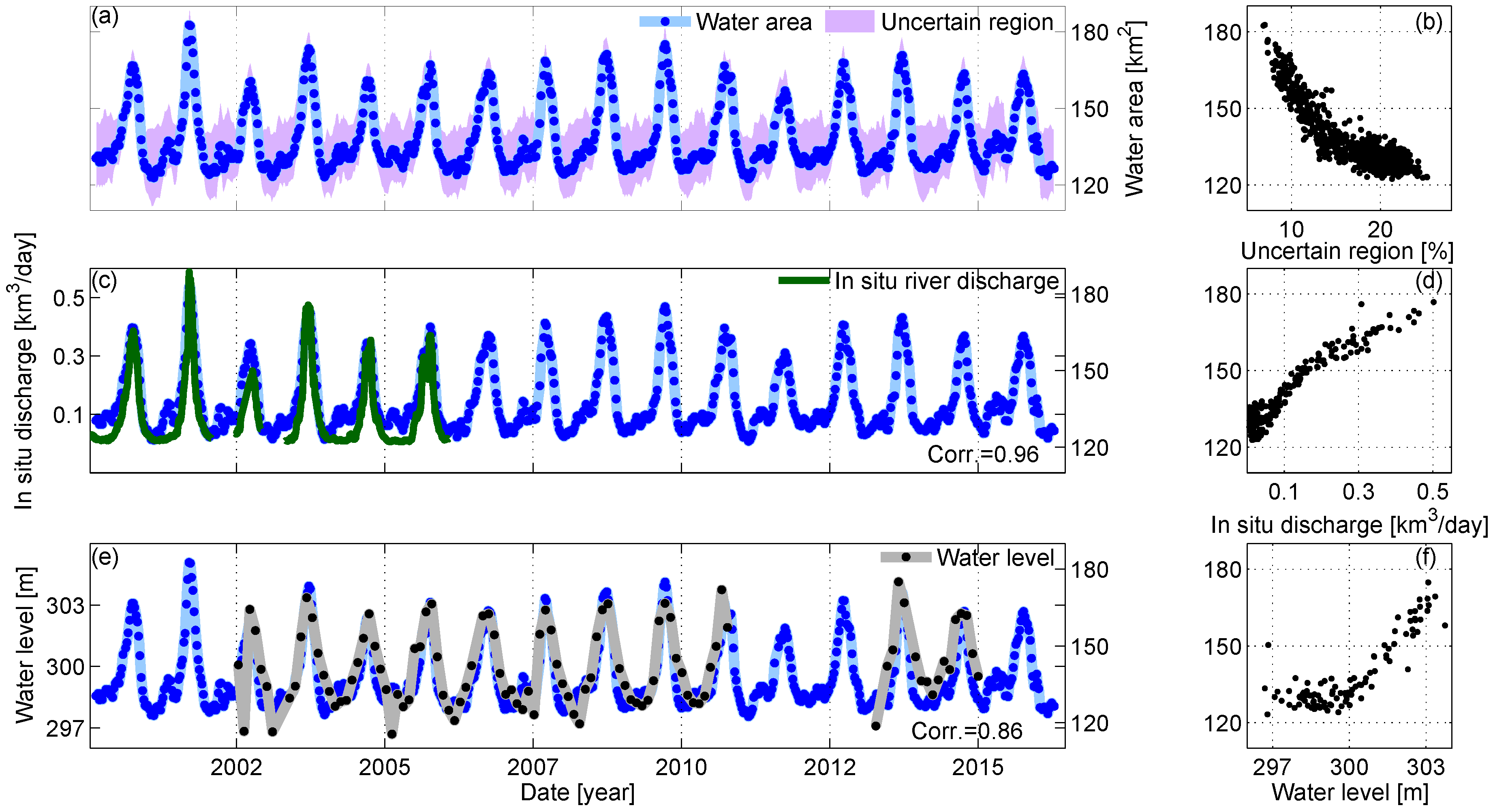
4.2. Niger River, Koulikoro Station
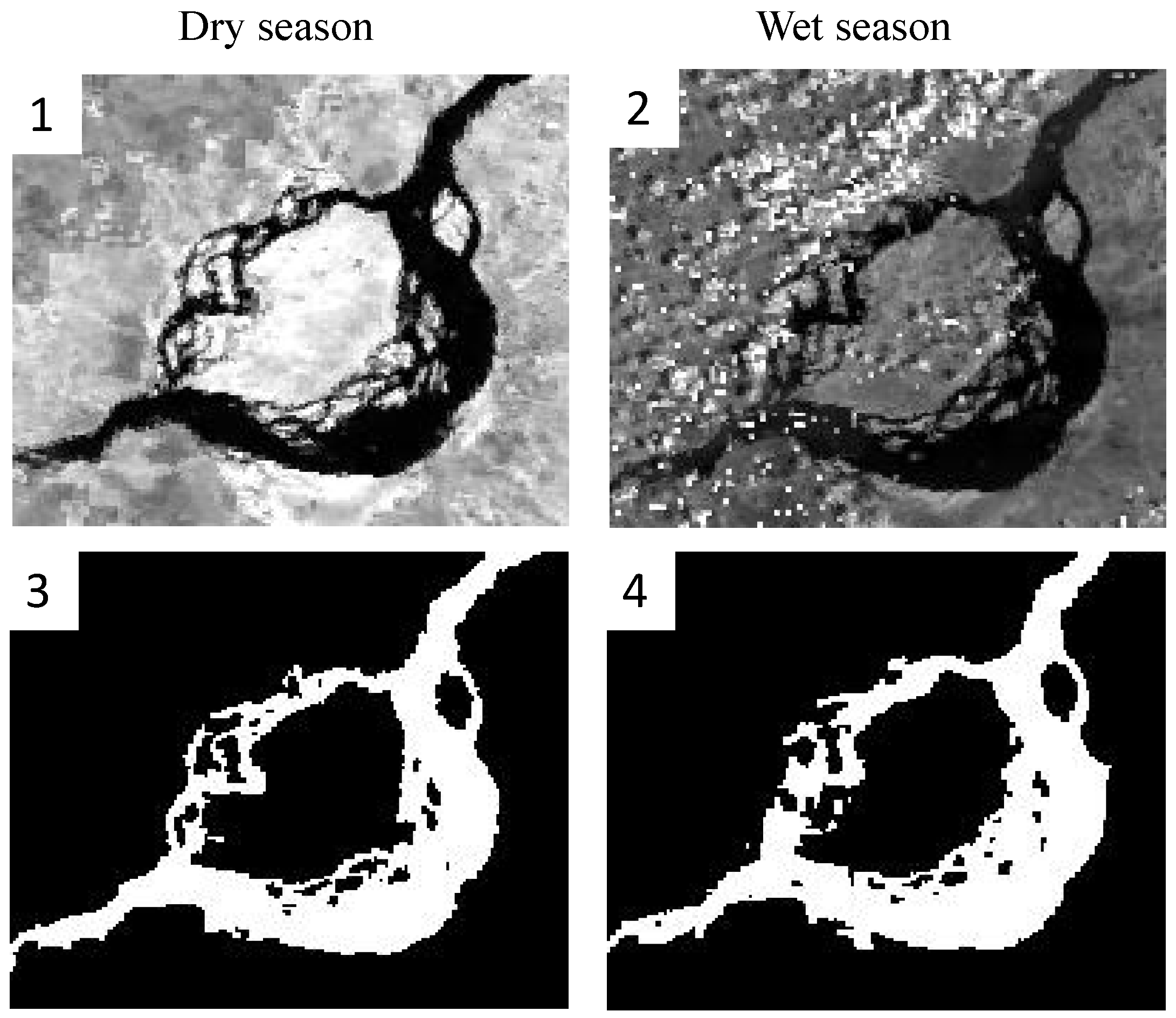
4.3. Congo River, Malebo Pool
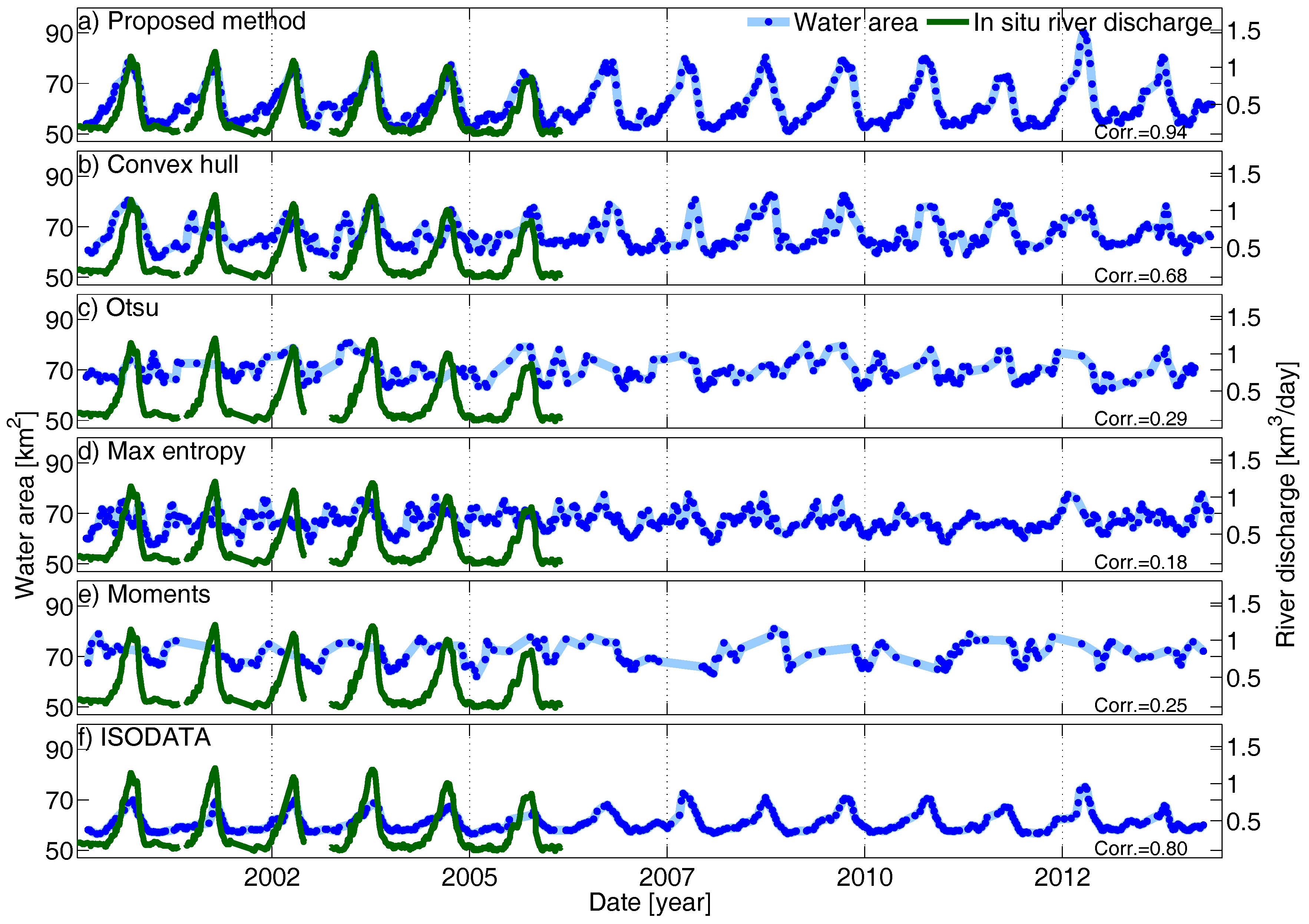
4.4. Comparison with Other Methods
- Convex hull thresholding is a method based on shape of the images histogram. After calculating the convex hull of the image histogram, the biggest difference between gray value frequency and convex hull is selected as threshold [71].
- Otsu thresholding is a clustering-based method which assumes that the image contains two bimodal histograms. Then, the optimum threshold is defined in such a way that the variance within the classes is minimized [72].
- Maximum entropy thresholding considers the image as two different sources of data, so when the sum of the two class entropies reaches its maximum. The image is optimally segmented into two classes [73].
- Moments thresholding: in this method, an image is considered as the blurred version of an ideal binary image. Then, the threshold value is defined by matching the first three moments of input image and binary map [74]. This method is considered as an object attribute-based thresholding algorithm.
- ISODATA: as one of the most advanced unsupervised classification methods, ISODATA is selected because of its ability to modify the clusters with respect to the situation of the river [75].
5. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Prigent, C.; Papa, F.; Aires, F.; Rossow, W.; Matthews, E. Global inundation dynamics inferred from multiple satellite observations, 1993–2000. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Rodríguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Sneeuw, N.; Lorenz, C.; Devaraju, B.; Tourian, M.J.; Riegger, J.; Kunstmann, H.; Bárdossy, A. Estimating runoff using hydro-geodetic approaches. Surv. Geophys. 2014, 35, 1333–1359. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Xie, H.; Zhang, K.; Zhu, F. Lakes’ state and abundance across the Tibetan Plateau. Chin. Sci. Bull. 2014, 59, 3010–3021. [Google Scholar] [CrossRef]
- Liu, G.; Schwartz, F.W.; Tseng, K.H.; Shum, C. Discharge and water-depth estimates for ungauged rivers: Combining hydrologic, hydraulic, and inverse modeling with stage and water-area measurements from satellites. Water Resour. Res. 2015, 51, 6017–6035. [Google Scholar] [CrossRef]
- Zhang, G.; Xie, H.; Kang, S.; Yi, D.; Ackley, S.F. Monitoring lake level changes on the Tibetan Plateau using ICESat altimetry data (2003–2009). Remote Sens. Environ. 2011, 115, 1733–1742. [Google Scholar] [CrossRef]
- Li, C.H.; Lee, C.K. Minimum cross entropy thresholding. Pattern Recognit. 1993, 26, 617–625. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondizio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2401. [Google Scholar] [CrossRef]
- Sandholt, I.; Nyborg, L.; Fog, B.; Lô, M.; Bocoum, O.; Rasmussen, K. Remote sensing techniques for flood monitoring in the Senegal River Valley. Geogr. Tidsskr. Dan. J. Geogr. 2003, 103, 71–81. [Google Scholar] [CrossRef]
- Bonn, F.; Dixon, R. Monitoring flood extent and forecasting excess runoff risk with RADARSAT-1 data. Nat. Hazards 2005, 35, 377–393. [Google Scholar] [CrossRef]
- Martinis, S.; Twele, A.; Strobl, C.; Kersten, J.; Stein, E. A Multi-Scale Flood Monitoring System Based on Fully Automatic MODIS and TerraSAR-X Processing Chains. Remote Sens. 2013, 5, 5598–5619. [Google Scholar] [CrossRef]
- Garay, M.J.; Diner, D.J. Multi-angle Imaging SpectroRadiometer (MISR) time-lapse imagery of tsunami waves from the 26 December 2004 Sumatra-Andaman earthquake. Remote Sens. Environ. 2007, 107, 256–263. [Google Scholar] [CrossRef]
- Munyati, C. Use of principal component analysis (PCA) of remote sensing images in wetland change detection on the Kafue Flats, Zambia. Geocarto Int. 2004, 19, 11–22. [Google Scholar] [CrossRef]
- Wang, Y. Seasonal change in the extent of inundation on floodplains detected by JERS-1 Synthetic Aperture Radar data. Int. J. Remote Sens. 2004, 25, 2497–2508. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Ryu, J.H.; Won, J.S.; Min, K.D. Waterline extraction from Landsat TM data in a tidal flat: A case study in Gomso Bay, Korea. Remote Sens. Environ. 2002, 83, 442–456. [Google Scholar] [CrossRef]
- Kuenzer, C.; Guo, H.; Huth, J.; Leinenkugel, P.; Li, X.; Dech, S. Flood Mapping and Flood Dynamics of the Mekong Delta: ENVISAT-ASAR-WSM Based Time Series Analyses. Remote Sens. 2013, 5, 687–715. [Google Scholar] [CrossRef] [Green Version]
- Kuenzer, C.; Klein, I.; Ullmann, T.; Georgiou, E.F.; Baumhauer, R.; Dech, S. Remote sensing of river delta inundation: Exploiting the potential of coarse spatial resolution, temporally-dense MODIS Time Series. Remote Sens. 2015, 7, 8516–8542. [Google Scholar] [CrossRef]
- Gao, H.; Birkett, C.; Lettenmaier, D.P. Global monitoring of large reservoir storage from satellite remote sensing. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Tourian, M.; Elmi, O.; Chen, Q.; Devaraju, B.; Roohi, S.; Sneeuw, N. A spaceborne multisensor approach to monitor the desiccation of Lake Urmia in Iran. Remote Sens. Environ. 2015, 156, 349–360. [Google Scholar] [CrossRef]
- Klein, I.; Dietz, A.J.; Gessner, U.; Galayeva, A.; Myrzakhmetov, A.; Kuenzer, C. Evaluation of seasonal water body extents in Central Asia over the past 27 years derived from medium-resolution remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 335–349. [Google Scholar] [CrossRef]
- Doña, C.; Chang, N.B.; Caselles, V.; Sánchez, J.M.; Pérez-Planells, L.; Bisquert, M.D.M.; García-Santos, V.; Imen, S.; Camacho, A. Monitoring Hydrological Patterns of Temporary Lakes Using Remote Sensing and Machine Learning Models: Case Study of La Mancha Húmeda Biosphere Reserve in Central Spain. Remote Sens. 2016, 8, 618. [Google Scholar] [CrossRef]
- Carroll, M.; Wooten, M.; DiMiceli, C.; Sohlberg, R.; Kelly, M. Quantifying Surface Water Dynamics at 30 Meter Spatial Resolution in the North American High Northern Latitudes 1991–2011. Remote Sens. 2016, 8, 622. [Google Scholar] [CrossRef]
- Huang, C.; Chen, Y.; Zhang, S.; Li, L.; Shi, K.; Liu, R. Surface Water Mapping from Suomi NPP-VIIRS Imagery at 30 m Resolution via Blending with Landsat Data. Remote Sens. 2016, 8, 631. [Google Scholar] [CrossRef]
- McFeeters, S.K. Using the Normalized Difference Water Index (NDWI) within a Geographic Information System to Detect Swimming Pools for Mosquito Abatement: A Practical Approach. Remote Sens. 2013, 5, 3544–3561. [Google Scholar] [CrossRef]
- Kallio, K.; Attila, J.; Härmä, P.; Koponen, S.; Pulliainen, J.; Hyytiäinen, U.M.; Pyhälahti, T. Landsat ETM+ images in the estimation of seasonal lake water quality in boreal river basins. Environ. Manag. 2008, 42, 511–522. [Google Scholar] [CrossRef] [PubMed]
- Fisher, A.; Danaher, T. A Water Index for SPOT5 HRG Satellite Imagery, New South Wales, Australia, Determined by Linear Discriminant Analysis. Remote Sens. 2013, 5, 5907–5925. [Google Scholar] [CrossRef]
- Elmi, O. The Role of Multispectral Image Transformations in Change Detection. Master’s Thesis, University of Stuttgart, Stuttgart, Germany, 2015. [Google Scholar]
- Wohlfart, C.; Liu, G.; Huang, C.; Kuenzer, C. A River Basin over the Course of Time: Multi-Temporal Analyses of Land Surface Dynamics in the Yellow River Basin (China) Based on Medium Resolution Remote Sensing Data. Remote Sens. 2016, 8, 186. [Google Scholar] [CrossRef]
- Tourian, M.; Tarpanelli, A.; Elmi, O.; Qin, T.; Brocca, L.; Moramarco, T.; Sneeuw, N. Spatiotemporal densification of river water level time series by multimission satellite altimetry. Water Resour. Res. 2016. [Google Scholar] [CrossRef]
- Elmi, O.; Tourian, M.J.; Sneeuw, N. River discharge estimation using channel width from satellite imagery. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 727–730.
- Pavelsky, T.M. Using width-based rating curves from spatially discontinuous satellite imagery to monitor river discharge. Hydrol. Process. 2014, 28, 3035–3040. [Google Scholar] [CrossRef]
- Townsend, P.A. Mapping seasonal flooding in forested wetlands using multi-temporal Radarsat SAR. Photogram. Eng. Remote Sens. 2001, 67, 857–864. [Google Scholar]
- Brivio, P.A.; Colombo, R.; Maggi, M.; Tomasoni, R. Integration of remote sensing data and GIS for accurate mapping of flooded areas. Int. J. Remote Sens. 2002, 23, 429–441. [Google Scholar] [CrossRef]
- Cao, W. Change Detection Using SAR Data. Master’s Thesis, University of Stuttgart, Stuttgart, Germany, 2013. [Google Scholar]
- Weih, R.C., Jr.; Riggan, N.D., Jr. Object-based classification vs. pixel-based classification: Comparative importance of multi-resolution imagery. In Proceedings of the GEOBIA 2010: Geographic Object-Based Image Analysis, Ghent, Belgium, 29 June–2 July 2010; Volume 38, p. 6.
- Hogan, C.M. Niger River; McGinley, M., Ed.; National Council for Science and Environment: Washington, DC, USA, 2013. [Google Scholar]
- Cretaux, J.F.; Berge-Nguyen, M.; Leblanc, M.; Abarca Del Rio, R.; Delclaux, F.; Mognard, N.; Lion, C.; Pandey, R.K.; Tweed, S.; Calmant, S.; et al. Flood mapping inferred from remote sensing data. Int. Water Technol. J. 2011, 1, 48–62. [Google Scholar]
- O’Loughlin, F.; Trigg, M.; Schumann, G.P.; Bates, P. Hydraulic characterization of the middle reach of the Congo River. Water Resour. Res. 2013, 49, 5059–5070. [Google Scholar] [CrossRef]
- Da Silva, J.S.; Calmant, S.; Seyler, F.; Filho, O.C.R.; Cochonneau, G.; Mansur, W.J. Water levels in the Amazon basin derived from the ERS 2 and ENVISAT radar altimetry missions. Remote Sens. Environ. 2010, 114, 2160–2181. [Google Scholar] [CrossRef]
- Tourian, M.; Sneeuw, N.; Bárdossy, A. A quantile function approach to discharge estimation from satellite altimetry (ENVISAT). Water Resour. Res. 2013, 49, 4174–4186. [Google Scholar] [CrossRef]
- Veksler, O. Efficient Graph-Based Energy Minimization Methods in Computer Vision. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 1999. [Google Scholar]
- Geman, S.; Geman, D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 1984, PAMI-6, 721–741. [Google Scholar] [CrossRef]
- Ishikawa, H.; Geiger, D. Segmentation by grouping junctions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Santa Barbara, CA, USA, 25 June 1998; pp. 125–131.
- Couprie, C.; Grady, L.; Najman, L.; Talbot, H. Power watershed: A unifying graph-based optimization framework. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1384–1399. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boykov, Y.; Veksler, O.; Zabih, R. Markov random fields with efficient approximations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Santa Barbara, CA, USA, 25 June 1998; pp. 648–655.
- Boykov, Y.; Veksler, O.; Zabih, R. Fast approximate energy minimization via graph cuts. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 1222–1239. [Google Scholar] [CrossRef]
- Bruzzone, L.; Prieto, D.F. An adaptive semiparametric and context-based approach to unsupervised change detection in multitemporal remote-sensing images. IEEE Trans. Image Process. 2002, 11, 452–466. [Google Scholar] [CrossRef] [PubMed]
- Mota, G.L.; Feitosa, R.Q.; Coutinho, H.L.; Liedtke, C.E.; Müller, S.; Pakzad, K.; Meirelles, M.S. Multitemporal fuzzy classification model based on class transition possibilities. ISPRS J. Photogram. Remote Sens. 2007, 62, 186–200. [Google Scholar] [CrossRef]
- Solberg, A.H.S.; Taxt, T.; Jain, A.K. A Markov random field model for classification of multisource satellite imagery. IEEE Trans. Geosci. Remote Sens. 1996, 34, 100–113. [Google Scholar] [CrossRef]
- Martinis, S.; Twele, A. A hierarchical spatio-temporal Markov model for improved flood mapping using multi-temporal X-band SAR data. Remote Sens. 2010, 2, 2240–2258. [Google Scholar] [CrossRef]
- Besag, J. On the statistical analysis of dirty pictures. J. R. Stat. Soc. Ser. B (Methodol.) 1986, 48, 259–302. [Google Scholar] [CrossRef]
- Szeliski, R.; Zabih, R.; Scharstein, D.; Veksler, O.; Kolmogorov, V.; Agarwala, A.; Tappen, M.; Rother, C. A comparative study of energy minimization methods for markov random fields. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2006; pp. 16–29. [Google Scholar]
- Greig, D.; Porteous, B.; Seheult, A.H. Exact maximum a posteriori estimation for binary images. J. R. Stat. Soc. Ser. B 1989, 51, 271–279. [Google Scholar]
- Boykov, Y.; Kolmogorov, V. An experimental comparison of min-cut/max-flow algorithms for energy minimization in vision. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1124–1137. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, A.V.; Hed, S.; Kaplan, H.; Tarjan, R.E.; Werneck, R.F. Maximum flows by incremental breadth-first search. In Algorithms–ESA 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 457–468. [Google Scholar]
- Veksler, O. Image segmentation by nested cuts. IEEE Conf. Comput. Vis. Pattern Recognit. 2000, 1, 339–344. [Google Scholar]
- Kolmogorov, V.; Zabin, R. What energy functions can be minimized via graph cuts? IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 147–159. [Google Scholar] [CrossRef] [PubMed]
- Kohli, P.; Torr, P. Measuring uncertainty in graph cut solutions-efficiently computing min-marginal energies using dynamic graph cuts. In Proceedings of the 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 30–43.
- Boykov, Y.Y.; Jolly, M.P. Interactive graph cuts for optimal boundary & region segmentation of objects in ND images. In Proceedings of the Eighth IEEE International Conference on Computer Vision (ICCV 2001), Vancouver, BC, Canada, 7–14 July 2001; Volume 1, pp. 105–112.
- Besag, J. Spatial interaction and the statistical analysis of lattice systems. J. R. Stat. Soc. Ser. B (Methodol.) 1974, 36, 192–236. [Google Scholar]
- Boykov, Y.; Veksler, O. Graph cuts in vision and graphics: Theories and applications. In Handbook of Mathematical Models in Computer Vision; Springer: Berlin/Heidelberg, Germany, 2006; pp. 79–96. [Google Scholar]
- Li, S.Z. Markov Random Field Modeling in Image Analysis; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Ford, L.; Fulkerson, D.R. Flows in Networks; Princeton University Press: Princeton, NJ, USA, 1962. [Google Scholar]
- Goldberg, A.V.; Tarjan, R.E. A new approach to the maximum-flow problem. J. ACM 1988, 35, 921–940. [Google Scholar] [CrossRef]
- Dinits, E. Algorithm of solution to problem of maximum flow in network with power estimates. Dokl. Akad. Nauk SSSR 1970, 11, 1277–1280. [Google Scholar]
- Kohli, P.; Torr, P.H. Measuring uncertainty in graph cut solutions. Comput. Vis. Image Underst. 2008, 112, 30–38. [Google Scholar] [CrossRef]
- Tarlow, D.; Adams, R.P. Revisiting uncertainty in graph cut solutions. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 2440–2447.
- Leopold, L.B.; Maddock, T., Jr. The Hydraulic Geometry of Stream Channels and Some Physiographic Implications; US Geological Survey Professional Paper No. 252; Superintendent of Documents; U.S. Government Printing Office: Washington, DC, USA, 1953.
- Sezgin, M.; Sankur, B. Survey over image thresholding techniques and quantitative performance evaluation. J. Electron. Imaging 2004, 13, 146–168. [Google Scholar]
- Rosenfeld, A.; de La Torre, P. Histogram concavity analysis as an aid in threshold selection. IEEE Trans. Syst. Man Cybern. 1983, SMC-13, 231–235. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. Automatica 1975, 11, 23–27. [Google Scholar] [CrossRef]
- Glasbey, C.A. An analysis of histogram-based thresholding algorithms. CVGIP Graph. Models Image Process. 1993, 55, 532–537. [Google Scholar] [CrossRef]
- Tsai, W.H. Moment-preserving thresolding: A new approach. Comput. Vis. Graph. Image Process. 1985, 29, 377–393. [Google Scholar] [CrossRef]
- Ball, G.H.; Hall, D.J. ISODATA, A Novel Method of Data Analysis and Pattern Classification; Technical Report; DTIC Document: Fort Belvoir, VA, USA, 1965. [Google Scholar]
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T.M. The SWOT mission and its capabilities for land hydrology. Surv. Geophys. 2016, 37, 307–337. [Google Scholar] [CrossRef]






| Study | Sensor | Approach | Type |
|---|---|---|---|
| Flood and Inundation Area Monitoring | |||
| Sandholt et al. [9] | AVHRR | Linear spectral unmixing | Advanced model, unsupervised |
| ERS2 | Iterative Self-Organizing Data Analysis Technique (ISODATA) | Unsupervised | |
| Landsat 7 | Maximum likelihood | Supervised | |
| Bonn and Dixon [10] | RADARSAT-1 | Parallelliped classifier | Supervised |
| Martinis et al. [11] | MODIS | Dynamic thresholding | Algebra, unsupervised |
| TerraSAR-X | Dynamic thresholding | Algebra, unsupervised | |
| Garay and Diner [12] | MEdium Resolution Imaging Spectrometer (MERIS) | Visual analysis | Supervised |
| Munyati [13] | Landsat 5 | Principal component analysis (PCA) | Transformation, unsupervised |
| Wang [14] | Japanese Earth Resources Satellite 1 (JERS-1) | Decision tree | Supervised |
| Feyisa et al. [15] | Landsat 5 | Dynamic thresholding | Algebra, unsupervised |
| Ryu et al. [16] | Landsat 7 | Density slicing | Algebra, unsupervised |
| Künzer et al. [17] | ENVISAT ASAR | Dynamic thresholding | Algebra, unsupervised |
| Künzer et al. [18] | MODIS | Dynamic thresholding | Algebra, unsupervised |
| Lake and Reservoir Area Monitoring | |||
| Gao et al. [19] | MODIS | k-Means clustering | Unsupervised classification |
| Tourian et al. [20] | MODIS | ISODATA | Unsupervised |
| Klein et al. [21] | MODIS, AVHHR | Dynamic thresholding | Algebra, unsupervised |
| Doña et al. [22] | Landsat 7 | Parallelepiped, support vector machine (SVM) | Supervised |
| Genetic algorithm, maximum likelihood | Supervised | ||
| Minimum distance, artificial neural network | Supervised | ||
| ISODATA, k-means | Unsupervised | ||
| Carroll et al. [23] | Landsat 5, 7 | Random forest classifier | Supervised |
| Huang et al. [24] | Landsat 8 | Otsu Thresholding | Algebra, unsupervised |
| Zhang et al. [4] | Landsat 7 | Visual analysis | Supervised |
| McFeeters [25] | QuickBird | thresholding, GIS-based | GIS, supervised |
| Kallio et al. [26] | Landsat 7 | Dynamic thresholding | Algebra, unsupervised |
| Fisher and Danaher [27] | SPOT 5 | Dynamic thresholding | Algebra, unsupervised |
| River Area Monitoring | |||
| Elmi [28] | Landsat 7, MODIS | PCA, canonical correlation analysis (CCA) | Transformation, unsupervised |
| Wohlfart et al. [29] | MODIS | Random forest classifier | Supervised |
| Tourian et al. [30] | Landsat 7 | Tasseled cap transformation | Transformation, unsupervised |
| Elmi et al. [31] | MODIS | ISODATA | Unsupervised |
| Pavelsky [32] | RapidEye | Dynamic thresholding | Unsupervised |
| Case | Name | Reach Length (km) | In Situ Discharge | Altimetry | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Station | Lat () | Lon () | Period | Lat () | Lon () | Period | Mission | |||
| 1 | Niger | 20 | Lokaja | N | E | 2000–2006 | N | 2003–2011 | Envisat | |
| 2 | Niger | 115 | Koulikoro | N | W | 2000–2006 | N | 2002–2015 | Envisat, SARAL | |
| 3 | Congo | 50 | Kinshasa | S | E | 2000–2010 | S | 15.30E | 2002–2014 | Envisat, SARAL |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elmi, O.; Tourian, M.J.; Sneeuw, N. Dynamic River Masks from Multi-Temporal Satellite Imagery: An Automatic Algorithm Using Graph Cuts Optimization. Remote Sens. 2016, 8, 1005. https://doi.org/10.3390/rs8121005
Elmi O, Tourian MJ, Sneeuw N. Dynamic River Masks from Multi-Temporal Satellite Imagery: An Automatic Algorithm Using Graph Cuts Optimization. Remote Sensing. 2016; 8(12):1005. https://doi.org/10.3390/rs8121005
Chicago/Turabian StyleElmi, Omid, Mohammad J. Tourian, and Nico Sneeuw. 2016. "Dynamic River Masks from Multi-Temporal Satellite Imagery: An Automatic Algorithm Using Graph Cuts Optimization" Remote Sensing 8, no. 12: 1005. https://doi.org/10.3390/rs8121005
APA StyleElmi, O., Tourian, M. J., & Sneeuw, N. (2016). Dynamic River Masks from Multi-Temporal Satellite Imagery: An Automatic Algorithm Using Graph Cuts Optimization. Remote Sensing, 8(12), 1005. https://doi.org/10.3390/rs8121005







