Next Article in Journal
Mass Flux Solution in the Tibetan Plateau Using Mascon Modeling
Next Article in Special Issue
Distinguishing Land Change from Natural Variability and Uncertainty in Central Mexico with MODIS EVI, TRMM Precipitation, and MODIS LST Data
Previous Article in Journal
Hierarchical Coding Vectors for Scene Level Land-Use Classification
Previous Article in Special Issue
Simulation of the Impact of a Sensor’s PSF on Mixed Pixel Decomposition: 1. Nonuniformity Effect
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 8
Issue 5
10.3390/rs8050440
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Error-Component Analysis of TRMM-Based Multi-Satellite Precipitation Estimates over Mainland China

by
Bin Yong
1,2,*,
Bo Chen
1,
Yudong Tian
3,4,
Zhongbo Yu
1 and
Yang Hong
5
1
State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Nanjing 210098, China
2
State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, SOA, Hangzhou 310012, China
3
Earth System Science Interdisciplinary Center, University of Maryland, College Park, MD 20742, USA
4
NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
5
School of Civil Engineering and Environmental Sciences, University of Oklahoma, Norman, OK 73019, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2016, 8(5), 440; https://doi.org/10.3390/rs8050440
Submission received: 16 February 2016 / Revised: 25 April 2016 / Accepted: 17 May 2016 / Published: 23 May 2016
(This article belongs to the Special Issue Uncertainties in Remote Sensing)
Browse Figures
Versions Notes

Abstract

:
The Tropical Rainfall Measuring Mission (TRMM) Multi-Satellite Precipitation Analysis (TMPA) products have been widely used, but their error and uncertainty characteristics over diverse climate regimes still need to be quantified. In this study, we focused on a systematic evaluation of TMPA’s error characteristics over mainland China, with an improved error-component analysis procedure. We performed the analysis for both the TMPA real-time and research product suite at a daily scale and 0.25° × 0.25° resolution. Our results show that, in general, the error components in TMPA exhibit rather strong regional and seasonal differences. For humid regions, hit bias and missed precipitation are the two leading error sources in summer, whereas missed precipitation dominates the total errors in winter. For semi-humid and semi-arid regions, the error components of two real-time TMPA products show an evident topographic dependency. Furthermore, the missed and false precipitation components have the similar seasonal variation but they counter each other, which result in a smaller total error than the individual components. For arid regions, false precipitation is the main problem in retrievals, especially during winter. On the other hand, we examined the two gauge-correction schemes, i.e., climatological calibration algorithm (CCA) for real-time TMPA and gauge-based adjustment (GA) for post-real-time TMPA. Overall, our results indicate that the upward adjustments of CCA alleviate the TMPA’s systematic underestimation over humid region but, meanwhile, unfavorably increased the original positive biases over the Tibetan plateau and Tianshan Mountains. In contrast, the GA technique could substantially improve the error components for local areas. Additionally, our improved error-component analysis found that both CCA and GA actually also affect the hit bias at lower rain rates (particularly for non-humid regions), as well as at higher ones. Finally, this study recommends that future efforts should focus on improving hit bias of humid regions, false error of arid regions, and missed snow events in winter.

Graphical Abstract

1. Introduction

In China, flood and drought are two primary natural hazards, often causing heavy property damages and human casualties [1,2,3]. Accurate measurement of precipitation plays a critical role in flood forecasting, drought monitoring, and related emergency management. Unfortunately, with two-thirds of its total land area covered by mountains, hills, and plateaus, China suffers the common problem of uneven distribution of meteorological stations and weather radars, and these instruments are particularly sparse over the mountainous regions with complex terrains, especially for Western China. Satellite-based remote sensing offers an effective way to measure precipitation from space and it has been complementary to the conventional rain gauge networks and weather radars [4]. In the past two decades, several high-resolution satellite precipitation estimates have been produced by combining many international satellite platforms. The concept behind most of these multi-sensor algorithms relies upon the merging of passive microwave (PMW)- and infrared (IR)-based estimates. A typical example is the Tropical Rainfall Measuring Mission (TRMM) Multi-satellite Precipitation Analysis (TMPA), which merges the TRMM satellite’s estimates with those of other satellites, with TRMM serving as the calibration standard for modern satellite-based global precipitation measurements during the TRMM era (1998–2014). The current operational Version-7 TMPA system produces two standard user-level (Level 3) rainfall products at relatively fine resolution (0.25° × 0.25°, 3 h), i.e., the real-time 3B42RT (hereafter referred to as “RTV7”; 6–9 h after observation time) for the latitude band 60° N–60° S and the gauge-adjusted, post-real-time 3B42V7 for research purposes (hereafter “V7”; two months latency) with spatial coverage of 50° N–50° S [5,6]. Recently, these two quasi-global satellite precipitation products have been widely utilized in various hydrological and meteorological applications in China [7,8,9,10,11,12,13].
Over the years, there have been many efforts to compare and validate available satellite precipitation estimates at global, regional, or basin scales [9,10,14,15,16,17,18,19,20,21,22,23,24,25]. An essential point when trying to evaluate the data accuracy is to know where the retrieval errors are coming from. One particularly effective approach is the error-component analysis introduced by Tian et al. [26], which has close correspondence to the precipitation retrieval processes. In practice, the retrieval processes of both PMW and IR normally consist of two steps. The first step is screening, i.e., detecting raining and no-raining pixels. This step is prone to two types of errors. If raining pixels are not detected, it will result in missed precipitation (i.e., missed error). On the contrary, no-raining pixels might be mistaken as raining ones, which could lead to false precipitation (i.e., false error). Once rainy pixels are identified, then the second step is to establish the relationship between the observed brightness temperature (either from passive microwave or infrared sensors) and rain rate. Even when a raining pixel is correctly hit, there still exist retrieval errors in translating the brightness temperature reading to rain rate (i.e., hit error). The error-component analysis technique treats these error sources separately, which in turn track the error sources better than the conventional approaches. This helps both algorithm developers and data users to better understand the error features of satellite precipitation and their generation mechanisms.
Therefore, the goal of this paper is to systematically evaluate the Version-7 TMPA products over the entirety of mainland China, with the error-component analysis technique. We also made some improvements to the technique to better capture the effect of the two gauge correction schemes employed by TMPA. This paper is structured as follows: Section 2 introduces the data sources used, study area, and methodology. Section 3 presents the analysis results of three independent error components over different climate regions. Spatio-temporal characteristics, intensity distribution, and contribution ratios of error components are demonstrated in this section. Summarizing remarks and conclusions finalize the paper in Section 4.

2. Data Sources, Study Area, and Error-Decomposition Method

2.1. Data Sources

TMPA has three flavors, as a result of the dynamic evolution of its multi-sensor merging and correction algorithm. An important climatological calibration algorithm (CCA; A detailed description is provided in Appendix A of Yong et al. [27]) was applied to the real-time estimates on 17 February 2009 for reducing the systematic biases on a large scale, meanwhile maintaining the original near-real-time availability. With the launch of the Global Precipitation Measurement (GPM) mission satellite as the successor of TRMM, the CCA calibration scheme was also carried over to the early runs of the Integrated Multi-satellite Retrievals for GPM (IMERG) algorithm. Nevertheless, previous studies have indicated that the employment of the historical gauge data and the smooth-fill scheme in CCA could homogenize the highly-variable local rainstorm characteristics, despite that it can effectively reduce the TMPA’s systematic biases [28]. As a purely satellite-derived estimation, the uncalibrated RTV7 before CCA may help data users to conduct further investigations in their areas of interest. This uncalibrated dataset was actually provided as an additional field in the TMPA real-time estimates. Therefore, it seems important to further understand and examine the error characteristics of Version-7 TMPA on its three different processing stages, namely the real-time estimates before and after CCA (hereafter referred to as “RTV7-UC” and “RTV7-C”), and the post-real-time product V7.
All the three TMPA products (i.e., RTV7-UC, RTV7-C, and V7) are evaluated against one ground-based rain gauge product in our study. We selected the newly-released gridded China Gauge-based Daily Precipitation Analysis (CGDPA) developed by the National Meteorological Information Center (NMIC) of the China Meteorological Administration (CMA; [29]) as a ground reference. The daily CGDPA consists of two products with different spatial resolution (i.e., 0.25° × 0.25° and 0.5° × 0.5° respectively). The 0.25° dataset was developed from 2419 rainfall gauges over mainland China from April 2008 to present, while the other 0.5° product was based on 756 national standard meteorological stations with longer time series that can date back to 1955 (see http://cdc.cma.gov.cn/dataSetDetailed.do). We used the 0.25° × 0.25° version for our analysis.
The CGDPA system adopts a modified interpolation method of climatology-based optimal interpolation (OI) with topographic correction proposed by Xie et al. [30]. The OI algorithm performs better than the other techniques, exhibiting higher correlation to the independent gauge observation for various situations. The validation results of Shen et al. [29] indicated that the CGDPA apparently outperformed other two surface observation rainfall datasets, the Climate Prediction Center Unified gauge dataset [31] and the East Asia gauge analysis [30], due to the denser rainfall gauges involved. Relatively, CGDPA could better capture the precipitation structure and spatial patterns, particularly for strong rainy events at higher rain rates (>25 mm/day). At present, the CGDPA has been formally released as the official daily gridded precipitation product that is normally recommended as a readily available input to hydrological and meteorological applications over mainland China. The period analyzed covers five complete years from April 2008 through March 2013, during which both observed precipitation and the aforementioned satellite datasets are all available. Both the reference data and the satellite data are aggregated to daily amount, at their common 0.25° × 0.25° spatial resolution.

2.2. Study Area

China has diverse climate conditions due to its large area and varied topography, with the Tibet Plateau being the most prominent orographic feature. The elevation drastically descends from west to east. Figure 1a shows the topography and the number of reporting stations in each 0.25° grid box for the reference data. Figure 1b presents the spatial distribution of average annual precipitation (AAP) in China during the past 50 years (1960–2009). This AAP map was computed from the aforementioned 0.5° CGDPA dataset with long historical recorder. It is clear that dry climate generally dominates vast areas of northwestern China, while it is mainly humid and semi-humid in the southeastern part of the country, as documented in Zou et al. [32]. As shown in Figure 1b, the AAP gradually decreases toward the northwest direction except for some parts of Northwestern Xinjiang, where there are larger APP values than those of surrounding areas. Under the influence of the East Asian Monsoon, Southeastern China has a humid subtropical climate with plenty rainfall (AAP > 800 mm/year), while the annual precipitation of Northwestern China is mostly less than 400 mm [33,34].
Several prior studies have found the potential linkage between the climate regimes and the performance of satellite precipitation estimates. For instant, the results of Xie et al. [30] and Shen et al. [35] indicated that the mainstream satellite precipitation estimates exhibit better agreement with gauge observations over humid regions, whereas they perform rather poorly over arid and semi-arid regions. Chen et al. [10] found that there exists larger overestimation of RTV7-C in arid Northwestern China and only slight underestimation occurred in humid Southern China. Likewise, Gebregiorgis et al. [36] considered that the performance of satellite precipitation products is the most likely affected by different criteria such as climate regime, topography, and soil type. In China, the different climate regimes associated with different rainfall types might have a great effect on the retrieval skills of satellite precipitation. Therefore, a regional division based on climatic regime is essential to systematically investigate the error components of satellite precipitation over the vast territory.
Considering that a complex division of climate regions may confuse the analysis results, here we simply divided mainland China into four representative climate regions: (1) humid region (AAP > 800 mm/year), covering the Southeastern China; (2) semi-humid region (AAP of 400–800 mm), extending from the southeast Tibet Plateau into the Northeastern China; (3) semi-arid region (AAP of 200–400 mm), with a long narrow strip region from southwest Tibet Plateau to North Inner Mongolia and some parts of Northwestern Xinjiang; (4) arid region (AAP < 200 mm), including the major part of Xinjiang and southern part of Inner Mongolia (see Figure 1).

2.3. Error Decomposition

In this study, we adopt the simple but effective error decomposition scheme proposed by Tian et al. [26] to evaluate the satellite precipitation estimates. Theoretically, this approach decomposes the total precipitation error E (hereafter referred to as “total bias”) into three error components: hit bias H, missed precipitation −M, and false precipitation F. Figure 2 illustrates the concept of hit, missed, and false precipitation of satellite rainfall estimates against ground observation, based on a 2 × 2 contingency table [37]. In practice, two simple true values (i.e., 1 and 0) can be used to identify raining and no-raining for satellite estimates and ground observation, respectively. Thus, H represents observed rainfall events which are detected by both satellite and ground validation data, M shows missed rainfall events by the satellite but detected by the validation data, and F indicates false observation of rainfall events by the satellite which are not reported by the ground reference (see Figure 2). Moreover, Tian et al. [26] adopted a binary mask and Boolean complement approach to verify that these three components (H, −M and F) are independent to one another (refer to Equations (1)–(5) in [26]).
According to the derivation of Tian et al. [26], the relation between three independent error components and the total bias can be expressed as:
E = H − M + F
In this study, the total bias E is defined as satellite estimates minus ground observation. Hit bias H is defined as satellite estimates minus ground reference for hit events and, therefore, it could be positive or negative. Missed precipitation (−M) and false precipitation (F) are always negative and positive, respectively, by definition. More details about the theory of error components are in Wilks [37] and Tian et al. [26].
The relationship in Equation (1) implies that the total bias, the subject of most conventional studies, cannot completely characterize the performance of satellite precipitation estimates. As the missed precipitation (−M) and false precipitation (F) always have opposite signs, they could cancel each other, which may result in smaller total bias than the individual components. Therefore, separating the total bias into independent error components could help us better understand the error nature of satellite products and the uncertainties of retrieval processes. Thus this approach is applied here to analyze the error components of three TMPA products (RTV7-UC, RTV7-C, and V7) across four different climate regions in China. A threshold of 1.0 mm/day is used to determine the occurrence of rainfall event for any given day, as suggested by many previous studies [7,16,26,38,39].

3. Results

3.1. Spatial Analysis of Error Components

Figure 3 and Figure 4 display the spatial distribution of the error components, each averaged for the summer (June, July, and August—JJA) and winter (December, January, and February—DJF), respectively. As for summer (Figure 3), all the three TMPA products (i.e., RTV7-UC, RTV7-C, and V7) exhibit an apparent similarity between total bias (E) and hit bias (H), suggesting that the most important error contribution in the TMPA retrievals comes from hit events (refer to the first two columns in Figure 3). On the other hand, these three products share almost identical distributions of missed precipitation over the entire China (Figure 3c,g,k). This implies that both the CCA calibration in RTV7-C and the gauged adjustment in V7 failed to correct those rainy events undetected by the satellites in the first place, and this is understandable. Furthermore, the largest missed errors are situated at the northeastern and southeastern parts of Qinghai-Tibetan plateau. This is possibly due to the limitation of current satellite precipitation retrievals in catching the warm rain processes or short-lived convective storms over complex mountainous areas, as documented in Tian et al. [26]. More interestingly, the north borderline of this domain remains in good agreement with the 200-mm precipitation contour, which is the important separation line to differentiate arid and semi-arid regions (Figure 3c,g,k). The false precipitation (Figure 3, 4th column) shows that these three TMPA estimates have similar distributions over the middle and eastern parts of China, while their main differences appeared over the Tibetan plateau and Tianshan Mountains of Western China, with RTV7-C having the highest amplitude (Figure 3d,h,l).
To look further into the spatial difference of total bias between different products, one can see that the RTV7-UC systematically underestimated gauge observations over the most parts of humid region and the Northeastern Qinghai-Tibetan plateau (Figure 3a), while an opposite overestimation occurred in the RTV7-C estimates (Figure 3e). Most notably over the Tibetan plateau and Tianshan Mountains, the upward adjustments of the CCA calibration in RTV7-C significantly elevated the original positive biases in RTV7-UC despite the underestimation over the humid Southeastern China being effectively alleviated (Figure 3e). This finding is consistent with the global scale assessment of Yong et al. [4]. Moreover, the overestimation of RTV7-C over Tibetan plateau and Tianshan Mountains mainly comes from the hit and false rainy events (Figure 3f,h). Due to the lack of ground observations over these regions, we cannot directly quantify the error components of satellite precipitation estimates and analyze their error sources by the validation data CGDPA. The difference between different satellite estimates in total bias was especially remarkable over these areas, which might be primarily attributed to the gauge validation product rather than to the satellite retrieval algorithm [40]. In our knowledge, there certainly exist large uncertainties for the satellite rainfall evaluation over regions where gauge network is very sparse. In general, the post-real-time V7, relative to the real-time RTV7-UC and RTV7-C estimates, exhibits much better performance over most parts of mainland China. This result demonstrates that the gauge-based adjustments in V7 can substantially improve the error structures and components for local areas, particularly with the underestimation of hit events over humid region (Figure 3b,f,j).
For winter, all the three TMPA estimates have relatively lower biases when compared to their summer counterpart (Figure 4, first column), which is primarily attributed to the obvious reduction of hit bias (Figure 4, second column). However, RTV7-UC still heavily underestimates the precipitation over the humid region in Southeastern China (Figure 4a). The first row of Figure 4 demonstrates such underestimation is mainly caused by missed precipitation, which is different from that of summer. We speculate this can mostly be attributed to the inability of TRMM-based constellation satellites to measure snowfall, or the low-level cloudiness and warm rain processes in winter which may not have a strong signature of ice particles. With respect to RTV7-C, the underestimation in humid region is evidently alleviated but the original slight overestimation over the arid and semi-arid regions is unfavorably increased. This is primarily due to the upward adjustments of the CCA on false precipitation (Figure 4d,h). Similar to summer, V7 also apparently outperformed RTV7-UC and RTV7-C during winter according to the spatial distributions of total bias (Figure 4i). However, note here the gauge adjustment in V7 tends to excessively elevate the positive hit errors of RTV7-UC over the humid region so as to compensate the negative bias of missed precipitation. Generally speaking, for winter, the underestimation of satellite precipitation over humid regions is mainly determined by missed precipitation, while the overestimation over arid and semi-arid regions mostly comes from false precipitation.
On the other hand, the error distribution of satellite precipitation estimates in Figure 3 and Figure 4 seems linked to topography (especially for the real-time RTV7 estimates). It would be useful to explore the error components’ dependency on elevation [41]. To this end, we plotted total bias and three error components with respect to elevation for the entire China in Figure 5. It is apparent that the error components of real-time RTV7-UC and RTV7-C generally demonstrate an evident topographic dependency (Figure 5, first two rows), while such feature is not significant in post-real-time V7 (Figure 5e,f). The total biases in RTV7-UC and RTV7-C gradually increase toward the higher elevations. Moreover, it can be seen that the hit bias keeps the similar tendency with that of total bias in summer. But, in winter, it shows substantially less dependence on elevation, while the false precipitation plays the dominant role. From the topographic analysis of error components, we can conclude that the CCA algorithm applied to RTV7-UC is primarily effective in balancing the error and bias at the large scale, rather than correcting the systematic errors caused by some local factors, such as topography. Especially over regions with higher elevations, the error components are more sensitive to the CCA algorithm. For example, the hit bias of RTV7-C estimates rapidly increases beyond 3000 m and the false precipitation has a significant increase starting from 4500 m. In contrast, the GA approach used in V7 seems to alleviate the topographic dependency and improve the error structures of satellite precipitation estimates to some degree.

3.2. Temporal Analysis of Error Components

Next, we investigated the temporal variations of error components for the three TMPA products during our entire study period (from April 2008 through March 2013). Figure 6 depicts the time series of area-averaged error components as well as the total bias over the four different climate regions. For smoothing and reducing visual clutter, a 31-day moving average was applied to the entire time series, similar to Tian et al. [26]. In general, there exists an obvious seasonality in the error components, particularly for the summer and winter months. Almost all of the error components and total bias show higher values in the summer and lower ones in winter. For spring and autumn, the error components in two real-time TMPA products show a smooth transition between the range of −1~1 mm/day, while such dynamic varying range is limited within about ±0.5 mm/day for the post-real-time V7 product. Generally speaking, the error behaviors during spring and autumn are largely in between the summer and winter, quite as expected. Such significant warm-season-driven error structure is primarily due to the majority of the rainfall in China occurring during the summer months.
In terms of the satellite-only RTV7-UC, the changing tendency of hit bias generally agrees well with that of total bias. Over the humid region, the larger negative hit and missed errors are the main contributors to the total bias of RTV7-UC, while the positive false error is relatively much lower (Figure 6a). With respect to the semi-humid and semi-arid regions, the positive false error and the negative missed error have rather similar seasonal variability. Furthermore, they look so symmetric that their overestimation and underestimation may cancel each other (Figure 6b,c). As a result, the curve of hit bias is very close to those of total bias. For the arid region, the overestimation of total errors in RTV7-UC is primarily from false precipitation, as the other two components (hit bias and missed precipitation) are considerably smaller (Figure 6d).
With respect to RTV7-C, the most outstanding feature is the upward adjustments for total bias and hit bias. Moreover, one can see that such adjustment mainly occurred in the warm months, suggesting that the CCA calibration in RTV7-C might yield larger effects on the summer rainy events with higher rain rates. Taking the humid region as example, opposite positive total bias and hit bias (corresponding to that of RTV7-UC in Figure 6a) appear in summer. Moreover, the overestimation of total errors is more remarkable for other three climate regions (Figure 6f–h), which is consistent with the spatial patterns show in Figure 3. In winter, RTV7-C still underestimates precipitation compared with gauges in the humid region (Figure 6a), but the steady overestimation occurs in the non-humid regions (Figure 6f–h), as seen from above Figure 4.
Over the four different climate regions, all the time series indicate that the V7 product has the best performance (see third row of Figure 6). Specifically, the gauge-based adjustment in V7 effectively reduces the hit bias, and then substantially improves the error structure of the TMPA output. As can be seen from Figure 6i–l), the area-averaged total biases of V7 are limited within 1.0 mm/day for the four climate regions during the entire study period. Thus, we can conclude that the gauge-based adjustment of V7 apparently outperforms the climatology-based CCA calibration of RTV7-C in removing the local errors of satellite-only precipitation data. Over the entirety of mainland China, the CCA calibration generally seems to overcorrect the RTV7-UC estimates.

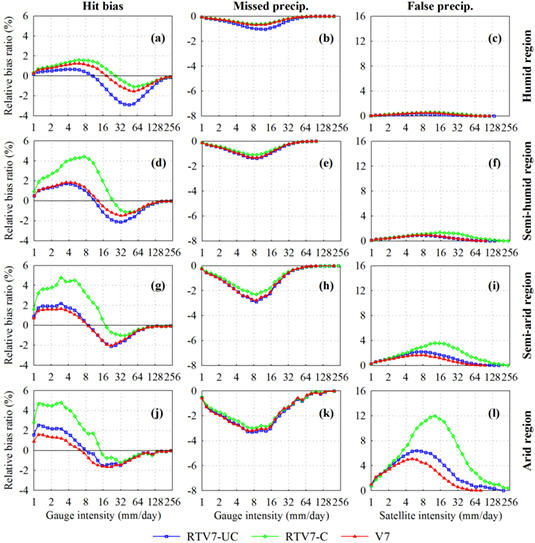
3.3. Intensity Distribution of Error Components

To further understand the error features at event-scale, we computed the distributions of the hit, missed, and false precipitation, together with the total precipitation amount, as functions of daily rainfall intensity (or rain rate) for different climate regions during the summer and winter seasons (Figure 7 and Figure 8). The rain rates exceeding the rain/no-rain threshold (1 mm/day) were presented on the x-axis across the range of 1–256 mm/day. The logarithmic scale was used to bin the precipitation rates. The precipitation amount on the y-axis stands for the accumulated daily precipitation of each bin, which is derived from the total days in the corresponding season.
For summer, the intensity distributions of total precipitation are generally similar to those of hit precipitation, further verifying the dominant role of hit bias in TMPA’s error components (Figure 7). However, the arid region is an exception, whose false precipitation seems to account for a considerable proportion (last row in Figure 7). For the humid region (first row, Figure 7), the intensity distribution of V7 is closest to that of gauge, and RTV7-UC grossly underestimates the precipitation for intensities over 8 mm/day (Figure 7a). The CCA algorithm in RTV7-C significantly raises the intensity distribution of hit precipitation at medium-high rain rates, but an unfavorable overcorrection occurs at higher rain rates (>30 mm/day; see Figure 7b). For the non-humid regions, the RTV7-UC distribution, as well as V7, remains in good agreement with the gauge, while the overestimation of RTV7-C at higher rain rates became the most outstanding feature in the intensity distribution of the total and hit precipitation. Additionally, one can note that the CCA calibration in RTV7-C and the gauge adjustment in V7 seem not to change the summer intensity distributions at lower rain rate (approximately less than 8 mm/day for most of China).
For winter, the total precipitation and the hit precipitation have quite similar patterns in their intensity distributions over the humid region (Figure 8a,b). Different from summer, the missed precipitation possesses considerable proportion in winter (Figure 8c). This feature is closely corresponding to the spatial distribution in Figure 3. Importantly, it was found that the purely satellite-derived RTV7-UC obviously underestimates the observed precipitation throughout the entire rain-rate range (Figure 8a,b). Even with CCA algorithm or gauge adjustment (GA), there still exist noticeable underestimates at lower rain rates and overestimates at higher ones between the calibrated estimates (RTV7-C and V7) and gauge observation (see Figure 8a). Therefore, accurately measuring the winter rainfall information was still a challenging issue for the current satellite precipitation estimates. As for the non-humid regions, the intensity distribution of total precipitation seems to be similar to that of false precipitation, while the daily hit and missed precipitation only account for a relative smaller proportion (Figure 8e–p). This suggests that the winter’s overestimation of two TMPA real-time estimates over the non-humid regions mainly comes from false precipitation. Interestingly, the V7 exhibits a rather good performance in tracing the in tracing the rain-rate changes of observed precipitation over the non-humid regions, which is different from that of the humid region (Figure 8e,i,m). The gauge-based adjustment technique looks more effective in reducing the error and bias of false precipitation than the CCA calibration over the non-humid areas.

3.4. Contribution Ratio of Error Components

An improvement to the original error decomposition of Tian et al. [26] is to examine the intensity distributions of the relative bias ratio (hereafter referred to as “RBR”). Specific details of the RBR definition and computation are given in Appendix A. This enhancement can provide unique insights into quantifying the specific contribution of each error component to the total bias of satellite precipitation estimates at different ranges of rain rates. The RBR distributions of the three error components for four different climate regions during summer and winter are shown in Figure 9 and Figure 10, respectively.
First, one can see that the hit bias distributions of all the three TMPA estimates have an evident tendency to overestimate lower rain rates (<10 mm/day) and underestimate medium to higher ones (10–128 mm/day) (first column in Figure 9 and Figure 10), which is a common error feature of satellite-based retrievals [42,43,44]. This is possibly due to the non-unique relation between surface precipitation and brightness temperature (TB). The observed brightness temperature (TB), either from passive microwave or infrared sensors, reflects the integrated effects of surface emission and water paths emission/scattering, not the surface rain rate [45]. In other words, different combinations of surface background and precipitation profiles can result in exactly same surface rain rate [46]. Due to this non-unique relation, the heavy precipitation will be underestimated since some light precipitation possesses very similar TB signatures to that from heavy precipitation, and vice versa.
For the humid region, the largest contribution from the negative hit bias occurs at high rain rates (peak value at approximately 50 mm/day for summer and 32 mm/day for winter, respectively; see Figure 9a and Figure 10a). The CCA calibration and gauge adjustment effectively reduce this primary contribution from hit precipitation so as to improve the satellite-only RTV7-UC estimates. When the climate becomes drier and drier, the peak value of contribution ratio dynamically moves toward the lower rain rates as the small rainy events gradually play the dominant role (refer to first column in Figure 9 and Figure 10).
Additionally, Figure 9a and Figure 10a suggest that, for the humid region, the CCA and GA algorithms tend to primarily affect the hit error of RTV7-UC at higher rain rates. This result is consistent with the analysis of above Figure 7. However, it is worth noting that both CCA and GA actually also affect the hit bias at lower rain rates, especially for the non-humid regions (Figure 9d,g,j and Figure 10d,g,j), which was not revealed by previous studies [26,28]. This arises because the commonly-used intensity distributions of precipitation amount cannot give the real variations of bias ratio before and after adjustments. Taking the summer of the semi-humid region for an example, some small rain events might be changed to larger ones at higher rain-rate range after CCA or GA corrections (see Figure 7f). Figure 9d can clearly show the contribution of these changed small rain events to the total bias. To look further into the first column of Figure 9 and Figure 10, we can conclude that the impact of the CCA on the hit bias at lower rain rates is greater for the non-humid regions.
For the missed precipitation, all these three TMPA products have basically identical intensity distributions of RBR over the different climate regions during both summer (Figure 9b,e,h,k) and winter (Figure 10b,e,h,k). This result further confirms that both CCA and GA almost failed to act on the missed rainy events in the TMPA’s retrieval process, which has been deduced by the spatial analyses in above Figure 3 and Figure 4. Specifically, the contribution of missed precipitation to the total bias shows strong seasonal and regional dependencies. For the same climate region, the contribution ratio of missed precipitation is evidently larger in winter than that in summer. On the other hand, for the same season, the contribution of missed precipitation seems to be grossly higher over drier regions. Such error dependency features are also shown in the false distribution (see last column in Figure 9 and Figure 10). This could be attributed to two major reasons. (1) In most parts of mainland China, the rainy events with medium-high rain rates in winter are significantly less than those in other seasons. The current satellite-based precipitation retrieval tends to misrepresent the sparse and small rain events; and (2) similarly, the direr regions have less rainfall than humid areas that will inevitably result in relatively larger proportions of missed and false error in the total bias.
Finally, the contribution ratios of the error components to the total bias of the three TMPA products were summarized in Table 1. It is notable that the negative hit bias (−20.3%) contributes mainly to the total error (−28.2%) of TMPA in the summer season over the humid region. This underestimation for hit precipitation was reduced to only 2.2% by the gauge adjustment (GA) in V7, while the overcorrection of the CCA calibration in RTV7-C changed this ratio to 12.3%. However, there is a gradually increasing tendency for the contribution ratios of the missed and false precipitation events with a transition from the humid region to the drier and drier regions. The false precipitation is the dominant error component in the arid region. For example, the false bias is only 4.8% for the humid region, while the corresponding value of the arid region is 92.6%, indicating a difference of 87.8%. For winter, the contribution of missed precipitation to the total bias is the largest one for the humid region. Moreover, we found that it is difficult to effectively remove this missed error by present calibrated approaches. Similar to summer, the relative biases of the missed and false precipitation also gradually increase in the winter season for the drier and drier climate regions. Amongst of them, the false precipitation has the largest contribution ratios to the total bias of all the satellite estimates in the arid region.

4. Conclusions and Recommendations

In this paper, we systematically investigated three independent error components in the latest Version-7 TMPA estimates (namely RTV7-UC, RTV7-C, and V7) over mainland China for a period of five years (April 2008 to March 2013). The error-decomposition method of Tian et al. [26] was used, with further improvements, for the study. We analyzed the seasonal error characteristics of the error components over four different climate regions (i.e., humid region, semi-humid region, semi-arid region, and arid region), and identified their contributions to the total errors of satellite precipitation.
The key findings can be summarized as follows:
Generally speaking, the error components of the TMPA estimates show strong seasonal and regional differences over mainland China. For the summer season, the underestimation of satellite-only RTV7-UC over humid region is caused by both hit bias and missed precipitation, while the overestimation in non-humid regions comes from hit bias and false precipitation. As for winter, the underestimation over humid region is mainly determined by missed precipitation, while the overestimation in arid and semi-arid regions mostly comes from false precipitation. Overall, the current CCA calibration in RTV7-C effectively reduces negative biases over Southeastern China but, meanwhile, significantly elevates the original positive biases over the Tibetan plateau and Tianshan Mountains. Relatively, the gauge adjustment in V7 worked rather well over all the climate regions, having effectively reduced the hit and false biases of TMPA real-time estimates. However, both of these two correction schemes cannot make up the rainfall missed by the satellites. Additionally, our topographic analysis shows the error components of the real-time RTV7-UC and RTV7-C exhibit an evident topographic dependency, while such a feature is not significant in the post-real-time V7.
The time series analyses clearly illustrate the total errors resulted from the interaction of the three independent components. For the humid region, the hit bias and missed precipitation work together to enhance the negative total bias of the satellite-only RTV7-UC, while for arid area false precipitation is apparently the dominant error sources. For the semi-humid and semi-arid areas, the seasonality of the error components is especially remarkable and consistent and the missed bias and false errors seem to cancel each other. Thus, the hit bias remains in good agreement with the total errors throughout the study period. In addition, the CCA calibration primarily changes the hit bias in warm seasons, resulting in an overall overestimation of RTV7-C. Since the gauge adjustment effectively reduces the hit and false bias for all seasons, the total bias of V7 varies around the zero.
From the perspective of intensity distribution, the key improvement of CCA manifests in changing the distribution pattern of the underestimated hit precipitation across the range of medium-high rain rates (>16 mm/day) over the humid region. For the non-humid regions, the satellite-only RTV7-UC distribution fits the intensity of gauge very well at higher rain rates, and the main discrepancy between them appears at lower rain rates. Consequently, the upward adjustment of CCA for higher rain rates worsened the performance of RTV7-UC instead. In practice, how to improve the hit precipitation at lower rain rates (<20 mm/day) is the crucial issue for non-humid areas in summer. Unfortunately, both CCA calibration and gauge adjustment (GA) cannot lessen the differences of hit precipitation distributions between TMPA real-time estimates and the gauge observations at lower rain rates. In addition, the false precipitation is the chief error source for the non-humid areas in winter. One can see that the incorporation of rain gauge data in V7 can effectively remove such winter-related false errors over the non-humid regions.
The relative-bias ratio (RBR, refer to Appendix A) analysis of the error components indicated that the hit bias of satellite-only RTV7-UC estimates accounts for approximately 72% of the total error over the humid region during summer. This negative hit bias was significantly improved by the gauge correction scheme (GA) in V7, with a drop from −20.3% before adjustment to 2.2% after adjustment, while the overcorrection of the CCA calibration in RTV7-C can only suppress this bias to 12.3%. On the other hand, there is a gradually increasing tendency for the contribution ratios of both missed and false precipitation with a transition from the humid region to the drier and drier regions. In addition, one should note that the CCA calibration and gauge adjustment (GA) scheme also affect the error structure at lower rain rates, particularly for the non-humid regions. Yet, this point is not obvious with the ordinary intensity analysis, because some small rainy events might be adjusted to larger ones at higher rain-rate range. Such change of small rainy events cannot be clearly exhibited in intensity distribution of precipitation amounts.
In summary, the climatological calibration algorithm in the real-time RTV7-C and the gauge-based adjustment in the post-real-time V7 are normally regarded as two crucial bias correction techniques to improve the data accuracy in the TMPA system. However, currently, the CCA improvement is primarily in the sense of simply balancing the error and bias at the large scale, rather than completely and fully correcting the systematic errors of satellite precipitation at the local scale. Comparatively, the GA approach could substantially improve the error structures and components for local areas. Taking mainland China as an example, the gauge adjustment in V7 effectively reduced both the underestimation of hit events over the humid region and the overestimation of false events at Himalayan and Tianshan Mountains. However, the CCA’s superiority lies in maintaining the near-real-time availability of TMPA estimates (e.g., the RTV7-C with 6–9 h latency over the globe). Consequently, hydrologic users of satellite precipitation are suggested to employ local high-resolution (e.g., daily or sub-daily) observed rainfall data in combination with the purely satellite-derived RTV7-UC (similar to the GA approach in V7) to create new precipitation products for satisfying their applications.
Although all the results drawn from this study may be specific to the four climate regions of Mainland China, they are likely to be also applicable to other similar areas in the globe. Based on our findings, we recommend that the future correction efforts should focus on further improving hit bias of humid regions, false error of arid regions, and missed snowing events in winter. The structures and features of error components revealed here are expected to serve for the development of quantitative error models and bias reduction algorithms in the GPM era.

Acknowledgments

The TMPA data used in this study were provided by the NASA/Goddard Space Flight Center’s laboratory for Atmospheres and PPS, which develop and compute the TMPA as a contribution to TRMM. This work was financially supported by National Natural Science Foundation of China (91547101, 51379056, and 91437214). Also this work is partially sponsored by the Open Fund of State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, SOA (SOED1601) and the Fundamental Research Funds for the Central Universities (2015B24614). The authors gratefully acknowledge three anonymous reviewers and the editor for their helpful suggestions.

Author Contributions

Bin Yong and Yudong Tian designed the study; Bin Yong, Bo Chen, and Yudong Tian conducted the analysis and wrote the manuscript; Zhongbo Yu and Yang Hong contributed to discussions and revisions, providing important feedbacks and suggestions.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A: Improving Error-component Analysis with Relative Bias Ratio (RBR)

We extended the work reported in Tian et al. [26] by computing the relative contribution of each error component to the total errors as the function of rain rates. Since the probability distribution of rain rate is closer to lognormal than to Gaussian, we first divided the range of rain rate into N + 1 consecutive logarithm-scaled bins, with the following bin boundaries:
{ T h 0 = r m i n T h n = T h 0 × F n , ( n = 1 , 2 , ⋯ , N )
where rmin is the rain/no-rain threshold (we used 1 mm/day here), and F > 1 denotes the constant ratio between two adjacent boundaries (or constant difference in logarithm-scale). We used rmin =1 mm/day and F = 1.2 in this study.
Then, given a precipitation field, R ( x → , t ) , one can derive a binary-valued precipitation event mask for the entire range of rain rates, P, and for each value falling into the nth rain rate bin, P t h n , respectively:
P = { 1   if   R ( x → , t ) ∈ ( T h 0 , T h M ] 0   if   R ( x → , t ) ∉ ( T h 0 , T h M ]
P t h n = { 1   if   R ( x → , t ) ∈ ( T h n − 1 , T h n ] 0   if   R ( x → , t ) ∉ ( T h n − 1 , T h n ] , ( n ≥ 1 )
where T h M denotes the maximum critical value, computed from Equation (A1), for all of the records of rain rates within both satellite estimates and observations. It is easy to see that the mask of each bin is independent to one another. If we use footnote “1” and “2” to denote the “observations” and the “satellite estimates”, respectively, the relative bias ratio (RBR) of hit bias H, missed precipitation −M, and false precipitation F can be expressed as:
R B R H n = P 1 T h n × ( R 2 − R 1 ) × P 2 T × 100 %
R B R M n = P 1 T h n × R 1 × P 2 ¯ T × 100 %
R B R F n =   P 2 T h n × R 2 × P 1 ¯ T × 100 %
where T is the areal and temporally total observation precipitation. P 1 ¯ and P 2 ¯ denote the Boolean complement of a binary mask in Equation (A2) for satellite estimates and for observations, respectively.
In this study, Equations (A4)–(A6) constitute the additional metrics to the original Tian et al. [26] scheme, and they were used to calculate the relative contribution of each error component as a function of rain rate shown in Figure 9 and Figure 10. The following Equations (A7)–(A10) were used to calculate the three error components and total bias listed in the Table 1:
R B R H = ∑ n = 1 N R B R H n = ∑ n = 1 N P 1 T h n × ( R 2 − R 1 ) × P 2 T   = P 12 × R 2 − R 1 T = H T
R B R M = ∑ n = 1 N R B R M n = ∑ n = 1 N P 1 T h n × R 1 × P 2 ¯ T = P 1 2 ¯ × R 1 T = M T
R B R F = ∑ n = 1 N R B R F n = ∑ n = 1 N P 2 T h n × R 2 × P 1 ¯ T = P 1 ¯ 2 × R 2 T = F T
R B R H − R B R M + R B R F =   E / T
where RBRH, RBRM, and RBRF represent the area-averaged contribution ratios (%) of three error components (i.e., hit, missed, and false) to the total bias of satellite precipitation estimates, respectively. N is the number of rain rate bins on the x-axis in Figure 9 and Figure 10. Other symbols are the same as above Equations (A4)–(A6).

References

  1. Zhai, P.; Zhang, X.; Wan, H.; Pan, X. Trends in Total Precipitation and Frequency of Daily Precipitation Extremes over China. J. Clim. 2005, 18, 1096–1108. [Google Scholar] [CrossRef]
  2. Piao, S.; Ciais, P.; Huang, Y.; Shen, Z.; Peng, S.; Li, J.; Zhou, L.; Liu, H.; Ma, Y.; Ding, Y.; et al. The impacts of climate change on water resources and agriculture in China. Nature 2010, 467, 43–51. [Google Scholar] [CrossRef] [PubMed]
  3. Ma, S.; Zhou, T. Observed trends in the timing of wet and dry season in China and the associated changes in frequency and duration of daily precipitation. Int. J. Climatol. 2015, 35, 4631–4641. [Google Scholar] [CrossRef]
  4. Yong, B.; Liu, D.; Gourley, J.J.; Tian, Y.; Huffman, G.J.; Ren, L.; Hong, Y. Global View Of Real-Time TRMM Multisatellite Precipitation Analysis: Implications For Its Successor Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2015, 96, 283–296. [Google Scholar] [CrossRef]
  5. Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
  6. Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Adler, R.F. Highlights of the Version 7 TRMM Multi-satellite Precipitation Analysis (TMPA). In Proceedings of the 5th International Precipitation Working Group Workshop, Hamburg, Germany, 11–15 October 2010; pp. 11–15.
  7. Yong, B.; Ren, L.; Hong, Y.; Wang, J.; Gourley, J.J.; Jiang, S.; Chen, X.; Wang, W. Hydrologic evaluation of Multisatellite Precipitation Analysis standard precipitation products in basins beyond its inclined latitude band: A case study in Laohahe basin, China. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
  8. Huang, Y.; Chen, S.; Cao, Q.; Hong, Y.; Wu, B.; Huang, M.; Qiao, L.; Zhang, Z.; Li, Z.; Li, W.; et al. Evaluation of Version-7 TRMM Multi-Satellite Precipitation Analysis Product during the Beijing Extreme Heavy Rainfall Event of 21 July 2012. Water 2013, 6, 32–44. [Google Scholar] [CrossRef]
  9. Li, Z.; Yang, D.; Hong, Y. Multi-scale evaluation of high-resolution multi-sensor blended global precipitation products over the Yangtze River. J. Hydrol. 2013, 500, 157–169. [Google Scholar] [CrossRef]
  10. Chen, S.; Hong, Y.; Cao, Q.; Gourley, J.J.; Kirstetter, P.-E.; Yong, B.; Tian, Y.; Zhang, Z.; Shen, Y.; Hu, J.; Hardy, J. Similarity and difference of the two successive V6 and V7 TRMM multisatellite precipitation analysis performance over China. J. Geophys. Res. 2013, 118, 13060–13074. [Google Scholar] [CrossRef]
  11. Zhao, T.; Yatagai, A. Evaluation of TRMM 3B42 product using a new gauge-based analysis of daily precipitation over China. Int. J. Climatol. 2014, 34, 2749–2762. [Google Scholar] [CrossRef]
  12. Yang, X.; Yong, B.; Hong, Y.; Chen, S.; Zhang, X. Error analysis of multi-satellite precipitation estimates with an independent raingauge observation network over a medium-sized humid basin. Hydrol. Sci. J. 2015. [Google Scholar] [CrossRef]
  13. Zhang, X.; Tang, Q. Combining satellite precipitation and long-term ground observations for hydrological monitoring in China. J. Geophys. Res. Atmos. 2015, 120, 6426–6443. [Google Scholar] [CrossRef]
  14. Bellerby, T.J.; Sun, J. Probabilistic and ensemble representations of the uncertainty in an IR/Microwave satellite precipitation product. J. Hydrometeorol. 2005, 6, 1032–1044. [Google Scholar] [CrossRef]
  15. Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of Near-Real-Time Precipitation Estimates from Satellite Observations and Numerical Models. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
  16. Tian, Y.; Peters-Lidard, C.D.; Choudhury, B.J.; Garcia, M. Multitemporal Analysis of TRMM-Based Satellite Precipitation Products for Land Data Assimilation Applications. J. Hydrometeorol. 2007, 8, 1165–1183. [Google Scholar] [CrossRef]
  17. Turk, F.J.; Arkin, P.; Sapiano, M.R.P.; Ebert, E.E. Evaluating High-Resolution Precipitation Products. Bull. Am. Meteorol. Soc. 2008, 89, 1911–1916. [Google Scholar] [CrossRef]
  18. Clarke, R.T.; Bulhoes Mendes, C.A.; Costa Buarque, D. A comparison of extreme rainfall characteristics in the Brazilian Amazon derived from two gridded data sets and a national rain gauge network. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
  19. Gourley, J.J.; Hong, Y.; Flamig, Z.L.; Li, L.; Wang, J. Intercomparison of Rainfall Estimates from Radar, Satellite, Gauge, and Combinations for a Season of Record Rainfall. J. Appl. Meteorol. Climatol. 2010, 49, 437–452. [Google Scholar] [CrossRef]
  20. Scheel, M.L.M.; Rohrer, M.; Huggel, C.; Santos Villar, D.; Silvestre, E.; Huffman, G.J. Evaluation of TRMM Multi-satellite Precipitation Analysis (TMPA) performance in the Central Andes region and its dependency on spatial and temporal resolution. Hydrol. Earth Syst. Sci. 2011, 15, 2649–2663. [Google Scholar] [CrossRef] [Green Version]
  21. Sorooshian, S.; AghaKouchak, A.; Arkin, P.; Eylander, J.; Foufoula-Georgiou, E.; Harmon, R.; Hendrickx, J.M.H.; Imam, B.; Kuugowski, R.; Skahill, B.; et al. Advanced Concepts on Remote Sensing of Precipitation at Multiple Scales. Bull. Am. Meteorol. Soc. 2011, 92, 1353–1357. [Google Scholar] [CrossRef]
  22. Ward, E.; Buytaert, W.; Peaver, L.; Wheater, H. Evaluation of precipitation products over complex mountainous terrain: A water resources perspective. Adv. Water Res. 2011, 34, 1222–1231. [Google Scholar] [CrossRef]
  23. Chen, S.; Hong, Y.; Gourley, J.J.; Huffman, G.J.; Tian, Y.D.; Cao, Q.; Yong, B.; Kirstetter, P.-E.; Hu, J.; Hardy, J.; et al. Evaluation of the successive V6 and V7 TRMM multisatellite precipitation analysis over the Continental United States. Water Resour. Res. 2013, 49, 8174–8186. [Google Scholar] [CrossRef]
  24. Xue, X.; Hong, Y.; Limaye, A.S.; Gourley, J.J.; Huffman, G.J.; Khan, S.I.; Dorji, C.; Chen, S. Statistical and hydrological evaluation of TRMM-based Multi-satellite Precipitation Analysis over the Wangchu Basin of Bhutan: Are the latest satellite precipitation products 3B42V7 ready for use in ungauged basins? J. Hydrol. 2013, 499, 91–99. [Google Scholar] [CrossRef]
  25. Zulkafli, Z.; Buytaert, W.; Onof, C.; Manz, B.; Tarnavsky, E.; Lavado, W.; Guyot, J.-L. A Comparative Performance Analysis of TRMM 3B42 (TMPA) Versions 6 and 7 for Hydrological Applications over Andean–Amazon River Basins. J. Hydrometeorol. 2014, 15, 581–592. [Google Scholar] [CrossRef]
  26. Tian, Y.; Peters-Lidard, C.D.; Eylander, J.B.; Joyce, R.J.; Huffman, G.J.; Adler, R.F.; Hsu, K.-L.; Turk, F.J.; Garcia, M.; Zeng, J. Component analysis of errors in satellite-based precipitation estimates. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
  27. Yong, B.; Hong, Y.; Ren, L.; Gourley, J.J.; Huffman, G.J.; Chen, X.; Wang, W.; Khan, S.I. Assessment of evolving TRMM-based multisatellite real-time precipitation estimation methods and their impacts on hydrologic prediction in a high latitude basin. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
  28. Yong, B.; Ren, L.; Hong, Y.; Gourley, J.J.; Tian, Y.; Huffman, G.J.; Chen, X.; Wang, W.; Wen, Y. First evaluation of the climatological calibration algorithm in the real-time TMPA precipitation estimates over two basins at high and low latitudes. Water Resour. Res. 2013, 49, 2461–2472. [Google Scholar] [CrossRef]
  29. Shen, Y.; Xiong, A. Validation and comparison of a new gauge-based precipitation analysis over mainland China. Int. J. Climatol. 2016, 36, 252–265. [Google Scholar] [CrossRef]
  30. Xie, P.; Chen, M.; Yang, S.; Yatagai, A.; Hayasaka, T.; Fukushima, Y.; Liu, C. A Gauge-Based Analysis of Daily Precipitation over East Asia. J. Hydrometerol. 2007, 8, 607–626. [Google Scholar] [CrossRef]
  31. Chen, M.; Shi, W.; Xie, P.; Silva, V.B.S.; Kousky, V.E.; Wayne Higgins, R.; Janowiak, J.E. Assessing objective techniques for gauge-based analyses of global daily precipitation. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
  32. Zou, X.; Zhai, P.; Zhang, Q. Variations in droughts over China: 1951–2003. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
  33. Qian, W.; Lin, X. Regional trends in recent precipitation indices in China. Meteorol. Atmos. Phys. 2005, 90, 193–207. [Google Scholar] [CrossRef]
  34. Zhou, T.; Yu, R.; Chen, H.; Dai, A.; Pan, Y. Summer Precipitation Frequency, Intensity, and Diurnal Cycle over China: A Comparison of Satellite Data with Rain Gauge Observations. J. Clim. 2008, 21, 3997–4010. [Google Scholar] [CrossRef]
  35. Shen, Y.; Xiong, A.; Wang, Y.; Xie, P. Performance of high-resolution satellite precipitation products over China. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
  36. Gebregiorgis, A.S.; Tian, Y.; Peters-Lidard, C.D.; Hossain, F. Tracing hydrologic model simulation error as a function of satellite rainfall estimation bias components and land use and land cover conditions. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
  37. Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: San Diego, CA, USA, 1995. [Google Scholar]
  38. Dai, A.G. Precipitation Characteristics in Eighteen Coupled Climate Models. J. Clim. 2006, 19, 4605–4630. [Google Scholar] [CrossRef]
  39. Dai, A.G.; Lin, X.; Hsu, K.-L. The frequency, intensity, and diurnal cycle of precipitation in surface and satellite observations over low- and mid-latitudes. Clim. Dyn. 2007, 29, 727–744. [Google Scholar] [CrossRef]
  40. Krakauer, N.Y.; Pradhanang, S.M.; Panthi, J.; Lakhankar, T.; Jha, A.K. Probabilistic Precipitation Estimation with a Satellite Product. Climate 2015, 3, 329–348. [Google Scholar] [CrossRef]
  41. Krakauer, N.Y.; Pradhanang, S.M.; Lakhankar, T.; Jha, A.K. Evaluating Satellite Products for Precipitation Estimation in Mountain Regions: A Case Study for Nepal. Remote Sens. 2013, 5, 4107–4123. [Google Scholar] [CrossRef]
  42. McCollum, J.R.; Krajewski, W.F.; Ferraro, R.R.; Ba, M.B. Evaluation of biases of satellite rainfall estimation algorithms over the Continental United States. J. Appl. Meteorol. 2002, 41, 1065–1080. [Google Scholar] [CrossRef]
  43. Tang, L.; Tian, Y.; Lin, X. Validation of precipitation retrievals from satellite-based passive microwave sensors. J. Geophys. Res. Atmos. 2014, 119, 4546–4567. [Google Scholar] [CrossRef]
  44. Yong, B.; Chen, B.; Gourley, J.J.; Ren, L.; Hong, Y.; Chen, X.; Wang, W.; Chen, S.; Gong, L. Intercomparison of the Version-6 and Version-7 TMPA precipitation products over high and low latitudes basins with independent gauge networks: Is the newer version better in both real-time and post-real-time analysis for water resources and hydrologic extremes? J. Hydrol. 2014, 508, 77–87. [Google Scholar]
  45. You, Y.; Liu, G. The relationship between surface rainrate and water paths and its implications to satellite rainrate retrieval. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
  46. Kummerow, C.D.; Ringerud, S.; Crook, J.; Randel, D.; Berg, W. An Observationally Generated A Priori Database for Microwave Rainfall Retrievals. J. Atmos. Ocean. Technol. 2011, 28, 113–130. [Google Scholar] [CrossRef]
Remotesensing 08 00440 g001 1024
Figure 1. (a) Digital elevation map (DEM) of China and distribution of station density; and (b) spatial distributions of average annual precipitation (AAP) and the corresponding climate regions for mainland China for the past 50 years (1960–2009).
Figure 1. (a) Digital elevation map (DEM) of China and distribution of station density; and (b) spatial distributions of average annual precipitation (AAP) and the corresponding climate regions for mainland China for the past 50 years (1960–2009).
Remotesensing 08 00440 g001
Remotesensing 08 00440 g002 1024
Figure 2. Simple 2 × 2 contingency table that shows how three independent error components (hit, miss, and false) are identified by dichotomous variables (satellite rainfall estimates and ground observation).
Figure 2. Simple 2 × 2 contingency table that shows how three independent error components (hit, miss, and false) are identified by dichotomous variables (satellite rainfall estimates and ground observation).
Remotesensing 08 00440 g002
Remotesensing 08 00440 g003 1024
Figure 3. Seasonally averaged error components of three TMPA estimates (i.e., RTV7-UC, RTV7-C, V7) for the summers (JJA) of five years (April 2008 through March 2013): total bias (E; (first column)); hit bias (H; (second column)); missed precipitation (−M; (third column)); and false precipitation (F; (fourth column)).
Figure 3. Seasonally averaged error components of three TMPA estimates (i.e., RTV7-UC, RTV7-C, V7) for the summers (JJA) of five years (April 2008 through March 2013): total bias (E; (first column)); hit bias (H; (second column)); missed precipitation (−M; (third column)); and false precipitation (F; (fourth column)).
Remotesensing 08 00440 g003
Remotesensing 08 00440 g004 1024
Figure 4. Same as Figure 3 but for winter (DJF).
Figure 4. Same as Figure 3 but for winter (DJF).
Remotesensing 08 00440 g004
Remotesensing 08 00440 g005 1024
Figure 5. Variation of the error components for the three TMPA estimates by elevation for summer seasons (first column) and winter seasons (second column): (a,b) RTV7-UC; (c,d) RTV7-C and (e,f) V7.
Figure 5. Variation of the error components for the three TMPA estimates by elevation for summer seasons (first column) and winter seasons (second column): (a,b) RTV7-UC; (c,d) RTV7-C and (e,f) V7.
Remotesensing 08 00440 g005
Remotesensing 08 00440 g006 1024
Figure 6. Time series of the error components for the three TMPA estimates, spatially averaged over four climate regions: (first column) humid region; (second column) semi-humid region; (third column) semi-arid region; and (fourth column) arid region. A 31-day running average is applied to each time series to reduce visual cluttering.
Figure 6. Time series of the error components for the three TMPA estimates, spatially averaged over four climate regions: (first column) humid region; (second column) semi-humid region; (third column) semi-arid region; and (fourth column) arid region. A 31-day running average is applied to each time series to reduce visual cluttering.
Remotesensing 08 00440 g006
Remotesensing 08 00440 g007 1024
Figure 7. Daily intensity distribution of the hit, missed, and false precipitation, together with the total precipitation for the summers of time period (April 2008 to March 2013) over four climate regions: (a–d) humid region; (e–h) semi-humid region; (i–l) semi-arid region; and (m–p) arid region. The total observed precipitation amount (black line) is also shown in the first two columns.
Figure 7. Daily intensity distribution of the hit, missed, and false precipitation, together with the total precipitation for the summers of time period (April 2008 to March 2013) over four climate regions: (a–d) humid region; (e–h) semi-humid region; (i–l) semi-arid region; and (m–p) arid region. The total observed precipitation amount (black line) is also shown in the first two columns.
Remotesensing 08 00440 g007
Remotesensing 08 00440 g008 1024
Figure 8. Same as Figure 7, but for winter seasons.
Figure 8. Same as Figure 7, but for winter seasons.
Remotesensing 08 00440 g008
Remotesensing 08 00440 g009 1024
Figure 9. Intensity distributions of relative bias ratio for the error components of three TMPA estimates over four climate regions: (a–d) humid region; (e–h) semi-humid region; (i–l) semi-arid region; and (m–p) arid region. The results are computed from the five summers during April 2008 and March 2013.
Figure 9. Intensity distributions of relative bias ratio for the error components of three TMPA estimates over four climate regions: (a–d) humid region; (e–h) semi-humid region; (i–l) semi-arid region; and (m–p) arid region. The results are computed from the five summers during April 2008 and March 2013.
Remotesensing 08 00440 g009
Remotesensing 08 00440 g010 1024
Figure 10. Intensity distributions of relative bias ratio for the error components of three TMPA estimates over four climate regions: (a–d) humid region; (e–h) semi-humid region; (i–l) semi-arid region; and (m–p) arid region. The results are computed from the five winters during the study period (April 2008 to March 2013).
Figure 10. Intensity distributions of relative bias ratio for the error components of three TMPA estimates over four climate regions: (a–d) humid region; (e–h) semi-humid region; (i–l) semi-arid region; and (m–p) arid region. The results are computed from the five winters during the study period (April 2008 to March 2013).
Remotesensing 08 00440 g010
Table
Table 1. Area-averaged contribution ratios (%) of the error components (i.e., hit, missed, and false) to total bias of three TMPA products for summer and winter over different climate regions of mainland China.
Table 1. Area-averaged contribution ratios (%) of the error components (i.e., hit, missed, and false) to total bias of three TMPA products for summer and winter over different climate regions of mainland China.
Climate RegionProductSummerWinter
H (%)−M (%)F (%)E = H − M + F (%)H (%)−M (%)F (%)E = H − M + F (%)
Humid RegionRTV7-UC−20.3−12.74.8−28.2−21.0−62.76.3−77.4
RTV7-C12.3−8.08.813.110.5−53.121.1−21.5
V72.2−8.67.30.921.5−48.313.5−13.3
Semi-humid RegionRTV7-UC−1.4−16.112.6−4.915.3−61.9138.591.9
RTV7-C44.9−13.221.553.242.4−59.9214.8197.3
V77.1−15.412.84.510.3−58.968.019.4
Semi-arid RegionRTV7-UC3.3−33.731.10.710.1−74.6229.6165.1
RTV7-C46.5−27.754.172.925.1−73.5297.1248.7
V7−0.2−32.823−10.06.9−79.283.411.1
Arid RegionRTV7-UC7.4−50.492.649.616.3−74.8476.4417.9
RTV7-C42.8−45.2173170.643.5−71.4698.3670.4
V7−5.0−49.064.610.624.1−78.7152.297.6

Share and Cite

MDPI and ACS Style

Yong, B.; Chen, B.; Tian, Y.; Yu, Z.; Hong, Y. Error-Component Analysis of TRMM-Based Multi-Satellite Precipitation Estimates over Mainland China. Remote Sens. 2016, 8, 440. https://doi.org/10.3390/rs8050440

AMA Style

Yong B, Chen B, Tian Y, Yu Z, Hong Y. Error-Component Analysis of TRMM-Based Multi-Satellite Precipitation Estimates over Mainland China. Remote Sensing. 2016; 8(5):440. https://doi.org/10.3390/rs8050440

Chicago/Turabian Style

Yong, Bin, Bo Chen, Yudong Tian, Zhongbo Yu, and Yang Hong. 2016. "Error-Component Analysis of TRMM-Based Multi-Satellite Precipitation Estimates over Mainland China" Remote Sensing 8, no. 5: 440. https://doi.org/10.3390/rs8050440

APA Style

Yong, B., Chen, B., Tian, Y., Yu, Z., & Hong, Y. (2016). Error-Component Analysis of TRMM-Based Multi-Satellite Precipitation Estimates over Mainland China. Remote Sensing, 8(5), 440. https://doi.org/10.3390/rs8050440

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop