Mapping Clearances in Tropical Dry Forests Using Breakpoints, Trend, and Seasonal Components from MODIS Time Series: Does Forest Type Matter?

Abstract

Tropical environments present a unique challenge for optical time series analysis, primarily owing to fragmented data availability, persistent cloud cover and atmospheric aerosols. Additionally, little is known of whether the performance of time series change detection is affected by diverse forest types found in tropical dry regions. In this paper, we develop a methodology for mapping forest clearing in Southeast Asia using a study region characterised by heterogeneous forest types. Moderate Resolution Imaging Spectroradiometer (MODIS) time series are decomposed using Breaks For Additive Season and Trend (BFAST) and breakpoints, trend, and seasonal components are combined in a binomial probability model to distinguish between cleared and stable forest. We found that the addition of seasonality and trend information improves the change model performance compared to using breakpoints alone. We also demonstrate the value of considering forest type in disturbance mapping in comparison to the more common approach that combines all forest types into a single generalised forest class. By taking a generalised forest approach, there is less control over the error distribution in each forest type. Dry-deciduous and evergreen forests are especially sensitive to error imbalances using a generalised forest model i.e., clearances were underestimated in evergreen forest, and overestimated in dry-deciduous forest. This suggests that forest type needs to be considered in time series change mapping, especially in heterogeneous forest regions. Our approach builds towards improving large-area monitoring of forest-diverse regions such as Southeast Asia. The findings of this study should also be transferable across optical sensors and are therefore relevant for the future availability of dense time series for the tropics at higher spatial resolutions.

1. Introduction

Forests provide many important regional to global ecosystem services including biodiversity [1,2], water supply [3], climate regulation [4], and carbon storage [5,6,7]. Monitoring forest cover and associated changes over time has therefore become a key component of many environmental management strategies, including Reduced Emission from Deforestation and Forest Degradation (REDD+). Optical imagery from earth observation satellites provides the primary source of spatially explicit data used for on-going forest monitoring. Continuing sensor advancements since the 1970s offer an increasingly broader range of mapping capabilities [8]. However, equally important has been the coinciding progression in methodologies used to monitor forest and change dynamics. Earlier approaches that largely focused on bi-temporal change analysis [9,10] are being superseded by advanced methods taking a more dense time-series approach [11,12,13,14,15].

Time series change detection methods can be generally divided into two categories: those that search for deviations from stable conditions, and those that characterise the entire time series using trends and/or trend segments. Methods focussed on seeking deviations have often used annual or biennial time-steps [11,16,17,18] and are generally suited for the detection of abrupt change events such as clear-cutting, fire damage, flooding, and wind throw. Methods that use trends describe complete time series trajectories [19,20], and when multiple trend segments are used, are capable of capturing both abrupt and gradual change [12,15] including forest degradation, disease and insect attack, climatic adaptation, and regeneration.

A commonality among studies using annual or biennial time-steps is that they aim to minimize the effect of vegetation seasonality and sun angle differences by using consistent anniversary-date time steps [11,12,15,16,19,20]. Others have embraced the inherent seasonality through the integration of seasonal models in the time series analysis [13,14,21]. Using this approach, time series of intra-annual observations spanning multiple years are decomposed into trend and seasonal components. Major shifts in trends are represented as breakpoints, with each breakpoint separating meaningful time series segments. Breakpoints are derived using a variety of statistical tests and can often include false or low magnitude detections. Many studies therefore employ a second thresholding procedure based on the break magnitude to eliminate undesired breaks. Optimal magnitude thresholds for abrupt change events can be determined empirically using a calibration data set of known stable and change samples [22,23]. This can be further extended to thresholding of longer duration linear trend segments to identify more gradual change events [12,24]. Besides break magnitude and trends, changes in seasonality have been reliable indicators of forest change [21,25,26,27,28]. Previous forest monitoring studies have used either a single change indicator to map change (e.g., breakpoints) or a combination of two change indicators (e.g., breakpoints and linear trends). To our knowledge, combining breakpoints, trend, and seasonal components in a single change detection model has not been explored before, and may be useful for further distinguishing disturbance events from stable conditions.

The vast majority of forest monitoring systems have been facilitated by MODIS and Landsat sensors, each lending to a number of different methodological approaches. Despite limitations related to low resolution bias [29], MODIS remains highly useful for rapid large area forest monitoring [30,31,32]. While insufficient for direct area estimation, MODIS maps have been used extensively to identify deforestation hotspots. Such maps can feed into probability based sampling approaches combining higher spatial resolution data to efficiently estimate deforestation area [33,34]. With near-daily coverage of the entire earth’s surface a major benefit of MODIS is in the temporal domain. This is especially necessary for near real-time monitoring programs [35,36,37,38]. High temporal resolution is also advantageous in areas prone to persistent cloud cover such as the tropics where Landsat can have as few as zero to five cloud free observations per year [39]. On-going optical sensor advancements, however, means that Landsat-scale time series will soon be available at comparable temporal resolutions to MODIS for the humid tropics. Imagery from Landsat 7 and 8 along with Sentinel-2A and -B will substantially increase the availability and frequency of medium resolution observations [40]. With fusion of Landsat and Sentinel datasets it will be possible to have 20–30 m optical time series with around three day intervals in the near future [14]. Furthermore, the Landsat Global Archive Consolidation program is currently consolidating unique scenes stored in data holdings from numerous international ground stations, bolstering the amount of imagery available in many areas previously lacking coverage in the USGS archive [41], and improving capabilities for retrospective time series analysis. Refining time series methods using MODIS data offers mutual benefits for future Landsat-scale applications in the tropics based on dense intra-annual time series.

Recently, there has been an emphasis on large area disturbance mapping using optical time series. Mapping forest disturbance over large areas requires an understanding of the sensitivity and generalisability of the change detection model across different forest types found throughout the region. Most change models opt for a generalised forest definition including all forest types, and choose a single universal threshold that distinguishes between change and no change pixels [15,23,37,42]. While this approach is likely to perform well in areas characterised by forest with similar spectral responses to disturbance, studies have shown using a single change/no change threshold can be problematic in areas defined by heterogeneous forest types leading to lower accuracies [11,43]. In a region like Southeast Asia, forest type is likely to have a significant impact on change detection accuracy using a generalised forest approach due the close proximities of forests with major differences in intra-annual spectral response [44].

The objective of this study was to assess the suitability of MODIS time series data for mapping forest clearances (i.e., clear-cutting) in dynamic and diverse tropical monsoon landscapes of Southeast Asia. Specifically, we were interested in addressing two main methodological questions:

(1)

Forest clearing can be detected using the break magnitude, trend segment slope and/or changes in the seasonal component. Can combining these three components in a single change model improve detection accuracies compared to using only a single component?

(2)

It is reasonable to assume that specialized models outperform more general models, but it is not clear to what degree this is true with respect to forest types. Since a forest-type specific approach would require additional inputs, a generalised approach may be preferable for large-area mapping if accurate enough. Is it beneficial to map forest changes separately by forest type or is a single generalised change model sufficiently accurate?

2. Study Area

The study area is located on the Cambodian-Vietnamese border and includes a number of typical forest types found throughout the larger region, including evergreen (29%), mixed-deciduous (22%), and dry-deciduous (15%) forest (Figure 1). Additionally, a significant proportion of tree cover is composed of plantation forest and forest regrowth (34%). Previous analysis has shown the area experienced significant forest loss from 2000–2012, mainly in the form of large-scale frontier forest clearing [45]. Seasons are divided into three distinct periods including a hot/dry season (March–May), a rainy season (May–October), and a cool/dry season (March–November). The study region is relatively flat with peaks of up to 900 m found mainly to the northeast.

3. Materials and Methods

We used Breaks For Additive Season and Trend (BFAST) [13,21] to extract breakpoint magnitude, trend, and seasonal components from filtered MODIS time series. We then used these as explanatory variables to predict per-pixel cleared forest probabilities using a non-parametric statistical model—Multivariate Adaptive Regression Splines (MARS). To assess the influence of forest type on change detection, we built separate change models for each forest type and then we compared the results with a generalised forest change model that ignored forest type.

3.1. MODIS Data and Processing

The 250-m MODIS 16-day Vegetation Indices (MOD13Q1) time series (February 2000–December 2012) was downloaded for tile ID h28v07 from the USGS server using the MODIS Reverb tool (http://reverb.echo.nasa.gov/reverb). Additional to the well-known Normalised Difference Vegetation Index (NDVI) [46] and Enhanced Vegetation Index (EVI) [47], we calculated the Land Surface Water Index (LSWI). A number of studies have used LSWI time series for land cover mapping [48,49]. The LSWI is sensitive to equivalent water thickness (g H₂O/m²) and is therefore useful for detecting canopy water content or water stress, in contrast to canopy greenness. We used the NIR and resampled SWIR band provided by the MOD13Q1 product to calculate the LSWI:

$$\frac{{\text{NIR}}_{\mathrm{b}2}-{\text{ SWIR}}_{\mathrm{b}7}}{{\text{NIR}}_{\mathrm{b}2}+{\text{ SWIR}}_{\mathrm{b}7}}$$

(1)

These three indices provided the basis for MODIS time series analysis. We smoothed the time series using a weighted Savitsky–Golay filter and introduced seasonally adjusted window sizes for improved fitting during dry and wet seasons. For a detailed description of the MODIS processing and the filtering procedure, see Appendix A.

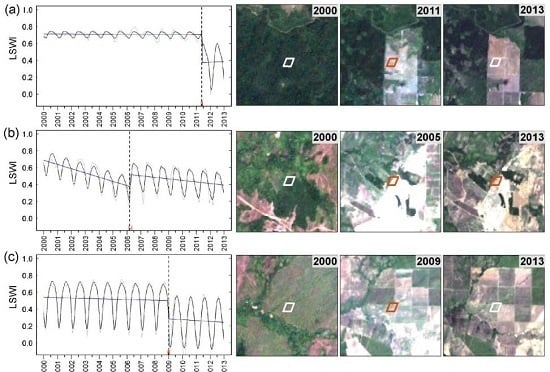
3.2. Extracting Breakpoints and Time Series Components Using BFAST

Time series analysis was performed on the filtered MODIS data using BFAST [13,21]. BFAST is an algorithm that combines structural break detection in time series with methods for decomposing the signal into seasonal, trend and remainder components. Piecewise linear trend and seasonal models are fitted to the time series using an additive decomposition model in the general form of:

$${\mathrm{Y}}_{\mathrm{t}}={\mathrm{T}}_{\mathrm{t}}+{\mathrm{S}}_{\mathrm{t}}+{\mathrm{e}}_{\mathrm{t}},\mathrm{t}=1,\dots ,\mathrm{n}$$

(2)

where Y_t is the observed data at time t, T_t is the trend component, S_t is the seasonal component, and e_t is the remainder component. The remainder component is the remaining variation in the data beyond what is explained by the seasonal and trend components. Before seasonal and trend models are fitted to the data, BFAST performs a test for abrupt changes in the time series. A number of different tests are available to detect structural breaks, including the Ordinary Least Squares (OLS) residuals-based Cumulative Sum (CUSUM) or Moving Sum (MOSUM) tests. If the test indicates a statistically significant change, breakpoints are estimated using the method of Bai and Perron [50], whereby the Bayesian Information Criterion is minimised to determine the optical number of breaks and break positions. We used a specific version of BFAST described by De Jong et al. [24], which is optimized to detect the most influential trend break in the time series. BFAST produces fitted seasonal and trend models based on the input time series (Figure 2). If there is an abrupt change in the time series it is indicated by a breakpoint. Optimal seasonal and trend models are then fitted for both time series segments on either side of the breakpoint. We used the ordinary least squares-moving sums (OLS-MOSUM) test with a significance level of 0.05 for detecting structural change within the MODIS time series. The MOSUM test for break detection is based upon the moving sums of OLS residuals within a user defined temporal window, or bandwidth. Similar to De Jong et al. [24], we choose the bandwidth of 40 observations. Since the number of 16-day time steps per year is 23, this gave a temporal window of just less than two years (i.e., 40/23).

We extracted three variables from the BFAST output that were potential predictors of forest clearing (Figure 2): the magnitude of the trend break (bmag), the seasonal amplitude difference between before and after a break (sdiff), and the most negative slope between each of the two trend segments (slp) (e.g., this would be the slope of second segment in Figure 2c). These three time series components were used as predictor variables for forest clearance modelling. The timing of clearances was estimated using the detected breakpoint.

BFAST is an open-source coding project available as an R package. For further details on its use and practical application see http://bfast.R-Forge.R-project.org/.

3.3. Classification for Comparing General and Forest-Type Specific Models

To address the question of whether forest-type specific change models improve the detection accuracy over a general change model, we classified the forest area into four classes for year 2000/2001: evergreen forest, mixed-deciduous forest, dry-deciduous forest, and a combined planted forest and forest regrowth class (see Appendix B for further details). We defined the forest area based upon the 30 m Vegetation Continuous Field (VCF) product for year 2000 [51] using a threshold of >15% tree cover [52]. All MODIS pixels with forest area above 75% were chosen for further analysis. For classification, we chose a random sample of 150 pixels per class and labelled them manually using a combination of Landsat and high resolution imagery from Google Earth. We used random forest [53] to classify each MODIS pixel using the above sample as training data and the three filtered time series (NDVI, EVI and LSWI) from February 2000–February 2001 as input data.

3.4. Change Model Training and Validation Data

For model training and validation we used a Landsat-based forest clearing map covering our study region created by Grogan et al. [45]. The map was produced by segmentation of Landsat time series using LandTrendr [12], and identifies stable forest and year of annual forest clearings in the period 2000–2012 with an overall accuracy of 86%. The forest area of the reference map was identical to that described in the previous classification step (Section 3.3). The reference map was aggregated from the original 30-m to the 250-m spatial resolution of the MODIS pixels. For this, we first projected the Landsat map to the MODIS sinusoidal projection. For each MODIS pixel we then calculated the cleared forest area proportion (C_p) for each year. The reference pixels with C_p values ≤0.05 were used as reference for stable forest, and pixels with C_p values >0.05 as reference for cleared forest.

Fully cleared MODIS pixels (C_p = 1) were more easily detected than partially cleared pixels (C_p < 1). To make the model results comparable between forest types, it was important that the training and validation sample for each forest type contained equal proportions of samples with similar C_p values. We selected a stratified random sample of 2000 pixels within each of the four forest types: 1000 forest clearance pixels and 1000 stable forest pixels. For the cleared forest sample we had five strata based on Cp value intervals: 0.05–0.24 (n = 130), 0.25–0.49 (n = 170), 0.50–0.75 (n = 200), 0.75–0.99 (n = 270) and 1 (n = 230). The sample size (n) for each clearance strata was proportional to the Cp frequency distribution using the same strata intervals for all forest clearance pixels (i.e., without distinguishing between forest type). We split the cleared and stable forest sample in half for each forest type, 50% for model training and 50% for model validation.

To ensure a minimal error in the training and validation samples, we manually screened all samples using time series of Landsat image chips (similar to Cohen et al. [54]), temporal-spectral profiles, and additional imagery from Google Earth where available. We removed and replaced any change or stable samples that were incorrectly labelled.

3.5. Modelling Forest Clearance Using Time Series Components

To discriminate between changed and stable forest pixels we modelled our binary response (cleared or stable) as a function of three predictor variables, bmag, sdiff, and slp. The relationships between the predictor variables and the binary response varied among forest type and were often non-linear. For example, clearance events were associated with both positive and negative sdiff values. A regression method capable of handling more complex interactions was therefore required. In this study we used Multivariate Adaptive Regression Splines (MARS). MARS is a non-parametric adaptive regression technique in which non-linear relationships between response and predictor variables are described via a series of piecewise spline basis functions [55,56]. Each segment of the fitted function is separated by a “knot” in a model that initially over-fits the training data. The final model is then simplified using a step-wise cross-validation procedure which incorporates a penalty term dependent on model complexity. The MARS model assumed a binomial error distribution, which ensured the values of the response variable were constrained between 0 and 1. For our models, predicted probabilities closer to 1 indicated higher likelihood of being cleared, while values closer to 0 were more likely to be stable forest.

3.5.1. Analysis of the Relative Importance of Time Series Components Clearance Predictions

To understand how well each individual variable predicts forest clearance, we first built separate forest-type specific change models using single variables only. We proceeded to combine predictor variables to test whether this improved the predictive power of the model and to assess which variable combination provided the most accurate results. We evaluated the performance of each model using receiver operating characteristic (ROC) curves. ROC curves illustrate the performance of binary response models by plotting the model sensitivity (true positive rate) against specificity (true negative rate) as the predicted probability threshold is varied. The area under the ROC curve (AUC) is a measure of the models predictive performance, with values of 0.5 indicating no discriminatory ability, and values of 1 indicating perfect discrimination. We made ROC curves using the validation data to assess model performance.

3.5.2. Comparison of Forest-Type Specific and Generalised Models

To determine the effect of forest type on clearance detection accuracies, we combined all training data to train a generalised forest change model using the same predictor variable combinations. Using the validation sample we then analysed the distribution of commission and omission errors among each forest type. Because our model (MARS) predicts class probabilities, it was necessary to translate the probabilities into discrete class memberships, but rather than selecting a single threshold value of probability (e.g., one that maximizes the overall accuracy), we estimated commission and omission errors for the entire range of probability thresholds (i.e., from 0–1). The resulting error curves were then plotted to examine differences between the forest-type specific and general approaches and to identify suitable probability thresholds. Although, the definition of a suitable threshold is user-specific, we selected thresholds that lead to balanced commission and omission errors.

3.6. SPATIAL/Temporal Accuracy and the Effects of Sub-Pixel Clearances

We used the validation sample to explore the effects of sub-pixel clearances on spatial accuracy (detection of clearing location) and timing of forest clearance. To analyse the effects of sub-pixel forest clearings on locational detection accuracy we generated histograms of omission error for the cleared forest class using C_p intervals of 10%. The temporal accuracy of the MODIS forest clearing map can be defined in a number of different ways when considering the effects of low resolution bias. If a single clearance occurs within a pixel then the mapped year of clearance using BFAST should relate to the actual year of the forest clearing. If however, there are multiple clearing events spanning two or more years, assigning a year label is not unambiguous. We assessed the temporal accuracy of the MODIS forest clearing map using two methods: (1) the year of maximum cleared area; and (2) the first year of forest clearing. We considered the timing of the clearance correct if it matched the reference sample year ± 1.

4. Results

4.1. Time Series Components and Their Effect on Forest Clearing Detection Accuracy

All three time series component variables: break magnitude (bmag), seasonal amplitude difference (sdiff), and negative trend slope (slp), were found to be associated with forest clearances (Figure 3). High magnitudes breaks were the most common indicator of change (Figure 3c,d) and were often accompanied by a significant change in the seasonal amplitude (Figure 3a). Forest clearance was also associated with steep negative trends before or after the breakpoints (e.g., Figure 3b). Among the spectral indices tested, LSWI performed best overall when compared to NDVI and EVI. In the interest of brevity, we present results using the LSWI only. Model results (ROC curves and AUCs) using NDVI and EVI can be found in Appendix C.

Overall, bmag was the best performing single predictor of forest clearance (Figure 4). sdiff was a slightly better predictor of clearance than bmag in evergreen forest and gave comparable accuracies to bmag in mixed forest, but was much less effective in planted and regrowth forest and especially so in dry-deciduous forest. The slp variable was the least effective single indicator of change in evergreen and mixed forest, but performed slightly better than sdiff in dry-deciduous forest and forest regrowth.

Using multiple predictors improved the performance of the change models in each forest type. Combining bmag and sdiff as explanatory variables improved model results with AUC increases ranging from 0.01 in dry-deciduous forest to 0.04 in mixed forest when compared to using bmag alone (

Table 1. Area under curve (AUC) estimates for regression models using different parameters and combinations of parameters, by forest type. AUCs for all models are derived using receiver operating characteristic (ROC) curves presented in Figure 4.

Variables	Evergreen Forest	Mixed Forest	Deciduous Forest	Planted and Regrowth
bmag + sdiff + slp	0.98	0.96	0.89	0.92
bmag + slp	0.97	0.96	0.89	0.92
bmag + sdiff	0.96	0.94	0.79	0.87
bmag	0.93	0.90	0.78	0.83
sdiff	0.94	0.86	0.61	0.72
slp	0.79	0.70	0.68	0.74

). Combining bmag and slp variables showed further increases in predictive power, with AUC increases ranging from 0.04 in evergreen forest to 0.11 in dry-deciduous forest when compared to using bmag alone. Using a combination of all three variables only slightly improved the model performance in evergreen forest compared to the bmag + slp model, with no further improvements gained in the other three forest types. Although the models performed very well in each forest type, there was notable variability. Higher AUCs were present in evergreen (0.98) and mixed (0.96) forest, and comparably lower values were found in planted and regrowth forest (0.92) and dry-deciduous forest (0.89).

4.2. Generalised versus Forest-Type Specific Models

By plotting omission versus commission errors for each model, any point on each error curve corresponds to a specific model probability threshold (Figure 5). Using forest-type specific models, errors were lowest in evergreen forest, followed by mixed forest, planted and regrowth forest and then dry-deciduous forest (Figure 5a). The shapes of the curves highlight the differences in model error sensitivity. For example, for forest clearance commission errors ranging between 0.05 and 0.25 the range of omission error in the dry deciduous forest was largest at 0.42–0.18 showing high sensitivity. Conversely, the corresponding range of omission error for evergreen forest was lowest at 0.09–0.02, displaying much lower sensitivity. When probability thresholds were chosen that balanced commission and omission errors, evergreen forest showed the lowest error at 0.08, increasing slightly for mixed forest (0.11), followed by planted and regrowth forest (0.16) and dry-deciduous forest (0.19) (Figure 5a). The average error balance for all validation samples using forest-type specific models was 0.14.

When using the generalised forest model, there is only one error curve, which represents the overall omission versus commission error curve, i.e., all forest without respect to forest type (Figure 5b). When a probability threshold was selected that balanced commission and omission errors, the generalised forest model achieved almost the same overall error rate as the forest-type specific models (0.15). Figure 6, however, illustrates how commission and omission errors using the generalised model were distributed between the four forest classes across a range of probability thresholds, allowing a comparison to the forest-type specific models. When the overall balanced error from the generalised model of 0.15 was separated by forest type, the errors were notably unbalanced and varied considerably, summarised in

Table 2. Forest clearance commission errors (CE) and omission errors (OE) for different forest types using forest-type specific models and the generalised forest model. The example presented chooses probability thresholds (P) with the goal of balancing commission and omission error. Data for the table are illustrated as points in Figure 5 and Figure 6. Errors and probabilities are rounded to two decimal places.

	Forest-Type Specific			Generalised Forest
	CE	OE	P	CE	OE	P
Evergreen Forest	0.08	0.08	0.35	0.04	0.13	0.40
Mixed Forest	0.11	0.11	0.41	0.10	0.11
Deciduous Forest	0.19	0.19	0.40	0.28	0.14
Planted and Regrowth	0.16	0.16	0.42	0.14	0.21
Overall	0.14	0.14		0.15	0.15

. Evergreen and dry-deciduous forest types were the two most affected by error imbalances, ranging from 0.09 to 0.14, respectively. The regrowth class was slightly less affected by the imbalance, while the mixed forest class remained virtually unaffected.

When compared to forest-type specific models, the generalised model consistently favoured higher commission/lower omission error in dry-deciduous forest, balanced mainly by a lower commission/higher omission error in evergreen forest. Overall, mixed forest and planted and regrowth forest error rates were less impacted by the choice of model. Using data represented in Figure 5 and Figure 6, a further two example tables are provided in Appendix D showing that this result holds true across a range of possible user-defined thresholds.

4.3. Forest clearance Mapping and Sub-Pixel Change

We mapped forest clearance using the forest-type specific model with bmag and slp as predictor variables and choosing a balanced commission and omission error. There was generally good agreement between the Landsat reference map and the 250-m MODIS map (Figure 7). The majority of change omission error was caused by clearances that occurred at the sub-pixel level and is therefore product of inherent low resolution bias (Figure 8). For clearance pixels that have C_p levels below 50%, the omission error was highest at between 0.17 (evergreen) and 0.40 (dry-deciduous). Omission error decreased linearly as C_p increased reaching a minimum ranging from 0.01 (evergreen) to 0.08 (dry-deciduous) for C_p values of 90%–100%.

Sub-pixel forest clearance also affected the timing assigned to clearance pixels since multiple clearances may occur at different times within the same MODIS pixel. When only one annual clearance occurred within a MODIS pixel the timing agreement using LSWI matched the validation data ±1 year for 70% of the samples (Figure 9). As the number of annual sub-pixel clearances increased, the timing labels assigned to cleared pixels were largely shared between the year with the greatest C_p value and the year of the first C_p occurrence. Agreements using these two matching criteria remained above 60% as the number of annual clearances increased.

5. Discussion

5.1. Combining Break Magnitude, Trend, and Seasonal Components

Combining trend and seasonal information with the break magnitude improved model performance, albeit to varying degrees, depending on forest type. A high break magnitude (bmag) was typical of the sudden deforestation events in the study area described by Grogan et al. [45], primarily large-scale rubber plantation expansion and smallholder clearances for agriculture. Linear trends have shown to be highly useful change indicators by many studies [12,15,19,20]. Overall, we found the addition of the negative trend variable (slp) enhanced model performance more than the addition of the seasonal amplitude difference (sdiff). Previous forest disturbance studies have modelled seasonality with the primary aim of removing the seasonal affects from the underlying trends [22,23]. Here we incorporated pre- and post-disturbance seasonal information into the change model and showed that it can also be a useful indicator of change, especially in low seasonality forest.

5.2. Model Sensitivity to Forest Type and Seasonality

Each model displayed consistently poorer performance moving from low to high seasonality forest (Table 2). This suggests an association between model accuracy and the gradient of forest seasonality, or degree of deciduousness, ranging from dry-deciduous to evergreen forest. Dry season leaf senescence can cause confusion in forest change analysis which can lead to higher error frequently reported in deciduous classes [57,58,59]. Besides seasonal variation in reflectance increasing with forest deciduousness [60], there can also be considerable natural inter-annual variation linked to changing climate and variable rainfall patterns [61,62,63]. This presents a major challenge for methods that use ridged seasonal models as they often model a constant average seasonality, failing to capture the natural variation. In tropical-dry forests characterized by high inter-annual seasonal variability, it does not seem ideal to use a seasonal model that assumes regular or stable seasonality—as does BFAST and other seasonal model approaches (see Zhu et al. [23] and Zhu and Woodcock [14]). Zhu and Woodcock [14] mapped land cover change with high accuracies in a humid continental climate using an approach that assumed phenology was consistent over time for stable land covers, but noted this could be problematic for drier regions. To address these shortcomings Jamali et al. [64] used a seasonal-trend decomposition procedure which allowed the seasonal model to vary from season to season. However, although this approach may better account for inter-annual forest variability, it remains uncertain if the variation captured in the seasonal model is due to natural variation or human induced change. This uncertainty has the potential to mask real disturbances from being evident in the trend component. A promising alternative might be to account for seasonal variation in the model by using external regressors. Dutrieux et al. [65] take such an approach in a recent Landsat-based change detection study in tropical dry forests by adjusting the seasonal NDVI model using MODIS based measures of inter-annual variability, with encouraging results. They also tested a measure of rainfall variability as an external regressor but with poorer results. Despite this, the use of climatic variables (e.g., soil moisture) to account for inter-annual variability in optical time series remains to be fully explored and further investigation may yield more favourable outcomes.

5.3. Model Sensitivity to Spectral Indices

We found that change models using LSWI time series performed better overall compared to the more commonly used NDVI and EVI. The LSWI is based on the spectral differences found between the NIR and SWIR bands. SWIR bands and associated indices are sensitive to canopy moisture and forest structure [66], and have been shown to be more responsive to a variety of disturbance types compared to indices based on NIR and VIS bands which target canopy greenness [12,45,67,68]. A possible explanation for this is that tropical vegetation greenness can recover rapidly soon after forest clearing as the herb layer and young saplings grow vigorously due to increased light levels, leading to an overall reduction in sensitivity when using greenness as a disturbance indicator. Hais et al. [68] demonstrated this affect in forests of Central Europe and found SWIR based indices to be more sensitive to forest disturbances. Another major advantage of SWIR based indices (and SWIR emphasizing transformations such as tasselled cap wetness) are their relative robustness to atmospheric water vapour and aerosols [69]. This property can further enhance the signal-to-noise ratio [70], leading to better characterisation of forest conditions and ultimately contributing to higher mapping accuracies.

5.4. Generalised versus Forest-Type Specific Models

Although overall accuracies were similar using forest-type specific models and a generalised forest model, applying separate models allowed more control over the error distribution among the different forest types. Compared to forest-type specific models, the generalised model consistently mapped forest clearance in dry-deciduous forest favouring lower omission error, but higher commission error. This was balanced by favouring lower commission/higher omission error in mainly evergreen forest. Our results suggest that accounting for forest type can improve forest clearance mapping in areas characterised by diverse forest types such as Southeast Asia. It seems particularly important to separate dry-deciduous and evergreen, seen as they have the largest swing of error imbalances using the generalised approach (Table 2). We gave equal weight to each forest type in our analysis. When considering discriminating forest type for forest clearance mapping thought should be given to the proportion of different forest types in the study region to evaluate the trade-offs in potential improved error distribution versus applying an extra classification step. This is likely more important for large area mapping where forest type can vary considerably. Discrimination of forest type can be made using a base map, as used in this study, or done on-the-fly during the time series analysis using the spectral information.

5.5. Forest Disturbance Mapping Using BFAST

Previous forest disturbance based studies using BFAST have mapped on the Landsat scale using breakpoints alone (i.e., no magnitude thresholding) to detect change [65,71]. However, DeVries et al. [22] showed that thresholding the break magnitude can be an important step distinguishing change from stable forest. Here we demonstrate how multiple BFAST components, combined with thresholding, can be used for effective forest monitoring using in MODIS time series. We used the single most influential break to identify forest clearance. Using multiple breakpoints may offer a more detailed summary of the pixel history—e.g., ability to capture multiple disturbances and trajectories. We also confined our study to monitor forest clearing, but the approach could also be adapted to include forest recovery, similar to DeVries et al. [72]. Although BFAST can handle unfiltered data, we found in the preliminary testing phase of our analysis that applying a smoothing filter improved forest clearance detections. MODIS 16-day time series products can be exceptionally noisy in the tropics, in part due to errors related to deficiencies in aerosol and cloud screening [73,74,75]. Time series composites generated using more advanced cloud screening and atmospheric correction techniques have shown to dramatically reduced time series noise [75] and may eliminate the need for data filtering.

Another shortcoming of BFAST and other similar time series models is that by using linear segments to describe underlying trends, they assume vegetation trends are linear processes. It has been known for some time that land cover change can often occur along non-linear multidirectional pathways [76]. Both abrupt and slowly occurring disturbances in land cover such as forest clear-cutting, fires, insect outbreaks and logging can result in non-linear changes to vegetation cover [77]. Similarly, natural climatic processes such as short- or long-term changes in rainfall patterns or temperature may induce a non-linear response form vegetation cover. Jamali et al. [78] tried to account for such non-linear processes by describing long term trends using polynomials and found it to adequately describe general non-linear change trajectories in the Sahel. The future challenge will be to incorporate non-linear change processes into change detection time series models.

5.6. Relevance for Forest Monitoring Systems

Robust forest monitoring systems are becoming increasingly more important, especially for conservation efforts and global climate initiatives such as REDD+. Tropical environments such as Southeast Asia present a unique challenge for retrospective and on-going forest monitoring, primarily due to data availability. For example Broich et al. [39] have shown cloud free Landsat observations for Indonesia are between 0 and 5 per year. Such data scarcity limits the capabilities of Landsat time series in these regions. Further monitoring limitations arise from technical capacities and budget constraints. For these reasons many advocate the combined use of sensors [79], drawing from the advantages of each in an integrated monitoring system. Such data-fusion approaches have been developed, e.g., by Hansen et al. [33], who integrated Landsat and MODIS to estimate forest clearing area in the humid tropics; or Potapov et al. [80], who used a similar approach in North America. Our results demonstrate how MODIS can be used to provide valuable information on location and timing of forest clearance events with high accuracy in a tropical dry environment. Our study region was relatively small however, so it is necessary to test if the approach can be successfully applied to a national or regional scale. Such forest clearance maps at the 250-m scale can be used to provide fast, up-to-date information on deforestation hotspots, where mapping efforts can be concentrated, or used as a stratification tool for estimating forest change area using probability based sampling [33,81,82]. It should be noted, however, that low resolution bias can limit the capacity of the MODIS sensor in regions with clearances occurring at smaller scales (e.g., mosaic forest clearing, or shifting cultivation). Dense intra-annual time series at medium resolution (20–30 m) will soon be available for the tropics pending the fusion of Landsat and Sentinel imagery, which will improve the ability to capture these smaller scale clearances at high temporal resolutions. Given the spectral similarities between MODIS and Landsat/Sentinel sensors the methods described in this manuscript should be readily transferable to future medium resolution applications.

6. Conclusions

Methods for forest monitoring using dense time series are advancing rapidly. This study demonstrates how combining break magnitude, trend, and seasonal components can improve forest clearance mapping when compared to using just the break magnitude alone. Our study indicates that forest type has significant influence on model performance, with lower accuracies in dry-deciduous forest and higher accuracies in evergreen forest, with mixed forest and forest regrowth accuracies lying in between. This suggests a relationship between the model performance and the gradient of seasonality. We also demonstrate that modelling forest clearance with respect to forest type, as opposed to using a generalised forest model, offers a more flexible approach and can ensure that the error levels within each forest type are optimally distributed by the user by choosing forest-type specific thresholds. The division of forest type is therefore important for regions such as Southeast Asia where diverse forest types with different phenology and spectral response to forest clearing can be found. It is especially relevant for large area mapping as there is a higher likelihood different forest types will be included in the analysis. From a forest monitoring perspective, the accuracies achieved using our approach show promising potential; however, it remains to be tested if the models can be applied over larger regions, while maintaining similar performance levels. Our methodological approach shows the potential usefulness of MODIS for rapid assessment of timing and location of forest cover change over large areas which can form part of an integrated monitoring system. These methods can also be useful for future medium resolution applications based on Landsat and Sentinel datasets.