Deformable ConvNet with Aspect Ratio Constrained NMS for Object Detection in Remote Sensing Imagery

Abstract

Convolutional neural networks (CNNs) have demonstrated their ability object detection of very high resolution remote sensing images. However, CNNs have obvious limitations for modeling geometric variations in remote sensing targets. In this paper, we introduced a CNN structure, namely deformable ConvNet, to address geometric modeling in object recognition. By adding offsets to the convolution layers, feature mapping of CNN can be applied to unfixed locations, enhancing CNNs’ visual appearance understanding. In our work, a deformable region-based fully convolutional networks (R-FCN) was constructed by substituting the regular convolution layer with a deformable convolution layer. To efficiently use this deformable convolutional neural network (ConvNet), a training mechanism is developed in our work. We first set the pre-trained R-FCN natural image model as the default network parameters in deformable R-FCN. Then, this deformable ConvNet was fine-tuned on very high resolution (VHR) remote sensing images. To remedy the increase in lines like false region proposals, we developed aspect ratio constrained non maximum suppression (arcNMS). The precision of deformable ConvNet for detecting objects was then improved. An end-to-end approach was then developed by combining deformable R-FCN, a smart fine-tuning strategy and aspect ratio constrained NMS. The developed method was better than a state-of-the-art benchmark in object detection without data augmentation.

1. Introduction

Object detection is one of the main tasks in remote sensing. Accurate identification and localization of land targets enables applications in urban planning [1], environmental management [2] and military uses [3,4]. Development of very high resolution remote sensing images provide us more detailed geo-spatial objects information, including diversities in scale, orientation and shape. Therefore, a key challenge in VHR (Very High Resolution) visual recognition is to build geometric aware models for high level object understanding.

The traditional object detection framework has three major components: feature representation, classification and localization. In the past, researchers have modeled geometric variations with two methods, both based on feature representation. The first method involves adding geometric priors in training samples, which is usually completed by manually rotating or performing transformation the training objects in two-dimensional (2D) or three-dimensional (3D) space [5]. The second method involves extracting transform invariance features. By finding scale-invariant feature transform descriptors, researchers created scaleinvariant feature transform (SIFT) [6] and histograms of oriented gradients (HOG) [7], which are widely used in computer vision and other image related areas.

The two modeling ways above are not without their weaknesses. For the first method, all the geometric diversities learned in the classifier are obtained from manual operations, making the prior less reliable. As a strong supervision model, the classifier cannot recognize unknown orientations. The complex time-consuming rotation procedures also limit the performance of the first method. The second method also shares problems created by manual inputs: SIFT and HOG features are built based on artificial selection of gradients between pixels, which does not comprehensively represent both variance and invariance in object shapes.

In object detection, the popularity of convolutional neural networks (CNNs) has instigated the end-to-end model design and benchmark beating. As the strongest classifiers to date, CNN uses convolution as a sampling approach, generating massive weights through connected convolution layers and fully connected network layers. Massive weights are defined as a massive information stream. CNN is able to store abundant structural information through training, which enables powerful complex object classification. In remote sensing images, AlexNet [8] was first introduced to very high resolution (VHR) optical images and beated Bag-of-Words (BoW) [9], spatial sparse coding BoW (SSCBoW) [10], Fisher discrimination dictionary learning (FDDL) [11] and the collection of part detectors (COPD) [12] model in object detection [5]. The success of AlexNet opened the field of deep learning to remote sensing. Since then, an increasing number of CNN structures such as region-based CNN (R-CNN) [13], Fast R-CNN [14] and Faster R-CNN [15] have been introduced to improve the precision in VHR object detection. Recently, R-P-Faster R-CNN was proposed by Han et al. [16]. With region proposal networks (RPN) added to the Faster R-CNN architecture, R-P-Faster has achieved higher precision than all other CNN models in NWPU (Northwestern Polytechnical University) VHR-10 datasets [5,17]. Its high quality performance makes R-P-CNN a state-of-the-art object recognition approach in VHR images. CNN’s continuous benchmark beating and structural innovation inspired us to determine if geometric variation or transformations can be learned end-to-end through structural augmentation in CNN. In Girshick et al. [18], the deformable parts model (DPM) was created as a special CNN structure, revealing that CNN is able to represent 2D layout of object parts, which provides a theoretical milestone for geometric modeling.

However, CNN has inherent limitations in modeling geometric variations shown in visual appearance. As described in Cheng et al. [5], CNN is problematic while being applied to VHR object detection directly. To remedy this issue, Rotation Invariant CNN (RICNN) is developed in [5], which augmented training objects by rotating them 360 degrees. RICNN was similar to the first geometric modeling method mentioned above. These approaches achieve better performance than pure AlexNet and performance close to that of R-P-Faster CNN, but strong supervision was added to the training process, breaking the end-to-end CNN framework. In fact, RICNN does not solve the inherent limitation in CNN and uses the most insufficient process to model geometric variation. The fundamental problem of CNN modeling geometric transformation lies in CNN’s convolution because all convolution operations conducted within CNNs are fixed locations sampling. These locations do not easily deform to fit objects in shapes and orientations. As long as a traditional CNN structure such as AlexNet is used, the only method available is artificially deforming training samples. Therefore, feature mapping in convolution must be reformed to fit the geometric proprieties of VHR targets.

The appearance of deformable convolution overcomes the mapping limitations in CNN [19]. By adding 2D offsets to the regular convolution grid, deformable convolution sample features from flexible locations instead of fixed locations, allowing free deformation in forms in the sampling grid. In other words, deformable convolution refines traditional convolution by adding preceding offsets layers. The deformable convolution modules substitute part of the convolution layers in CNN and form deformable ConvNets (DCN), which contain massive internal transform parameters to model geometric proprieties of objects. Compared to RICNN or previous methods such as DPM, deformable ConvNets build a deep and end-to-end geometric aware CNN model. We believe deformable ConvNets will have excellent performance when used in VHR remote sensing images.

In this work, we propose an end-to-end workflow to address the geometric modeling problem in object detection for VHR remote sensing imagery. Deformable ConvNet with deformable convolution layers embedded on Region-based Fully Convolutional Networks (R-FCN) is introduced in the field of remote sensing for object detection. After experimenting on several VHR annotated images, we found that deformable R-FCN has false positive bounding boxes in distorted aspect ratio. Some of the boxes have limited width, making them lines. To solve this problem, we proposed aspect ratio constrained non maximum suppression (NMS) to eradicate false results and improve precision. The deformable R-FCN, together with aspect ratio constrained NMS (arcNMS) form our complete solution to geometric variant object detection in VHR remote sensing images.

Our major contribution includes introducing deformable ConvNet to object detection in VHR remote sensing imagery. An end-to-end CNN approach without artificial augment is introduced in our paper. Geometric variation modeling is completed within the convolution sampling layers. Feature maps extracted by deformable ConvNet contain more information about the objects’ scale, orientation, and shape. Meanwhile, structurally, the proposed deformable ConvNet is an end-to-end model that directly obtains raw images as input and output bounding boxes and labels without artificial operations.

Our other contribution is the improvement of deformable ConvNet’s performance in VHR remote sensing imagery by using an efficient network training strategy. To make full use of the limited annotated VHR optical imagery resources, we propose a time and computation saving fine-tuning approach. The deformable ConvNet was constructed by substituting convolution layers in R-FCN with deformable convolution layers. We used pre-trained ImageNet R-FCN model parameters as the initial parameters for all regular convolution models. We added one offset layer next to one of the regular convolution layers, and the offset layer parameters were trained from scratch. With this method, objects in VHR remote sensing images are better understood by deformable ConvNet in less time and require less computation resources. Our work proposes an aspect ratio constrained NMS to improve deformable ConvNet’s performance in remote sensing areas. By modeling the logarithm of the bounding boxes’ aspect ratio during training annotations, arcNMS detects anomaly bounding boxes generated by deformable ConvNet and deletes them, constraining the number of false positive proposals in VHR remote sensing images and improving the precision of deformable ConvNet.

The proposed deformable ConvNet with arcNMS is evaluated and compared to established VHR object detection methods in the NWPU VHR-10 dataset [5,17] . The experiment results confirm our assumptions and prove that deformable ConvNets outperforms state-of-the-art CNN models in object detection tasks without data augmentation.

The rest of our paper is described as follows. Section 2 describes the proposed deformable ConvNet and arcNMS method, Section 3 presents the dataset and experimental settings for object recognition performance evaluation and comparison on VHR remote sensing imagery. The results of deformable ConvNets, and other approaches in the NWPU VHR-10 and RSOD (Remote Sensing Object Detection) datasets, are presented in Section 4. Section 5 provides our conclusion.

2. Proposed Method

The architecture of previous CNN models applied for object detection can be summarized as three major components: features, detectors and post-processing. In this section, we introduce our proposed deformable ConvNet in these three components. First, we present the fundamental concepts of deformable convolution and its use in image feature sampling. Then, we introduce our deformable ConvNet detector, which contains deformable convolution layers, pre-trained parameters and fine-tuning mechanisms. Lastly, an arcNMS post-processing step is described to illustrate how lines like false region proposals can be eradicated.

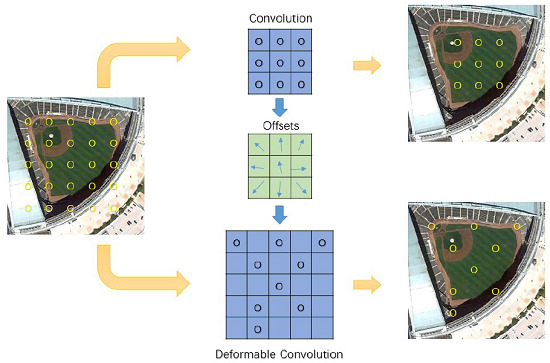
2.1. Deformable Convolution

For image processing, convolution can be regarded as 2D spatial sampling. Given the sampling grid $\Psi$, convolution of weights $w\left[n_i,n_j\right]$ and input feature map $f(x,y)$ is

$$u\left[x,y\right]=\sum _{\left(n_i,n_j\right)\in \Psi }w\left[n_i,n_j\right]f\left[x-n_i,y-n_j\right],$$

(1)

where $u\left[x,y\right]$ represents the output of convolution between weights grid and the input; in tasks such as denoising, smoothing and edge detection [20], grid $\Psi$ is usually recognized as kernels.

In Dai et al. [19], deformable convolution was achieved by augmenting the input feature map with 2D offsets during convolution. For better understanding from the image processing perspective, we formulized the deformable convolution as follows:

$$u\left[x,y\right]=\sum _{\left(n_i,n_j\right)\in \Psi }w\left[n_i,n_j\right]f\left[x-n_i-\Delta n_i,y-n_j-\Delta n_j\right],$$

(2)

where convolution becomes the weighted sampling of unfixed locations of the input feature grid, which generate its diversities.

However, as the offsets might be non-integer, the value of $f\left[x-n_i-\Delta n_i,y-n_j-\Delta n_j\right]$ remains to be determined. In our work, we used bilinear interpolation to obtain the fractional location between integer pixels. If points $(x,y)$ fall into a 2 × 2 pixels area, x ranges from $x_i$ to $x_i+1$ and y from $y_j$ to $y_j+1$. The value of $f\left[x,y\right]$ by bilinear interpolation is approximately

$$\begin{array}{cc}\hfill f\left[x,y\right]& \approx f\left[x_i,y_j\right](1-x+x_i)(1-y+y_j)+f\left[x_i+1,y_j\right](x-x_i)(1-y+y_j)\hfill \\ & +f\left[x_i,y_j+1\right](1-x+x_i)(y-y_j)+f\left[x_i+1,y_j+1\right](x-x_i)(y-y_j).\hfill \end{array}$$

(3)

To express this function generally, we have

$$f\left[x,y\right]\approx \sum _{\left(x_t,y_t\right)\in \Phi }g(x_t,x)·g(y_t,y)·f\left[x_t,y_t\right],$$

(4)

where $\Phi$ enumerates all integer points clique near $f\left[x,y\right]$. The interpolation kernel is decomposed into 2 kernels in the x and y dimensions. Kernels $g(a,b)$ in two dimensions are defined as

$$g(a,b)=max(0,1-|a-b\left|\right).$$

(5)

With deformable convolution function determined, the next step was to learn the offsets through training. In Figure 1, how to obtain offsets by augmenting convolution layers with additional offsets field according to Equation (2) is illustrated. With offsets vectors having the same spatial resolution as input feature maps, the original sampling points spread outward to focus on the objects. With offsets and convolution weights being fully learned, CNN obtains better geometric variation features. Therefore, in the test procedure, deformable ConvNets were able to generate more accurate bounding boxes according to deformable feature mapping.

2.2. Deformable R-FCN

For image recognition, convolutional Neural Networks have been continuously enhanced since AlexNet [8] and visual geometry group (VGG) Nets [21]. In contrast to these two nets that consist of convolutional subnetworks with Region-of-Interest (RoI) pooling and fully connected layers, image classification CNN such as GoogeLeNets [22] and ResNets [23] are fully convolutional. However, for object detection, state-of-the-art architectures like Faster R-CNN [24] are still using RoI subnetworks with hidden, computational unshared layers. To remedy this issue, Dai et al. developed Region-based Fully Convolutional Networks (R-FCN) [25] for object detection. The key aspects of R-FCN are position-sensitive score maps that encode positioning information using banks of specialized convolutional layers. Position-sensitive RoI pooling is also used in R-FCN to gather all information contained in feature score maps. With these two aspects, R-FCN realizes an end-to-end fully convolutional network with all computation shares on the entire image instead of hundreds of region-based subnetworks. Results have shown that, by using the ResNet-101 model pre-trained on ImageNet, R-FCN outperforms Faster R-CNN and other network structures on both VOC (Visual Object Classes) and COCO (Common Objects in Context) object detection datasets.

In our work, the CNN architecture was developed according to Dai et al. [19], but a different training strategy is used. As shown in Figure 2, based on R-FCN that contains fully convolutional feature maps, RoI pooling and RPN, we used ResNet101 ImageNet pre-trained parameters as the initial values and substitute res5, res4b22, res4b21 and res4b20 layers by deformable convolution layers. Then, the deformable R-FCN architecture was fine-tuned using NWPU VHR-10 images as input.

This procedure provides a fine-tuning strategy to fully use powerful CNN architecture and pre-trained natural image classification models. Fine-tuning is motivated by the earlier features of ConvNet containing more generic features such as edge detectors or color blob detectors that should be useful for many tasks. We initialized all regular convolution layers with pre-trained ImageNet R-FCN model parameters, added one offset layer adjacent to one of the regular convolution layers and the offset layer parameters were trained from scratch. This strategy helped CNN learn the basic region invariance of both objects and background from well-established natural image models, which reduced computation time. Then, the objects’ geometric proprieties were modeled by deformable convolution layers, enhancing CNN’s locality. Therefore, higher precision object detection was realized when VHR remote sensing imagery was used with the limited training dataset.

2.3. Aspect Ratio Constrained NMS

2.3.1. Lines like False Region Proposals

To test the architecture of deformable ConvNets, we conducted experiments on the NWPU VHR-10 dataset with non maximum suppression. Interesting line like false region proposals (LFRP) were found in results. After examining the concepts of deformable convolution, we found a possible explanation for the LFRP. Due to deformable convolution samples features from flexible locations, sets of irrelevant points may be recognized as objects if they are exactly moved to object points by offsets field. This coincidence is illustrated in Figure 3. When the baseball diamond feature points in the test set match parameters trained in CNN, they will be recognized in remote sensing images. However, deformable ConvNets also recognize deviated points as correct. In the following layers, the deviated points in a line will be recognized as objects no matter how the CNN was changed.

Li et al. [26] attempted remedy strange LFRP generated by CNN. The bounding boxes in unnatural aspect ratios were explained as confusion of global contexts. For instance, if the context of a baseball diamond is similar to a harbor or a road, the false ship or car regions are proposed and most of these proposals will have thin and long shapes. Li et al. [26] summarized this problem as challenges easily overcome using the traditional DPM method, which is usually ignored by region-based CNNs. Therefore, an aspect ratio and context aware fully convolutional network (ARCFCN) is developed to add the aspect ratio and context aware part-based models into FCN. Experiments have shown that ARCFCN benefits from FCN and Faster R-CNN frameworks in precision.

However, augmenting FCN with context aware part-based models increases the computation complexities of the CNN architecture, thus increasing the computation time. The ARCFCN reduces the false positive region proposals, which will only improve the precision but not the recall rates. To create a simpler solution for the LFRP problem, we focused on refining the non maximum suppression instead of the CNN architecture. NMS is one of the key post-processing steps in computer vision applications including edge detection, object detection and semantic segmentation [27]. NMS provides an Intersection over Union (IoU) based workflow to select region proposals to get the accurate object localization. Once NMS considers the aspect ratio during selecting, LFRP may be eliminated.

2.3.2. Aspect Ratio Constrained NMS

In our work, an aspect ratio constrained NMS was developed and applied to augment deformable ConvNet’s performance in VHR object detection. To construct the appropriate aspect ratio constraints, we calculated the logarithm of the aspect ratios in both training and test boxes as

$$AR=log({\displaystyle \frac{length}{width+{\delta }_t}}),$$

(6)

where $length$ and $width$ represent the distance in the x and y dimensions between lower left and upper right vertexes of the bounding boxes and ${\delta }_t$ is the fractional coefficient in case the denominator becomes zero. In our experiment, we set ${\delta }_t$ as 10⁻⁴⁶. Then, we derived the distribution of $AR$ in both training and test sets. As Figure 4 shows, $AR$s appear to fall within normal distribution with a large peak at zero. Zero $AR$ means these boxes have the same length and width. However, in the distribution shown in Figure 5, the $AR$s proposed by deformable ConvNets have three peaks in locations other than zero. These three peaks represent LFRP generated in deformable ConvNet. Once these peaks are omitted in NMS, the precision of deformable ConvNet will improve.

Therefore, for all deformable ConvNet proposed regions, the aspect ratio constraint is developed as

$$c_t=\left\{\begin{array}{ccc}1,\hfill & \mathrm{if}& \left|A{R}_t-\mu \right|<3\sigma ,\hfill \\ 0,\hfill & \mathrm{if}& \left|A{R}_t-\mu \right|>3\sigma ,\hfill \end{array}\right.$$

(7)

where $\mu$ and $\sigma$ are mean value and standard deviation of $AR$s in training annotations, respectively. For each of the bounding boxes proposed by deformable ConvNets, if the difference between its $AR$ and $\mu$ exceeds $3\sigma$, the region proposal is recognized as an LFRP. Then, the constraint $C_t$ becomes zero.

Then, the input to NMS algorithm is refined as

$$\left(b_t,s_t\right)=c_t·\left(b_t,s_t\right),$$

(8)

where $B=\left\{b_1,b_2,\dots b_n\right\}$ is the list of initial detection boxes and $S=\left\{s_1,s_2,\dots s_n\right\}$ represents the corresponding scores of the proposed boxes. For each $b_t\in B$ and $s_t\in S$, constraint $c_t$ is added to $\left(b_t,s_t\right)$, which deletes all of the LFRPs by setting them to zero. Then, the lists of region proposals and corresponding scores are selected according to Intersection over Union (IoU). Based on the arcNMS post-processing step, the precision of deformable ConvNet in object localization increases. The deformable network structure provides powerful benchmark beating capacities in object detection.

3. Dataset and Experimental Settings

To evaluate and validate the effectiveness of deformable ConvNet and arcMNS on VHR remote sensing imagery, the dataset, experimental settings, and the corresponding evaluation indicators of the experimental results are described in this section.

3.1. Dataset and Implementation Details

To compare the performance of various approaches developed for object detection in remote sensing images, many datasets are available for researchers to conduct further investigations [3,28,29,30,31]. These datasets promote the development of object detection methods in remote sensing imagery, but have obvious drawbacks. First, the volume of annotations in these datasets are limited, which constrain the power of CNN because it requires large scale training samples. Datasets are specialized as certain types of objects such as vehicles, planes or roads, but lacks a comprehensive benchmark for remote sensing imagery.

In our work, we selected an NWPU VHR-10 dataset used in prior studies [5] as benchmarks based on the considerations listed above. The advantages of NWPU VHR-10 dataset can be summarized as:

• Source and resolution diversity. NWPU VHR-10 dataset not only contains optical remote sensing images, but also includes pan-sharped color infrared images. In addition, 715 images were downloaded from Google Earth Pro (Version 7.3, Google, Mountainview, California, US) with spatial resolutions from 0.5 m to 2.0 m. Meanwhile, 85 pan-sharpened color infrared images were acquired from the Vaihingen data with a 0.08 m spatial resolution.
• Comprehensive object types. NWPU VHR-10 dataset contains 10 different types of objects, including airplane, ship, storage tank, baseball diamond, tennis court, basketball court, ground track field, harbor, bridge, and vehicle.
• Abundant object annotations.The NWPU VHR-10 dataset contains 650 annotated images, within each image containing at least one target to be recognized. For the image set in VOC 2007 formula, 757 airplanes, 302 ships, 655 storage tanks, 390 baseball diamonds, 524 tennis courts, 150 basketball courts, 163 ground track fields, 224 harbors, 124 bridges, and 477 vehicles have been manually annotated with rectangular bounding boxes, and were utilized as the training samples and testing ground truth.

With Cheng et al. [5] being cited more than 60 times, the NWPU VHR-10 dataset has become the widely applied open source VHR remote sensing image dataset for object detection. Han et al. [16] reported that CNNs attained an accuracy of about 70% in object detection. Objects such as airplanes, baseball diamonds, and ground track fields have higher precision than objects like storage tanks and bridges. The state-of-the-art benchmark of mAP (mean Average Precision) for end-to-end CNNs is 76.3%.

To evaluate deformable ConvNet in comparison to RICNN and R-P-Faster R-CNN, we established the same experiment environments as Han et al. [16]. The ratios of training, validation and testing dataset were set to 20%, 20% and 60%, respectively. Then, we randomly selected 130, 130 and 390 images in NWPU VHR-10 dataset to fill the three subsets, respectively. Deformable ConvNets and comparison models were implemented on a server with an Nvidia GTX 1080Ti GPU (graphics processing unit). In the training of deformable ConvNet, we set the learning rate to 0.0005 and perform fine-tuning based on ResNet-101 pre-trained models. The RPN parameters in deformable ConvNet were same as in Dai et al. [19]. To compare deformable ConvNet’s fine-tuned efficiency, we used transferred AlexNet, newly trained AlexNet, RICNN with and without fine-tuning on ImageNet, and R-P-Faster R-CNN with Zeiler and Fergus (ZF) model or the visual geometry group (VGG) model fine-tuned on ImageNet.

However, results a in single dataset may not be enough to evaluate the performance of deformable R-FCN. To address the dataset constraints, we chose an RSOD dataset proposed by Long et al. [32], who annotated oil tanks, aircrafts, overpasses, and playgrounds on 2326 images collected from Google Earth. The ratios of the training, validation and testing dataset were set to 25%, 25% and 50%. In this experiment, we compared deformable R-FCN with two previous CNN structures that have the highest meanAP in the NWPU VHR-10 dataset.

3.2. Evaluation Indicators

To quantitatively evaluate the performance of different CNNs in object detection, we used the precision–recall curve (PRC) and average precision (AP), which are are two well-known and widely applied standard measures approaches for comparisons [11].

3.2.1. Precision—Recall Curve

PRC is obtained from four well-established evaluation components in information retrieval, true positive (TP), false positive (FP), false negative (FN), and true negative (TN). TP and FP represent the correctly and falsely detected objects’ ratio in all region proposals. FN is the sum of regions not proposed. Based on these four components, we provide the definition of precision and recall rate as

$$Precision={\displaystyle \frac{TP}{(TP+FP)}},$$

(9)

$$Recall={\displaystyle \frac{TP}{(TP+FN)}}.$$

(10)

PRC is built as a detection map developed on precision and recall. If the ratio of overlap between proposals and ground truth exceeds 0.5, the proposals are recognized as TP; otherwise, they are FP. Typically, precision and recall are inversely related, so, as precision increases, recall falls and vice-versa. A balance between these two must be achieved by the IR system, and the precision–recall curves allow the comparison of performance to achieve this balance. The relationship between precision and recall has been displayed in PRC in many experiments. The PRC provides a detailed inspection of a model’s performance in object detection.

3.2.2. Average Precision

The AP computes the average value of precision over the interval from recall = 0 to recall = 1, i.e., the area under the PRC. Mean AP (mAP) computes the average value of AP over all object categories. AP and mAP are used as the quantitative indicators in object detection [6,9]. Most papers recognize higher AP as proof of benchmark beating. Except AP for value, Han et el. [16] used accuracy from image classification for performance comparison as follows:

$$Accuracy={\displaystyle \frac{TP+TN}{(TP+TN+FP+FN)}}.$$

(11)

However, accuracy is questionable for object detection. Object detection is different from image classification or retrieval. The detector will not draw true negative bounding boxes in training and testing. Accuracy is meaningless as an indicator. Moreover, the accuracy in Han et al. [16] does not match the equation when TN is zero. Therefore, accuracy was not applied in our work.

4. Results

Visualization of the objects detected by deformable R-FCN in an NWPU VHR-10 dataset is shown in Figure 6. From Figure 6, deformable R-FCN shows better detection results in orientation variant targets such as airplanes (top left), ships (top right), bridges (bottom left), and vehicles (bottom right). Deformable R-FCN has better performance in recognizing adjacent or overlapping objects such as harbors, storage tanks, and ball courts. In the following subsection, quantitative and qualitative analysis will be presented to evaluate the performance of deformable R-FCN.

4.1. Quantitative Evaluation of NWPU VHR-10 Dataset

Quantitative comparisons measured by AP values and average running time per image are displayed in

Table 1. The AP (Average Precision) values of the object detection methods.

	BoW	SSC BoW	FDDL	CPOD	Transfered AlexNet	Newly Trained AlexNet	RICNN without Fine-Tuning	RICNN with Fine-Tuning	R-P-Faster R-CNN (ZF)	R-P-Faster R-CNN (Double) (VGG16)	R-P-Faster R-CNN (Single) (VGG16)	R-FCN (ResNet-101)	Deformable R-FCN (ResNet-101)	Deformable R-FCN (ResNet-101) with arcNMS
Airplane	0.025	0.506	0.292	0.623	0.661	0.701	0.860	0.884	0.803	0.906	0.904	0.817	0.861	0.873
Ship	0.585	0.508	0.376	0.689	0.569	0.637	0.760	0.773	0.681	0.762	0.750	0.806	0.816	0.814
Storage tank	0.632	0.334	0.770	0.637	0.843	0.843	0.850	0.853	0.359	0.403	0.444	0.662	0.626	0.636
Baseball diamond	0.090	0.435	0.258	0.833	0.816	0.836	0.873	0.881	0.906	0.908	0.899	0.903	0.904	0.904
Tennis court	0.047	0.003	0.028	0.321	0.350	0.355	0.396	0.408	0.715	0.797	0.79	0.802	0.816	0.816
Basketball court	0.032	0.150	0.036	0.363	0.459	0.468	0.579	0.585	0.677	0.774	0.776	0.697	0.724	0.741
Ground track field	0.078	0.101	0.201	0.853	0.800	0.812	0.855	0.867	0.892	0.880	0.877	0.898	0.898	0.903
Harbor	0.530	0.583	0.254	0.553	0.620	0.623	0.665	0.686	0.769	0.762	0.791	0.786	0.722	0.753
Bridge	0.122	0.125	0.215	0.148	0.423	0.454	0.585	0.615	0.572	0.575	0.682	0.478	0.714	0.714
Vehicle	0.091	0.336	0.045	0.440	0.429	0.448	0.680	0.711	0.646	0.666	0.732	0.783	0.757	0.755
mean AP	0.246	0.308	0.245	0.546	0.597	0.618	0.710	0.726	0.702	0.743	0.765	0.763	0.784	0.791

and

Table 2. Computation time comparisons for objects’ detection methods.

	BoW	SSC BoW	FDDL	CPOD	Transfered CNN	Newly Trained CNN	RICNN without Fine-Tuning	RICNN with Fine-Tuning	R-P-Faster R-CNN (ZF)	R-P-Faster R-CNN (Double) (VGG16)	R-P-Faster R-CNN (Single) (VGG16)	R-FCN (ResNet-101)	Deformable R-FCN (ResNet-101)	Deformable R-FCN (ResNet-101) with arcNMS
Average running time per image (second)	5.32	40.32	7.17	1.06	5.24	8.77	8.77	8.77	0.005	0.155	0.155	0.156	0.201	0.201

. As the NMS process has no impact on TP and FN, recall rate of deformable R-FCN, both with and without arcNMS, were the same. The recall rate value is shown in Figure 7. In addition to the ZF model, the R-P-Faster R-CNN used VGG16 training mechanism, which includes single fine-tuning and double fine-tuning [21]. The RICNN with fine-tuning uses AlexNet pre-trained on ImageNet. From Table 1, among all the object detection methods, the proposed deformable R-FCN, fine-tuned once on the ImageNet dataset, obtains the best mean AP value of 78.4% among all the object detection methods. ArcNMS enhances deformable R-FCN in the detection and pushes the benchmark into 79.1%. After arcNMS was added to deformable R-FCN, the APs among the objects all increased, including airplane (0.861 to 0.873), basketball court (0.724 to 0.741), ground track field (0.898 to 0.903), and harbor (0.722 to 0.753) are all increased. The best mean AP value among all objects was obtained by deformable R-FCN with arcNMS that was fine-tuned on the ResNet-101 ImageNet pre-trained model.

Table 2 shows the average running time of all previous approaches. For object detection in remote sensing, the running time per image of deformable R-FCN was slightly slower than R-FCN and R-P-Faster R-CNN given its additional offsets layers. However, deformable R-FCN’s time cost is generally acceptable compared to traditional methods and AlexNet. Figure 7 displays the recall values of the proposed deformable R-FCN, obtaining an overall recall rate of 87.96%. Compared to R-P-Faster R-CNN R-CNN [16] and RICNN [13], the average recall rate is lower than R-P-Faster R-CNN with the VGG model and RICNN, but higher than R-P-Faster R-CNN with the ZF model. Overall, deformable R-FCN had increased precision in object detection of VHR remote sensing images, especially for geometrically variant objects such as bridges, vehicles, and baseball diamonds. We confirmed that arcNMS also enhances deformable R-FCN. Obviously, a trade-off exists between precision and recall, and the following PRC further explains the problem of evaluating the performance of various CNN structures.

4.2. PRC Evaluation of NWPU VHR-10 Dataset

For object detection approaches, PRC is one of the primary indicators of robustness and effectiveness. In PRCs, the precision vector generated in experiments is measured on the y axis and the recall rates on the x axis. The curve at the top of the PRCs indicates a better performance. In previous papers [5,16], COPD, FDDL, SSCBoW, BoW, and AlexNet are displayed for comparison. Too many curves make the recognition and comparison of established approaches with state-of-the-art CNNs difficult. From Table 1, only R-P-Faster R-CNN, R-FCN and deformable R-FCN have mean AP higher than 0.76. Given its performance, deformable ConvNet was only compared with R-P-Faster R-CNN.

In this paper, we focused on the top three object detection methods outlined in Table 1: deformable R-FCN with arcNMS, deformable R-FCN and R-P-Faster R-CNN trained on VGG16 model in single fine-tuning mode. Figure 8 shows the PRCs of these three methods. Most of the classes in deformable R-FCN had better detection performance than R-P-Faster R-CNN. However, for storage tanks, basketball courts, vehicles and harbors, deformable R-FCN requires improvements. Moreover, arcNMS was proved to be effective in improving the AP value by preventing PRC from decreasing. By jointly analyzing the AP values, the recall rate, and the PRCs, the proposed deformable R-FCN with arcNMS algorithm shows a superior detection performance for VHR remote sensing objects.

4.3. Evaluation on RSOD Dataset

The results of R-P-Faster R-CNN and both deformable and regular R-FCN on RSOD dataset are displayed in

Table 3. The AP (Average Precision) values of the object detection methods on the RSOD (Remote Sensing Object Detection) dataset.

	R-P-Faster R-CNN (Single) (VGG16)	R-FCN (ResNet-101)	Deformable R-FCN (ResNet-101)	Deformable R-FCN (ResNet-101) with arcNMS
Aircraft	0.7084	0.7148	0.7150	0.7187
Oiltank	0.9019	0.9023	0.9026	0.9035
Overpass	0.7874	0.7684	0.8148	0.8959
Playground	0.9809	0.9770	0.9953	0.9988
mean AP	0.8447	0.8407	0.8570	0.8792

. The proposed deformable R-FCN method fine-tuned once on the ImageNet dataset obtained the best mean AP value of 85.70%. ArcNMS enhanced detection of deformable R-FCN, pushing the benchmark into 87.92%. After arcNMS was added to deformable R-FCN, the APs among objects such as Overpasses (0.8148–0.8792) increased considerably. The best mean AP value among all objects, thus, was obtained by deformable R-FCN with arcNMS fine-tuned on the ResNet-101 ImageNet pre-trained model. The performance of our method on another dataset validates its improvement compared to established approaches and reveals its robustness for various remote sensing object detection tasks.

5. Conclusions

In this paper, an end-to-end deformable convolutional neural network structure is presented for modeling geometric variations in VHR remote sensing objects. As standard convolution sampling is substituted by flexible feature mapping with 2D offsets, the CNN is capable of recognizing remote sensing objects with a more complicated visual appearance. We also proposed VHR remote sensing objects transfer mechanism. Deformable ConvNets are more effective when fine-tuned on pre-trained natural image CNN models. Finally, a post-processing arcNMS was developed to delete outlier LFRP and improve precision.

Our workflow was evaluated using the NWPU-VHR-10 dataset. The results show that the proposed deformable R-FCN with arcNMS approach outperforms state-of-the-art benchmarks for object detection. A detailed investigation proved that deformable R-FCN has better performance for geometrically diverse objects such as bridges, harbors and baseball diamonds. Additionally, arcNMS was also proved to enhance deformable ConvNets. Experiments on running time and PRC confirm that deformable ConvNets are efficient and effective. The explanation and visualization of deformable CNN may be researched in future works.