A Digital Twin of the Coaxial Lamination Mixer for the Systematic Study of Mixing Performance and the Prediction of Precipitated Nanoparticle Properties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Digital Geometry of the CLM
2.2. Flow and Mixing Analysis
2.3. Quantification of Progressive Mixing
3. Results and Discussion
3.1. Mesh Convergence Testing
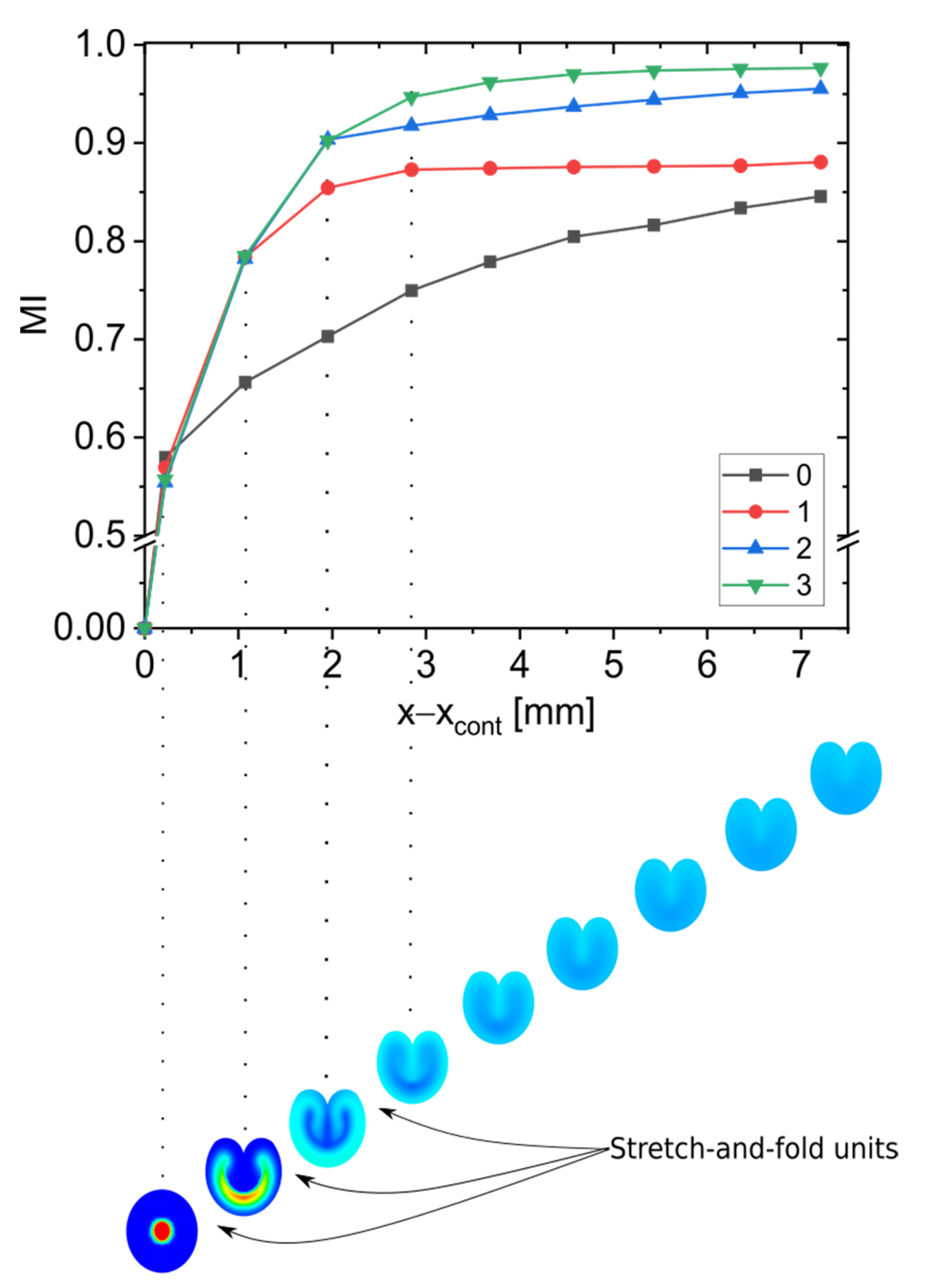
3.2. Effect of Multiple Stretch-and-Fold Units on the Mixing Performance
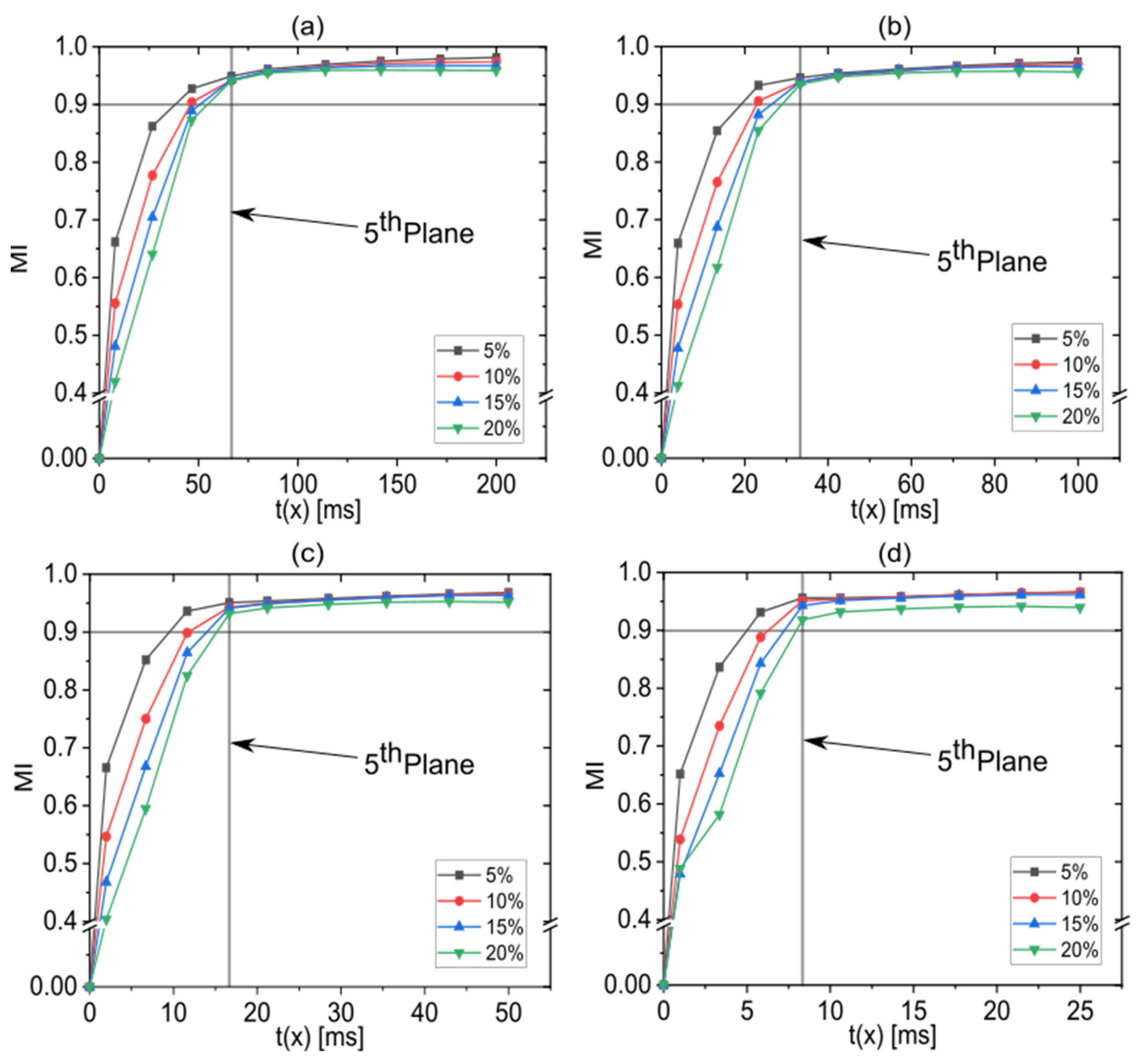
3.3. Effect of the Flow Rate Ratio on the Mixing
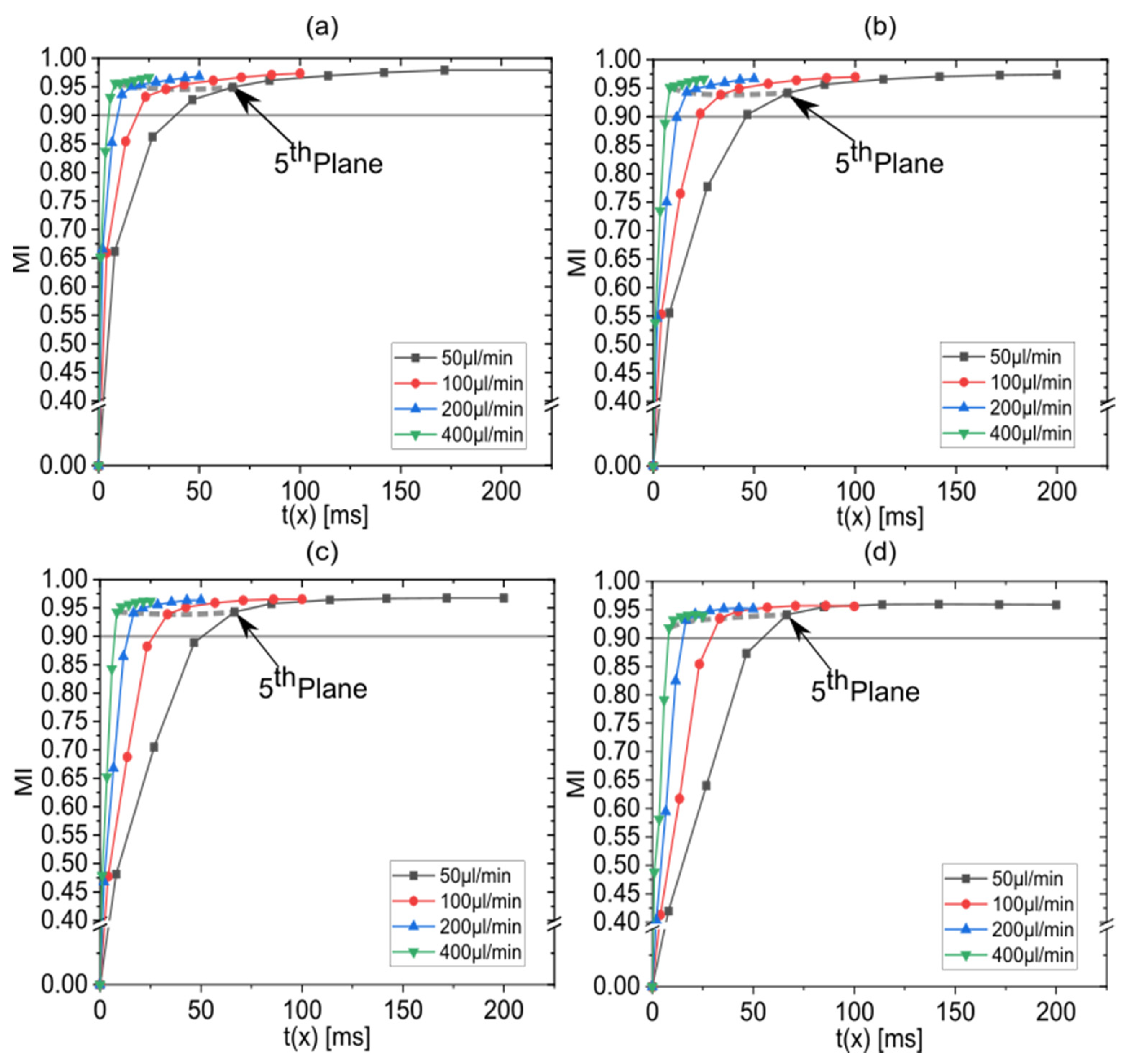
3.4. Effect of the Total Flow Rate on the Mixing Performance
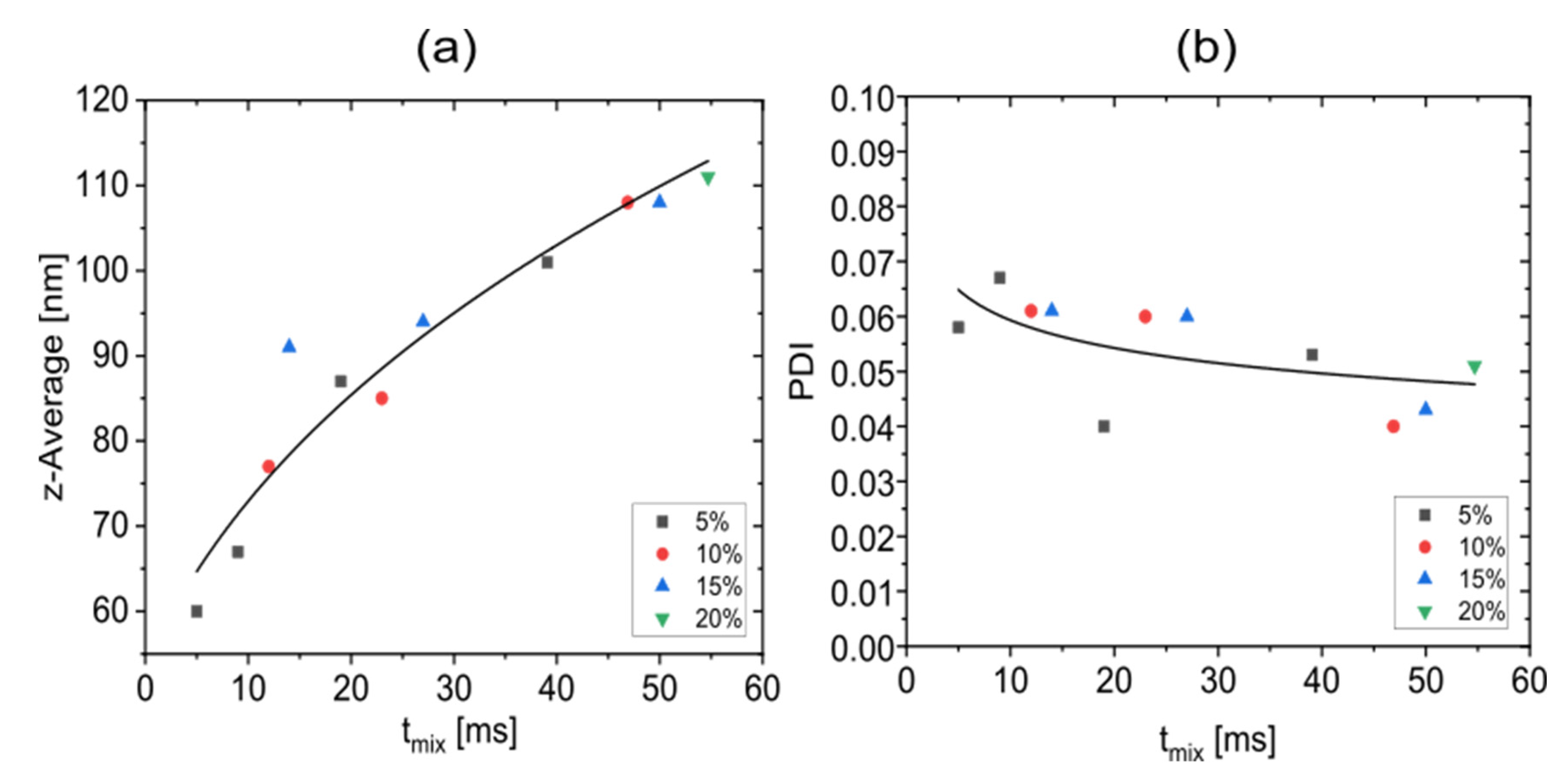
3.5. Correlation between Nanoparticle Properties and the Mixing Time
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cai, G.; Xue, L.; Zhang, H.; Lin, J. A Review on Micromixers. Micromachines 2017, 8, 274. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.-Y.; Chang, C.-L.; Wang, Y.-N.; Fu, L.-M. Microfluidic mixing: A review. Int. J. Mol. Sci. 2011, 12, 3263–3287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bayareh, M.; Ashani, M.N.; Usefian, A. Active and passive micromixers: A comprehensive review. Chem. Eng. Process.-Process Intensif. 2020, 147, 107771. [Google Scholar] [CrossRef]
- Kumar, V.; Paraschivoiu, M.; Nigam, K. Single-phase fluid flow and mixing in microchannels. Chem. Eng. Sci. 2011, 66, 1329–1373. [Google Scholar] [CrossRef]
- Gupta, V.K.; Bhadauria, B.S.; Hasim, I.; Jawdat, J.; Singh, A.K. Chaotic convection in a rotating fluid layer. Alex. Eng. J. 2015, 54, 981–992. [Google Scholar] [CrossRef] [Green Version]
- Jafari, S.; Sprott, J.C.; Molaie, M. A Simple Chaotic Flow with a Plane of Equilibria. Int. J. Bifurc. Chaos 2016, 26, 1650098. [Google Scholar] [CrossRef]
- Lee, K.H.; Yang, G.; Wyslouzil, B.E.; Winter, J.O. Electrohydrodynamic Mixing-Mediated Nanoprecipitation for Polymer Nanoparticle Synthesis. ACS Appl. Polym. Mater. 2019, 1, 691–700. [Google Scholar] [CrossRef]
- Karnik, R.; Gu, F.; Basto, P.; Cannizzaro, C.; Dean, L.; Kyei-Manu, W.; Langer, R.; Farokhzad, O.C. Microfluidic platform for controlled synthesis of polymeric nanoparticles. Nano Lett. 2008, 8, 2906–2912. [Google Scholar] [CrossRef]
- Lu, M.; Ozcelik, A.; Grigsby, C.L.; Zhao, Y.; Guo, F.; Leong, K.W.; Huang, T.J. Microfluidic Hydrodynamic Focusing for Synthesis of Nanomaterials. Nano Today 2016, 11, 778–792. [Google Scholar] [CrossRef]
- Ying, Y.; Chen, G.; Zhao, Y.; Li, S.; Yuan, Q. A high throughput methodology for continuous preparation of monodispersed nanocrystals in microfluidic reactors. Chem. Eng. J. 2008, 135, 209–215. [Google Scholar] [CrossRef]
- Gradl, J.; Schwarzer, H.-C.; Schwertfirm, F.; Manhart, M.; Peukert, W. Precipitation of nanoparticles in a T-mixer: Coupling the particle population dynamics with hydrodynamics through direct numerical simulation. Chem. Eng. Process. Process Intensif. 2006, 45, 908–916. [Google Scholar] [CrossRef]
- Johnson, B.K.; Prud’homme, R.K. Mechanism for rapid self-assembly of block copolymer nanoparticles. Phys. Rev. Lett. 2003, 91, 118302. [Google Scholar] [CrossRef]
- Johnson, B.K.; Prud’homme, R.K. Chemical processing and micromixing in confined impinging jets. AIChE J. 2003, 49, 2264–2282. [Google Scholar] [CrossRef]
- Han, J.; Zhu, Z.; Qian, H.; Wohl, A.R.; Beaman, C.J.; Hoye, T.R.; Macosko, C.W. A simple confined impingement jets mixer for flash nanoprecipitation. J. Pharm. Sci. 2012, 101, 4018–4023. [Google Scholar] [CrossRef]
- Kumar, S.L. Microfluidics Technology for Nanoparticles and Equipment. In Emerging Technologies for Nanoparticle Manufacturing; Springer: Cham, Switzerland, 2021; pp. 67–98. [Google Scholar]
- Hamdallah, S.I.; Zoqlam, R.; Erfle, P.; Blyth, M.; Alkilany, A.M.; Dietzel, A.; Qi, S. Microfluidics for pharmaceutical nanoparticle fabrication: The truth and the myth. Int. J. Pharm. 2020, 584, 119408. [Google Scholar] [CrossRef]
- Maged, A.; Abdelbaset, R.; Mahmoud, A.A.; Elkasabgy, N.A. Merits and advances of microfluidics in the pharmaceutical field: Design technologies and future prospects. Drug Deliv. 2022, 29, 1549–1570. [Google Scholar] [CrossRef]
- Gimondi, S.; Guimarães, C.F.; Vieira, S.F.; Gonçalves, V.M.F.; Tiritan, M.E.; Reis, R.L.; Ferreira, H.; Neves, N.M. Microfluidic mixing system for precise PLGA-PEG nanoparticles size control. Nanomedicine 2022, 40, 102482. [Google Scholar] [CrossRef]
- Belliveau, N.M.; Huft, J.; Lin, P.J.; Chen, S.; Leung, A.K.; Leaver, T.J.; Wild, A.W.; Lee, J.B.; Taylor, R.J.; Tam, Y.K.; et al. Microfluidic Synthesis of Highly Potent Limit-size Lipid Nanoparticles for In Vivo Delivery of siRNA. Mol. Ther.-Nucleic Acids 2012, 1, e37. [Google Scholar] [CrossRef]
- Yun, J.; Zhang, S.; Shen, S.; Chen, Z.; Yao, K.; Chen, J. Continuous production of solid lipid nanoparticles by liquid flow-focusing and gas displacing method in microchannels. Chem. Eng. Sci. 2009, 64, 4115–4122. [Google Scholar] [CrossRef]
- Erfle, P.; Riewe, J.; Bunjes, H.; Dietzel, A. Stabilized Production of Lipid Nanoparticles of Tunable Size in Taylor Flow Glass Devices with High-Surface-Quality 3D Microchannels. Micromachines 2019, 10, 220. [Google Scholar] [CrossRef]
- Lopes, C.; Cristóvão, J.; Silvério, V.; Lino, P.R.; Fonte, P. Microfluidic production of mRNA-loaded lipid nanoparticles for vaccine applications. Expert Opin. Drug Deliv. 2022, 19, 1381–1395. [Google Scholar] [CrossRef] [PubMed]
- Maeki, M.; Uno, S.; Niwa, A.; Okada, Y.; Tokeshi, M. Microfluidic technologies and devices for lipid nanoparticle-based RNA delivery. J. Control. Release 2022, 344, 80–96. [Google Scholar] [CrossRef] [PubMed]
- Ali, H.S.M.; York, P.; Blagden, N. Preparation of hydrocortisone nanosuspension through a bottom-up nanoprecipitation technique using microfluidic reactors. Int. J. Pharm. 2009, 375, 107–113. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Wang, J.-X.; Wang, Q.-A.; Chen, J.-F.; Yun, J. Controlled Liquid Antisolvent Precipitation of Hydrophobic Pharmaceutical Nanoparticles in a Microchannel Reactor. Ind. Eng. Chem. Res. 2007, 46, 8229–8235. [Google Scholar] [CrossRef]
- Dev, S.; Prabhakaran, P.; Filgueira, L.; Iyer, K.S.; Raston, C.L. Microfluidic fabrication of cationic curcumin nanoparticles as an anti-cancer agent. Nanoscale 2012, 4, 2575–2579. [Google Scholar] [CrossRef]
- Haberkorn, H.; Franke, D.; Frechen, T.; Goesele, W.; Rieger, J. Early stages of particle formation in precipitation reactions—Quinacridone and boehmite as generic examples. J. Colloid Interface Sci. 2003, 259, 112–126. [Google Scholar] [CrossRef]
- Lorenz, T.; Bojko, S.; Bunjes, H.; Dietzel, A. An inert 3D emulsification device for individual precipitation and concentration of amorphous drug nanoparticles. Lab Chip 2018, 18, 627–638. [Google Scholar] [CrossRef]
- Jahn, A.; Lucas, F.; Wepf, R.A.; Dittrich, P.S. Freezing continuous-flow self-assembly in a microfluidic device: Toward imaging of liposome formation. Langmuir 2013, 29, 1717–1723. [Google Scholar] [CrossRef]
- Jahn, A.; Reiner, J.E.; Vreeland, W.N.; DeVoe, D.L.; Locascio, L.E.; Gaitan, M. Preparation of nanoparticles by continuous-flow microfluidics. J. Nanopart. Res. 2008, 10, 925–934. [Google Scholar] [CrossRef]
- Jahn, A.; Vreeland, W.N.; Gaitan, M.; Locascio, L.E. Controlled vesicle self-assembly in microfluidic channels with hydrodynamic focusing. J. Am. Chem. Soc. 2004, 126, 2674–2675. [Google Scholar] [CrossRef]
- Jahn, A.; Stavis, S.M.; Hong, J.S.; Vreeland, W.N.; DeVoe, D.L.; Gaitan, M. Microfluidic mixing and the formation of nanoscale lipid vesicles. ACS Nano 2010, 4, 2077–2087. [Google Scholar] [CrossRef]
- Othman, R.; Vladisavljević, G.T.; Hemaka Bandulasena, H.C.; Nagy, Z.K. Production of polymeric nanoparticles by micromixing in a co-flow microfluidic glass capillary device. Chem. Eng. J. 2015, 280, 316–329. [Google Scholar] [CrossRef] [Green Version]
- Erfle, P.; Riewe, J.; Bunjes, H.; Dietzel, A. Goodbye fouling: A unique coaxial lamination mixer (CLM) enabled by two-photon polymerization for the stable production of monodisperse drug carrier nanoparticles. Lab Chip 2021, 21, 2178–2193. [Google Scholar] [CrossRef]
- Ottino, J.M. The Kinematics of Mixing: Stretching, Chaos, and Transport; Reprinted; Cambridge University Press: Cambridge, UK, 1997; ISBN 0521363357. [Google Scholar]
- Fan, Y.; Hassan, I. The Numerical Simulation of a Passive Interdigital Micromixer With Uneven Lamellar Width. In Proceedings of the 7th International Conference on Nanochannels, Microchannels and Minichannels—2009, Pohang, Republic of Korea, 22–24 June 2009; ASME: New York, NY, USA, 2009; pp. 813–819. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; Wiley: New York, NY, USA, 2007; ISBN 0470115394. [Google Scholar]
- Sahu, K.C.; Ding, H.; Valluri, P.; Matar, O.K. Linear stability analysis and numerical simulation of miscible two-layer channel flow. Phys. Fluids 2009, 21, 42104. [Google Scholar] [CrossRef] [Green Version]
- Minakov, A.V.; Rudyak, V.Y.; Gavrilov, A.A.; Dekterev, A.A. Mixing in a T-shaped micromixer at moderate Reynolds numbers. Thermophys. Aeromech. 2012, 19, 385–395. [Google Scholar] [CrossRef]
- Van Doormaal, J.P.; Raithby, G.D. Enhancements of the simple method for predicting incompressible fluid flows. Numer. Heat Transf. 1984, 7, 147–163. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 2018; ISBN 9781315275130. [Google Scholar]
- Van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Hossain, S.; Husain, A.; Kim, K.-Y. Optimization of Micromixer with Staggered Herringbone Grooves on Top and Bottom Walls. Eng. Appl. Comput. Fluid Mech. 2011, 5, 506–516. [Google Scholar] [CrossRef] [Green Version]
- Rafeie, M.; Welleweerd, M.; Hassanzadeh-Barforoushi, A.; Asadnia, M.; Olthuis, W.; Ebrahimi Warkiani, M. An easily fabricated three-dimensional threaded lemniscate-shaped micromixer for a wide range of flow rates. Biomicrofluidics 2017, 11, 14108. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.J.; Chen, C.H.; Shie, S.R. Optimal designs of staggered dean vortex micromixers. Int. J. Mol. Sci. 2011, 12, 3500–3524. [Google Scholar] [CrossRef]
- Bayareh, M. Artificial diffusion in the simulation of micromixers: A review. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 5288–5296. [Google Scholar] [CrossRef]
- Noll, B. Numerische Strömungsmechanik: Grundlagen; Springer: Berlin/Heidelberg, Germany, 1993; ISBN 9783642849602. [Google Scholar]
- Fletcher, C.A.J. Computational Techniques for Fluid Dynamics 2: Specific Techniques for Different Flow Categories, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1991; ISBN 9783642582394. [Google Scholar]
- Virag, Z.; Trincas, G. An improvement of the exponential differencing scheme for solving the convection-diffusion equation. Adv. Eng. Softw. 1994, 19, 1–20. [Google Scholar] [CrossRef]
- Barz, D.P.J.; Zadeh, H.F.; Ehrhard, P. Laminar flow and mass transport in a twice–folded microchannel. AIChE J. 2008, 54, 381–393. [Google Scholar] [CrossRef]
- Schönfeld, F.; Hardt, S. Simulation of helical flows in microchannels. AIChE J. 2004, 50, 771–778. [Google Scholar] [CrossRef]
- Adrover, A.; Cerbelli, S.; Giona, M. A spectral approach to reaction/diffusion kinetics in chaotic flows. Comput. Chem. Eng. 2002, 26, 125–139. [Google Scholar] [CrossRef]
- Hardt, S.; Schönfeld, F. Laminar mixing in different interdigital micromixers: II. Numerical simulations. AIChE J. 2003, 49, 578–584. [Google Scholar] [CrossRef]
- Dietzel, A. Microsystems for Pharmatechnology: Manipulation of Fluids, Particles, Droplets, and Cells; Springer: Cham, Switzerland, 2016; ISBN 9783319269207. [Google Scholar]
- Layek, A.; Mishra, G.; Sharma, A.; Spasova, M.; Dhar, S.; Chowdhury, A.; Bandyopadhyaya, R. A Generalized Three-Stage Mechanism of ZnO Nanoparticle Formation in Homogeneous Liquid Medium. J. Phys. Chem. C 2012, 116, 24757–24769. [Google Scholar] [CrossRef]
- Burke, J.E.; Turnbull, D. Recrystallization and grain growth. Prog. Met. Phys. 1952, 3, 220–292. [Google Scholar] [CrossRef]
- Erfle, P.; Riewe, J.; Cai, S.; Bunjes, H.; Dietzel, A. Horseshoe lamination mixer (HLM) sets new standards in the production of monodisperse lipid nanoparticles. Lab Chip 2022, 22, 3025–3044. [Google Scholar] [CrossRef]


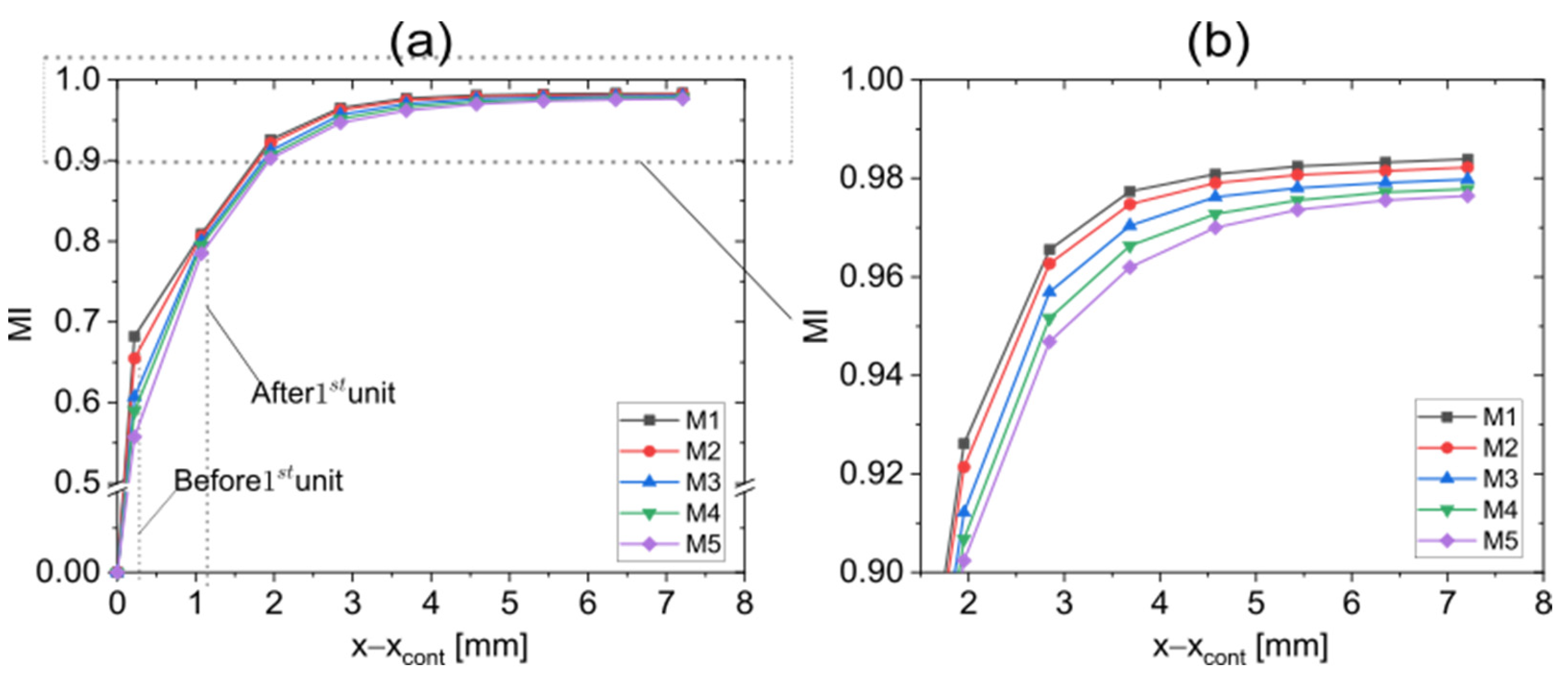



| Fluid | Density [kg m−3] | Viscosity [kg m−1s−1] | Diffusivity [m−2s−1] |
|---|---|---|---|
| Water | 9.998 × 102 | 0.9 × 10−3 | 1.2 × 10−9 |
| Ethanol | 7.890 × 102 | 1.2 × 10−3 | 1.2 × 10−9 |
| Meshing Level | |||
|---|---|---|---|
| M1 | 5 | 46 | 644 |
| M2 | 4.2 | 38 | 541 |
| M3 | 3.4 | 31 | 438 |
| M4 | 2.6 | 23 | 335 |
| M5 | 2.2 | 20 | 283 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, S.; Erfle, P.; Dietzel, A. A Digital Twin of the Coaxial Lamination Mixer for the Systematic Study of Mixing Performance and the Prediction of Precipitated Nanoparticle Properties. Micromachines 2022, 13, 2076. https://doi.org/10.3390/mi13122076
Cai S, Erfle P, Dietzel A. A Digital Twin of the Coaxial Lamination Mixer for the Systematic Study of Mixing Performance and the Prediction of Precipitated Nanoparticle Properties. Micromachines. 2022; 13(12):2076. https://doi.org/10.3390/mi13122076
Chicago/Turabian StyleCai, Songtao, Peer Erfle, and Andreas Dietzel. 2022. "A Digital Twin of the Coaxial Lamination Mixer for the Systematic Study of Mixing Performance and the Prediction of Precipitated Nanoparticle Properties" Micromachines 13, no. 12: 2076. https://doi.org/10.3390/mi13122076






