Miniaturized Band Pass Filter Design Using Half Mode Substrate Integrated Coaxial Resonators
Abstract
:1. Introduction
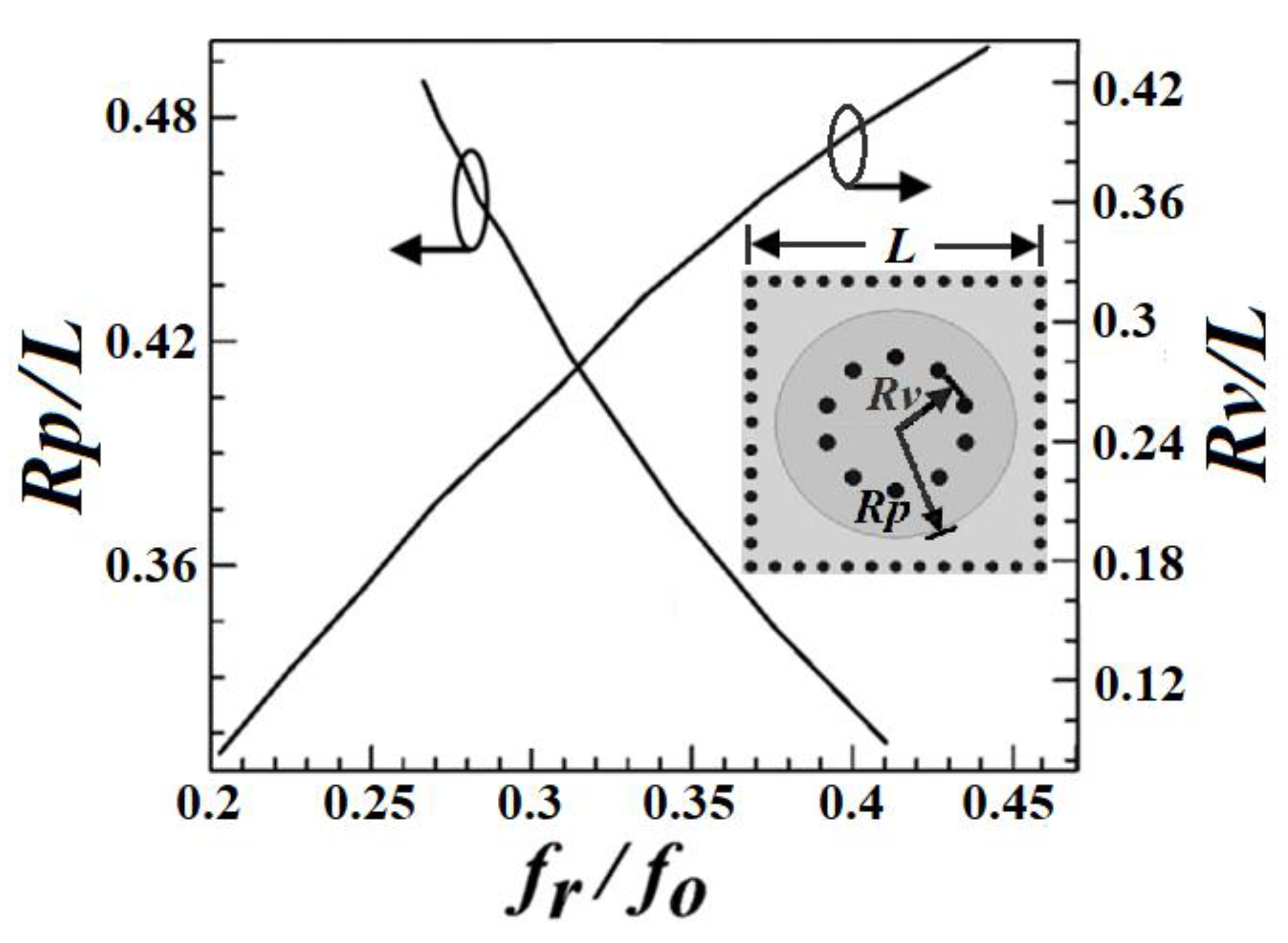
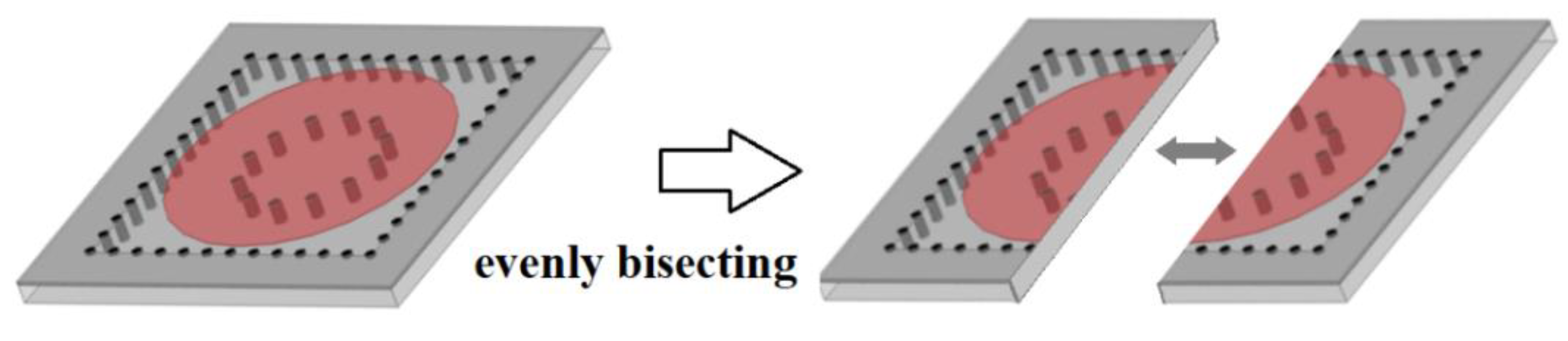
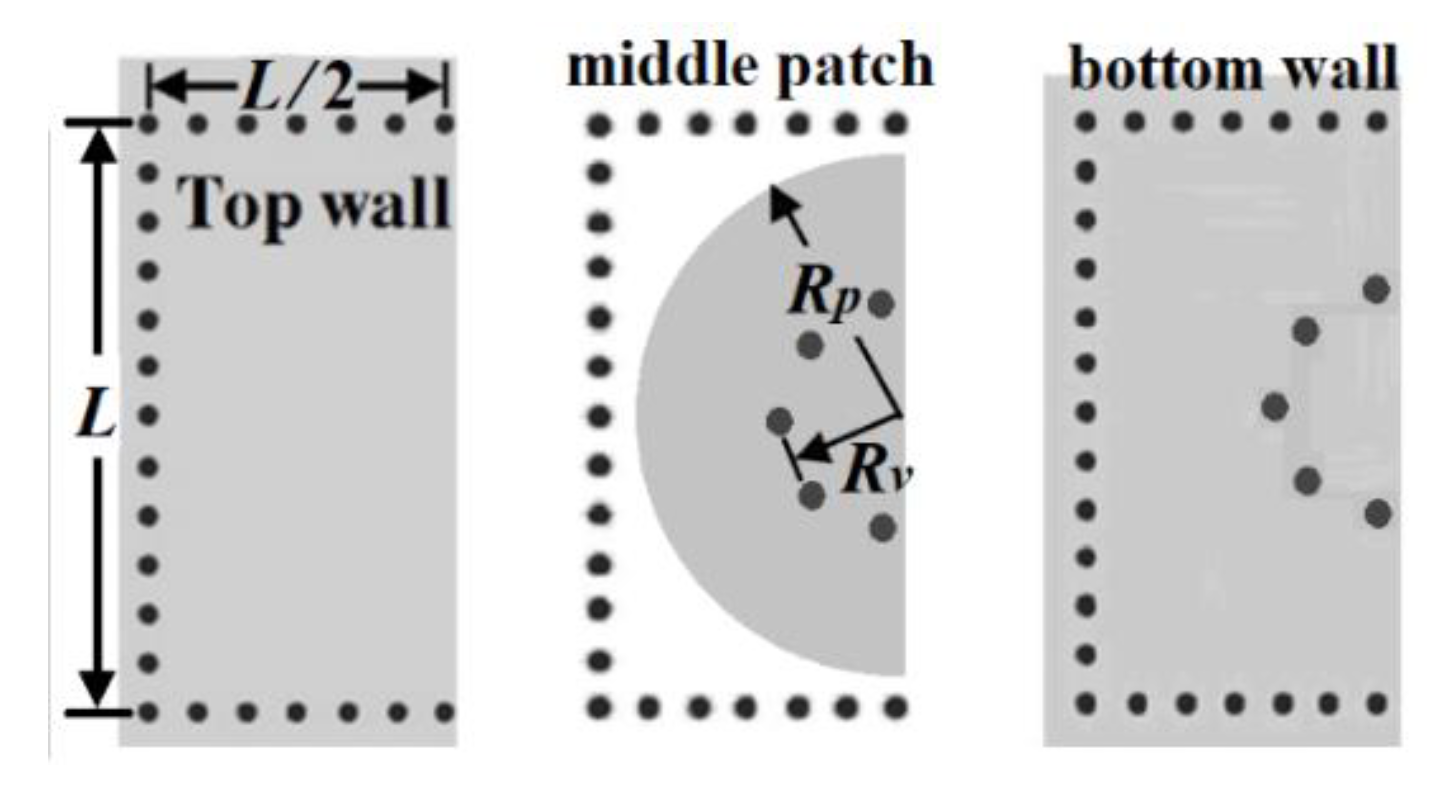
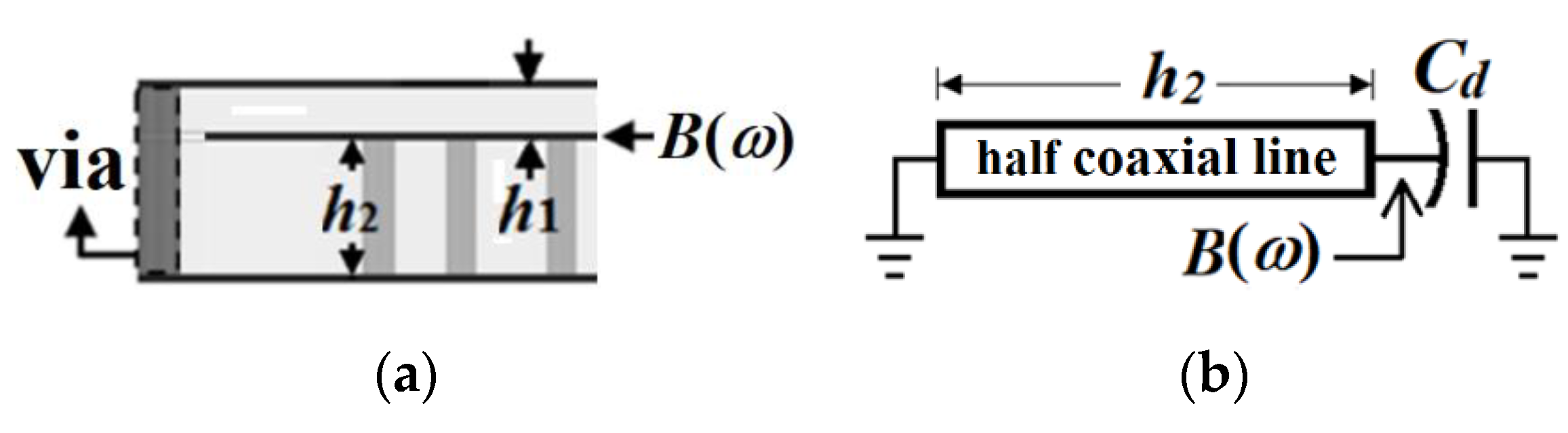
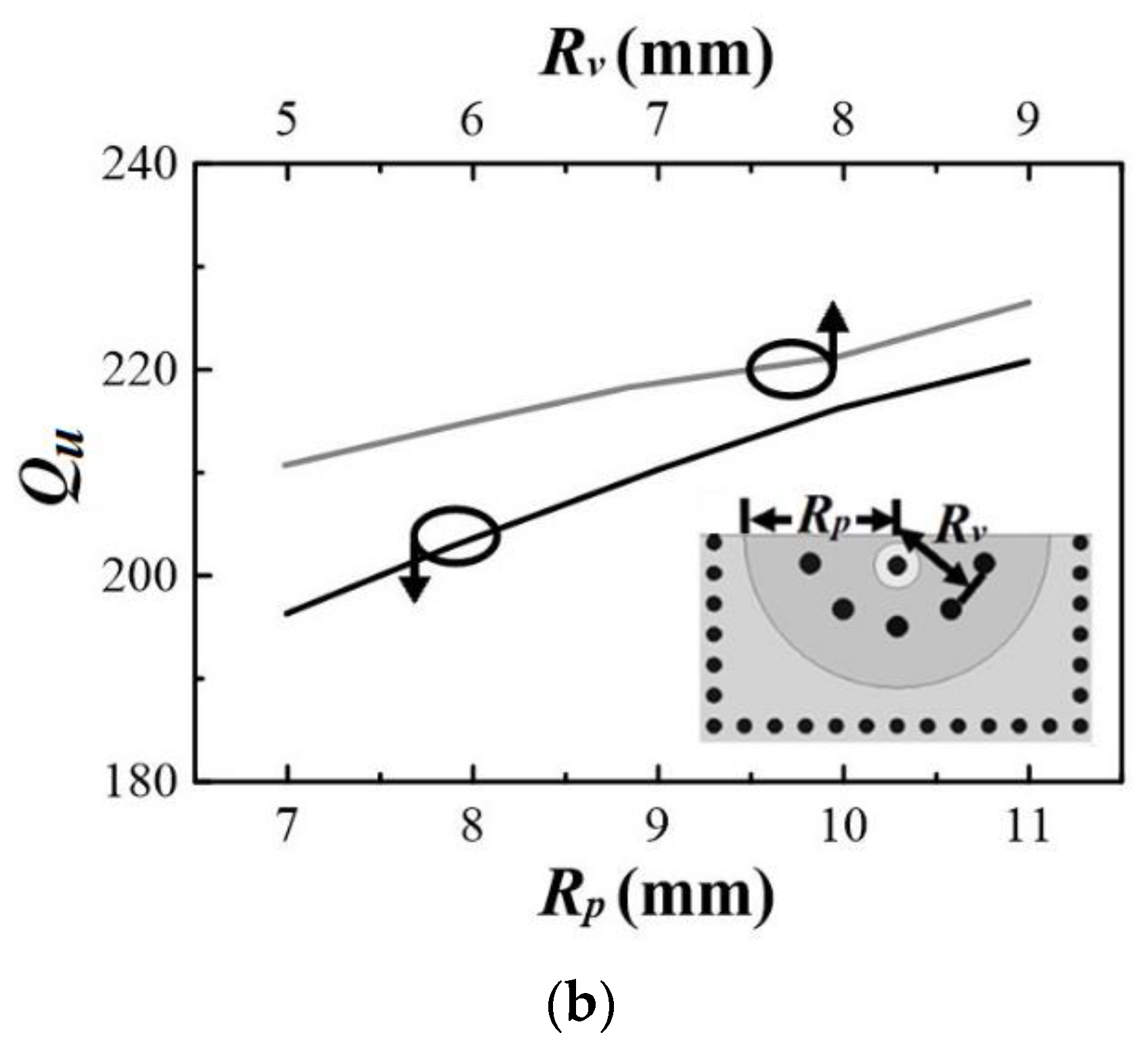
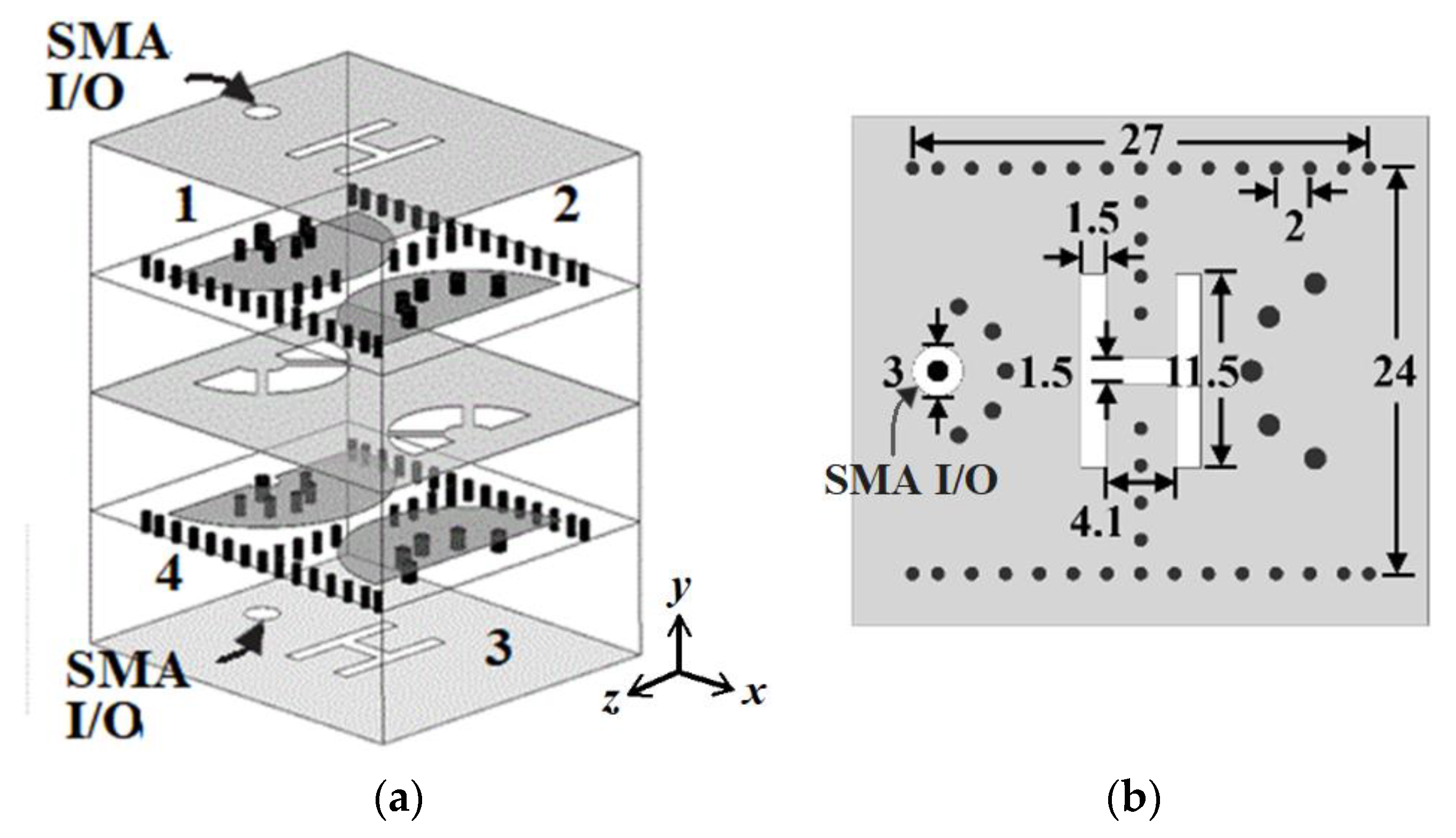
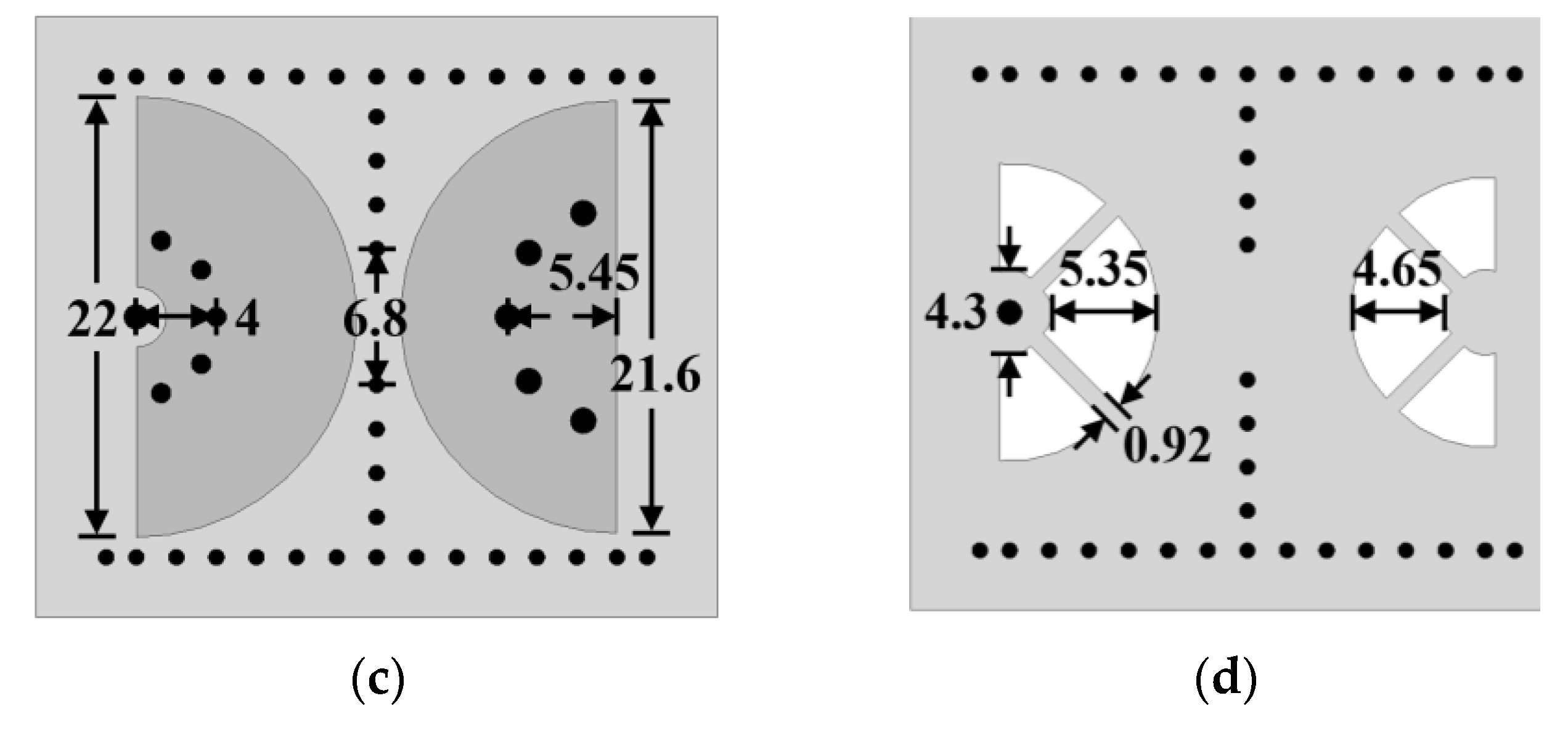
2. Half-Mode Substrate Integrated Coaxial Resonator
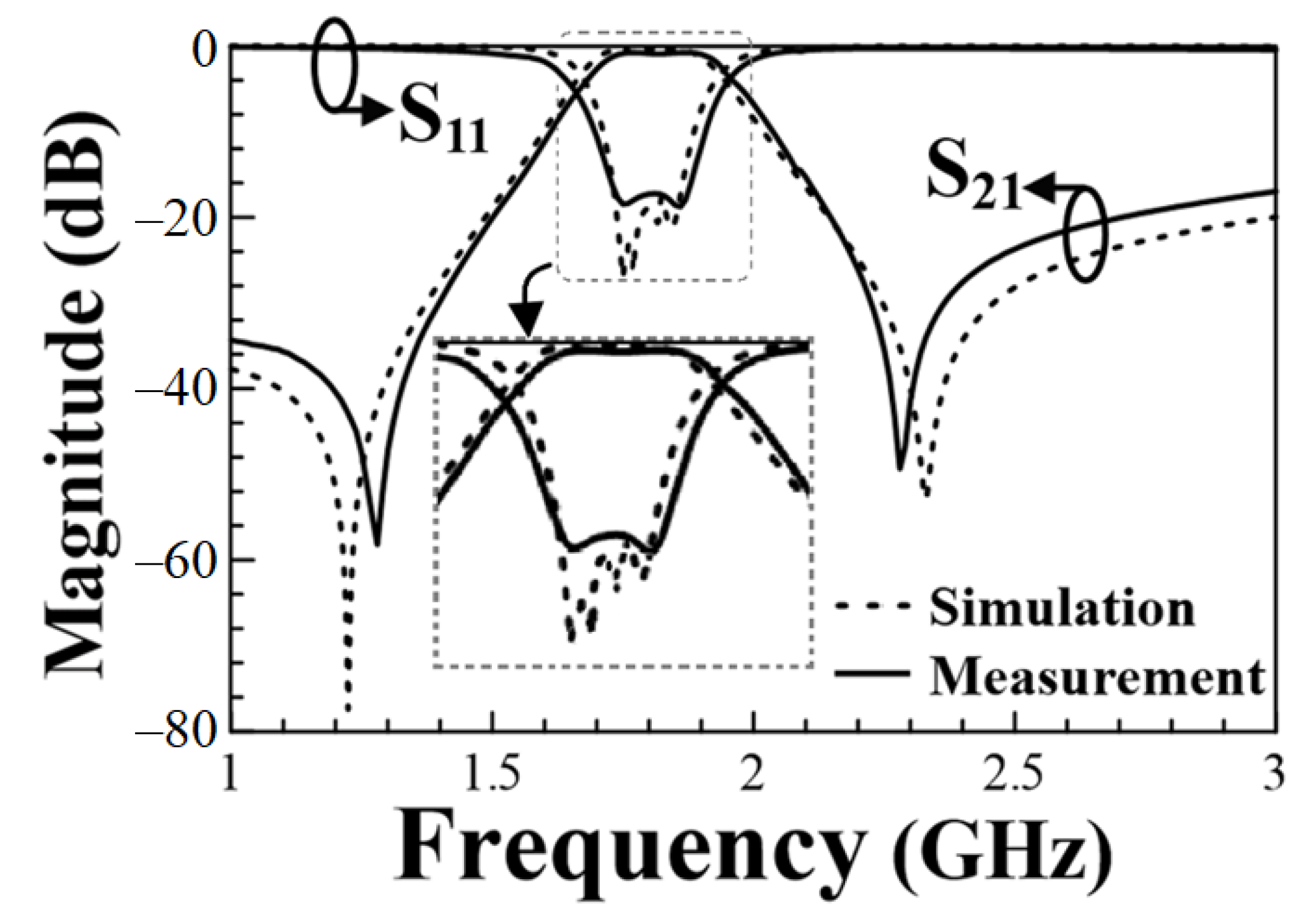
3. Sample Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marcuvitz, N. Waveguide Handbook; Peter Peregrinus Ltd.: London, UK, 1993. [Google Scholar]
- Piloto, A.; Leahy, K.; Flanick, B.; Zaki, K.A. Waveguide Filters Having a Layered Dielectric Structure. U.S. Patent 5,382,931, 17 January 1995. [Google Scholar]
- Hirokawa, J.; Ando, M. Single-layer feed waveguide consisting of posts for plane TEM wave excitation in parallel plates. IEEE Trans. Ant. Propagat. 1998, 46, 625–630. [Google Scholar] [CrossRef]
- Uchimura, H.; Takenoshita, T.; Fujii, M. Development of the “laminated waveguide”. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, Baltimore, MD, USA, 7–12 June 1998; pp. 2438–2443. [Google Scholar]
- Deslands, D.; Wu, K. Single-substrate integration technique of planar circuits and waveguide filters. IEEE Trans. Microw. Theory Tech. 2003, 51, 593–596. [Google Scholar] [CrossRef]
- Dong, Y.D.; Yang, T.; Itoh, T. Substrate integrated waveguide loaded by complementary split-ring resonators and its applications to miniaturized waveguide filters. IEEE Trans. Microw. Theory Tech. 2009, 57, 2211–2223. [Google Scholar] [CrossRef]
- Zhang, Q.-L.; Yin, W.-Y.; He, S.; Wu, L.-S. Compact substrate integrated waveguide (SIW) bandpass filter with complementary split-ring resonators (CSRRs). IEEE Microw. Wireless Compon. Lett. 2010, 20, 426–428. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, W.; Dong, Y.; Liu, B.; Tang, H.J.; Chen, J.; Yin, X.; Wu, K. Half mode substrate integrated waveguide (HMSIW) bandpass filter. IEEE Microw. Wireless Compon. Lett. 2007, 17, 265–267. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, N.; Wu, K.K. 5-GHz bandpass filter demonstration using quarter-mode substrate integrated waveguide cavity for wireless system. In Proceedings of the IEEE Radio and Wireless Symposium, San Diego, CA, USA, 18–22 January 2009; pp. 95–98. [Google Scholar]
- Jin, C.; Shen, Z. Compact triple-mode filter based on quarter-mode substrate integrated waveguide. IEEE Trans. Microw. Theory Tech. 2014, 62, 37–45. [Google Scholar] [CrossRef]
- Martínez, J.D.; Sirci, S.; Taroncher, M.; Boria, V.E. Compact CPW-fed combline filter in substrate integrated waveguide technology. IEEE Microw. Wireless Compon. Lett. 2012, 22, 7–9. [Google Scholar] [CrossRef] [Green Version]
- Yang, T.; Ho, K.; Rebeiz, G.M. Compact self-shielded 2–3 GHz high-Q coaxial fixed and tunable filters. IEEE Trans. Microw. Theory Tech. 2014, 62, 3370–3379. [Google Scholar] [CrossRef]
- Ho, M.-H.; Li, J.-C.; Chen, Y.-C. Miniaturized SIW cavity resonator and its application in filter design. IEEE Microw. Wireless Compon. Lett. 2018, 28, 651–653. [Google Scholar] [CrossRef]
- Saghati, A.P.; Saghati, A.P.; Entesari, K. Ultra-miniature SIW cavity resonators and filters. IEEE Trans. Microw. Theory Tech. 2015, 63, 4329–4340. [Google Scholar] [CrossRef]
- Li, M.; Chen, C.; Chen, W. Miniaturized dual-band filter using dual-capacitively loaded SIW cavities. IEEE Microw. Wireless Compon. Lett. 2017, 27, 344–346. [Google Scholar] [CrossRef]
- High Frequency Structure Simulator (HFSS), version 21.0; ANSYS Inc.: Canonsburg, PA, USA, 2021.
- Chang, C.-Y.; Hsu, W.-C. Novel planar, square-shaped, dielectric-waveguide, single-, and dual-mode filters. IEEE Trans. Microw. Theory Tech. 2002, 50, 2527–2536. [Google Scholar] [CrossRef]
- Chen, X.-P.; Wu, K. Substrate integrated waveguide cross-coupled filter with negative coupling structure. IEEE Trans. Microw. Theory Tech. 2013, 61, 125130–125149. [Google Scholar] [CrossRef]
- Potelon, B.; Favennec, J.; Quendo, C.; Rius, E.; Person, C.; Bohorquez, J. Design of a substrate integrated waveguide (SIW) filter using a novel topology of coupling. IEEE Microw. Wirel. Compon. Lett. 2008, 18, 596–598. [Google Scholar] [CrossRef]
- You, C.J.; Chen, Z.N.; Zhu, X.W.; Gong, K. Single-layered SIW post-loaded electric coupling-enhanced structure and its filter applications. IEEE Tran. Microw. Theory Tech. 2013, 61, 125–130. [Google Scholar] [CrossRef]
- Shen, Y.-L.; Hung, J.-T.; Ho, M.-H.; Hsu, C.-I.G. Miniaturized substrate integrated waveguide cavities in dual-band filter and diplexer design. IET Microw. Ant. Propagat. 2020, 14, 428–434. [Google Scholar] [CrossRef]
- Ho, M.-H.; Tang, K.-H. Miniaturized SIW cavity tri-band filter design. IEEE Microw. Wireless Compon. Lett. 2020, 30, 589–592. [Google Scholar] [CrossRef]
- Hong, J.-S.; Lancaster, M.J. Microstrip Filters for RF/Microwave Applications; Chapters 10 & 11; John Wiley & Sons Inc.: New York, NY, USA, 2001. [Google Scholar]
- Kurzok, R.M. General four-resonator filters at microwave frequencies. IEEE Trans. Microw. Theory Tech. 1966, 14, 295–296. [Google Scholar] [CrossRef]
- Levy, R. Direct synthesis of cascaded quadruplet (CQ) filters. IEEE Trans. Microw. Theory Tech. 1995, 43, 2940–2944. [Google Scholar] [CrossRef]
- Hong, J.-S.; Lancaster, M.J. Compact microwave elliptic function filter using novel microstrip meander open-loop resonators. Electron. Lett. 1996, 32, 563–564. [Google Scholar] [CrossRef]





| fc (GHz) | FBW (%) | IL (dB) | Circuit Order | Circuit Size (λd × λd) | USB BW (S21 ≤ –20 dB) | |
|---|---|---|---|---|---|---|
| [7] Figure 6 | 3.52 | 6.25 | 1.45 | 4 | 0.45 × 0.79 | |
| [8] Figure 2b | 8.79 | 40 | 1.2 | 5 | 1.15 × 0.33 | |
| [10] Figure 12 | 5.2 | 38 | 0.74 | 3 | 0.99 × 0.99 | |
| [12] Figure 6 | 3.58 | 6.5 | 1.7 | 3 | 0.35 × 0.47 | ~1.28 fc |
| [13] Figure 4 | 1.658 | 9.1 | 1.56 | 4 | 0.41 × 0.41 | 6.17 fc |
| [13] Figure 6 | 1.04 | 4.6 | 1.84 | 4 | 0.26 × 0.26 | 3 fc |
| This work | 1.81 | 14.8 | 0.6 | 4 | 0.24 × 0.22 | 0.4 fc |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ho, M.-H.; Hsu, C.-I.G.; Tang, K.-H.; Hong, W. Miniaturized Band Pass Filter Design Using Half Mode Substrate Integrated Coaxial Resonators. Micromachines 2022, 13, 389. https://doi.org/10.3390/mi13030389
Ho M-H, Hsu C-IG, Tang K-H, Hong W. Miniaturized Band Pass Filter Design Using Half Mode Substrate Integrated Coaxial Resonators. Micromachines. 2022; 13(3):389. https://doi.org/10.3390/mi13030389
Chicago/Turabian StyleHo, Min-Hua, Chung-I G. Hsu, Kun-Hua Tang, and Wanchu Hong. 2022. "Miniaturized Band Pass Filter Design Using Half Mode Substrate Integrated Coaxial Resonators" Micromachines 13, no. 3: 389. https://doi.org/10.3390/mi13030389






