A Novel Remote-Controlled Vascular Interventional Robotic System Based on Hollow Ultrasonic Motor
Abstract
:1. Introduction
2. System Design
2.1. Working Principle of RVIR
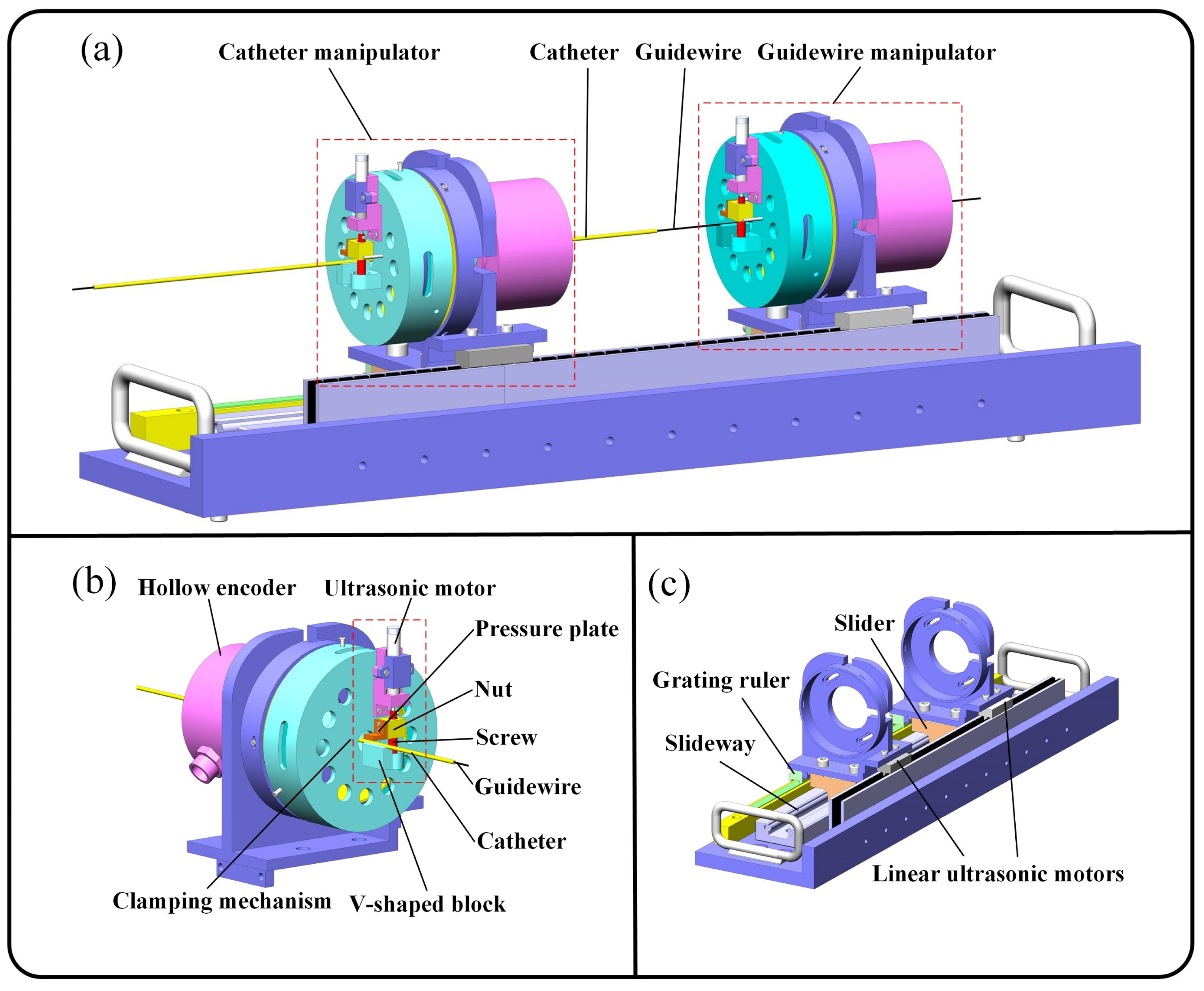
2.2. Slave Robot Design
2.3. Master Robot Design
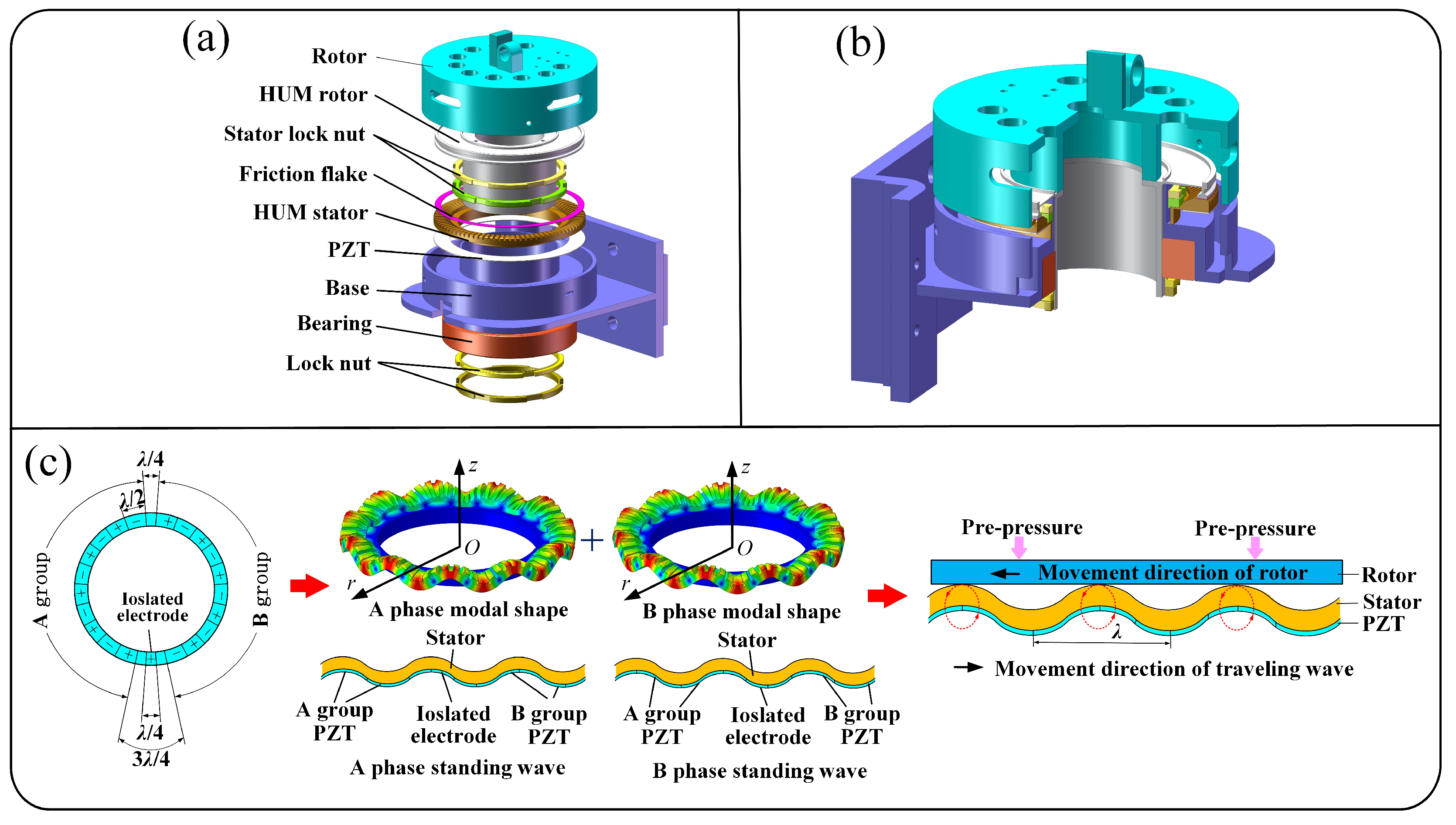
3. Design and Optimization of the HUM
3.1. The Structure and Motion Mechanism of the HUM
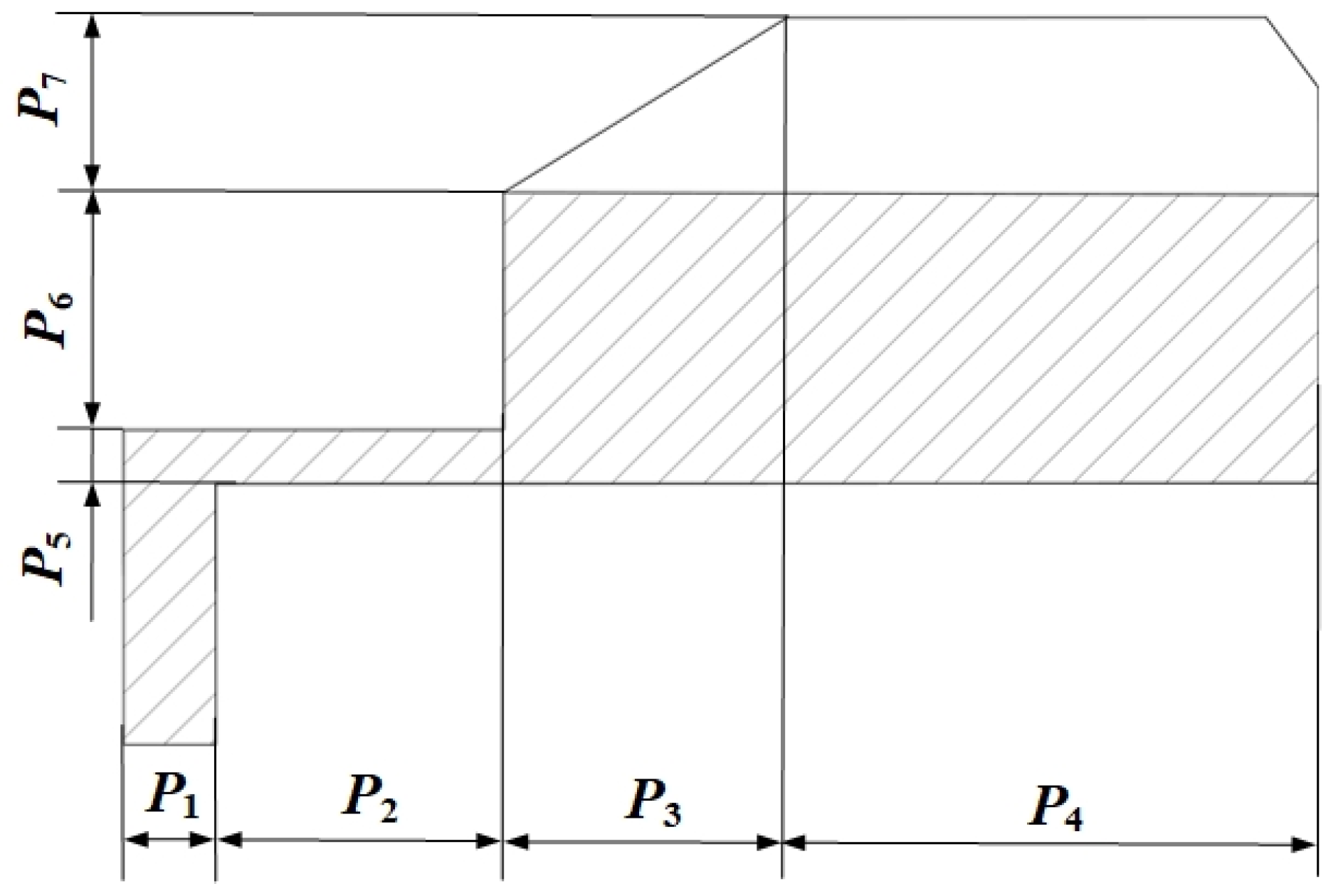
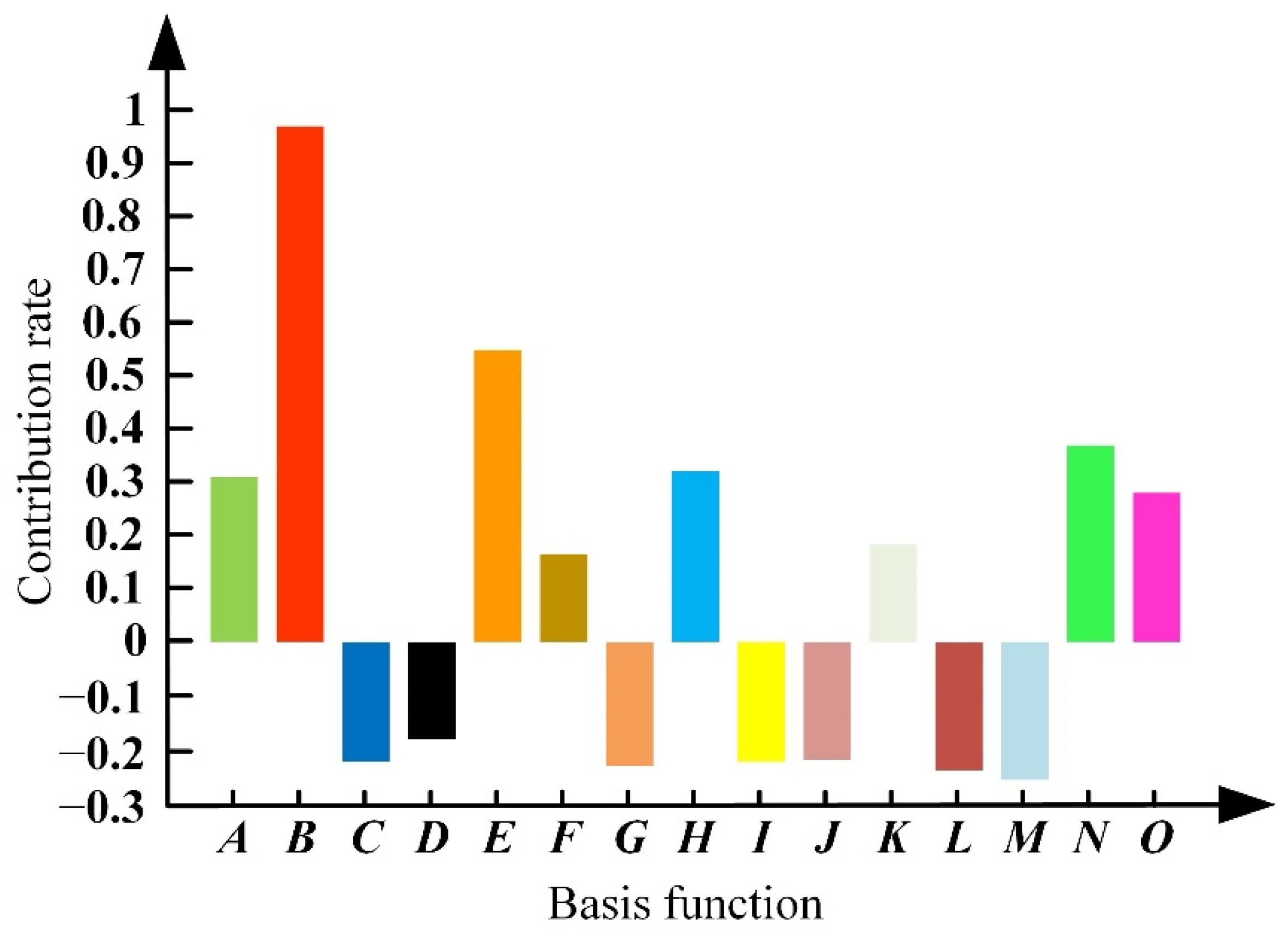
3.2. Optimization of the HUM
4. Experimental Performance Evaluation
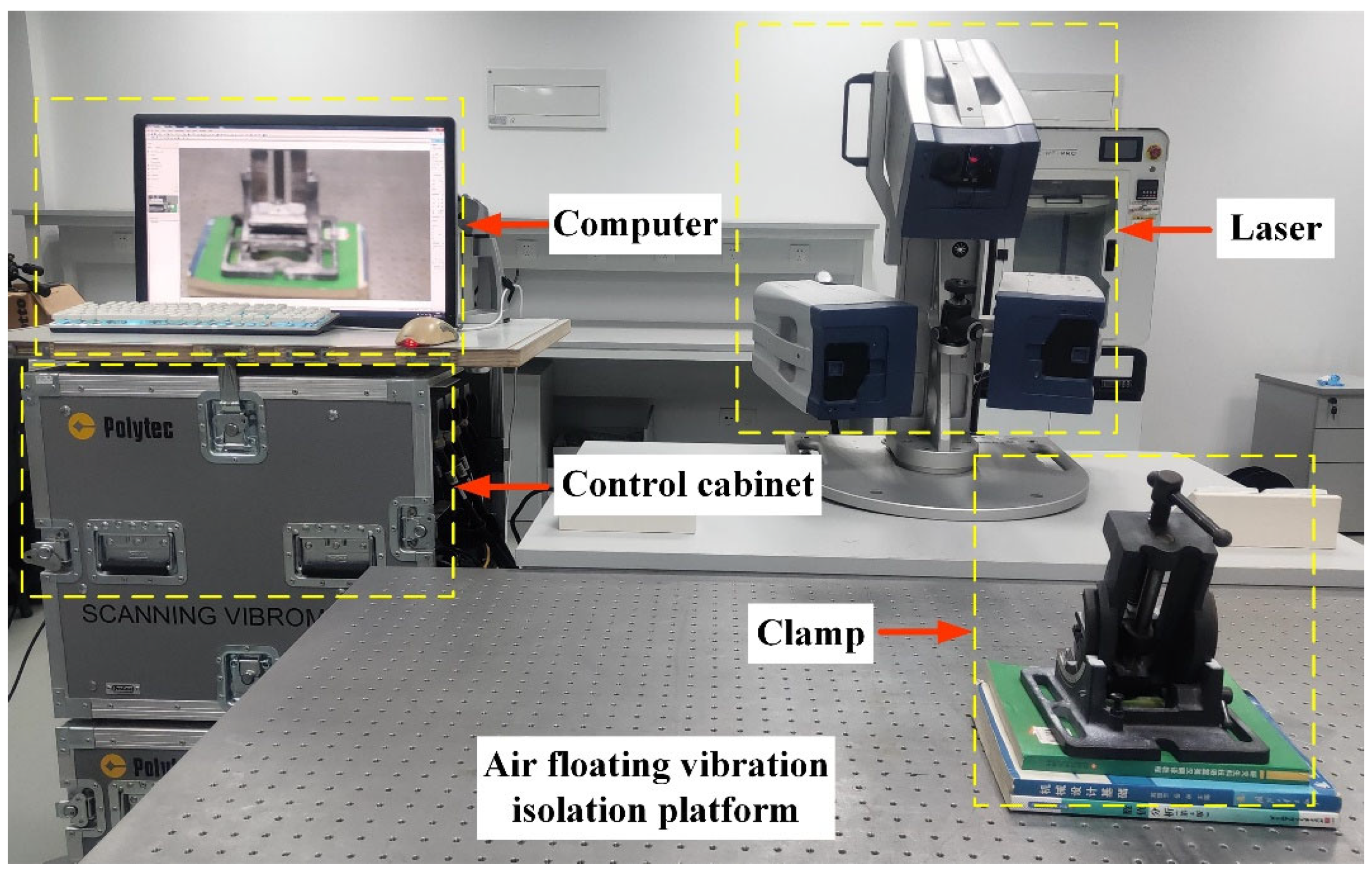
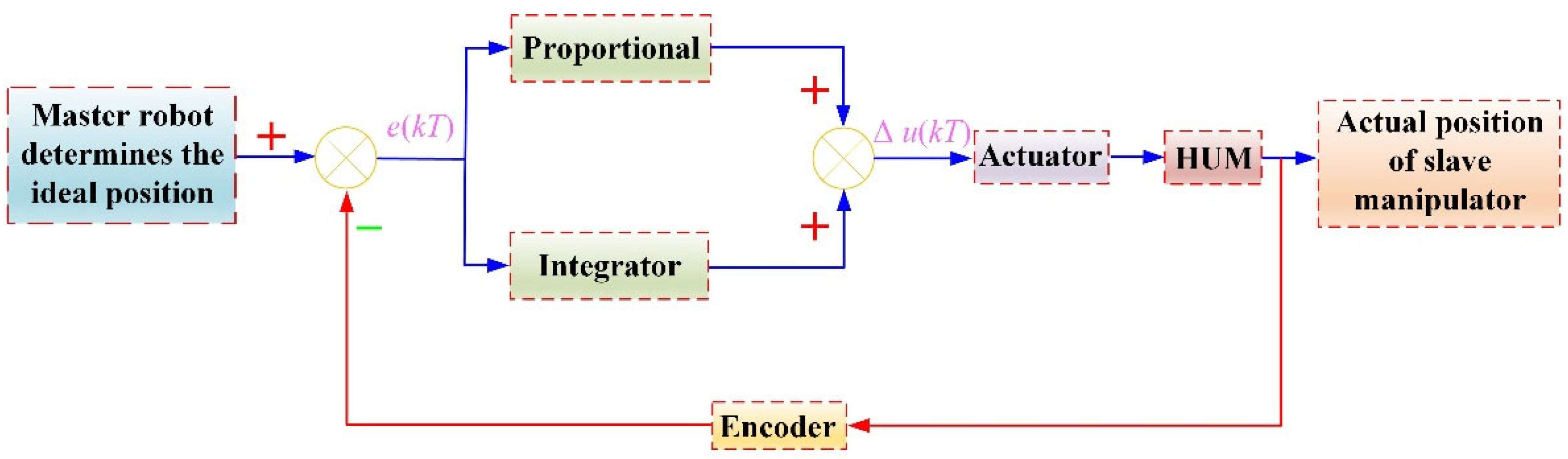
4.1. Experimental Platform and Control Algorithm
4.2. Slave Robot Driving Accuracy Test Experiment
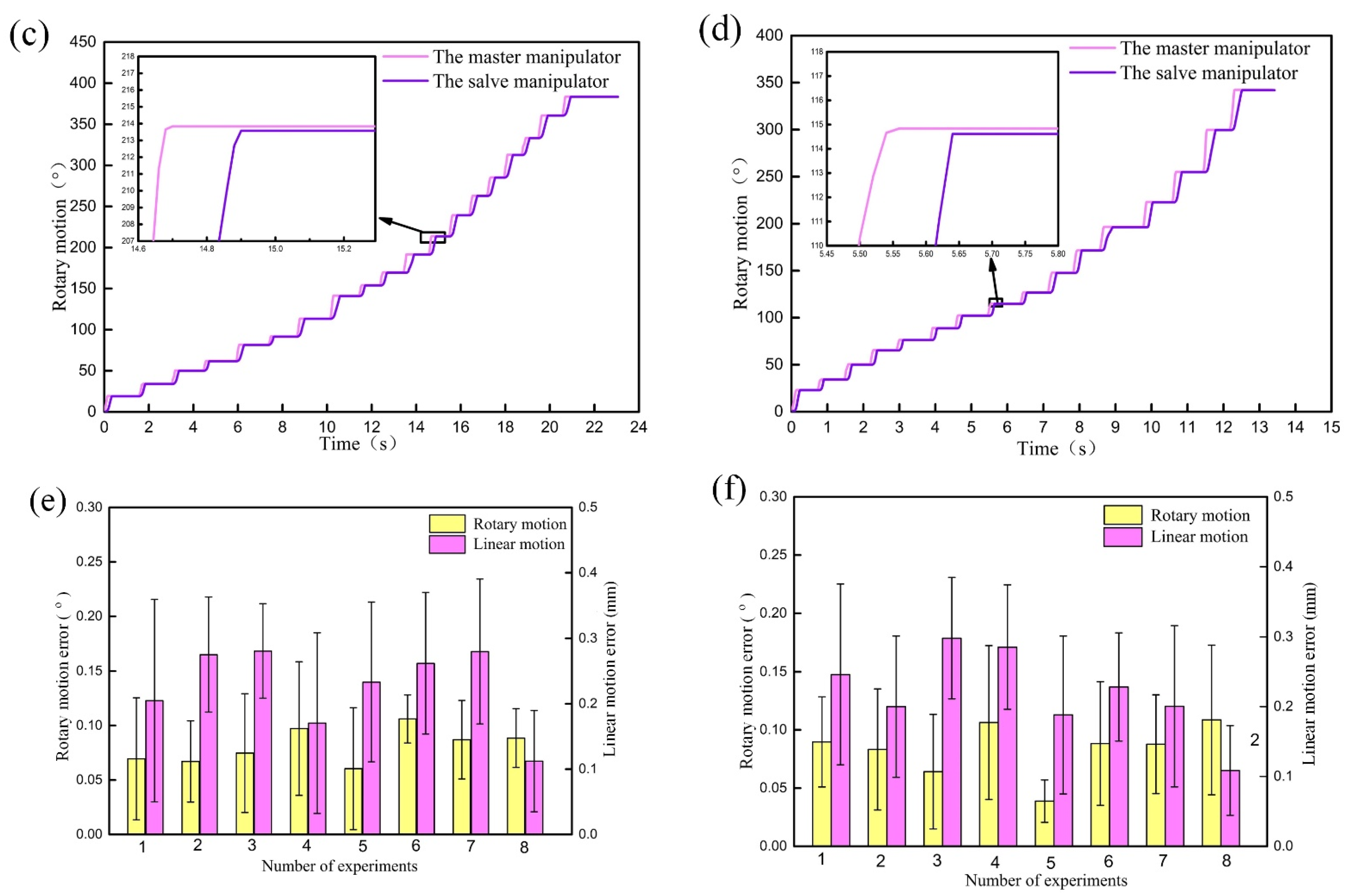
4.3. Master-Slave Tracking Test Experiment
4.4. Cooperative Control Motion Test Experiment
4.5. Vascular Intervention Simulation Experiment
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Guo, J.; Guo, S.; Xiao, N.; Ma, X.; Kawanishi, M. A novel robotic catheter system with force and visual feedback for vascular interventional surgery. Int. J. Mechatron. Autom. 2012, 2, 15–24. [Google Scholar] [CrossRef] [Green Version]
- Bian, G.B.; Xie, X.L.; Feng, Z.Q.; Hou, Z.G.; Tan, M. An enhanced dual-finger robotic Hand for Catheter manipulating in vascular intervention: A preliminary study. In Proceedings of the IEEE International Conference on Information & Automation, Yinchuan, China, 27 January 2014. [Google Scholar]
- Miller, D.L. Why use remote guidance to steer catheters and guide wires? Radiology 2004, 232, 313. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beyar, R.; Gruberg, L.; Dan, D.; Roguin, A.; Almagor, Y.; Cohen, S.; Kumar, G.; Wenderow, T. Remote-control percutaneous coronary interventions: Concept, validation, and first-in-humans pilot clinical trial. J. Am. Coll. Cardiol. 2006, 47, 296–300. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tanimoto, M.; Arai, F.; Fukuda, T.; Itoigawa, K.; Hashimoto, M.; Takahashi, I.; Negoro, M. Telesurgery System for Intravascular Neurosurgery. In Proceedings of the International Conference on Medical Image Computing & Computer-Assisted Intervention, Berlin, Germany, 11 October 2000. [Google Scholar]
- Abdelaziz, M.; Stramigioli, S.; Yang, G.Z.; Kundrat, D.; Riga, C. Toward a Versatile Robotic Platform for Fluoroscopy and MRI-Guided Endovascular Interventions: A Pre-Clinical Study. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 4–8 November 2019. [Google Scholar]
- Shang, W.; Hao, S.; Gang, L.; Fischer, G.S. Teleoperation System with Hybrid Pneumatic-Piezoelectric Actuation for MRI-Guided Needle Insertion with Haptic Feedback. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots & Systems, Tokyo, Japan, 3–7 November 2013. [Google Scholar]
- Yang, X.; Wang, H.; Sun, L.; Yu, H. Operation and Force Analysis of the Guide Wire in a Minimally Invasive Vascular Interventional Surgery Robot System. Chin. J. Mech. Eng. 2015, 28, 249–257. [Google Scholar] [CrossRef]
- Rafii-Tari, H.; Payne, C.J.; Yang, G.Z. Current and Emerging Robot-Assisted Endovascular Catheterization Technologies: A Review. Ann. Biomed. Eng. 2014, 42, 697–715. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.C. The role of robotic surgical system in the management of vascular disease. Ann. Vasc. Surg. 2013, 27, 976–983. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, D.; Wang, T. Overview of the vascular interventional robot. Int. J. Med. Robot. Comput. Assist. Surg. 2010, 4, 289–294. [Google Scholar]
- Lee, K.H.; Fu, K.; Guo, Z.; Dong, Z.; Leong, M.C.W.; Cheung, C.L.; Lee, P.W.; Luk, W.; Kwok, K.W. MR Safe Robotic Manipulator for MRI-guided Intra-cardiac Catheterization. IEEE/ASME Trans. Mechatron. 2018, 23, 586–595. [Google Scholar] [CrossRef]
- Wijnmaalen, A.P.; van der Geest, R.J.; van Huls van Taxis, C.F.; Siebelink, H.M.J.; Kroft, L.J.; Bax, J.J.; Reiber, J.H.; Schalij, M.J.; Zeppenfeld, K. Head-to-head comparison of contrast-enhanced magnetic resonance imaging and electroanatomical voltage mapping to assess post-infarct scar characteristics in patients with ventricular tachycardias: Real-time image integration and reversed registration. Eur. Heart J. 2011, 32, 104–114. [Google Scholar] [CrossRef] [Green Version]
- Radau, P.E.; Pintilie, S.; Flor, R.; Biswas, L.; Wright, G.A. VURTIGO: Visualization Platform for Real-Time, MRI-Guided Cardiac Electroanatomic Mapping. In Proceedings of the International Workshop on Statistical Atlases & Computational Models of the Heart, Berlin, Germany, 22 September 2011. [Google Scholar]
- Lardo, A.C.; Mcveigh, E.R.; Jumrussirikul, P.; Berger, R.D.; Calkins, H.; Lima, J.; Halperin, H.R. Visualization and Temporal/Spatial Characterization of Cardiac Radiofrequency Ablation Lesions Using Magnetic Resonance Imaging. Circulation 2000, 102, 698–705. [Google Scholar] [CrossRef] [Green Version]
- Ranjan, R.; Kholmovski, E.G.; Blauer, J.; Vijayakumar, S.; Volland, N.A.; Salama, M.E.; Parker, D.L.; MacLeod, R.; Marrouche, N.F. Identification and Acute Targeting of Gaps in Atrial Ablation Lesion Sets Using a Real-Time Magnetic Resonance Imaging System. Circ. Arrhythmia Electrophysiol. 2012, 5, 1130–1135. [Google Scholar] [CrossRef] [Green Version]
- Zia, M.I.; Ghugre, N.R.; Connelly, K.A.; Strauss, B.H.; Sparkes, J.D.; Dick, A.J.; Wright, G.A. Characterizing myocardial edema and hemorrhage using quantitative T2 and T2* mapping at multiple time intervals post ST-segment elevation myocardial infarction. Circ. Cardiovasc. Imaging 2012, 5, 566–572. [Google Scholar] [CrossRef] [Green Version]
- Linet, M.S.; Kim, K.P.; Miller, D.L.; Kleinerman, R.A.; Simon, S.L.; Gonzalez, A.D. Historical review of occupational exposures and cancer risks in medical radiation workers. Radiat. Res. 2010, 174, 793–808. [Google Scholar] [CrossRef] [Green Version]
- Yoshinaga, S.; Mabuchi, K.; Sigurdson, A.J.; Doody, M.M.; Ron, E. Cancer risks among radiologists and radiologic technologists: Review of epidemiologic studies. Radiology 2004, 233, 313–321. [Google Scholar] [CrossRef]
- Ramanathan, V.; Almeida, S.M.; Fernando, K. Occupational dose measurement for radiographers during cardiac catheterization procedures. Int. J. Sci. Res. Publ. 2021, 11, 476. [Google Scholar] [CrossRef]
- Bhagirath, P.; van der Graaf, M.; Karim, R.; Rhode, K.; Piorkowski, C.; Razavi, R.; Schwitter, J.; Götte, M. Interventional Cardiac Magnetic Resonance Imaging in Electrophysiology: Advances Toward Clinical Translation. Circ. Arrhythmia Electrophysiol. 2015, 8, 203–211. [Google Scholar] [CrossRef] [Green Version]
- Akoum, N.; Daccarett, M.; Mcgann, C.; Segerson, N.; Vergara, G.; Kuppahally, S.; Badger, T.; Burgon, N.; Haslam, T.; Kholmovski, E.; et al. Atrial Fibrosis Helps Select the Appropriate Patient and Strategy in Catheter Ablation of Atrial Fibrillation: A DE-MRI Guided Approach. J. Cardiovasc. Electrophysiol. 2011, 22, 16–22. [Google Scholar] [CrossRef]
- Arujuna, A.; Karim, R.; Caulfield, D.; Knowles, B.; Rhode, K.; Schaeffter, T.; Kato, B.; Rinaldi, C.A.; Cooklin, M.; Razavi, R. Acute pulmonary vein isolation is achieved by a combination of reversible and irreversible atrial injury after catheter ablation: Evidence from magnetic resonance imaging. Circ. Arrhythmia Electrophysiol. 2012, 5, 691–700. [Google Scholar] [CrossRef] [Green Version]
- Harrison, J.L.; Jensen, H.K.; Peel, S.A.; Amedeo, C.; Grøndal, A.K.; Bloch, L.Ø.; Pedersen, S.F.; Bentzon, J.F.; Christoph, K.; Rashed, K. Cardiac magnetic resonance and electroanatomical mapping of acute and chronic atrial ablation injury: A histological validation study. Eur. Heart J. 2014, 35, 1486–1495. [Google Scholar] [CrossRef]
- Tavallaei, M.A.; Lavdas, M.K.; Gelman, D.; Drangova, M. Magnetic resonance imaging compatible remote catheter navigation system with 3 degrees of freedom. Int. J. Comput. Assist. Radiol. Surg. 2016, 11, 1537–1545. [Google Scholar] [CrossRef]
- Liu, T.; Poirot, N.L.; Franson, D.; Seiberlich, N.; Griswold, M.A.; Avuolu, M.C.N. Modeling and Validation of the Three Dimensional Deflection of an MRI-Compatible Magnetically-Actuated Steerable Catheter. IEEE Trans. Bio-Med. Eng. 2015, 63, 2142–2154. [Google Scholar]
- Bao, X.; Guo, S.; Xiao, N.; Li, Y.; Yang, C.; Jiang, Y. A cooperation of catheters and guidewires-based novel remote-controlled vascular interventional robot. Biomed. Microdevices 2018, 20, 20. [Google Scholar] [CrossRef]
- Magnusson, P.; Johansson, E.; Nsson, S.M.; Petersson, J.S.; Chai, C.M.; Hansson, G.; Axelsson, O.; Golman, K. Passive catheter tracking during interventional MRI using hyperpolarized 13C. Magn. Reson. Med. 2010, 57, 1140–1147. [Google Scholar] [CrossRef]
- Khan, E.M.; Frumkin, W.; Ng, G.A.; Neelagaru, S.; Abi-Samra, F.M.; Lee, J.; Giudici, M.; Gohn, D.; Winkle, R.A.; Sussman, J.; et al. First experience with a novel robotic remote catheter system: Amigo™ mapping trial. J. Interv. Card. Electrophysiol. 2013, 37, 121–129. [Google Scholar] [CrossRef]
- Granada, J.F.; Delgado, J.A.; Uribe, M.P.; Fernandez, A.; Blanco, G.; Leon, M.B.; Weisz, G. First-in-human evaluation of a novel robotic-assisted coronary angioplasty system. JACC Cardiovasc. Interv. 2011, 4, 460–465. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Riga, C.V.; Bicknell, C.D.; Hamady, M.S.; Cheshire, N. Evaluation of robotic endovascular catheters for arch vessel cannulation. J. Vasc. Surg. 2011, 54, 799–809. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Riga, C.V.; Bicknell, C.D.; Rolls, A.; Cheshire, N.J.; Hamady, M.S. Robot-assisted Fenestrated Endovascular Aneurysm Repair (FEVAR) Using the Magellan System. J. Vasc. Interv. Radiol. 2013, 24, 191–196. [Google Scholar] [CrossRef] [PubMed]
- Srimathveeravalli, G.; Kesavadas, T.; Li, X. Design and fabrication of a robotic mechanism for remote steering and positioning of interventional devices. Int. J. Med. Robot. Comput. Assist. Surg. 2010, 6, 160–170. [Google Scholar] [CrossRef] [PubMed]
- Uchino, K. MicroMechatronics, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2003; pp. 465–522. [Google Scholar]
- Jūrėnas, V.; Kazokaitis, G.; Mažeika, D. 3DOF Ultrasonic Motor with Two Piezoelectric Rings. Sensors 2020, 20, 834. [Google Scholar] [CrossRef] [Green Version]
- Delibas, B.; Koc, B. L1B2 piezo motor using D33 effect. In Proceedings of the 16th International Conference on New Actuators, Bremen, Germany, 25–27 June 2018; pp. 1–4, ISBN 9783800746750. [Google Scholar]
- Tian, X.; Liu, Y.; Deng, J.; Wang, L.; Chen, W. A review on piezoelectric ultrasonic motors for the past decade: Classification, operating principle, performance, and future work perspectives. Sens. Actuators A Phys. 2020, 306, 111971. [Google Scholar] [CrossRef]
- Deibel, K.R.; Wegener, K. Methodology for shape optimization of ultrasonic amplifier using genetic algorithms and simplex method. J. Manuf. Syst. 2013, 32, 523–528. [Google Scholar] [CrossRef] [Green Version]
- Zhou, G.D.; Yi, T.H.; Li, H.N. Wireless Sensor Placement for Bridge Health Monitoring Using a Generalized Genetic Algorithm. Int. J. Struct. Stab. Dyn. 2014, 14, 1440011. [Google Scholar] [CrossRef]






| Analysis Process | |
|---|---|
| Step 1 | Determine the optimal design space of the stator |
| Step 2 | Establish the optimization model of the stator |
| Step 3 | Use Latin hypercube sampling to obtain sample points |
| Step 4 | Calculate the response of the sample points |
| Step 5 | Filter data points |
| Step 6 | Build response surface model |
| Step 7 | Use a genetic algorithm to find the optimal solution in the whole domain |
| Design Variable | Initial Size/mm | Design Space/mm |
|---|---|---|
| P1 | 0.9 | 0.81–0.99 |
| P2 | 2.5 | 2.00–2.90 |
| P3 | 2.5 | 2.25–2.75 |
| P4 | 4.5 | 4.00–5.00 |
| P5 | 0.5 | 0.42–0.58 |
| P6 | 1.5 | 1.30–1.70 |
| P7 | 1.5 | 1.35–1.65 |
| Frequency/kHz | Amplitude/μm | Stress/Mpa | |||||
|---|---|---|---|---|---|---|---|
| Ff | Fb | FA | FB | W0 | σin | ||
| FEA | Initial | 37.25 | 39.05 | 38.62 | 38.62 | 0.81 | 15.23 |
| Optimized | 36.52 | 40.64 | 38.43 | 38.43 | 2.79 | 11.17 | |
| TEST | Initial | 37.11 | 39.01 | 38.55 | 38.55 | 0.93 | — |
| Optimized | 36.37 | 40.53 | 38.43 | 38.43 | 3.12 | — | |
| Object | Motion | Mean | SD | Cumulation |
|---|---|---|---|---|
| GM | Linear/mm | 0.12 | 0.035 | 0.57 |
| Rotary/° | 0.08 | 0.027 | 0.35 | |
| CM | Linear/mm | 0.13 | 0.029 | 0.45 |
| Rotary/° | 0.11 | 0.023 | 0.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Q.; Sun, Z.; Zhang, J.; Zhang, J.; Zheng, J.; Qian, F. A Novel Remote-Controlled Vascular Interventional Robotic System Based on Hollow Ultrasonic Motor. Micromachines 2022, 13, 410. https://doi.org/10.3390/mi13030410
Lu Q, Sun Z, Zhang J, Zhang J, Zheng J, Qian F. A Novel Remote-Controlled Vascular Interventional Robotic System Based on Hollow Ultrasonic Motor. Micromachines. 2022; 13(3):410. https://doi.org/10.3390/mi13030410
Chicago/Turabian StyleLu, Qing, Zhijun Sun, Jialiang Zhang, Jiacheng Zhang, Juju Zheng, and Feng Qian. 2022. "A Novel Remote-Controlled Vascular Interventional Robotic System Based on Hollow Ultrasonic Motor" Micromachines 13, no. 3: 410. https://doi.org/10.3390/mi13030410





