An Accelerometer Based on All Silica In-Line Fiber Fabry-Perot Etalon for High Temperature up to 800 °C
Abstract
:1. Introduction
2. Fabrication and Principle
3. Results
3.1. Testing System
3.2. Experimental Results
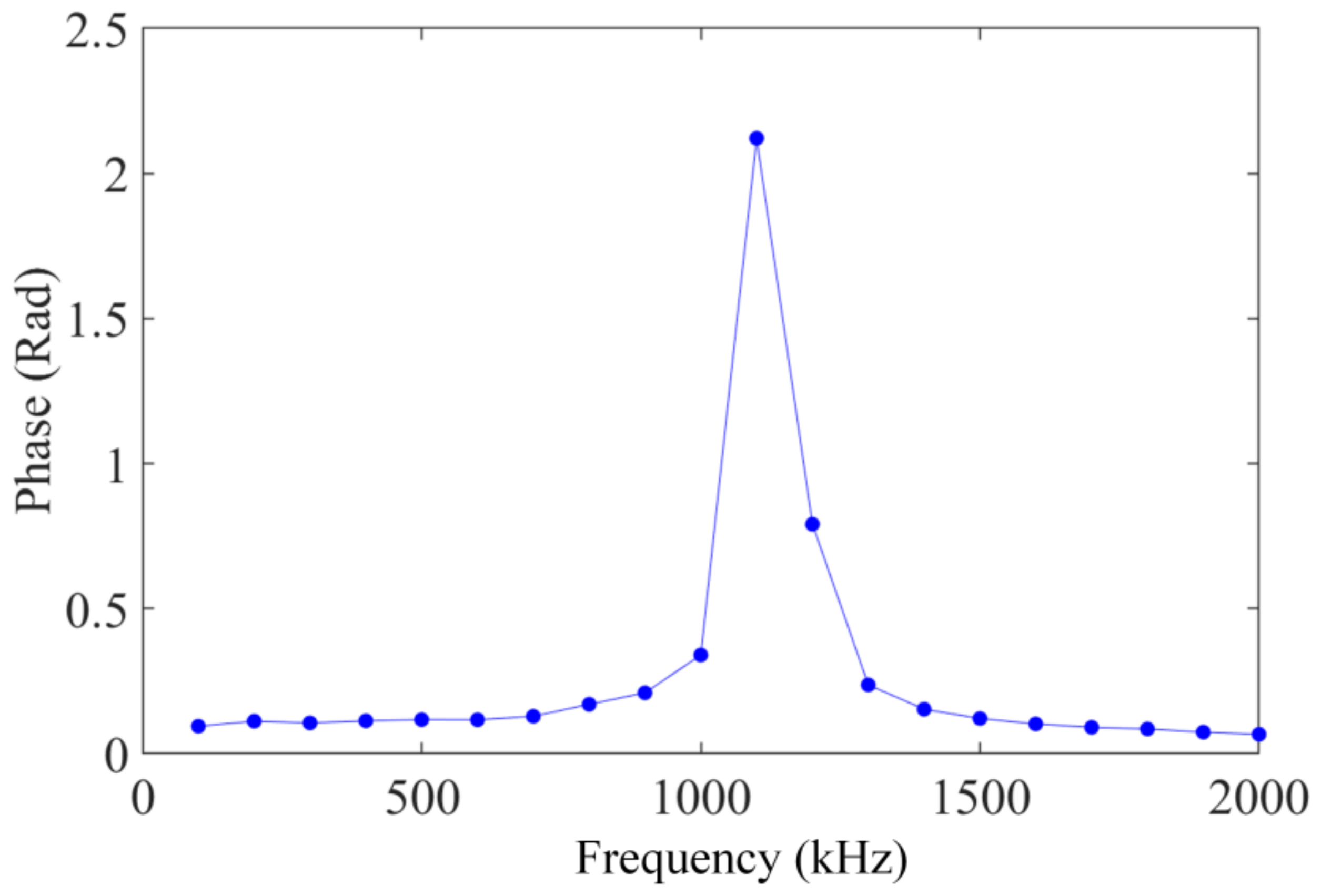
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, D.F.; Lin, L.J. Thermal/vibration joint experimental investigation on lightweight ceramic insulating material for hypersonic vehicles in extremely high-temperature environment up to 1500 °C. Cream. Int. 2020, 46, 14439–14447. [Google Scholar] [CrossRef]
- Miah, K.; Potter, D. A Review of Hybrid Fiber-Optic Distributed Simultaneous Vibration and Temperature Sensing Technology and Its Geophysical Applications. Sensors 2021, 17, 2511. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, D.; Qian, J.; Liu, J.; Chen, B.J.; An, G.W.; Hong, Y.P.; Jia, P.G.; Xiong, J.J. An in-line fiber optic fabry-perot sensor for high-temperature vibration measurement. Micromachines 2020, 11, 252. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kitada, Y.; Hirotani, T.; Iguchi, M. Models test on dynamic structure structure interaction of nuclear power plant buildings. Nucl. Eng. Des. 1999, 192, 205–216. [Google Scholar] [CrossRef]
- Johnson, R.W.; Evans, J.L.; Jacobsen, P.; Thompson, J.R.; Christopher, M. The Changing Automotive Environment: High-temperature Electronics. IEEE Trans. Electron. Packag. Manuf. 2004, 27, 164–176. [Google Scholar] [CrossRef]
- Om, P.P.; Jagannath, N.; Sundarrajan, A. Design and Validation of a Novel High Sensitivity Self-Temperature Compensated Fiber Bragg Grating Accelerometer. IEEE Sens. J. 2019, 19, 6197–6204. [Google Scholar]
- Rokicki, E.; Przysowa, R.; Kotkowski, J.; Majewski, P. High Temperature Magnetic Sensors for the Hot Section of Aeroengines. Aerospace 2021, 8, 261. [Google Scholar] [CrossRef]
- Ranganath, K.; Samuel, H.H.; William, H.V. System health monitoing and prognostics-A review of current paradigms and practices. Int. J. Adv. Manuf. Technol. 2006, 28, 1012–1024. [Google Scholar]
- Howuk, K.; Sean, K.; Mohamed, B.; Jiang, X.N. AlN Single Crystal Accelerometer for Nuclear Power Plants. IEEE Trans. Ind. Electronic. 2021, 68, 5346–5354. [Google Scholar]
- Jiang, C.; Liu, X.L.; Yu, F.P.; Zhang, S.J.; Fang, H.R.; Cheng, X.F.; Zhao, X. High-temperature Vibration Sensor Based on Ba2TiSi2O8 Piezoelectric Crystal with Ultra-Stable Sensing Performance up to 650 °C. IEEE Trans. Ind. Electron. 2021, 68, 12850–12859. [Google Scholar] [CrossRef]
- Eklund, E.J.; Shkel, A.M. Single-mask fabrication of high-G piezoresistive accelerometers with extended temperature range. J. Micromech. Microeng. 2007, 17, 730–736. [Google Scholar] [CrossRef] [Green Version]
- Alexander, U.; Christian, W.; Alexander, S.; Mir, M.; Michael, K.; Rainer, K. A high-precision and high-bandwidth MEMS-based capacitive accelerometer. IEEE Sens. J. 2018, 18, 6533–6539. [Google Scholar]
- Shi, C.H.; Zhu, T.; Rao, Y.J.; Deng, M. Fiber optic accelerometer based on long period fiber grating induced by CO2 laser pulses. Microw. Opt. Technol. 2011, 53, 841–845. [Google Scholar] [CrossRef]
- Zhang, T.X.; Zhao, Y.F.; Wei, D.M.; Pan, J. Fiber-Optic Michelson Accelerometer Based on Frequency Modulation. IEEE Photonics Technol. Lett. 2014, 26, 2361–2364. [Google Scholar] [CrossRef]
- Shang, Y.L.; Wang, J.B.; Tu, S.; Chen, D.Y. A novel micromachined differential resonant accelerometer with flexural mechanisms fabricated by SOI-mems technology. In Proceedings of the 2011 IEEE Sensors, Limerick, Ireland, 28–31 October 2011. [Google Scholar]
- Wang, D.H.; Jia, P.G. Fiber optic extrinsic Fabry–Perot accelerometer using laser emission frequency modulated phase generated carrier demodulation scheme. Opt. Eng. 2013, 52, 0550040-1–0550040-9. [Google Scholar] [CrossRef]
- Liu, Y.F.; Li, B.; Liu, S.X. Study on a Single-axis Fabry-perot Fiber-optic Accelerometer and its Signal Demodulation Method. In Proceedings of the International Conference on Computer Engineering & Information Systems, Shanghai, China, 1 January 2016. [Google Scholar]
- Wang, Z.G.; Zhang, W.T.; Han, J.; Huang, W.Z.; Li, F. Diaphragm-Based Fiber Optic Fabry–Perot Accelerometer With High Consistency. J. Lightwave Technol. 2014, 32, 4810–4815. [Google Scholar] [CrossRef]
- Ren, Q.Y.; Jia, P.G.; An, G.W.; Liu, J.; Fang, G.C.; Liu, W.Y.; Xiong, J.J. Dual-wavelength demodulation technique for interrogating a shortest cavity in multi-cavity fiber-optic Fabry-Perot sensors. Opt. Express. 2021, 20, 32658–32669. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.Y.; Ren, Q.Y.; Jia, P.G.; Hong, Y.P.; Liang, T.; Liu, J.; Xiong, J.J. Least square fitting demodulation technique for the interrogation of an optical fiber Fabry–Perot sensor with arbitrary reflectivity. Appl. Opt. 2020, 59, 1301–1306. [Google Scholar] [CrossRef] [PubMed]
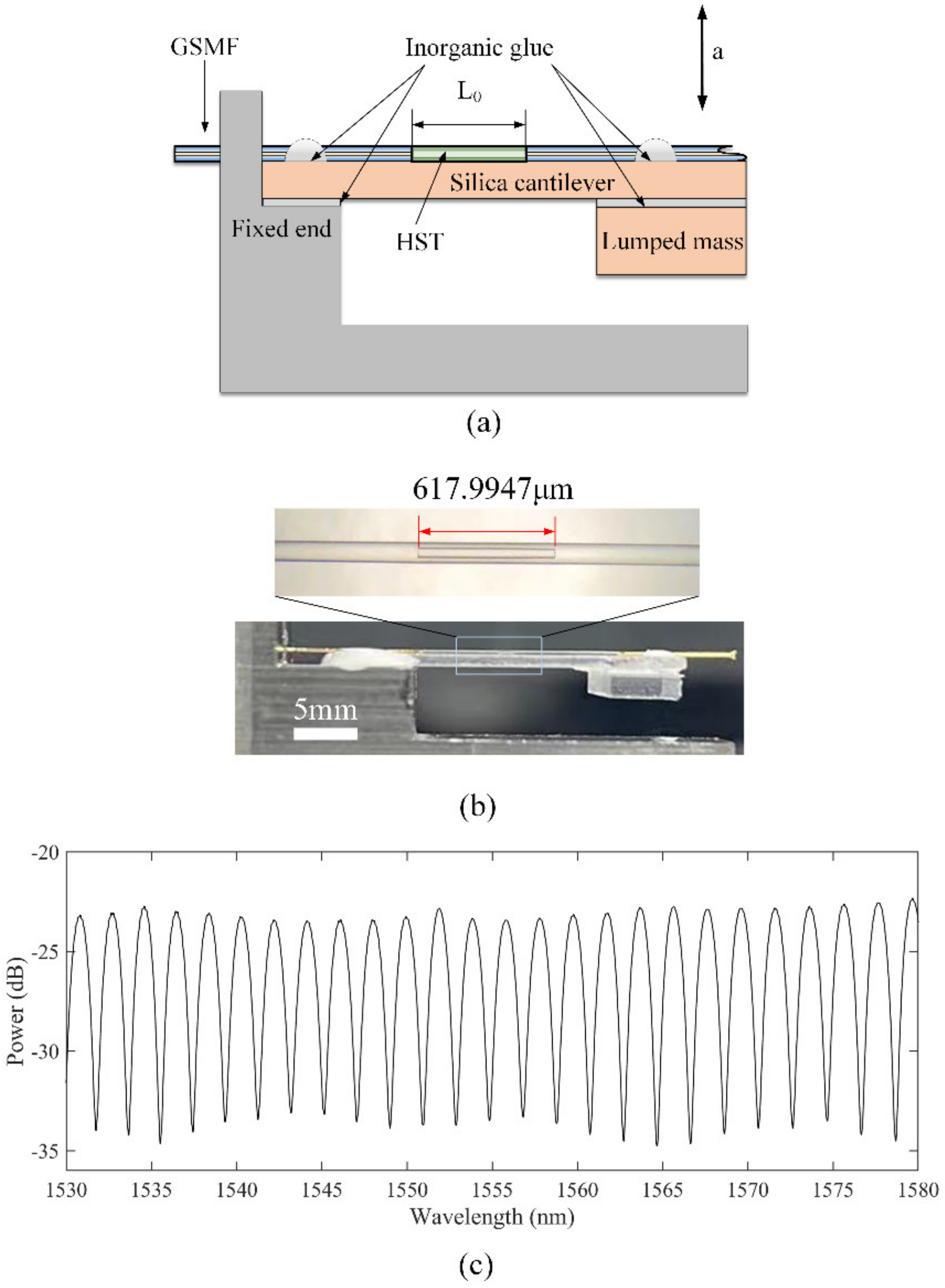

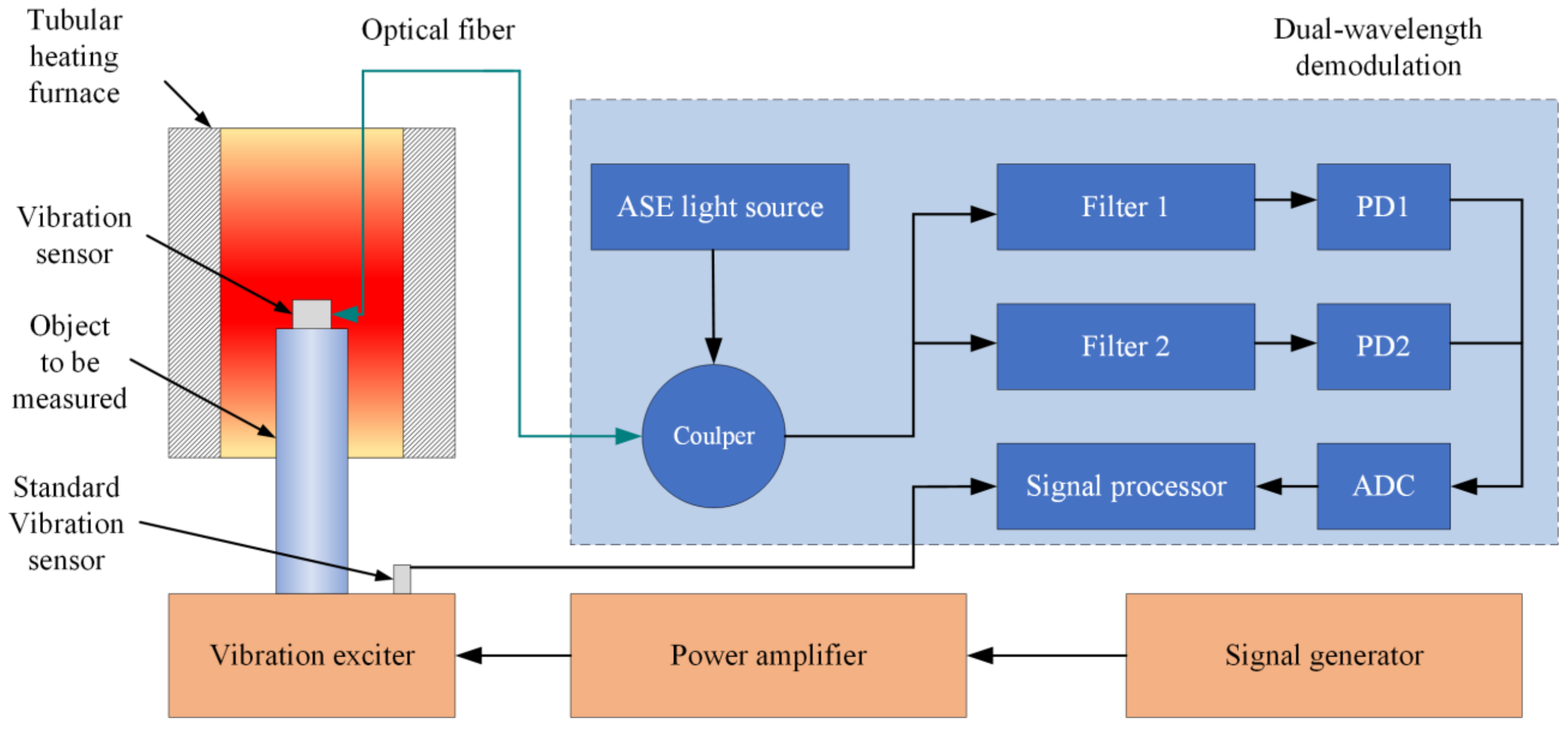
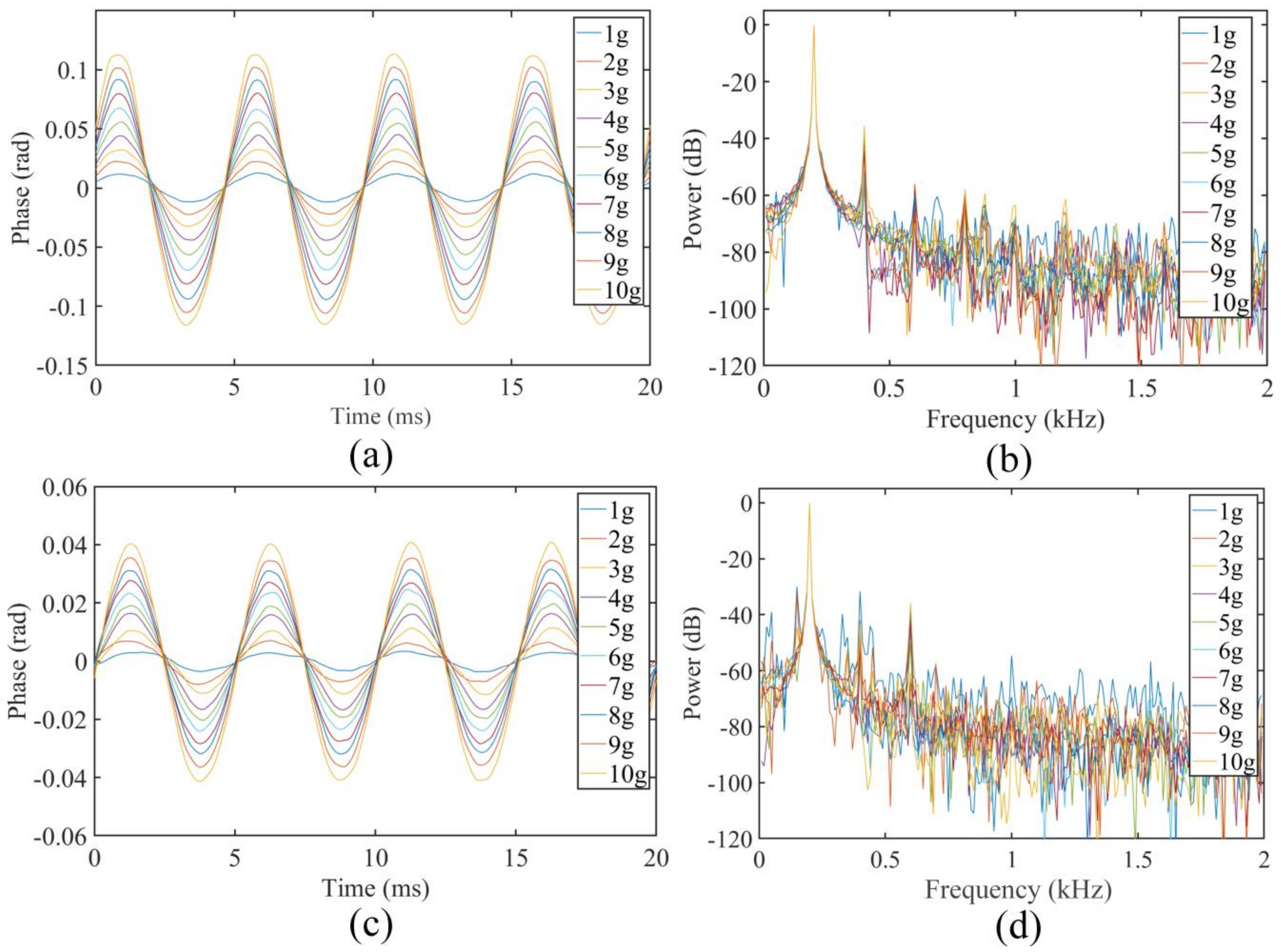

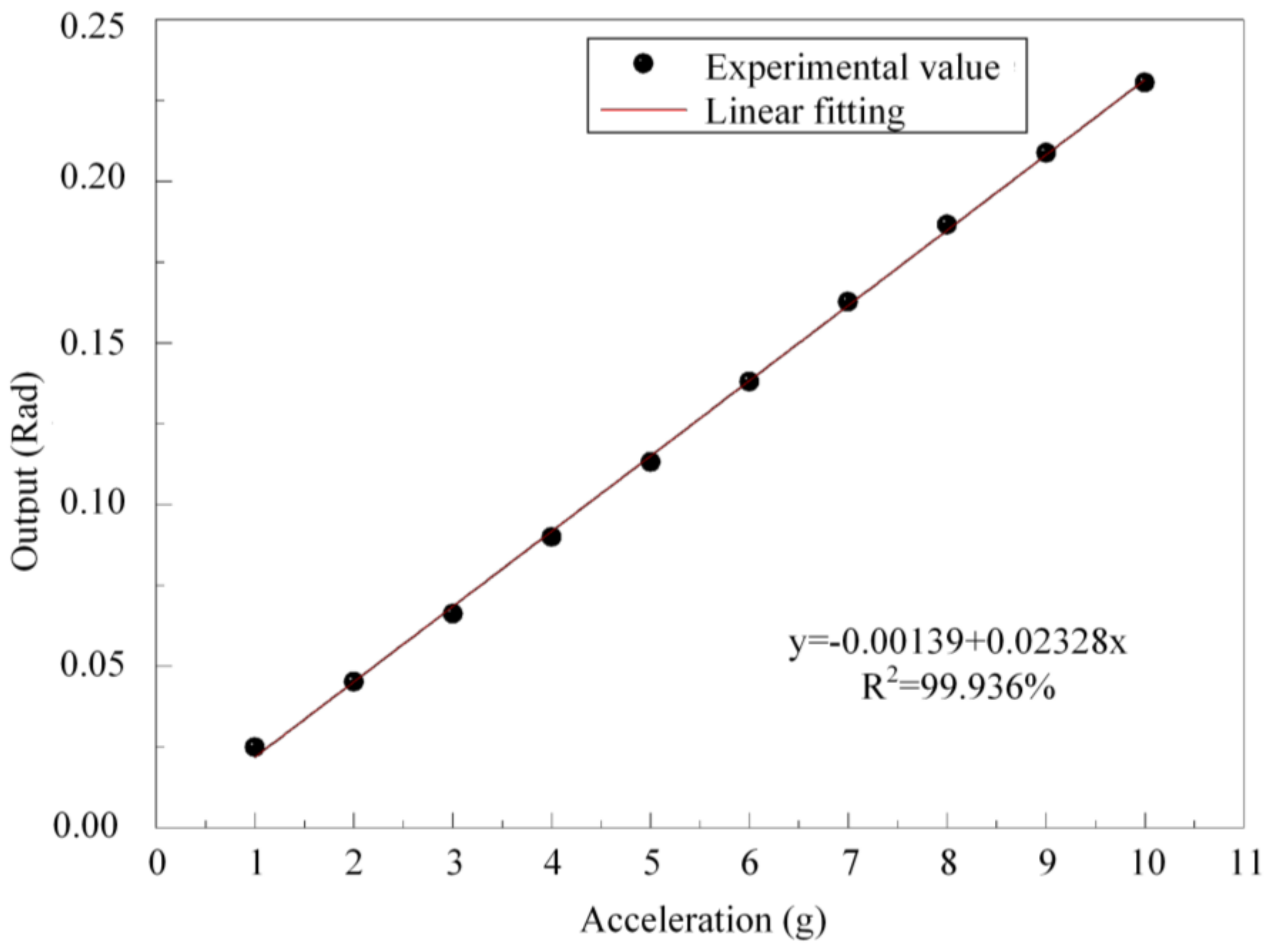
| Parameters | Symbol | Units | Value |
|---|---|---|---|
| Length of beam | mm | 9 | |
| Width of beam | mm | 5 | |
| Thickness of beam | mm | 0.3 | |
| Density of monocrystalline silica | kg/m3 | 2203 | |
| Length of mass | mm | 5 | |
| Width of mass | mm | 5 | |
| Thickness of mass | mm | 1 | |
| Initial length of FP cavity | mm | 0.618 | |
| Young’s modulus of silica | GPa | 69.6 | |
| Sensitivity | rad/g | 0.02 | |
| Resonance frequency | Hz | 1146.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, J.; Jia, P.; Ren, Q.; Liu, H.; Qin, L.; Xiong, J. An Accelerometer Based on All Silica In-Line Fiber Fabry-Perot Etalon for High Temperature up to 800 °C. Micromachines 2022, 13, 548. https://doi.org/10.3390/mi13040548
Qian J, Jia P, Ren Q, Liu H, Qin L, Xiong J. An Accelerometer Based on All Silica In-Line Fiber Fabry-Perot Etalon for High Temperature up to 800 °C. Micromachines. 2022; 13(4):548. https://doi.org/10.3390/mi13040548
Chicago/Turabian StyleQian, Jiang, Pinggang Jia, Qianyu Ren, Hua Liu, Li Qin, and Jijun Xiong. 2022. "An Accelerometer Based on All Silica In-Line Fiber Fabry-Perot Etalon for High Temperature up to 800 °C" Micromachines 13, no. 4: 548. https://doi.org/10.3390/mi13040548






