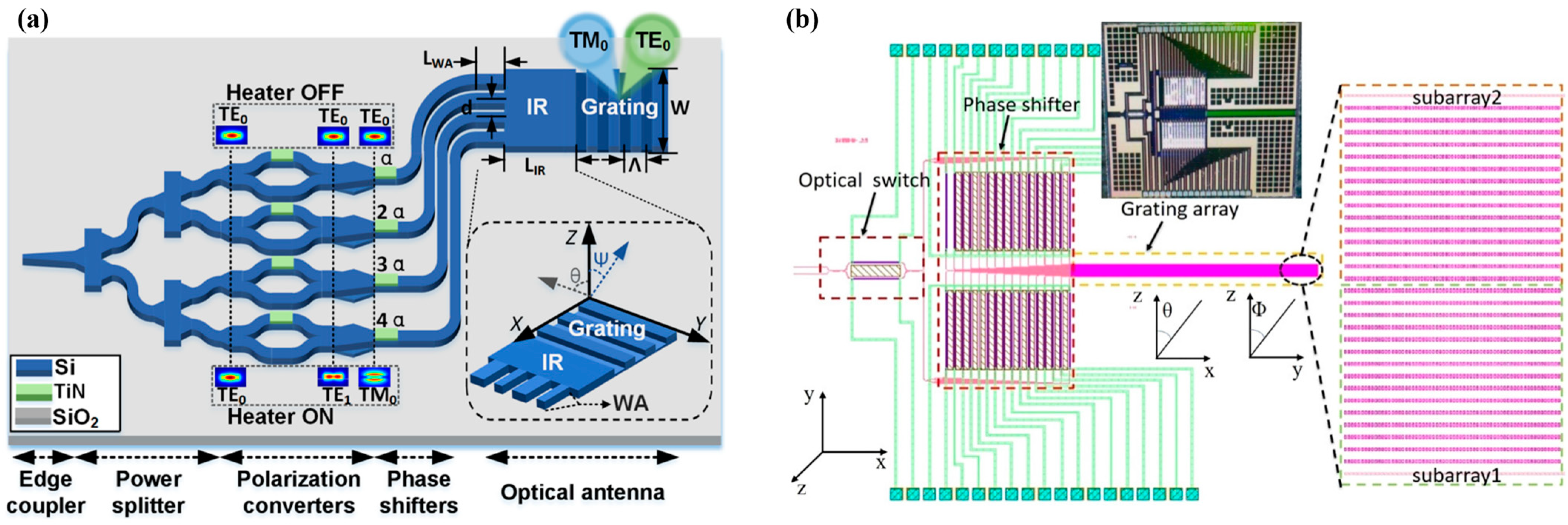
Beam Steering Technology of Optical Phased Array Based on Silicon Photonic Integrated Chip
Abstract
1. Introduction
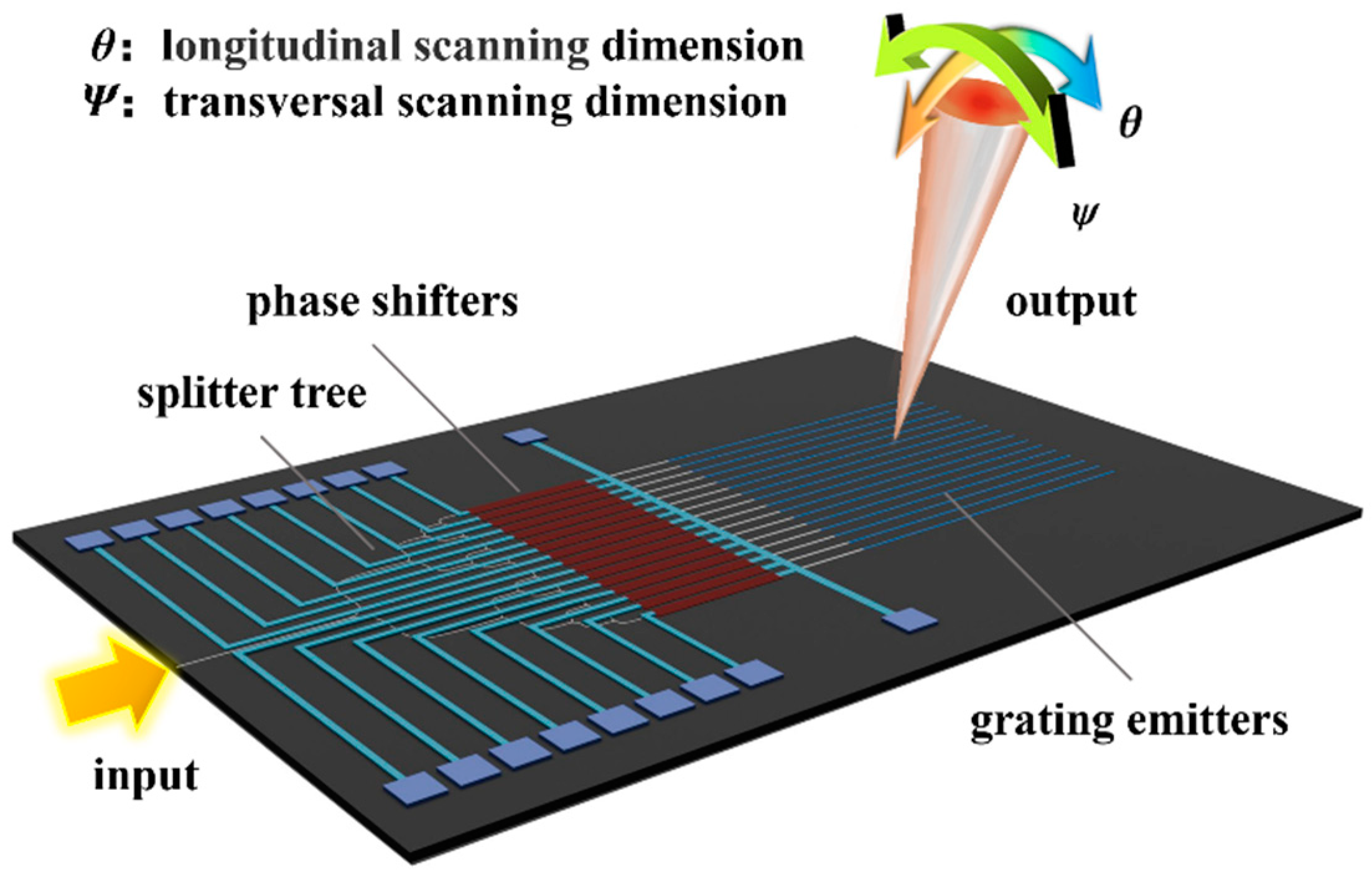
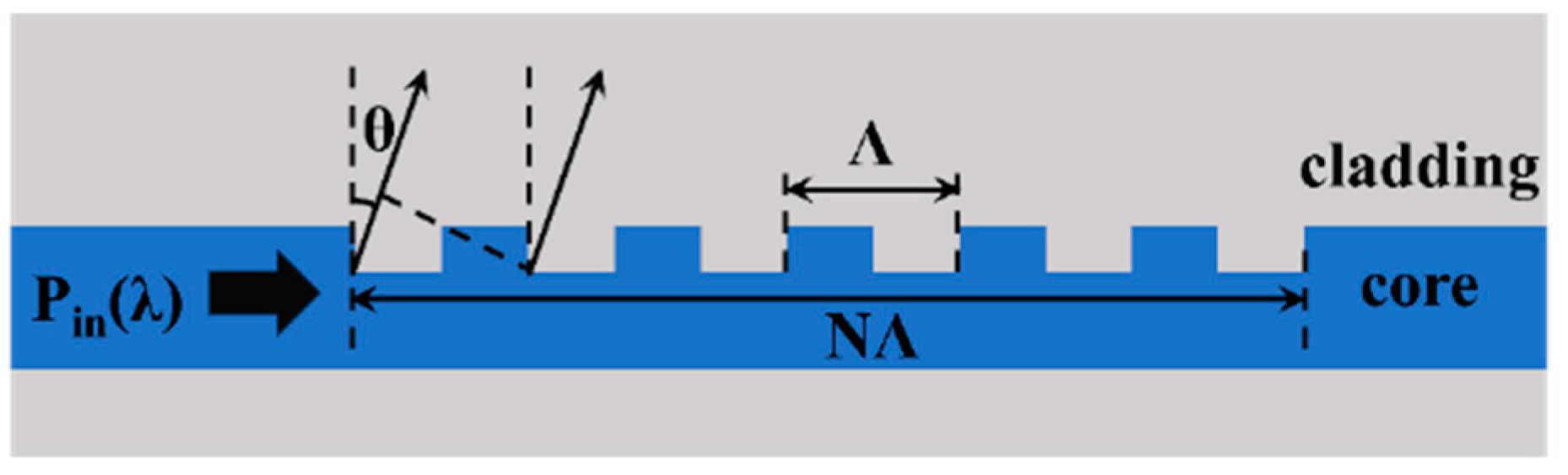
2. Scanning Principle of PIC OPA
3. Schemes and Review for Improving OPA Device Performance
3.1. Improving Beam Quality of Longitudinal Dimension
3.1.1. Expanding Scanning Range of Longitudinal Dimension
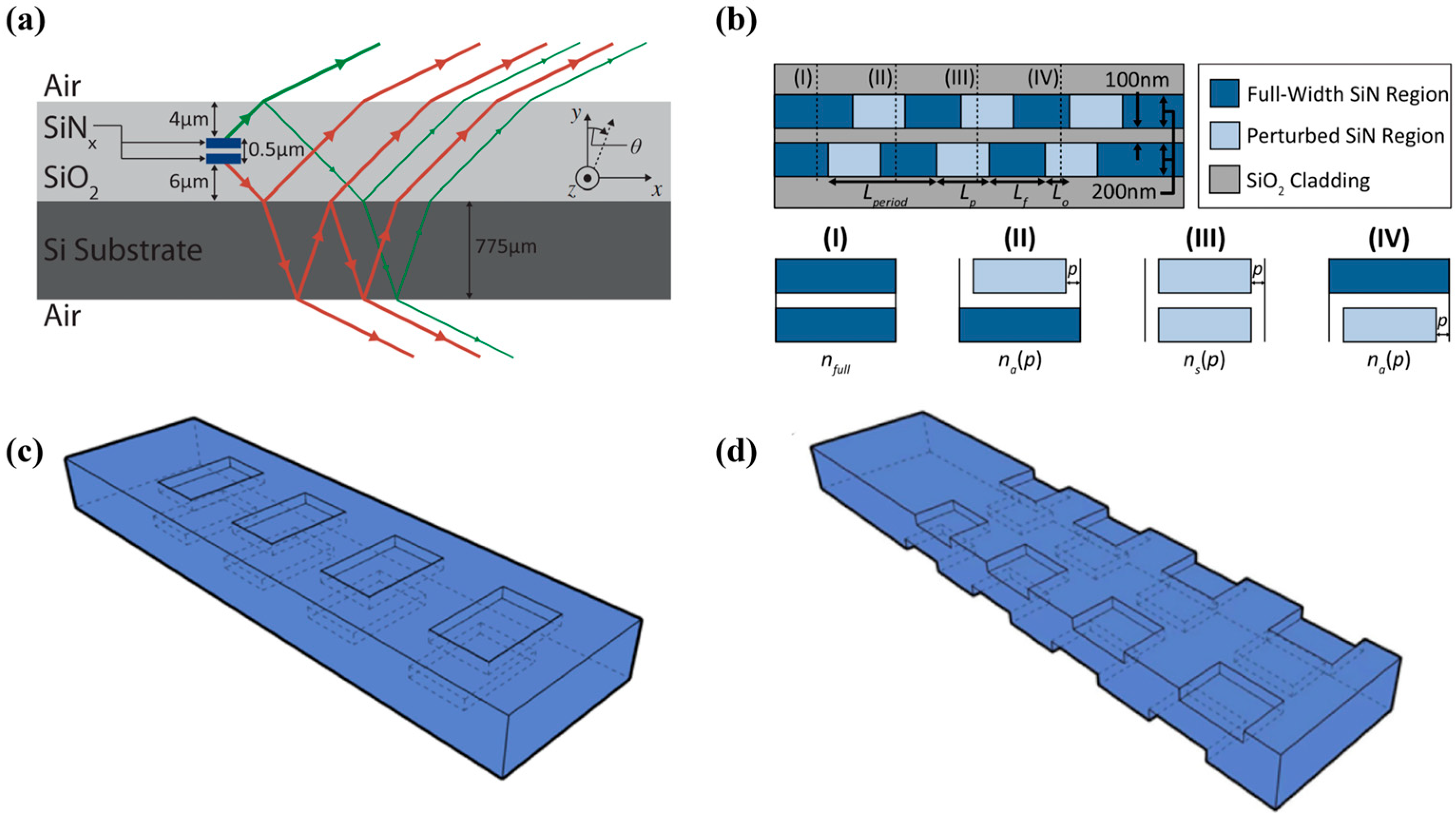
3.1.2. Reducing Divergence Angle of Longitudinal Dimension
3.2. Improving Beam Quality of the Transversal Dimension
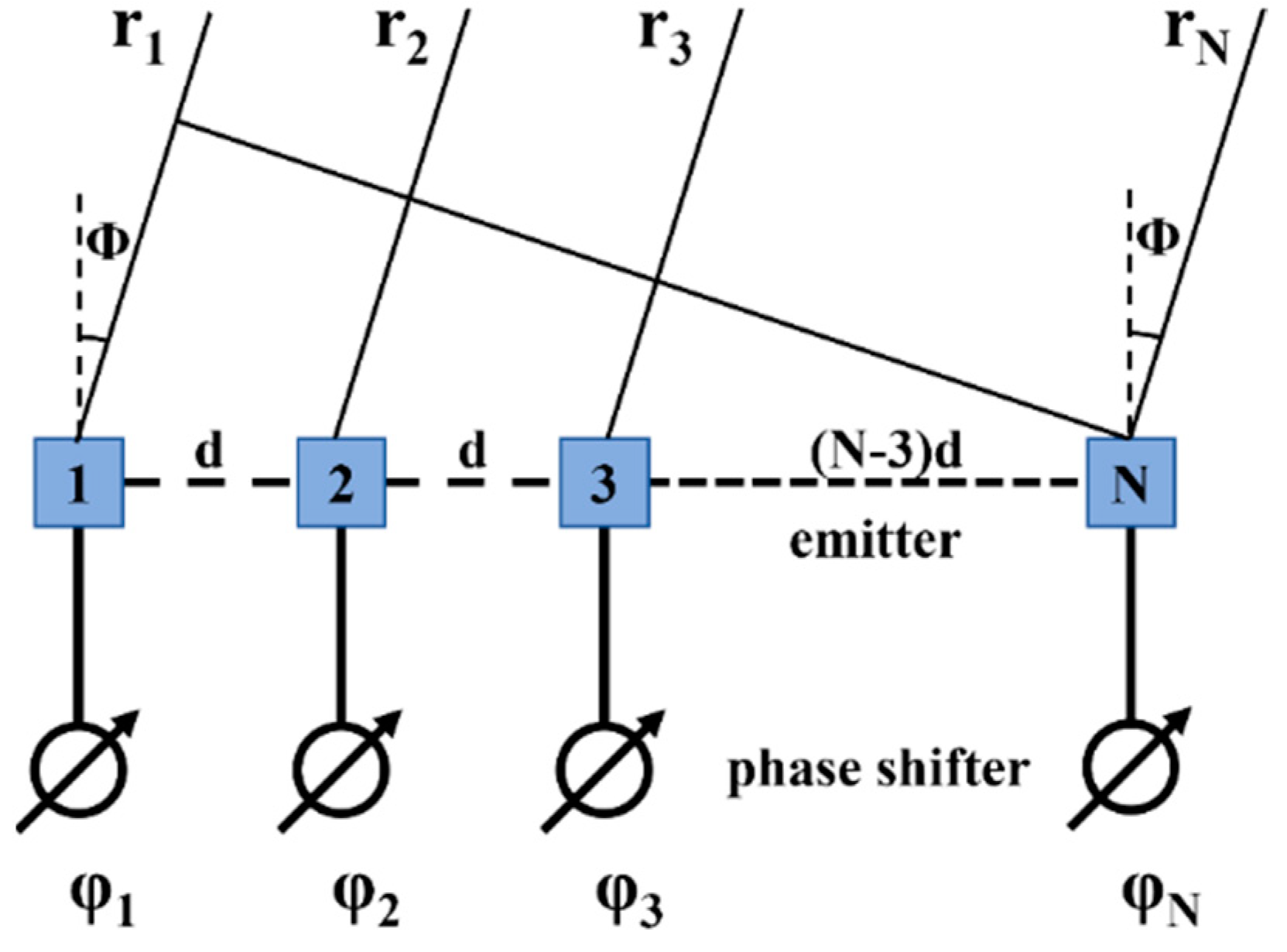
3.2.1. Distributing Array Periodically with Small Spacing to Expand the Transversal Scanning Range
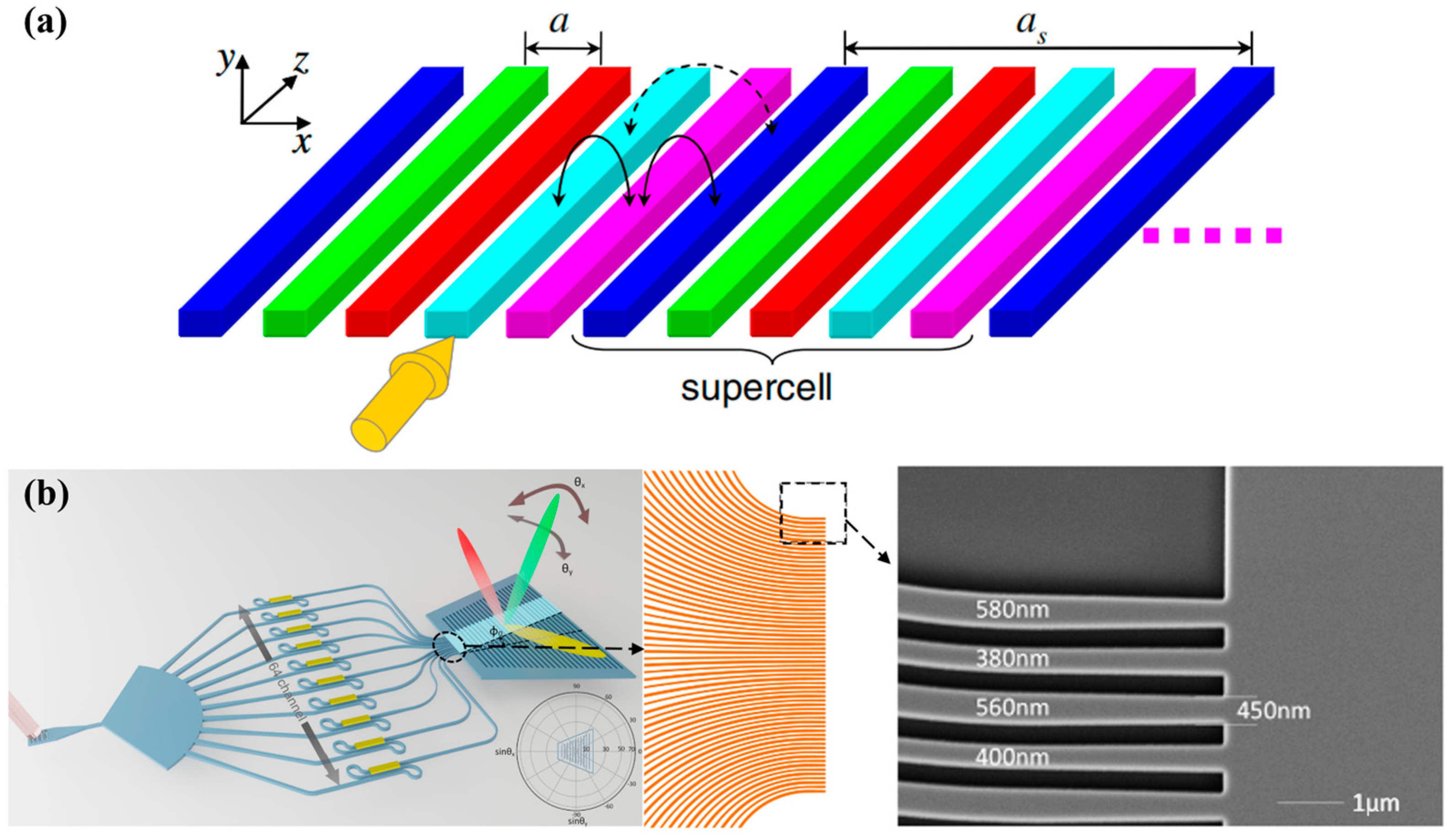
3.2.2. Distributing Array Unevenly with Large Spacing to Expand the Transversal Scanning Range
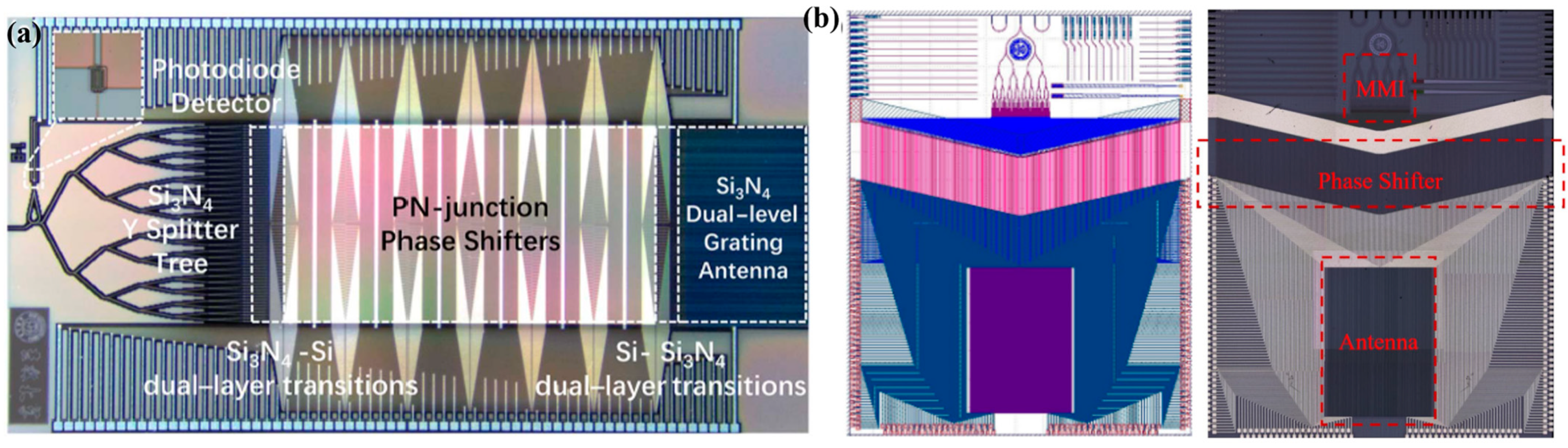
3.3. Unidirectionality of WGA and OPA Chips
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chang, Y.-P.; Liu, C.-N.; Pei, Z.; Lee, S.-M.; Lai, Y.-K.; Han, P.; Shih, H.-K.; Cheng, W.-H. New scheme of LiDAR-embedded smart laser headlight for autonomous vehicles. Opt. Express 2019, 27, A1481–A1489. [Google Scholar] [CrossRef] [PubMed]
- Isaac, B.J.; Song, B.; Pinna, S.; Coldren, L.A.; Klamkin, J. Indium Phosphide Photonic Integrated Circuit Transceiver for FMCW LiDAR. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 8000107. [Google Scholar] [CrossRef]
- Hsu, C.-P.; Li, B.; Solano-Rivas, B.; Gohil, A.R.; Chan, P.H.; Moore, A.D.; Donzella, V. A Review and Perspective on Optical Phased Array for Automotive LiDAR. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 8300416. [Google Scholar] [CrossRef]
- Fukui, T.; Kohno, Y.; Tang, R.; Nakano, Y.; Tanemura, T. Single-Pixel Imaging through Multimode Fiber using Silicon Optical Phased Array Chip. In Proceedings of the 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8–12 March 2020. [Google Scholar]
- Yoon, J.; Yoon, H.; Kim, J.Y.; Kim, J.; Kang, G.; Kwon, N.H.; Kurt, H.; Park, H.H. Demonstration of high-accuracy 3D imaging using a Si optical phased array with a tunable radiator. Opt. Express 2023, 31, 9935–9944. [Google Scholar] [CrossRef] [PubMed]
- Rogers, C.; Piggott, A.Y.; Thomson, D.J.; Wiser, R.F.; Opris, I.E.; Fortune, S.A.; Compston, A.J.; Gondarenko, A.; Meng, F.; Chen, X.; et al. A universal 3D imaging sensor on a silicon photonics platform. Nature 2021, 590, 256–261. [Google Scholar] [CrossRef]
- Kim, S.M.; Lee, E.S.; Chun, K.W.; Jin, J.; Oh, M.C. Compact solid-state optical phased array beam scanners based on polymeric photonic integrated circuits. Sci. Rep. 2021, 11, 10576. [Google Scholar] [CrossRef]
- Pierrottet, D.F.; Amzajerdian, F.; Petway, L.; Barnes, B.; Lockard, G.; Rubio, M. Linear FMCW Laser Radar for Precision Range and Vector Velocity Measurements. MRS Online Proc. Libr. 2008, 1076, 10760406. [Google Scholar] [CrossRef]
- Li, Y.; Chen, B.; Na, Q.; Tao, M.; Liu, X.; Zhi, Z.; Peng, T.; Li, X.; Luo, X.; Lo, G.-Q.; et al. High-Data-Rate and Wide-Steering-Range Optical Wireless Communication via Nonuniform-Space Optical Phased Array. J. Light. Technol. 2023, 41, 4933–4940. [Google Scholar] [CrossRef]
- Derakhshandeh, A.; Pachnicke, S.; Hoeher, P.A. Underwater Wireless Laser-Based Communications Using Optical Phased Array Antennas. IEEE Photonics J. 2023, 15, 7304309. [Google Scholar] [CrossRef]
- Ren, W.; Liang, Q.; Feng, J.; Liu, H.; Hu, J.; Yuan, S.; Xia, X.; Jiang, W.; Zhan, Q.; Zeng, H. Free-space beam shaping and steering based on a silicon optical phased array. Photonics Res. 2023, 11, 2093–2099. [Google Scholar] [CrossRef]
- Poulton, C.V.; Yaacobi, A.; Cole, D.B.; Byrd, M.J.; Raval, M.; Vermeulen, D.; Watts, M.R. Coherent solid-state LIDAR with silicon photonic optical phased arrays. Opt. Lett. 2017, 42, 4091–4094. [Google Scholar] [CrossRef]
- Poulton, C.V.; Byrd, M.J.; Russo, P.; Timurdogan, E.; Khandaker, M.; Vermeulen, D.; Watts, M.R. Long-Range LiDAR and Free-Space Data Communication With High-Performance Optical Phased Arrays. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 7700108. [Google Scholar] [CrossRef]
- Raval, M.; Yaacobi, A.; Watts, M.R. Integrated visible light phased array system for autostereoscopic image projection. Opt. Lett. 2018, 43, 3678–3681. [Google Scholar] [CrossRef] [PubMed]
- Omaki, M.; Kajiyama, Y.; Imaki, M.; Inoue, Y.; Nakahara, S.; Honda, N.; Niikura, E.; Hirata, Y.; Nomura, J.; Yoshida, M.; et al. Compact and MEMS-Scanner-Based 3-D Imaging LiDAR With Wide Scanning Angle of 147.5° × 11.6° Using Multiple Transmitters and a Single Small Photodetector With Diameter of 0.5 mm. IEEE Sens. J. 2022, 22, 20389–20400. [Google Scholar] [CrossRef]
- Gour, A.; Menard, M.; Nabki, F. A High-Speed Chip-Scale Rotary Polygon Optical Scanner Based on a Micromotor Integrated With a Micro-Polyhedron Mirror. J. Microelectromech. Syst. 2022, 31, 486–499. [Google Scholar] [CrossRef]
- Heck, M.J.R. Highly integrated optical phased arrays: Photonic integrated circuits for optical beam shaping and beam steering. Nanophotonics 2017, 6, 93–107. [Google Scholar] [CrossRef]
- Tao, M.; Peng, T.; Ding, C.; Guan, J.; Li, Y.; Zhang, L.; Chena, B.; Gao, L.; Li, X.; Song, J.; et al. A Large-Range Steering Optical Phased Array Chip and High-Speed Controlling System. IEEE Trans. Instrum. Meas. 2022, 71, 2001212. [Google Scholar] [CrossRef]
- Raptakis, A.; Gounaridis, L.; Weigel, M.; Kleinert, M.; Georgiopoulos, M.; Mylonas, E.; Groumas, P.; Tsokos, C.; Keil, N.; Avramopoulos, H.; et al. 2D Optical Phased Arrays for Laser Beam Steering Based on 3D Polymer Photonic Integrated Circuits. J. Light. Technol. 2021, 39, 6509–6523. [Google Scholar] [CrossRef]
- Sun, J.; Timurdogan, E.; Yaacobi, A.; Hosseini, E.S.; Watts, M.R. Large-scale nanophotonic phased array. Nature 2013, 493, 195–199. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, G.; Zhang, X.; Kwon, K.; Blanche, P.-A.; Triesault, N.; Yu, K.-S.; Wu, M.C. 2D broadband beamsteering with large-scale MEMS optical phased array. Optica 2019, 6, 557–562. [Google Scholar] [CrossRef]
- Ashtiani, F.; Aflatouni, F. N × N optical phased array with 2N phase shifters. Opt. Express 2019, 27, 27183–27190. [Google Scholar] [CrossRef]
- Zhang, X.; Kwon, K.; Henriksson, J.; Luo, J.; Wu, M.C. A large-scale microelectromechanical-systems-based silicon photonics LiDAR. Nature 2022, 603, 253–258. [Google Scholar] [CrossRef]
- Van Acoleyen, K.; Rogier, H.; Baets, R. Two-dimensional optical phased array antenna on silicon-on-insulator. Opt. Express 2010, 18, 13655–13660. [Google Scholar] [CrossRef] [PubMed]
- Morris, R.; Jones, C.; Nagaraj, M. Liquid Crystal Devices for Beam Steering Applications. Micromachines 2021, 12, 247. [Google Scholar] [CrossRef] [PubMed]
- Poulton, C.V.; Russo, P.; Timurdogan, E.; Whitson, M.; Byrd, M.J.; Hosseini, E.; Moss, B.; Su, Z.; Vermeulen, D.; Watts, M.R. High-Performance Integrated Optical Phased Arrays for Chip-Scale Beam Steering and LiDAR. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 13 May 2018; p. ATu3R.2. [Google Scholar]
- Gozzard, D.R.; Roberts, L.E.; Spollard, J.T.; Sibley, P.G.; Shaddock, D.A. Fast beam steering with an optical phased array. Opt. Lett. 2020, 45, 3793–3796. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Dostart, N.; Khilo, A.; Brand, M.; Qubaisi, K.A.; Onural, D.; Feldkhun, D.; Popović, M.A.; Wagner, K. Serpentine Optical Phased Array Silicon Photonic Aperture Tile with Two-Dimensional Wavelength Beam Steering. In Proceedings of the 2019 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 3–7 March 2019; pp. 1–3. [Google Scholar]
- Guglielmon, J.; Byrd, M.J.; Moss, B.R.; Tran, J.; Millman, R.P.; Watts, M.R.; Poulton, C.V. Optical Phased Array Super-Cell Beyond the Reticle Limit. In Proceedings of the 2023 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 7–12 May 2023; pp. 1–2. [Google Scholar]
- Lim, A.E.J.; Song, J.; Fang, Q.; Li, C.; Tu, X.; Duan, N.; Chen, K.K.; Tern, R.P.C.; Liow, T.Y. Review of Silicon Photonics Foundry Efforts. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 405–416. [Google Scholar] [CrossRef]
- Fard, S.T.; Murray, K.; Caverley, M.; Donzella, V.; Flueckiger, J.; Grist, S.M.; Huante-Ceron, E.; Schmidt, S.A.; Kwok, E.; Jaeger, N.A.F.; et al. Silicon-on-insulator sensors using integrated resonance-enhanced defect-mediated photodetectors. Opt. Express 2014, 22, 28517–28529. [Google Scholar] [CrossRef] [PubMed]
- Soref, R. Mid-infrared photonics in silicon and germanium. Nat. Photonics 2010, 4, 495–497. [Google Scholar] [CrossRef]
- Vivien, L.; Polzer, A.; Marris-Morini, D.; Osmond, J.; Hartmann, J.M.; Crozat, P.; Cassan, E.; Kopp, C.; Zimmermann, H.; Fédéli, J.M. Zero-bias 40Gbit/s germanium waveguide photodetector on silicon. Opt. Express 2012, 20, 1096–1101. [Google Scholar] [CrossRef] [PubMed]
- Virot, L.; Benedikovic, D.; Szelag, B.; Alonso-Ramos, C.; Karakus, B.; Hartmann, J.-M.; Le Roux, X.; Crozat, P.; Cassan, E.; Marris-Morini, D.; et al. Integrated waveguide PIN photodiodes exploiting lateral Si/Ge/Si heterojunction. Opt. Express 2017, 25, 19487–19496. [Google Scholar] [CrossRef]
- Abediasl, H.; Hashemi, H. Monolithic optical phased-array transceiver in a standard SOI CMOS process. Opt. Express 2015, 23, 6509–6519. [Google Scholar] [CrossRef]
- Van Acoleyen, K.; Bogaerts, W.; Jágerská, J.; Le Thomas, N.; Houdré, R.; Baets, R. Off-chip beam steering with a one-dimensional optical phased array on silicon-on-insulator. Opt. Lett. 2009, 34, 1477–1479. [Google Scholar] [CrossRef]
- Xiao, F.; Hu, W.; Xu, A. Optical phased-array beam steering controlled by wavelength. Appl. Opt. 2005, 44, 5429–5433. [Google Scholar] [CrossRef] [PubMed]
- Doylend, J.K.; Heck, M.J.R.; Bovington, J.T.; Peters, J.D.; Bowers, J.E. Free-space beam steering using silicon waveguide surface gratings. In Proceedings of the IEEE Photonic Society 24th Annual Meeting, Arlington, VA, USA, 9–13 October 2011; pp. 547–548. [Google Scholar]
- Wang, Q.; Wang, S.; Zeng, Y.; Wang, W.; Cai, Y.; Tu, Z.; Yue, W.; Wang, X.; Fang, Q.; Yu, M. Dual-layer waveguide grating antenna with high directionality for optical phased arrays. Appl. Opt. 2019, 58, 5807–5811. [Google Scholar] [CrossRef] [PubMed]
- Zadka, M.; Chang, Y.-C.; Mohanty, A.; Phare, C.T.; Roberts, S.P.; Lipson, M. On-chip platform for a phased array with minimal beam divergence and wide field-of-view. Opt. Express 2018, 26, 2528–2534. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Li, Y.; Zhang, L.; Li, Y.; Liu, X.; Tao, M.; Hou, Y.; Tang, H.; Zhi, Z.; Gao, F.; et al. Unidirectional large-scale waveguide grating with uniform radiation for optical phased array. Opt. Express 2021, 29, 20995–21010. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Chen, J.; Shi, Y. All-Solid-State Beam Steering via Integrated Optical Phased Array Technology. Micromachines 2022, 13, 894. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yu, L.; Yang, Y.; Ma, P.; Cui, L.; Luo, S.; Ji, Z.; Song, Z.; Su, Y.; Pan, J.; et al. Wide field of view optical phased array with a high-directionality antenna. Opt. Express 2023, 31, 21192–21199. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Chen, B.; Na, Q.; Xie, Q.; Tao, M.; Zhang, L.; Zhi, Z.; Li, Y.; Liu, X.; Luo, X.; et al. Wide-steering-angle high-resolution optical phased array. Photonics Res. 2021, 9, 2511–2518. [Google Scholar] [CrossRef]
- Yan, X.; Chen, J.; Dai, D.; Shi, Y. Polarization Multiplexing Silicon-Photonic Optical Phased Array for 2D Wide-Angle Optical Beam Steering. IEEE Photonics J. 2021, 13, 6600506. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, J.; Shi, Y. Dual Polarization and Bi-Directional Silicon-Photonic Optical Phased Array with Large Scanning Range. IEEE Photonics J. 2022, 14, 6620905. [Google Scholar] [CrossRef]
- Guo, X.; Li, Z.; Chen, H.; Li, Y.; Ye, M.; Zhang, X.; Yu, Y. Two-dimensional silicon optical phased array with large field of view. Opt. Express 2022, 30, 28049–28056. [Google Scholar] [CrossRef]
- Zhao, S.; Lian, D.; Chen, J.; Dai, D.; Shi, Y. Polarization multiplexing silicon photonic optical phased array with a wide scanning range. Opt. Lett. 2023, 48, 6092–6095. [Google Scholar] [CrossRef] [PubMed]
- Tan, K.; Huang, Y.; Lo, G.Q.; Lee, C.; Yu, C. Three-dimensional polarization splitter and rotator based on multi-layer Si3N4-on-SOI platform. In Proceedings of the 2016 International Conference on Optical MEMS and Nanophotonics (OMN), Singapore, 31 July–4 August 2016; pp. 1–2. [Google Scholar]
- Sun, X.; Alam, M.Z.; Aitchison, J.S.; Mojahedi, M. Compact and broadband polarization beam splitter based on a silicon nitride augmented low-index guiding structure. Opt. Lett. 2016, 41, 163–166. [Google Scholar] [CrossRef]
- Tyler, N.A.; Fowler, D.; Malhouitre, S.; Garcia, S.; Grosse, P.; Rabaud, W.; Szelag, B. SiN integrated optical phased arrays for two-dimensional beam steering at a single near-infrared wavelength. Opt. Express 2019, 27, 5851–5858. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Wang, S.; Jia, L.; Cai, Y.; Yue, W.; Yu, M. Increasing wavelength-controlled steering range of an optical phasedarray by using two subarrays. Appl. Opt. 2021, 60, 5424–5429. [Google Scholar] [CrossRef] [PubMed]
- Luo, G.; Yu, L.; Ma, P.; Wang, R.; Cui, L.; Wang, Z.; Yu, H.; Zhou, X.; Wang, P.; Zhang, Y.; et al. A Large-Scale Passive Optical Phase Array With 1024 Channels. IEEE Photonics Technol. Lett. 2023, 35, 927–930. [Google Scholar] [CrossRef]
- Yu, L.; Ma, P.; Luo, G.; Cui, L.; Zhou, X.; Wang, P.; Zhang, Y.; Pan, J. Adoption of large aperture chirped grating antennas in optical phase array for long distance ranging. Opt. Express 2022, 30, 28112–28120. [Google Scholar] [CrossRef]
- Qiu, H.; Liu, Y.; Meng, X.; Guan, X.; Ding, Y.; Hu, H. Bidirectional high sidelobe suppression silicon optical phased array. Photonics Res. 2023, 11, 659–668. [Google Scholar] [CrossRef]
- Raval, M.; Poulton, C.V.; Watts, M.R. Unidirectional waveguide grating antennas with uniform emission for optical phased arrays. Opt. Lett. 2017, 42, 2563–2566. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Li, J.; Yao, Y.; Sun, Y.; Tian, J.; Zou, Y.; Zhao, X.; Xu, X. Subwavelength structure enabled ultra-long waveguide grating antenna. Opt. Express 2021, 29, 15133–15144. [Google Scholar] [CrossRef]
- Zhang, Y.; Ling, Y.-C.; Zhang, K.; Gentry, C.; Sadighi, D.; Whaley, G.; Colosimo, J.; Suni, P.; Ben Yoo, S.J. Sub-wavelength-pitch silicon-photonic optical phased array for large field-of-regard coherent optical beam steering. Opt. Express 2019, 27, 1929–1940. [Google Scholar] [CrossRef]
- Wang, P.F.; Luo, G.Z.; Yu, H.Y.; Li, Y.J.; Wang, M.Q.; Zhou, X.L.; Chen, W.X.; Zhang, Y.J.; Pan, J.Q. Improving the performance of optical antenna for optical phased arrays through high-contrast grating structure on SOI substrate. Opt. Express 2019, 27, 2703–2712. [Google Scholar] [CrossRef]
- Yaacobi, A.; Sun, J.; Moresco, M.; Leake, G.; Coolbaugh, D.; Watts, M.R. Integrated phased array for wide-angle beam steering. Opt. Lett. 2014, 39, 4575–4578. [Google Scholar] [CrossRef]
- Song, W.; Gatdula, R.; Abbaslou, S.; Lu, M.; Stein, A.; Lai, W.Y.C.; Provine, J.; Pease, R.F.W.; Christodoulides, D.N.; Jiang, W. High-Density Low-Crosstalk Waveguide Superlattice. In Proceedings of the Frontiers in Optics 2015, San Jose, CA, USA, 18 October 2015; p. FM1F.6. [Google Scholar]
- Yang, N.; Yang, H.; Hu, H.; Zhu, R.; Chen, S.; Zhang, H.; Jiang, W. Theory of high-density low-cross-talk waveguide superlattices. Photonics Res. 2016, 4, 233–239. [Google Scholar] [CrossRef]
- Phare, C.T.; Shin, M.C.; Sharma, J.; Ahasan, S.; Krishnaswamy, H.; Lipson, M. Silicon Optical Phased Array with Grating Lobe-Free Beam Formation Over 180 Degree Field of View. In Proceedings of the 2018 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 13–18 May 2018; pp. 1–2. [Google Scholar]
- Kim, Y.; Yoon, H.; You, J.-B.; Kim, M.; Park, H.-H. Wide-Angle Beam-Steering Using an Optical Phased Array with Non-Uniform-Width Waveguide Radiators. Photonics 2020, 7, 56. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, W.; Xia, J.; Huang, Q. Optical phased array antenna with wide steering range using grating array superlattices. In Proceedings of the Sixth International Conference on Optical and Photonic Engineering (icOPEN 2018), Shanghai, China, 8–11 May 2018. [Google Scholar]
- Yi, X.; Zeng, H.; Gao, S.; Qiu, C. Design of an ultra-compact low-crosstalk sinusoidal silicon waveguide array for optical phased array. Opt. Express 2020, 28, 37505–37513. [Google Scholar] [CrossRef] [PubMed]
- Liang, D.; Li, W.; Wang, X.; Zhao, X.; Guo, Z.; Han, X.E.; Chen, J.; Dai, D.; Shi, Y. Grating lobe-free silicon optical phased array with periodically bending modulation of dense antennas. Opt. Express 2023, 31, 11423–11430. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Luo, G.; Xu, Y.; Li, Y.; Su, Y.; Ma, J.; Wang, R.; Yang, Z.; Zhou, X.; Zhang, Y.; et al. Design and fabrication of a SiN-Si dual-layer optical phased array chip. Photonics Res. 2020, 8, 912–919. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, H. Silicon optical phased array with a 180-degree field of view for 2D optical beam steering. Optica 2022, 9, 903–907. [Google Scholar] [CrossRef]
- Zhuang, D.; Zhagn, L.; Han, X.; Li, Y.; Li, Y.; Liu, X.; Gao, F.; Song, J. Omnidirectional beam steering using aperiodic optical phased array with high error margin. Opt. Express 2018, 26, 19154–19170. [Google Scholar] [CrossRef]
- Dong, T.; He, J.; He, X.; Xu, Y.; Zhou, J. Hybrid design approach of optical phased array with wide beam steering range and low side-lobe level. Opt. Lett. 2022, 47, 806–809. [Google Scholar] [CrossRef]
- Xu, W.; Guo, Y.; Li, X.; Liu, C.; Lu, L.; Chen, J.; Zhou, L. Fully Integrated Solid-State LiDAR Transmitter on a Multi-Layer Silicon-Nitride-on-Silicon Photonic Platform. J. Light. Technol. 2023, 41, 832–840. [Google Scholar] [CrossRef]
- Hutchison, D.N.; Sun, J.; Doylend, J.K.; Kumar, R.; Heck, J.; Kim, W.; Phare, C.T.; Feshali, A.; Rong, H. High-resolution aliasing-free optical beam steering. Optica 2016, 3, 887–890. [Google Scholar] [CrossRef]
- Kwong, D.; Hosseini, A.; Zhang, Y.; Chen, R. 1 × 12 Unequally spaced waveguide array for actively tuned optical phased array on a silicon nanomembrane. Appl. Phys. Lett. 2011, 99, 051104. [Google Scholar] [CrossRef]
- Hosseini, A.; Kwong, D.; Zhao, Y.; Chen, Y.S.; Crnogorac, F.; Pease, R.F.W.; Chen, R.T. Unequally Spaced Waveguide Arrays for Silicon Nanomembrane-Based Efficient Large Angle Optical Beam Steering. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 1439–1446. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, P.; Yang, Y.; Cui, L.; Yu, L.; Luo, G.; Wang, P.; Pan, J.; Su, Y.; Zhang, Y. Non-uniform optical phased array with a large steering angle and high side mode suppression ratio. Appl. Opt. 2022, 61, 10788–10793. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Wang, S.; Jia, L.; Cai, Y.; Yue, W.; Yu, M. Silicon nitride assisted 1 × 64 optical phased array based on a SOI platform. Opt. Express 2021, 29, 10509–10517. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Li, Y.; Chen, B.; Wang, Y.; Li, H.; Hou, Y.; Tao, M.; Li, Y.; Zhi, Z.; Liu, X.; et al. Two-dimensional multi-layered SiN-on-SOI optical phased array with wide-scanning and long-distance ranging. Opt. Express 2022, 30, 5008–5018. [Google Scholar] [CrossRef] [PubMed]
- Han, K.; Yurlov, V.; Yu, N.E. Highly directional waveguide grating antenna for optical phased array. Curr. Appl. Phys. 2018, 18, 824–828. [Google Scholar] [CrossRef]
- Li, W.-L.; Liu, J.-W.; Cheng, G.-A.; Huang, Q.-Z.; Zheng, R.-T.; Wu, X.-L. Diffraction gratings based on a multilayer silicon nitride waveguide with high upward efficiency and large effective length. Appl. Opt. 2022, 61, 2604–2609. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yang, Y.; Cui, L.; Yu, L.; Ma, P.; Luo, S.; Wang, P.; Song, Z.; Ji, Z.; Pan, J.; et al. High-directionality SiN-assisted grating antenna for optical phased array. J. Opt. Soc. Am. B 2023, 40, 1994–1998. [Google Scholar] [CrossRef]
- Bo, Y.; Wang, Q.; Wang, J.; Cai, Y.; Yue, W.; Wang, S.; Wang, W.; Yu, M. Multilayered High-directional Waveguide Grating Antenna Based on Interleaved Etching for Optical Phased Arrays. Curr. Opt. Photon. 2023, 7, 157–165. [Google Scholar]
- Zhang, L.; Li, Y.; Hou, Y.; Wang, Y.; Tao, M.; Chen, B.; Na, Q.; Li, Y.; Zhi, Z.; Liu, X.; et al. Investigation and demonstration of a high-power handling and large-range steering optical phased array chip. Opt. Express 2021, 29, 29755–29765. [Google Scholar] [CrossRef]


| Ref | Platform | Scheme | Divergence | Length of WGA | Scanning Rang | |
|---|---|---|---|---|---|---|
| Expanding scanning range | [45] | Si | Polarization Multiplexed | / | / | 28.2° |
| [46] | Si | Polarization Multiplexed | / | / | 54.5° | |
| [54] | Si | Polarization multiplexed | / | / | 15.62° + 16.08° | |
| [48] | Si | Polarization multiplexed | 2.0° | / | 28° | |
| [52] | Si-Si3N4 | Wavelength multiplexing | 0.067° | / | 32.6° | |
| Reducing longitudinal divergence angle | [56] | Si3N4 | Apodized WGA | / | 3 mm | / |
| [57] | Si | Subwavelength WGA | 0.081° | 1 mm | 0.17°/nm | |
| [41] | Si3N4 | Apodized WGA | 0.029° [44] | 3 mm | / | |
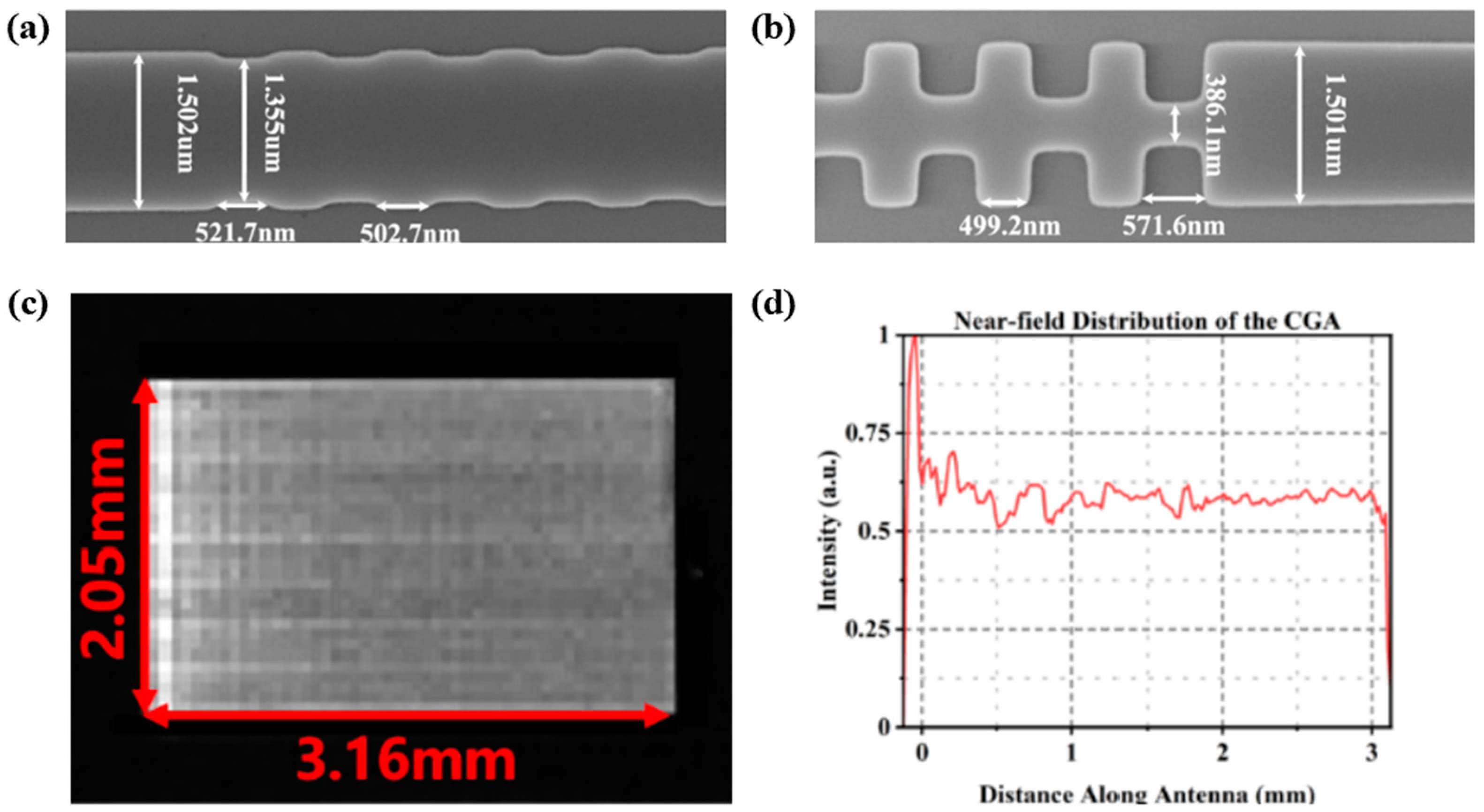
| [54] | Si3N4 | Apodized WGA | 0.04° | 3.16 mm | 0.064°/nm | |
| [55] | Si | Gaussian apodized WGA | 0.07° | 2 mm | 13.2° | |
| [53] | Si- Si3N4 | Uniform periodic WGA | 0.05° | 5 mm | 15.1° |
| Ref | Platform | Scheme | Divergence Angle | Number of Channels | Scanning Range |
|---|---|---|---|---|---|
| [60] | Si | Periodic | 3.3° | 16 | 51° |
| [63] | Si | Periodic | 1.2° | 64 | 120° |
| [77] | Si-Si3N4 | Periodic | 0.69° | 64 | 35.5° |
| [78] | Si-Si3N4 | Periodic | 1.9° | 64 | 96° |
| [53] | Si-Si3N4 | Periodic | 0.04° | 1024 | 40° |
| [68] | Si-Si3N4 | Si slab array | 2.3° | 32 | 96° |
| [69] | Si | Si slab array | 2.1° | 64 | 180° |
| [73] | Si | Aperiodic | 0.14° | 128 | 80° |
| [44] | Si-Si3N4 | Aperiodic | 0.021° | 128 | 140° |
| [43] | Si3N4 | Aperiodic | 0.066° | 256 | 150° |
| [72] | Si-Si3N4 | Aperiodic | 0.051° | 256 | 140° |
| Ref | Platform | Scheme | Unidirectionality | |
|---|---|---|---|---|
| Simulation | [79] | Si | Etching upper SiO2 cladding | >70% |
| [39] | Si-Si3N4 | Shallow etching Si3N4 grating | >89% | |
| [59] | Si-poly-Si | High contrast grating | 93.94% | |
| [82] | Si-Si3N4 | Interleaved etching of Si3N4 grating | 97% | |
| Fabrication and testing | [56] | Si3N4 | Dual-layer Si3N4 grating with offset | >90% |
| [41] | Si3N4 | Etching dual-level Si3N4 grating with offset | ~80–90% | |
| [43] | Si3N4 | Dual-layer Si3N4 grating with offset | >92% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Song, R.; Li, X.; Yue, W.; Cai, Y.; Wang, S.; Yu, M. Beam Steering Technology of Optical Phased Array Based on Silicon Photonic Integrated Chip. Micromachines 2024, 15, 322. https://doi.org/10.3390/mi15030322
Wang J, Song R, Li X, Yue W, Cai Y, Wang S, Yu M. Beam Steering Technology of Optical Phased Array Based on Silicon Photonic Integrated Chip. Micromachines. 2024; 15(3):322. https://doi.org/10.3390/mi15030322
Chicago/Turabian StyleWang, Jinyu, Ruogu Song, Xinyu Li, Wencheng Yue, Yan Cai, Shuxiao Wang, and Mingbin Yu. 2024. "Beam Steering Technology of Optical Phased Array Based on Silicon Photonic Integrated Chip" Micromachines 15, no. 3: 322. https://doi.org/10.3390/mi15030322
APA StyleWang, J., Song, R., Li, X., Yue, W., Cai, Y., Wang, S., & Yu, M. (2024). Beam Steering Technology of Optical Phased Array Based on Silicon Photonic Integrated Chip. Micromachines, 15(3), 322. https://doi.org/10.3390/mi15030322