A Phase Model of the Bio-Inspired NbOx Local Active Memristor under Weak Coupling Conditions
Abstract
:1. Introduction
2. The Kuramoto Model
3. The Dynamical Characteristics of the Memristor
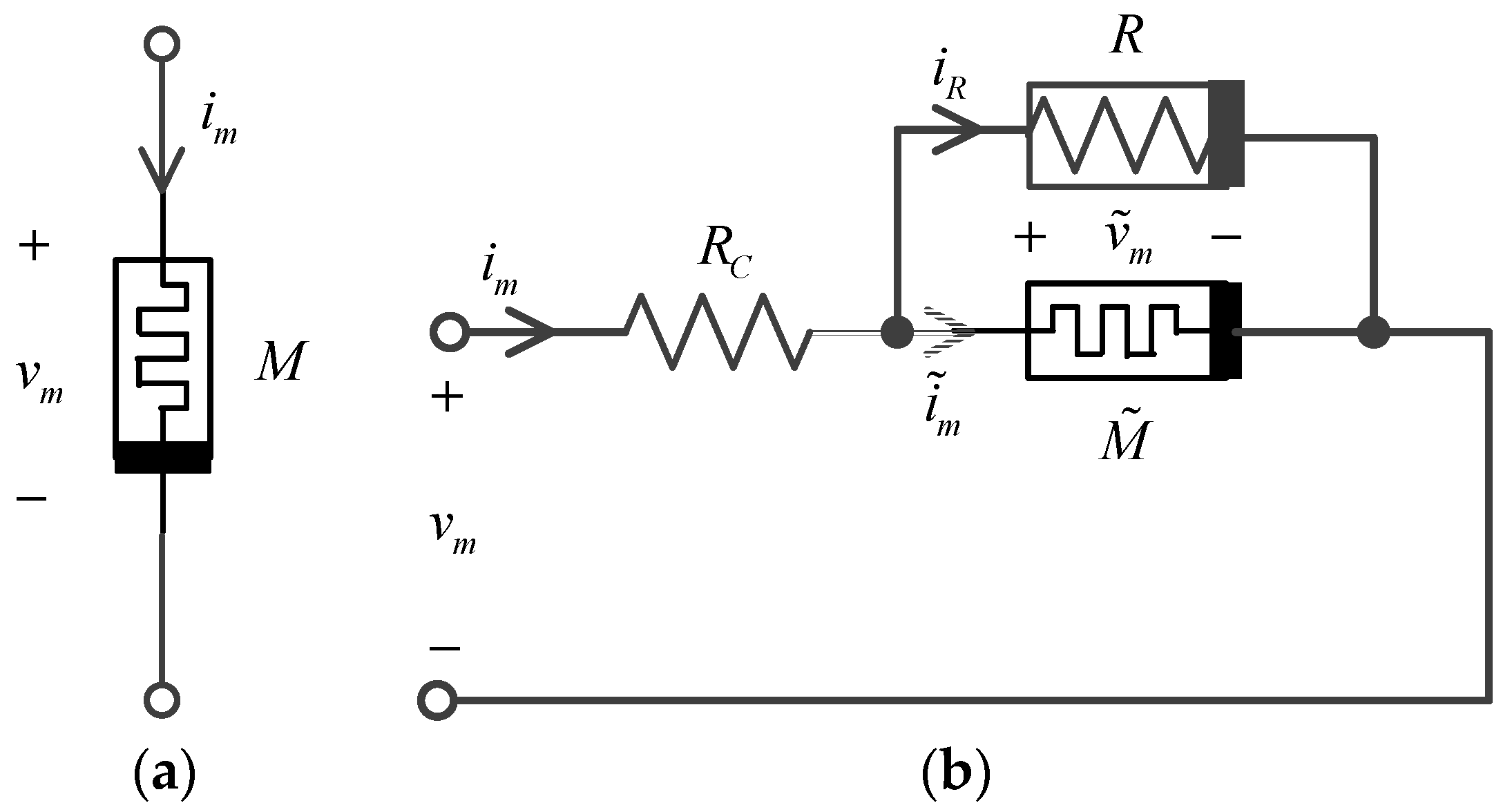
3.1. Chua’s Unfolding Model of the Memristor
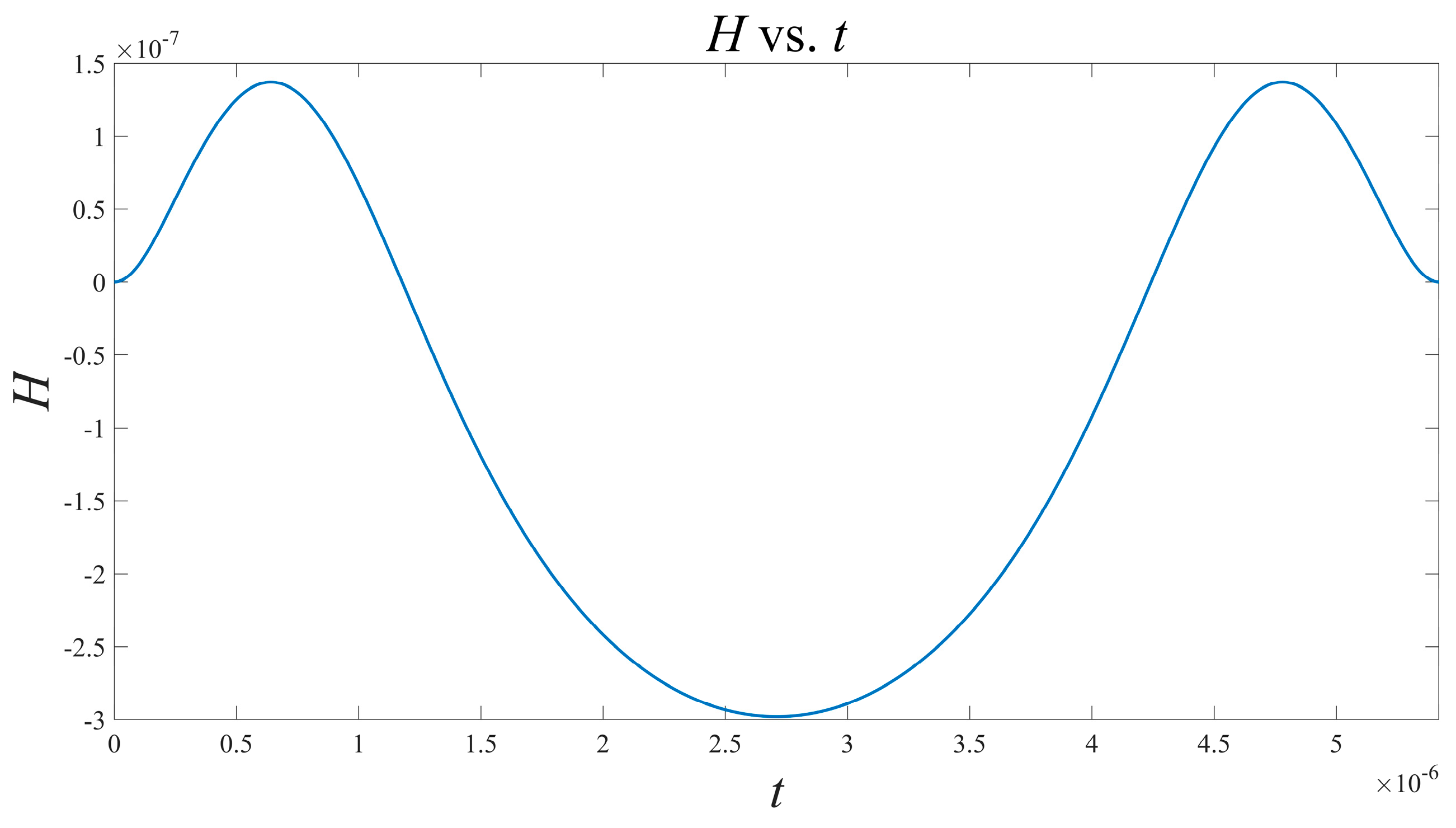
3.2. The Weak Coupling Theory
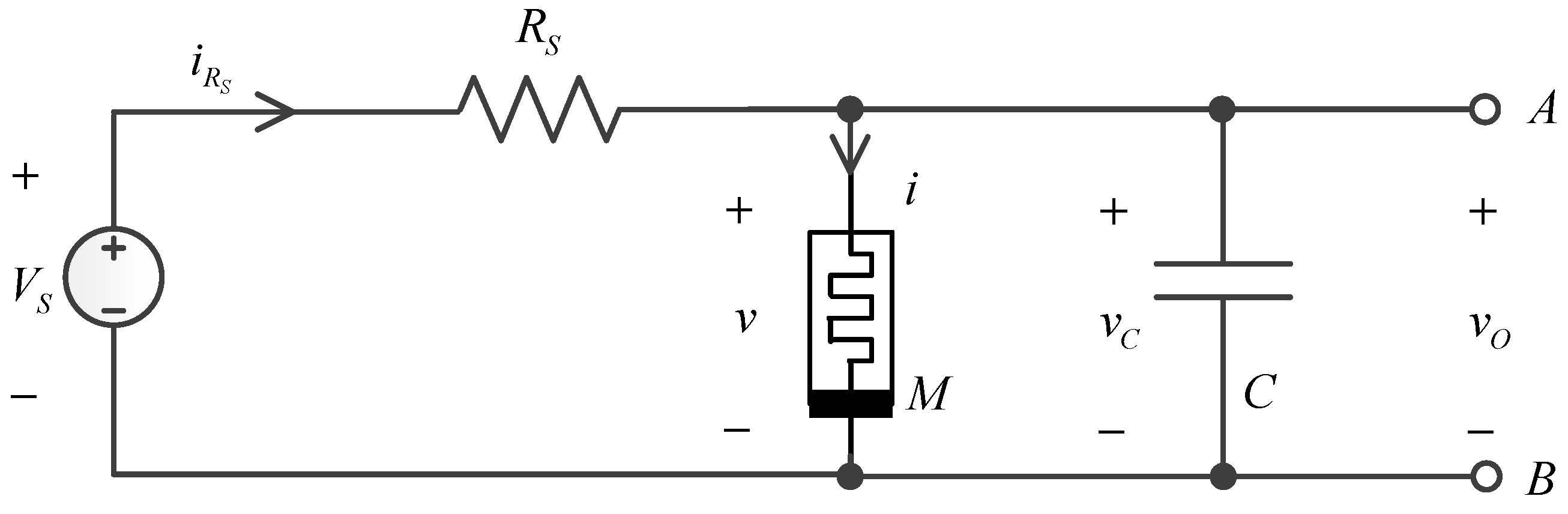
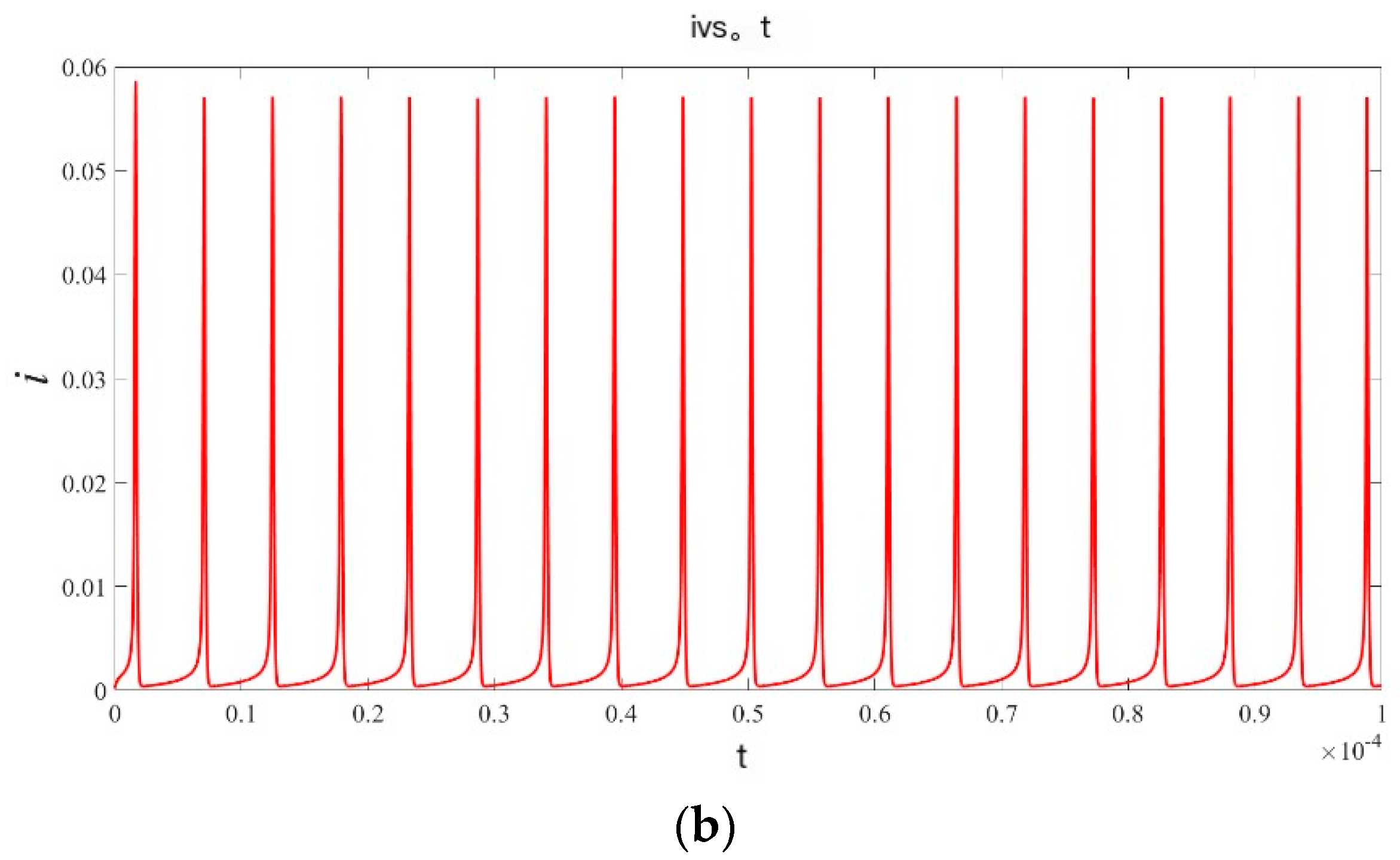
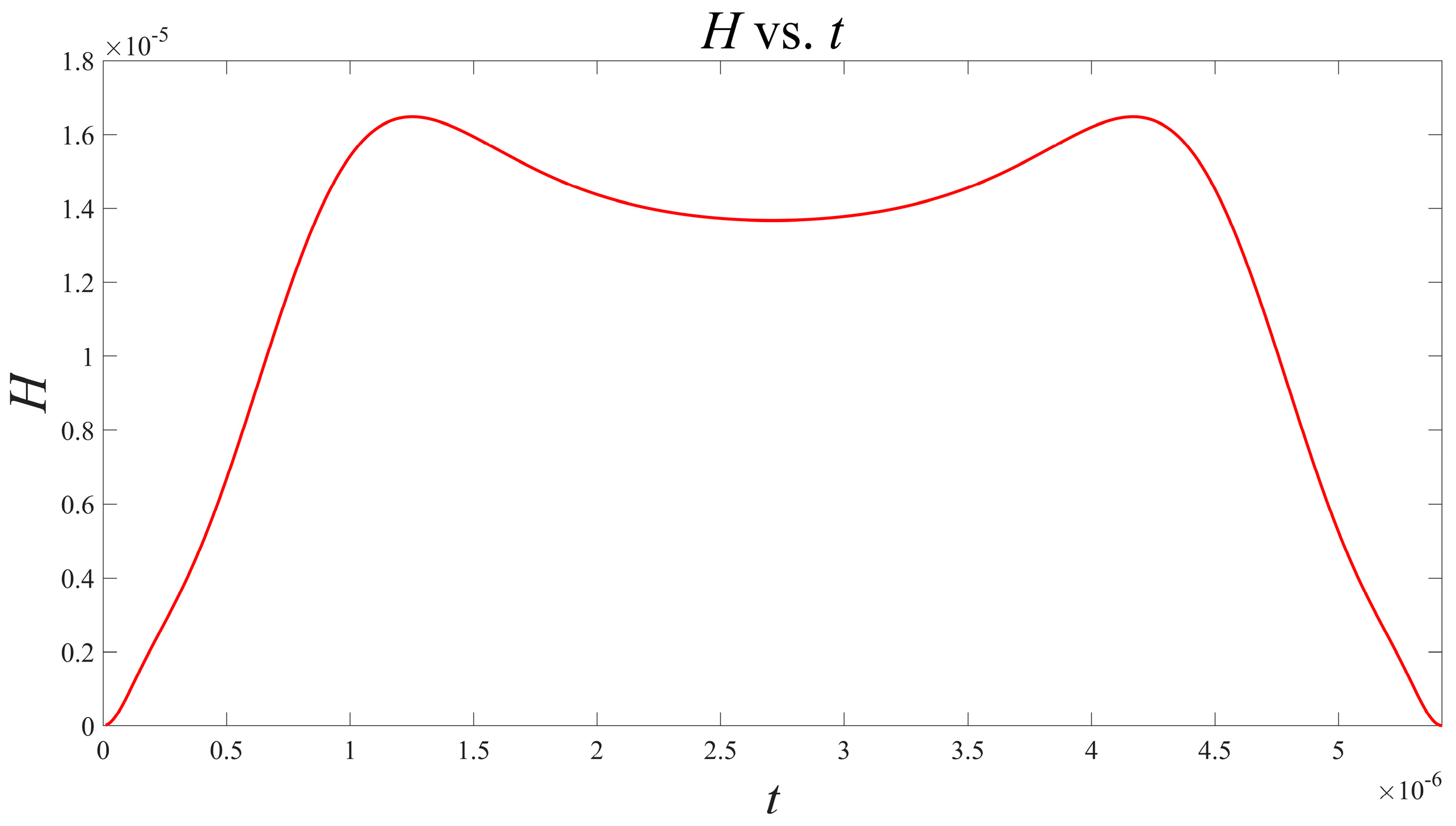
3.3. Single Memristor Oscillator
3.4. Phase Model of the Oscillator Pair
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chua, L.O. Memristor—The missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Chua, L.O.; Kang, S.M. Memristive devices and systems. IEEE Proc. 1976, 64, 209–223. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- James, M.T.; He, T. The fourth element. Nature 2008, 453, 42–43. [Google Scholar]
- Yang, J.J.; Pickett, M.D.; Li, X.; Ohlberg, D.A.A.; Stewart, D.R.; Williams, R.S. Memristive switching mechanism for metal/oxide/metal nanodevices. Nat. Nanotechnol. 2008, 3, 429–433. [Google Scholar] [CrossRef]
- Joglekar, Y.N.; Wolf, S.J. The elusive memristor: Signatures in basic electrical circuits. Eur. J. Phys. 2009, 30, 661–675. [Google Scholar] [CrossRef]
- Chua, L.O. If it’s pinched it’s a memristor. Semicond. Sci. Technol. 2014, 29, 104001. [Google Scholar] [CrossRef]
- Vourkas, I.; Sirakoulis, G.C. Memristor-Based Nanoelectronic Computing Circuits and Architectures; Springer International Publishing: Cham, Switzerland, 2016; pp. 101–103. [Google Scholar]
- Pi, S.; Lin, P.; Xia, Q. Cross point arrays of 8 nm × 8 nm memristive devices fabricated with nano imprint lithography. J. Vac. Sci. Technol. B 2013, 31, 06FA02. [Google Scholar] [CrossRef]
- Vourkas, I.; Sirakoulis, G.C. Emerging memristor-based logic circuit design approaches: A review. IEEE Circuits Syst. Mag. 2016, 16, 15–30. [Google Scholar] [CrossRef]
- Slavova, A. Memristor CNN Model for Image Denoising. In Proceedings of the 2019 26th IEEE International Conference on Electronics, Circuits, and Systems (ICECS), Genoa, Italy, 27–29 November 2019. [Google Scholar]
- Sah, M.P.; Kim, H.; Chua, L.O. Brains are made of memristors. IEEE Circuits Syst. Mag. 2014, 14, 12–36. [Google Scholar] [CrossRef]
- Prezioso, M.; Merrikh-Bayat, F.; Strukov, D.B. Training and operation of an integrated neuromorphic network based on metal-oxide memristors. Nature 2015, 521, 61–64. [Google Scholar] [CrossRef]
- Corinto, F.; Forti, M. Memristor circuits: Flux—Charge analysis method. IEEE Trans. Circuits Syst. I Reg. Pap. 2016, 63, 1997–2009. [Google Scholar] [CrossRef]
- Corinto, F.; Forti, M. Memristor circuits: Bifurcations without parameters. IEEE Trans. Circuits Syst. I Reg. Pap. 2017, 64, 1540–1551. [Google Scholar] [CrossRef]
- Pham, V.-T.; Vaidyanathan, S.; Volos, C.K.; Hoang, T.M. A novel memristive time–delay chaotic system without equilibrium points. Eur. Phys. J. Spec. Top. 2016, 225, 127–136. [Google Scholar] [CrossRef]
- Chen, M.; Li, M.Y.; Yu, Q.; Bao, B.C.; Xu, Q.; Wang, J. Dynamics of self-excited attractors and hidden attractors in generalized memristor based Chua’s circuit. Nonlinear Dyn. 2015, 81, 215–226. [Google Scholar] [CrossRef]
- Kumar, S.; Strachan, J.P.; Williams, R.S. Chaotic dynamics in nanoscale NbO2 Mott memristors for analogue computing. Nature 2017, 548, 318–321. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Williams, R.S.; Wang, Z. Third-order nanocircuit elements for neuromorphic engineering. Nature 2020, 585, 518–523. [Google Scholar] [CrossRef]
- Ventra, M.D.; Pershin, Y.V.; Chua, L.O. Circuit elements with memory: Memristors, memcapacitors, and meminductors. Proc. IEEE 2009, 97, 1717–1724. [Google Scholar] [CrossRef]
- Julian, M.R.; Pershin, Y.V. Bistable nonvolatile elastic-membrane memcapacitor exhibiting a chaotic behavior. IEEE Trans. Electron Devices 2011, 58, 1809–1812. [Google Scholar]
- Theis, T.N.; Solomon, P.M. In Quest of the ‘Next Switch’: Prospects for Greatly Reduced Power Dissipation in a Successor to the Silicon Field-Effect Transistor. Proc. IEEE 2010, 98, 2005–2014. [Google Scholar] [CrossRef]
- Zhirnov, V.V.; Cavin, R.K.; Hutchby, J.A.; Bourianoff, G.I. Limits to binary logic switch scaling—A gedanken model. Proc. IEEE 2003, 91, 1934–1939. [Google Scholar] [CrossRef]
- Ercsey-Ravasz, M.; Toroczkai, Z. Optimization hardness as transient chaos in an analog approach to constraint satisfaction. Nat. Phys. 2011, 7, 966–970. [Google Scholar] [CrossRef]
- Nikonov, D.E.; Csaba, G.; Porod, W.; Shibata, T.; Voils, D.; Hammerstrom, D.; Young, I.N. Coupled-Oscillator Associative Memory Array Operation for Pattern Recognition. IEEE J. Explor. Solid-State Comput. Devices Circuits 2015, 1, 85–93. [Google Scholar] [CrossRef]
- Welser, J.J.; Bourianoff, G.I.; Zhirnov, V.V.; Cavin, R.K. The quest for the next information processing technology. J. Nanopart. Res. 2007, 10, 1–10. [Google Scholar] [CrossRef]
- Srinivasan, G.; Sengupta, A.; Roy, K. Magnetic Tunnel Junction Based Long-Term Short- Term Stochastic Synapse for a Spiking Neural Network with On-Chip STDP Learning. Sci. Rep. 2016, 6, 29545. [Google Scholar] [CrossRef]
- Sharad, M.; Augustine, C.; Roy, K. Boolean and non-Boolean computation with spin devices. In Proceedings of the 2012 International Electron Devices Meeting, San Francisco, CA, USA, 10–13 December 2012; pp. 11.6.1–11.6.4. [Google Scholar]
- Bian, Z.; Chudak, F.; Macready, W.G.; Rose, G. The Ising model: Teaching an old problem new tricks. D-Wave Syst. 2010, 2, 1–32. [Google Scholar]
- Johnson, M.W.; Amin, M.H.; Gildert, S.; Lanting, T.; Hamze, F.; Dickson, N.; Harris, R.; Berkley, A.J.; Johansson, J.; Bunyk, P.; et al. Quantum annealing with manufactured spins. Nature 2011, 473, 194–198. [Google Scholar] [CrossRef] [PubMed]
- Boothby, K.; Bunyk, P.; Raymond, J.; Roy, A. Next-Generation Topology of D-Wave Quantum Processors. arXiv 2020, arXiv:2003.00133. [Google Scholar]
- Bian, Z.; Chudak, F.; Israel, R.; Lackey, B.; Macready, W.G.; Roy, A. Discrete optimization using quantum annealing on sparse Ising models. Front. Phys. 2014, 2, 56. [Google Scholar] [CrossRef]
- Marandi, A.; Wang, Z.; Takata, K.; Byer, R.L.; Yamamoto, Y. Network of time-multiplexed optical parametric oscillators as a coherent Ising machine. Nat. Photonics 2014, 8, 937–942. [Google Scholar] [CrossRef]
- Wang, T.; Roychowdhury, J. Oscillator-based Ising Machine. arXiv 2017, arXiv:1709.08102. [Google Scholar]
- Wang, T.; Wu, L.; Roychowdhury, J. New Computational Results and Hardware Prototypes for Oscillator-based Ising Machines. In Proceedings of the 56th Annual Design Automation Conference, Las Vegas, NV, USA, 2–6 June 2019; pp. 239:1–239:2. [Google Scholar]
- Wang, T.; Wu, L.; Nobel, P.; Roychowdhury, J. Solving combinatorial optimisation problems using oscillator based Ising machines. Nat. Comput. 2021, 20, 287–306. [Google Scholar] [CrossRef]
- Afoakwa, R.; Zhang, Y.; Vengalam, U.K.R.; Ignjatovic, Z.; Huang, M. BRIM: Bistable Resistively Coupled Ising Machine. In Proceedings of the 2021 IEEE International Symposium on High-Performance Computer Architecture (HPCA), Seoul, Republic of Korea, 27 February–3 March 2021; pp. 749–760. [Google Scholar]
- Singh, A.K.; Jamieson, K.; Venturelli, D.; McMahon, P. Ising Machines’ Dynamics and Regularization for Near-Optimal Large and Massive MIMO Detection. arXiv 2021, arXiv:2105.10535v1. [Google Scholar]
- Kim, M.; Venturelli, D.; Jamieson, K. Leveraging quantum annealing for large MIMO processing in centralized radio access networks. In Proceedings of the ACM Special Interest Group on Data Communication, Beijing, China, 19–23 August 2019; ACM: New York, NY, USA, 2019; pp. 241–255. [Google Scholar]
- Goto, H. Bifurcation-based adiabatic quantum computation with a nonlinear oscillator network. Sci. Rep. 2016, 6, 21686. [Google Scholar] [CrossRef]
- Ashwin, P.; Coombes, S.; Nicks, R. Mathematical Frameworks for Oscillatory Network Dynamics in Neuroscience. J. Math. Neurosci. 2016, 6, 2. [Google Scholar] [CrossRef]
- Arnaudon, A.; Peach, R.L.; Petri, G.; Expert, P. Connecting Hodge and Sakaguchi-Kuramoto through a mathematical framework for coupled oscillators on simplicial complexes. Commun. Phys. 2022, 5, 211. [Google Scholar] [CrossRef]
- Takemura, N.; Takata, K.; Takiguchi, M.; Notomi, M. Emulating the local Kuramoto model with an injection-locked photonic crystal laser array. Sci. Rep. 2021, 11, 8587. [Google Scholar] [CrossRef] [PubMed]
- Markdahl, J.; Proverbio, D.; Mi, L.; Goncalves, J. Almost global convergence to practical synchronization in the generalized Kuramoto model on networks over the n-sphere. Commun. Phys. 2021, 4, 187. [Google Scholar] [CrossRef]
- Ódor, G.; Kelling, J. Critical synchronization dynamics of the Kuramoto model on connectome and small world graphs. Sci. Rep. 2019, 9, 19621. [Google Scholar] [CrossRef]
- Ratas, I.; Pyragas, K.; Tass, P.A. Multistability in a star network of Kuramoto-type oscillators with synaptic plasticity. Sci. Rep. 2021, 11, 9840. [Google Scholar] [CrossRef]
- Park, Y.; Ermentrout, B. Weakly coupled oscillators in a slowly varying world. J. Comput. Neurosci. 2016, 40, 269–281. [Google Scholar] [CrossRef] [PubMed]
- Ermentrout, B.; Park, Y.; Wilson, D. Recent advances in coupled oscillator theory. Philos. Trans. R. Soc. 2019, 377, 20190092. [Google Scholar] [CrossRef] [PubMed]
- Ascoli, A.; Weiher, M.; Herzig, M.; Slesazeck, S.; Mikolajick, T.; Tetzlaff, R. Graph Coloring via Locally-Active Memristor Oscillatory Networks. J. Low Power Electron. Appl. 2022, 12, 22. [Google Scholar] [CrossRef]
- Ascoli, A.; Slesazeck, S.; Mähne, H.; Tetzlaff, R.; Mikolajick, T. Nonlinear Dynamics of a Locally-Active Memristor. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 1165–1174. [Google Scholar] [CrossRef]
- Ascoli, A.; Demirkol, A.S.; Tetzlaff, R.; Slesazeck, S.; Mikolajick, T.; Chua, L.O. On Local Activity and Edge of Chaos in a NaMLab Memristor. Front. Neurosci. 2021, 15, 651452. [Google Scholar] [CrossRef]
- Ascoli, A.; Demirkol, A.S.; Tetzlaff, R.; Chua, L. Analysis and Design of Bio-Inspired Circuits With Locally-Active Memristors. IEEE Trans. Circuits Syst. II Express Briefs 2023, 71, 1721–1726. [Google Scholar] [CrossRef]



| Initial Condition | |||
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Shen, Y. A Phase Model of the Bio-Inspired NbOx Local Active Memristor under Weak Coupling Conditions. Micromachines 2024, 15, 390. https://doi.org/10.3390/mi15030390
Ma X, Shen Y. A Phase Model of the Bio-Inspired NbOx Local Active Memristor under Weak Coupling Conditions. Micromachines. 2024; 15(3):390. https://doi.org/10.3390/mi15030390
Chicago/Turabian StyleMa, Xuetiao, and Yiran Shen. 2024. "A Phase Model of the Bio-Inspired NbOx Local Active Memristor under Weak Coupling Conditions" Micromachines 15, no. 3: 390. https://doi.org/10.3390/mi15030390







