Effective Permittivity for FDTD Calculation of Plasmonic Materials
Abstract
:1. Introduction
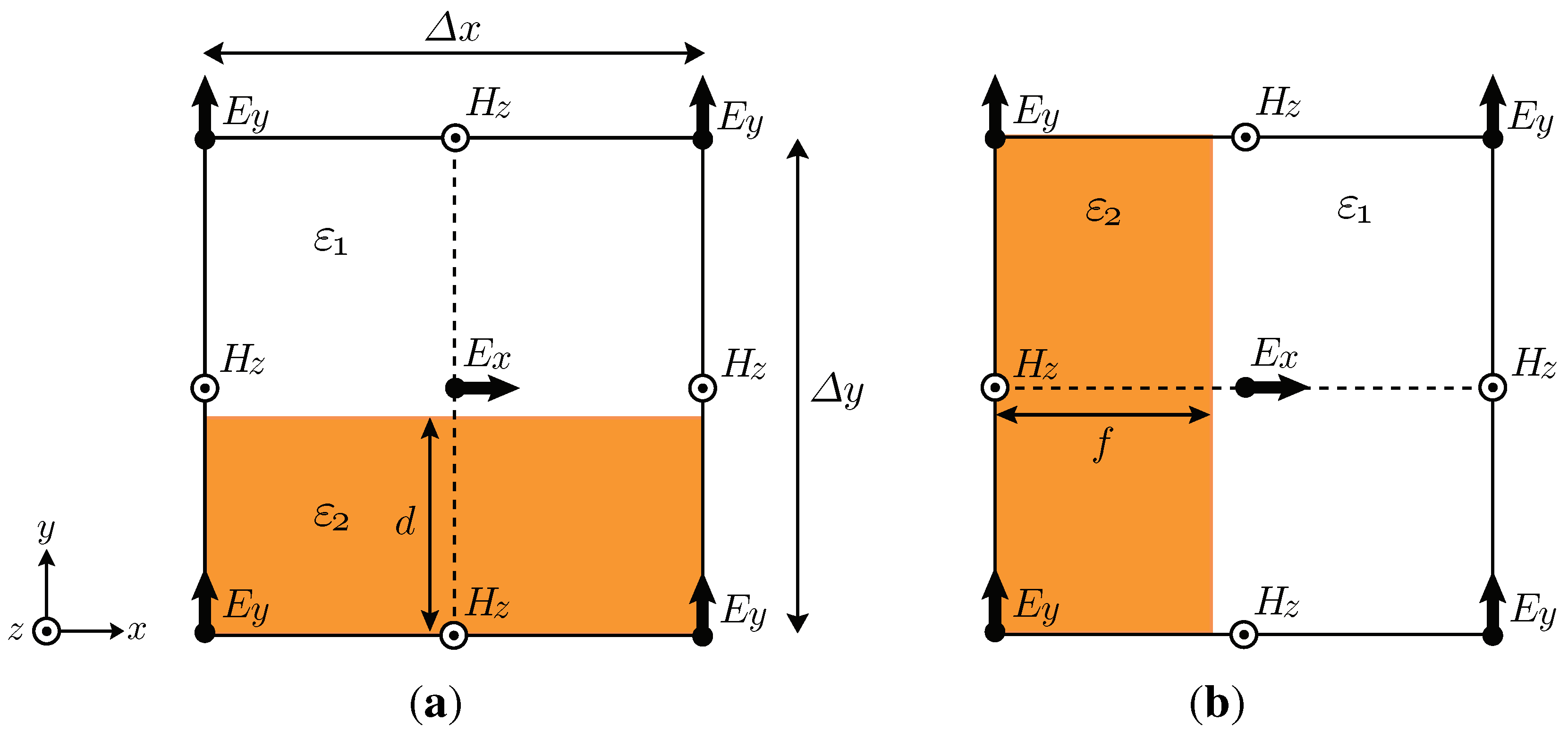
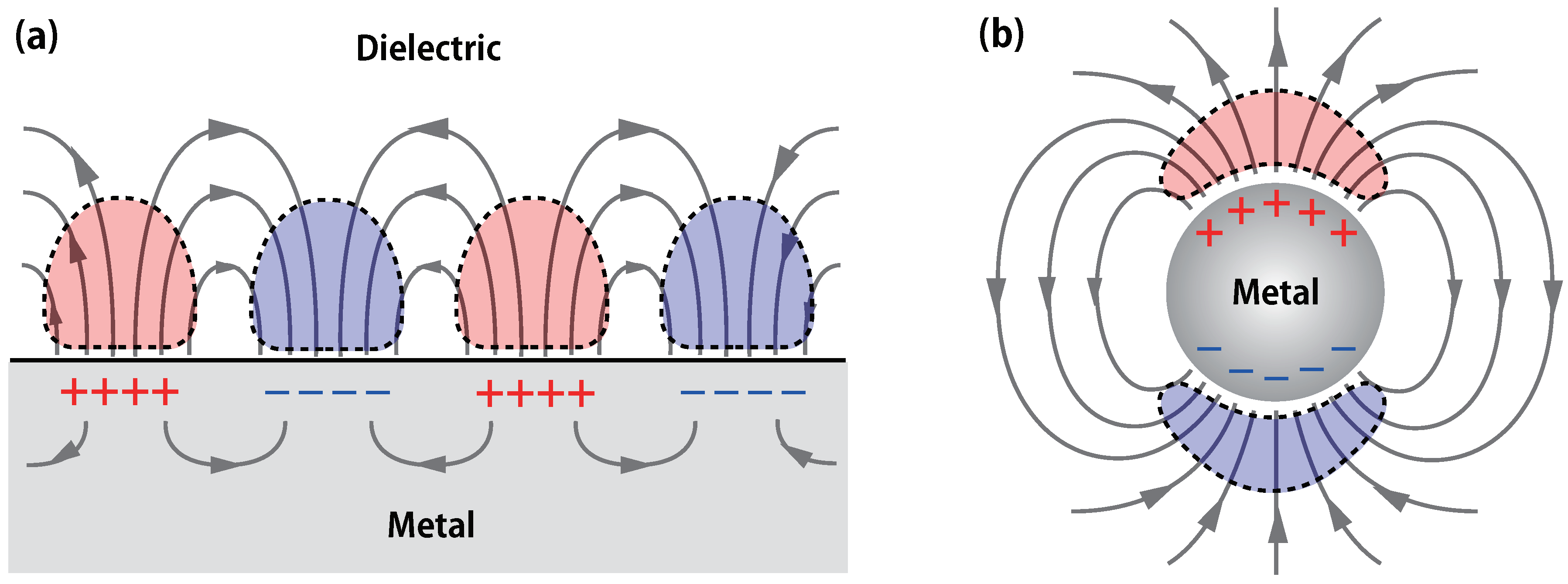
2. Effective Permittivity for Plasmonic Materials
3. Numerical Validations
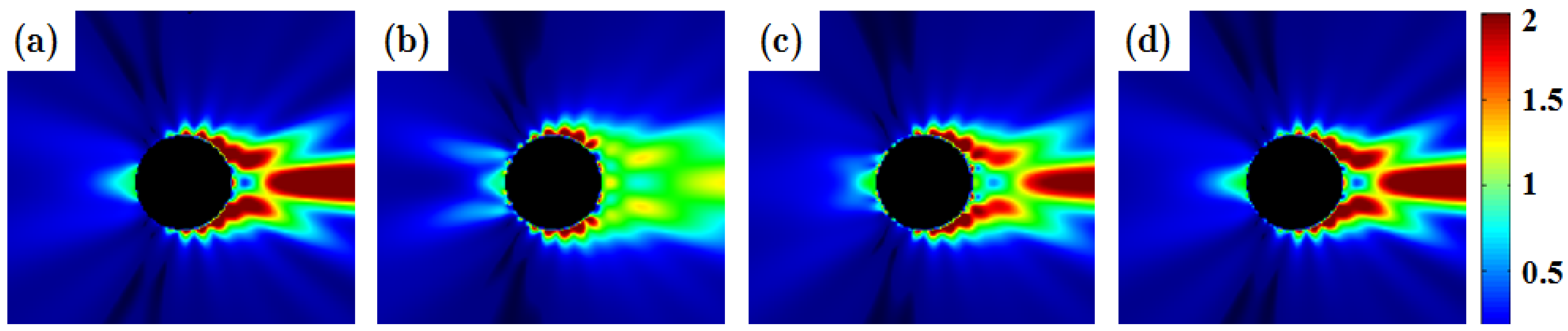
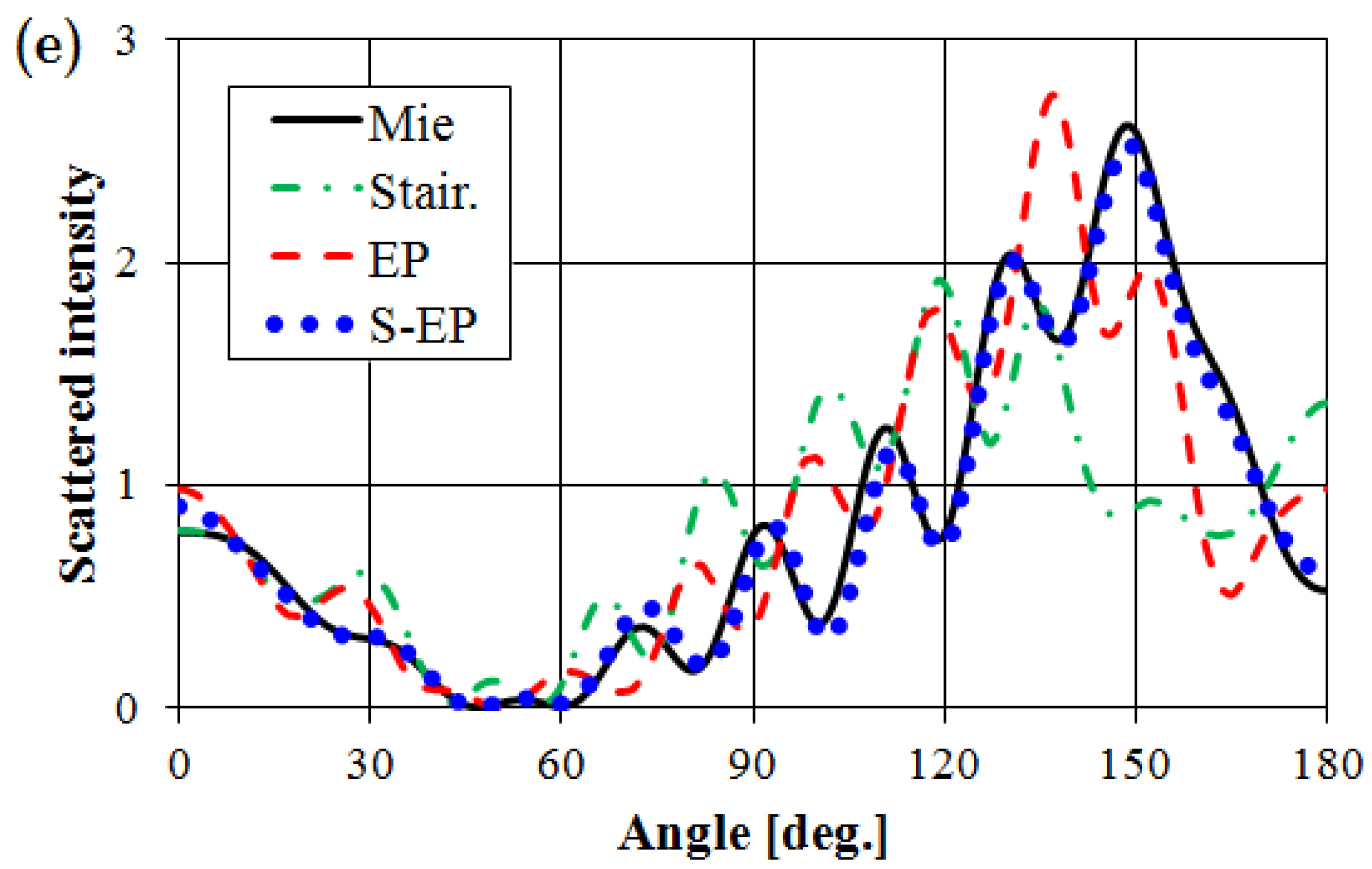
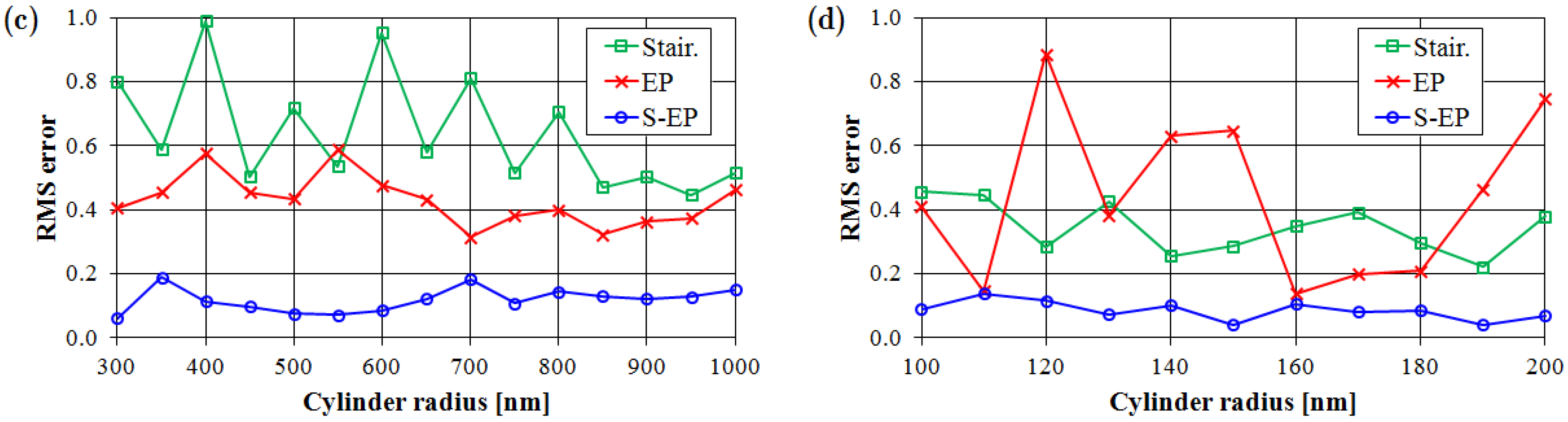
3.1. Infinitely-Long Ag Cylinder
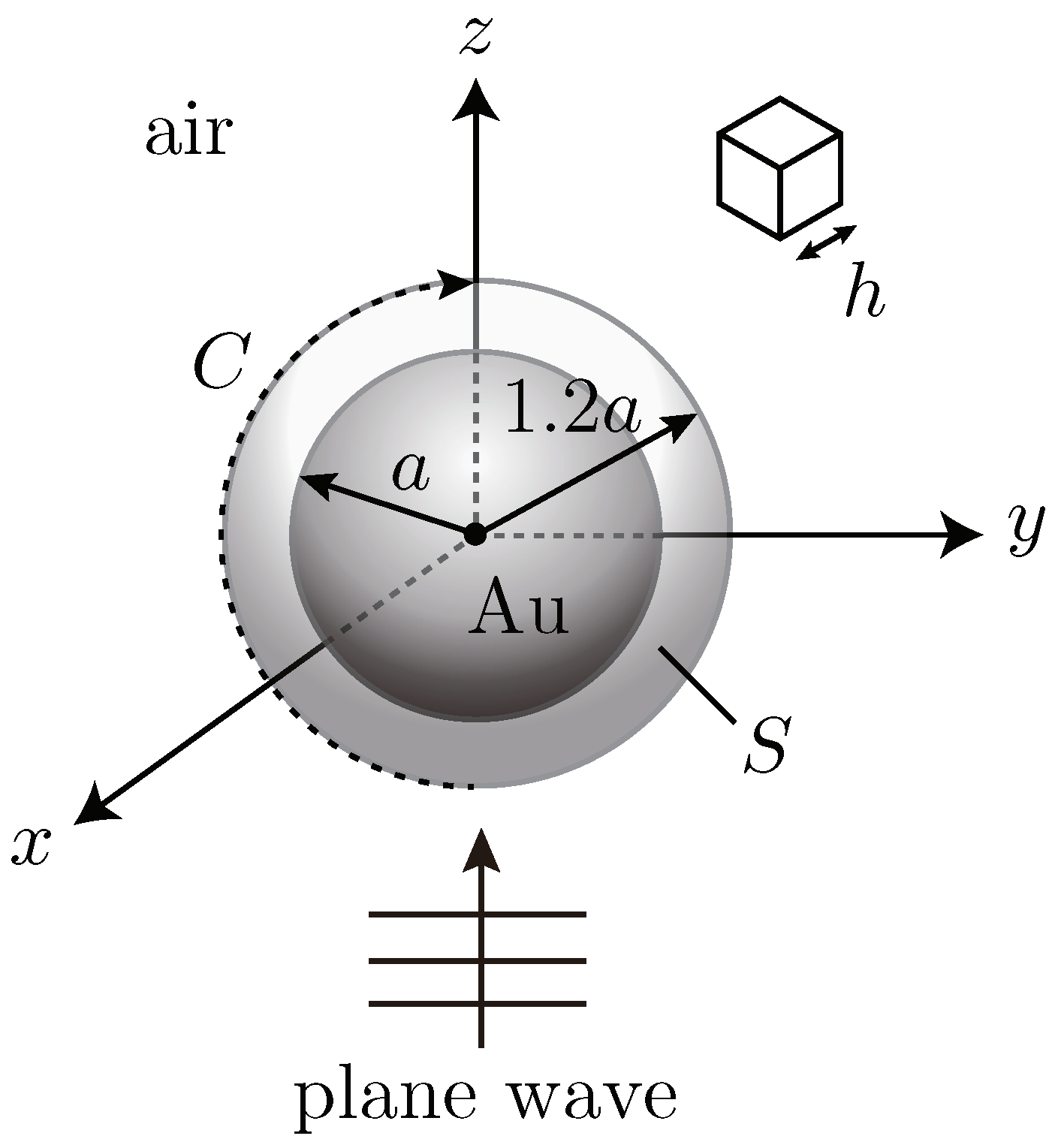
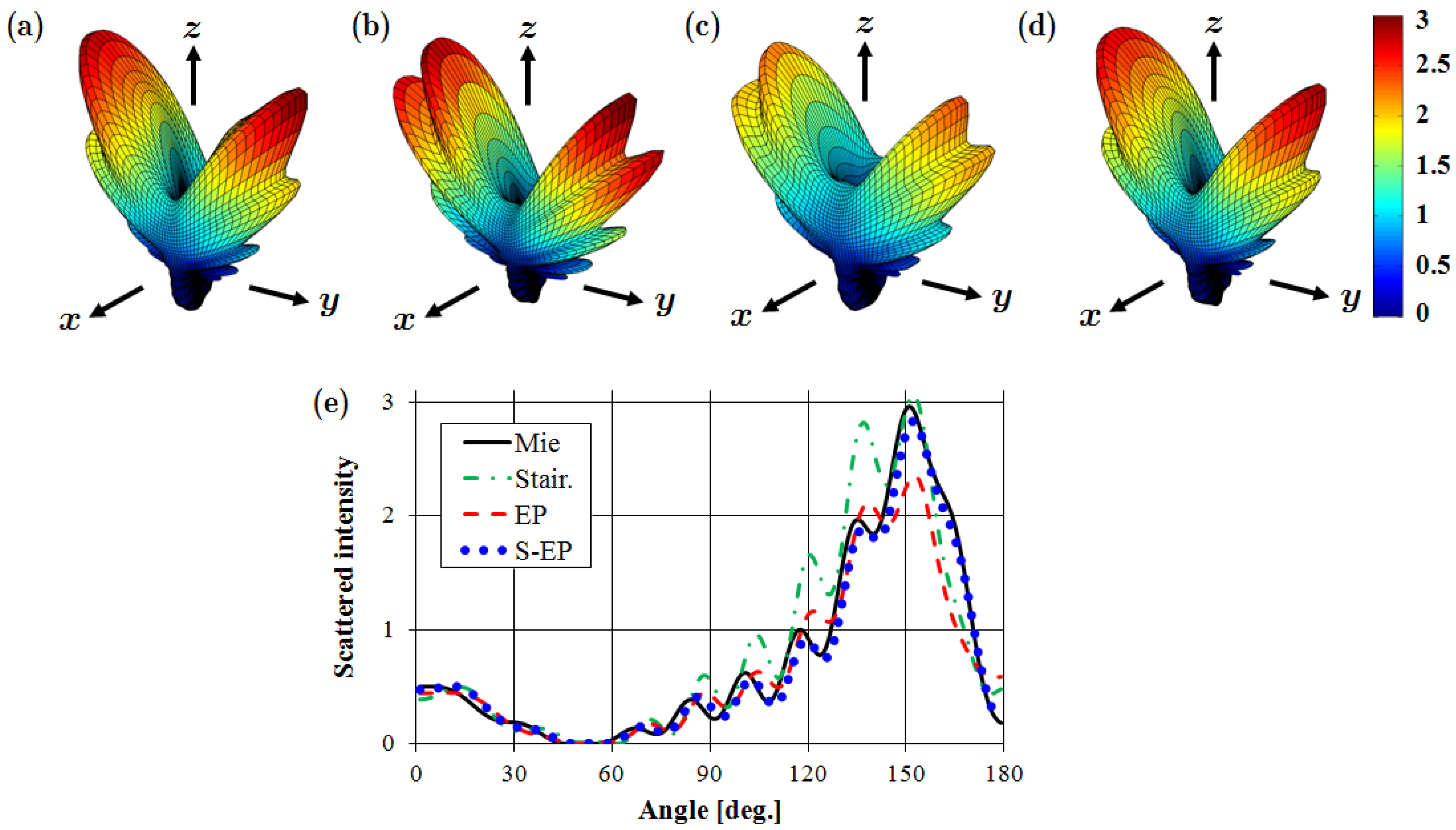
3.2. Au Sphere
4. Conclusions
Acknowledgments
References
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966–3969. [Google Scholar] [CrossRef] [PubMed]
- Homola, J.; Yee, S.S.; Gauglitz, G. Surface plasmon resonance sensors: Review. Sens. Actuat. B Chem. 1999, 54, 3–15. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Zouhdi, S.; Sihvola, A.; Vinogradov, A.P. Metamaterials and Plasmonics: Fundamentals, Modeling, Applications; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Brumfiel, G. Metamaterials: Ideal focus. Nature 2009, 459, 504–505. [Google Scholar] [CrossRef]
- Cai, W.; Shalaev, V. Optical Metamaterials: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Solymar, L.; Shamonina, E. Waves in Metamaterials; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Capolino, F. Applications of Metamaterials; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Sarid, D.; Challener, W. Modern Introduction to Surface Plasmons: Theory, Mathematica Modeling, and Applications; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Yee, K. Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Taflove, A.; Brodwin, M.E. Numerical solution of steady-state electromagnetic scattering problems using the time-dependent Maxwell’s equations. IEEE Trans. Microwave Theory Tech. 1975, 23, 623–630. [Google Scholar] [CrossRef]
- Taflove, A. Application of the finite-difference time-domain method to sinusoidal steady-state electromagnetic-penetration problems. IEEE Trans. Electromagnet. Compat. 1980, 22, 191–202. [Google Scholar] [CrossRef]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; Artech House: London, UK, 2005. [Google Scholar]
- Cole, J.B. High-accuracy Yee algorithm based on nonstandard finite differences: New developments and verifications. IEEE Trans. Antennas Propag. 2002, 50, 1185–1191. [Google Scholar] [CrossRef]
- Mei, K.K.; Cangellaris, A.; Angelakos, D.J. Finite-difference solution of Maxwell’s equations in generalized nonorthogonal coordinates. IEEE Trans. Nuclear Sci. 1983, 30, 4589–4591. [Google Scholar]
- Mei, K.K.; Cangellaris, A.; Angelakos, D.J. Conformal time domain finite difference method. Radio Sci. 1984, 19, 1145–1147. [Google Scholar] [CrossRef]
- Fusco, M. FDTD algorithm in curvilinear coordinates. IEEE Trans. Antennas Propag. 1990, 38, 76–89. [Google Scholar] [CrossRef]
- Jurgens, T.G.; Taflove, A.; Umashankar, K.; Moore, T.G. Finite-difference time-domain modeling of curved surfaces. IEEE Trans. Antennas Propag. 1992, 40, 357–366. [Google Scholar] [CrossRef]
- Jurgens, T.G.; Taflove, A.; Umashankar, K.; Moore, T.G. Three-dimensional contour FDTD modeling of scattering from single and multiple bodies. IEEE Trans. Antennas Propag. 1993, 41, 1703–1708. [Google Scholar] [CrossRef]
- Kim, I.S.; Hoefer, W.J.R. A local mesh refinement algorithm for the time domain-finite difference method using Maxwell’s curl equations. IEEE Trans. Microw. Theory Tech. 1990, 38, 812–815. [Google Scholar] [CrossRef]
- Zivanovic, S.S.; Yee, K.S.; Mei, K.K. A subgridding method for the time-domain finite-difference method to solve Maxwell’s equations. IEEE Trans. Microw. Theory Tech. 1991, 39, 471–479. [Google Scholar] [CrossRef]
- Chevalier, M.W.; Luebbers, R.J.; Cable, V.P. FDTD local grid with material traverse. IEEE Trans. Antennas Propag. 1997, 45, 411–421. [Google Scholar] [CrossRef]
- Kaneda, N.; Houshmand, B.; Itoh, T. FDTD analysis of dielectric resonators with curved surfaces. IEEE Trans. Microw. Theory Tech. 1997, 45, 1645–1649. [Google Scholar] [CrossRef]
- Hirono, T.; Shibata, Y.; Lui, W.W.; Seki, S.; Yoshikuni, Y. The second-order condition for the dielectric interface orthogonal to the Yee-lattice axis in the FDTD scheme. IEEE Microw. Guid. Wave Lett. 2000, 10, 359–361. [Google Scholar] [CrossRef]
- Hwang, K.P.; Cangellaris, A.C. Effective permittivities for second-order accurate FDTD equations at dielectric interfaces. IEEE Microw. Wirel. Compon. Lett. 2001, 11, 158–160. [Google Scholar] [CrossRef]
- Mohammadi, A.; Nadgaran, H.; Agio, M. Contour-path effective permittivities for the two-dimensional finite-difference time-domain method. Opt. Express 2005, 13, 10367–10381. [Google Scholar] [CrossRef]
- Okada, N.; Cole, J.B. Simulation of whispering gallery modes in the Mie regime using the nonstandard finite-difference time domain algorithm. J. Opt. Soc. Am. B 2010, 27, 631–639. [Google Scholar] [CrossRef]
- Capolino, F. Light Scattering Reviews 6; Springer: Berlin, Heidelberg, Germany, 2011. [Google Scholar]
- Maloney, J.G.; Smith, G.S. The efficient modeling of thin material sheets in the finite-difference time-domain (FDTD) method. IEEE Trans. Antennas Propag. 1992, 40, 323–330. [Google Scholar] [CrossRef]
- Dey, S.; Mittra, R. A conformal finite-difference time-domain technique for modeling cylindrical dielectric resonators. IEEE Trans. Microw. Theory Tech. 1999, 47, 1737–1739. [Google Scholar]
- Sun, W.; Fu, Q.; Chen, Z. Finite-difference time-domain solution of light scattering by dielectric particles with a perfectly matched layer absorbing boundary condition. Appl. Opt. 1999, 38, 3141–3151. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Dey, S.; Mittra, R. On the modeling of periodic structures using the finite-difference time-domain algorithm. Microw. Opt. Tech. Lett. 2000, 24, 151–155. [Google Scholar] [CrossRef]
- Yang, P.; Liou, K.N.; Mishchenko, M.I.; Gao, B.C. Efficient finite-difference time-domain scheme for light scattering by dielectric particles: Application to aerosols. Appl. Opt. 2000, 39, 3727–3737. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Mittra, R. A conformal finite difference time domain technique for modeling curved dielectric surfaces. IEEE Microw. Wirel. Compon. Lett. 2001, 11, 25–27. [Google Scholar]
- Yang, P.; Kattawar, G.W.; Liou, K.N.; Lu, J.Q. Comparison of cartesian grid configurations for application of the finite-difference time-domain method to electromagnetic scattering by dielectric particles. Appl. Opt. 2004, 43, 4611–4624. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Hao, Y. Finite-difference time-domain study of guided modes in nano-plasmonic waveguides. IEEE Trans. Antennas Propag. 2007, 55, 3070–3077. [Google Scholar] [CrossRef]
- Barber, P.W.; Hill, S.C. Light Scattering by Particles: Computational Methods; World Scientific: Singapore, 1989. [Google Scholar]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Etchegoin, P.G.; Ru, E.C.L.; Meyer, M. An analytic model for the optical properties of gold. J. Chem. Phys. 2006, 125. [Google Scholar] [CrossRef]
- Vial, A. Implementation of the critical points model in the recursive convolution method for modeling dispersive media with the finite-difference time domain method. J. Opt. A: Pure Appl. Opt. 2007, 9, 745–748. [Google Scholar] [CrossRef]
- Luebbers, R.; Hunsberger, F.P.; Kunz, K.S.; Standler, R.B.; Schneider, M. A frequency-dependent finite-difference time-domain formulation for dispersive materials. IEEE Trans. Electromagnet. Compat. 1990, 32, 222–227. [Google Scholar] [CrossRef]
- Kelley, D.F.; Luebbers, R.J. Piecewise linear recursive convolution for dispersive media using FDTD. IEEE Trans. Antennas Propag. 1996, 44, 792–797. [Google Scholar] [CrossRef]
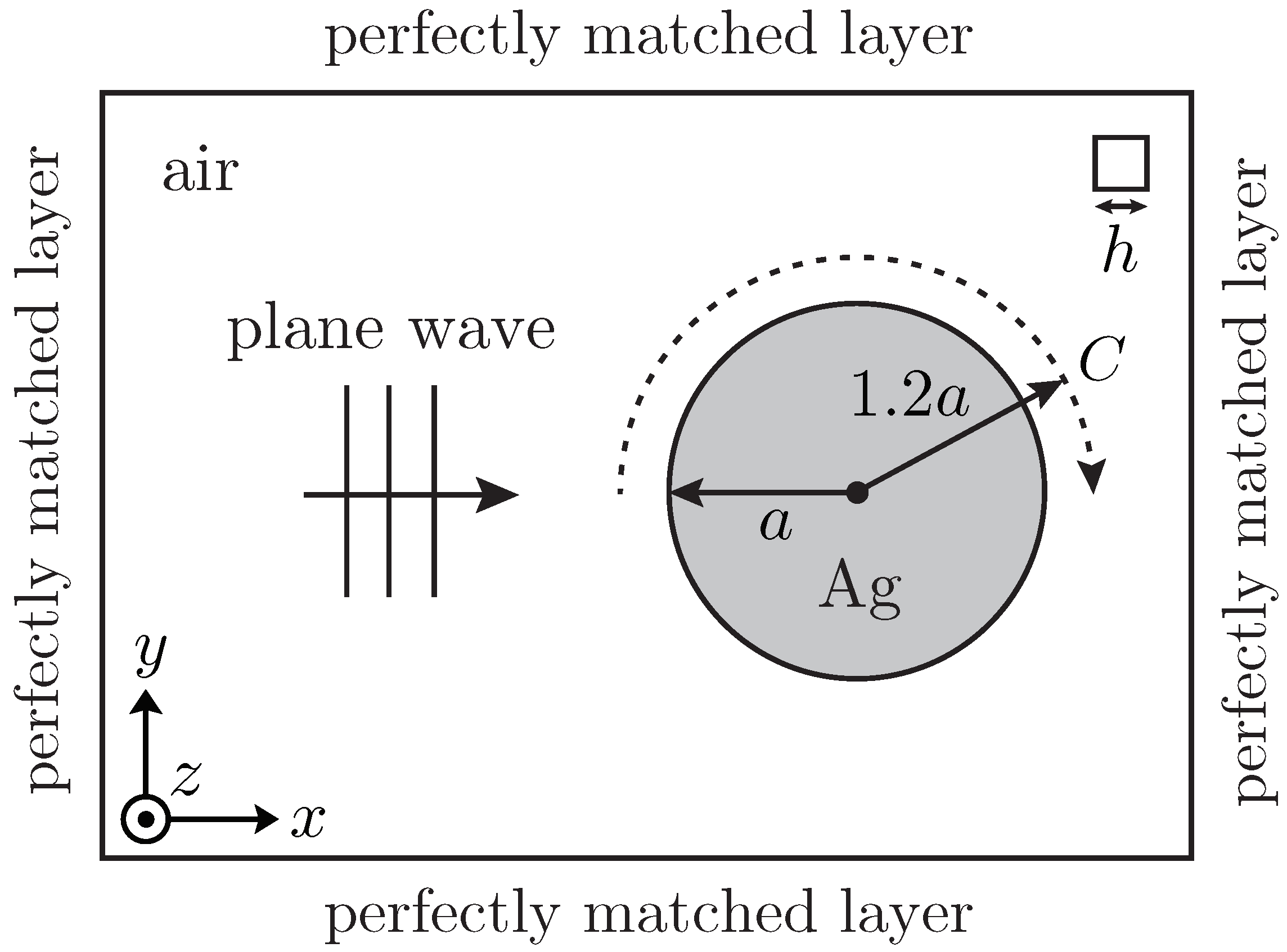

| Parameter | Input Value |
|---|---|
| permittivity of air | 1 |
| permittivity of Ag | −6.06 + i0.197 |
| wavelength | 430.501 nm |
| cylinder radius a | 538.126 nm |
| grid spacing h | 20 nm |
| Parameter | Input Value |
|---|---|
| permittivity of air | 1 |
| permittivity of Au | −10.662 + i1.374 |
| wavelength | 616.837 nm |
| cylinder radius a | 925.255 nm |
| grid spacing h | 20 nm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2012 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okada, N.; Cole, J.B. Effective Permittivity for FDTD Calculation of Plasmonic Materials. Micromachines 2012, 3, 168-179. https://doi.org/10.3390/mi3010168
Okada N, Cole JB. Effective Permittivity for FDTD Calculation of Plasmonic Materials. Micromachines. 2012; 3(1):168-179. https://doi.org/10.3390/mi3010168
Chicago/Turabian StyleOkada, Naoki, and James B. Cole. 2012. "Effective Permittivity for FDTD Calculation of Plasmonic Materials" Micromachines 3, no. 1: 168-179. https://doi.org/10.3390/mi3010168




