Optical Spectrum and Electric Field Waveform Dependent Optically-Induced Dielectrophoretic (ODEP) Micro-Manipulation
Abstract
:1. Introduction
2. ODEP Force and Its Dependence on Optical Spectrum and Electric Field Waveform


 is the gradient of the energy density of the electric field, and K(ω) the Clausius-Mossotti (CM) factor, expressed as:
is the gradient of the energy density of the electric field, and K(ω) the Clausius-Mossotti (CM) factor, expressed as: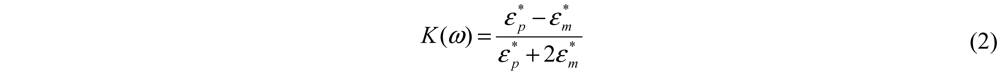
2.1. Optical Spectrum-Dependent ODEP Force
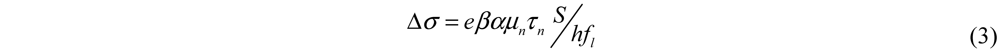
| Color | Wavelength (nm) | Averaged Absorption Coefficient (m−1) | Photoconductivity (S/m) |
|---|---|---|---|
| Red | Max: 700 | 1 × 106 | 1.1 × 10−5 |
| Mean: 660 | 1.7 × 106 | 1.8 × 10−5 | |
| Min: 620 | 3.1 × 106 | 3.1 × 10−5 | |
| Orange | Mean: 605 | 4.3 × 106 | 4.2 × 10−5 |
| Yellow | Mean: 580 | 5.7 × 106 | 5.3 × 10−5 |
| Green | Max: 570 | 6.8 × 106 | 6.3 × 10−5 |
| Mean: 530 | 1.1 × 107 | 9.6 × 10−5 | |
| Min: 495 | 1.7 × 107 | 1.3 × 10−4 | |
| Cyan | Mean: 485 | 1.9 × 107 | 1.5 × 10−4 |
| Blue | Mean: 463 | 2.5 × 107 | 1.8 × 10−4 |
| Purple | Max: 450 | 2.8 × 107 | 2.0 × 10−4 |
| Mean: 415 | 3.6 × 107 | 2.5 × 10−4 | |
| Min: 380 * | 4.5 × 107 * | 2.9 × 10−4 |


 ).
).
 ).
).
2.2. Dependence of ODEP Force on AC Electric Field Waveforms
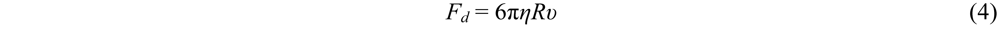
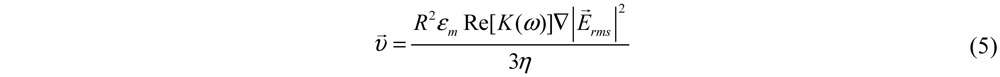
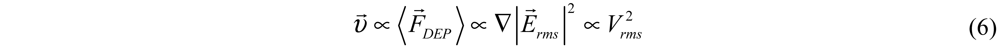
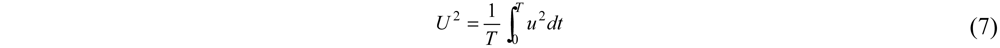
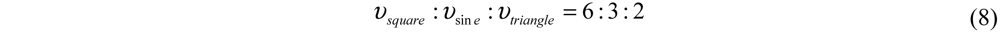



3. Experimental Results
3.1. ODEP Force Dependence on AC Waveforms

3.2. ODEP Force Dependence on Light Spectrum

4. Conclusions
Acknowledgments
References
- Chiou, P.Y.; Ohta, A.T.; Wu, M.C. Massively parallel manipulation of single cells and microparticles using optical images. Nature 2005, 436, 370–372. [Google Scholar] [CrossRef]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar]
- Wong, T.S.; Li, W.J. Bulk Carbon Nanotubes as Sensing Element for Temperature and Anemometry Micro Sensing. In Proceedings of the 16th IEEE International Conference Micro Electro Mechanical Systems, Kyoto, Japan, 19–23 January 2003; pp. 41–44.
- Lin, Y.H.; Lee, G.B. An integrated cell counting and continuous cell lysis device using an optically induced electric field. Sens. Actuat: B: Chem. 2010, 145, 854–860. [Google Scholar] [CrossRef]
- Lin, Y.H.; Lee, G.B. Optically induced flow cytometry for continuous microparticle counting and sorting. Biosens. Bioelectron. 2008, 24, 572–578. [Google Scholar] [CrossRef]
- Lin, Y.H.; Chang, C.M.; Lee, G.B. Manipulation of single DNA molecules by using optically projected images. Opt. Express 2009, 17, 15318–15329. [Google Scholar]
- Pauzauskie, P.J.; Jamshidi, A.; Valley, J.K.; Satcher, J.H.; Wu, M.C. Parallel trapping of multiwalled carbon nanotubes with optoelectronic tweezers. Appl. Phys. Lett. 2009, 95, 113104:1–113104:3. [Google Scholar]
- Lee, M.W.; Lin, Y.H.; Lee, G.B. Manipulation and patterning of carbon nanotubes utilizing optically induced dielectrophoretic forces. Microfluid. Nanofluid. 2010, 8, 609–617. [Google Scholar] [CrossRef]
- Jamshidi, A.; Pauzauskie, P.J.; Schuck, P.J.; Ohta, A.T.; Chiou, P.Y.; Chou, J.; Yang, P.D.; Wu, M.C. Dynamic manipulation and separation of individual semiconducting and metallic nanowires. Nature 2008, 2, 85–89. [Google Scholar]
- Jamshidi, A.; Neale, S.L.; Yu, K.; Pauzauskie, P.J.; Schuck, P.J.; Valley, J.K.; Hsu, H.Y.; Ohta, A.T.; Wu, M.C. Nanopen: Dynamic, low-Power, and light-actuated patterning of nanoparticles. Nano Lett. 2009, 9, 2921–2925. [Google Scholar]
- Hung, S.H.; Lin, Y.H.; Lee, G.B. A microfluidic platform for manipulation and separation of oil-in-water emulsion droplets using optically induced dielectrophoresis. J. Micromech. Microeng. 2010, 20, 1–8. [Google Scholar]
- Chiou, P.Y.; Ohta, A.T.; Jamshidi, A.; Hsu, H.Y.; Wu, M.C. Light-actuated AC electroosmosis for nanoparticle manipulation. J. Microelectromech. S 2008, 17, 525–531. [Google Scholar] [CrossRef]
- Hwang, H.; Park, J.K. Dynamic light-activated control of local chemical concentration in a fluid. Anal. Chem. 2009, 81, 5865–5870. [Google Scholar] [CrossRef]
- Hwang, H.; Park, J.K. Measurement of molecular diffusion based on optoelectrofluidic fluorescence microscopy. Anal. Chem. 2009, 81, 9163–9167. [Google Scholar] [CrossRef]
- Hwang, H.; Park, Y.H.; Park, J.K. Optoelectrofluidic control of colloidal assembly in an optically induced electric field. Langmuir 2009, 25, 6010–6014. [Google Scholar]
- Hwang, H.; Chon, H.; Choo, J.; Park, J.K. Optoelectrofluidic sandwich immunoassays for detection of human tumor marker using surface-enhanced Raman scattering. Anal. Chem. 2010, 82, 7603–7610. [Google Scholar] [CrossRef]
- Hwang, H.; Park, J.K. Rapid and selective concentration of microparticles in an optoelectrofluidic platform. Lab Chip 2009, 9, 199–206. [Google Scholar] [CrossRef]
- Ohta, A.T.; Chiou, P.Y.; Huan, L.P.; Sherwood, S.W.; Yang, J.M.; Lau, N.K.; Hsu, H.Y.; Jamshidi, A.; Wu, M.C. Optically controlled cell discrimination and trapping using optoelectronic tweezers. J. Sel. Top. Quantum 2007, 13, 235–243. [Google Scholar]
- Li, W.Y.; Lin, Y.H.; Lee, G.B. Separation of micro-particles utilizing spatial difference of optically induced dielectrophoretic forces. Microfluid. Nanofluid. 2010, 8, 217–229. [Google Scholar]
- Jone, T.B. Electromechanics of Particles; Cambridge University Press: New York, NY, USA, 1995; pp. 17–20. [Google Scholar]
- Stutzmann, M.; Jackson, W.B.; Tsai, C.C. Light-induced metastable defects in hydrogenated amorphous silicon: A system study. Phys. Rev. B 1985, 32, 23–47. [Google Scholar]
- Carlson, D.E.; Wronski, C.R. Amorphous silicon solar cell. Appl. Phys. Lett. 1976, 28, 671–673. [Google Scholar] [CrossRef]
- Hishikawa, Y.; Nakamura, N.; Tsuda, S.; Nakano, S.; Kishi, Y.; Kuwano, Y. Interference-free determination of optical absorption coefficient and the optical gap of amorphous silicon thin films. Jpn. J. Appl. Phys. 1991, 30, 1008–1014. [Google Scholar] [CrossRef]
- Adachi, S. Optical Properties of Crystalline and Amorphous Semiconductors: Materials and Fundamental Principles; Kluwer Academic Publishers: Boston, MA, USA, 1999; pp. 207–208. [Google Scholar]
- Liu, E.K. Semiconductor Physics, 6th ed; Publishing House of Electronics Industry: Beijing, China, 2005; pp. 333–335. [Google Scholar]
- Okamoto, H.; Kida, H.; Nonomura, S.; Fukumoto, K.; Hamakawa, Y. Mobility-lifetime product and interface property in amorphous silicon solar cells. J. Appl. Phys. 1983, 54, 3236–3243. [Google Scholar] [CrossRef]
- Liang, W.F.; Wang, S.E.; Qu, Y.L.; Dong, Z.L.; Lee, G.B.; Li, W.J. An Equivalent Electrical Model for Numerical Analyses of ODEP Manipulation. In Proceedings of the 6th IEEE International Conference Nano/Micro Engineered and Molecular Systems, Kaohsiung, Taiwan, 20-23 February 2011; pp. 825–830.
- Li, Q. Fundamentals of Circuit; Xi’an Jiaotong University Press: Beijing, China, 2004; pp. 132–134. [Google Scholar]
- Castellanos, A.; Ramos, A.; Gonzalez, A.; Green, N.G.; Morgan, H. Electrohydrodynamics and dielectrophoresis in microsystems: Scaling laws. J. Phys. D: Appl. Phys. 2003, 36, 2584–2597. [Google Scholar] [CrossRef]
- Zheng, L.F.; Li, S.D.; Brody, J.P.; Nakano, S.; Kishi, Y.; Kuwano, Y. Manipulating nanoparticles in solution with electrically contacted nano-tubes using dielectrophoresis. Langmuir 2004, 20, 8612–8619. [Google Scholar]
- Li, M.L.; Qu, Y.L.; Dong, Z.L.; Wang, Y.C.; Li, W.J. Limitations of Au particle nanoassembly using dielectrophoretic force-A parametric experimental and theoretical study. IEEE Trans. Nanotechnol. 2008, 7, 477–479. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liang, W.; Wang, S.; Dong, Z.; Lee, G.-B.; Li, W.J. Optical Spectrum and Electric Field Waveform Dependent Optically-Induced Dielectrophoretic (ODEP) Micro-Manipulation. Micromachines 2012, 3, 492-508. https://doi.org/10.3390/mi3020492
Liang W, Wang S, Dong Z, Lee G-B, Li WJ. Optical Spectrum and Electric Field Waveform Dependent Optically-Induced Dielectrophoretic (ODEP) Micro-Manipulation. Micromachines. 2012; 3(2):492-508. https://doi.org/10.3390/mi3020492
Chicago/Turabian StyleLiang, Wenfeng, Shue Wang, Zaili Dong, Gwo-Bin Lee, and Wen J. Li. 2012. "Optical Spectrum and Electric Field Waveform Dependent Optically-Induced Dielectrophoretic (ODEP) Micro-Manipulation" Micromachines 3, no. 2: 492-508. https://doi.org/10.3390/mi3020492
APA StyleLiang, W., Wang, S., Dong, Z., Lee, G.-B., & Li, W. J. (2012). Optical Spectrum and Electric Field Waveform Dependent Optically-Induced Dielectrophoretic (ODEP) Micro-Manipulation. Micromachines, 3(2), 492-508. https://doi.org/10.3390/mi3020492




