Tunable Clamped–Guided Arch Resonators Using Electrostatically Induced Axial Loads
Abstract
:1. Introduction
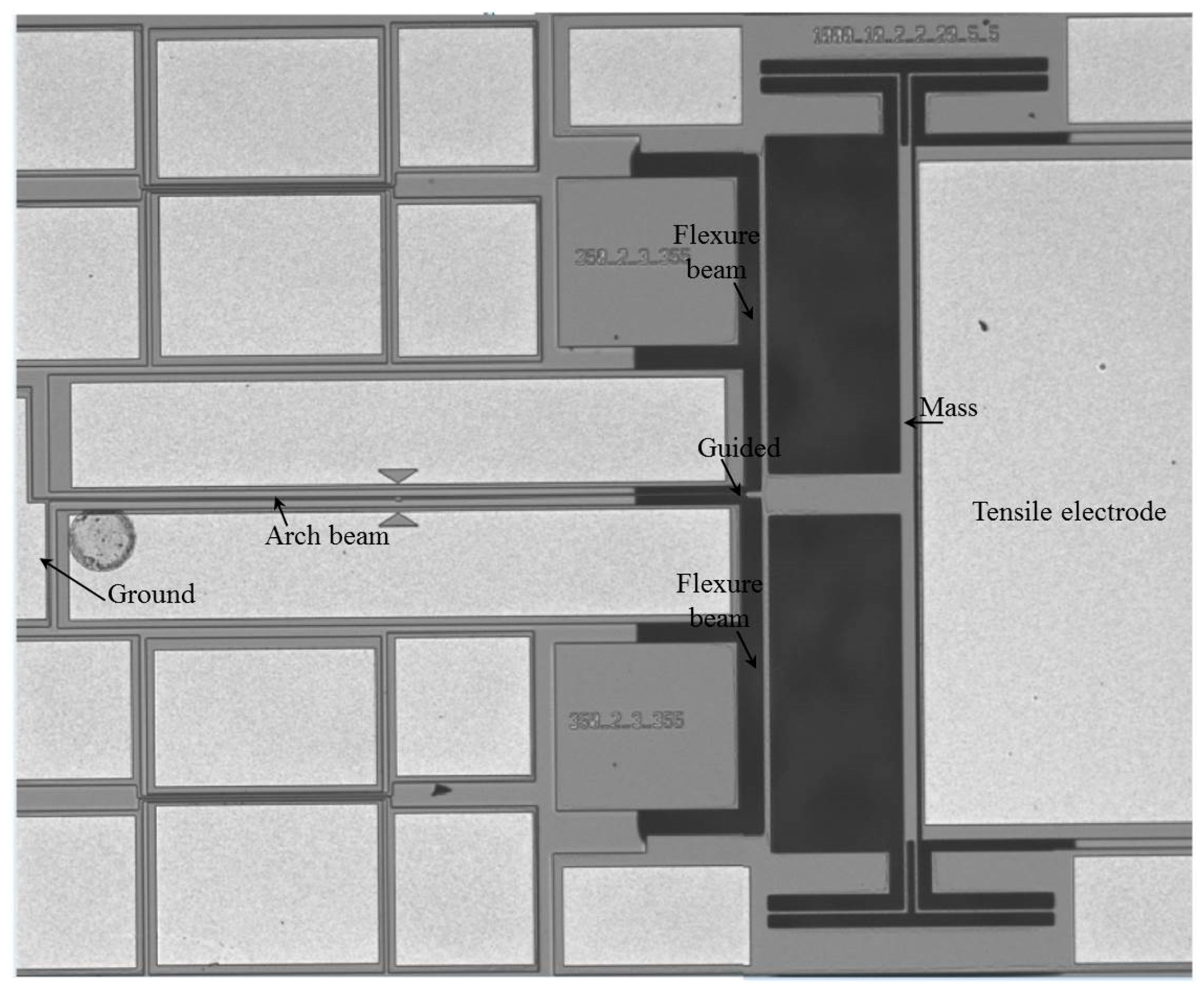
2. Design and Principle of the Tunable Microresonators
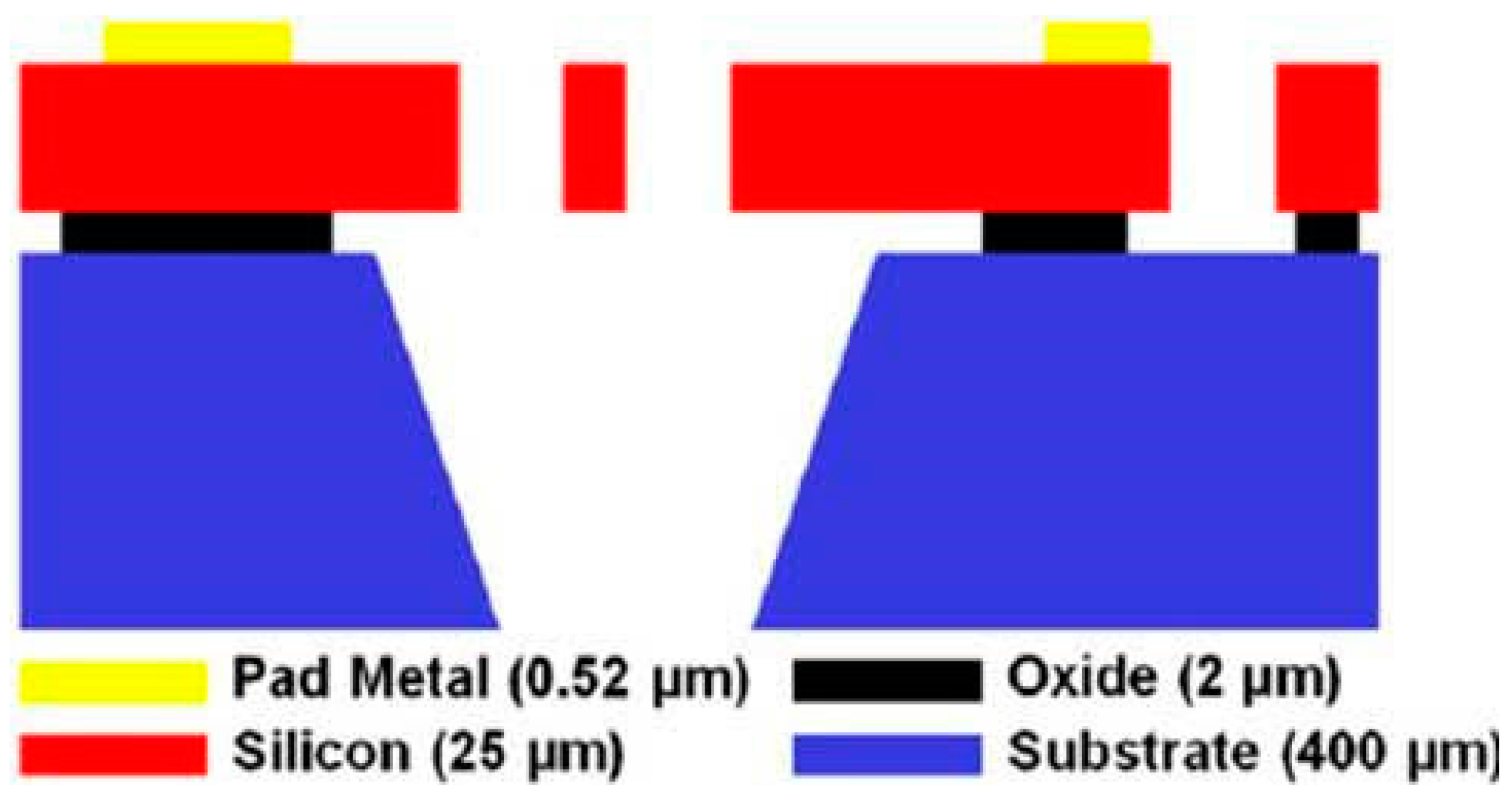
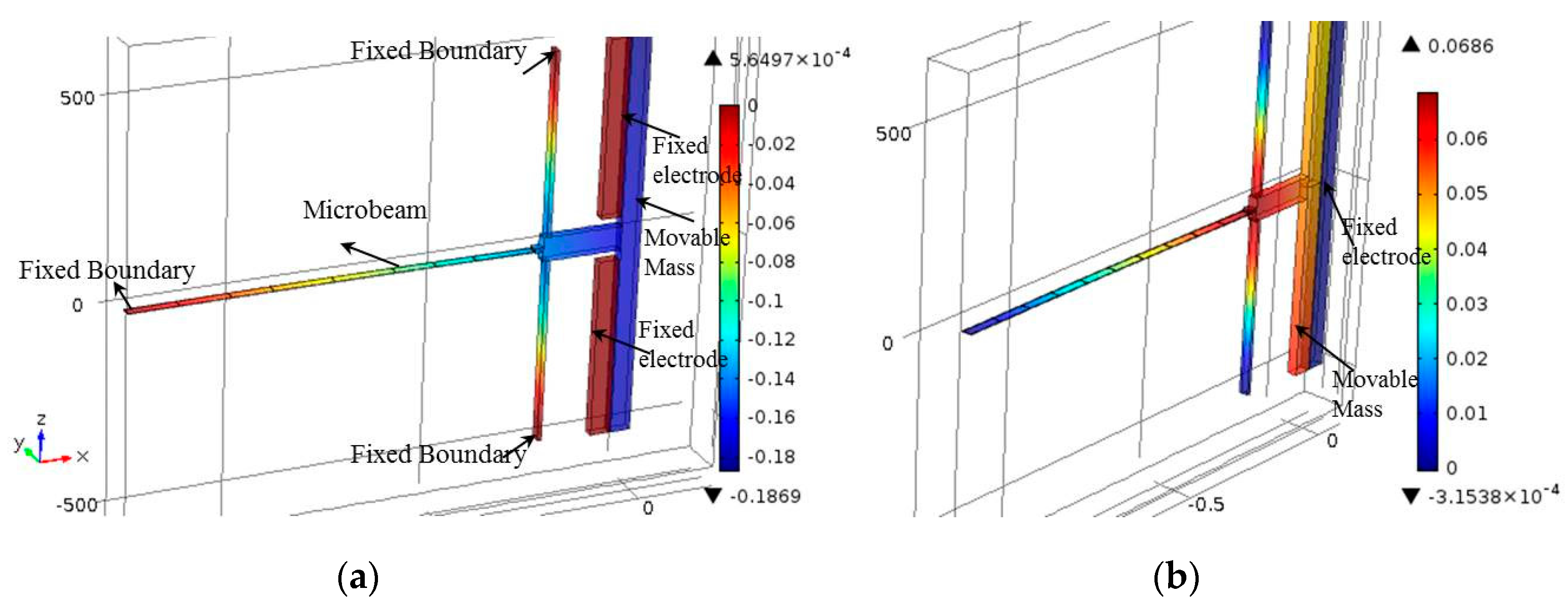
3. Finite Element Model
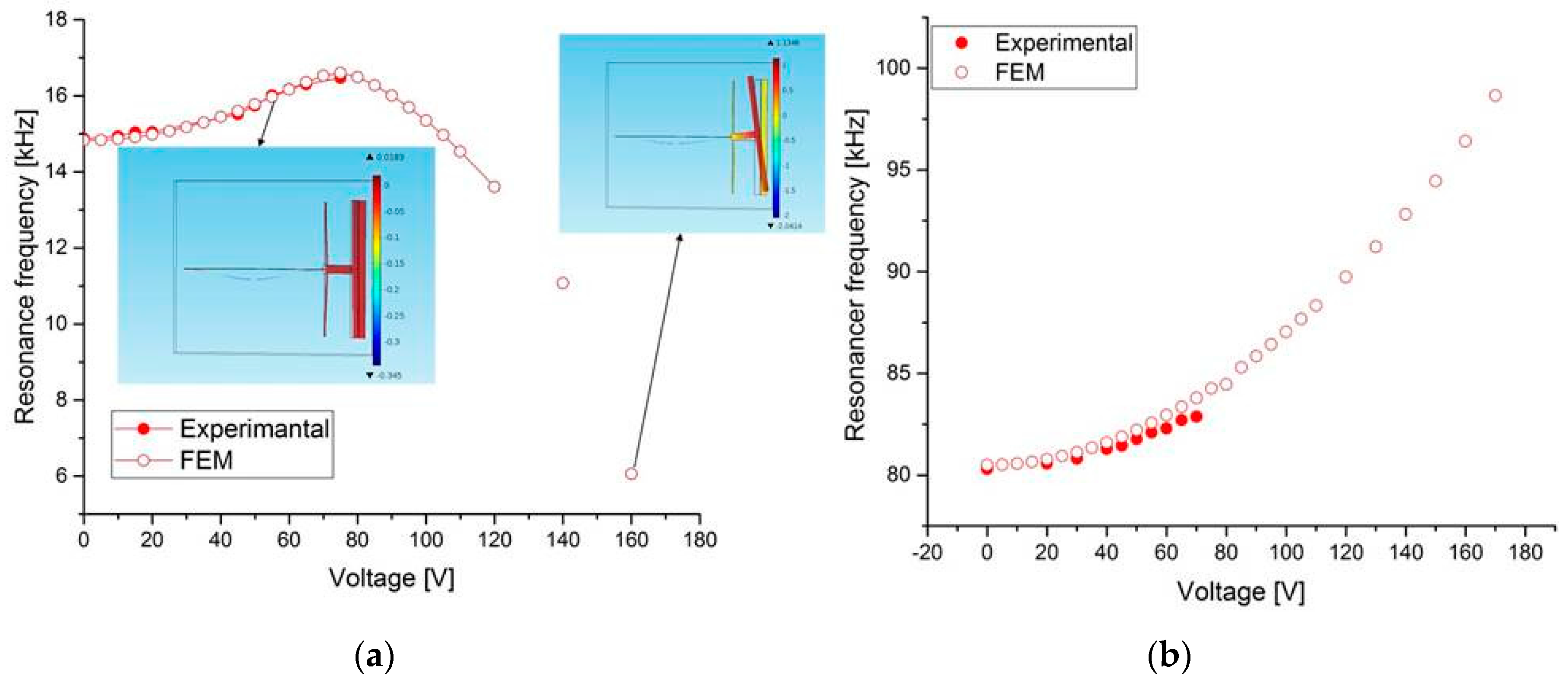
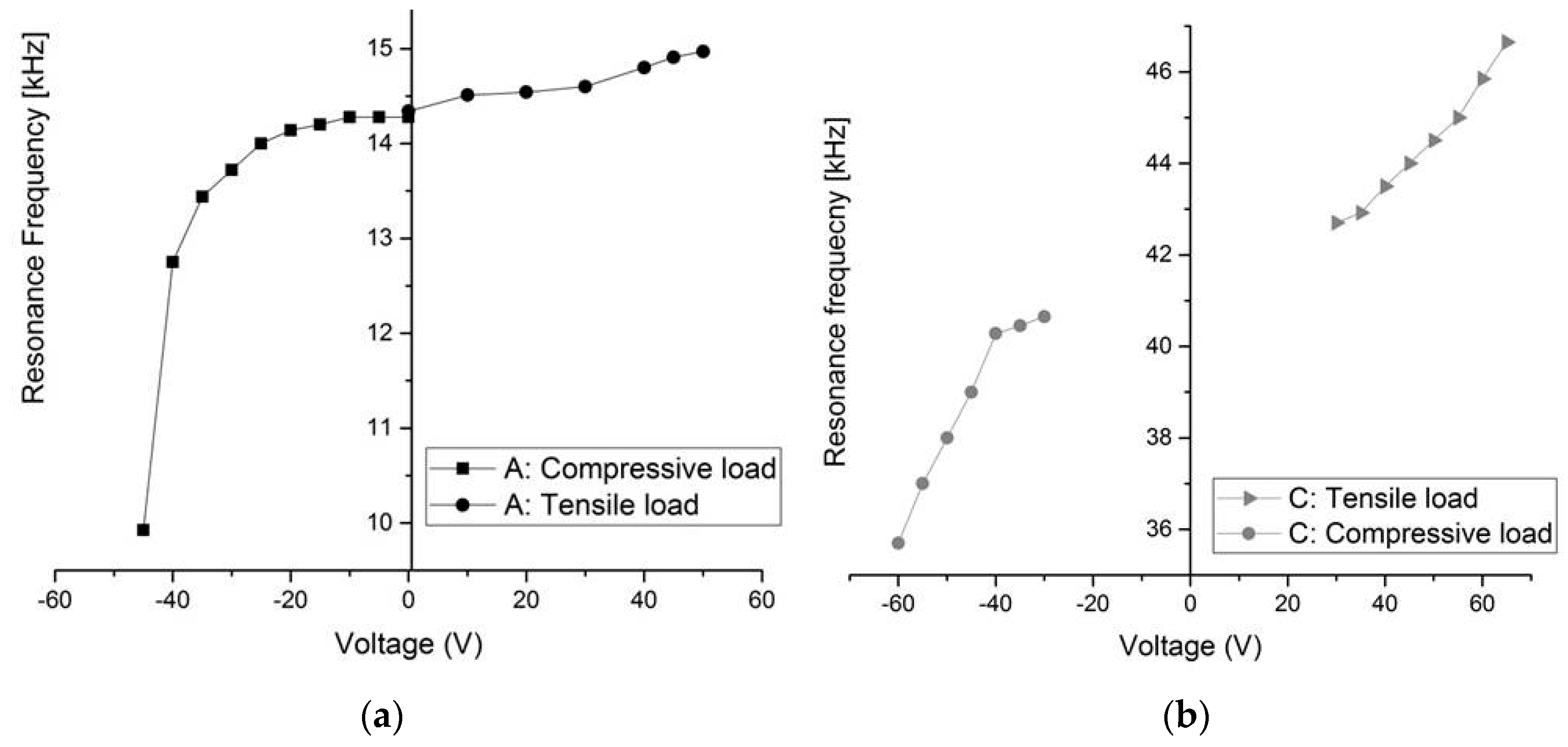
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, G.; Gaspar, J.; Chu, V.; Conde, J. Electrostatically actuated polymer microresonators. Appl. Phys. Lett. 2005, 87, 1–3. [Google Scholar] [CrossRef]
- Arlett, J.; Myers, E.; Roukes, M. Comparative advantages of mechanical biosensors. Nat. Nanotechnol. 2011, 6, 203–215. [Google Scholar] [CrossRef] [PubMed]
- Li, L. Recent development of micromachined biosensors. IEEE Sens. J. 2011, 11, 305–311. [Google Scholar] [CrossRef]
- Eom, K.; Park, H.S.; Yoon, D.S.; Kwon, T. Nanomechanical resonators and their applications in biological/chemical detection: Nanomechanics principles. Phys. Rep. 2011, 503, 115–163. [Google Scholar] [CrossRef]
- Heinisch, M.; Reichel, E.; Dufour, I.; Jakoby, B. Tunable resonators in the low kHz range for viscosity sensing. Sens. Actuators A Phys. 2012, 186, 111–117. [Google Scholar] [CrossRef]
- Rhoads, J.F.; Shaw, S.W.; Turner, K.L.; Baskaran, R. Tunable microelectromechanical filters that exploit parametric resonance. J. Vib. Acoust. 2005, 127, 423–430. [Google Scholar] [CrossRef]
- Athukorala, L.; Budimir, D. Compact dual-mode open loop microstrip resonators and filters. IEEE Microw. Wirel. Compon. Lett. 2009, 19, 698–700. [Google Scholar] [CrossRef]
- Harne, R.; Wang, K. A review of the recent research on vibration energy harvesting via bistable systems. Smart Mater. Struct. 2013, 22, 023001. [Google Scholar] [CrossRef]
- Al-Ashtari, W.; Hunstig, M.; Hemsel, T.; Sextro, W. Frequency tuning of piezoelectric energy harvesters by magnetic force. Smart Mater. Struct. 2012, 21, 035019. [Google Scholar] [CrossRef]
- Hafiz, M.; Kosuru, L.; Younis, M.I. Microelectromechanical reprogrammable logic device. Nat. Commun. 2016, 7, 11137. [Google Scholar] [CrossRef] [PubMed]
- Kozinsky, I.; Postma, H.C.; Bargatin, I.; Roukes, M. Tuning nonlinearity, dynamic range, and frequency of nanomechanical resonators. Appl. Phys. Lett. 2006, 88, 253101. [Google Scholar] [CrossRef]
- Brueckner, K.; Niebelschuetz, F.; Tonisch, K.; Foerster, C.; Cimalla, V.; Stephan, R.; Pezoldt, J.; Stauden, T.; Ambacher, O.; Hein, M. Micro-and nano-electromechanical resonators based on SiC and group III-nitrides for sensor applications. Phys. Status Solidi A 2011, 208, 357–376. [Google Scholar] [CrossRef]
- Rashvand, K.; Rezazadeh, G.; Mobki, H.; Ghayesh, M.H. On the size-dependent behavior of a capacitive circular micro-plate considering the variable length-scale parameter. Int. J. Mech. Sci. 2013, 77, 333–342. [Google Scholar] [CrossRef]
- Faroki, H.; Ghayesh, M.H. Nonlinear dynamical behavior of geometrically imperfect microplates based on modified couple stress theory. Int. J. Mech. Sci. 2015, 90, 133–144. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Faroki, H.; Alici, G. Subcritical parametric dynamics of microbeams. Int. J. Eng. Sci. 2015, 95, 36–48. [Google Scholar] [CrossRef]
- Huang, X.M.H.; Zorman, C.A.; Mehregany, M.; Roukes, M.L. Nanoelectromechanical systems: Nanodevice motion at microwave frequencies. Nature 2003, 421, 496. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.E.-Y.; Bahreyni, B.; Zhu, Y.; Seshia, A.A. A single-crystal-silicon bulk-acoustic-mode microresonator oscillator. IEEE Electron Device Lett. 2008, 29, 701–703. [Google Scholar] [CrossRef]
- Davila, A.P.; Jang, J.; Gupta, A.K.; Walter, T.; Aronson, A.; Bashir, R. Microresonator mass sensors for detection of Bacillus anthracic Sterne spores in air and water. Biosens. Bioelectron. 2007, 22, 3028–3035. [Google Scholar] [CrossRef] [PubMed]
- Ramos, D.; Arroyo-Hernandez, M.; Gil-Santos, E.; Duy Tong, H.; Van Rijn, C.; Calleja, M.; Tamayo, J. Arrays of dual nanomechanical resonators for selective biological detection. Anal. Chem. 2009, 81, 2274–2279. [Google Scholar] [CrossRef] [PubMed]
- Jun, S.C.; Huang, X.; Manolidis, M.; Zorman, C.; Mehregany, M.; Hone, J. Electrothermal tuning of Al–SiC nanomechanical resonators. Nanotechnology 2006, 17, 1506. [Google Scholar] [CrossRef]
- Remtema, T.; Lin, L. Active frequency tuning for micro resonators by localized thermal stressing effects. Sens. Actuators A Phys. 2001, 91, 326–332. [Google Scholar] [CrossRef]
- Sviličić, B.; Mastropaolo, E.; Zhang, R.; Cheung, R. Tunable MEMS cantilever resonators electrothermally actuated and piezoelectrically sensed. Microelectron. Eng. 2015, 145, 38–42. [Google Scholar] [CrossRef]
- Faroki, H.; Ghayesh, M.H. Thermo-mechanical dynamics of perfect and imperfect Timoshenko microbeams. Int. J. Eng. Sci. 2015, 91, 12–33. [Google Scholar] [CrossRef]
- Lee, W.S.; Kwon, K.C.; Kim, B.K.; Cho, J.H.; Youn, S.K. Frequency-shifting analysis of electrostatically tunable micro-mechanical actuator. Comp. Model. Eng. Sci. 2004, 5, 279–286. [Google Scholar]
- Kafumbe, S.; Burdess, J.; Harris, A. Frequency adjustment of microelectromechanical cantilevers using electrostatic pull down. J. Micromech. Microeng. 2005, 15, 1033. [Google Scholar] [CrossRef]
- Kao, P.H.; Dai, C.L.; Hsu, C.C.; Lee, C.Y. Fabrication and characterization of a tunable in-plane resonator with low driving voltage. Sensors 2009, 9, 2062–2075. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.; Roberts, S.; Tudor, M.J.; Beeby, S.P. Design and experimental characterization of a tunable vibration-based electromagnetic micro-generator. Sens. Actuators A Phys. 2010, 158, 284–293. [Google Scholar] [CrossRef]
- Hajjaj, A.Z.; Alcheikh, N.; Ramini, A.; Al Hafiz, M.A.; Younis, M.I. Highly tunable electrothermally and electrostatically actuated resonators. J. Microelectromech. Syst. 2016, 25, 1–10. [Google Scholar] [CrossRef]
- Pourkamali, S.; Hashimura, A.; Abdolvand, R.; Ho, G.K.; Erbil, A.; Ayazi, F. High-Q single crystal silicon HARPSS capacitive beam resonators with self-aligned sub-100-nm transduction gaps. J. Microelectromech. Syst. 2003, 12, 487–496. [Google Scholar] [CrossRef]
- Krylov, S.; Ilic, B.R.; Schreiber, D.; Seretensky, S.; Craighead, H. The pull-in behavior of electrostatically actuated bistable microstructures. J. Micromech. Microeng. 2008, 18, 055026. [Google Scholar] [CrossRef]
- Krylov, S.; Dick, N. Dynamic stability of electrostatically actuated initially curved shallow micro beams. Contin. Mech. Thermodyn. 2010, 22, 445–468. [Google Scholar] [CrossRef]
- Ouakad, H.M.; Younis, M.I. The dynamic behavior of MEMS arch resonators actuated electrically. Int. J. Non-Linear Mech. 2010, 45, 704–713. [Google Scholar] [CrossRef]
- Alkharabsheh, S.A.; Younis, M.I. Statics and dynamics of mems arches under axial forces. J. Vib. Acoust. 2013, 135, 021007. [Google Scholar] [CrossRef]
- Abu-Salih, S.; Elata, D. Experimental validation of electromechanical buckling. J. Microelectromech. Syst. 2006, 15, 1656–1662. [Google Scholar] [CrossRef]
- Krylov, S.; Ilic, B.R.; Lulinsky, S. Bistability of curved microbeams actuated by fringing electrostatic fields. Nonlinear Dyn. 2011, 66, 403–426. [Google Scholar] [CrossRef]
- Ramini, A.; Alcheikh, N.; Ilyas, S.; Younis, M.I. Efficient primary and parametric resonance excitation of bistable resonators. J. AIP Adv. 2016, 9, 1–9. [Google Scholar] [CrossRef]
- MEMSCAP. Available online: http://www.memscap.com (accessed on 29 December 2016).
- Polytech. Available online: http://www.polytec.com/us (accessed on 29 December 2016).
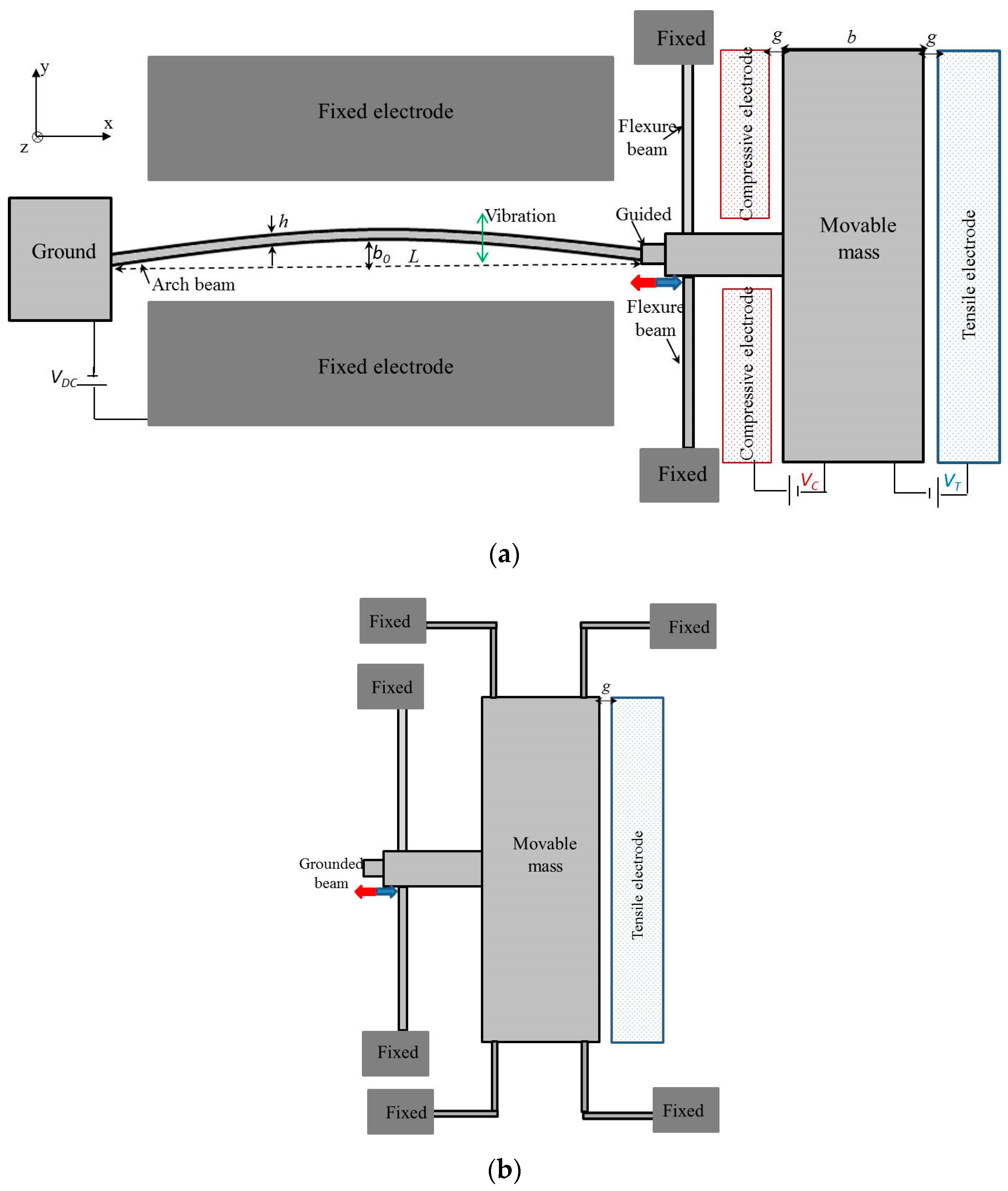
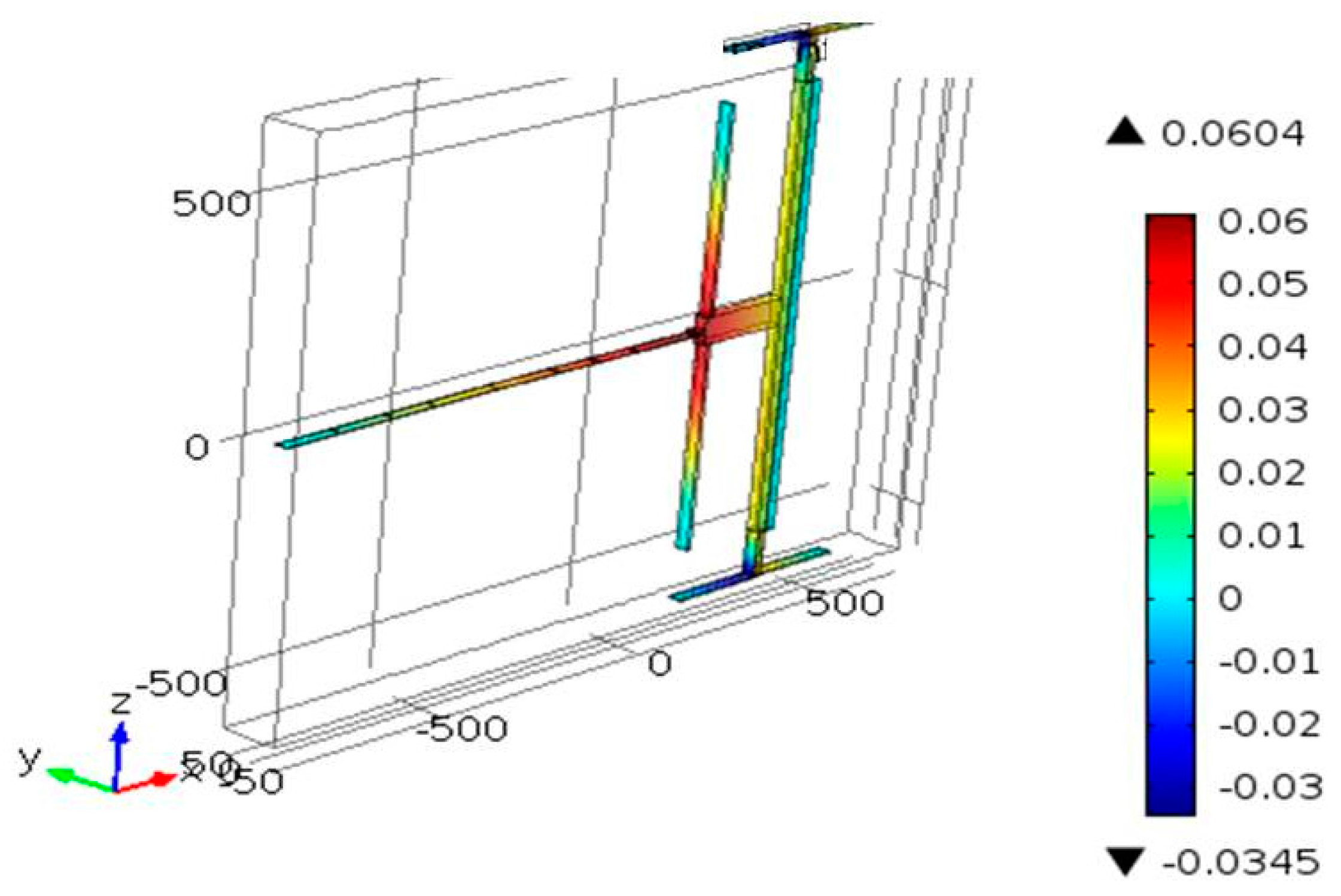
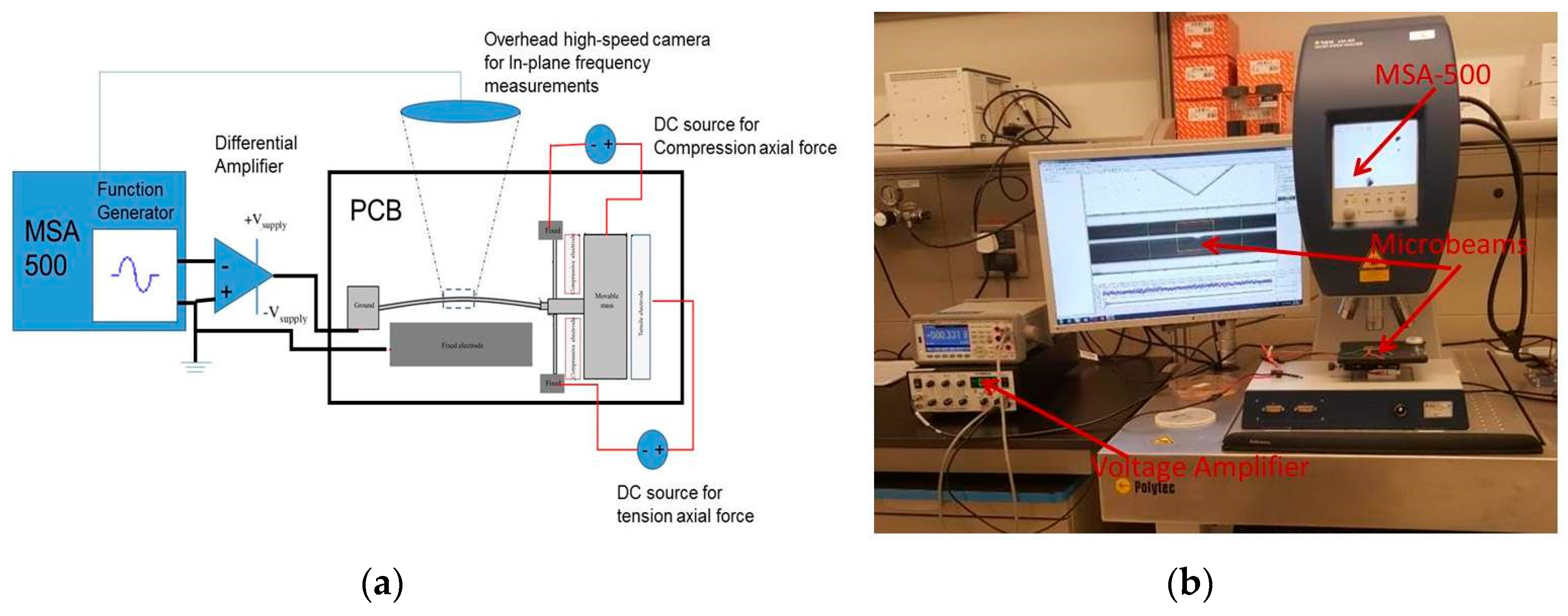
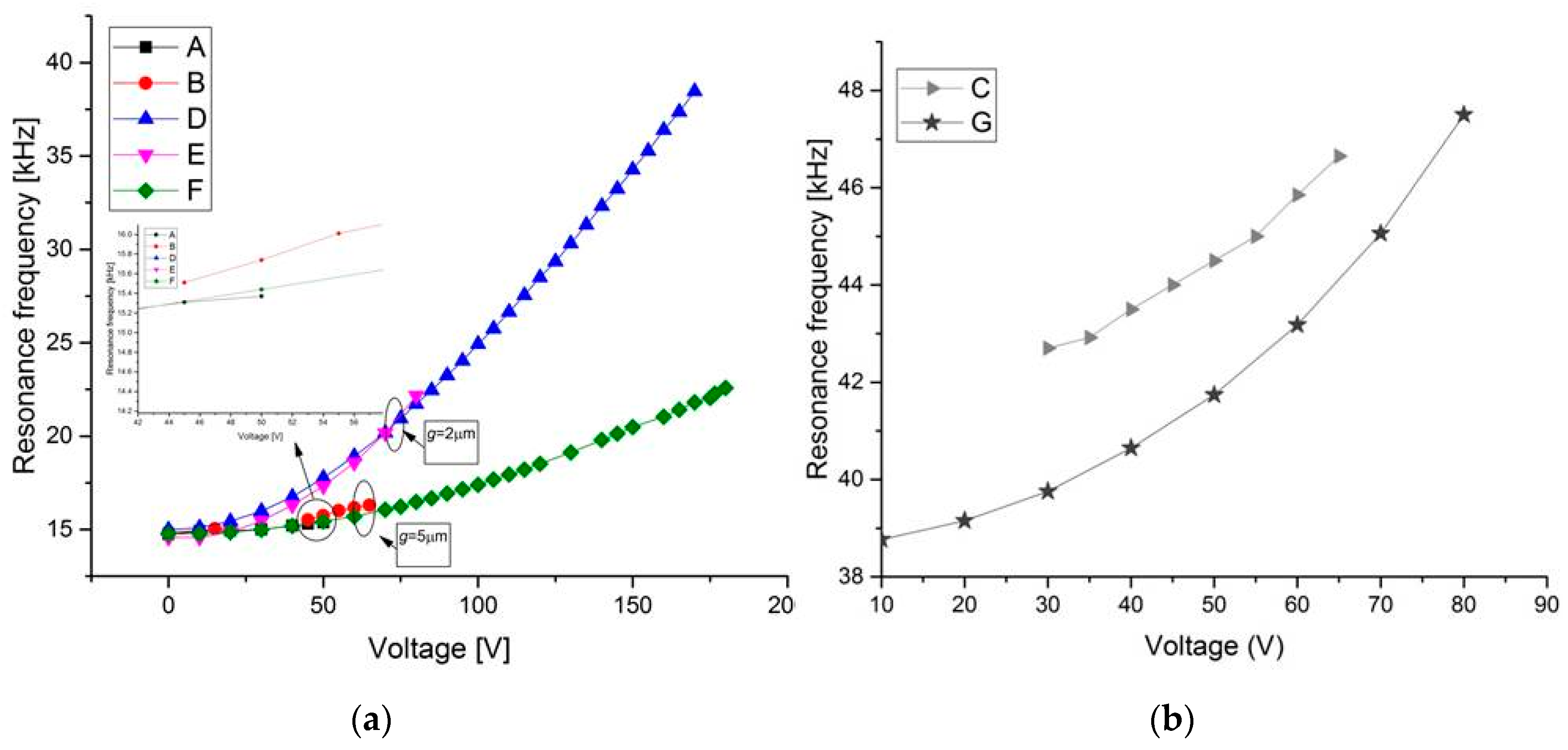
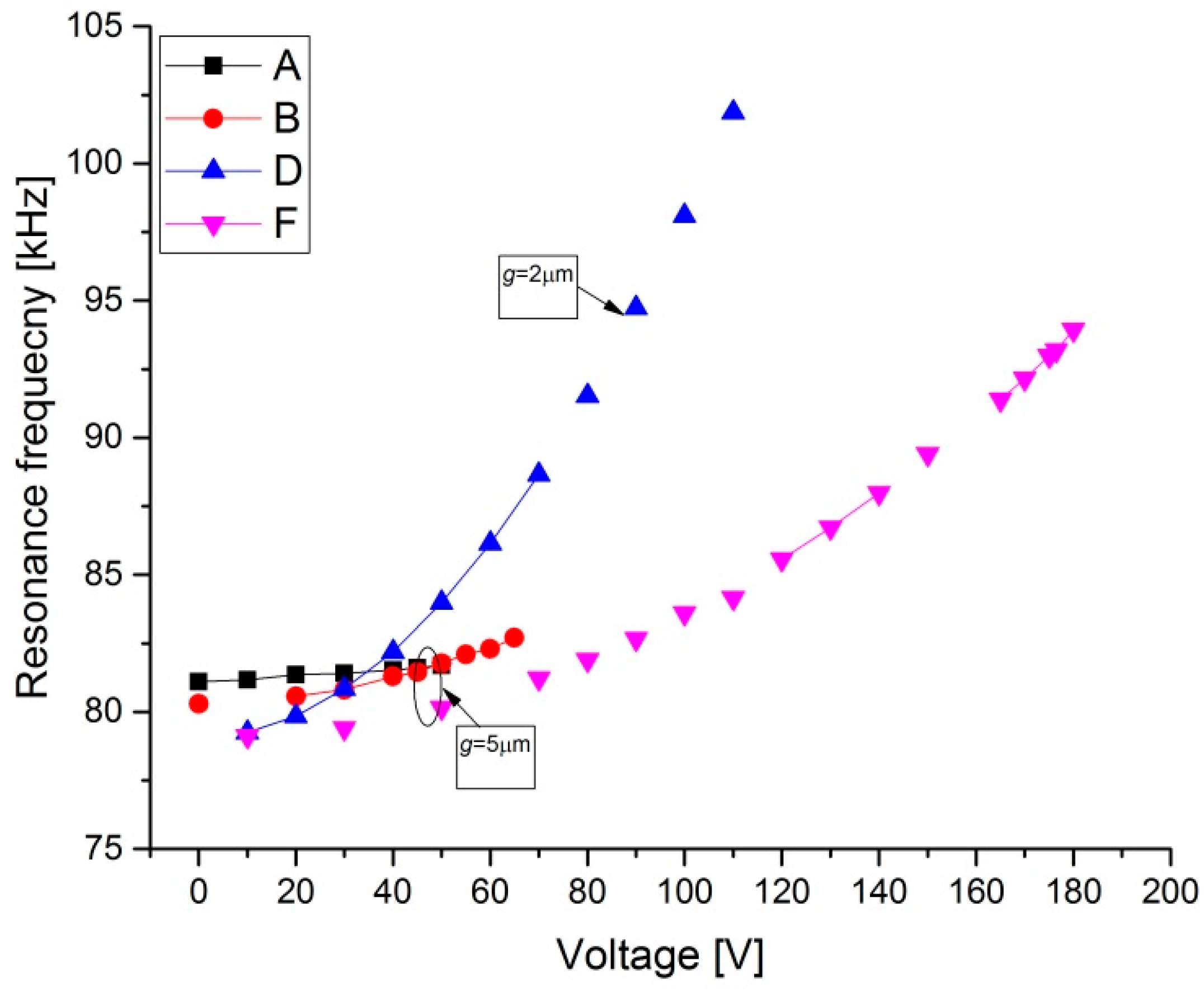

| Type 1 | L (μm) | h (μm) | b0 (μm) | b (μm) | g (μm) | f01 (kHz) |
| A | 1000 | 1.85 | 1.8 | 50 | 5 | 14.74 |
| B | 1000 | 1.85 | 2.6 | 50 | 5 | 14.87 |
| C | 600 | 1.85 | 1.8 | 50 | 2 | 42.7@30V |
| Type 2 | L (μm) | h (μm) | b0 (μm | b (μm) | g (μm) | f01 (kHz) |
| D | 1000 | 1.85 | 2.6 | 20 | 2 | 15 |
| E | 1000 | 1.85 | 2.6 | 10 | 2 | 14.2 |
| F | 1000 | 1.85 | 2.6 | 10 | 5 | 14.5 |
| G | 600 | 1.85 | 2.6 | 10 | 2 | 38.7 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alcheikh, N.; Ramini, A.; Hafiz, M.A.A.; Younis, M.I. Tunable Clamped–Guided Arch Resonators Using Electrostatically Induced Axial Loads. Micromachines 2017, 8, 14. https://doi.org/10.3390/mi8010014
Alcheikh N, Ramini A, Hafiz MAA, Younis MI. Tunable Clamped–Guided Arch Resonators Using Electrostatically Induced Axial Loads. Micromachines. 2017; 8(1):14. https://doi.org/10.3390/mi8010014
Chicago/Turabian StyleAlcheikh, Nouha, Abdallah Ramini, Md Abdullah Al Hafiz, and Mohammad I. Younis. 2017. "Tunable Clamped–Guided Arch Resonators Using Electrostatically Induced Axial Loads" Micromachines 8, no. 1: 14. https://doi.org/10.3390/mi8010014
APA StyleAlcheikh, N., Ramini, A., Hafiz, M. A. A., & Younis, M. I. (2017). Tunable Clamped–Guided Arch Resonators Using Electrostatically Induced Axial Loads. Micromachines, 8(1), 14. https://doi.org/10.3390/mi8010014





