A Novel Electroosmotic Micromixer with Asymmetric Lateral Structures and DC Electrode Arrays
Abstract
:1. Introduction
2. The Mathematical Model and Numerical Method
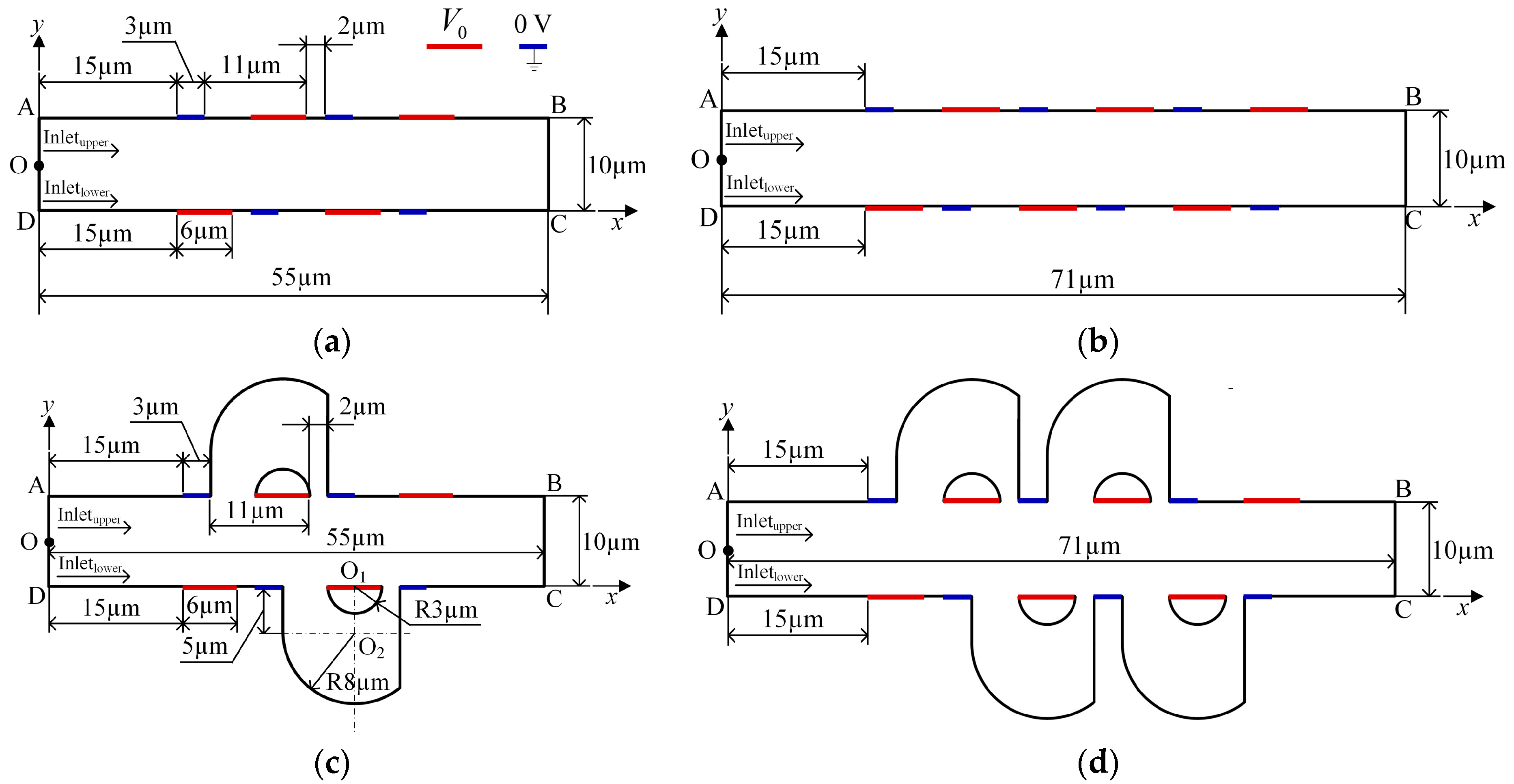
2.1. Mathematical Model
2.2. Numerical Method
3. Results and Discussion
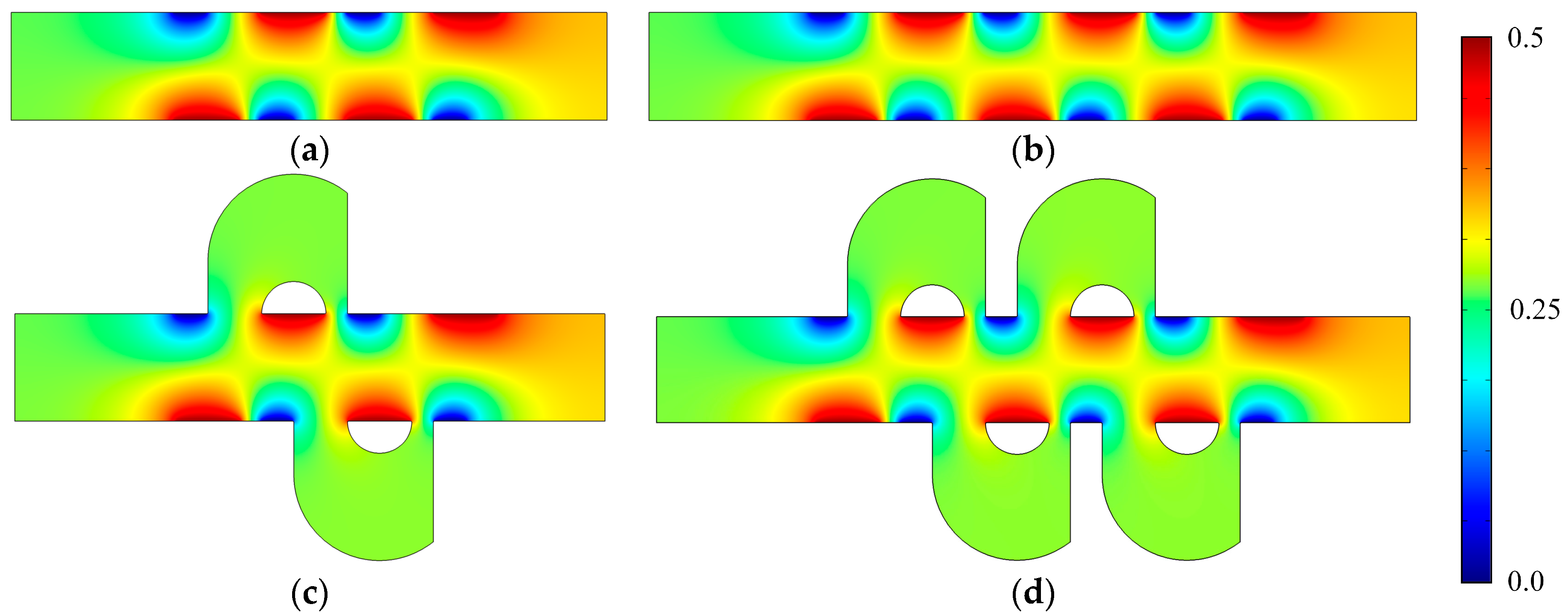
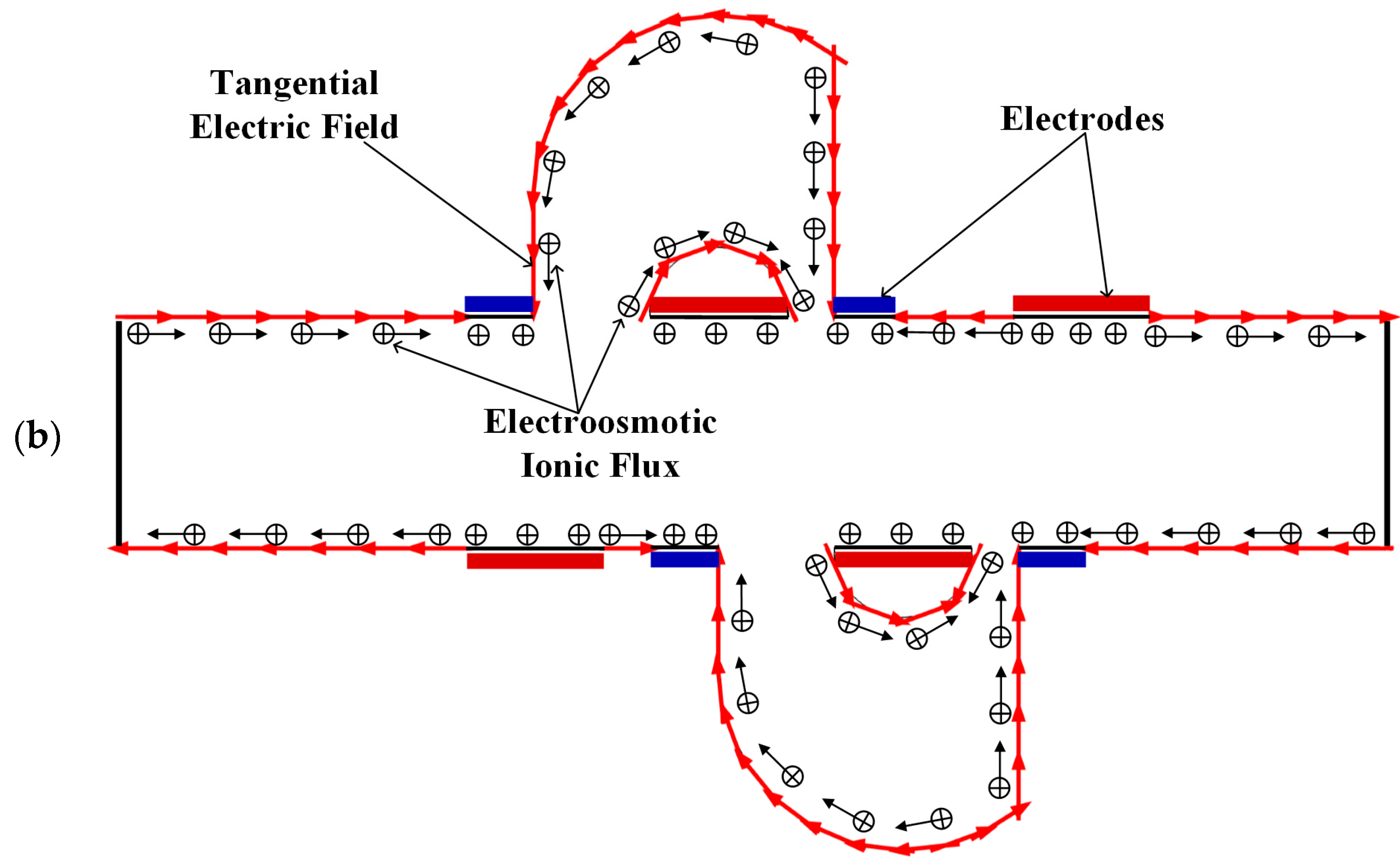
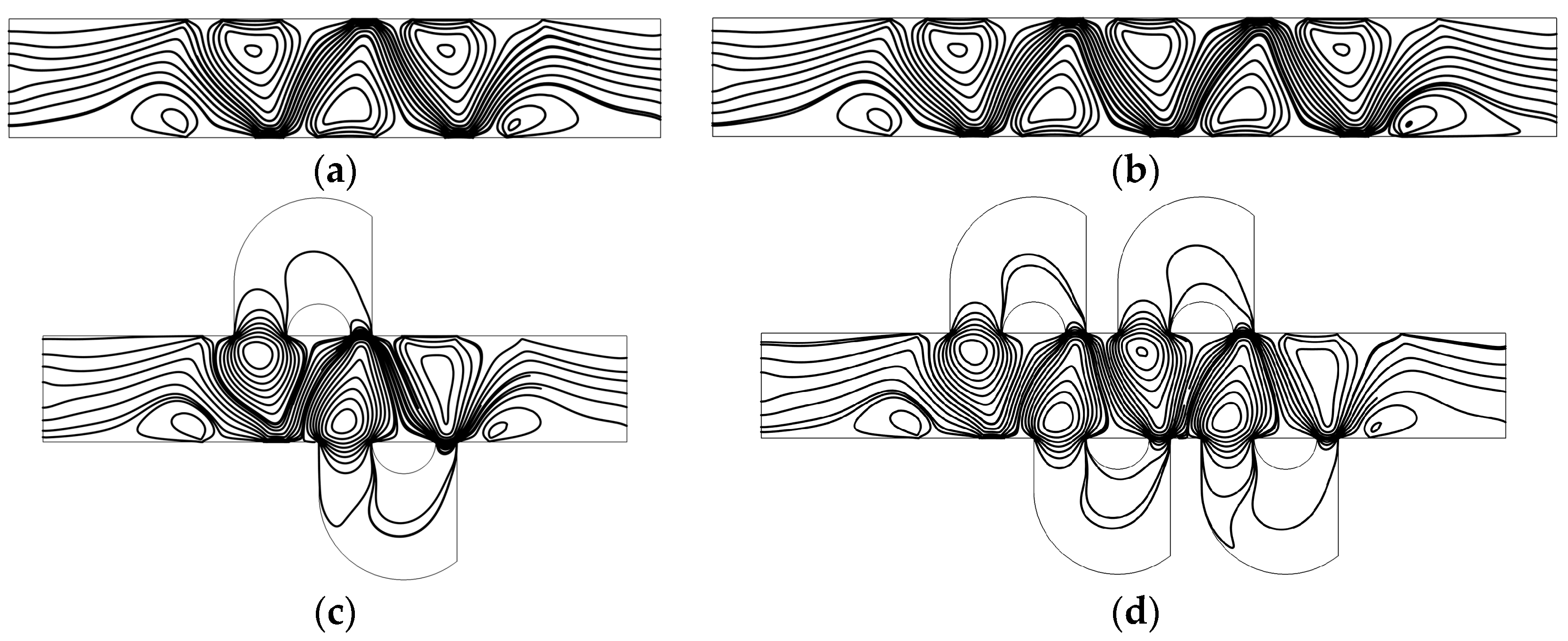
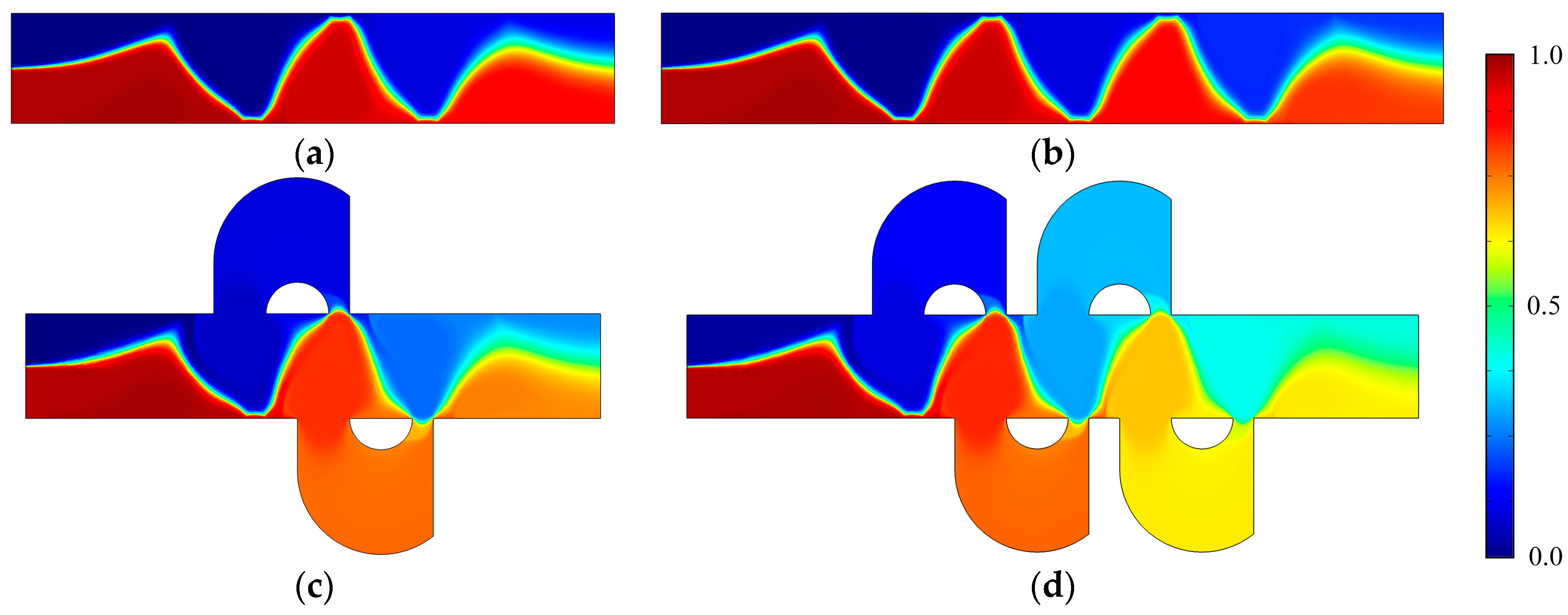
3.1. Mixing Mechanism
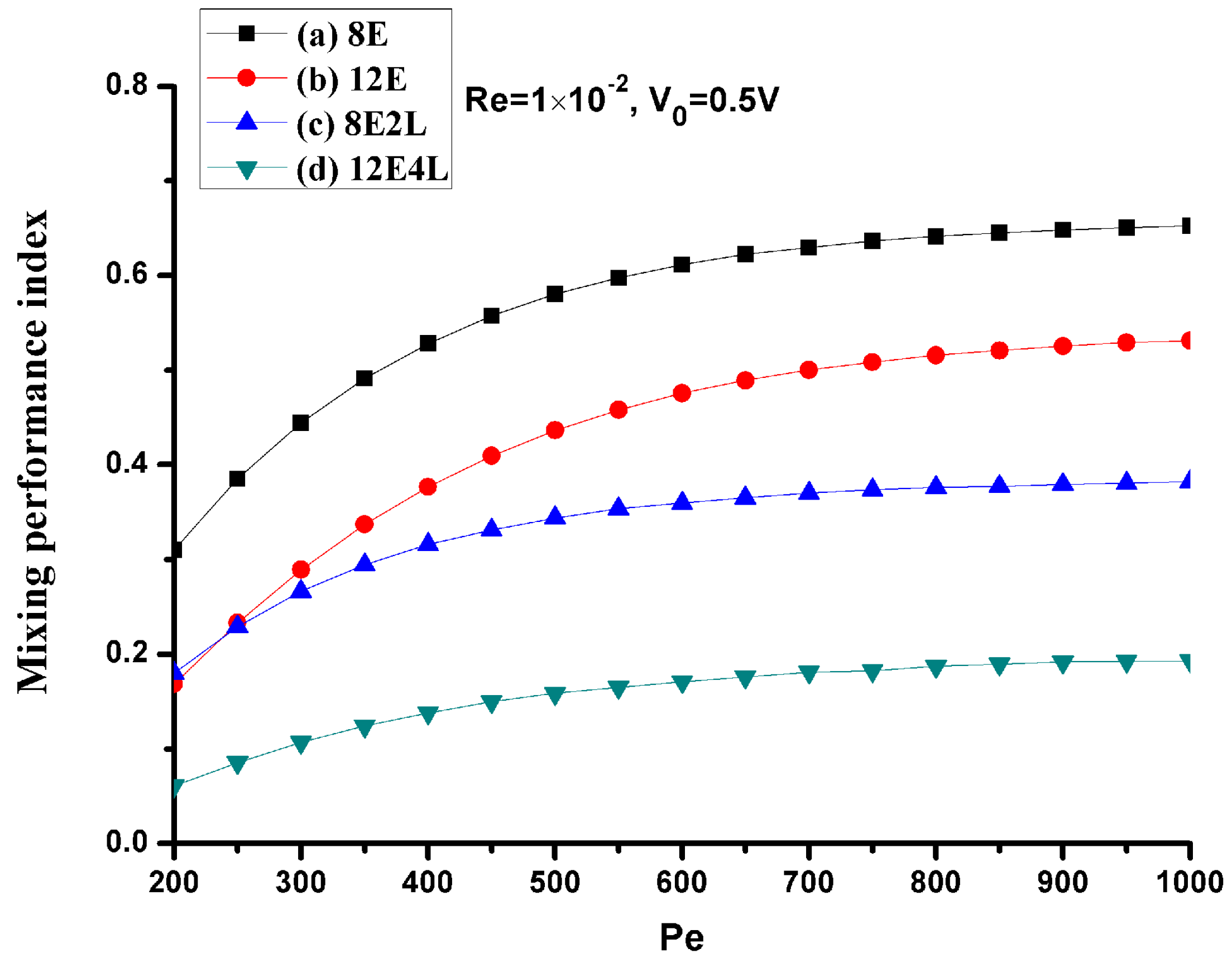
3.2. Mixing Performance
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Johnson, T.J.; Ross, D.; Locascio, L.E. Rapid microfluidic mixing. Anal. Chem. 2002, 74, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.-Y.; Chang, C.-L.; Wang, Y.-N.; Fu, L.-M. Microfluidic mixing: A review. Int. J. Mol. Sci. 2011, 12, 3263–3287. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, N.-T.; Wu, Z. Micromixers—A review. J. Micromech. Microeng. 2005, 15, 1–16. [Google Scholar] [CrossRef]
- Suh, Y.K.; Kang, S. A review on mixing in microfluidics. Micromachines 2010, 1, 82–111. [Google Scholar] [CrossRef]
- Zhou, T.; Yeh, L.H.; Li, F.C.; Mauroy, B.; Joo, S. Deformability-based electrokinetic particle separation. Micromachines 2016, 7, 170. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Wang, W.-T.; Liu, C.-C.; Fu, L.-M. Passive mixers in microfluidic systems: A review. Chem. Eng. J. 2016, 288, 146–160. [Google Scholar] [CrossRef]
- Song, H.; Cai, Z.; Noh, H.M.; Bennett, D.J. Chaotic mixing in microchannels via low frequency switching transverse electroosmotic flow generated on integrated microelectrodes. Lab Chip 2010, 10, 734–740. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, S.-S.; Huang, Y.-C. Passive mixing in micro-channels with geometric variations through μPIV and μLIF measurements. J. Micromech. Microeng. 2008, 18, 065017. [Google Scholar] [CrossRef]
- Zhou, T.; Liu, Z.; Wu, Y.; Deng, Y.; Liu, Y.; Liu, G. Hydrodynamic particle focusing design using fluid-particle interaction. Biomicrofluidics 2013, 7, 054104. [Google Scholar] [CrossRef] [PubMed]
- Glasgow, I.; Aubry, N. Enhancement of microfluidic mixing using time pulsing. Lab Chip 2003, 3, 114–120. [Google Scholar] [CrossRef] [PubMed]
- Mao, H.; Yang, T.; Cremer, P.S. A microfluidic device with a linear temperature gradient for parallel and combinatorial measurements. J. Am. Chem. Soc. 2002, 124, 4432. [Google Scholar] [CrossRef] [PubMed]
- Qian, S.; Bau, H.H. Magnetohydrodynamic flow of RedOx electrolyte. Phys. Fluids 2005, 17, 067105. [Google Scholar] [CrossRef]
- Qian, S.; Zhu, J.; Bau, H.H. A stirrer for magnetohydrodynamically controlled minute fluidic networks. Phys. Fluids 2002, 14, 3584–3592. [Google Scholar] [CrossRef]
- Qian, S.; Bau, H.H. Magneto-hydrodynamics based microfluidics. Mech. Res. Commun. 2009, 36, 10–21. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Matsumoto, S.; Goto, H.; Matsumoto, M.; Maeda, R. Ultrasonic micromixer for microfluidic systems. Sens. Actuators A Phys. 2001, 93, 266–272. [Google Scholar] [CrossRef]
- Zhu, X.; Kim, E.S. Acoustic-wave liquid mixer. In Microelectromechanical Systems (MEMS); Dynamic Systems and Control Division (DSC), American Society of Mechanical Engineers: Fairfield, NJ, USA, 1997; Volume 62, pp. 35–38. [Google Scholar]
- Jacobson, S.C.; McKnight, E.E.; Ramsey, J.M. Microfluidic devices for electrokinetically driven parallel and serial mixing. Anal. Chem. 1999, 71, 4455–4459. [Google Scholar] [CrossRef]
- Wu, Z.; Li, D. Micromixing using induced-charge electrokinetic flow. Electrochim. Acta 2008, 53, 5827–5835. [Google Scholar] [CrossRef]
- Daghighi, Y.; Li, D. Numerical study of a novel induced-charge electrokinetic micro-mixer. Anal. Chim. Acta 2013, 763, 28–37. [Google Scholar] [CrossRef] [PubMed]
- Oddy, M.H.; Santiago, J.G.; Mikkelsen, J.C. Electrokinetic instability micromixing. Anal. Chem. 2001, 73, 5822–5832. [Google Scholar] [CrossRef] [PubMed]
- Lim, C.Y.; Lam, Y.C.; Yang, C. Mixing enhancement in microfluidic channel with a constriction under periodic electro-osmotic flow. Biomicrofluidics 2010, 4, 014101. [Google Scholar] [CrossRef] [PubMed]
- Xuan, X.; Li, D. Analysis of electrokinetic flow in microfluidic networks. J. Micromech. Microeng. 2004, 14, 290–298. [Google Scholar] [CrossRef]
- Tang, Z.; Hong, S.; Djukic, D.; Modi, V.; West, A.C.; Yardley, J.; Osgood, R.M. Electrokinetic flow control for composition modulation in a microchannel. J. Micromech. Microeng. 2002, 12, 870–877. [Google Scholar] [CrossRef]
- Lee, M.G.; Choi, S.; Park, J.K. Rapid laminating mixer using a contraction-expansion array microchannel. Appl. Phys. Lett. 2009, 95, 051902. [Google Scholar] [CrossRef]
- Qian, S.; Bau, H.H. A chaotic electroosmotic stirrer. Anal. Chem. 2002, 74, 3616–3625. [Google Scholar] [CrossRef] [PubMed]
- Qian, S.; Bau, H.H. Theoretical investigation of electro-osmotic flows and chaotic stirring in rectangular cavities. Appl. Math. Model. 2005, 29, 726–753. [Google Scholar] [CrossRef]
- Kumar, D.T.; Zhou, Y.; Brown, V.; Lu, X.; Kale, A.; Yu, L.; Xuan, X. Electric field-induced instabilities in ferrofluid microflows. Microfluid. Nanofluid. 2015, 19, 43–52. [Google Scholar] [CrossRef]
- Ward, K.; Fan, Z.H. Mixing in microfluidic devices and enhancement methods. J. Micromech. Microeng. 2015, 25, 094001. [Google Scholar] [CrossRef] [PubMed]
- Chang, S.T.; Beaumont, E.; Petsev, N.D.; Velev, O.D. Remotely powered distributed microfluidic pumps and mixers based on miniature diodes. Lab Chip 2008, 8, 117–124. [Google Scholar] [CrossRef] [PubMed]
- Seo, H.-S.; Han, B.; Kim, Y.-J. Numerical study on the mixing performance of a ring-type electroosmotic micromixer with different obstacle configurations. J. Nanosci. Nanotechnol. 2012, 12, 4523–4530. [Google Scholar] [CrossRef] [PubMed]
- Yoon, M.S.; Kim, B.J.; Sung, H.J. Pumping and mixing in a microchannel using AC asymmetric electrode arrays. Int. J. Heat Fluid Flow 2008, 29, 269–280. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Y.; Mezic, I.; Meinhart, C.; Petzold, L. Numerical simulation of an electroosmotic micromixer. In Proceedings of the ASME 2003 International Mechanical Engineering Congress and Exposition, Washington, DC, USA, 15–21 November 2003; pp. 653–658. [Google Scholar]
- Erickson, D.; Li, D. Influence of surface heterogeneity on electrokinetically driven microfluidic mixing. Langmuir 2002, 18, 1883–1892. [Google Scholar] [CrossRef]
- Biddiss, E.; Erickson, D.; Li, D. Heterogeneous surface charge enhanced micromixing for electrokinetic Flows. Anal. Chem. 2004, 76, 3208–3213. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, S.; Hasanzadeh-Barforoushi, A.; Nejat, A.; Kowsary, F. Numerical study of mixing and heat transfer in mixed electroosmotic/pressure driven flow through T-shaped microchannels. Int. J. Heat Mass Transf. 2014, 75, 565–580. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Z.; Zhang, P.; Liu, Y.; Gao, Q.; Wu, Y. A flexible layout design method for passive micromixers. Biomed. Microdevices 2012, 14, 929–945. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Wang, H.; Shi, L.; Liu, Z.; Joo, S. An enhanced electroosmotic micromixer with an efficient asymmetric lateral structure. Micromachines 2016, 7, 218. [Google Scholar] [CrossRef]
- Zhou, T.; Xu, Y.; Liu, Z.; Joo, S.W. An enhanced one-layer passive microfluidic mixer with an optimized lateral structure with the Dean effect. J. Fluids Eng. 2015, 137, 091102. [Google Scholar] [CrossRef]
- Liu, Z.; Deng, Y.; Lin, S.; Xuan, M. Optimization of micro Venturi diode in steady flow at low Reynolds number. Eng. Optim. 2012, 44, 1389–1404. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, Q.; Zhang, P.; Xuan, M.; Wu, Y. Topology optimization of fluid channels with flow rate equality constraints. Struct. Multidiscip. Optim. 2011, 44, 31–37. [Google Scholar] [CrossRef]
- Zhou, T.; Liu, T.; Deng, Y.; Chen, L.; Qian, S.; Liu, Z. Design of microfluidic channel networks with specified output flow rates using the CFD-based optimization method. Microfluid. Nanofluid. 2017, 21, 11. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Z.; Wu, Y.; Zhou, T; Qian, S. Optimal control-based inverse determination of electrode distribution for electroosmotic micromixer. arXiv, 2016; arXiv:1601.03076v4. [Google Scholar]
- Chen, X.; Li, T. A novel design for passive misscromixers based on topology optimization method. Biomed. Microdevices 2016, 18, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Borrvall, T.; Petersson, J. Topology optimization of fluids in stokes flow. Int. J. Numer. Methods Fluids 2003, 41, 77–107. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, P.; Liu, Y.; Wu, Y.; Liu, Z. Optimization of unsteady incompressible Navier–Stokes flows using variational level set method. Int. J. Numer. Methods Fluids 2013, 71, 1475–1493. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Z.; Wu, Y. Topology optimization of steady and unsteady incompressible Navier–Stokes flows driven by body forces. Struct. Multidiscip. Optim. 2013, 47, 555–570. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Z.; Zhang, P.; Liu, Y.; Wu, Y. Topology optimization of unsteady incompressible Navier–Stokes flows. J. Comput. Phys. 2011, 230, 6688–6708. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Z.; Wu, J.; Wu, Y. Topology optimization of steady Navier–Stokes flow with body force. Comput. Methods Appl. Mech. Eng. 2013, 255, 306–321. [Google Scholar] [CrossRef]
- Gersborg-Hansen, A.; Sigmund, O.; Haber, R.B. Topology optimization of channel flow problems. Struct. Multidiscip. Optim. 2005, 30, 181–192. [Google Scholar] [CrossRef]
- Olesen, L.H.; Okkels, F.; Bruus, H. A high-level programming language implementation of topology optimization applied to steady-state Navier–Stokes flow. Int. J. Numer. Methods Eng. 2006, 65, 975–1001. [Google Scholar] [CrossRef]
- Liu, R.H.; Sharp, K.V.; Olsen, M.G.; Stremler, M.; Santiago, J.G.; Adrian, R.J.; Aref, H.; Beebe, D.J. Passive mixing in a three-dimensional serpentine microchannel. J. Microelectromech. Syst. 2000, 9, 190–197. [Google Scholar] [CrossRef]
- Stroock, A.D.; Dertinger, S.K.W.; Ajdari, A.; Mezic, I.; Stone, H.A.; Whitesides, G.M. Chaotic mixer for microchannels. Science 2002, 295, 647–651. [Google Scholar] [CrossRef] [PubMed]




© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Deng, Y.; Zhou, T.; Pan, H.; Liu, Z. A Novel Electroosmotic Micromixer with Asymmetric Lateral Structures and DC Electrode Arrays. Micromachines 2017, 8, 105. https://doi.org/10.3390/mi8040105
Chen L, Deng Y, Zhou T, Pan H, Liu Z. A Novel Electroosmotic Micromixer with Asymmetric Lateral Structures and DC Electrode Arrays. Micromachines. 2017; 8(4):105. https://doi.org/10.3390/mi8040105
Chicago/Turabian StyleChen, Limin, Yongbo Deng, Teng Zhou, Hui Pan, and Zhenyu Liu. 2017. "A Novel Electroosmotic Micromixer with Asymmetric Lateral Structures and DC Electrode Arrays" Micromachines 8, no. 4: 105. https://doi.org/10.3390/mi8040105
APA StyleChen, L., Deng, Y., Zhou, T., Pan, H., & Liu, Z. (2017). A Novel Electroosmotic Micromixer with Asymmetric Lateral Structures and DC Electrode Arrays. Micromachines, 8(4), 105. https://doi.org/10.3390/mi8040105






