Construction of Subgame-Perfect Mixed-Strategy Equilibria in Repeated Games
Abstract
:1. Introduction
2. The Model
2.1. Stage Games
- is the finite set of players,
- is the finite set of pure actions for player , and is the set of pure-action profiles. Also, a pure action of player i is called and a pure-action profile is called .
- is the payoff vector.
2.2. Equilibria in Stage Games

3. Repeated Games
3.1. Characterization of Equilibria in Repeated Games
3.2. Self-Supporting Sets and Monotonicity
- 1.
- , and
- 2.
- if player i plays an action outside (an observable deviation), while , then is player i’s punishment payoff .
- 3.
- if at least two players make an observable deviation, then the continuation payoff is a predetermined equilibrium payoff.
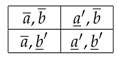
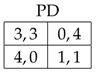
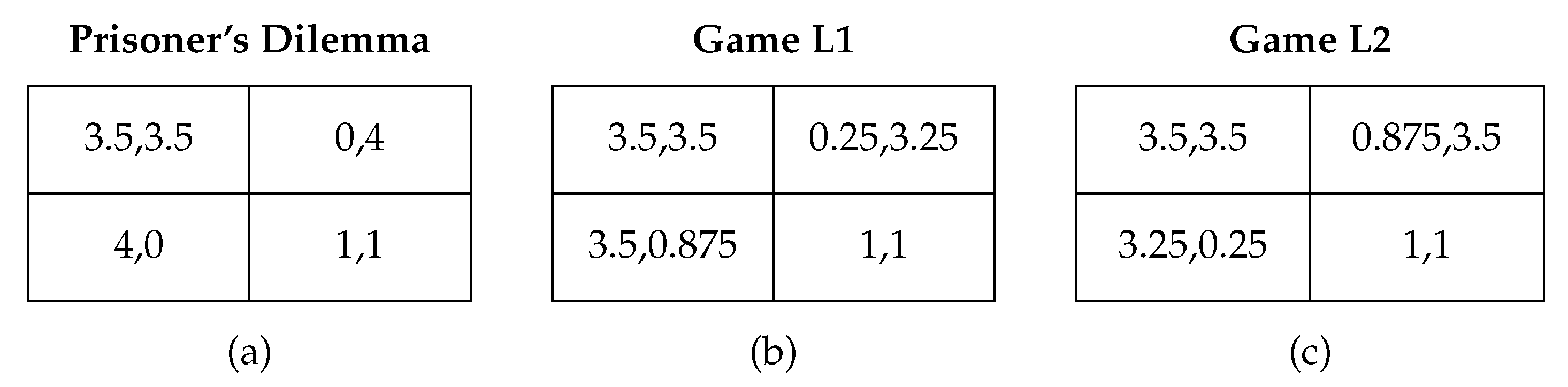
4. Strategies in the Repeated Prisoner’s Dilemma

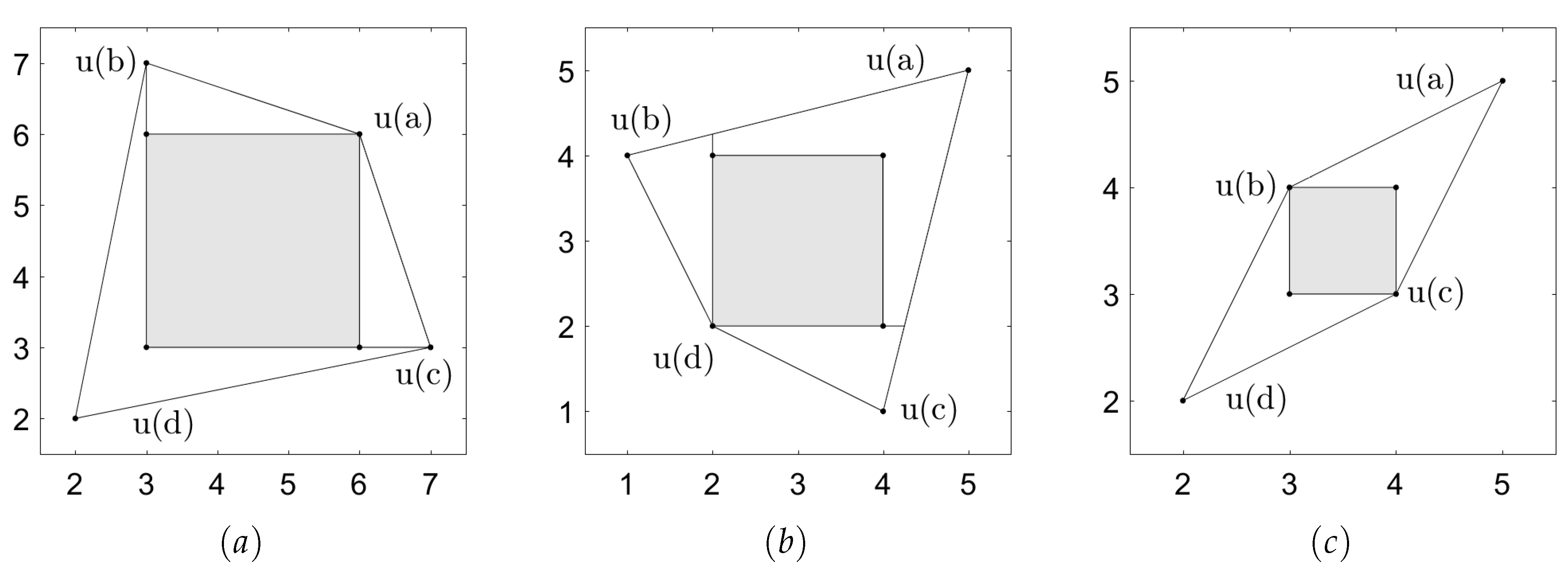
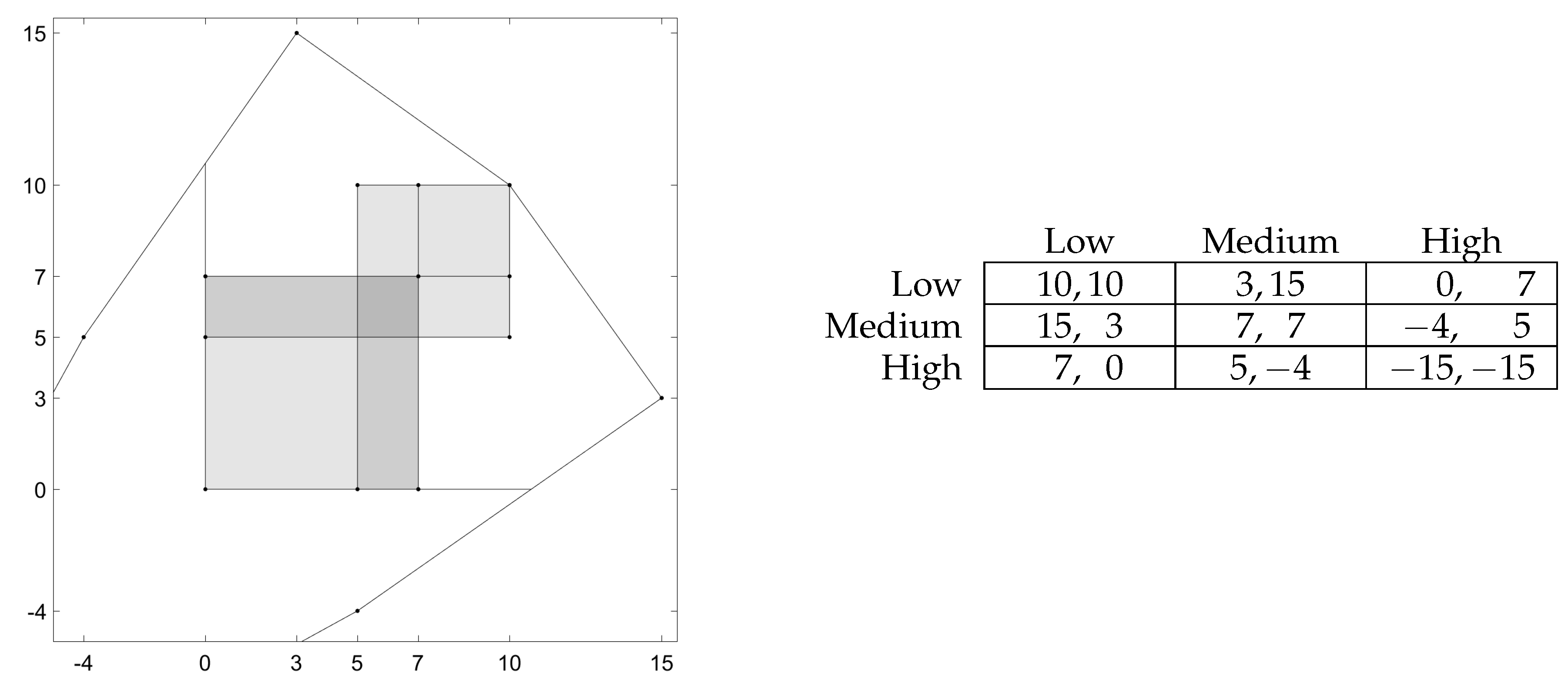
5. Example of a Duopoly Game
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Abreu, D.; Pearce, D.; Stacchetti, E. Optimal cartel equilibria with imperfect monitoring. J. Econ. Theory 1986, 39, 251–269. [Google Scholar] [CrossRef]
- Abreu, D.; Pearce, D.; Stacchetti, E. Toward a theory of discounted repeated games with imperfect monitoring. Econometrica 1990, 58, 1041–1063. [Google Scholar] [CrossRef]
- Mailath, G.J.; Samuelson, L. Repeated Games and Reputations: Long-Run Relationships; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Cronshaw, M.B.; Luenberger, D.G. Strongly symmetric subgame perfect equilibria in infinitely repeated games with perfect monitoring. Games Econ. Behav. 1994, 6, 220–237. [Google Scholar] [CrossRef]
- Cronshaw, M.B. Algorithms for finding repeated game equilibria. Comput. Econ. 1997, 10, 139–168. [Google Scholar] [CrossRef]
- Judd, K.; Yeltekin, Ş.; Conklin, J. Computing supergame equilibria. Econometrica 2003, 71, 1239–1254. [Google Scholar] [CrossRef]
- Burkov, A.; Chaib-draa, B. An approximate subgame-perfect equilibrium computation technique for repeated games. In Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010; pp. 729–736. [Google Scholar]
- Salcedo, B.; Sultanum, B. Computation of Subgame-Perfect Equilibria of Repeated Games with Perfect Monitoring and Public Randomization; Working Paper; The Pennsylvania State University: State College, PA, USA, 2012. [Google Scholar]
- Abreu, D.; Sannikov, Y. An algorithm for two player repeated games with perfect monitoring. Theor. Econ. 2014, 9, 313–338. [Google Scholar] [CrossRef]
- Berg, K.; Kitti, M. Equilibrium Paths in Discounted Supergames; Working Paper; Aalto University: Espoo, Finland, 2012; Available online: http://sal.aalto.fi/publications/pdf-files/mber09b.pdf (accessed on 24 October 2017).
- Berg, K.; Kitti, M. Computing equilibria in discounted 2 × 2 supergames. Comput. Econ. 2013, 41, 71–78. [Google Scholar] [CrossRef]
- Berg, K.; Kitti, M. Fractal geometry of equilibrium payoffs in discounted supergames. Fractals 2014, 22. [Google Scholar] [CrossRef]
- Fudenberg, D.; Maskin, E. The folk theorem in repeated games with discounting and incomplete information. Econometrica 1986, 54, 533–554. [Google Scholar] [CrossRef]
- Fudenberg, D.; Maskin, E. On the dispensability of public randomization in discounted repeated games. J. Econ. Theory 1991, 53, 428–438. [Google Scholar] [CrossRef]
- Gossner, O. The Folk Theorem for Finitely Repeated Games with Mixed Strategies. Int. J. Game Theory 1995, 24, 95–107. [Google Scholar] [CrossRef]
- Busch, L.-A.; Wen, Q. Negotiation games with unobservable mixed disagreement actions. J. Math. Econ. 2001, 35, 563–579. [Google Scholar] [CrossRef]
- Fudenberg, D.; Levine, D.; Maskin, E. The folk theorem with imperfect public information. Econometrica 1994, 62, 997–1039. [Google Scholar] [CrossRef]
- Sugaya, T. Characterizing the limit set of PPE payoffs with unequal discounting. Theor. Econ. 2015, 10, 691–717. [Google Scholar] [CrossRef]
- Chassang, S.; Takahashi, S. Robustness to incomplete information in repeated games. Theor. Econ. 2011, 6, 49–93. [Google Scholar] [CrossRef]
- Peski, M. Repeated games with incomplete information and discounting. Theor. Econ. 2014, 9, 651–694. [Google Scholar] [CrossRef]
- Dutta, P.K. A Folk theorem for stochastic games. J. Econ. Theory 1995, 66, 1–32. [Google Scholar] [CrossRef]
- Hörner, J.; Sugaya, T.; Takahashi, S.; Vieille, N. Recursive methods in discounted stochastic games: An algorithm for δ → 1 and a folk theorem. Econometrica 2011, 79, 1277–1318. [Google Scholar]
- Berg, K. Elementary subpaths in discounted stochastic games. Dyn. Games Appl. 2016, 6, 304–323. [Google Scholar] [CrossRef]
- Berg, K. Set-Valued Games and Mixed-Strategy Equilibria in Discounted Supergames; Working Paper; Aalto University: Espoo, Finland, 2017. [Google Scholar]
- Berg, K. Extremal pure strategies and monotonicity in repeated games. Comput. Econ. 2017, 49, 387–404. [Google Scholar] [CrossRef]
- Berg, K.; Kärki, M. An Algorithm for Computing the Minimum Pure-Strategy Payoffs in Repeated Games; Working Paper; Aalto University: Espoo, Finland, 2016; Available online: http://sal.aalto.fi/publications/pdf-files/mber14c.pdf (accessed on 24 October 2017).
- Ely, J.C.; Välimäki, J. A Robust Folk Theorem for the Prisoner’s Dilemma. J. Econ. Theory 2002, 102, 84–105. [Google Scholar] [CrossRef]
- Ely, J.C.; Hörner, H.; Olszewski, W. Belief-free equilibria in repeated games. Econometrica 2005, 73, 377–415. [Google Scholar] [CrossRef]
- Doraszelski, U.; Escobar, J.F. Restricted feedback in long term relationships. J. Econ. Theory 2012, 147, 142–161. [Google Scholar] [CrossRef]
- Sorin, S. On repeated games with complete information. Math. Oper. Res. 1986, 11, 147–160. [Google Scholar] [CrossRef]
- Stahl, D.O. The graph of prisoner’s dilemma supergame payoffs as a function of the discount factor. Games Econ. Behav. 1991, 3, 368–384. [Google Scholar] [CrossRef]
- Mailath, G.J.; Obara, I.; Sekiguchi, T. The maximum efficient equilibrium payoff in the repeated prisoners’ dilemma. Games Econ. Behav. 2002, 40, 99–122. [Google Scholar] [CrossRef]
- Berg, K.; Kärki, M. How Patient the Players Need to Be to Obtain All the Relevant Payoffs in Discounted Supergames? Working Paper; Aalto University: Espoo, Finland, 2014; Available online: http://sal.aalto.fi/publications/pdf-files/mber14b.pdf (accessed on 24 October 2017).
- Bhaskar, V.; Mailath, G.J.; Morris, S. Purification in the infinitely-repeated prisoners’ dilemma. Rev. Econ. Dyn. 2008, 11, 515–528. [Google Scholar] [CrossRef]
- Bhaskar, V.; Mailath, G.J.; Morris, S. A foundation for Markov equilibria in sequential games with finite social memory. Rev. Econ. Stud. 2013, 80, 925–948. [Google Scholar] [CrossRef]
- Robinson, D.; Goforth, D. The Topology of the 2 × 2 Games: A New Periodic Table; Routledge: Abingdon, UK, 2005. [Google Scholar]
- Borm, P. A classification of 2 × 2 bimatrix games. Cah. Cent. d’Etudes Rech. Oper. 1987, 29, 69–84. [Google Scholar]
- Abreu, D. On the theory of infinitely repeated games with discounting. Econometrica 1988, 56, 383–396. [Google Scholar] [CrossRef]
- Yamamoto, Y. The use of public randomization in discounted repeated games. Int. J. Game Theory 2010, 39, 431–443. [Google Scholar] [CrossRef]
| 1. | |
| 2. | Only the strategy on the equilibrium path is guaranteed to have a finite presentation but we are not aware of any result that the punishment strategies have a finite presentation. |
| 3. | Note that denotes the stage-game payoffs and the expected payoff of a mixed strategy q. |
| 4. | We thank Tadashi Sekiguchi for pointing this out. |
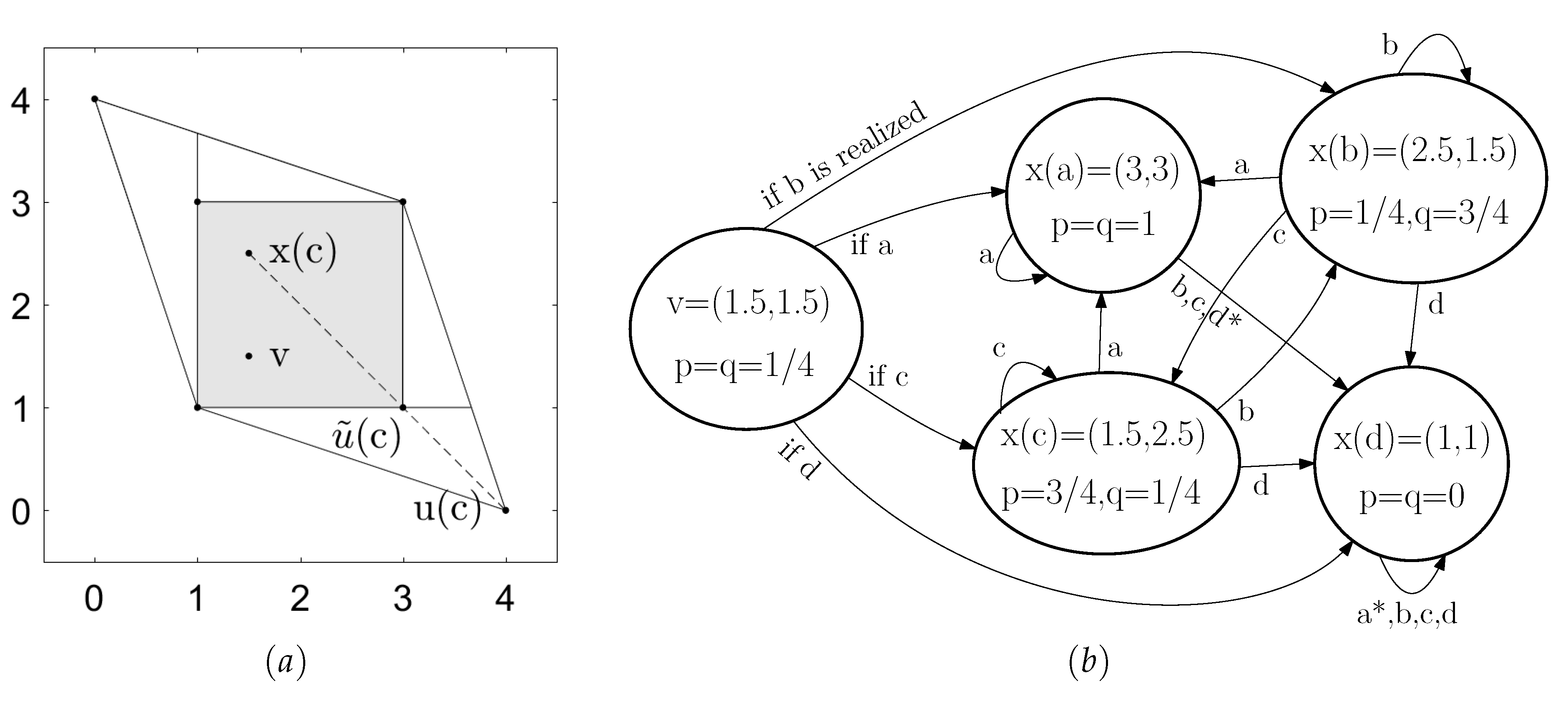
| 5. | Note that in general the continuation play involves mixed strategies even though pure strategies are enough in this example. Figure 3b shows an example where mixed actions are used after action profiles b and c. |
| 6. | The optimal pure punishment strategies in this game depend on the discount factors [26]. |

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berg, K.; Schoenmakers, G. Construction of Subgame-Perfect Mixed-Strategy Equilibria in Repeated Games. Games 2017, 8, 47. https://doi.org/10.3390/g8040047
Berg K, Schoenmakers G. Construction of Subgame-Perfect Mixed-Strategy Equilibria in Repeated Games. Games. 2017; 8(4):47. https://doi.org/10.3390/g8040047
Chicago/Turabian StyleBerg, Kimmo, and Gijs Schoenmakers. 2017. "Construction of Subgame-Perfect Mixed-Strategy Equilibria in Repeated Games" Games 8, no. 4: 47. https://doi.org/10.3390/g8040047
APA StyleBerg, K., & Schoenmakers, G. (2017). Construction of Subgame-Perfect Mixed-Strategy Equilibria in Repeated Games. Games, 8(4), 47. https://doi.org/10.3390/g8040047




