Defect-Free Phononic Crystal Waveguides on GaAs
Abstract
:1. Introduction
2. Materials and Methods
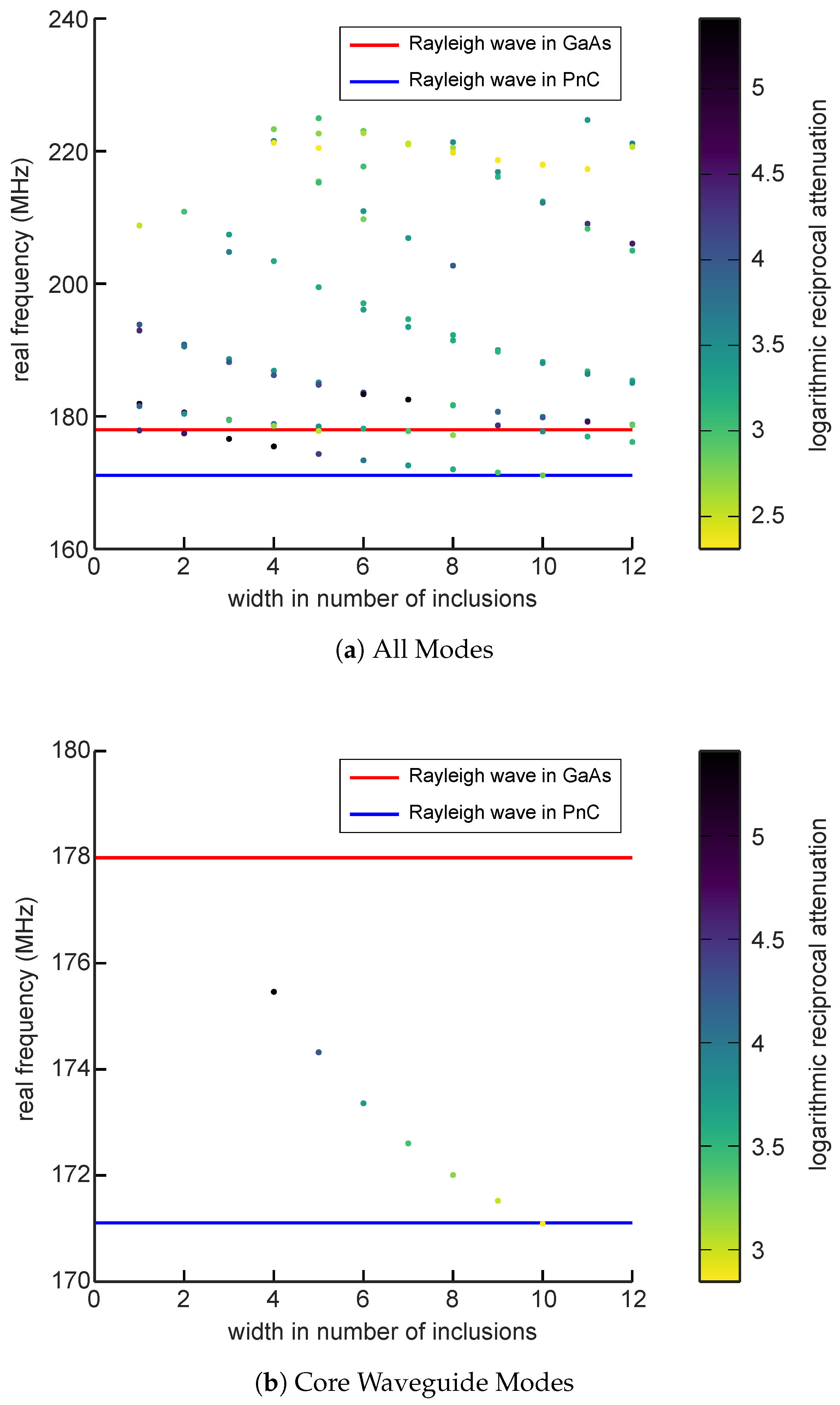
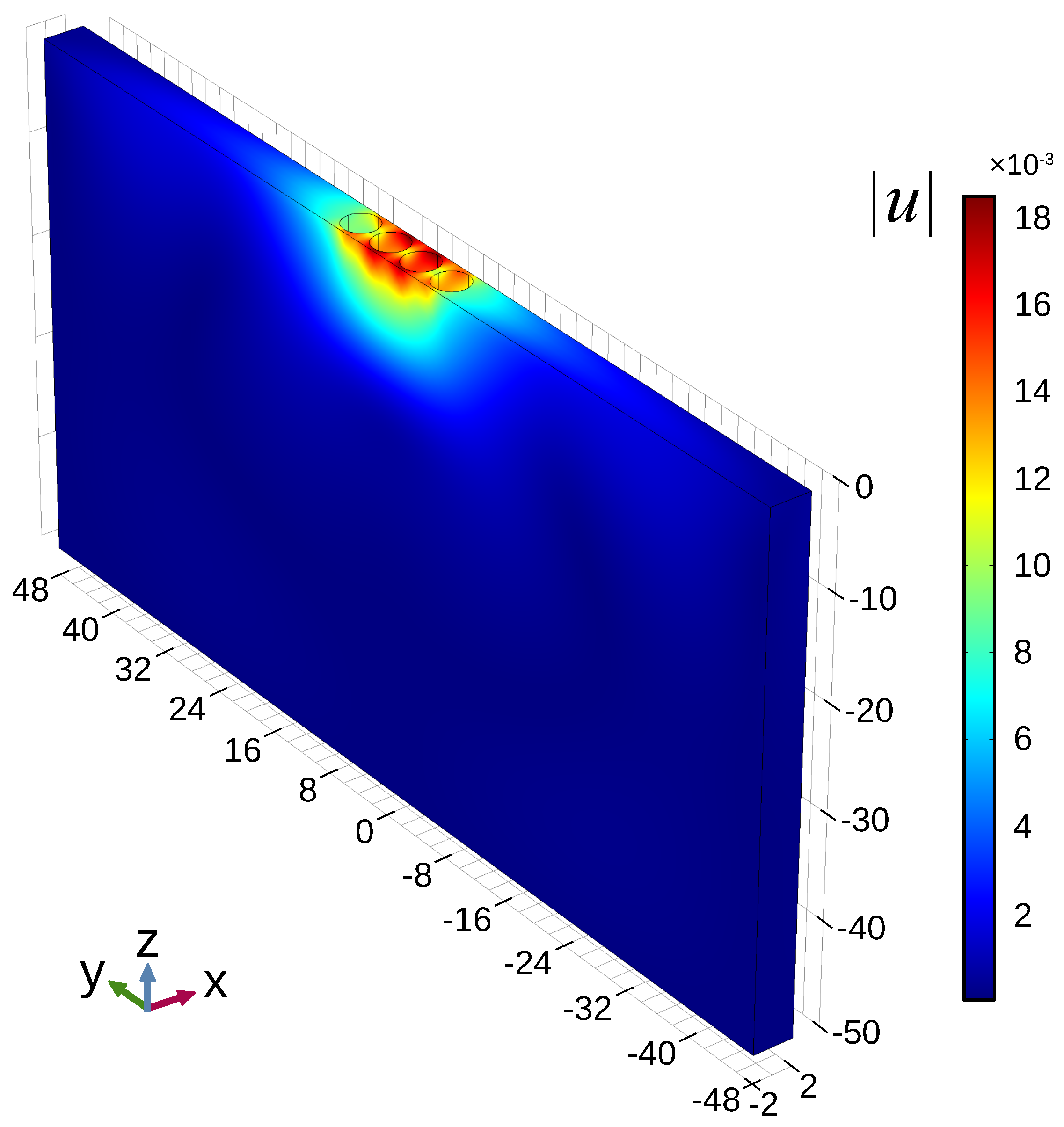
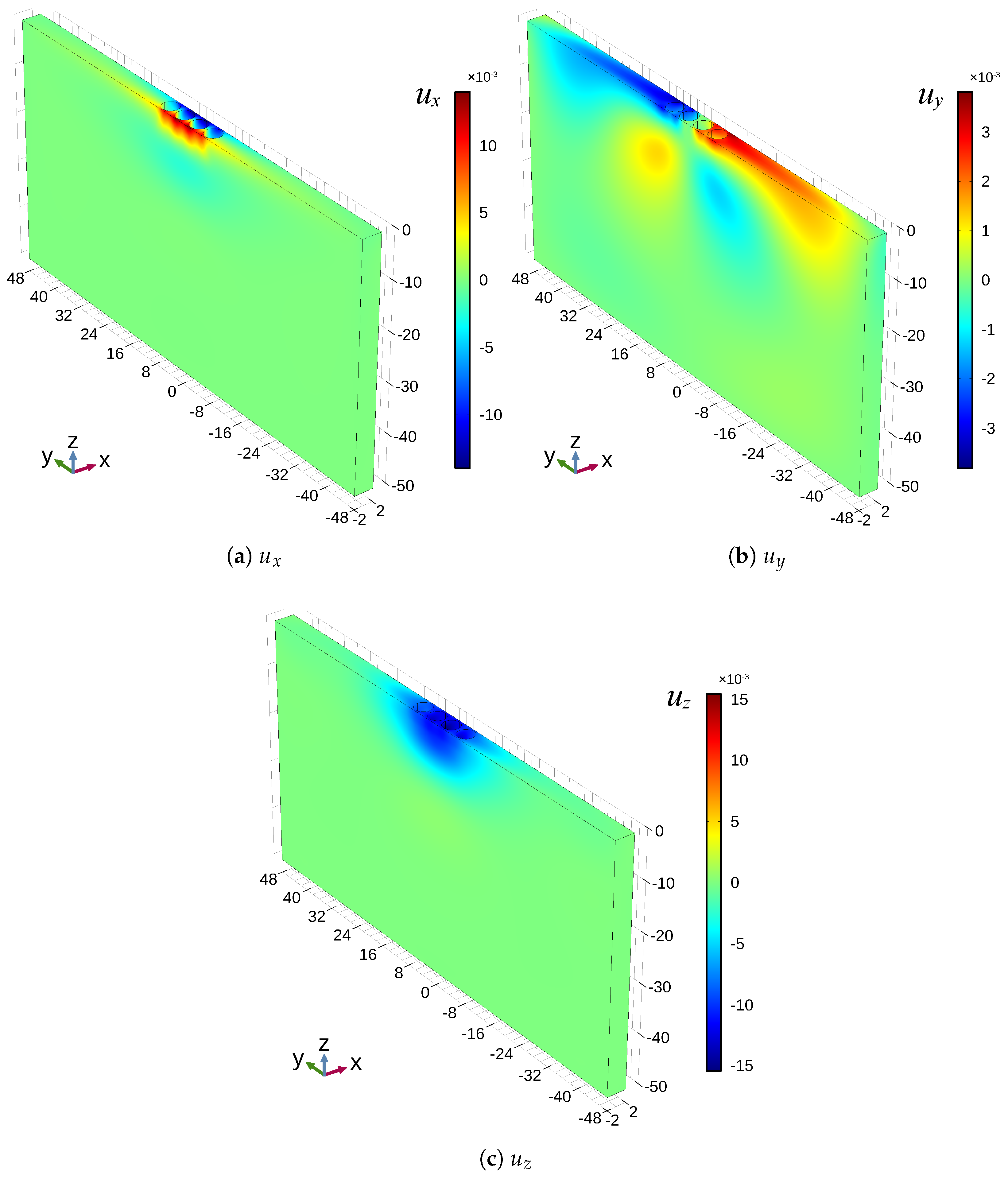
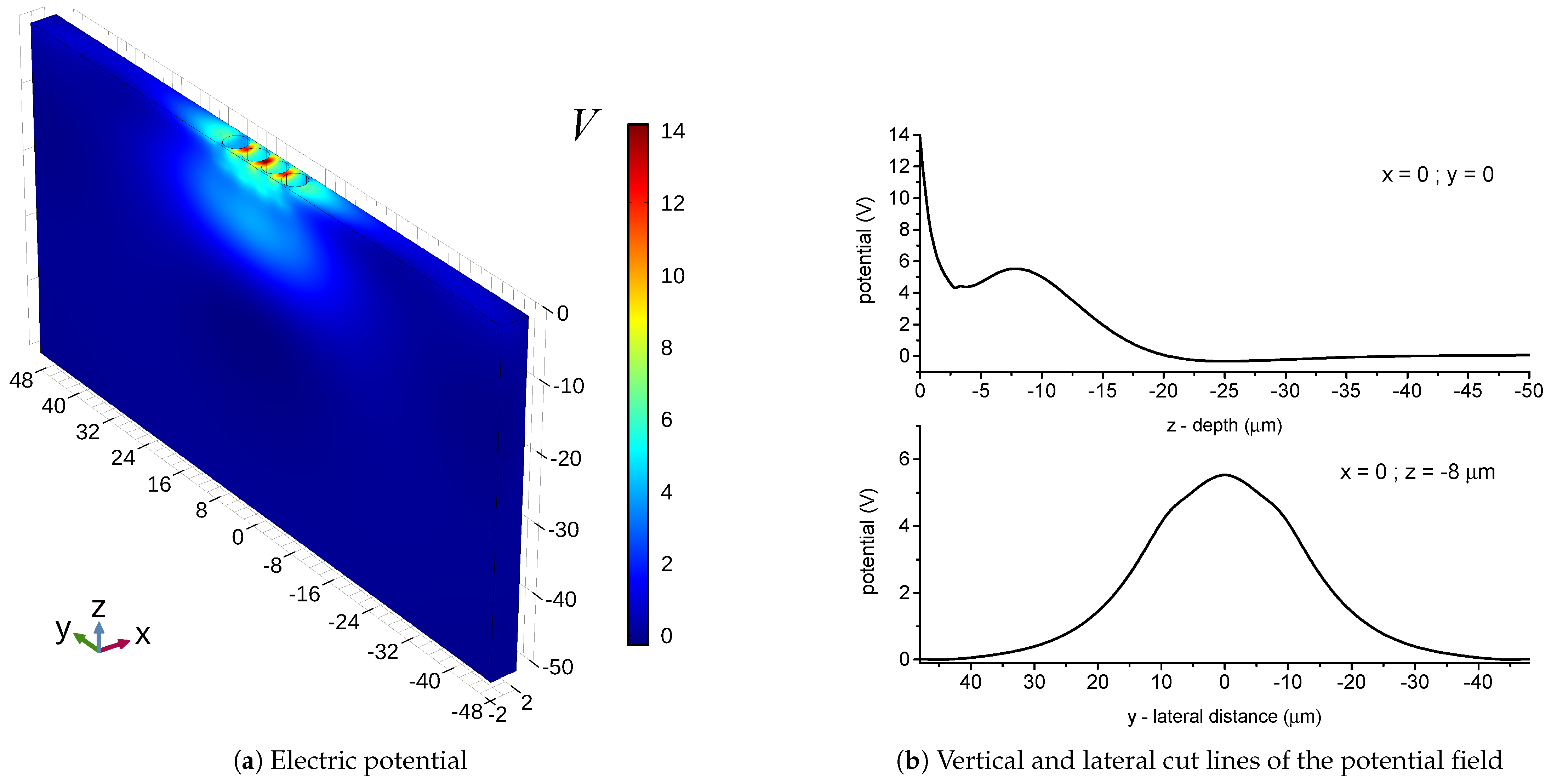
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RF | Radio-frequency |
| SAW | Surface acoustic wave |
| PnC | Phononic crystal |
| FEM | Finite element method |
References
- Vecchi, F.; Repossi, M.; Eyssa, W.; Arcioni, P.; Svelto, F. Design of Low-Loss Transmission Lines in Scaled CMOS by Accurate Electromagnetic Simulations. IEEE J. Solid-State Circuits 2009, 44, 2605–2615. [Google Scholar] [CrossRef]
- Webster, M.A.; Pafchek, R.M.; Sukumaran, G.; Koch, T.L. Low-loss quasi-planar ridge waveguides formed on thin silicon-on-insulator. Appl. Phys. Lett. 2005, 87, 231108. [Google Scholar] [CrossRef]
- Lin, S.Y.; Chow, E.; Hietala, V.; Villeneuve, P.R.; Joannopoulos, J.D. Experimental Demonstration of Guiding and Bending of Electromagnetic Waves in a Photonic Crystal. Science 1998, 282, 274–276. [Google Scholar] [CrossRef]
- Delsing, P.; Cleland, A.N.; Schuetz, M.J.A.; Knörzer, J.; Giedke, G.; Cirac, J.I.; Srinivasan, K.; Wu, M.; Balram, K.C.; Bäuerle, C.; et al. The 2019 surface acoustic waves roadmap. J. Phys. D Appl. Phys. 2019, 52, 353001. [Google Scholar] [CrossRef]
- Auld, B.A. Acoustic Fields and Waves in Solids, Vols. I and II; John Wiley & Sons, Inc.: New York, NY, USA, 1973. [Google Scholar]
- Ash, E.A.; De La Rue, R.M.; Humphryes, R.F. Microsound Surface Waveguides. IEEE Trans. Microw. Theory Tech. 1969, 17, 882–892. [Google Scholar] [CrossRef]
- Modica, G.; Zhu, R.; Horvath, R.; Beaudoin, G.; Sagnes, I.; Braive, R. Slow propagation of 2 GHz acoustical waves in a suspended GaAs phononic waveguide on insulator. Appl. Phys. Lett. 2020, 117, 193501. [Google Scholar] [CrossRef]
- Oliner, A.A. Waveguides for surface waves. In Acoustic Surface Waves; Springer: Berlin/Heidelberg, Germany, 1978; pp. 187–223. [Google Scholar] [CrossRef]
- Mei, J.; Friend, J. A review: Controlling the propagation of surface acoustic waves via waveguides for potential use in acoustofluidics. Mech. Eng. Rev. 2020, 7, 19-00402. [Google Scholar] [CrossRef]
- Porter, R.; Evans, D.V. Embedded Rayleigh–Bloch surface waves along periodic rectangular arrays. Wave Motion 2005, 43, 29–50. [Google Scholar] [CrossRef]
- Al Lethawe, M.; Addouche, M.; Benchabane, S.; Laude, V.; Khelif, A. Guidance of surface elastic waves along a linear chain of pillars. AIP Adv. 2016, 6, 121708. [Google Scholar] [CrossRef]
- Khelif, A.; Choujaa, A.; Benchabane, S.; Djafari-Rouhani, B.; Laude, V. Guiding and bending of acoustic waves in highly confined phononic crystal waveguides. Appl. Phys. Lett. 2004, 84, 4400–4402. [Google Scholar] [CrossRef]
- Olsson, R.H., III; El-Kady, I. Microfabricated phononic crystal devices and applications. Meas. Sci. Technol. 2009, 20, 012002. [Google Scholar] [CrossRef]
- Muzar, E.; Aval, G.A.; Stotz, J.A.H. Wet-etched phononic crystal waveguiding on GaAs. J. Phys. D Appl. Phys. 2018, 51, 044001. [Google Scholar] [CrossRef]
- Benchabane, S.; Gaiffe, O.; Salut, R.; Ulliac, G.; Laude, V.; Kokkonen, K. Guidance of surface waves in a micron-scale phononic crystal line-defect waveguide. Appl. Phys. Lett. 2015, 106, 081903. [Google Scholar] [CrossRef]
- Laude, V. Principles and properties of phononic crystal waveguides. APL Mater. 2021, 9, 080701. [Google Scholar] [CrossRef]
- Muzar, E.; Stotz, J.A.H. Surface acoustic wave modes in two-dimensional shallow void inclusion phononic crystals on GaAs. J. Appl. Phys. 2019, 126, 025104. [Google Scholar] [CrossRef]
- Eigenfrequency Analysis. 2018. Available online: https://www.comsol.com/multiphysics/eigenfrequency-analysis (accessed on 1 October 2023).
- Tanaka, Y.; Tamura, S. Surface acoustic waves in two-dimensional periodic elastic structures. Phys. Rev. B 1998, 58, 7958–7965. [Google Scholar] [CrossRef]
- COMSOL. Structural Mechanics Module User’s Guide: Version 5.3. 2017. Available online: https://doc.comsol.com/5.3/doc/com.comsol.help.sme/StructuralMechanicsModuleUsersGuide.pdf (accessed on 1 October 2023).
- Liu, T.W.; Tsai, Y.C.; Lin, Y.C.; Ono, T.; Tanaka, S.; Wu, T.T. Design and fabrication of a phononic-crystal-based Love wave resonator in GHz range. AIP Adv. 2014, 4, 124201. [Google Scholar] [CrossRef]
- Achaoui, Y.; Khelif, A.; Benchabane, S.; Laude, V. Polarization state and level repulsion in two-dimensional phononic crystals and waveguides in the presence of material anisotropy. J. Phys. D Appl. Phys. 2010, 43, 185401. [Google Scholar] [CrossRef]
- Laude, V. Phononic Crystals; De Gruyter: Berlin, Germany; Boston, MA, USA, 2015. [Google Scholar] [CrossRef]
- Maznev, A.A.; Every, A.G. Surface acoustic waves in a periodically patterned layered structure. J. Appl. Phys. 2009, 106, 113531. [Google Scholar] [CrossRef]
- Hermelin, S.; Takada, S.; Yamamoto, M.; Tarucha, S.; Wieck, A.D.; Saminadayar, L.; Bäuerle, C.; Meunier, T. Electrons surfing on a sound wave as a platform for quantum optics with flying electrons. Nature 2011, 477, 435–438. [Google Scholar] [CrossRef]
- Couto, O.D.D.; Lazić, S.; Iikawa, F.; Stotz, J.A.H.; Jahn, U.; Hey, R.; Santos, P.V. Photon anti-bunching in acoustically pumped quantum dots. Nat. Photonics 2009, 3, 645–648. [Google Scholar] [CrossRef]
- Stotz, J.A.H.; Hey, R.; Santos, P.V.; Ploog, K.H. Coherent spin transport through dynamic quantum dots. Nat. Mater. 2005, 4, 585–588. [Google Scholar] [CrossRef] [PubMed]
- Helgers, P.L.J.; Stotz, J.A.H.; Sanada, H.; Kunihashi, Y.; Biermann, K.; Santos, P.V. Flying electron spin control gates. Nat. Commun. 2022, 13, 5384. [Google Scholar] [CrossRef] [PubMed]
- Stotz, J.A.H.; Hey, R.; Santos, P.V.; Ploog, K.H. Enhanced spin coherence via mesoscopic confinement during acoustically induced transport. New J. Phys. 2008, 10, 093013. [Google Scholar] [CrossRef]
- Maznev, A.A. Dirac cone dispersion of acoustic waves in plates without phononic crystals. J. Acoust. Soc. Am. 2014, 135, 577–580. [Google Scholar] [CrossRef] [PubMed]
- Maznev, A.; Every, A. Existence of backward propagating acoustic waves in supported layers. Wave Motion 2011, 48, 401–407. [Google Scholar] [CrossRef]
- Eaton, J.W.; Bateman, D.; Hauberg, S.; Wehbring, R. GNU Octave Version 4.2.1 Manual: A High-Level Interactive Language for Numerical Computations. 2017. Available online: https://www.gnu.org/software/octave/doc/v4.2.1/ (accessed on 1 October 2023).

| Constant | Value | Unit |
|---|---|---|
| 5360 | kg/m3 | |
| 11.88 | Pa | |
| = = | 5.38 | Pa |
| 5.94 | Pa | |
| 0.139785 | C/m2 | |
| 12.459 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muzar, E.; Stotz, J.A.H. Defect-Free Phononic Crystal Waveguides on GaAs. Crystals 2023, 13, 1540. https://doi.org/10.3390/cryst13111540
Muzar E, Stotz JAH. Defect-Free Phononic Crystal Waveguides on GaAs. Crystals. 2023; 13(11):1540. https://doi.org/10.3390/cryst13111540
Chicago/Turabian StyleMuzar, Edward, and James A. H. Stotz. 2023. "Defect-Free Phononic Crystal Waveguides on GaAs" Crystals 13, no. 11: 1540. https://doi.org/10.3390/cryst13111540






