Electronic Structure of Cu(tmdt)2 Studied with First-Principles Calculations
1
Nanosystem Research Institute (NRI) “Research Initiative of Computational Sciences (RICS)”, National Institute of Advanced Industrial Science and Technology (AIST), 1-1-1 Umezono, Tsukuba, Ibaraki 305-8568, Japan
2
Japan Advanced Institute of Science and Technology (JAIST), 1-1 Asahidai, Nomi, Ishikawa923-1292, Japan
*
Author to whom correspondence should be addressed.
Crystals 2012, 2(3), 1210-1221; https://doi.org/10.3390/cryst2031210
Submission received: 13 April 2012
/
Revised: 9 August 2012
/
Accepted: 13 August 2012
/
Published: 21 August 2012
(This article belongs to the Special Issue Molecular Conductors)
Abstract
:We have studied the electronic structure of Cu(tmdt)2, a material related to single-component molecular conductors, by first-principles calculations. The total energy calculations for several different magnetic configurations show that there is strong antiferromagnetic (AFM) exchange coupling along the crystal a-axis. The electronic structures are analyzed in terms of the molecular orbitals near the Fermi level of isolated Cu(tmdt)2 molecule. This analysis reveals that the system is characterized by the half-filled pdσ(−) band whose intermolecular hopping integrals have strong one-dimensionality along the crystal a-axis. As the exchange splitting of the band is larger than the band width, the basic mechanism of the AFM exchange coupling is the superexchange. It will also be shown that two more ligand orbitals which are fairly insensitive to magnetism are located near the Fermi level. Because of the presence of these orbitals, the present calculation predicts that Cu(tmdt)2 is metallic even in its AFM state, being inconsistent with the available experiment. Some comments will be made on the difference between Cu(tmdt)2 and Cu(dmdt)2.
1. Introduction
Since the successful synthesis of Ni(tmdt)2 (tmdt = trimethylenetetrathiafulvalenedithiolate) which is the first single-component molecular conductor [1], related materials such as Au(tmdt)2 [2], Cu(dmdt)2 (dmdt = dimethyltetrathiafulvalenedithiolate) [3] and Zn(tmdt)2 [4] have been subsequently synthesized. Their electronic properties observed experimentally are wide-ranging. Briefly, Ni(tmdt)2 is a paramagnetic metal in the whole temperature range below room temperature. In contrast, Au(tmdt)2 undergoes a magnetic phase transition around 110 K. At low temperature, it is an antiferromagnetic metal [5]. (Note that in the early stage, semiconducting behavior was reported [2].) Cu(dmdt)2 behaves as a semiconductor and shows Curie–Weiss-type magnetic susceptibility with a magnetic moment of 0.84 μB/molecule. Zn(tmdt)2 is a semiconductor though there is a temperature-independent paramagnetic component in magnetic susceptibility measurements.
Their crystal structures can be classified into two categories. Ni(tmdt)2 and Au(tmdt)2 belonging to the first category have the crystal with the triclinic symmetry ( ![Crystals 02 01210 i001]()
) while Cu(dmdt)2 and Zn(tmdt)2 belonging to the second one have the crystal with the base-centered monoclinic symmetry (C2/c). The molecular shape therein is planar for the former while it is twisted for the latter. Recently, a new member Cu(tmdt)2 has been synthesized [6], whose crystal structure is similar to those of Ni(tmdt)2 and Au(tmdt)2 with its molecular shape being planar. It is quite interesting that Cu(dmdt)2 and Cu(tmdt)2 show different crystal structures and molecular shapes therein in spite of their chemical similarities. In Figure 1, chemical structural formulae of Cu(dmdt)2 and Cu(tmdt)2 and three-dimensional views (drawn with VESTA [7]) of a Cu(tmdt)2 molecule as well as the Cu(tmdt)2 crystal are shown. Magnetic susceptibility measurements imply that Cu(tmdt)2 is a one-dimensional antiferromagnetic Heisenberg system with the antiferromagnetic ordering temperature of 13 K [6].
) while Cu(dmdt)2 and Zn(tmdt)2 belonging to the second one have the crystal with the base-centered monoclinic symmetry (C2/c). The molecular shape therein is planar for the former while it is twisted for the latter. Recently, a new member Cu(tmdt)2 has been synthesized [6], whose crystal structure is similar to those of Ni(tmdt)2 and Au(tmdt)2 with its molecular shape being planar. It is quite interesting that Cu(dmdt)2 and Cu(tmdt)2 show different crystal structures and molecular shapes therein in spite of their chemical similarities. In Figure 1, chemical structural formulae of Cu(dmdt)2 and Cu(tmdt)2 and three-dimensional views (drawn with VESTA [7]) of a Cu(tmdt)2 molecule as well as the Cu(tmdt)2 crystal are shown. Magnetic susceptibility measurements imply that Cu(tmdt)2 is a one-dimensional antiferromagnetic Heisenberg system with the antiferromagnetic ordering temperature of 13 K [6].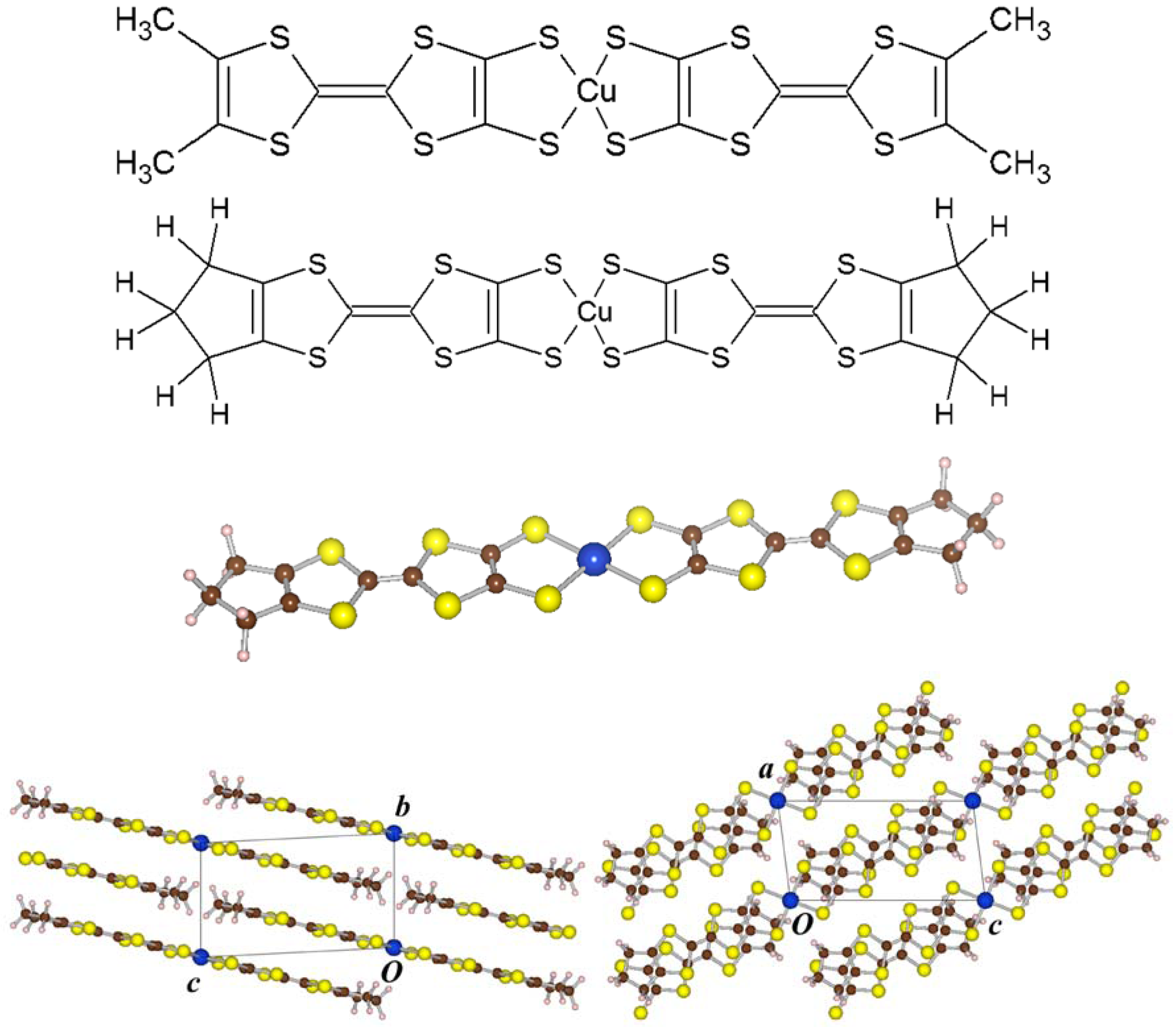
Figure 1.
Chemical formulae of Cu(dmdt)2 (first) and Cu(tmdt)2 (second) and three-dimensional views of a Cu(tmdt)2 molecule (third) and the Cu(tmdt)2 crystal (lower left and right).
Figure 1.
Chemical formulae of Cu(dmdt)2 (first) and Cu(tmdt)2 (second) and three-dimensional views of a Cu(tmdt)2 molecule (third) and the Cu(tmdt)2 crystal (lower left and right).
In the present paper, we investigate the electronic structure of this novel single-component molecular crystal Cu(tmdt)2 by means of first-principles calculations. We show that the magnetic property of this material is indeed characterized by a one-dimensional antiferromagnet along the crystal a-axis stabilized by superexchange. The obtained electronic structures are compared with our previous results [8,9,10] for other single-component conductors and existing experimental results [6].
2. Method
The calculations were carried out with our computational code QMAS (Quantum MAterials Simulator) [11], where the planewave basis and the projector augmented-wave (PAW) method [12,13,14] are adopted. As for the exchange and correlation energy for electrons, the generalized gradient approximation (GGA) [15] was used. The planewave cut-off energy was set to 20 hartree. For isolated molecules, κ-point sampling was Г point only and a supercell of the size of 30 Å × 13 Å × 10 Å was used. For self-consistent calculations of solid states, 128 κ-points were used in the 1/2 of the Brillouin zone. To obtain the electronic density of states, band dispersions and Fermi surfaces, calculations with fixed charge distribution were made at additional κ-points.
3. Results and Discussion
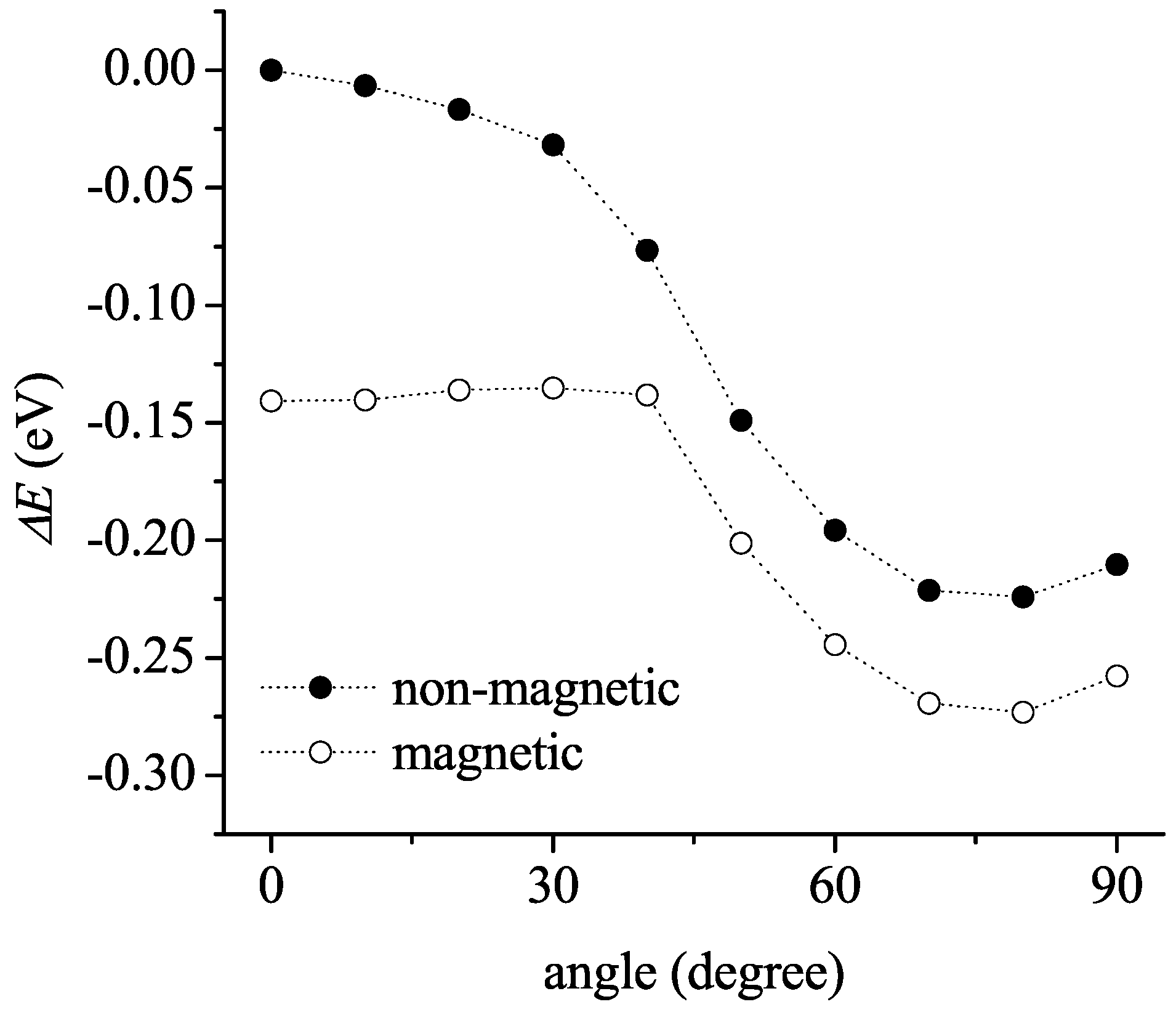
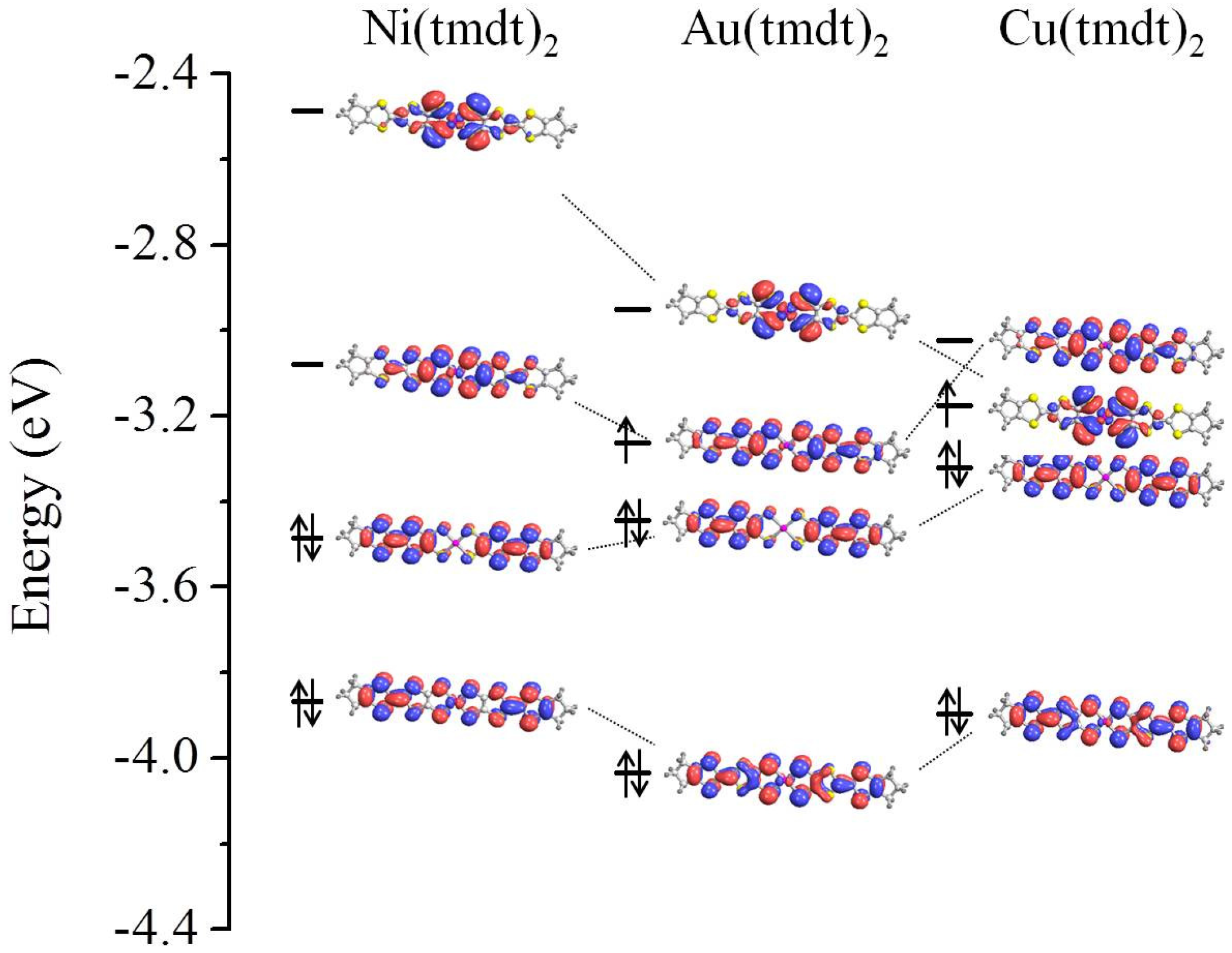
3.1. Isolated Molecule
The Cu(tmdt)2 molecule consists of three parts; one center metal and two ligands. The ligand “tmdt” is very similar to “dmdt”, and only the end part is different. Nonetheless, the crystal structures and the molecular shapes therein are different as mentioned above. As was the case of Cu(dmdt)2 [9], we have evaluated the total energy of a Cu(tmdt)2 molecule as a function of the dihedral angle between two ligands. The results are shown in Figure 2 for both non-magnetic and spin-polarized cases. These results are quite similar to those for Cu(dmdt)2. The energy minima are located around 80° for both the non-magnetic and spin-polarized cases. For the latter, there is a very shallow local minimum at 0°. The planar shape of Cu(tmdt)2 in its crystal form is thus ascribed to the so-called crystallization effect. The subtle difference at the end group produces significant difference in the condensed phase.
Figure 2.
Total energy variation with dihedral angle. Filled circles are for non-magnetic results while open circles are for spin-polarized results. ΔE is defined as the difference from the non-magnetic energy at 0°.
Figure 2.
Total energy variation with dihedral angle. Filled circles are for non-magnetic results while open circles are for spin-polarized results. ΔE is defined as the difference from the non-magnetic energy at 0°.
In Figure 3, for the planar molecules of Ni(tmdt)2, Au(tmdt)2 and Cu(tmdt)2, the energy levels and the shapes of the four molecular orbitals including the highest-/singly-occupied molecular orbital (HOMO/SOMO) and the lowest unoccupied molecular orbital (LUMO) from non-magnetic calculations are shown. The situation of Cu(tmdt)2 is very similar to that of Cu(dmdt)2 [9]. The relative position in energy space of the pdσ(−) state (for example, the highest level shown for Ni(tmdt)2 in Figure 3), which is an antibonding state between the center atom and the surrounding sulfur atoms, shifts down systematically from Ni(tmdt)2 to Cu(tmdt)2. In our previous paper [9], it was pointed out that the energy level ordering of pdσ(−) between Au(tmdt)2 and Cu(tmdt)2 is governed by the stronger pdσ(−) hybridization for the Au case than for the Cu case. Note that in the free atom case, Au 5d level is deeper than Cu 3d one by about 2 eV.
Figure 4 represents the results of spin-polarized calculations for the planar Cu(tmdt)2 molecule. It is shown that the pdσ(−) state (the SOMO in the non-magnetic calculation) is shifted toward opposite direction in energy space depending on the spin state by exchange splitting. As a result, one is occupied and the other is unoccupied. Again, this result is very similar to that of planar Cu(dmdt)2 [9]. There are a couple of important features to be noted. One is that, in contrast to the large exchange splitting of pdσ(−), other molecular states near the Fermi level is quite insensitive to the spin polarization of pdσ(−). This is because the difference in the exchange potential between up and down spin states produced by pdσ(−) state has large magnitude in the nodal plane of the ligand orbitals of π character. When Cu(tmdt)2 molecules form a solid, the direct effect of spin polarization exists only for pdσ(−) orbitals and the other states near the Fermi level are indirectly affected by the spin polarization through the hybridization with pdσ(−) orbitals. In Section 3.3, more extensive discussions will be given on the basic features of the electronic structures of Cu(tmdt)2 and some comparison with those of Cu(dmdt)2 will also be made.
Figure 3.
Non-magnetic wavefunctions and energy eigenvalues for planar Ni(tmdt)2, Au(tmdt)2 and Cu(tmdt)2 molecules. Four states including HOMO/SOMO and LUMO are shown for each molecule.
Figure 3.
Non-magnetic wavefunctions and energy eigenvalues for planar Ni(tmdt)2, Au(tmdt)2 and Cu(tmdt)2 molecules. Four states including HOMO/SOMO and LUMO are shown for each molecule.
Figure 4.
Spin-polarized wavefunctions and energy eigenvalues for planar Cu(tmdt)2 molecule.
3.2. Solid State
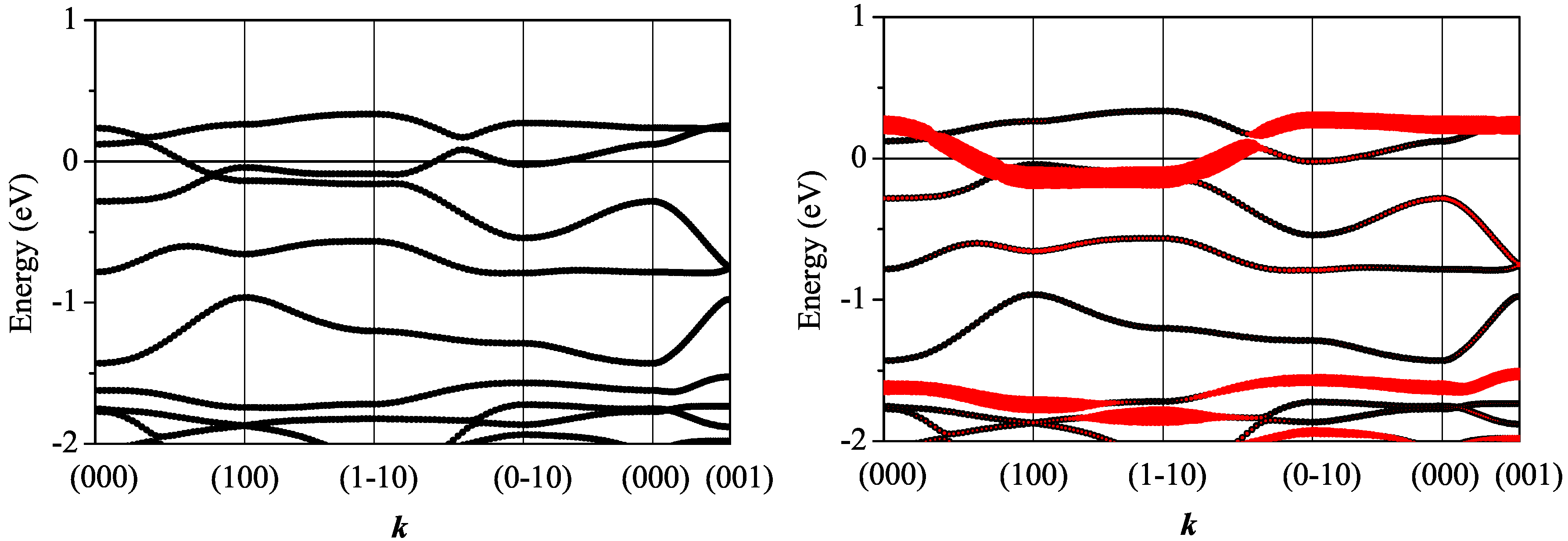
3.2.1. Non-Magnetic Results
Figure 5 represents non-magnetic (NM) electronic band dispersions for crystalline Cu(tmdt)2. The corresponding electronic density of states (DOS) is plotted in Figure 6. In the vicinity of the Fermi level, there are three overlapping bands with some hybridization. They originate from the upper three MO’s shown in Figure 3. In the right panel, the weight of Cu 3d states is indicated by the width of the red curve. Near the top of the band, the red curve corresponds to the dispersion of the pdσ(−) band. It is a typical one-dimensional cosine band along the a* direction and almost dispersionless along directions perpendicular to a*. The one-dimensional character of the pdσ(−) band is also reflected in the DOS as the two sharp peaks above and below the Fermi level. For reference, in the Ni(tmdt)2 case, the pdσ(−) band is isolated from the ligand-derived bands and shows a typical DOS shape for the one-dimensional dispersion [9]. The pdσ(−) band is nearly half-filled in Cu(tmdt)2. The Fermi surface (not shown here) clearly shows strong nesting feature coming from the one-dimensional character and the flat part of the Fermi surface faces the direction of the a-axis. However, as will be discussed below, this Fermi surface nesting does not play any important roles in the present system.
Figure 5.
Electronic band dispersions (left side) and Cu 3d contribution therein (right side) for non-magnetic Cu(tmdt)2. κ vectors are shown in units of ( a*/2, b*/2, c*/2).
Figure 5.
Electronic band dispersions (left side) and Cu 3d contribution therein (right side) for non-magnetic Cu(tmdt)2. κ vectors are shown in units of ( a*/2, b*/2, c*/2).
Figure 6.
Electronic density of states for non-magnetic Cu(tmdt)2 with partial densities of states from Cu 3d and four S atoms surrounding Cu (Sinner), respectively.
Figure 6.
Electronic density of states for non-magnetic Cu(tmdt)2 with partial densities of states from Cu 3d and four S atoms surrounding Cu (Sinner), respectively.
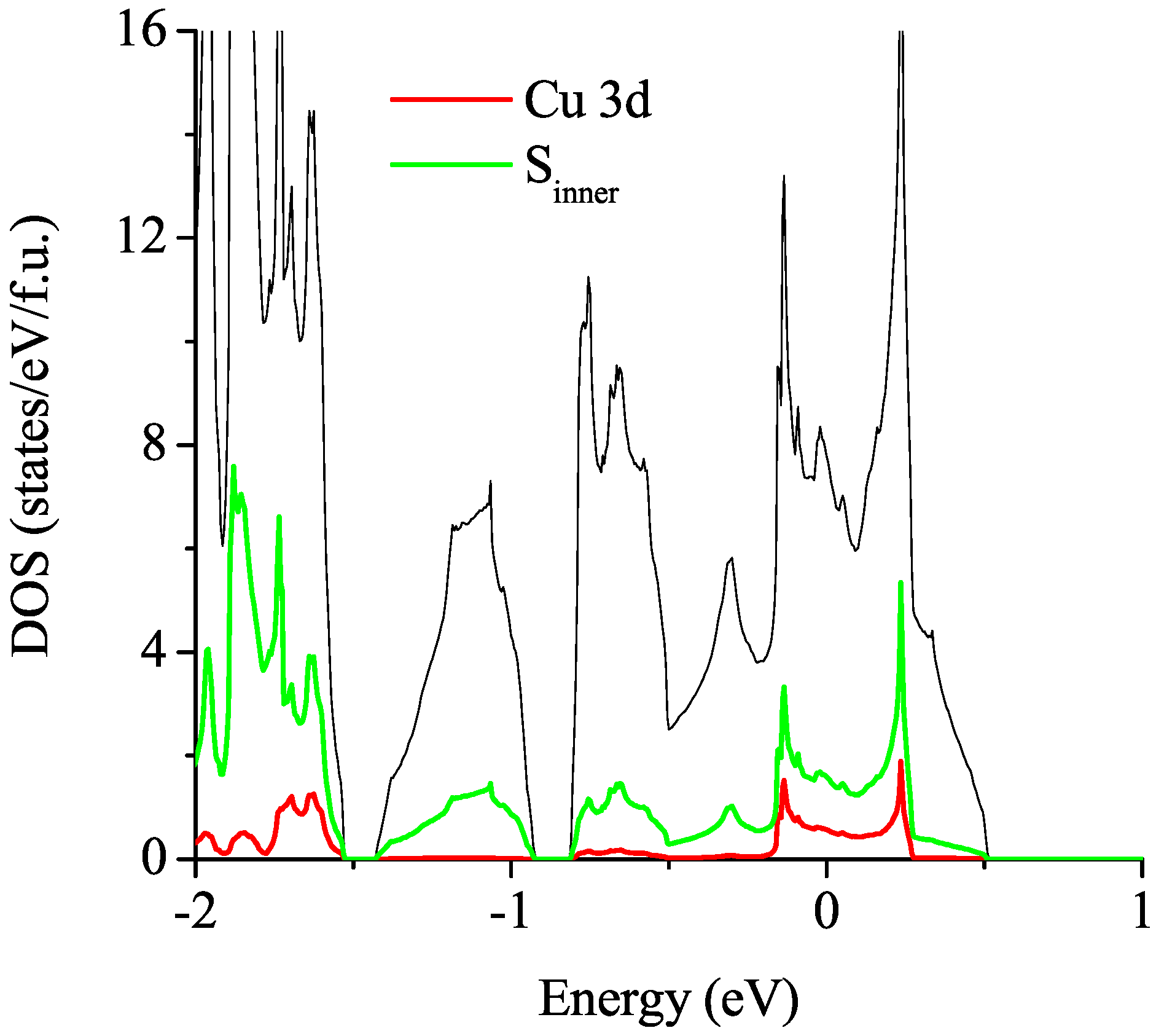
3.2.2. Spin-Polarized Results
First, we made spin-polarized calculations on the same unit cell as that for the NM calculations and obtained a ferromagnetic (FM) solution. The FM state is 9.3 meV/molecule more stable than the NM state. The DOS for the FM state is plotted in Figure 7. The quasi-one-dimensional pdσ(−) state shows significant exchange splitting of about 0.5 eV being comparable to the exchange splitting of a single molecule and larger than the pdσ(−) band width of about 0.4 eV. Therefore, the pdσ(−) band is completely spin polarized. The DOS for the FM state can be directly related to the energy-level scheme of the MO’s shown in Figure 4. The total magnetic moment per molecule is 0.944 μB. By Bader population analysis [16], 31.8% of the magnetic moment is distributed on Cu and 57.7% is on four surrounding S atoms.
Figure 7.
Electronic density of states for ferromagnetic Cu(tmdt)2 with partial densities of states from Cu 3d and four S atoms surrounding Cu (Sinner), respectively.
Figure 7.
Electronic density of states for ferromagnetic Cu(tmdt)2 with partial densities of states from Cu 3d and four S atoms surrounding Cu (Sinner), respectively.
Generally, the nearly half-filled band shows stronger tendency toward AFM order rather than FM order. In the present case, if the spin polarization is weak, AFM order along the a-axis may be further stabilized by the Fermi surface nesting. However, as pointed out for the FM case, pdσ(−) band is fully spin polarized. In such a case, the mechanism of AFM order is the superexchange. In order to evaluate the exchange coupling between the neighboring pdσ(−) spin magnetic moments, we investigated six types of AFM ordered phases whose unit-cell vectors are (2a, b, c), (a, 2b, c), (a, b, 2c), (a, b−c, b+c), (c+a, b, c−a) and (a, b−c, b+c), respectively. a, b and c represent the lattice vectors for the NM unit cell. For all the six cases, the unit cell volume is twice as that for the NM or FM phase and two molecules exist therein. Relative energies for the one FM and six AFM states against the NM state are listed in Table 1. All the seven magnetic states are more stable than the NM state (minus sign means more stable) and all the six AFM states are more stable than the FM state as expected. In addition, the stabilization energies can be classified into two groups. One has values around −10 ~ −9 meV/molecule and the other has those around −36 ~ −32 meV/molecule. It is clear that for the latter case, there is AFM ordering along the a-axis. Roughly speaking, the system becomes ~ 10 meV more stable by spin polarization, and, another ~ 20 meV energy gain is achieved by the AFM superexchange along the a-axis.
By assuming the following expression for the energy gain by magnetic ordering,
where Si denotes the spin at i-th pdσ(−) orbital, ![Crystals 02 01210 i003]()
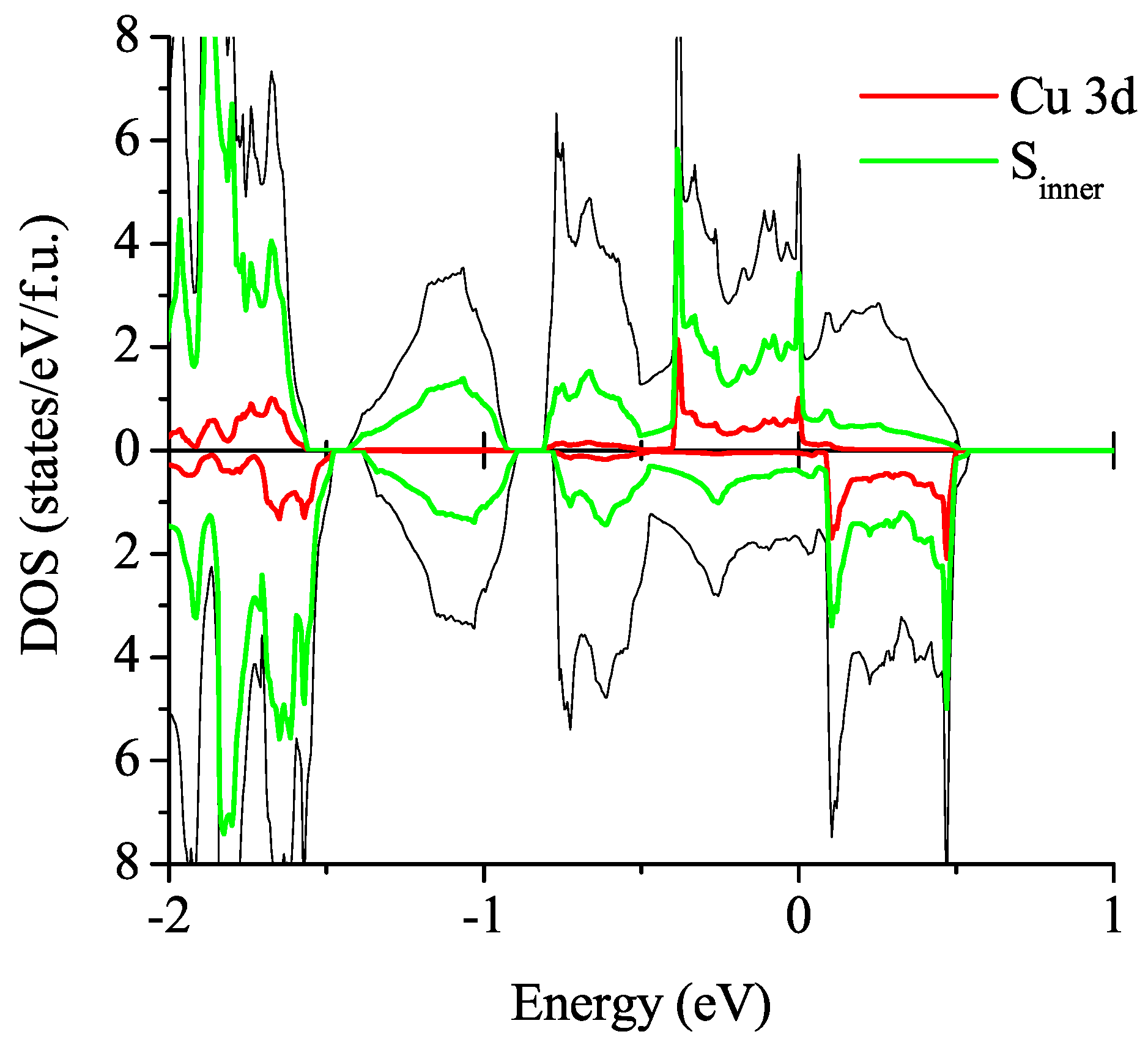
is the exchange coupling and C is the energy gain due to spin polarization. As the exchange couplings, we consider the following six contributions: three parameters for the first neighbors along each of the crystal axis, ![Crystals 02 01210 i004]()
, ![Crystals 02 01210 i005]()
and ![Crystals 02 01210 i006]()
; three parameters for the second neighbors in each crystal plane, ![Crystals 02 01210 i007]()
, ![Crystals 02 01210 i008]()
and ![Crystals 02 01210 i009]()
. Using the relative energies listed in Table 1, we can determine these six exchange couplings and the results are as follows: ![Crystals 02 01210 i010]()
meV, ![Crystals 02 01210 i011]()
meV, ![Crystals 02 01210 i012]()
meV, ![Crystals 02 01210 i013]()
meV, ![Crystals 02 01210 i014]()
meV, and ![Crystals 02 01210 i015]()
meV. Clearly the AFM exchange coupling along the a-axis dominates. Other coupling parameters are about one order magnitude smaller than ![Crystals 02 01210 i004]()
. Anyway, they cooperatively stabilize the AFM ordering along a by ferromagnetically coupling the neighboring AFM chains. From the temperature dependence of magnetic susceptibility, Zhou et al. [6] obtained 117 cm−1 (14.5 meV) as the AFM exchange coupling along the chain. Our value of ![Crystals 02 01210 i004]()
is about three times larger than this experimental value. Perhaps, for the present system, Coulomb corrected version like LDA+U may be better suited than simple GGA used in the present calculation. Then the exchange splitting will be enhanced and the superexchange coupling will be suppressed through the increase of energy denominator. Anyway, agreement within a numerical factor may be rather satisfactory.
is the exchange coupling and C is the energy gain due to spin polarization. As the exchange couplings, we consider the following six contributions: three parameters for the first neighbors along each of the crystal axis, 
, 
and 
; three parameters for the second neighbors in each crystal plane, 
, 
and 
. Using the relative energies listed in Table 1, we can determine these six exchange couplings and the results are as follows: 
meV, 
meV, 
meV, 
meV, 
meV, and 
meV. Clearly the AFM exchange coupling along the a-axis dominates. Other coupling parameters are about one order magnitude smaller than . Anyway, they cooperatively stabilize the AFM ordering along a by ferromagnetically coupling the neighboring AFM chains. From the temperature dependence of magnetic susceptibility, Zhou et al. [6] obtained 117 cm−1 (14.5 meV) as the AFM exchange coupling along the chain. Our value of is about three times larger than this experimental value. Perhaps, for the present system, Coulomb corrected version like LDA+U may be better suited than simple GGA used in the present calculation. Then the exchange splitting will be enhanced and the superexchange coupling will be suppressed through the increase of energy denominator. Anyway, agreement within a numerical factor may be rather satisfactory.
| Magneticorder | Unitcell | Relative energy (meV/molecule) |
|---|---|---|
| FM | (a, b, c) | −9:3 |
| AFM | (2a, b, c) | −35:8 |
| AFM | (a, 2b, c) | −10:0 |
| AFM | (a, b, 2c) | −10:0 |
| AFM | (a, b−c, b+c) | −9:6 |
| AFM | (c+a, b, c−a) | −32:7 |
| AFM | (a−b, a+b, c) | −32:9 |
In Figure 8, DOS’s for the two AFM states with the unit cells of (2a, b, c) and (a, 2b, c) are shown. The corresponding band dispersions are shown in Figure 9 only for the up-spin state. The weight of Cu(1) 3d and Cu(2) 3d states are indicated by the width of the red and purple curves, respectively. For the former AFM state, the AFM ordering is along the a-axis and the electron hopping between neighboring pdσ(−) orbitals is strongly suppressed to make the pdσ(−) band very narrow. The magnetic moment per molecule is reduced to 0.848 μB and the contributions to the magnetic moment from Cu and four S are 34.1% and 58.3%, respectively, being more or less similar to those for the FM case. On the other hand, the pdσ(−) band in the DOS for (a, 2b, c) keeps the width of original NM state because of the presence of large electron hopping along the a-axis. Accordingly, the magnetic moment per molecule and the partitioning of it to Cu and four S become closer to those of FM case: 0.920 μB, 32.4% and 58.1%. DOS’s for the rest four AFM states are similar to one of the two depending on the direction of AFM ordering.
Figure 8.
Electronic densities of states for antiferromagnetic Cu(tmdt)2 with the unit cells of (2a, b, c) (left) and (a, 2b, c) (right) with partial densities of states from Cu 3d and four S atoms surrounding Cu (Sinner), respectively. The labels (1) and (2) distinguish two Cu atoms in the unit cell.
Figure 8.
Electronic densities of states for antiferromagnetic Cu(tmdt)2 with the unit cells of (2a, b, c) (left) and (a, 2b, c) (right) with partial densities of states from Cu 3d and four S atoms surrounding Cu (Sinner), respectively. The labels (1) and (2) distinguish two Cu atoms in the unit cell.
Figure 9.
Electronic band dispersions (left) and Cu(1) 3d (center) and Cu(2) 3d (right) contributions therein for antiferromagnetic Cu(tmdt)2 with the unit cells of (2a, b, c) (upper) and (a, 2b, c) (lower). The labels (1) and (2) distinguish two Cu atoms in the unit cell. κ vectors are shown in units of (a*/2, b*/2, c*/2).
Figure 9.
Electronic band dispersions (left) and Cu(1) 3d (center) and Cu(2) 3d (right) contributions therein for antiferromagnetic Cu(tmdt)2 with the unit cells of (2a, b, c) (upper) and (a, 2b, c) (lower). The labels (1) and (2) distinguish two Cu atoms in the unit cell. κ vectors are shown in units of (a*/2, b*/2, c*/2).
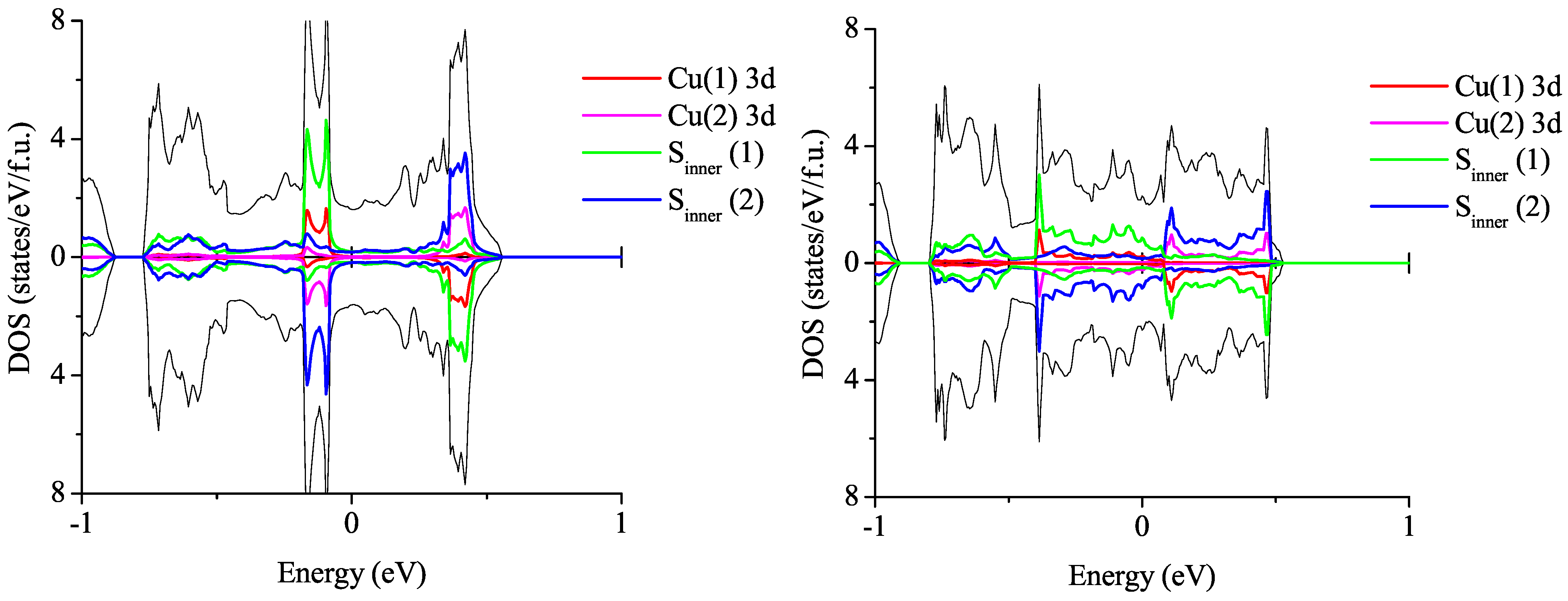
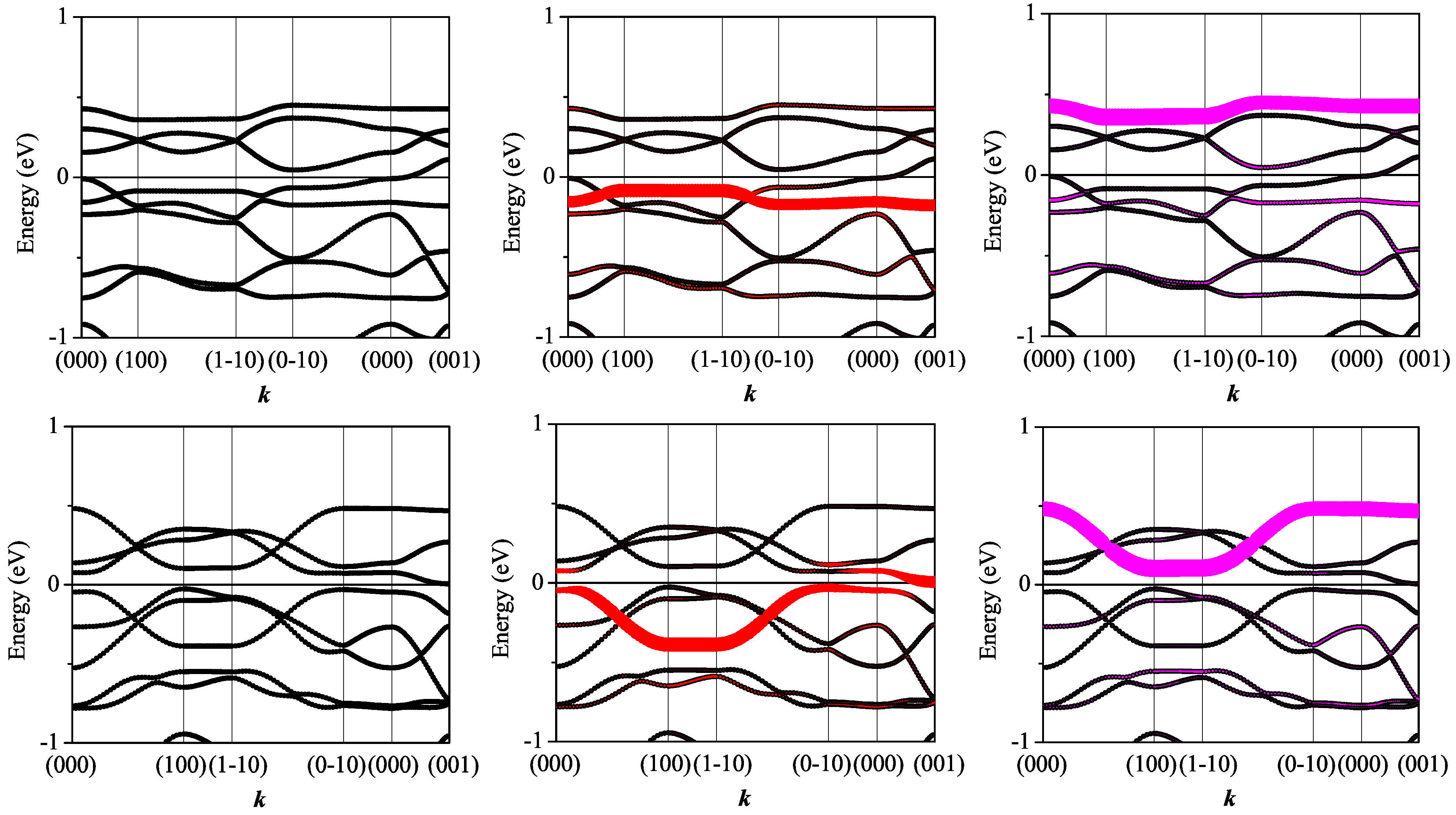
3.3. On the Qualitative Difference between Cu(tmdt)2 and Cu(dmdt)2
From the discussions so far, we have now a clear picture for the characteristic features in the electronic structures of Cu(tmdt)2. For the electronic properties, only the upper three molecular orbitals shown in Figure 3 are important. Three electrons are accommodated to these three orbitals. The energy separation between them is about 0.2 eV. When a solid is formed, these three molecular orbitals form three bands, each of which has roughly 0.4 eV band width. Therefore, the three bands overlap. However, the band overlap between the top band and the third band is rather small. The bottom band is nearly filled, the top band is nearly empty and the middle band which has mostly pdσ(−) character is nearly half filled. Only the pdσ(−) orbitals are magnetically active and its exchange splitting of more than 0.5 eV is larger than its band width. Because of the planar shape of Cu(tmdt)2 molecule in the solid together with the planar orbital shape of pdσ(−), electron hopping is significant only along the a-axis. The one-dimensional AFM chain along the a-axis caused by the superexchange is a consequence of these aspects. Because of the presence of orbitals with different characters near the Fermi level, the system may have some analogy with the s-d model.
The situation is radically different in Cu(dmdt)2, where the molecule is twisted. As discussed in our previous paper [9], the highest occupied states are doubly degenerate for the dihedral angle of 90° and one electron has to be accommodated to these states. The deviation of the dihedral angle from 90° is due to the Jahn–Teller effect and the resulting energy splitting of the two levels is about 0.1 eV. If the width of each band formed by the orbitals in a solid is small compared with the Jahn–Teller splitting, the lower band can be regarded as half filled. On the other hand, if the band width is larger than the Jahn–Teller splitting, the system moves toward a quarter filled situation. As these two molecular orbitals have smaller Cu 3d component compared with the pdσ(−) orbital in the planar configuration, the exchange splitting of these orbitals is only about 0.2 eV. Anyway, the two orbitals near the Fermi level are both directly affected by exchange splitting. We also note that the twisted form of Cu(dmdt)2 molecule makes the electron hopping at least two dimensional. Experimental efforts are still being made to clarify the low temperature magnetic behavior of Cu(dmdt)2 and more careful extensive theoretical study is our future task.
4. Conclusions
For an isolated molecule of Cu(tmdt)2 whose structure is assumed to be planar, the shape and the relative energy levels of molecular orbitals in the vicinity of SOMO are very similar to those for planar Cu(dmdt)2. The pdσ(−) state shows a strong exchange splitting in contrast with Au(tmdt)2 case. It is found that the stable molecular shape is twisted as in the Cu(dmdt)2 case. In the existing solid forms, the Cu(tmdt)2 molecule is planar while the Cu(dmdt)2 molecule is twisted. The subtle difference at the end group produces significant difference in the condensed phase.
Combining the information of molecular orbitals with that of the band structure of the NM state, we formed a clear picture for the electronic structures near the Fermi level. The pdσ(−) orbitals form a nearly half filled one-dimensional band along the crystal a-axis. A large exchange splitting in this one-dimensional band stabilizes the AFM chain configuration through superexchange as suggested by experiment. By performing total energy calculations for several magnetic configurations, we estimated the exchange interactions in the Heisenberg model. The calculated AFM exchange interaction is about three times larger than the experimentally estimated one. We also note that our calculation based on GGA does not give a finite band gap as a Mott insulator. In the present results, this is due to the presence of two additional molecular orbitals near the Fermi level which have ligand π character and are quite insensitive to the spin polarization of pdσ(−) orbitals. A couple of possible reasons are conceivable for the failure of reproducing the insulating nature. Perhaps the most plausible one is the well-known HOMO-LUMO gap underestimation of the density functional theory. Another possibility may be the arrangement of one-dimensional AFM chains in the a axis. In the present calculation of (2a, b, c) , all the AFM chains are ferromagnetically coupled. Even if the two molecular orbitals other than the pdσ(−) do not feel the exchange potential, their band structure will be modified through the hybridization with the pdσ(−) depending on the different arrangements of the AFM chains. This possibility will be tested by using larger supercells in the near future as an extension of the present calculation. In parallel with this line of study, analysis based on an extended Hubbard model is now being made to clarify the origin of the insulating nature of the system [17].
Acknowledgments
The authors are grateful to Akiko Kobayashi, Hayao Kobayashi, Biao Zhou, Hidetoshi Fukuyama, Hitoshi Seo and Kazushi Kanoda for fruitful discussions. This research was partially supported by Grant-in-Aid for Scientific Research on Innovative Areas (No. 20110003 and No. 22104010) from the Ministry of Education, Science, Sports and Culture (MEXT), by the Strategic Programs for Innovative Research (SPIRE), MEXT, and by the Computational Materials Science Initiative (CMSI), Japan.
References
- Tanaka, H.; Okano, Y.; Kobayashi, H.; Suzuki, W.; Kobayashi, A. A three-dimensional synthetic metallic crystal composed of single-component molecules. Science 2001, 291, 285–287. [Google Scholar]
- Suzuki, W.; Fujiwara, E.; Kobayashi, A.; Fujishiro, Y.; Nishibori, E.; Takata, M.; Sakata, M.; Fujiwara, H.; Kobayashi, H. Highly conducting crystals based on single-component gold complexes with extended-TTF dithiolateligands. J. Am. Chem. Soc. 2003, 125, 1486–1487. [Google Scholar]
- Tanaka, H.; Kobayashi, H.; Kobayashi, A. A conducting crystal based on a single-component paramagnetic molecule, [Cu(dmdt)2] (dmdt = Dimethyltetrathiafulvalenedithiolate). J. Am. Chem. Soc. 2002, 124, 10002–10003. [Google Scholar] [CrossRef]
- Yamamoto, K.; Fujiwara, E.; Kobayashi, A.; Fujishiro, Y.; Nishibori, E.; Sakata, M.; Takata, M.; Tanaka, H.; Okano, Y.; Kobayashi, H. Single-component molecular conductor [Zn(tmdt)2] and related Zn complexes. Chem. Lett. 2005, 34, 1090–1091. [Google Scholar] [CrossRef]
- Tanaka, H.; Hara, S.; Tokumoto, M.; Kobayashi, A.; Kobayashi, H. Resistance measurements of microcrystals of single-component molecular metals using finely patterned interdigitated electrodes. Chem. Lett. 2007, 36, 1006–1007. [Google Scholar] [CrossRef]
- Zhou, B.; Yajima, H.; Kobayashi, A.; Okano, Y.; Tanaka, H.; Kumashiro, T.; Nishibori, E.; Sawa, H.; Kobayashi, H. Single-component molecular conductor [Cu(tmdt)2] containing an antiferromagnetic heisenberg chain. Inorg. Chem. 2010, 49, 6740–6747. [Google Scholar]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Ishibashi, S.; Tanaka, H.; Kohyama, M.; Tokumoto, M.; Kobayashi, A.; Kobayashi, H.; Terakura, K. Ab initio electronic structure calculation for single-component molecular conductors Au(tmdt)2 (tmdt = trimethylenetetrathiafulvalenedithiolate). J. Phys. Soc. Jpn. 2005, 74, 843–846, 1879. [Google Scholar] [CrossRef]
- Ishibashi, S.; Terakura, K.; Kobayashi, A. Electronic structures of single component molecular metals based on Ab initio calculation. J. Phys. Soc. Jpn. 2008, 77, 024702:1–024702:7. [Google Scholar]
- Seo, H.; Ishibashi, S.; Okano, Y.; Kobayashi, H.; Kobayashi, A.; Fukuyama, H.; Terakura, K. Single-component molecular metals as multiband π-d systems. J. Phys. Soc. Jpn. 2008, 77, 023714:1–023714:4. [Google Scholar]
- QMAS (Quantum MAterials Simulator). Available online: http://www.qmas.jp (accessed on 17 August 2012).
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Holzwarth, N.A.W.; Matthews, G.E.; Dunning, R.B.; Tackett, A.R.; Zeng, Y. Comparison of the projector augmented-wave, pseudopotential, and linearized augmented-plane-wave formalisms for density-functional calculations of solids. Phys. Rev. B 1997, 55, 2005–2017. [Google Scholar]
- Kresse, G.; Joubert, D. From ultrasoftpseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Seo, H. Private communication. The Institute of Physical and Chemical Research (RIKEN): Japan, 2012. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
MDPI and ACS Style
Ishibashi, S.; Terakura, K. Electronic Structure of Cu(tmdt)2 Studied with First-Principles Calculations. Crystals 2012, 2, 1210-1221. https://doi.org/10.3390/cryst2031210
AMA Style
Ishibashi S, Terakura K. Electronic Structure of Cu(tmdt)2 Studied with First-Principles Calculations. Crystals. 2012; 2(3):1210-1221. https://doi.org/10.3390/cryst2031210
Chicago/Turabian StyleIshibashi, Shoji, and Kiyoyuki Terakura. 2012. "Electronic Structure of Cu(tmdt)2 Studied with First-Principles Calculations" Crystals 2, no. 3: 1210-1221. https://doi.org/10.3390/cryst2031210
APA StyleIshibashi, S., & Terakura, K. (2012). Electronic Structure of Cu(tmdt)2 Studied with First-Principles Calculations. Crystals, 2(3), 1210-1221. https://doi.org/10.3390/cryst2031210
