The Origin of Raman D Band: Bonding and Antibonding Orbitals in Graphene

Abstract

In Raman spectroscopy of graphite and graphene, the D band at ~ 1355 cm⁻¹ is used as the indication of the dirtiness of a sample. However, our analysis suggests that the physics behind the D band is closely related to a very clear idea for describing a molecule, namely bonding and antibonding orbitals in graphene. In this paper, we review our recent work on the mechanism for activating the D band at a graphene edge.

1. Introduction

Bonding and antibonding orbitals are basic ideas for describing molecules. Bonding orbitals contribute to the formation of a molecule, whereas antibonding orbitals weaken the bonding and destabilize a molecule. Normally, bonding orbitals are more stable than antibonding orbitals in terms of energy and thus a molecule is stable unless sufficient electrons occupy the antibonding orbitals.

Graphene [1,2] is unique with respect to its molecular orbitals. The bonding and antibonding orbitals in graphene are degenerate, and various types of linear combination of these orbitals form the Fermi surface expressed by the isoenergy sections of Dirac cones. This degeneracy plays an essential role in various phenomena. For example, graphene is stable with respect to a large shift of the Fermi energy position [3]. Another notable example is that graphene exhibits high mobility. Elastic backward scattering between the bonding and antibonding orbitals induced by long-range impurity potential is suppressed because they are orthogonal [4]. In this paper, we show that the bonding and antibonding orbitals in graphene are key factors in the activation mechanism of the D band observed at a graphene edge.

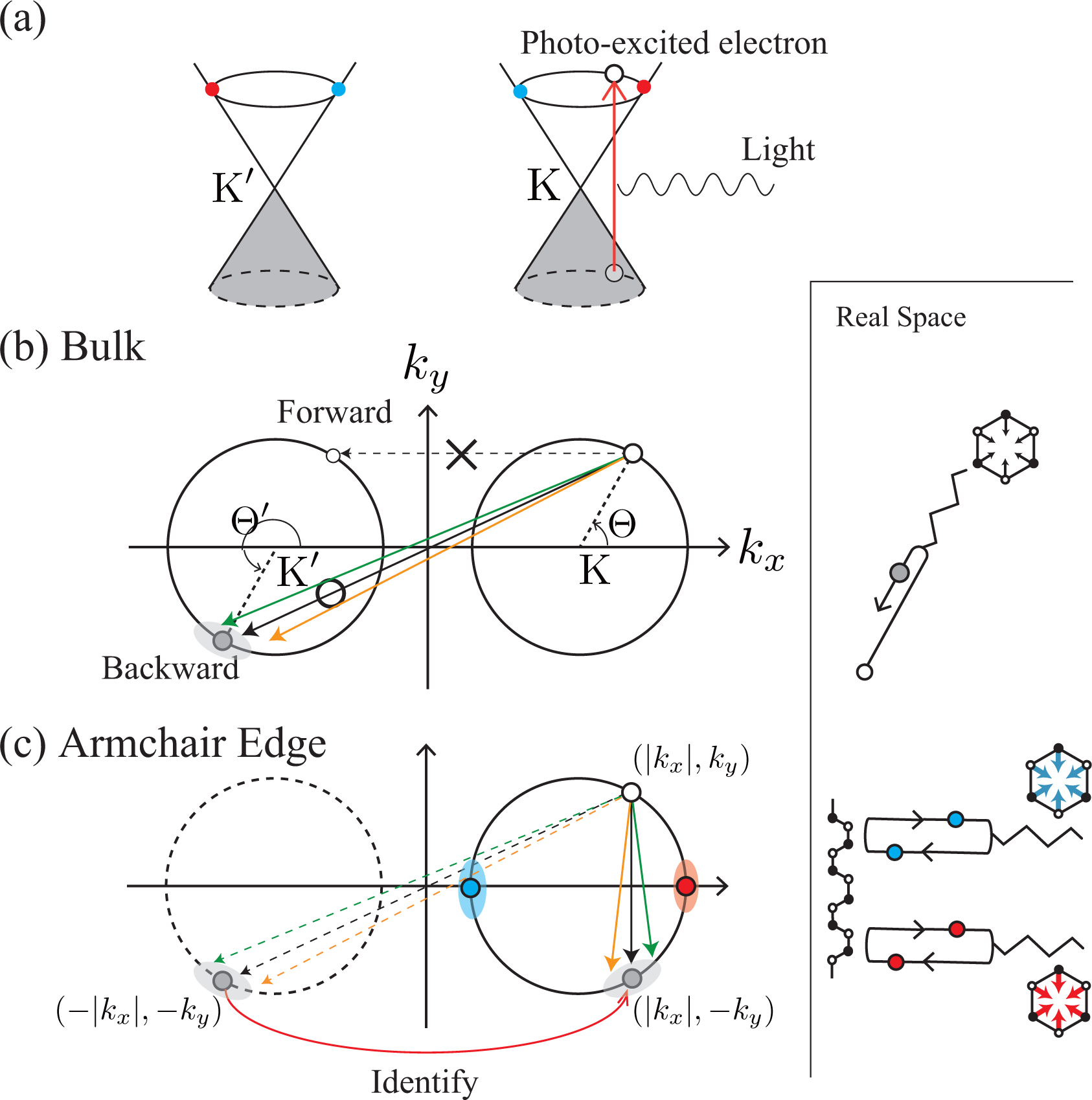
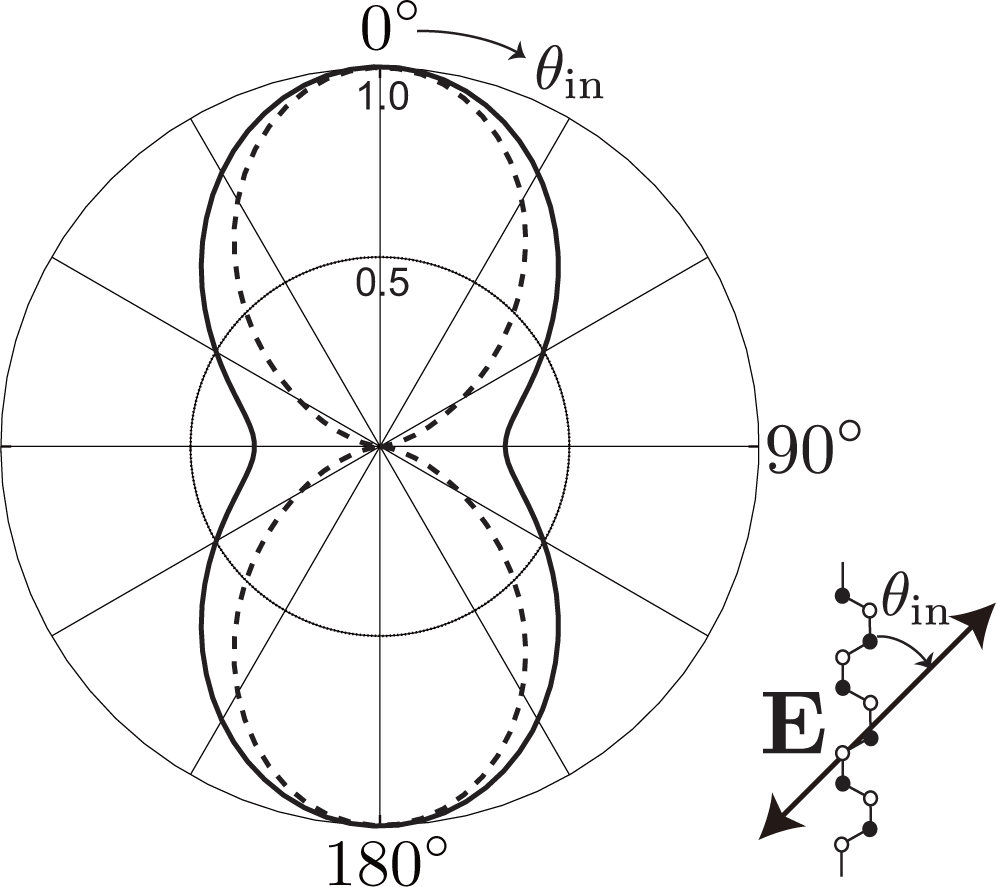
Since the discovery of the D band, much interest has focused on its origin. Tuinstra and Koenig attributed the D band to an A_1g zone-boundary mode at the edge of a sample (see Figure 1) on the grounds that the Raman intensity is proportional to the edge percentage and that the edge causes a relaxation of the momentum conservation needed for activating a zone-boundary phonon [5]. Katagiri et al. confirmed that the D band originates from an edge (or discontinuity in the carbon network) by observing the light polarization dependence of the D band intensity at graphite edge planes [6]. The atomic arrangement of an edge has two principal axes: armchair and zigzag edges. Cançado et al. showed that the armchair (zigzag) edge is relevant (irrelevant) to the relaxation of the momentum conservation for a zone-boundary phonon [7]. In addition, they found that the D band Raman intensity depends on the polarization of laser light, that is, the intensity is maximum (minimum) when the polarization is parallel (perpendicular) to the armchair edge. The light polarization dependence of the D band is also observed ubiquitously at the armchair edges of a single layer of graphene, which suggests that out-of-plane coupling in graphite is not essential to the origin of the D band [8–10].

A model of the D band must at least explain the observed properties: the D band intensity increases only at an armchair edge and is dependent on the laser light polarization.

The current D band model is a double resonance model [11]. In this model, a photo-excited electron passes through two resonance states, which enhances the Raman intensity of a phonon with nonzero wave vector q ≠ 0. This model is not concerned with the details of electron-phonon and electron-light matrix elements, and it does not provide clear explanations of the properties of the D band. Also, the intensity calculated with this model is dependent on the lifetime of the resonance states. Usually, the lifetime is determined in such a manner that a calculated result reproduces experimental data. In this sense, the double resonance model is phenomenological. Because the lifetime is shorter in a defective graphene sample, double resonance does not necessarily mean an enhancement of the D band Raman intensity. On the other hand, the model can account for the so-called dispersive behavior of the D band [11]. However, as we will show in this paper, dispersive behavior is characteristic of A_1g modes, rather than an inherent property of the D band. In fact, dispersive behavior is observed also for the 2D band [12], and the excitation does not need an edge, which is in contrast to the D band.

In this paper we show that the observed properties of the D band are naturally explained in terms of simple ideas based on molecular orbitals and momentum conservation. In our formulation, the D band is excited from a photo-excited electron through a single resonance process in the same way as the G band. (Negri et al. took the same approach to the resonance Raman process of the D band of polycyclic aromatic hydrocarbons [13]) It is concluded that, without invoking an artificial assumption, the D band is closely related to (1) the orbital dependence of the electron-phonon matrix element; (2) the special nature of the armchair edge; and (3) optical anisotropy [14].

This paper is organized as follows. In Section 2 we observe that a graphene molecular orbital and wave vector are closely correlated. This correlation is both an important factor in terms of understanding the D band and an essential feature of graphene. In Section 3 the properties of the D band are deduced from three factors (1,2,3). The importance of the electron-phonon matrix element and the role of the armchair edge in the excitation mechanism of the D band are explained in detail. In Section 4 we show some predictions obtained with our model. Future prospects and our conclusion are given in Section 5 and Section 6, respectively. We give some notes on resonant condition in Appendix A.

2. Bonding and Antibonding Orbitals

Graphene’s hexagonal unit cell has two carbon atoms, denoted by A and B in Figure 1, and the electron’s wave function ψ is written as a linear combination of 2p_z atomic orbitals of the A and B atoms, χ_A and χ_B. When we apply Bloch’s theorem to graphene, we obtain ψ and the band structure as a function of the wave vector k [15,16]. In the Brillouin zone (BZ) of graphene, there are two points, namely the K and K′ points, where the conduction and valence bands touch each other. The orbitals of the states near the K point take the form of

$${\psi }_K^s(k)=\frac{1}{\sqrt{2}}(e^{-i\Theta (k)}{\chi }_{{\rm A}}+s{\chi }_{{\rm B}})$$

(1)

where the phase Θ(k) ∈ [0, 2π] is the polar angle between vector k measured from the K point and the k_x-axis (see Figure 1); and s = ±1 is the band index (s = +1 is the π*-band and s = −1 π-band). The orbitals of the states near the K′ point are written as

$${\psi }_{K^{\prime }}^s(k)=\frac{1}{\sqrt{2}}(e^{-i{\Theta }^{\prime }(k)}{\chi }_{{\rm A}}+s{\chi }_{{\rm B}})$$

(2)

where Θ^′(k) is the polar angle defined with respect to the K′ point as shown in Figure 1.

In Equation (1), the bonding and antibonding orbitals (χ_A + χ_B and −χ_A + χ_B) are located at Θ = 0 and π, respectively, on the iso-energy section of the π^*-band (s = +1). The orbital with a general Θ is a linear combination of the bonding and antibonding orbitals. In Equation (2), the bonding and antibonding orbitals are located at Θ′ = π and 0, respectively, on the iso-energy section of the π^*-band. As we can see in Figure 1, the bonding (antibonding) orbitals are located symmetrically on the k_x-axis with respect to the Γ point, which is one of the most important characteristics of the BZ of graphene [i.e., mirror symmetry with respect to the replacement, x ↔ −x].

The orbital Equations (1) and (2) can be derived from an effective model for graphene, that is, a massless Dirac equation, in the following manner. The energy eigenequation is written as

$$E\psi =\widehat{H}\psi =v_F\left(\begin{array}{cc}\sigma \cdot \widehat{p}& 0\\ 0& {\sigma }^{\prime }\cdot \widehat{p}\end{array}\right)\left(\begin{array}{c}{\psi }_K(r)\\ {\psi }_{K^{\prime }}(r)\end{array}\right)$$

(3)

where v_F is the Fermi velocity; $\widehat{p}=({\widehat{p}}_x,{\widehat{p}}_y)$ is a momentum operator; 0 in the off-diagonal terms represents a 2 × 2 null matrix; and $\sigma =({\sigma }_x,{\sigma }_y)$ and ${\sigma }^{\prime }=(-{\sigma }_x,{\sigma }_y)$ are 2 × 2 Pauli spin matrices:

$${\sigma }_x=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),{\sigma }_y=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right).$$

(4)

The massless Dirac equation in Equation (3) is decomposed into two Weyl’s equations for the K and K′ valleys: $E{\psi }_K(r)=v_F\sigma \cdot \widehat{p}{\psi }_K(r)$ and $E{\psi }_{K^{\prime }}(r)=v_F{\sigma }^{\prime }\cdot \widehat{p}{\psi }_{K^{\prime }}(r),$ respectively. To reproduce Equation (1), we assume the plane wave solution ${\psi }_K(r)=e^{ik\cdot r}{\psi }_K(k)/\sqrt{V},$ and obtain the energy eigenequation ħv_Fσ·kψ_K(k)= Eψ_K(k). Then, the corresponding energy eigenvalue and eigenstate are easy to find using $k_x\mp i{k}_y=\left|k\right|e^{\mp i\Theta (k)}$ as E=sħv_F|k| and

$${\psi }_K^s(k)=\frac{1}{\sqrt{2}}\left(\begin{array}{c}{e}^{-i\Theta (k)}\\ s\end{array}\right).$$

(5)

This is identical to Equation (1) by setting

$${\chi }_A=\left(\begin{array}{c}1\\ 0\end{array}\right),{\chi }_B=\left(\begin{array}{c}0\\ 1\end{array}\right).$$

(6)

Similarly, we can check that Equation (2) is the solution of ħv_Fσ′·kψ_K′(k)= Eψ_K′(k), which is given by

$${\psi }_{K^{\prime }}^s(k)=\frac{1}{\sqrt{2}}\left(\begin{array}{c}{e}^{-i{\Theta }^{\prime }(k)}\\ s\end{array}\right).$$

(7)

The Dirac equation is very helpful as regards understanding the mechanism of a result in terms of symmetry and momentum conservation. In particular, the fact that the Dirac equation is composed of a multiplication of the Pauli matrices (for the A and B atoms) and momentum operators makes it easy to recognize that the orbital (the pattern of the linear combination of χ_A and χ_B) is dependent on the wave vector of the particle. In the following, we refer to the Dirac equation for graphene in order to capture the essential features of a result. The graphene Dirac equation differs from the original Dirac equation in the following respect: the wave function ψ in the graphene Dirac equation has 4 components consisting of two orbitals (χ_A and χ_B) and two valleys (K and K′), while those in the original Dirac equation are two spin states (up and down spins) and two chiralities (left- and right-handed) [17]. Thus, the orbital degree of graphene is commonly referred to as pseudo-spin. (We define the bonding and antibonding orbitals by the molecular orbitals of nearest neighbor atoms having the same position in the x-axis (as shown in Figure 1). Although our definition is not appropriate for the bonds between nearest neighbor atoms having different positions in the x-axis, those are not so important in discussing the D band at armchair edge [14]. Note also that our definition connects smoothly to the definition of π and π^* bands at the Γ point, where any nearest neighbor carbon atoms form the bonding (antibonding) orbital in the π (π^*) band.)

3. Light Polarization Dependence of D Band Intensity

In this section we show that the light polarization dependence of the D band originates from three factors. The first factor concerns the nature of the electron-phonon interaction for the A_1g mode, which will be explained in Section 3.1. The second factor is a modification of the BZ by the armchair edge, which will be explored in Section 3.2. In Section 3.3, we describe the third factor, which concerns the interaction between electrons and a polarized laser light. In Section 3.4, we construct the D band polarization formula, by combining the three factors.

3.1. Dominance of Intervalley Backward Scattering

Suppose that an electron has been excited into the π^*-band by a laser light [Figure 2a]. When a photo-excited electron emits an A_1g mode, there is a strong probability that the electron will undergo (intervalley) backward scattering, as shown by the real space diagram in Figure 2b. In the k-space, the change in the exact (approximate) intervalley backward scattering is denoted by the black (orange and green) solid arrow. Although the forward scattering denoted by the dashed arrow may be allowed by momentum conservation, it never takes place because orbitals suppress the corresponding electron-phonon matrix element. This dominance of intervalley backward scattering originates from the characteristic feature of an A_1g mode, namely that the vibration consists only of bond shrinking/stretching motions, as shown by the displacement vectors in Figure 1. Mathematically, this characteristic of the A_1g mode is described by the fact that the electron-phonon interaction, Ĥ_ep(D), satisfies

$${\chi }_A^{†}{\widehat{H}}_{ep}{(D)}_{{\chi }_B}={\chi }_B^{†}{\widehat{H}}_{ep}{(D)}_{{\chi }_A}=g_{ep}$$

(8)

$${\chi }_A^{†}{\widehat{H}}_{ep}{(D)}_{{\chi }_A}={\chi }_B^{†}{\widehat{H}}_{ep}{(D)}_{{\chi }_B}=0$$

(9)

where gep is a coupling constant for bond stretching. With these Ĥ_ep(D) conditions, we obtain the electron-phonon matrix element squared $|M{|}^2=|{\psi }_{K^{\prime }}^{s^{\prime }}{({\Theta }^{\prime })}^{†}{\widehat{H}}_{ep}(D){\psi }_K^s(\Theta ){|}^2$ using Equations (1) and (2) as

$$|M{|}^2=\frac{g_{\text{ep}}^2}{2}\{1-s{s}^{\prime }\cos ({\Theta }^{\prime }-\Theta )\}.$$

(10)

Equation (10) shows that, for intraband scattering (ss′ = 1), the scattering probability of the exact backward scattering (Θ′ = Θ + π) is maximum, while that of the exact forward scattering (Θ′ = Θ) vanishes.

When the energy of a photo-excited electron is much larger than the phonon energy (≃ 0.15 eV), we can assume that no significant energy shift occurs as a result of the inelastic scattering. For the exact backward scattering, the A_1g wave vector relates to the photo-excited electron wave vector as q = −2k, where q (k) is the wave vector of the A_1g mode (photo-excited electron) measured from the K point. This relationship between k and q shows that the orbitals effectively relate the electron wave vector k to the A_1g wave vector q. (Thus, the orbital dependence of the electron-phonon matrix element justifies the basic idea of the quasi-selection rule for the D band proposed by several authors [18,19]. The relationship between k and q (q = −2k) shows that ħv_F|q| changes linearly with changing excitation energy E_L because 2ħv_F|k| is approximately equal to E_L. It becomes important when we discuss the dispersive behavior of the D band in Section 4.1).

It is straightforward to reproduce Equation (10) in the framework of the graphene Dirac equation. The electron-phonon interaction for an A_1g mode with wave vector q is written as [20]

$${\widehat{H}}_{ep}(D_q)=g_{ep}\left(\begin{array}{cc}0& e^{-iq\cdot r}{\sigma }_x\\ e^{iq\cdot r}{\sigma }_x& 0\end{array}\right)$$

(11)

and the matrix element M is given by

$$\begin{array}{c}M={\displaystyle {\int }_V{d}^{2}r{\psi }_{K^{\prime }}^{s^{\prime }}}{(r)}^{†}{\widehat{H}}_{ep}(D_q){\psi }_K^s(r)\\ =\left(\frac{1}{V}{\displaystyle {\int }_V{d}^{2}r}{e}^{i(k+q-k^{\prime })\cdot r}\right)\left({\psi }_{K^{\prime }}^{s^{\prime }}{(k^{\prime })}^{†}{\sigma }_x{\psi }_K^s(k)\right).\end{array}$$

(12)

The last line is written as a multiplication of two parts: the first part represents momentum conservation and the wave vector of the scattered electron k′ is given by k^′ = k + q. The second part gives Equation (10). In addition to momentum conservation, we can use energy conservation to obtain v_F|k^′| = v_F|k| − ω_q, where ω_q is the frequency of A_1g. Thus, when ħv_F|k| ≫ ħω_q, we have |k^′| ≃ |k|. Since the orbital part results in the dominance of intervalley backward scattering, we obtain k^′ ≃ −k. As a result, q ≃ −2k is satisfied.

3.2. Brillouin Zone Folding

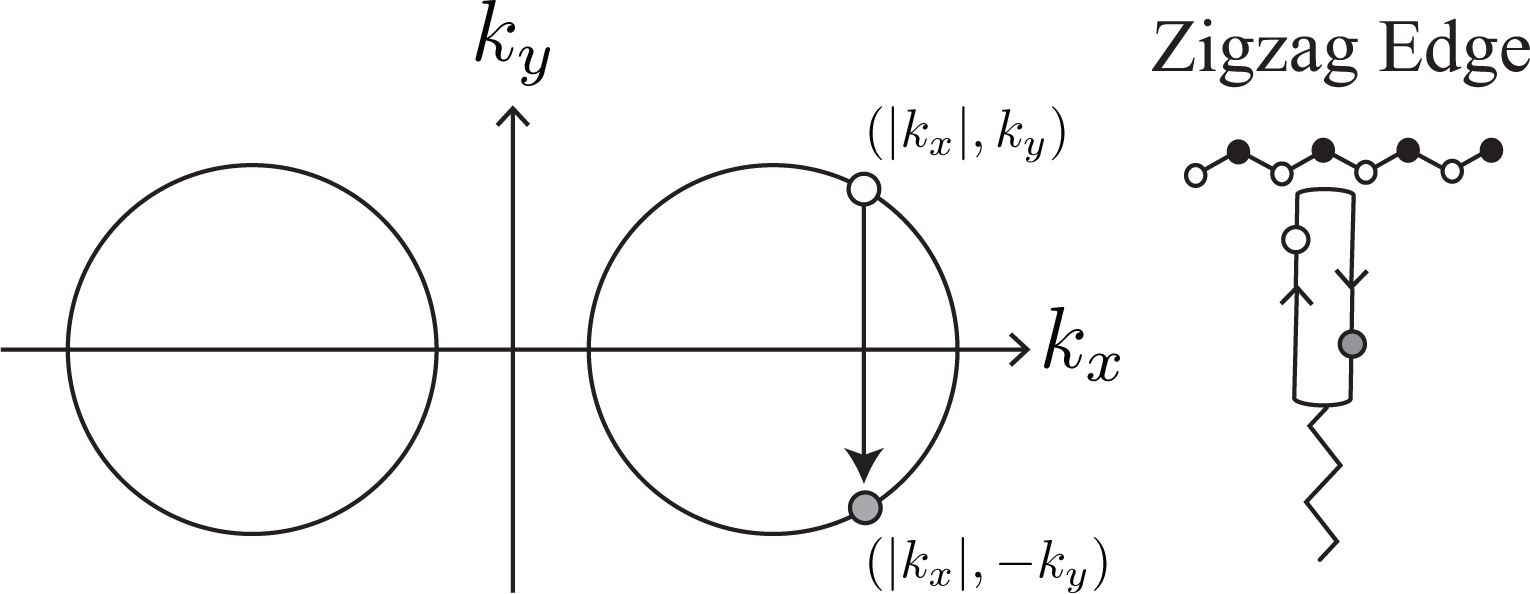
The dominance of intervalley backward scattering causes an enhancement of the D band Raman intensity if Brillouin zone folding (BZF) by the armchair edge is taken into account [14]. Here, BZF means that, in the BZ of graphene shown in Figure 1, a state with (k_x, k_y) is identical to a state with (−k_x, k_y) and that the correct BZ is given by the positive k_x region of the original BZ of graphene [21]. In Figure 2c, as a consequence of BZF, the final state in the intervalley backward scattering event is identified with the state near the K point. Namely, the state with (−|k_x|, −k_y) near the K′ point is identified with the state with (|k_x|, −k_y) near the K point. So, in the folded BZ, the change of a photo-excited electron is (|k_x|, k_y) → (|k_x|, −k_y), as shown by the solid arrow in Figure 2c. Generally, the probability of a process in the folded BZ is given by replacing Θ′ with π − Θ′ in Equation (10) as

$$|M_{BZF}{|}^2=\frac{g_{ep}^2}{2}\{1+s{s}^{\prime }\cos ({\Theta }^{\prime }+\Theta )\}$$

(13)

and this transition probability is indeed maximum when Θ′ = −Θ. When Θ′ = Θ and s′ = s in Equation (13), the final state coincides with the initial state, which is the condition of a first-order Raman process. In this case, the probability is given by

$$|M_{BZF}{|}^2=g_{ep}^2{\cos }^2\Theta$$

(14)

which takes its maximum value for Θ = 0 and π. This shows that the states near the k_x-axis (or the states with bonding and antibonding orbitals) can contribute to the D band intensity through a first-order Raman process.

BZF originates from the fact that a special standing wave is formed by an armchair edge. The standing wave is constructed by the antisymmetric combination of an incident plane wave with k = (k_x, k_y) and a scattered plane wave with k′ = (−k_x, k_y) as $e^{i{k}_{y}y}(e^{i{k}_{x}x}-e^{-e^{i{k}_{x}x}})\propto e^{i{k}_{y}y}\sin (k_{x}x).$ A symmetric combination does not satisfy the boundary condition for the armchair edge [21]. Note that sin(k_xx) does not change when k_x is replaced with −k_x, except for the unimportant change in the overall sign. More importantly, the orbital part Equation (1) does not change when there is the reflection at the armchair edge, as we can confirm by replacing Θ′ with π − Θ in Equation (2) [21,22]. The same orbitals are superposed to form a standing wave at the armchair edge. Thus, the total wave function becomes

$${\psi }_a^s(k)=N\left\{e^{ik\cdot r}\left(\begin{array}{c}{e}^{-i\Theta (k)}\\ s\end{array}\right)-e^{i{k}^{\prime }\cdot r}\left(\begin{array}{c}{e}^{-i{\Theta }^{\prime }{(k)}^{\prime }}\\ s\end{array}\right)\right\}=N^{\prime }{e}^{i{k}_{y}y}\sin (k_{x}x)\left(\begin{array}{c}{e}^{-i\Theta (k)}\\ s\end{array}\right)$$

(15)

where N (N′) is a normalization constant. The standing wave does not change with the replacement k_x → −k_x, and therefore the correct BZ of the standing wave is given solely by the positive k_x region to avoid double counting. It is noteworthy that BZF is specific to the armchair edge and is not applicable to a zigzag edge. The absence of BZF at a zigzag edge is due to the orbital part changes with the reflection of an electron at the zigzag edge and the different orbitals are superposed to form a standing wave [22,23]. The standing wave for a zigzag edge is written as

$${\psi }_a^s(k)=N{e}^{i{k}_{x}x}\left\{e^{i{k}_{y}y}\left(\begin{array}{c}{e}^{-i\Theta (k)}\\ s\end{array}\right)-e^{-i{k}_{y}y}\left(\begin{array}{c}{e}^{i\Theta (k)}\\ s\end{array}\right)\right\}=N^{\prime }{e}^{i{k}_{x}x}\left(\begin{array}{c}\sin (k_{y}y-\Theta (k)))\\ s\sin (k_{y}y)\end{array}\right)$$

(16)

which is not invariant with the replacement k_y → −k_y unless Θ = 0 or π. Thus, it needs a second-order process to activate a phonon mode with nonzero q (see Figure 3) and a first-order Raman band (except the G band) cannot appear at the zigzag edge. Although the intensity is not comparable to that of G or D bands, we can expect a second-order band to appear at the zigzag edge. The D′ band [24,25] (not the D band) may be such a second-order Raman band that can be described by the double resonance model.

The standing wave at the armchair edge can be expressed in the framework of the Dirac equation as

$${\psi }_{a,k}^s(r)=N{e}^{i{k}_{y}y}\left(\begin{array}{c}{e}^{+i{k}_{x}x}{e}^{-i\Theta (k)}\\ e^{+i{k}_{x}x}s\\ e^{-i{k}_{x}x}{e}^{-i\Theta (k)}\\ e^{-i{k}_{x}x}s\end{array}\right)=N{e}^{i{k}_{y}y}\left(\begin{array}{c}{e}^{+i{k}_{x}x}\\ e^{-i{k}_{x}x}\end{array}\right)\otimes \frac{1}{\sqrt{2}}\left(\begin{array}{c}{e}^{-i\Theta (k)}\\ s\end{array}\right)$$

(17)

where k denotes the wave vector measured from the Dirac point in the folded BZ and ⊗ represents the direct product of the valley and the orbital. It can be confirmed that Equation (17) reproduces Equation (13), by calculating the expectation value of Ĥ_ep(D_q) of Equation (11) with respect to Equation (17),

$$\begin{array}{c}{M}_{BZF}={\displaystyle {\int }_V{d}^{2}r{\psi }_{a,K^{\prime }}^{s^{\prime }}}{(r)}^{†}{\widehat{H}}_{ep}(D_q){\psi }_{a,K}^s(r)\\ =\delta (q_x-k_x-{k^{\prime }}_x)\frac{1}{2}\{\delta (k_y+q_y-{k^{\prime }}_y)+\delta (k_y-q_y-{k^{\prime }}_y)\}\frac{g_{ep}}{2}\left(e^{i{\Theta }^{\prime }}s+s^{\prime }{e}^{-i\Theta }\right)\end{array}$$

(18)

where we used $N^2{\displaystyle \int dy{e}^{i(k_y\pm q_y-{k^{\prime }}_y)y}}{\displaystyle \int dx{e}^{\pm i(q_x-k_x-{k^{\prime }}_x)x}}=(1/2)\delta (k_y\pm q_y-{k^{\prime }}_y)\delta (q_x-k_x-{k^{\prime }}_x).$ For k′ = k (i.e., for a first order Raman process), Equation (14) is reproduced, and momentum conservation gives q = (2k_x, 0).

3.3. Optical Anisotropy

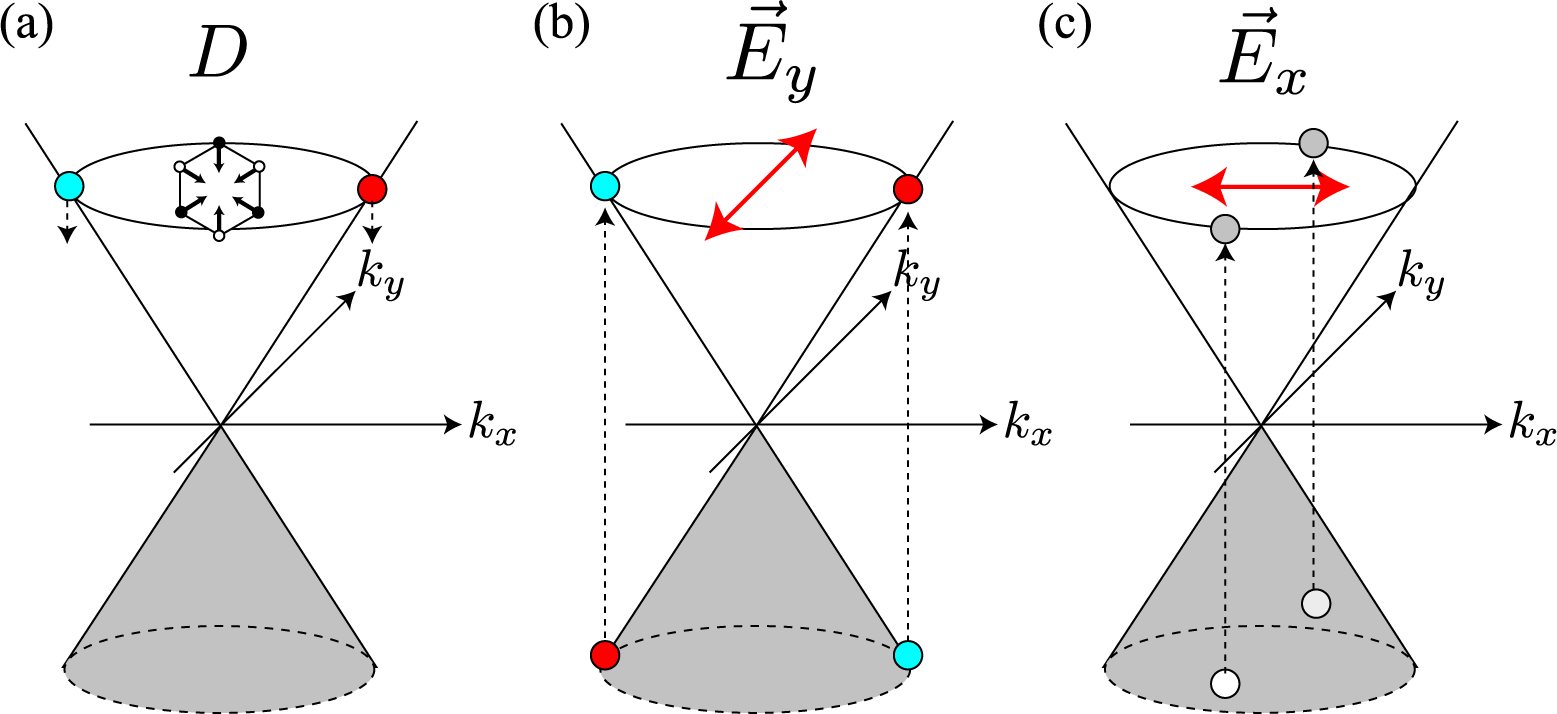
The third factor is the polarization dependence of optical transitions. To supply photo-excited electrons to the states with bonding and antibonding orbitals on the k_x-axis, the polarization of incident laser light must be set parallel to the armchair edge (y-axis), as shown in Figure 4b. The photo-excited electrons on the k_x-axis emit A_1g modes without changing their positions [see Figure 4a]. Meanwhile, when the polarization of the incident laser light is set perpendicular to the armchair edge, the x-polarized light supplies the states on the k_y-axis with photo-excited electrons [see Figure 4c]. The electrons near the k_y-axis change their positions in the folded BZ when they emit A_1g modes [see Figure 2b], and these electrons on the k_y-axis do not contribute to the D band intensity. As a result, the D band can be strongly dependent on the laser light polarization: the D band intensity is enhanced (suppressed) when the polarization of the incident laser light is parallel (perpendicular) to the armchair edge.

The optical anisotropy is due to the Θ dependence of the optical matrix element [26]. Namely, for y (x) polarized light, ${\overrightarrow{E}}_y({\overrightarrow{E}}_x),$ the optical matrix element squared is proportional to cos² Θ (sin² Θ) as

$$|M_{opt}{|}^2=\{\begin{array}{cc}{g}_{e\gamma }^2{\cos }^2\Theta & for{\overrightarrow{E}}_y\\ g_{e\gamma }^2{\sin }^2\Theta & for{\overrightarrow{E}}_x\end{array}$$

(19)

where g_eγ denotes an electron-light coupling constant. The electrons near the k_x (k_y)-axis are dominantly photo-excited by ${\overrightarrow{E}}_y({\overrightarrow{E}}_x)$ [see Figure 4b,c]. For the general polarization direction of incident laser light E, M_opt is proportional to the vector product of E and $\widehat{k}(\equiv k/|k|)$as $M_{opt}\propto E\times \widehat{k}.$M_opt ∝ E × kˆ.

Although Equation (19) was derived without taking account of the edge, it turns out that a similar optical matrix element is obtained for the standing waves [27]. Here, let us use the Dirac equation of Equation (3) to obtain the matrix element that includes the effect of the armchair edge. The electron-light interaction is given by replacing $\widehat{p}$ with $\widehat{p}-eA$ in Equation (3) as

$$\widehat{H}=v_F\left(\begin{array}{cc}\sigma \cdot (\widehat{p}-eA)& 0\\ 0& {\sigma }^{\prime }\cdot (\widehat{p}-eA)\end{array}\right)$$

(20)

where A is the vector potential of light. Since the Maxwell equation gives E = −∂A/∂t, the vector directions of E and A are the same. The optical matrix element is defined using Equation (17) as

$$M_{opt}=-e{v}_F{\displaystyle \int d^{2}r{\psi }_{a,k^{\prime }}^{+1}}{(r)}^{†}\left(\begin{array}{cc}\sigma \cdot A& 0\\ 0& {\sigma }^{\prime }\cdot A\end{array}\right){\psi }_{a,k}^{-1}(r).$$

(21)

For the y-polarized light A = (0, A_y), M_opt is nonzero only for a direct transition (k′ = k) and the orbital gives cos Θ. For the x-polarized light A = (A_x, 0), M_opt includes the integral $(1/L){\displaystyle {\int }_0^{L}dx}\sin (k_x-{k^{\prime }}_x)x$and the orbital gives (−e^iΘ′ + e^−iΘ)/2. Since the integral vanishes when k_x = k_x′, a direct transition does not take place. The possible transitions are indirect transitions k_x ≠k_x^′. For k_x − k_x′ = nπ/L (n is an odd number), we obtain 2/(nπ) by performing the integral. The momentum change in an indirect transition is inversely proportional to the distance (L) from the armchair edge where the standing wave is a good approximation. Since the change in the wave vector is negligible when L is large, we may assume Θ′ ≃ Θ. Then the orbital leads to −i sin Θ, which reproduces Equation (19). This feature of the indirect transition for the x-polarized light has been examined with a more mathematically rigorous method using a lattice tight-binding model [27].

3.4. D Band Polarization Formula

We combine Equations (14) and (19) to derive the polarization formula of the D band. The probability of a first-order Raman process that an electron with Θ in the π-band is excited into the π*-band by $\overrightarrow{E}(i=\{x,y\}),$ and then the photo-excited electron emits the A_1g mode, and finally the electron with Θ emits a light with ${\overrightarrow{E}}_j,$is given by

$$|M_{ji}(\Theta ){|}^2=|M_{opt}({\overrightarrow{E}}_j){|}^2|M_{BZF}(\Theta ){|}^2|M_{opt}({\overrightarrow{E}}_i){|}^2=g_{e\gamma }^4{g}_{ep}^4\{\begin{array}{l}{\cos }^6\Theta (ji)=(yy)\\ {\cos }^4\Theta {\sin }^2\Theta (xy)\text{(}yx\text{)}\\ {\cos }^2\Theta {\sin }^4\Theta (xx).\end{array}$$

(22)

Note that the wave vector of the A_1g mode is completely fixed by Θ and |k| (or E_L) as

$$q_x=-2\left|k\right|\cos \Theta .$$

(23)

Phonons with different momenta are distinguishable in principle. We have different final states for different Θ values, and to calculate the D band intensity, we need to sum over all possible final states by operating |M_ji(Θ)|² with ${\displaystyle \int {}_0^{2\pi }}d\Theta$. Because ${\displaystyle {\int }_0^{2\pi }{\cos }^2\Theta {\sin }^4\Theta d\Theta /{\displaystyle {\int }_0^{2\pi }{\cos }^6\Theta d\Theta }}=1/5$, the polarization dependence of the D band intensity is written as

$$I_D({\theta }_{out},{\theta }_{in})\propto ({\cos }^2{\theta }_{out}{\sin }^2{\theta }_{out})\left(\begin{array}{cc}1& 1/5\\ 1/5& 1/5\end{array}\right)\left(\begin{array}{c}{\cos }^2{\theta }_{in}\\ {\sin }^2{\theta }_{in}\end{array}\right)$$

(24)

where θ_in (θ_out) denotes the angle of an incident (scattered) electric field with respect to the armchair edge. (In calculating the D band Raman intensity, it is incorrect to sum over intermediate states specified by the electron’s wave vector k, such as $|{\displaystyle {\sum }_k{M}_{ji}(\Theta (\mathbf{k}))}{|}^2.$Because the phonon wave vector relates to the electron wave vector through q = −2k, ${\displaystyle \sum {}_k}$actually means a summation for different phonons (final states). Thus, the Raman intensity is proportional to ${\displaystyle {\sum }_q|M_{ji}(\Theta (q)){|}^2}$ or ${\displaystyle \int {}_0^{2\pi }}d\Theta |M_{ji}(\Theta ){|}^2.)$ (The polarization dependence of the D band near the edge has been calculated by Basko [28], and the result is different from our result. The difference may arise from the fact that here we did not sum over the intermediate states nor take into account the energy denominators of the perturbation theory; instead, we have assumed a resonant Raman process, that is, we select a particular intermediate state for each final phonon state. We show that the application of resonance condition is validated unless the mean lifetime of intermediate state is extremely short in Appendix A.) When the VV configuration (θ_out = θ_in) is used, the polarization dependence is approximated by $I_D^{VV}({\theta }_{in})\simeq I{\cos }^4{\theta }_{in}.$ On the other hand, when the VH configuration (θ_out = θ_in + π/2) is used, the polarization dependence is approximated by $I_D^{VH}({\theta }_{in})\simeq I{\cos }^2{\theta }_{in}{\sin }^2{\theta }_{in}.$ These results are consistent with the experiment reported by Cançado et al [7]. Without a polarizer for the scattered light, we have

$$I_D({\theta }_{in})\propto \left({\displaystyle {\int }_0^{2\pi }d\Theta {\cos }^4\Theta }\right){\cos }^2({\theta }_{in})+\left({\displaystyle {\int }_0^{2\pi }d\Theta {\cos }^2\Theta {\sin }^2\Theta }\right){\sin }^2({\theta }_{in})$$

(25)

because ${\displaystyle {\int }_0^{2\pi }{\cos }^2\Theta {\sin }^2\Theta d\Theta /}{\displaystyle {\int }_0^{2\pi }{\cos }^4\Theta d\Theta =1/3,}$ it may be rewritten as I_D(θ_in) ∝ cos²(θ_in) + (1/3) sin²(θ_in)

$$I_D({\theta }_{\text{in}})\propto {\text{cos}}^2({\theta }_{\text{in}})+b{\text{sin}}^2({\theta }_{\text{in}})+c$$

(26)

where c is a constant, which probably originates from a defect beside the edge. The constants b and c determine the depolarization ratio: I_D(90^◦)/I_D(0^◦) = (b + c)/(1 + c) [see Figure 5]. When c is much larger than unity, the polarization behavior is obscured. If c is negligible, a smaller depolarization ratio (b = 1/5) is expected when a polarizer is used for the scattered light.

4. Predictions of Our Model

We have seen that the D band has a direct relationship to the bonding and antibonding orbitals (that is, an A_1g mode is excited through the first-order Raman process only from these orbitals). This conclusion has been derived based on two factors: the dominance of intervalley backward scattering (Section 3.1), and BZF by the armchair edge (Section 3.2). In this section, we report some consequences that are derived from these factors.

4.1. The Origin of Dispersive Behavior

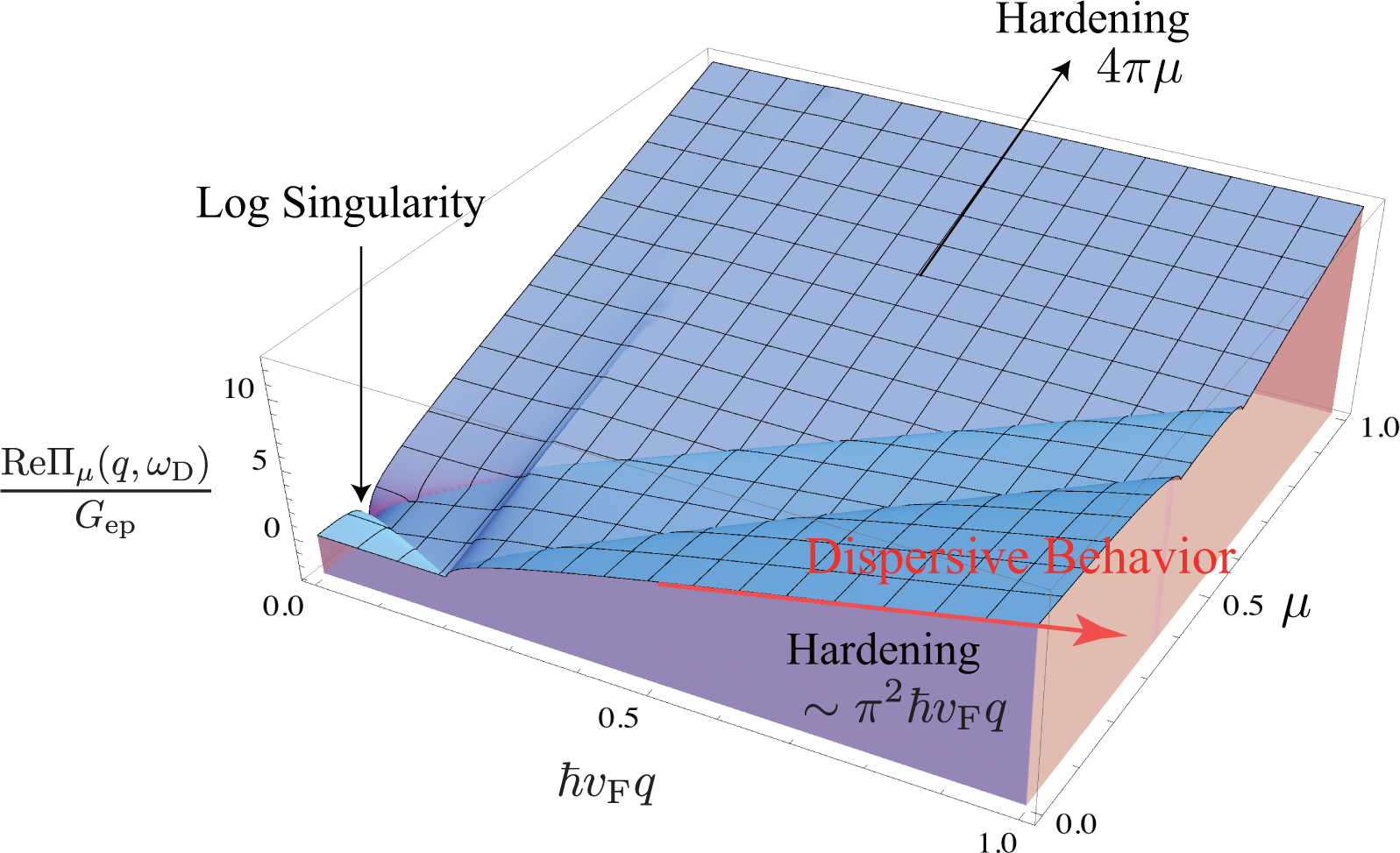
The D band frequency ω_D increases linearly with increasing excitation energy E_L as ∂ω_D/∂E_L ∼ 50 cm⁻¹/eV, which is known as dispersive behavior [9,12,29,30]. In a previous paper [31], we pointed out that the dispersive behavior is mainly attributed to a quantum mechanical correction (self-energy) to the A_1g frequency. The modified energy of the A_1g mode is written as ħω + ReΠ_μ(q, ω), where ω is the bare frequency (Calculation suggests that the bare frequency contains a term quadratic in q, which is consistent with inelastic X-ray scattering data for graphite [32].) and Π_μ(q, ω) represents the self-energies of the A_1g modes induced by electron-phonon interaction. The self-energy of an A_1g mode with q = |q| is defined as

$${\displaystyle {\prod }_{\mu }(q,\omega )}\equiv {\displaystyle \sum _{s,s^{\prime }}{\displaystyle \sum _k\frac{(f_{k,\mu }^s-f_{k+q,\mu }^{s^{\prime }})g_s|M{|}^2}{\hslash \omega +s\hslash v_{F}k-s^{\prime }\hslash v_F|k+q|+i\in }}}$$

(27)

where ϵ is a positive infinitesimal; $f_{k,\mu }^s={\lim }_{\beta \to \infty }{(1+e^{\beta (sv|k|-\mu )})}^{-1}$ is the Fermi distribution function with finite doping μ; and g_s = 2 represents spin degeneracy. The electron-phonon matrix element squared |M|² is constructed in Equation (10) as $|M{|}^2=\frac{g_{ep}^2}{2}\{1-s{s}^{\prime }\cos ({\Theta }^{\prime }(k+q)-\Theta (k))\}.$

In the continuum limit of k, Π_μ(q, ω) is calculated analytically. The expression of the real part is given by

$$\begin{array}{l}\mathrm{Re}{\displaystyle {\prod }_{\mu }(q,\omega )}/G_{ep}=4\pi \mu \\ +\hslash \pi \sqrt{{\omega }^2-v_F^2{q}^2}{\theta }_{\omega -v_{F}q}\left[-g\left(\frac{\hslash \omega +2\mu }{\hslash v_{F}q}\right)+{\theta }_{\frac{\hslash \omega -\hslash v_{F}q}{2}-\mu }g\left(\frac{\hslash \omega -2\mu }{\hslash v_{F}q}\right)+{\theta }_{\mu -\frac{\hslash \omega +\hslash v_{F}q}{2}}g\left(\frac{2\mu -\hslash \omega }{\hslash v_{F}q}\right)\right]\\ +\hslash \pi \sqrt{v_F^2{q}^2-{\omega }^2}{\theta }_{v_{F}q-\omega }\left\{{\theta }_{\frac{\hslash v_{F}q-\hslash \omega }{2}-\mu }\left[\frac{\pi }{2}-{\sin }^{-1}\left(\frac{\hslash \omega +2\mu }{\hslash v_{F}q}\right)\right]+{\theta }_{\frac{\hslash v_{F}q+\hslash \omega }{2}-\mu }\left[\frac{\pi }{2}-{\sin }^{-1}\left(\frac{2\mu -\hslash \omega }{\hslash v_{F}q}\right)\right]\right\}\end{array}$$

(28)

where θ_x denotes a step function satisfying θ_x≥0 = 1; and θ_x<0 = 0, $g(x)\equiv \ln (x+\sqrt{x^2+1})$;and $G_{ep}\equiv g_{ep}^{2}V/{(2\pi \hslash v_F)}^2$ is a (dimensionless) coupling constant. A 3d plot of ReΠ_μ(q, ω_D)/G_ep is shown in Figure 6. Interestingly, ReΠ_μ(q, ω_D) increases as we increase q. In fact, near the Dirac point, ReΠ_μ(q, ω_D) follows

$$\mathrm{Re}{\displaystyle {\prod }_{\mu \sim 0}(q,\omega )}\simeq G_{ep}{\pi }^2\hslash v_{F}q.$$

(29)

Since ħv_Fq ≃ E_L, the self-energy contributes to the dispersive behavior of the D (or 2D) band [9,12,29,30,33]. If we use G_ep = 5 cm⁻¹/eV, which is obtained from the broadening data published by Chen et al. [3], the self-energy can account for ∼60% of the dispersion because ReΠ_μ≃0(q, ω_q)≃G_epπ²E_L and G_epπ² ≃ 30 cm⁻¹/eV. It should be emphasized that the self-energy is calculated using only Equation (10), and any artificial assumption, such as an adiabatic approximation, is not employed when calculating the self-energy. The physical origin of the dispersive behavior is easy to be understood with shifted Dirac cones [31]. In perturbation theory, the mechanism of dispersive behavior is almost the same as the mechanism where the G band exhibits hardening with increasing |μ|.

The dispersive behavior is not an inherent property of the D band but rather is a property of the A_1g mode. The armchair edge is involved in the activation of the D band. However, the dispersive behavior itself has nothing to do with the edge. In other words, there are processes that can exhibit dispersive behavior, besides the Raman D band. A good example is the 2D band, for which dispersive behavior is observed [12] because the 2D band consists of two A_1g modes.

4.2. Intravalley Phonons

In addition to the zone-boundary A_1g mode, we can determine the effect of BZF on zone-center (intravalley) optical phonon modes: BZF forbids an intravalley transverse optical (TO) mode to appear as a prominent Raman band at the armchair edge. The Dirac equation is the most useful way of showing this. The electron-phonon interactions for the LO and TO modes with (nonzero) momentum (q_x, q_y) are written as

$${\widehat{H}}_{LO}(q)=g_{ep}\frac{e^{iq\cdot r}}{\left|q\right|}\left(\begin{array}{cc}{\sigma }_x{q}_y-{\sigma }_y{q}_x& 0\\ 0& {\sigma }_x{q}_y+{\sigma }_y{q}_x\end{array}\right)$$

(30)

$${\widehat{H}}_{LO}(q)=g_{ep}\frac{e^{iq\cdot r}}{\left|q\right|}\left(\begin{array}{cc}{\sigma }_x{q}_x+{\sigma }_y{q}_y& 0\\ 0& {\sigma }_x{q}_x-{\sigma }_y{q}_y\end{array}\right)$$

(31)

and their matrix elements are obtained from Equation (17) as

$$\begin{array}{c}{M}_{LO}(q)=\frac{g_{ep}}{\left|q\right|}\delta \left(-{k^{\prime }}_y+q_y+k_y\right)\times \\ \left\{\delta \left(-{k^{\prime }}_x+q_x+k_x\right)[\langle {\sigma }_x\rangle q_y-\langle {\sigma }_y\rangle q_x]+\delta \left(-{k^{\prime }}_x-q_x+k_x\right)[\langle {\sigma }_x\rangle q_y+\langle {\sigma }_y\rangle q_x]\right\}\end{array}$$

(32)

$$\begin{array}{c}{M}_{TO}(q)=\frac{g_{ep}}{\left|q\right|}\delta \left(-{k^{\prime }}_y+q_y+k_y\right)\times \\ \left\{\delta \left(-{k^{\prime }}_x+q_x+k_x\right)[\langle {\sigma }_x\rangle q_x+\langle {\sigma }_y\rangle q_y]+\delta \left(-{k^{\prime }}_x-q_x+k_x\right)[\langle {\sigma }_x\rangle q_x-\langle {\sigma }_y\rangle q_y]\right\}\end{array}$$

(33)

where ⟨σ_x⟩ ≡ (se^iΘ′ + s^′e^−Θ)/2 and ⟨σ_y⟩ ≡ −i(se^iΘ′ − s^′e^−Θ)/2. For the TO mode, M_TO(q) vanishes in the q_x → 0 limit, due to the interference between the valleys. In the q_y → 0 limit, Θ^′ = π − Θ holds, and the orbital of the matrix element, ⟨σ_x⟩, vanishes when s^′ = s. Thus, the electron-phonon matrix element for the Γ point TO mode is suppressed compared with that of the LO mode: the Γ point TO mode is missing in the G band at the armchair edge [10,22,34,35].

4.3. D Band Splitting

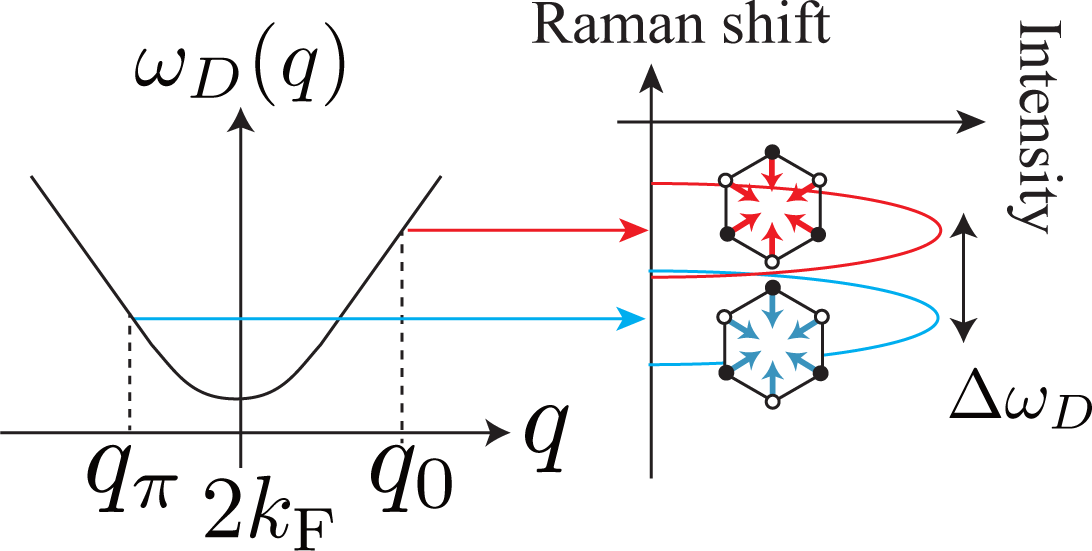
The D band is composed of the (two) A_1g modes that are emitted from two electronic states with bonding or antibonding orbitals (Θ = 0 or π). This fact results in the splitting of the D band if the trigonal warping effect is taken into account [14]. The splitting width increases with increasing incident laser energy E_L as

$$\Delta {\omega }_D=25{\left(\frac{E_L}{{\gamma }_0}\right)}^2[c{m}^{-1}]$$

(34)

where γ₀ (≃ 3 eV) is the hopping integral between nearest neighbor atoms. This formula is derived by noting that the wave vectors for the two A_1g modes that originate from the bonding and antibonding orbitals are different due to the trigonal warping effect. The difference is estimated with the lattice tight-binding model as [14]

$$\Delta q=\frac{\sqrt{3}}{a}{\left(\frac{E_L}{3{\gamma }_0}\right)}^2.$$

(35)

For simplicity, let us assume that the phonon dispersion relation for the D band is isotropic about the Dirac point. From Figure 7 it is clear that the two phonon modes with q₀ and q_π have different phonon energies, which results in the double peak structure of the D band. The difference between the energy of the phonon mode with q₀ and that with q_π is approximated by

$$\Delta {\omega }_D=\frac{\partial {\omega }_D}{\partial q}\Delta q$$

(36)

where ∂ω_D/∂q is the slope of the phonon energy dispersion. We interpret the dispersive behavior that occurs as a result of the dispersion relation of the phonon mode. Then we have

$$\frac{\partial {\omega }_D}{\partial q}=\frac{\partial E_L}{\partial q}\frac{\partial {\omega }_D}{\partial E_L}.$$

(37)

Putting |∂E_L/∂q| = ħv_F in Equation (37), and combining it with Equations (35) and (36), we obtain Equation (34). Actual splitting can be smaller than Equation (34) due to several factors, such as (i) the phonon dispersion relation for the D band not being exactly isotropic around the Dirac point [32]; (ii) Θ not exactly limited by 0 or π.

5. Prospects

The D band has a close relationship with the energy gap. A direct relationship between the zone-boundary A_1g mode and the energy gap is seen in the Pierls instability at armchair nanoribbons [36,37]. In the Dirac equation, an energy gap is represented by a Dirac mass term that appears in the off-diagonal terms as

$$\widehat{H}=\left(\begin{array}{cc}{v}_F\sigma \cdot \widehat{p}& m{\sigma }_x\\ m\ast {\sigma }_x& v_F{\sigma }^{\prime }\cdot \widehat{p}\end{array}\right).$$

(38)

The spectrum has an energy gap 2|m|, because the energy dispersion is given by $\pm \sqrt{{(\hslash v_{\mathrm{F}}q)}^2+|m{|}^2}.$ The zone-boundary A_1g mode is related to the Dirac mass because the electron-phonon interaction [Equation (11)] appears as a mass term in the Dirac equation: m → g_epe^−iq·r. The dominance of intervalley backward scattering becomes clear with respect to the mass term, because a nonzero mass tends to stop a massless particle by backward scattering.

Interestingly, the armchair edge itself can be modeled as a singular mass term in the Dirac equation, whereby Equation (17) is obtained as a solution of the model [38]. This theoretical framework leads us to find a relationship between the dominance of intervalley backward scattering represented by Equation (10) and BZF. To see a connection between them, it is important to recognize that in deriving Equation (10), the orbital structures of Equations (1) and (2) play a decisive role. These orbitals have to relate to each other by mirror symmetry with respect to the x-axis [x → −x or k_x → −k_x] in Figure 1. In fact, Equation (2) is constructed by replacing Θ with π − Θ′ in Equation (1). The orbital should be invariant under this replacement.

Defects, such as a lattice vacancy and a topological defect, are considered to be sources that increase the D band intensity [c-term in Equation (26)]. This speculation is reasonable, because creating a lattice vacancy inevitably involves the antibonding orbital. Unfortunately, the wave functions and the corresponding BZ in the presence of defects are difficult to construct rigidly in the framework of a tight-binding lattice model. This difficulty prevents us from calculating the electron-phonon matrix element exactly. However, there is the possibility of obtaining a good approximation of the matrix element using the Dirac equation [39–43].

6. Conclusions

An orbital and wave vector are the basic idea for a molecular and a crystal, respectively. Knowing the correlation between them is the key to understand the D band. The D band originates from two orbitals: the bonding and antibonding orbitals on the k_x-axis. Observing the D band is the same thing as selecting the two orbitals from the various orbitals that compose the iso-energy section of the Dirac cone. This idea leads us to expect the optical control of edge chiralities [44]. A slight asymmetry between the bonding and antibonding orbitals, induced by the trigonal warping effect, may be important in terms of understanding the stability of the armchair edge under laser light irradiation. A closer study of the D band based on the Dirac equation will be fruitful for a further investigation of the physics of the D band.