Kinetics and Morphology of Flow Induced Polymer Crystallization in 3D Shear Flow Investigated by Monte Carlo Simulation
Abstract
:1. Introduction
2. Mathematical Model and Numerical Method
2.1. Morphology Evolution Model for Spherulites and Shish-Kebabs
2.2. Amorphous Phase and Semi-Crystalline Phase Model
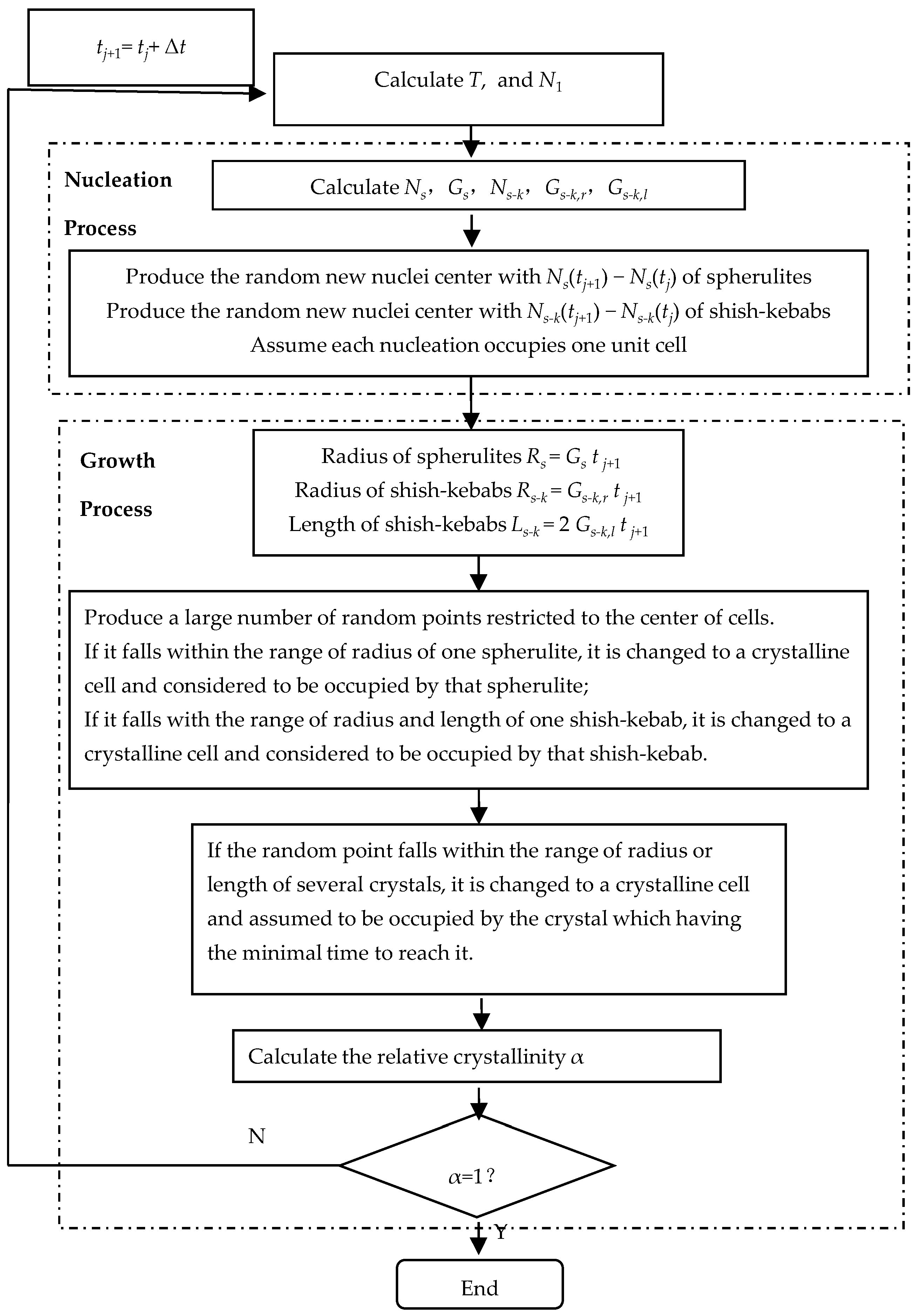
2.3. Numerical Method
2.3.1. Monte Carlo Method
2.3.2. Finite Difference Method
3. Results and Discussion
3.1. Parameters
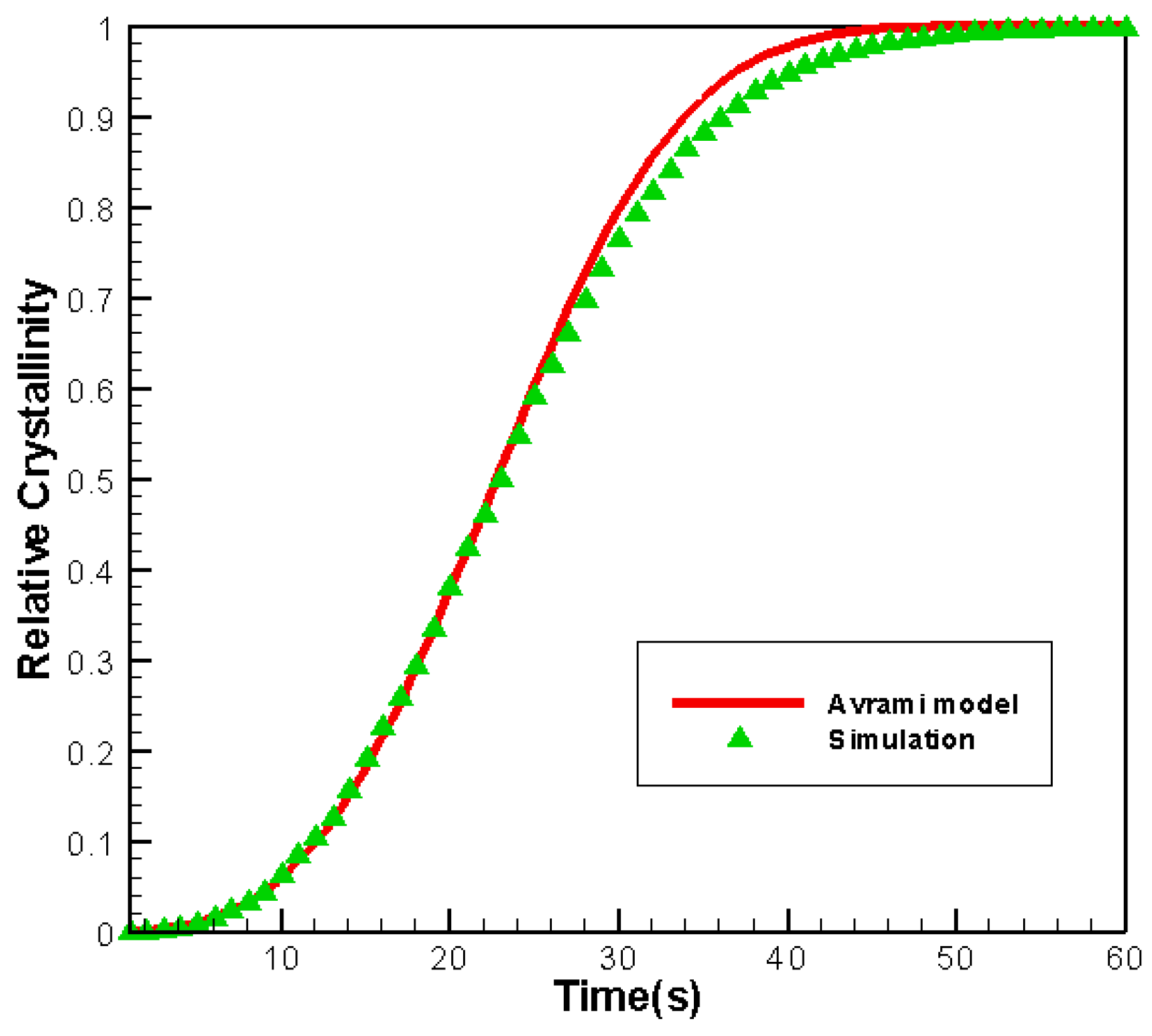
3.2. Validity of the Simulation
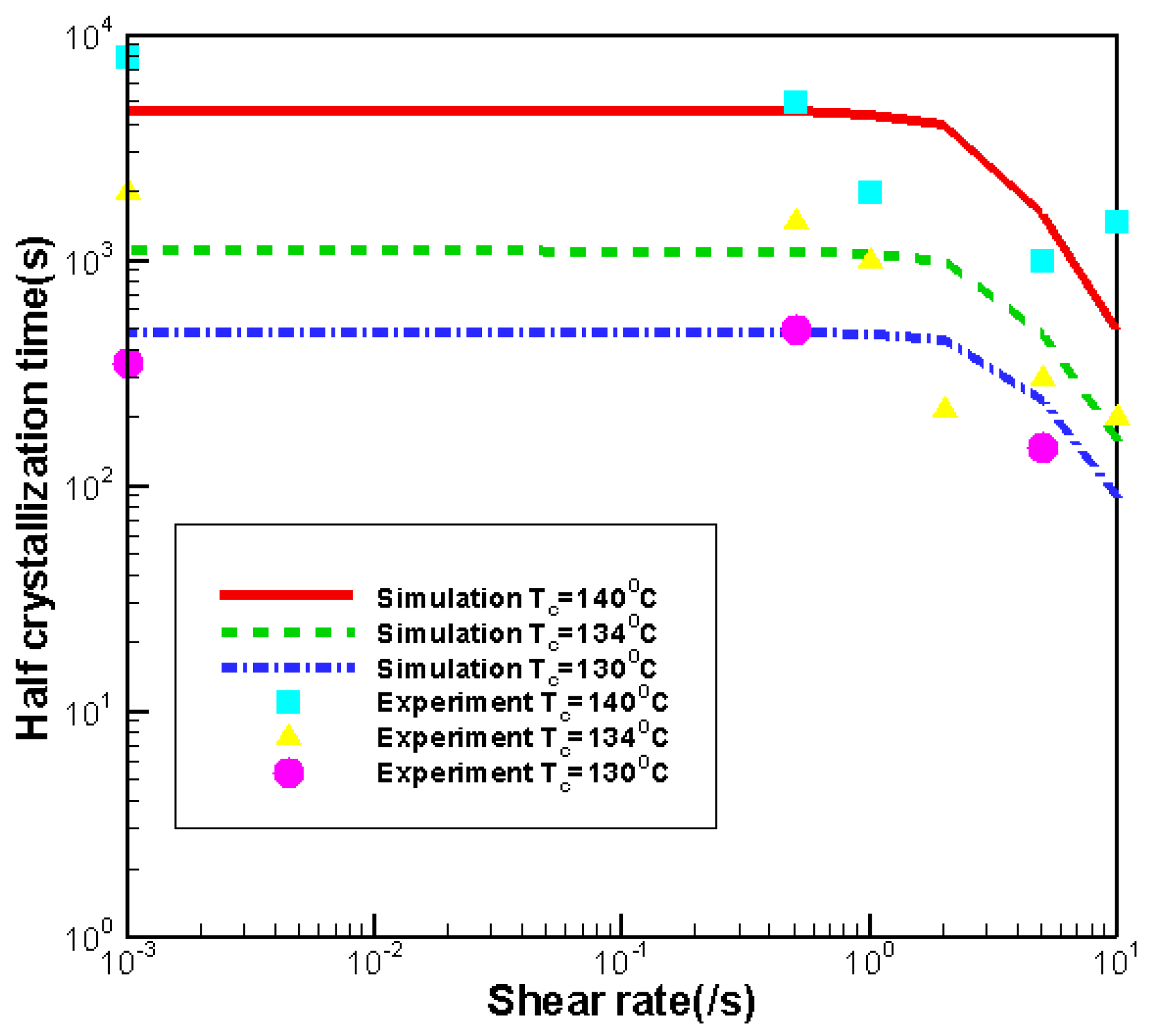
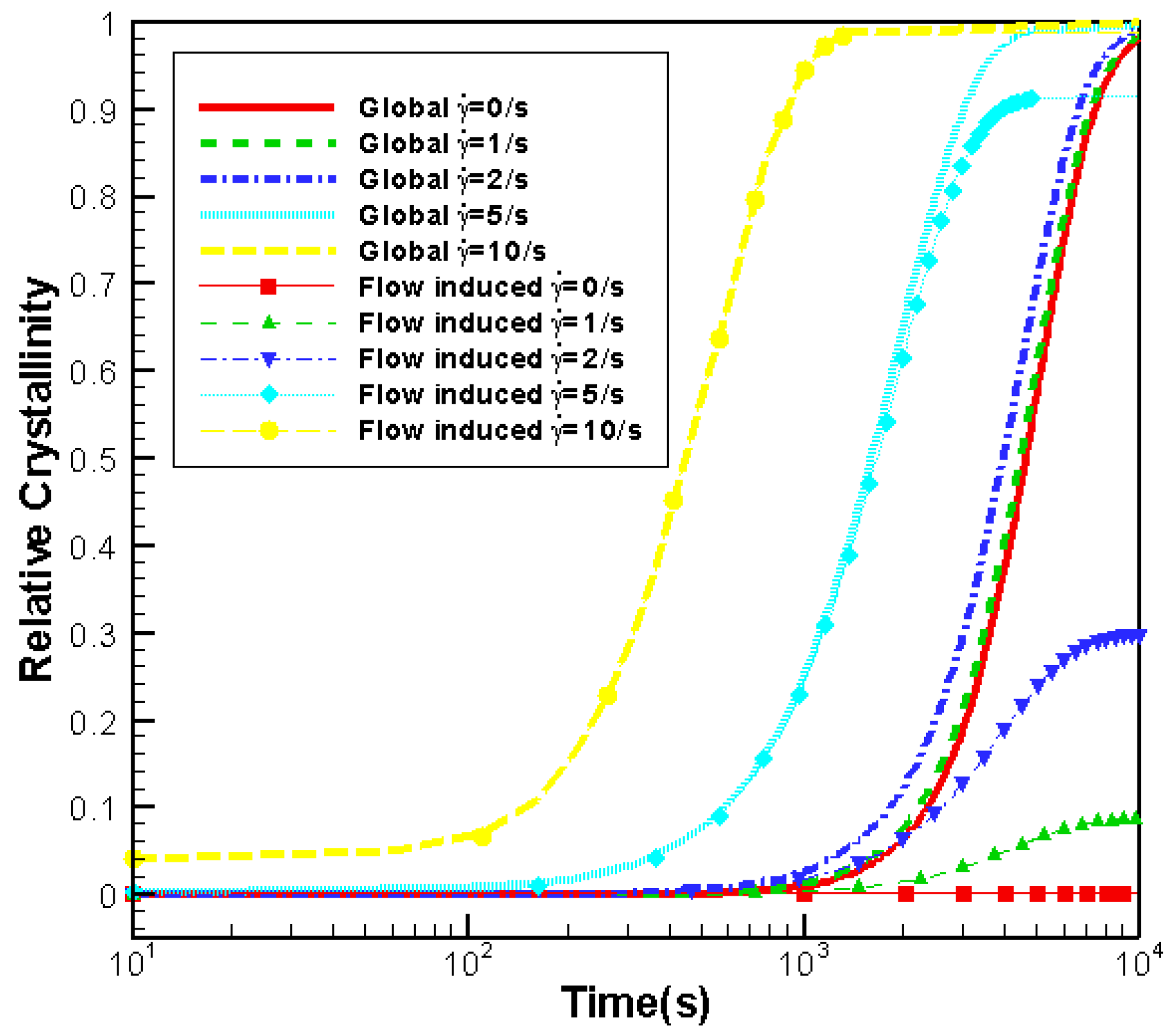
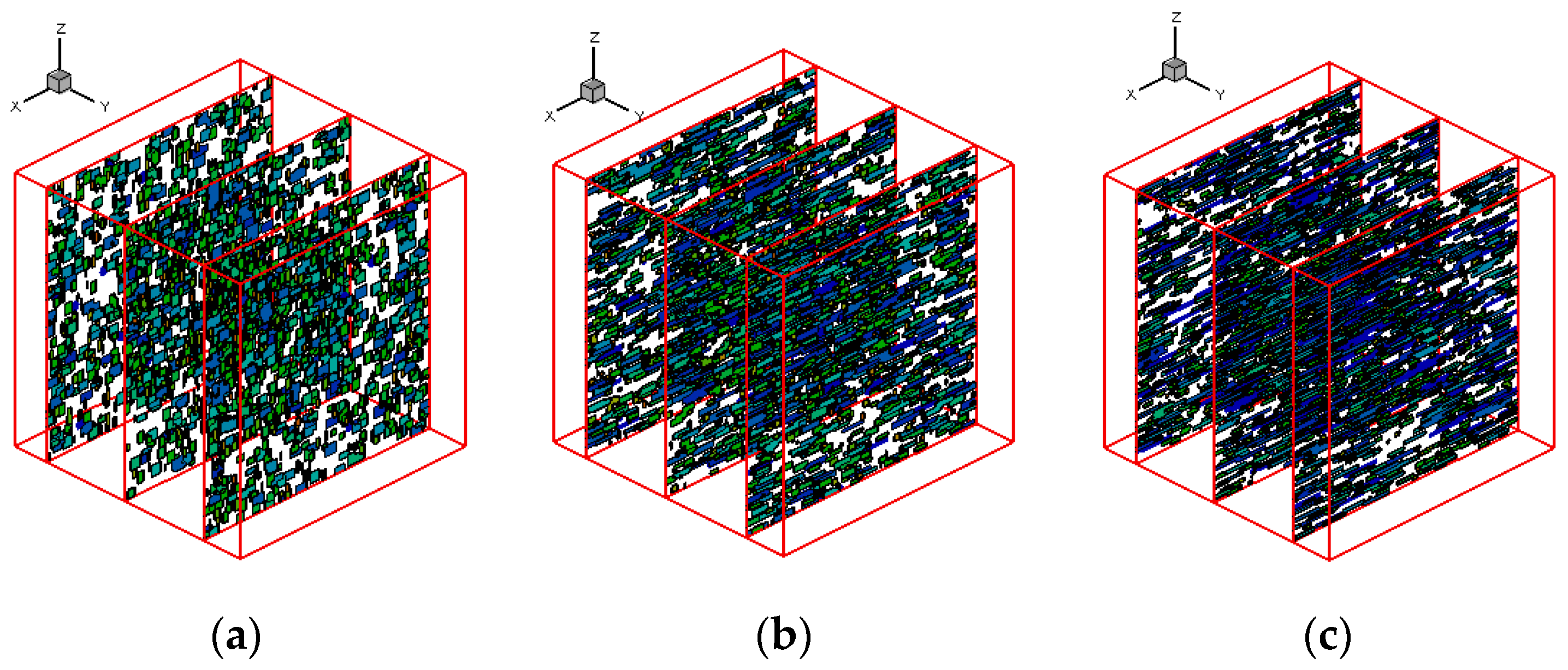
3.3. Effects of Shear Rate
3.3.1. Effects of Shear Rate on Crystallization
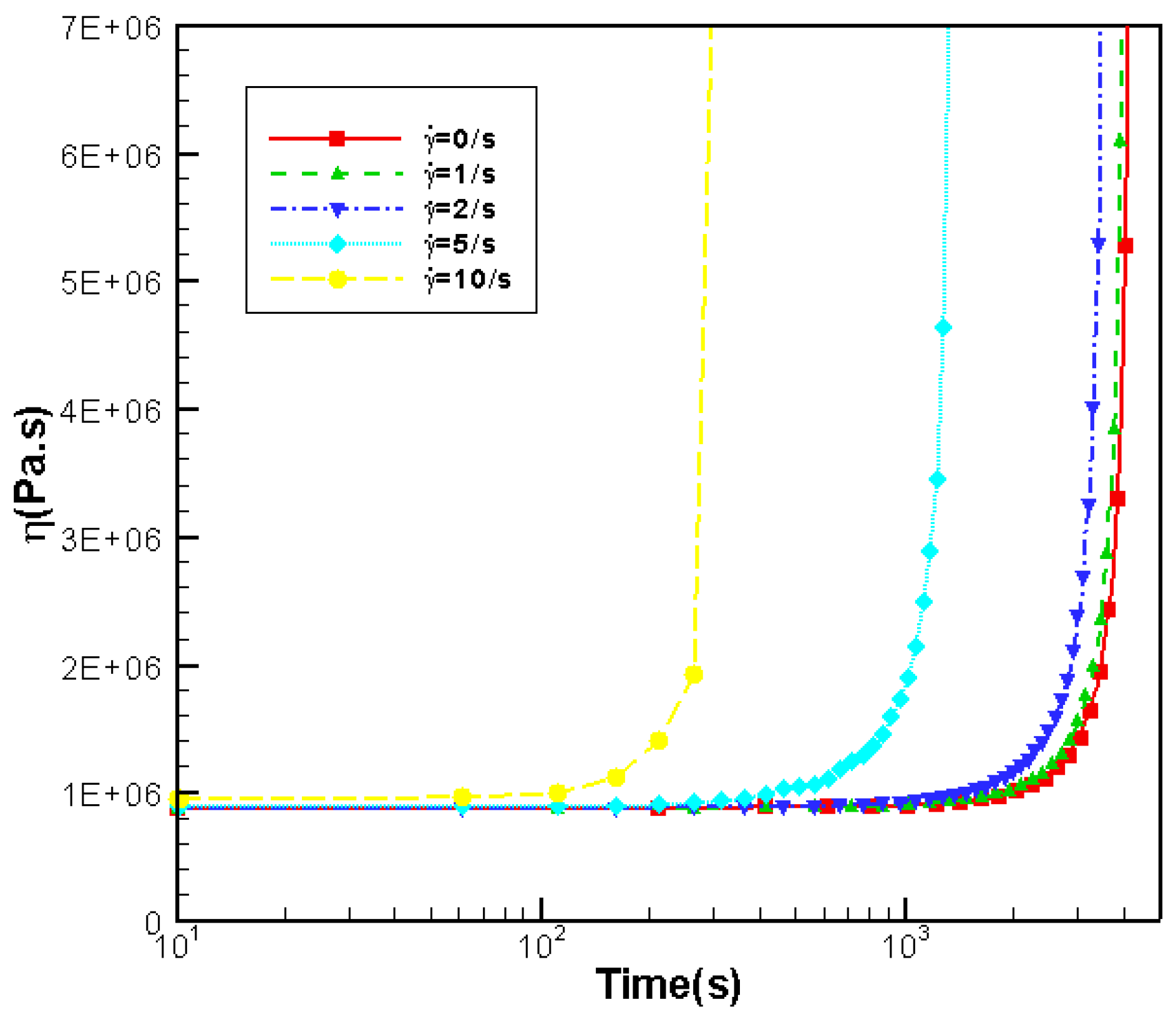
3.3.2. Effects of Shear Rate on Rheology
3.4. Effects of Shear Time
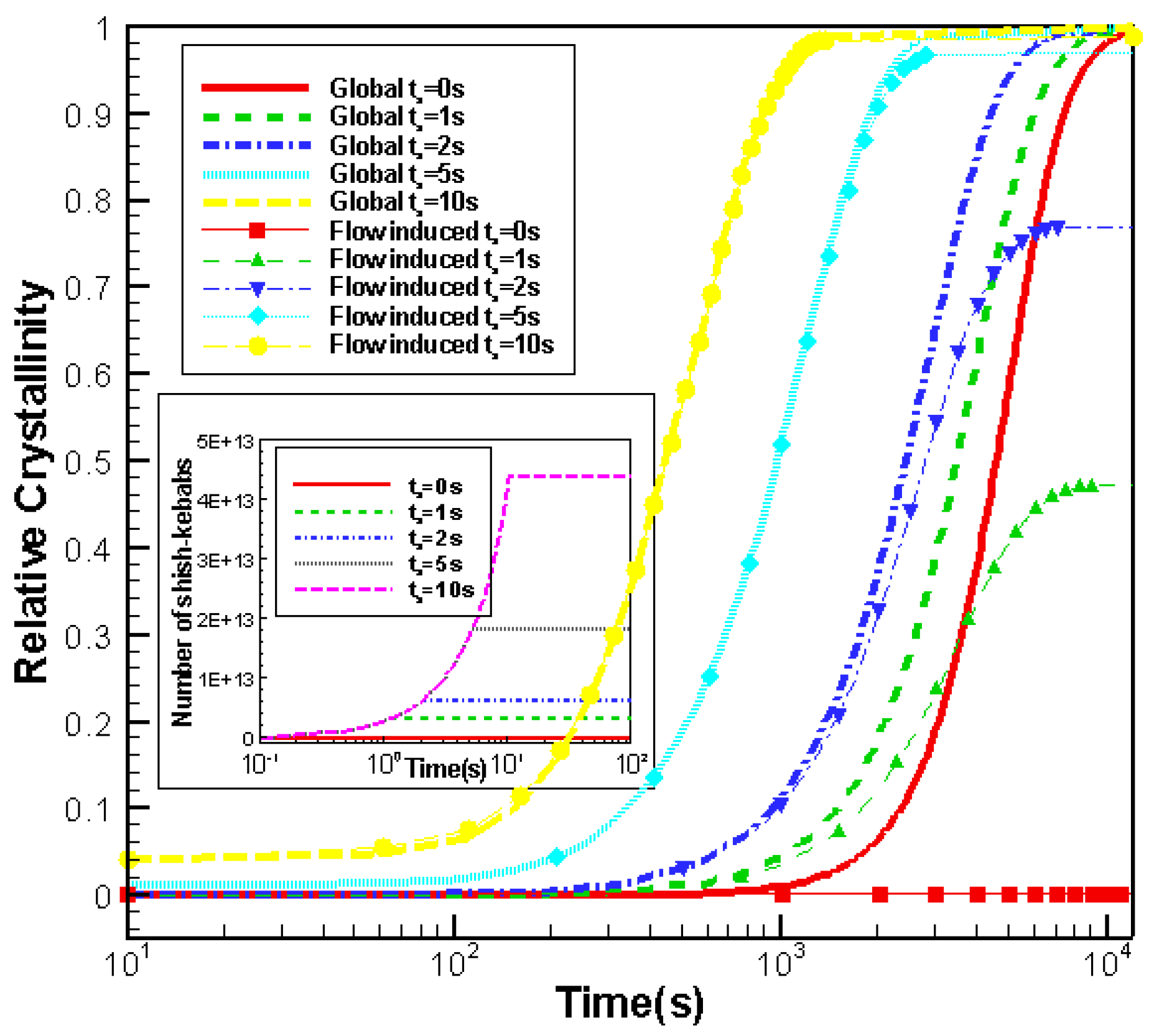
3.4.1. Effects of Shear Time on Crystallization
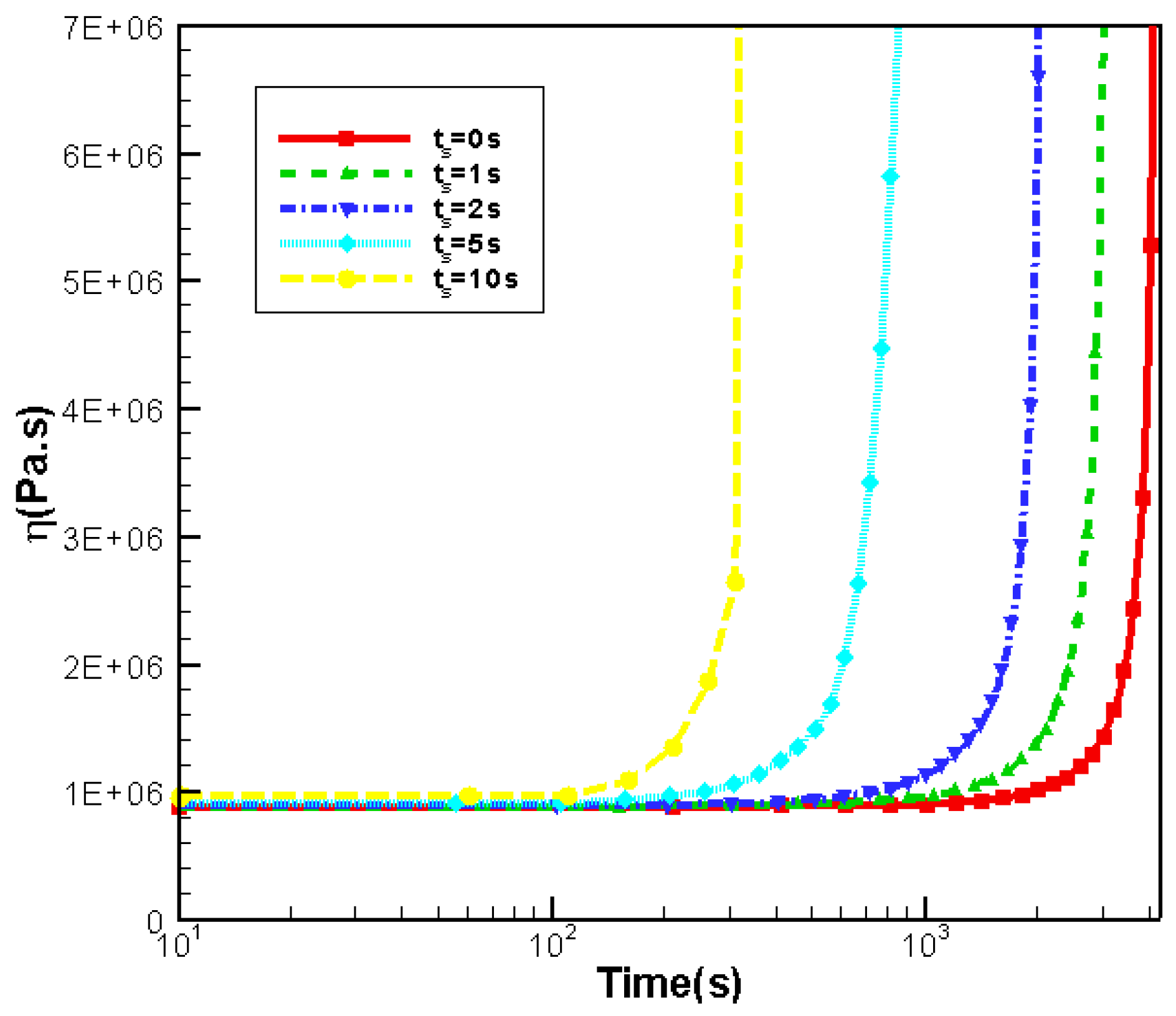
3.4.2. Effects of Shear Time on Rheology
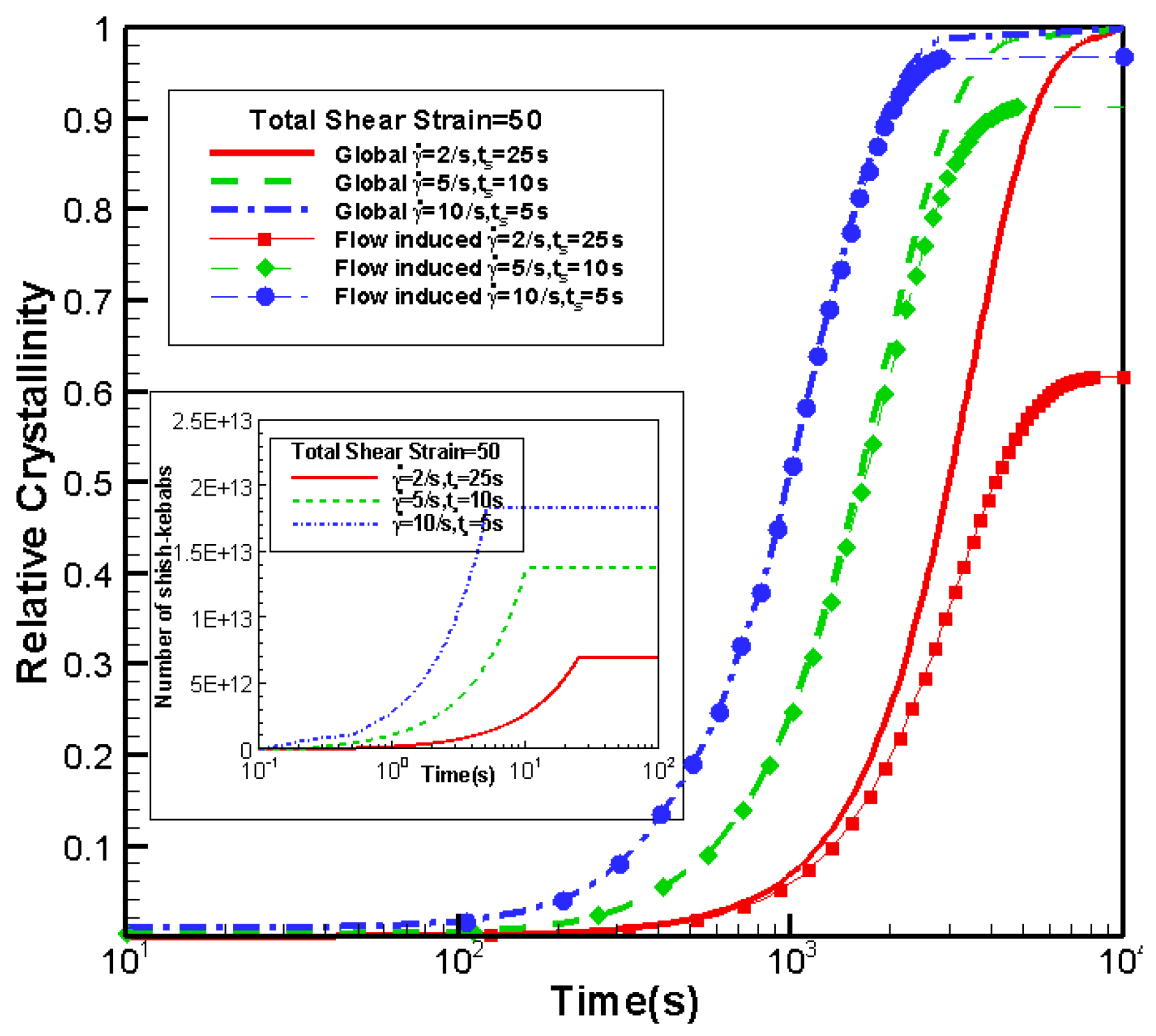
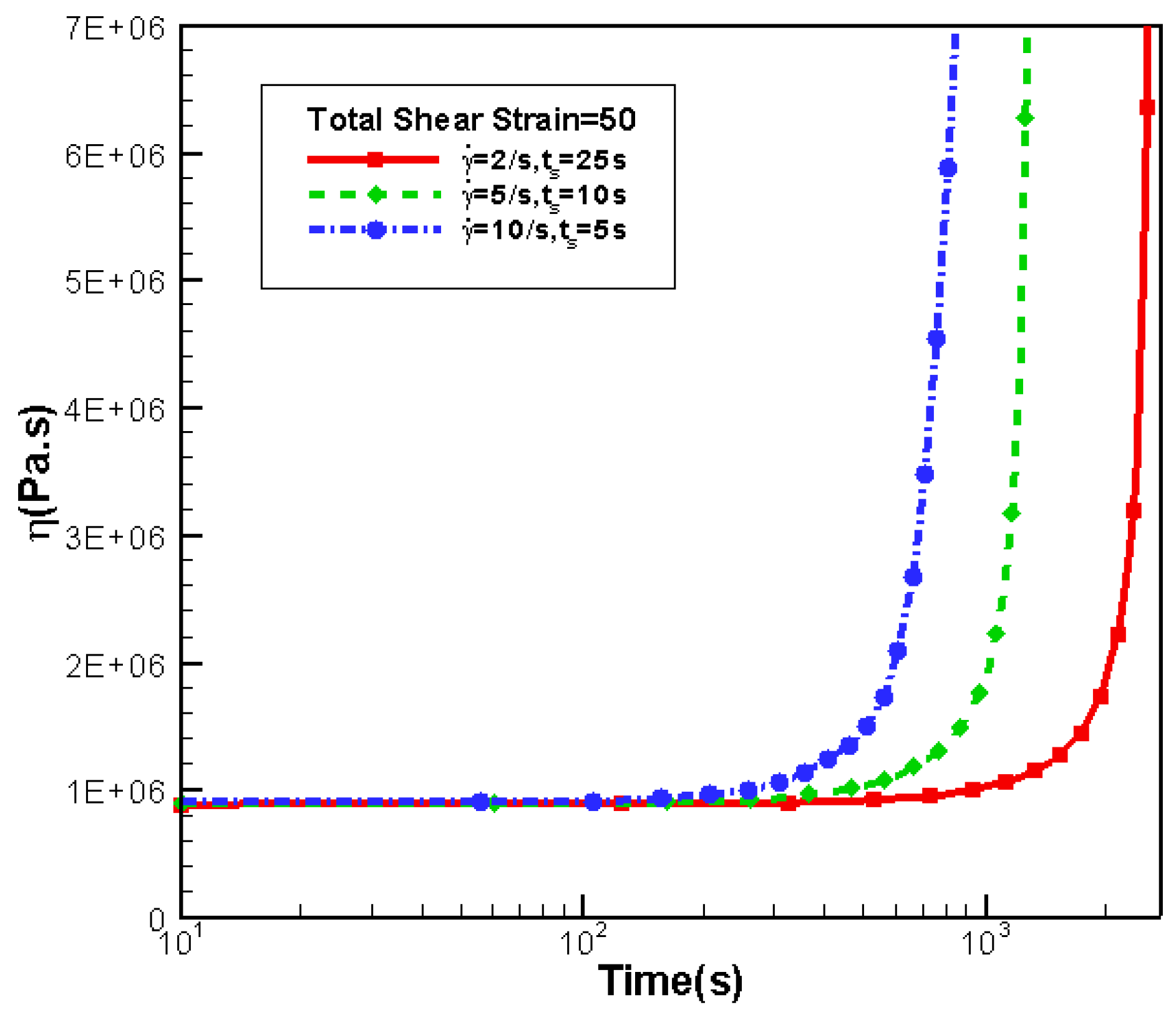
3.5. Effects of Shear Strain
3.5.1. Effects of Shear Strain on Crystallization
3.5.2. Effects of Shear Strain on Rheology
4. Conclusions
- (1)
- The evolution model and Monte Carlo method established are effective and reliable. With the evolution model and Monte Carlo algorithm, we obtain reliable crystallization kinetics and detailed crystal morphology.
- (2)
- Effects of shear rate, shear time and shear strain on crystallization and rheology obtained here is in agreement with other numerical work and experimental results. We show the great influence of shear rate and shear time on the crystallization kinetics, crystal morphology and rheology of the system. In a higher shear rate or longer shear time case, the contribution of shish-kebabs to both crystallization kinetics and morphology becomes more significant and the sudden increase of viscosity occurs earlier. Under the same shear strain, the case with higher shear rate and shorter shear time can lead to a quicker crystallization rate and an earlier occurrence of sudden increase of viscosity.
Acknowledgments
Conflicts of Interest
References
- Eder, G.; Janeschitz-Kriegl, H. Materials Science and Technology; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Zheng, R.; Tanner, R.I.; Fan, X.J. Injection Molding: Integration of Theory and Modeling Methods; Springer: Berlin, Germany, 2011. [Google Scholar]
- Pantanin, R.; Coccorullo, I.; Speranza, V.; Titomanlio, G. Modeling of morphology evolution in the injection molding process of thermoplastic polymers. Prog. Polym. Sci. 2005, 30, 1185–1222. [Google Scholar] [CrossRef]
- Doufas, A.K.; Mchugh, A.J.; Miller, C. Simulation of melt spinning including flow-induced crystallization. Part 1. Model development and predictions. J. Non-Newtonian Fluid Mech. 2000, 92, 27–66. [Google Scholar] [CrossRef]
- Tanner, R.I. A suspension model for low shear rate polymer solidification. J. Non-Newtonian Fluid Mech. 2002, 102, 397–408. [Google Scholar] [CrossRef]
- Ziabicki, A.; Janecki, L.; Sorrentino, A. The role of flow-induced crystallization in melt spinning. e-Ploymers 2004, 4, 823–836. [Google Scholar]
- Koscher, E.; Fulchiron, R. Influence of shear on polypropylene crystallization: Morphology development and kinetics. Polymer 2002, 43, 6931–6942. [Google Scholar] [CrossRef]
- Zheng, R.; Kennedy, P.K. A model for post-flow induced crystallization: General equations and predictions. J. Rheol. 2004, 48, 823–842. [Google Scholar] [CrossRef]
- Schneider, W.; Koppl, A.; Berger, J. Non-isothermal crystallization of polymers. Int. Polym. Process 1988, 3, 151–154. [Google Scholar]
- Zuidema, H.; Peters, G.W.M.; Meijer, H.E.H. Development and validation of a recoverable strain-based model for flow induced crystallization of polymers. Macromol. Theory Simul. 2001, 10, 447–460. [Google Scholar] [CrossRef]
- Boutaous, M.; Bourgin, P.; Zinet, M. Thermally and flow induced crystallization of polymers at low shear rate. J. Non-Newtonian Fluid Mech. 2010, 165, 227–237. [Google Scholar] [CrossRef]
- Raabe, D. Mesoscale simulation of spherulite growth during polymer crystallization by use of a cellular automaton. Acta Mater. 2004, 52, 2653–2664. [Google Scholar] [CrossRef]
- Raabe, D.; Godara, A. Mesoscale simulation of the kinetics and topology of spherulite growth during crystallization of isotactic polypropylene (iPP) by using a cellular automaton. Model. Simul. Mater. Sci. Eng. 2005, 13, 733–751. [Google Scholar] [CrossRef]
- Raabe, D. Simulation of spherulite growth during polymer crystallization by use of a cellular automaton. Mater. Sci. Forum 2004, 467, 603–608. [Google Scholar] [CrossRef]
- Lin, J.X.; Wang, C.Y.; Zheng, Y.Y. Prediction of isothermal crystallization parameters in monomer cast nylon 6. Comput. Chem. Eng. 2008, 32, 3023–3029. [Google Scholar] [CrossRef]
- Spina, R.; Spekowius, M.; Hopmann, C. Multi-scale thermal simulation of polymer crystallization. Int. J. Mater. Form 2015, 8, 497–504. [Google Scholar] [CrossRef]
- Spina, R.; Spekowius, M.; Hopmann, C. Multiphysics simulation of thermoplatic polymer crystallization. Mater. Des. 2016, 95, 455–469. [Google Scholar]
- Liu, Z.J.; Ouyang, J.; Zhou, W.; Wang, X.D. Simulation of polymer crystallization under isothermal and temperature gradient conditions using praticle level set method. Crystals 2016, 6, 90. [Google Scholar] [CrossRef]
- Liu, Z.J.; Ouyang, J.; Ruan, C.; Liu, Q.S. Numerical simulation of the polymer crystallization during cooling stage by using level set method. Comput. Mater. Sci 2015, 97, 245–253. [Google Scholar] [CrossRef]
- Micheletti, A.; Burger, M. Stochastic and deterministic simulation of nonisothermal crystallization of polymers. J. Math. Chem. 2001, 30, 169–193. [Google Scholar] [CrossRef]
- Ruan, C. Multiscale numerical study of 3D polymer crystallization during cooling stage. Math. Probl. Eng. 2012, 2012, 802420. [Google Scholar] [CrossRef]
- Ruan, C.; Ouyang, J.; Liu, S. Computer modeling of isothermal crystallization in short fiber reinforced composites. Comput. Chem. Eng. 2011, 35, 2306–2317. [Google Scholar] [CrossRef]
- Ketdee, S.; Anantawaraskul, S. Simulation of crystallization kinetics and morphological development during isothermal crystallization of polymers: Effect of number of nuclei and growth rate. Chem. Eng. Commun. 2008, 195, 1315–1327. [Google Scholar] [CrossRef]
- Ruan, C.; Liu, C.; Zheng, G. Monte Carlo simulation for the morphology and kinetics of spherulites and shish-kebabs in isothermal polymer crystallization. Math. Probl. Eng. 2015, 2015, 50624. [Google Scholar] [CrossRef]
- Godara, A.; Raabe, D.; Van Puyvelde, P.; Moldenaers, P. Influence of flow on the global crystallization kinetics of iso-tactic polypropylene. Polym. Test. 2006, 25, 460–469. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Miller, R.L. Kinetics of crystallization from the melt and chain folding in polyethylene fractions revisited: theory and experiment. Polymer 1997, 38, 3151–3212. [Google Scholar] [CrossRef]
- Owens, R.G.; Phillips, T.N. Computational Rheology; Imperial College Press: London, UK, 2002. [Google Scholar]
- Chung, D.H.; Kwon, T.H. Invariant-based optimal fitting closure approximation for the numerical prediction of flow-induced fiber orientation. J. Rheol. 2002, 46, 169–194. [Google Scholar] [CrossRef]
- Tanner, R.I.; Qi, F. A comparison of some models for describing polymer crystallization at low deformation rates. J. Non-Newtonian Fluid Mech. 2005, 127, 131–141. [Google Scholar] [CrossRef]
- Rong, Y.; He, H.P.; Cao, W.; Shen, C.Y.; Chen, J.B. Multi-scale molding and numerical simulation of the flow-induced crystallization. Comput. Mater. Sci 2013, 67, 35–39. [Google Scholar] [CrossRef]


| Variables | Definition | Values | Variables | Definition | Values |
|---|---|---|---|---|---|
| Equation (4) | Equation (12) | ||||
| Equation (4) | Equation (12) | ||||
| Equation (5) | Equation (12) | ||||
| Equation (5) | Equations (11) and (13) | ||||
| Equation (5) | Equation (13) | ||||
| Equation (5) | Equation (13) | ||||
| Equation (5) | Equations (15) and (18) | ||||
| Equation (8) | Equations (15) and (18) | ||||
| Equation (10) | Equations (15) and (18) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, C. Kinetics and Morphology of Flow Induced Polymer Crystallization in 3D Shear Flow Investigated by Monte Carlo Simulation. Crystals 2017, 7, 51. https://doi.org/10.3390/cryst7020051
Ruan C. Kinetics and Morphology of Flow Induced Polymer Crystallization in 3D Shear Flow Investigated by Monte Carlo Simulation. Crystals. 2017; 7(2):51. https://doi.org/10.3390/cryst7020051
Chicago/Turabian StyleRuan, Chunlei. 2017. "Kinetics and Morphology of Flow Induced Polymer Crystallization in 3D Shear Flow Investigated by Monte Carlo Simulation" Crystals 7, no. 2: 51. https://doi.org/10.3390/cryst7020051





