Design of Spin-Frustrated Monomer-Type C60•? Mott Insulator
Abstract
:1. Introduction: Quantum Spin Liquid State
- 1)
- the system has a low spin state (S = 1/2),
- 1)
- the system should be a Mott insulator in ambient conditions,
- 1)
- its Mott insulating state has both a partial CT state close to the itinerant region and a small Mott gap,
- 1)
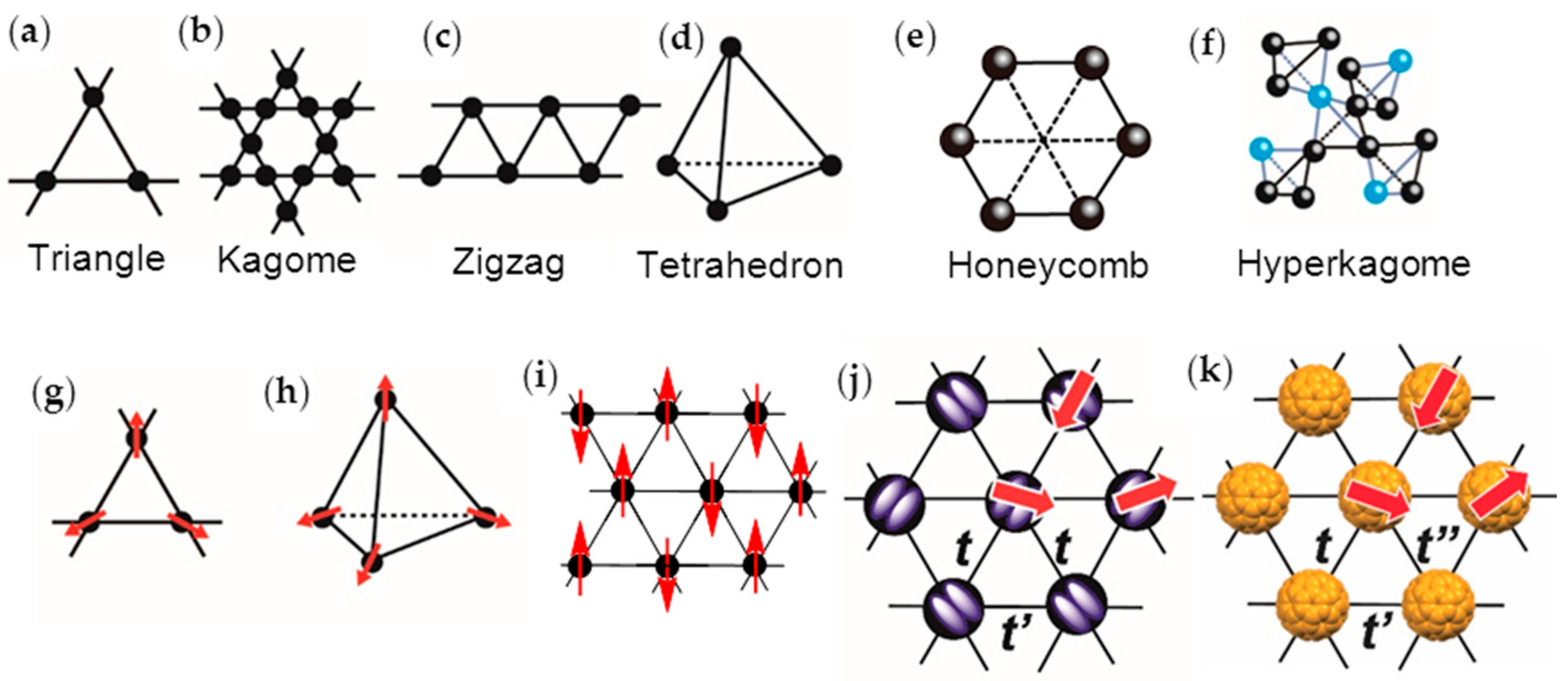
- the spin lattice should have a geometry that affords a strong geometrical frustration, i.e., t′/t ~ 1 for a triangular spin lattice,
- 1)
- a high |ΘCW| or high |J| value to observe the QSL state at the experimentally available temperatures, and
- 1)
- the material must maintain weak energy dispersion along the weakest direction for the magnetic interactions of the 2D system, i.e., negligibly weak magnetic interaction perpendicular to the 2D magnetic layer in order to keep the geometry of spin-frustrated spin lattice down to low temperatures.
2. Characteristic Features of C60: Superconductors and Other Functions for C60 Charge-Transfer Materials
3. Requirements for Spin-Frustrated Spin Lattice of C60•−
3.1. Competition among Bond-Formation, Itinerancy, Localization, and Frustration in Fulleride Solids
- (I)
- existence of C60•− or low-spin state of C603− (S = 1/2),
- (II)
- no polymerization between C60 molecules,
- (III)
- triangular or hexagonal packing of C60 with equal interfullerene distance r, or t′/t ~ 1, and
- (IV)
- strong AF interactions.
3.2. Charged State of C60 and Effective On-Site Coulomb Repulsion
3.3. Packing of C60 and Magnetic Interactions in Fulleride Solids
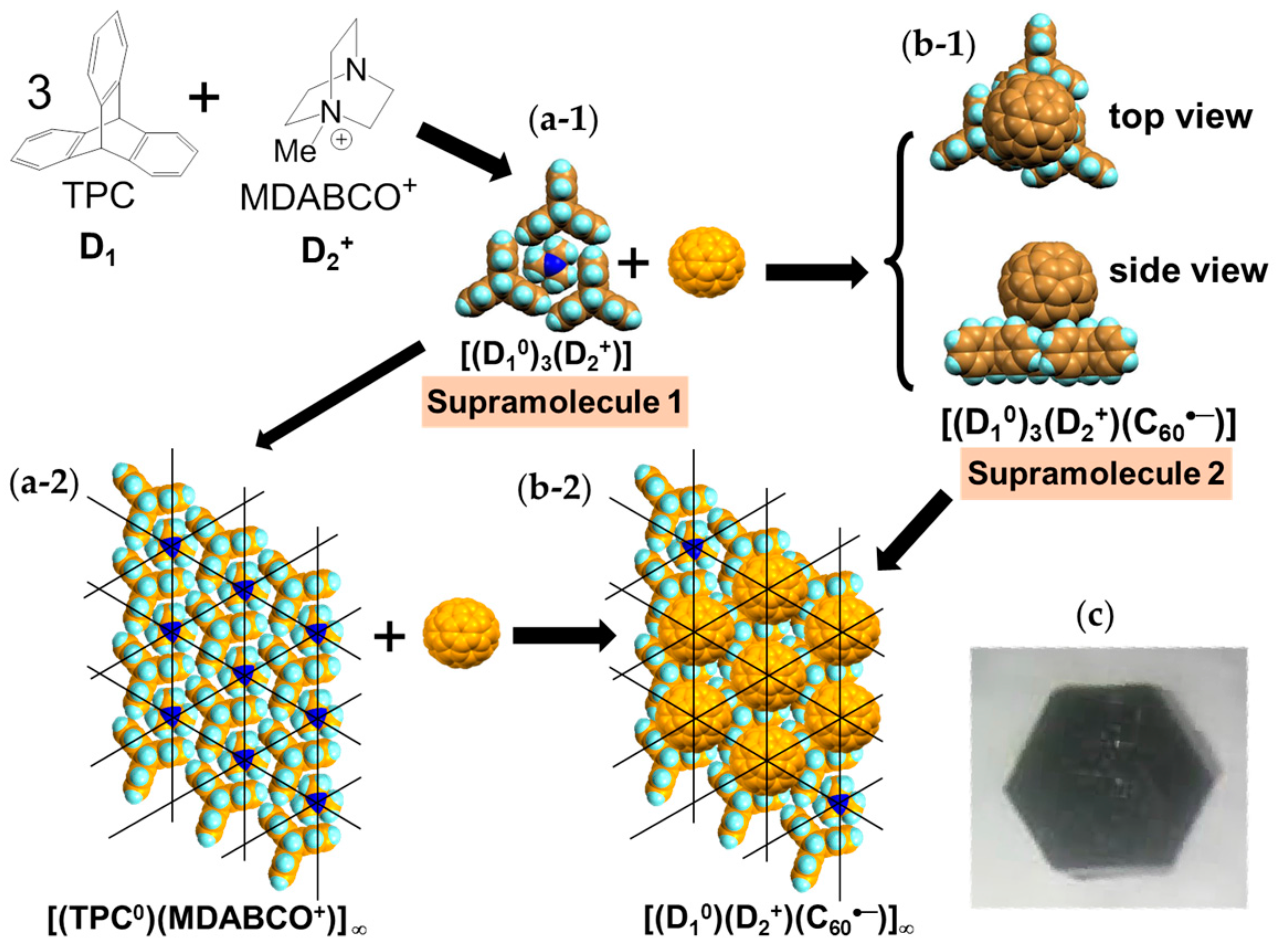
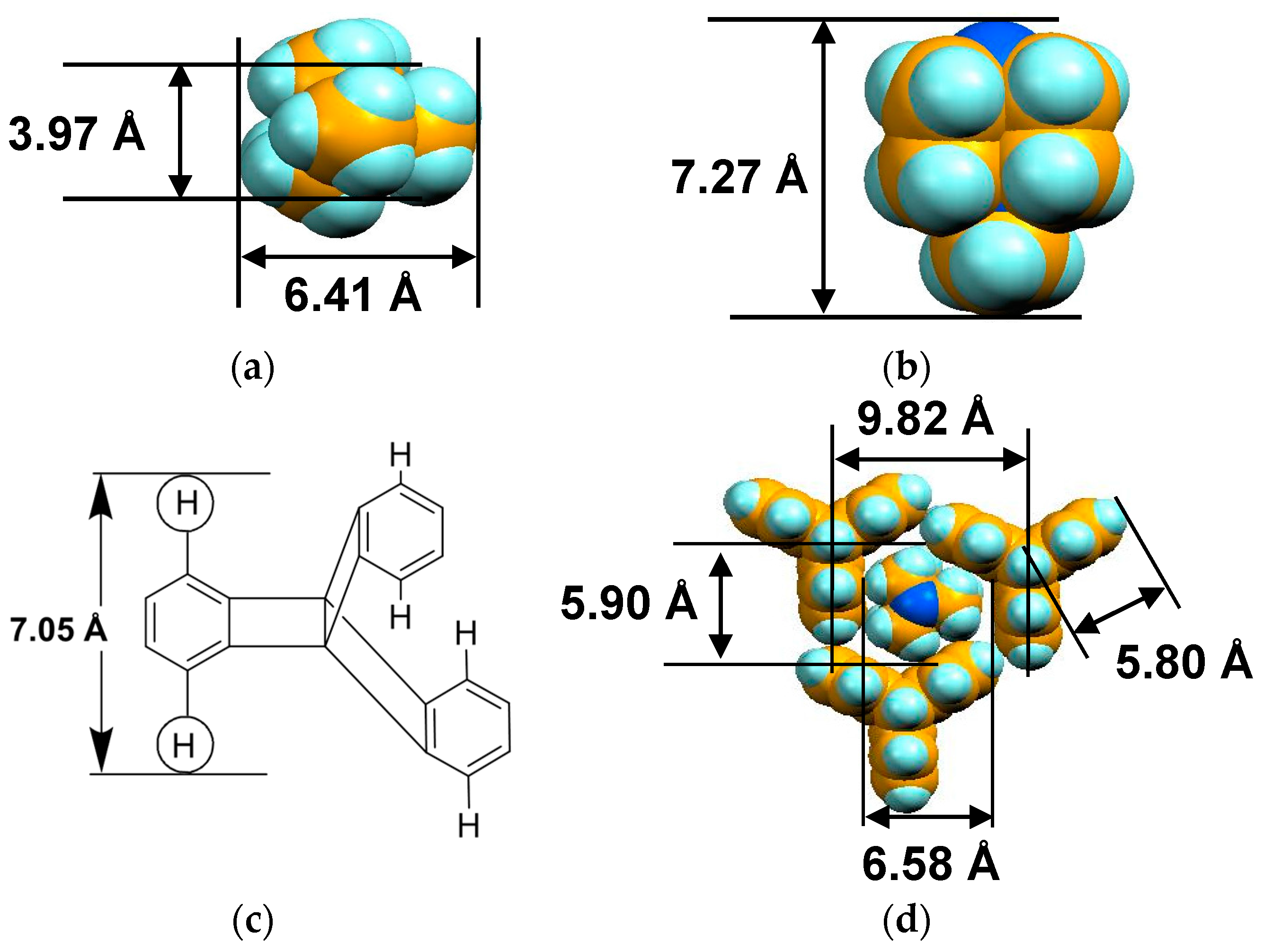
3.4. Requirements for Triangular or Hexagonal Packing of C60•− by Key-Keyhole Relation: 2D or 3D Polycationic Template
4. Key-Keyhole Relations in C60•− Charge-Transfer Solids
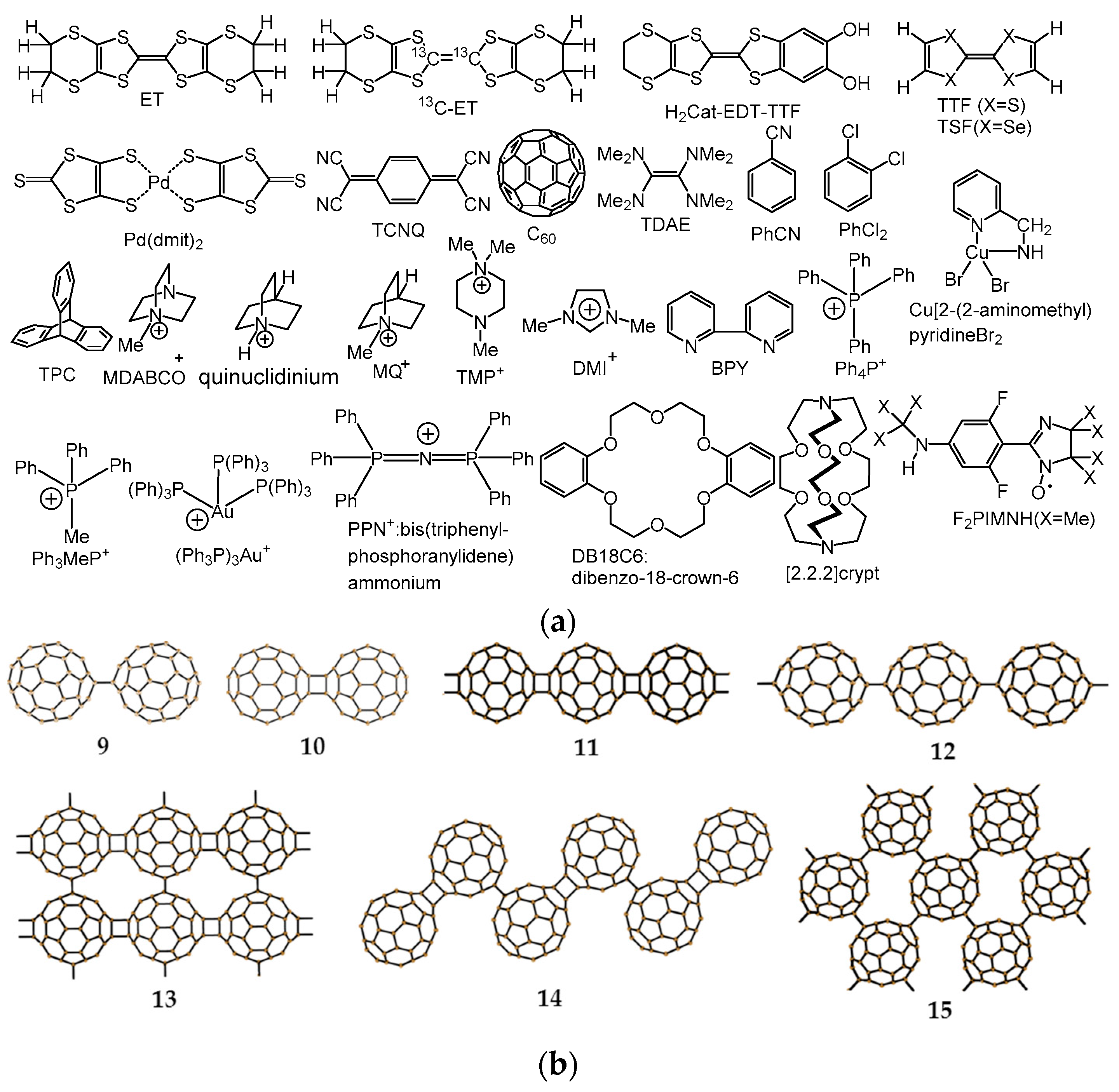
4.1. Three-Component Materials
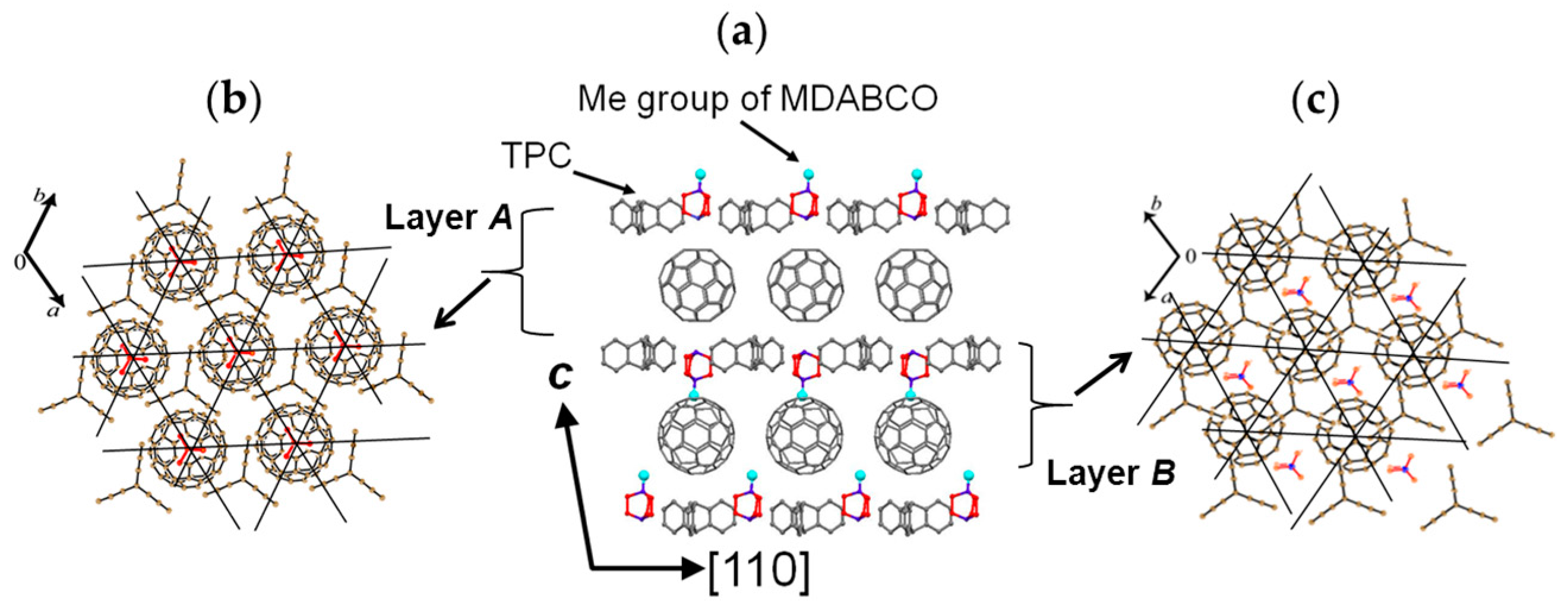
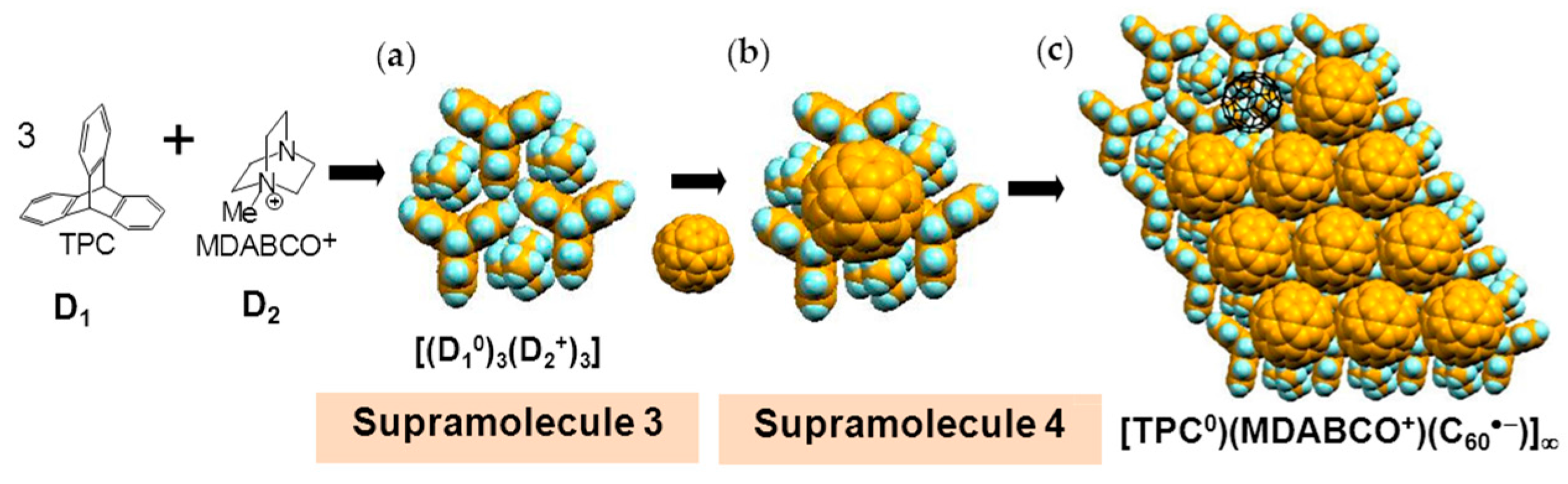
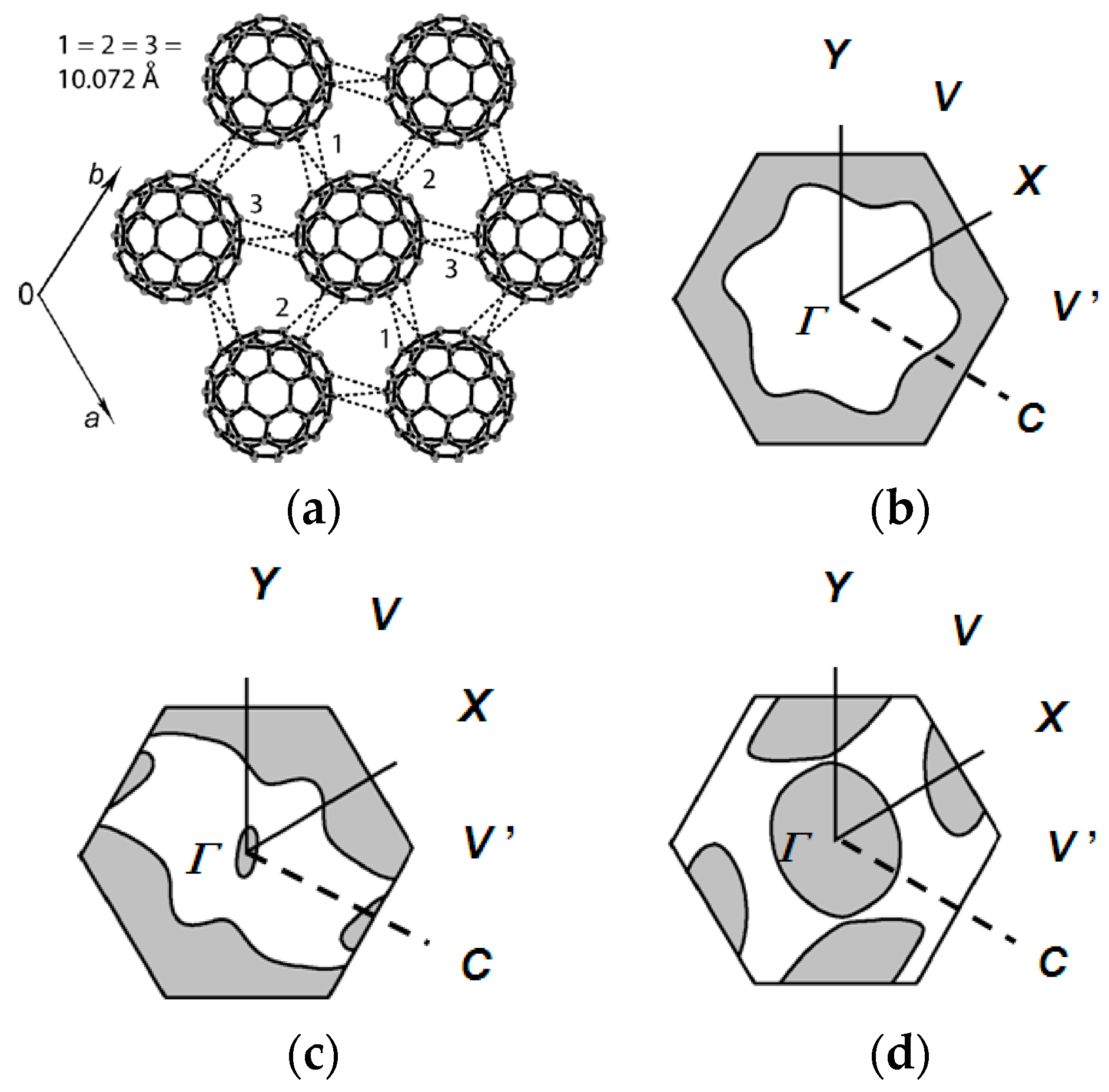
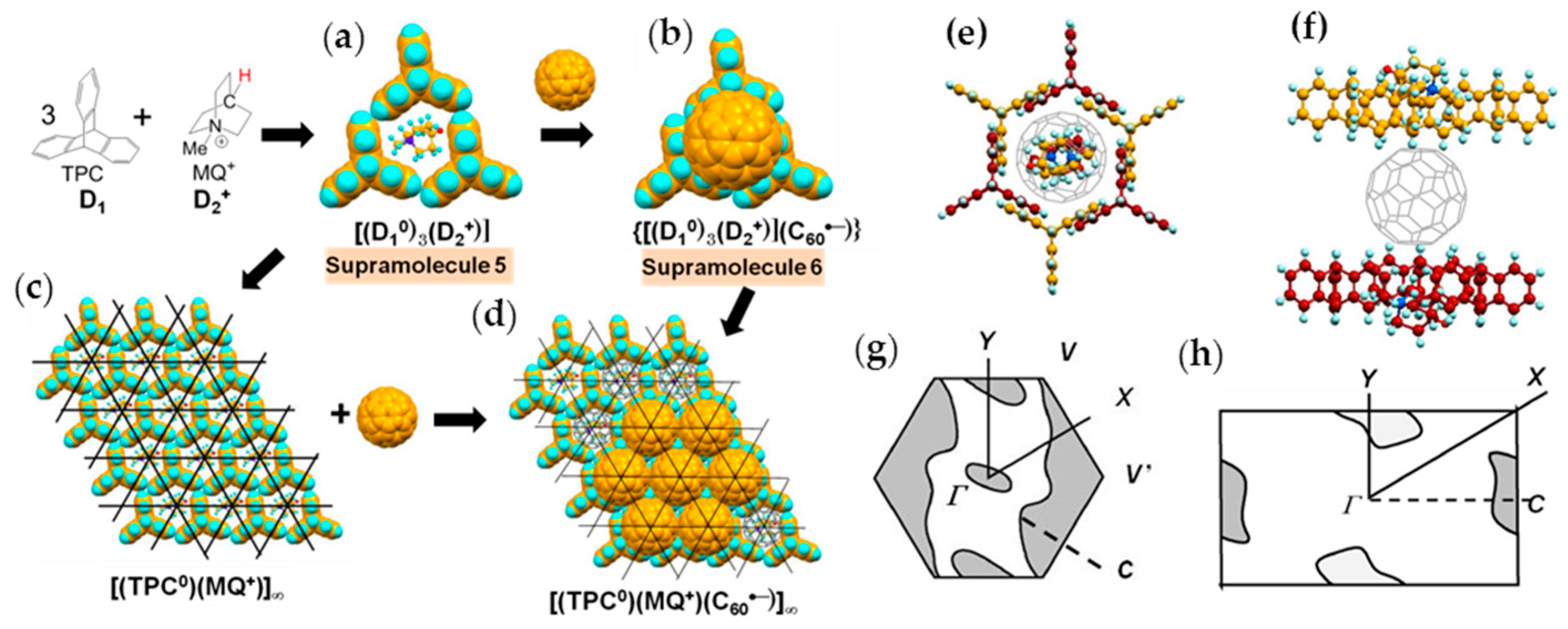
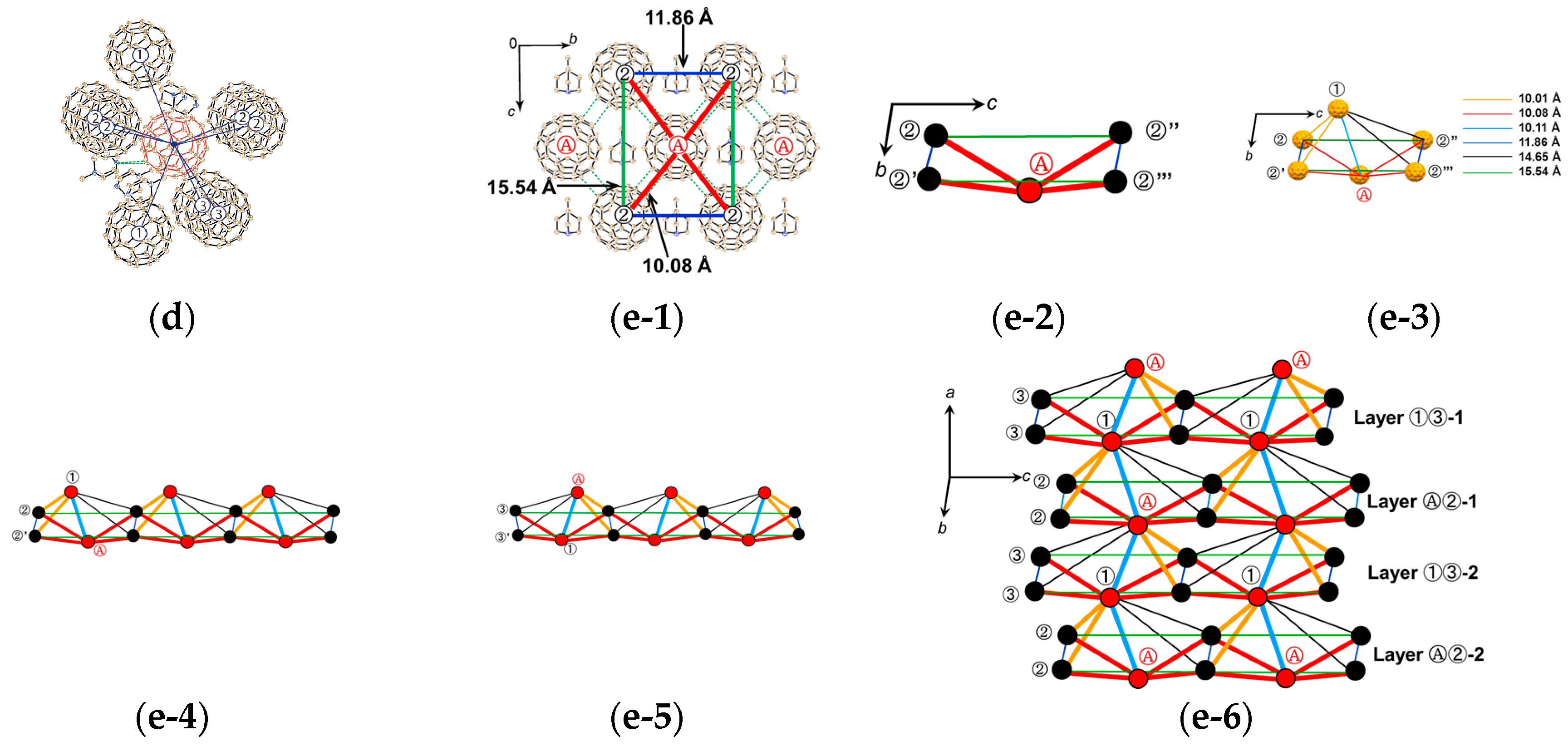
4.1.1. Coexistence of Itinerant and Frustrated Spins in 2D Hexagonal Packing of C60•− in (TPC0)(MDABCO+)(C60•−)
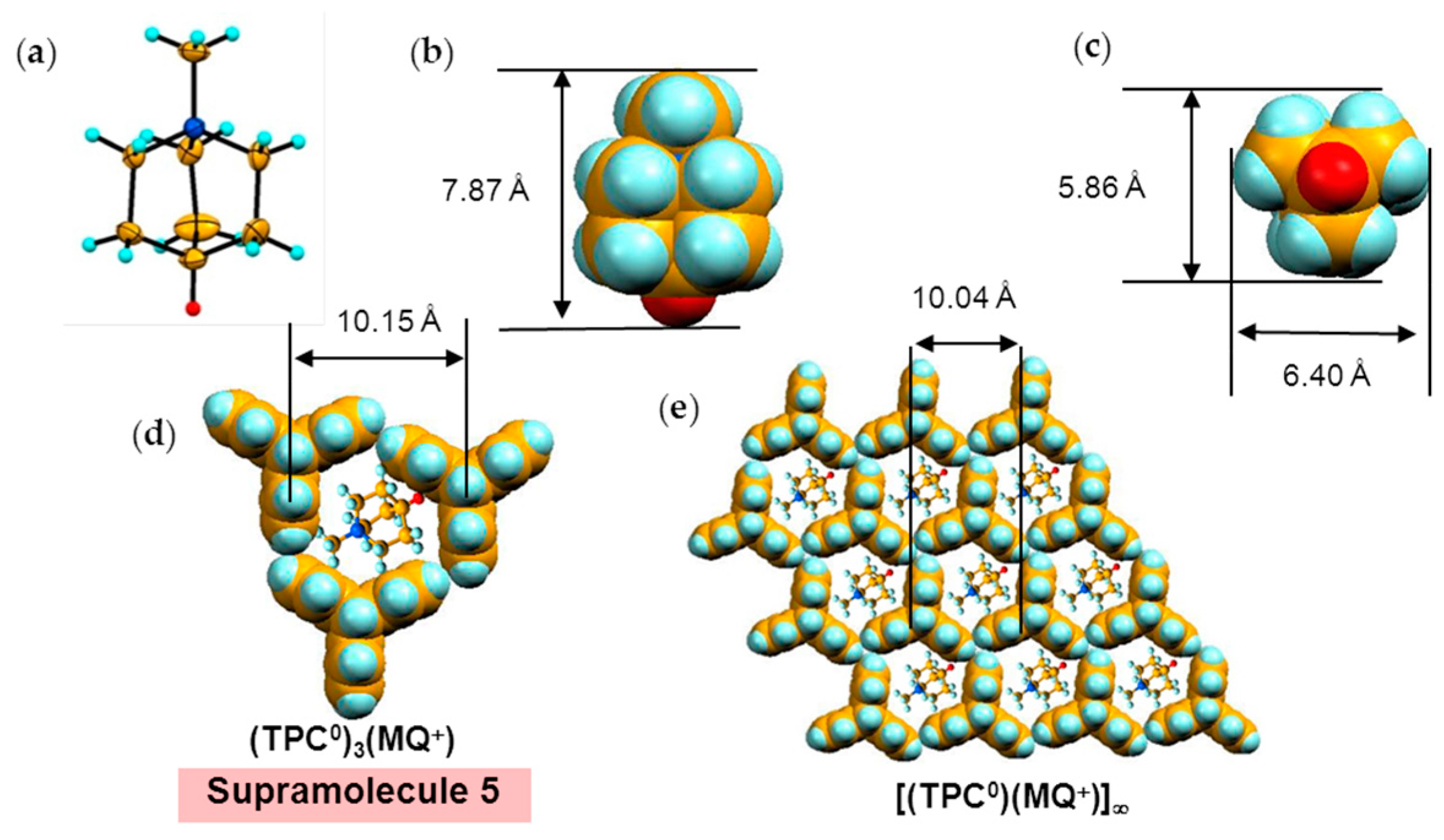
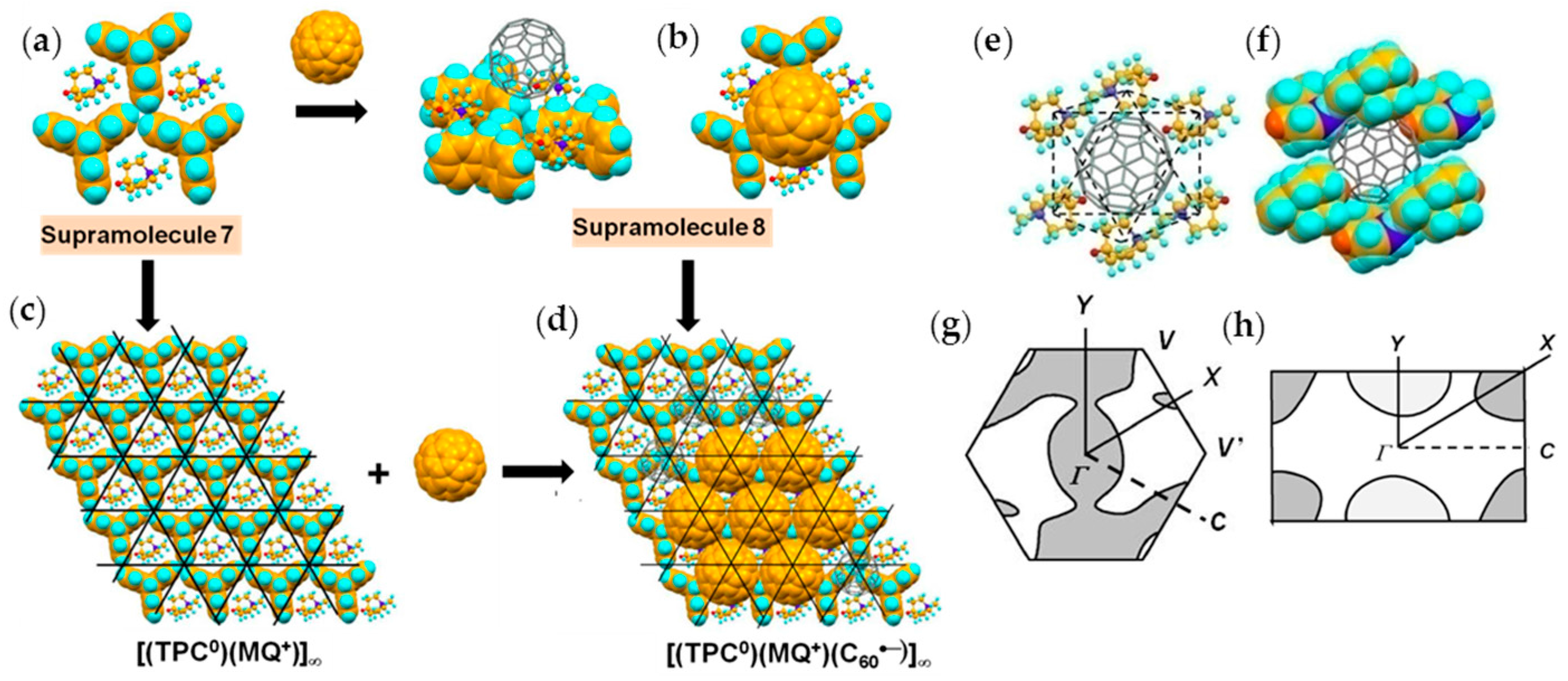
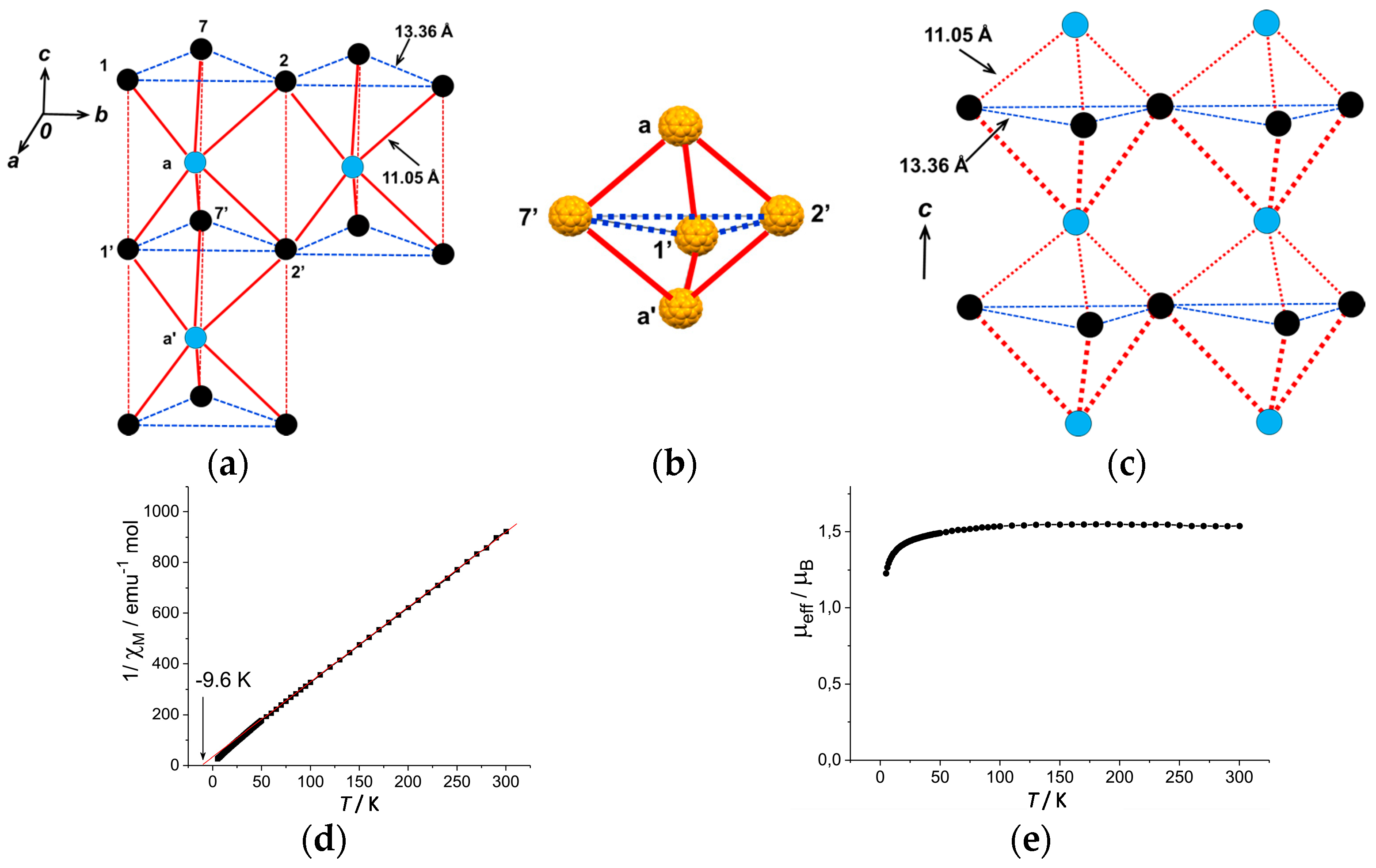
4.1.2. Only Frustrated Spins in 2D Hexagonal Packing of C60•− in (TPC0)(MQ+)(C60•−)
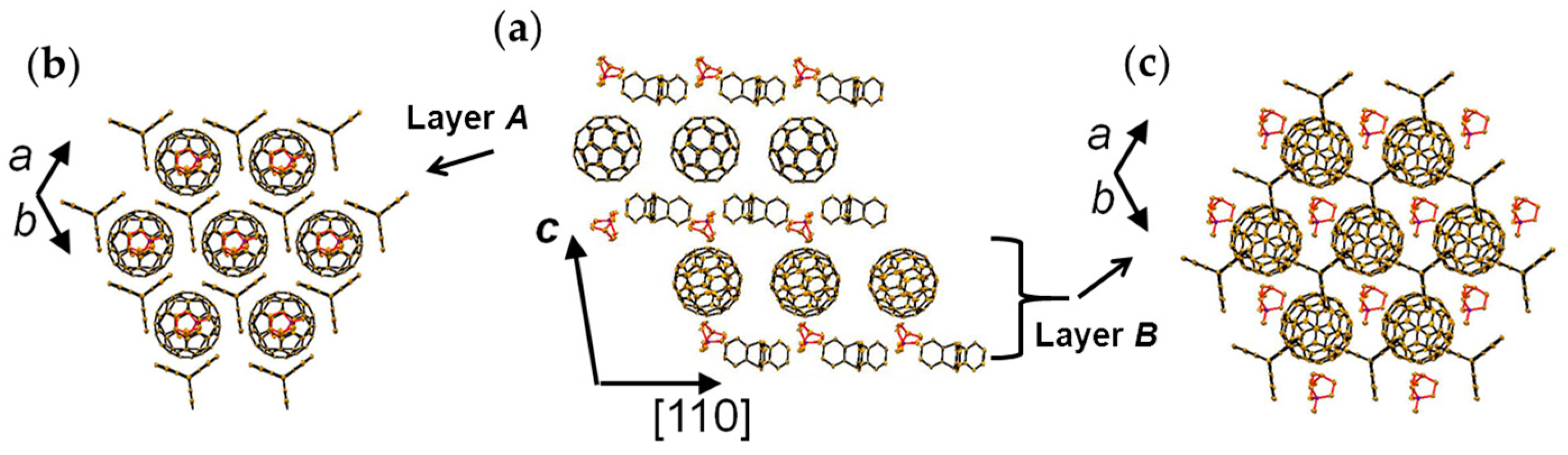
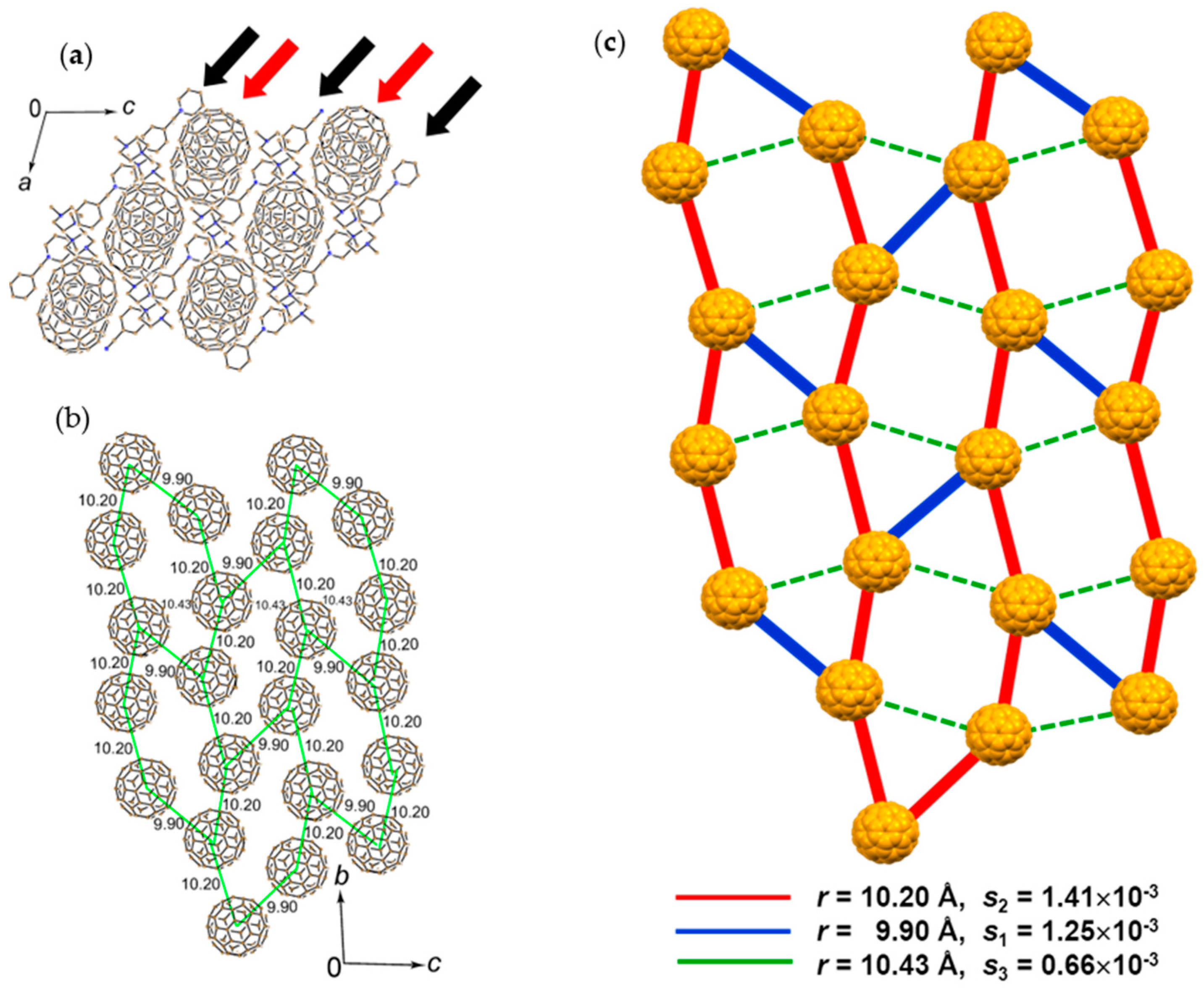
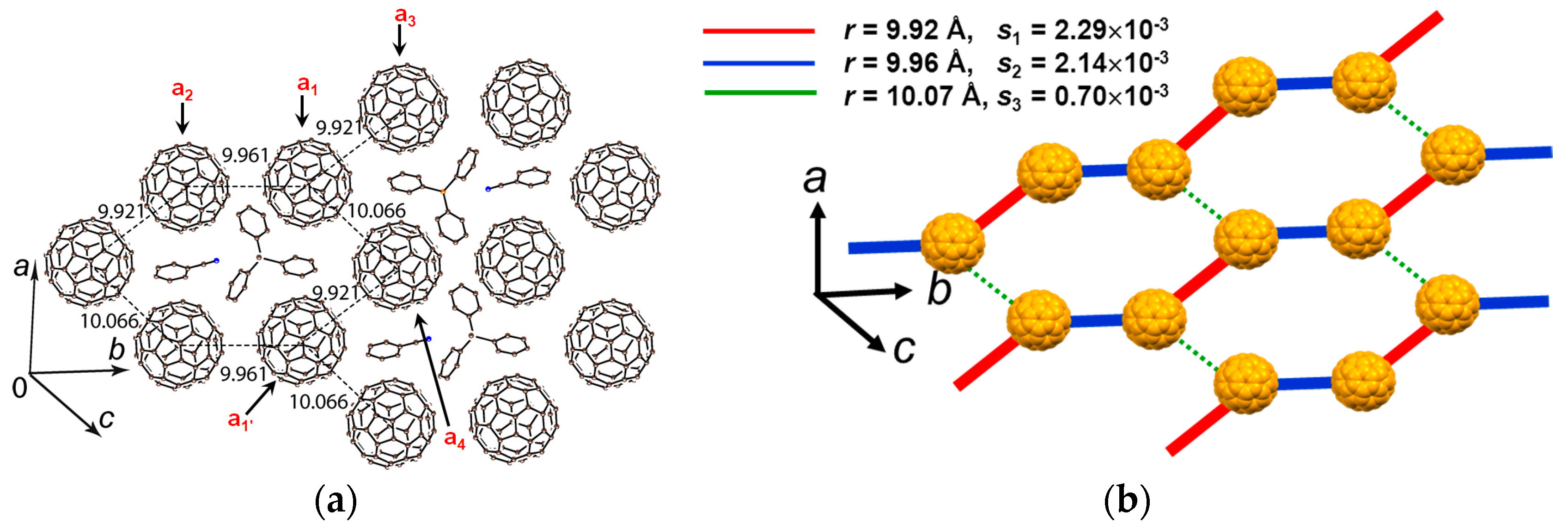
4.1.3. Distorted Hexagonal Packing of C60•− in (PhCN0)(TMP+)(C60•−), (PhCN0)(Ph3MeP+)(C60•−), and (PhCl20)[(Ph3P)3Au+]2(C60•−)2(C60)
(PhCN0)(TMP+)(C60•−)
(PhCN0)(Ph3MeP+)(C60•−)
(PhCl20){(Ph3P)3Au+}2(C60•−)2(C60)
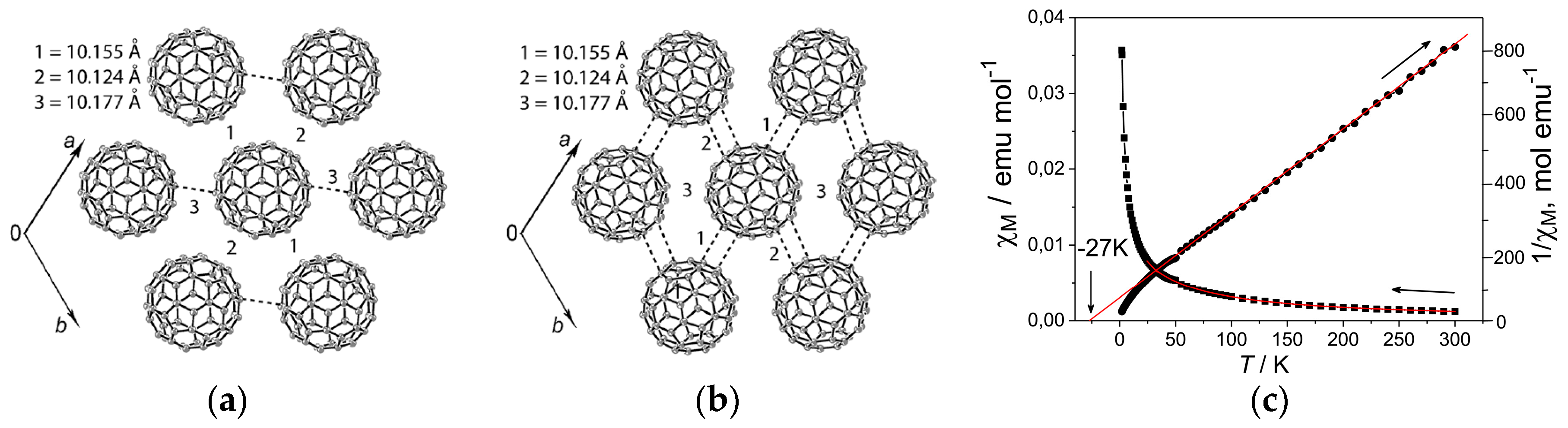
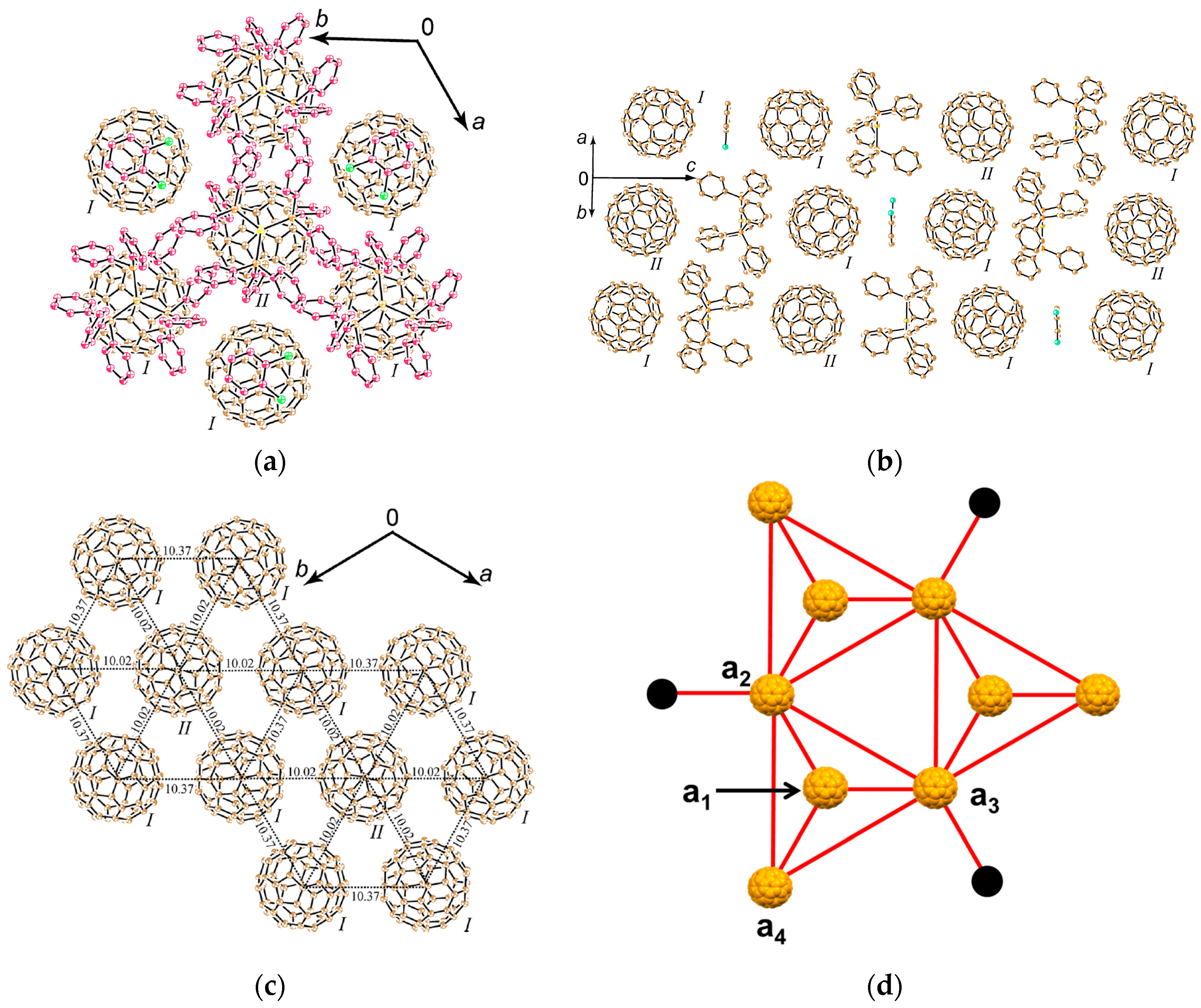
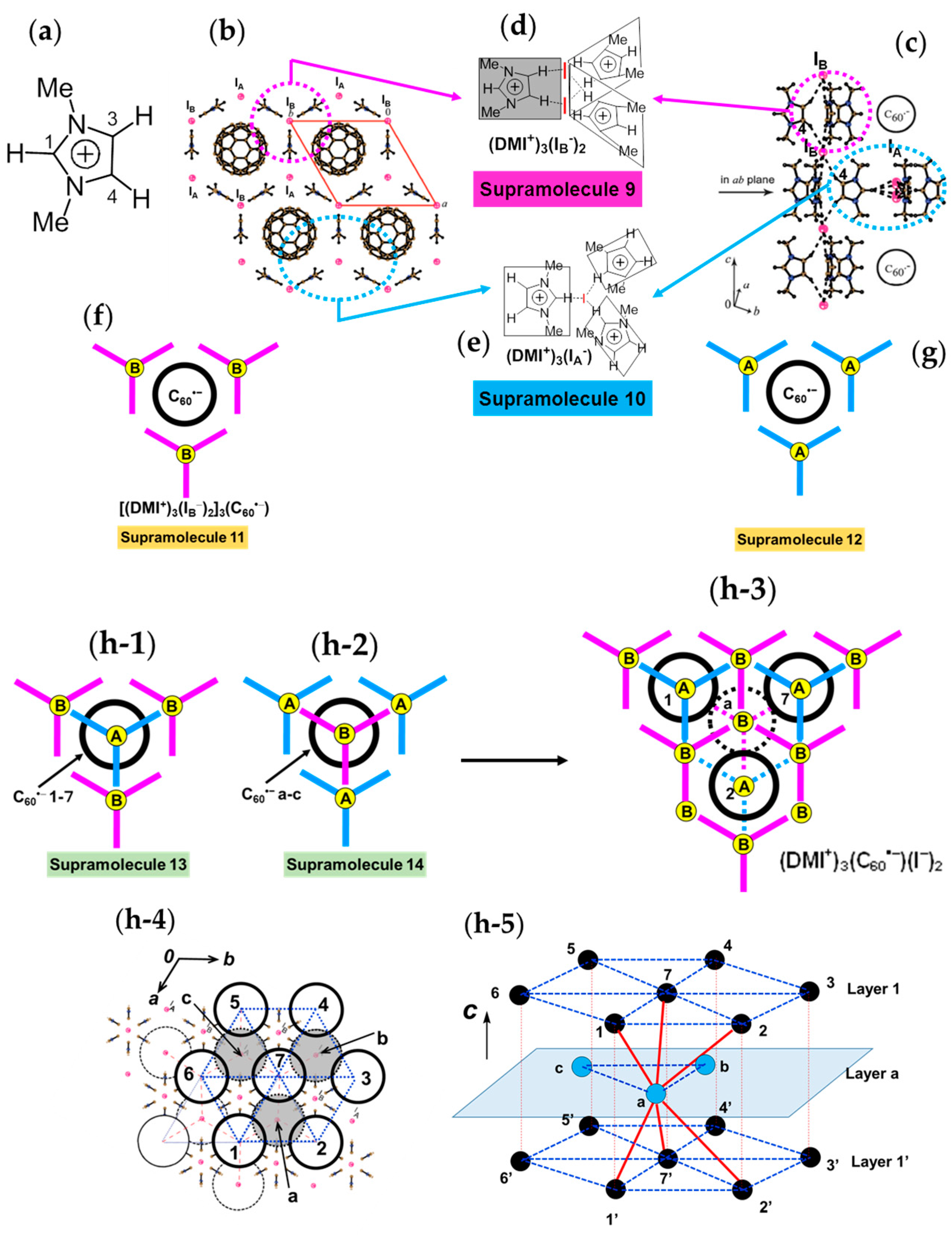
4.1.4. Frustrated Spins in 3D Hexagonal Packing of C60•− in (DMI+)3(C60•−)(I−)2
4.2. Two-Component Materials
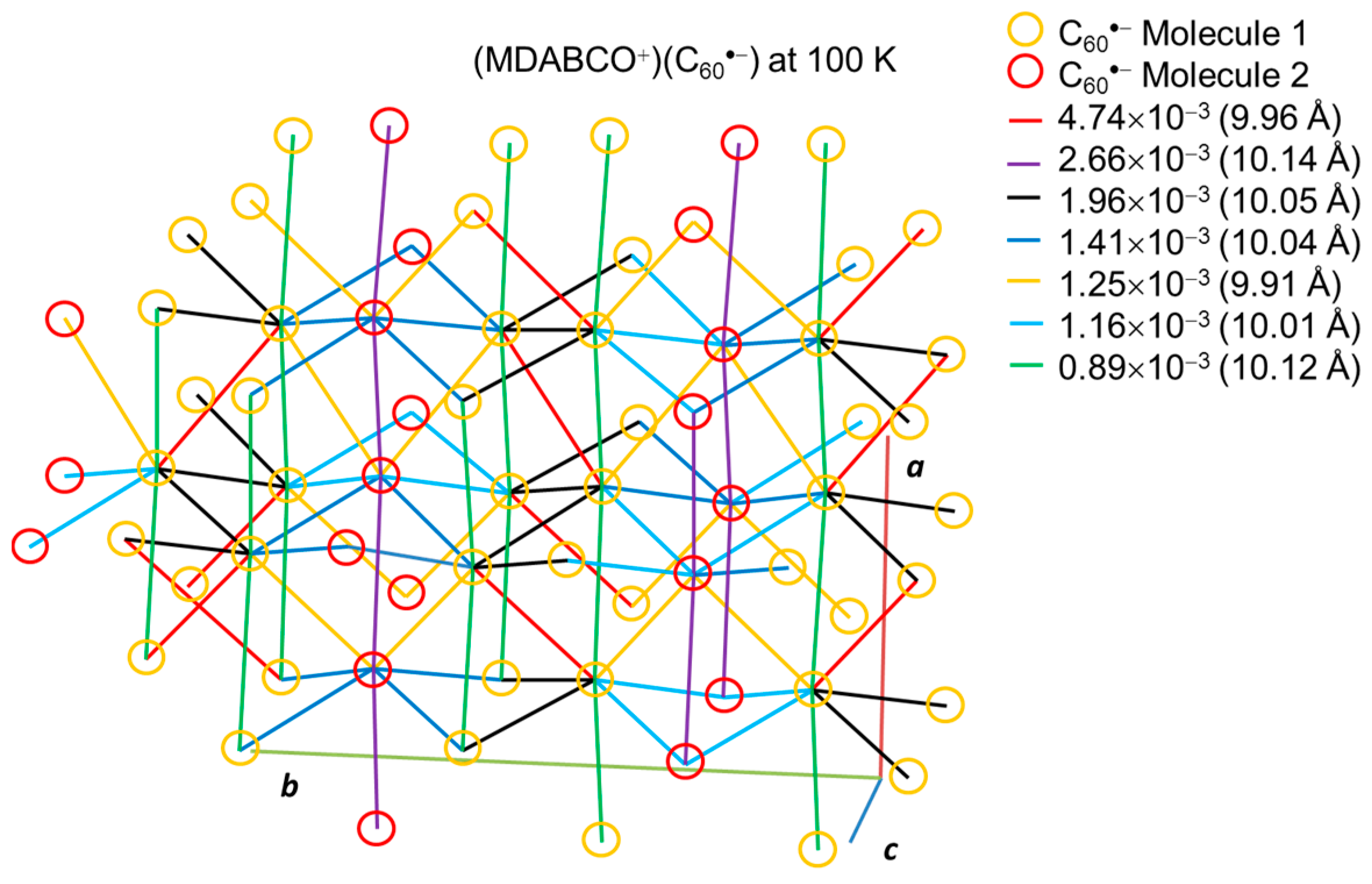
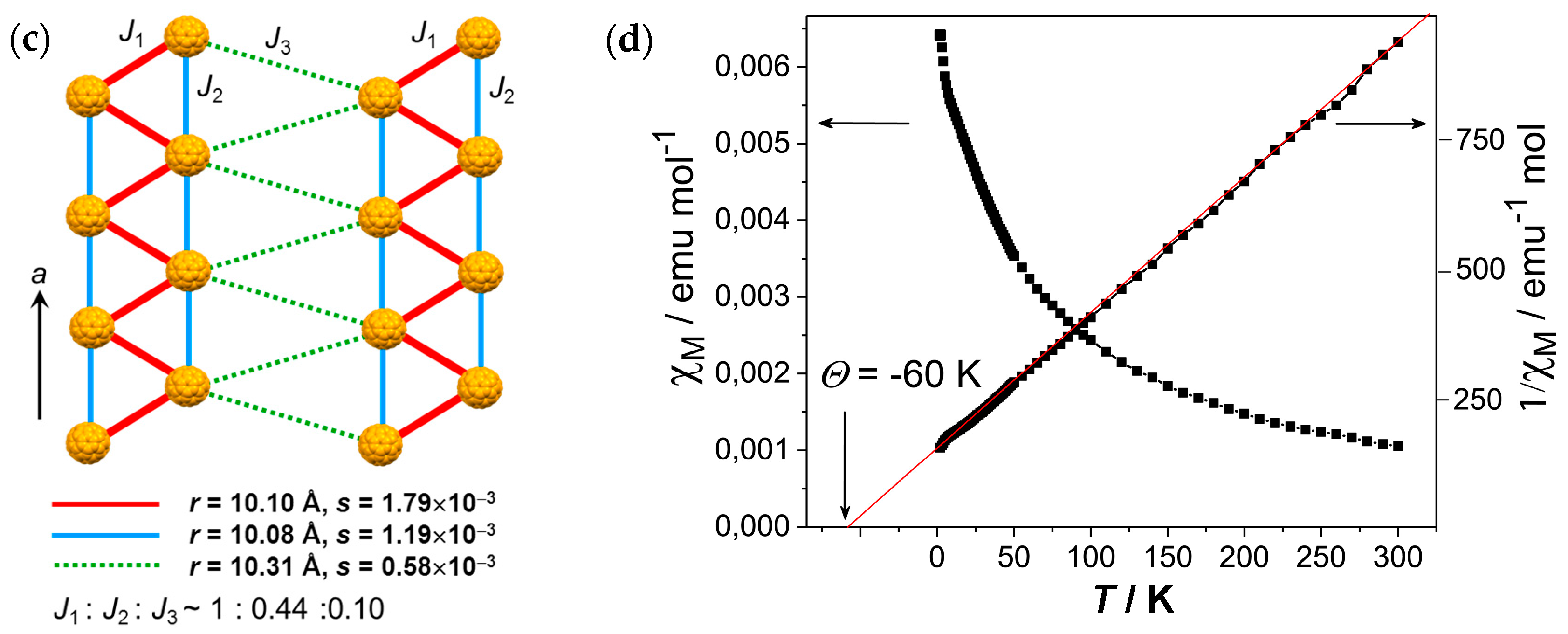
4.2.1. Frustrated Spins in 3D Corrugated Packing of C60•− in (MDABCO+)(C60•−) 3D Spin Lattice
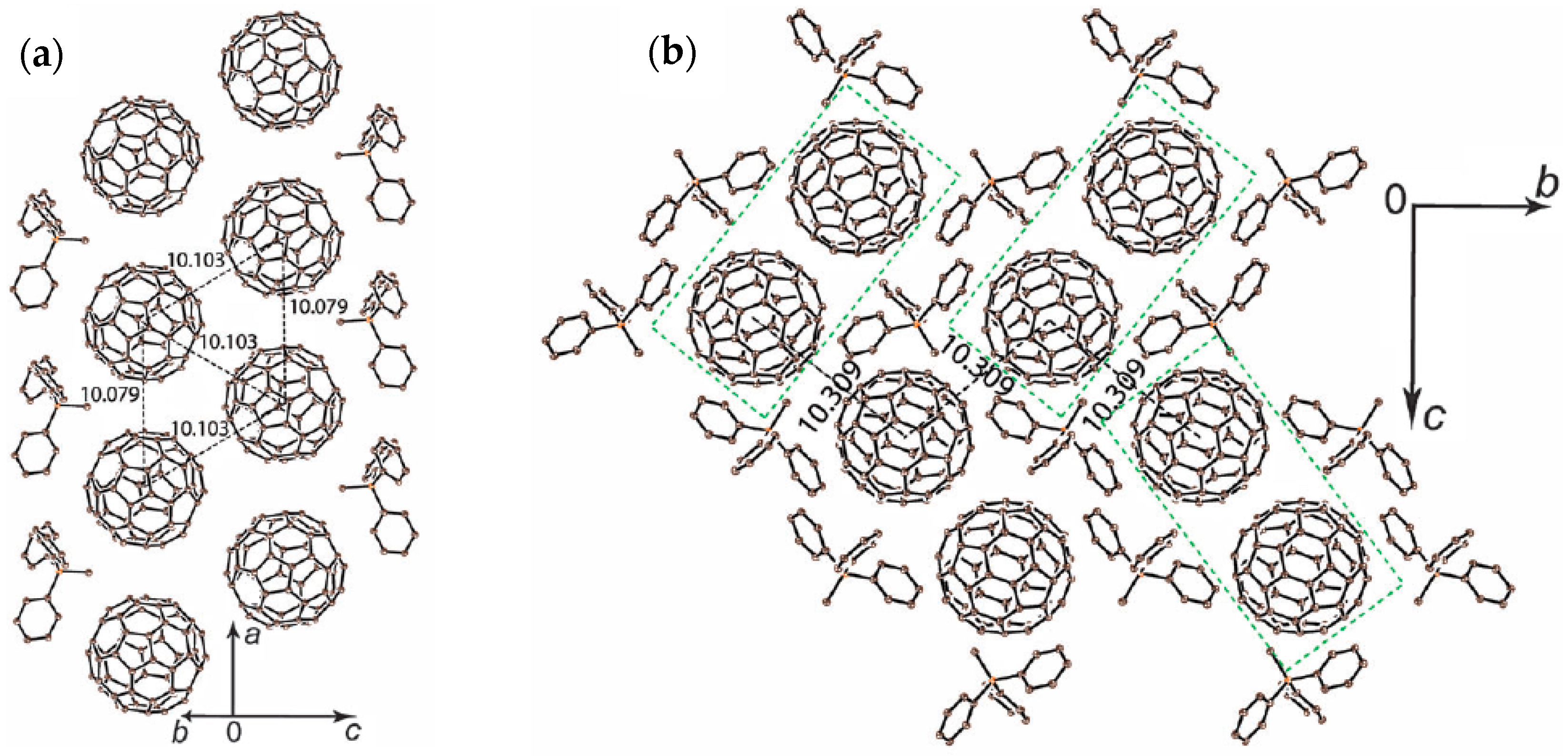
4.2.2. Frustrated Spins in Double Chains of Triangles from C60•− in (Ph3MeP+)(C60•−): Weakly Coupled Zigzag Chains
5. Summary
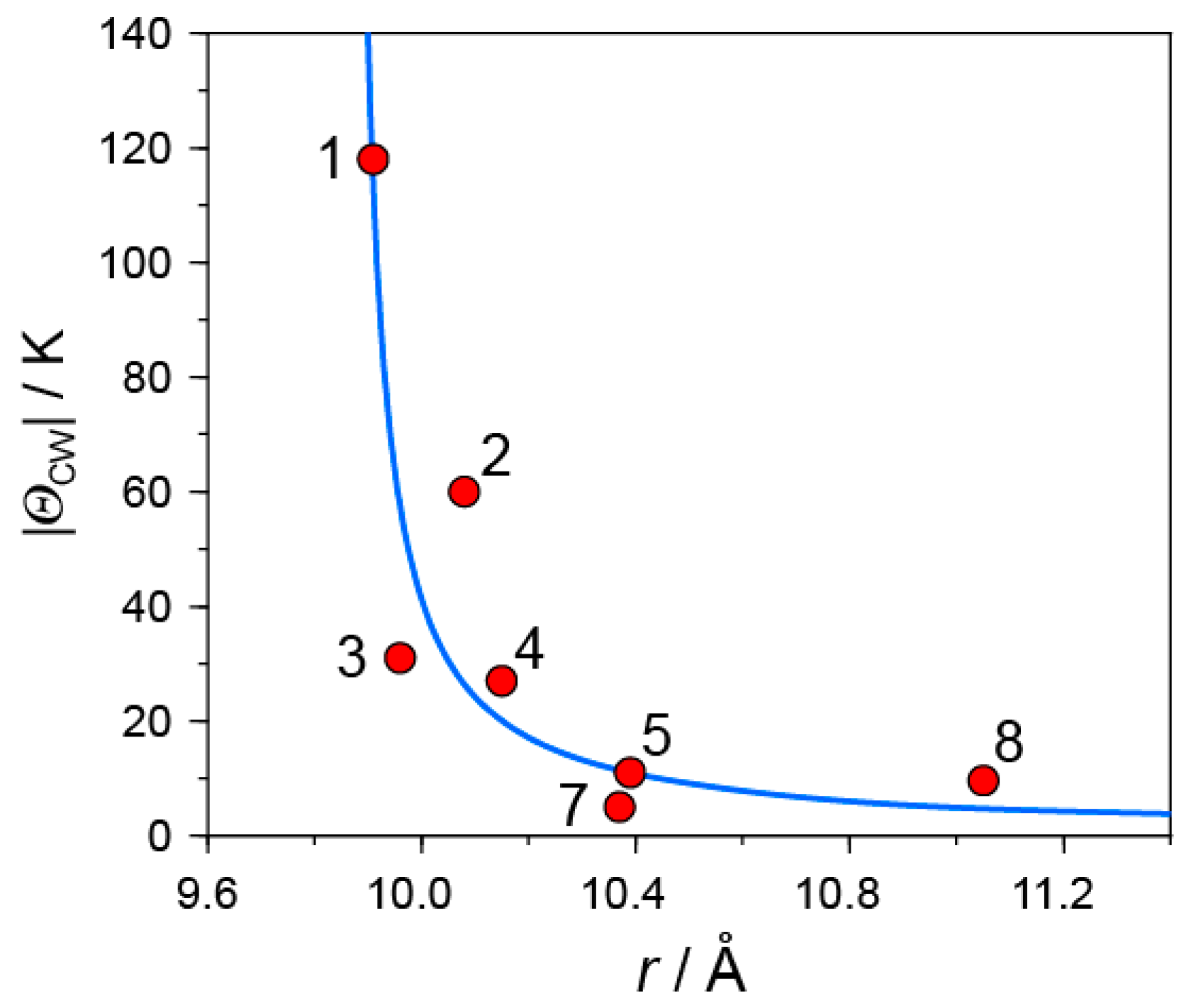
- |ΘCW| seems to increase rapidly when r < 10 Å and magnetic dimensionality is 3D. Such low values of r were realized for two-component CT solids with cation molecules of small size with threefold symmetry. However, it is difficult to find a good key-keyhole relation to provide uniform triangular or hexagonal packing of C60•− for the two-component case. Furthermore, single crystals of CT solids were not always obtainable. For example, a quinuclidinium cation, which is smaller than MDABCO+ and MQ+, gave no CT solids so far.
- The cationic supramolecular template with threefold symmetry leads to uniform triangular or hexagonal packing of C60•− for three-component case based on the key-keyhole relation. For three-component case, it is critical to decrease the r value and increase the magnetic dimensionality.
Acknowledgments
Conflicts of Interest
References
- Anderson, P.W. Resonating valence bonds: A new kind of insulator? Mater. Res. Bull. 1973, 8, 153–160. [Google Scholar] [CrossRef]
- Fazekas, P.; Anderson, P.W. On the ground state properties of the anisotropic triangular antiferromagnet. Philos. Mag. 1974, 30, 423–440. [Google Scholar] [CrossRef]
- Wannier, G.H. Antiferromagnetism. The triangular ising net. Phys. Rev. 1950, 79, 357–364. [Google Scholar] [CrossRef]
- Greedan, J.E. Geometrically frustrated magnetic materials. J. Mater. Chem. 2001, 11, 37–53. [Google Scholar] [CrossRef]
- Anderson, P.W. Ordering and antiferromagnetism in ferrites. Phys. Rev. 1956, 102, 1008–1013. [Google Scholar] [CrossRef]
- Hirakawa, K.; Yoshizawa, H.; Ubukoshi, K. Magnetic and neutron scattering study of one-dimensional heisenberg antiferromagnet CsVCl3. J. Phys. Soc. Jpn. 1982, 51, 1119–1122. [Google Scholar] [CrossRef]
- Ferey, G.; De Pape, R.; Leblanc, M.; Pannetier, J. Ordered magnetic frustration: VIII. Crystal and magnetic structures of the pyrochlore form of iron trifluoride between 2.5 and 25 K from powder neutron diffraction. Comparison with the other varieties of FeF3. Rev. Chim. Miner. 1986, 23, 474–484. [Google Scholar]
- Huse, D.; Elser, V. Simple variational wave functions for two-dimensional heisenberg spin-1/2 antiferromagnets. Phys. Rev. Lett. 1988, 60, 2531–2534. [Google Scholar] [CrossRef] [PubMed]
- Tocchio, L.F.; Gros, C.; Valentif, R.; Becca, F. One-dimensional spin liquid, collinear, and spiral phases from uncoupled chains to the triangular lattice. Phys. Rev. B 2014, 89, 235107. [Google Scholar] [CrossRef]
- Yamada, A. Magnetic properties and Mott transition in the Hubbard model on the anisotropic triangular lattice. Phys. Rev. B 2014, 89, 195108. [Google Scholar] [CrossRef]
- Yamada, A. Magnetic properties and Mott transition of the Hubbard model for weakly coupled chains on the anisotropic triangular lattice. Phys. Rev. B 2014, 90, 235138. [Google Scholar] [CrossRef]
- Konarev, D.V.; Khasanov, S.S.; Otsuka, A.; Maesato, M.; Uruichi, M.; Yakushi, K.; Shevchun, A.F.; Yamochi, H.; Saito, G.; Lyubovskaya, R.N. Metallic and Mott insulating spin-frustrated antiferromagnetic states in ionic fullerene complexes with a two-dimensional hexagonal C60•− packing motif. Chem. Eur. J. 2014, 20, 7268–7277. [Google Scholar] [CrossRef] [PubMed]
- Ramirez, A.P. strongly geometrically frustrated magnets. Annu. Rev. Mater. Sci. 1994, 24, 453–480. [Google Scholar] [CrossRef]
- Schiffer, P.; Ramirez, A.P. Recent experimental progress in the study of geometrical magnetic frustration. Comments Condens. Matter Phys. 1996, 18, 21–50. [Google Scholar]
- Hirakawa, K.; Kadowaki, H.; Ubukoshi, K. Study of frustration effects in two-dimensional triangular lattice antiferromagnets-neutron powder diffraction study of VX2, X≡Cl, Br and I. J. Phys. Soc. Jpn. 1983, 52, 1814–1824. [Google Scholar] [CrossRef]
- Ajiro, Y.; Asano, T.; Takagi, T.; Mekata, M.; Katori, H.A.; Goto, T. High-field magnetization process in the triangular lattice antiferromagnet CuFeO2 up to 100 T. Physica B 1994, 201, 71–74. [Google Scholar] [CrossRef]
- Kimura, T.; Lashley, J.C.; Ramirez, A.P. Inversion-symmetry breaking in the noncollinear magnetic phase of the triangular-lattice antiferromagnet CuFeO2. Phys. Rev. B 2006, 73, 220401. [Google Scholar] [CrossRef]
- Mitamura, H.; Mitsuda, S.; Kanetsuki, S.; Katori, H.A.; Sakakibara, T.; Kindo, K. Dielectric polarization measurements on the antiferromagnetic triangular lattice system CuFeO2 in pulsed high magnetic fields. J. Phys. Soc. Jpn. 2007, 76, 094709. [Google Scholar] [CrossRef]
- Hirakawa, K.; Kadowaki, H.; Ubukoshi, K. Experimental studies of triangular lattice antiferromagnets with S = 1/2: NaTiO2 and LiNiO2. J. Phys. Soc. Jpn. 1985, 54, 3526–3536. [Google Scholar] [CrossRef]
- Tauber, A.; Moller, W.M.; Banks, E. Magnetic ordering in LiCr1−xFexO2. J. Solid State Chem. 1972, 4, 138–152. [Google Scholar] [CrossRef]
- Ajiro, Y.; Kikuchi, H.; Sugiyama, S.; Nakashima, T.; Shamoto, S.; Nakayama, N.; Kiyama, M.; Yamamoto, N.; Oka, Y. Z2 Vortex-induced broadening of the EPR linewidth in the two-dimensional triangular lattice antiferromagnets, HCrO2 and LiCrO2. J. Phys. Soc. Jpn. 1988, 57, 2268–2271. [Google Scholar] [CrossRef]
- Moreno, N.O.; Israel, C.; Pagliuso, P.G.; Garcia-Adeva, A.J.; Rettori, C.; Sarrao, J.L.; Thompson, J.D.; Oseroff, S.B. Magnetic properties of the frustrated antiferromagnet LiCrO2. J. Mag. Mag. Mater. 2004, 272–276, e1023–e1024. [Google Scholar] [CrossRef]
- Mekata, M. Antiferro-ferrimagnatic transition in triangular ising lattice. J. Phys. Soc. Jpn. 1977, 42, 76–82. [Google Scholar] [CrossRef]
- Plakhty, V.P.; Kulda, J.; Visser, D.; Moskvin, E.V.; Wosnitza, J. Chiral critical exponents of the triangular-lattice antiferromagnet CsMnBr3 as determined by polarized neutron scattering. Phys. Rev. Lett. 2000, 85, 3942–3945. [Google Scholar] [CrossRef] [PubMed]
- Müller, A.; Kögerler, P.; Dress, A.W.M. Giant metal-oxide-based spheres and their topology: From pentagonal building blocks to keplerates and unusual spin systems. Coord. Chem. Rev. 2001, 222, 193–218. [Google Scholar] [CrossRef]
- Takano, M.; Shinjo, T.; Kiyama, M.; Takada, T. Magnetic properties of jarosites, RFe3(OH)6(SO4)2(R = NH4, Na or K). J. Phys. Soc. Jpn. 1968, 25, 902. [Google Scholar] [CrossRef]
- Townsend, M.G.; Longworth, G.; Roudaut, E. Triangular-spin, kagome plane in jarosites. Phys. Rev. B 1986, 33, 4919–4926. [Google Scholar] [CrossRef]
- Maegawa, S.; Nishiyama, M.; Tanaka, N.; Oyamada, A.; Takano, M. Observation of successive phase transitions in kagomé lattice antiferromagnets RFe3(OH)6(SO4)2 [R = NH4, Na, K]. J. Phys. Soc. Jpn. 1996, 65, 2776–2778. [Google Scholar] [CrossRef]
- Matan, K.; Ono, T.; Fukumoto, Y.; Sato, T.J.; Yamaura, J.; Yano, M.; Morita, K.; Tanaka, H. Pinwheel valence-bond solid and triplet excitations in the two-dimensional deformed kagome lattice. Nat. Phys. 2010, 6, 865–869. [Google Scholar] [CrossRef]
- Nakatsuji, S.; Nambu, Y.; Tonomura, H.; Sakai, O.; Jonas, S.; Broholm, C.; Tsunetsugu, H.; Qiu, Y.; Maeno, Y. Spin Disorder on a triangular lattice. Science 2005, 309, 1697–1700. [Google Scholar] [CrossRef] [PubMed]
- Manson, J.L.; Ressouche, E.; Miller, J.S. Spin Frustration in MII[C(CN)3]2 (M = V, Cr). A magnetism and neutron diffraction study. Inorg. Chem. 2000, 39, 1135–1141. [Google Scholar] [CrossRef] [PubMed]
- Ramirez, A.P.; Espinosa, G.P.; Cooper, A.S. Strong Frustration and dilution-enhanced order in a quasi-2D spin glass. Phys. Rev. Lett. 1990, 64, 2070–2073. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, Y.; Nohara, M.; Aruga-Katori, H.; Takagi, H. Spin-liquid state in the S = 1/2 hyperkagome antiferromagnet Na4Ir3O8. Phys. Rev. Lett. 2007, 99, 137207. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, Y.; Yoshida, H.; Hiroi, Z. Vesignieite BaCu3V2O8(OH)2 as a candidate spin-1/2 kagome antiferromagnet. J. Phys. Soc. Jpn. 2009, 78, 033701. [Google Scholar] [CrossRef]
- Yoshida, H.; Yamaura, J.; Isobe, M.; Okamoto, Y.; Nilsen, G.J.; Hiroi, Z. Orbital switching in a frustrated magnet. Nat. Commun. 2012, 3, 860. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, Y.; Miyagawa, K.; Kanoda, K.; Maesato, M.; Saito, G. Spin liquid state in an organic mott insulator with a triangular lattice. Phys. Rev. Lett. 2003, 91, 107001. [Google Scholar] [CrossRef] [PubMed]
- Konarev, D.V.; Khasanov, S.S.; Otsuka, A.; Saito, G. The Reversible Formation of a single-bonded (C60−)2 dimer in ionic charge transfer complex: Cp*2Cr·C60(C6H4Cl2)2. The molecular structure of (C60−)2. J. Am. Chem. Soc. 2002, 124, 8520–8521. [Google Scholar] [CrossRef] [PubMed]
- Konarev, D.V.; Khasanov, S.S.; Otsuka, A.; Saito, G.; Lyubovskaya, R.N. Negatively charged π-(C60−)2 Dimer with biradical state at room temperature. J. Am. Chem. Soc. 2006, 128, 9292–9293. [Google Scholar] [CrossRef] [PubMed]
- Stephens, P.W.; Bortel, G.; Faigel, G.; Tegze, M.; Jánossy, A.; Pekker, S.; Oszlanyi, G.; Forró, L. Polymeric fullerene chains in RbC60 and KC60. Nature 1994, 370, 636–639. [Google Scholar] [CrossRef]
- Bommeli, F.; Degiorgi, L.; Wachter, P.; Legeza, Ö.; Jánossy, A.; Oszlanyi, G.; Chauvet, O.; Forro, L. Metallic conductivity and metal-insulator transition in (AC60)n (A = K, Rb, and Cs) linear polymer fullerides. Phys. Rev. B 1995, 51, 14794–14797. [Google Scholar] [CrossRef]
- Bendele, G.M.; Stephens, P.W.; Prassides, K.; Vavekis, K.; Kortados, K.; Tanigaki, K. Effect of charge state on polymeric bonding geometry: The ground state of Na2RbC60. Phys. Rev. Lett. 1998, 80, 736–739. [Google Scholar] [CrossRef]
- Margadonna, S.; Pontiroli, D.; Belli, M.; Shiroka, T.; Riccò, M.; Brunelli, M. Li4C60: A polymeric fulleride with a two-dimensional architecture and mixed interfullerene bonding motifs. J. Am. Chem. Soc. 2004, 126, 15032–15033. [Google Scholar] [CrossRef] [PubMed]
- Riccò, R.; Pontiroli, D.; Mazzani, M.; Gianferrari, F.; Pagliari, M.; Goffredi, A.; Brunelli, M.; Zandomeneghi, G.; Meier, B.H.; Shiroka, T. Fullerenium salts: A new class of C60-based compounds. J. Am. Chem. Soc. 2010, 132, 2064–2068. [Google Scholar] [CrossRef] [PubMed]
- Oszlányi, G.; Baumgartner, G.; Faigel, L.; Forró, L. Na4C60: An alkali intercalated two-dimensional polymer. Phys. Rev. Lett. 1997, 78, 4438–4441. [Google Scholar] [CrossRef]
- Ohira, S.; Shimizu, Y.; Kanoda, K.; Saito, G. Spin liquid state in κ-(BEDT-TTF)2Cu2(CN)3 studied by muon spin relaxation method. J. Low Temp. Phys. 2006, 142, 153–158. [Google Scholar] [CrossRef]
- Pratt, F.L.; Baker, P.J.; Blundell, S.J.; Lancaster, T.; Ohira-Kawamura, S.; Baines, C.; Shimizu, Y.; Kanoda, K.; Watanabe, I.; Saito, G. Magnetic and non-magnetic phases of a quantum spin liquid. Nature 2011, 471, 612–616. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, Y.; Maesato, M.; Saito, G.; Drozdova, O.; Ouahab, L. Transport properties of a Mott insulator κ-(ET)2Cu2(CN)3 under the uniaxial strain. Synth. Met. 2003, 133, 225–226. [Google Scholar] [CrossRef]
- Saito, G.; Maesato, M. Organic superconductors. Mol. Cryst. Liq. Cryst. 2006, 455, 31–46. [Google Scholar] [CrossRef]
- Shimizu, Y.; Maesato, M.; Saito, G. Uniaxial strain effects on mott and superconducting transitions in κ-(ET)2Cu2(CN)3. J. Phys. Soc. Jpn. 2011, 80, 074702. [Google Scholar] [CrossRef]
- Kurosaki, Y.; Shimizu, Y.; Miyagawa, K.; Kanoda, K.; Saito, G. Mott transition from a spin liquid to a fermi liquid in the spin-frustrated organic conductor κ-(ET)2Cu2(CN)3. Phys. Rev. Lett. 2005, 95, 177001. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, Y.; Kasahara, H.; Furuta, T.; Miyagawa, K.; Kanoda, K.; Maesato, M.; Saito, G. Pressure-induced superconductivity and Mott transition in spin-liquid κ-(ET)2Cu2(CN)3 probed by 13C NMR. Phys. Rev. B 2010, 81, 224508. [Google Scholar] [CrossRef]
- Saito, G.; Yoshida, Y. Development of conductive organic molecular assemblies: Organic metals, superconductors, and exotic functional materials. Bull. Chem. Soc. Jpn. 2007, 80, 1–137. [Google Scholar] [CrossRef]
- Saito, G.; Yoshida, Y. Organic superconductors. Chem. Rec. 2011, 11, 124–145. [Google Scholar] [CrossRef] [PubMed]
- Hiramatsu, T.; Yoshida, Y.; Saito, G.; Otsuka, A.; Yamochi, H.; Maesato, M.; Shimizu, Y.; Ito, H.; Kishida, H. Quantum spin liquid: Design of a quantum spin liquid next to a superconducting state based on a dimer-type ET Mott insulator. J. Mater. Chem. C 2015, 3, 1378–1388. [Google Scholar] [CrossRef]
- Balents, L. Spin liquids in frustrated magnets. Nature 2010, 464, 199–208. [Google Scholar] [CrossRef] [PubMed]
- Norman, M.R. The Challenge of unconventional superconductivity. Science 2011, 332, 196–200. [Google Scholar] [CrossRef] [PubMed]
- Powell, B.J.; McKenzie, R.H. Quantum frustration in organic Mott insulators: From spin liquids to unconventional superconductors. Rep. Prog. Phys. 2011, 74, 056501. [Google Scholar] [CrossRef]
- Isono, T.; Kamo, H.; Ueda, A.; Takahashi, K.; Kimata, M.; Tajima, H.; Tsuchiya, S.; Terashima, T.; Uji, S.; Mori, H. Gapless quantum spin liquid in an organic spin-1/2 triangular-lattice κ-H3(Cat-EDT-TTF)2. Phys. Rev. Lett. 2014, 112, 177201. [Google Scholar] [CrossRef] [PubMed]
- Itou, T.; Oyamada, A.; Maegawa, S.; Tamura, M.; Kato, R. Spin-liquid state in an organic spin-1/2 system on a triangular lattice, EtMe3Sb[Pd(dmit)2]2. J. Phys. Condens. Matter 2007, 19, 145247. [Google Scholar] [CrossRef]
- Shores, M.P.; Nytko, E.A.; Bartlett, B.M.; Nocera, D.G. A structurally perfect S = 1/2 kagomé antiferromagnet. J. Am. Chem. Soc. 2005, 127, 13462–13463. [Google Scholar] [CrossRef] [PubMed]
- Mandels, P.; Bert, F. Quantum kagome antiferromagnet ZnCu3(OH)6Cl2. J. Phys. Soc. Jpn. 2010, 79, 011001. [Google Scholar] [CrossRef]
- Han, T.-H.; Helton, J.S.; Chu, S.; Nocera, D.G.; Rodriguez-Rivera, J.A.; Broholm, C.; Lee, Y.S. Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet. Nature 2012, 492, 406–410. [Google Scholar] [CrossRef] [PubMed]
- Clark, L.; Orain, J.C.; Bert, F.; De Vries, M.A.; Aidoudi, F.H.; Morris, R.E.; Lightfoot, P.; Lord, J.S.; Telling, M.T.F.; Bonville, P.; et al. Gapless spin liquid ground State in the S = 1/2 vanadium oxyfluoride kagome antiferromagnet [NH4]2[C7H14N][V7O6F18]. Phys. Rev. Lett. 2013, 110, 207208. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Baker, P.J.; Zhang, Y.; Wang, D.; Wang, Z.; Su, S.; Zhu, D.; Pratt, F.L. Quantum spin liquid from a three-dimensional copper-oxalate framework. J. Am. Chem. Soc. 2018, 140, 122–125. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, Y.; Hiramatsu, T.; Maesato, M.; Otsuka, A.; Yamochi, H.; Ono, A.; Itoh, M.; Yoshida, M.; Takigawa, M.; Yoshida, Y.; et al. Pressure-tuned exchange coupling of a quantum spin liquid in the molecular triangular lattice κ-(ET)2Ag2(CN)3. Phys. Rev. Lett. 2016, 117, 107203. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Jawad, M.; Terasaki, I.; Sasaki, T.; Yoneyama, N.; Kobayashi, N.; Uesu, Y.; Hotta, C. Anomalous dielectric response in the dimer Mott insulator κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. B 2010, 82, 125119. [Google Scholar] [CrossRef]
- Hiramatsu, H.; Yoshida, Y.; Saito, G.; Otsuka, A.; Yamochi, H.; Shimizu, Y.; Hattori, Y.; Nakamura, Y.; Kishida, H.; Ito, H.; et al. Spin frustration in antiperovskite systems: (TTF•+ or TSF•+)3[(Mo6X14)2−Y−]. J. Mater. Chem. C 2015, 3, 11046–11054. [Google Scholar] [CrossRef]
- Bray, J.W.; Interrante, L.V.; Jacobs, I.S.; Bonner, J.C. The Spin-Peierls Transition. In Extended Linear Chain Compounds: Volume 3; Miller, J.S., Ed.; Plenum Press: New York, NY, USA, 1983; pp. 353–415. [Google Scholar]
- Batail, P.; Livage, C.; Parkin, S.S.P.; Coulon, C.; Martin, J.D.; Canadell, E. Antiperovskite structure with ternary tetrathiafulvalenium salts: construction, distortion, and antiferromagnetic ordering. Angew. Chem. Int. Ed. Engl. 1991, 30, 1498–1500. [Google Scholar] [CrossRef]
- Conwell, E. (Ed.) Semiconductors and Semimetals: Volume 27, Highly Conducting Quasi-One-Dimensional Organic Crystals; Academic Press: Boston, MA, USA, 1988. [Google Scholar]
- Kosaka, M.; Tanigaki, K.; Tanaka, T.; Atake, T.; Lappas, A.; Prassides, K. Conducting phase of rapidly cooled AC60 (A = Cs and Rb). Phys. Rev. B 1995, 51, 12018–12021. [Google Scholar] [CrossRef]
- Brouet, V.; Alloul, H.; Forró, L. Coexistence of spin singlets and metallic behavior in simple cubic CsC60. Phys. Rev. B 2002, 66, 155123. [Google Scholar] [CrossRef]
- Gunnarsson, O.; Koch, E.; Martin, R.M. Mott transition in degenerate Hubbard models: Application to doped fullerenes. Phys. Rev. B 1996, 54, R11026–R11029. [Google Scholar] [CrossRef]
- Gunnarsson, O. Superconductivity in fullerides. Rev. Mod. Phys. 1997, 69, 575–606. [Google Scholar] [CrossRef]
- Tinkham, M. Introduction to Superconductivity, 2nd ed.; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Rosseinsky, M.J.; Ramirez, A.P.; Glarum, S.H.; Murphy, D.W.; Haddon, R.C.; Hebard, A.F.; Palstra, T.T.M.; Kortan, A.R.; Zahurak, S.M.; Makhija, A.V. Superconductivity at 28 K in RbxC60. Phys. Rev. Lett. 1991, 66, 2830–2832. [Google Scholar] [CrossRef] [PubMed]
- Tanigaki, K.; Ebbesen, T.W.; Saito, S.; Mizuki, J.; Tsai, J.S.; Kubo, Y.; Kuroshima, S. Superconductivity at 33 K in CsxRbyC60. Nature 1991, 352, 222–223. [Google Scholar] [CrossRef]
- Rosseinsky, M.J. Recent developments in the chemistry and physics of metal fullerides. Chem. Mater. 1998, 10, 2665–2685. [Google Scholar] [CrossRef]
- Andreoni, W. (Ed.) The Physics of Fullerene-Based and Fullerene-Related Materials; Springer: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Reed, C.A.; Bolskar, R.D. Discrete fulleride anions and fullerenium cations. Chem. Rev. 2000, 100, 1075–1120. [Google Scholar] [CrossRef] [PubMed]
- Fleming, R.M.; Ramirez, A.P.; Rosseinsky, M.J.; Murphy, D.W.; Haddon, R.C.; Zahurak, S.M.; Makhija, A.V. Relation of structure and superconducting transition temperatures in A3C60. Nature 1991, 352, 787–788. [Google Scholar] [CrossRef]
- Ganin, A.Y.; Takabayashi, Y.; Khimyak, Y.Z.; Margadonna, S.; Tamai, A.; Rosseinsky, M.J.; Prassides, K. Bulk superconductivity at 38 K in a molecular system. Nat. Mater. 2008, 7, 367–371. [Google Scholar] [CrossRef] [PubMed]
- Ganin, A.Y.; Takabayashi, Y.; Jeglič, Y.; Arčon, D.; Potočnik, A.; Baker, P.J.; Ohishi, Y.; McDonald, M.T.; Tzirakis, M.D.; McLennan, A.; et al. Polymorphism control of superconductivity and magnetism in Cs3C60 close to the Mott transition. Nature 2010, 466, 221–225. [Google Scholar] [CrossRef] [PubMed]
- Özdaş, E.; Kortan, A.R.; Kopylov, N.; Ramirez, A.P.; Siegrist, T.; Rabe, K.M.; Bair, H.E.; Schuppler, S.; Citrin, P.H. Superconductivity and cation-vacancy ordering in the rare-earth fulleride Yb2.75C60. Nature 1995, 375, 126–129. [Google Scholar] [CrossRef]
- Chen, X.H.; Roth, G. Superconductivity at 8 K in samarium-doped C60. Phys. Rev. B 1995, 52, 15534–15536. [Google Scholar] [CrossRef]
- Brown, C.M.; Taga, S.; Gogia, B.; Kordatos, K.; Margadonna, S.; Prassides, K.; Iwasa, Y.; Tanigaki, K.; Fitch, A.N.; Pattison, P. Structural and electronic properties of the noncubic superconducting fullerides A’4C60 (A’ = Ba, Sr). Phys. Rev. Lett. 1999, 83, 2258–2261. [Google Scholar] [CrossRef]
- Baenitz, M.; Heinze, M.; Lüders, K.; Werner, H.; Schlögl, R.; Weiden, M.; Sparn, G.; Steglich, F. Superconductivity of Ba doped C60—Susceptibility results and upper critical field. Solid State Commun. 1995, 96, 539–544. [Google Scholar] [CrossRef]
- Iwasa, Y.; Hayashi, H.; Furudate, T.; Mitani, T. Superconductivity in K3Ba3C60. Phys. Rev. B 1996, 54, 14960–14962. [Google Scholar] [CrossRef]
- Ksari-Habiles, Y.; Claves, D.; Chouteau, G.; Touzain, P.; Jeandey, C.; Oddou, J.L.; Stepanov, A. Superexchange and magnetic relaxation in novel Eu-DOPED C60 phases. J. Phys. Chem. Solids 1997, 58, 1771–1778. [Google Scholar] [CrossRef]
- Maruyama, Y.; Motohashi, S.; Sakai, N.; Watanabe, K.; Suzuki, K.; Ogata, H.; Kubozono, Y. Possible competition of superconductivity and ferromagnetism in CexC60 compounds. Solid State Commun. 2002, 123, 229–233. [Google Scholar] [CrossRef]
- Zadik, R.H.; Takabayashi, Y.; Klupp, G.; Colman, R.H.; Ganin, A.Y.; Potočnik, A.; Jeglič, P.; Arčon, D.; Matus, P.; Kamarás, K.; et al. Optimized unconventional superconductivity in a molecular Jahn-Teller metal. Sci. Adv. 2015, 1, e1500059. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, S.; Matsuda, A.; Chu, C.W. Fermi-liquid behavior and BCS s-wave pairing of K3C60 observed by 13C-NMR. J. Phys. Soc. Jpn. 1994, 63, 1670–1673. [Google Scholar] [CrossRef]
- Kiefl, R.F.; MacFarlane, W.A.; Chow, K.H.; Dunsiger, S.; Duty, T.L.; Johnston, T.M.S.; Schneider, J.W.; Sonier, J.; Brard, L.; Strongin, R.M.; et al. Coherence Peak and Superconducting energy gap in Rb3C60 observed by muon spin relaxation. Phys. Rev. Lett. 1993, 70, 3987–3990. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Allemand, P.-M.; Khemani, K.C.; Koch, A.; Wudl, F.; Holczer, K.; Donovan, S.; Grüner, G.; Thompson, J.D. Organic Molecular Soft ferromagnetism in a fullerene C60. Science 1991, 253, 301–303. [Google Scholar] [CrossRef] [PubMed]
- Konerav, D.V.; Lyubovskaya, R.N. Molecular design, study of the structures and properties of ionic fullerene compounds. Rus. Chem. Rev. 2012, 81, 336–366. [Google Scholar] [CrossRef]
- Prassides, K. Polymer and Dimer Phases in Doped Fullerenes. In The Physics of Fullerene-Based and Fullerene-Related Materials; Andreoni, W., Ed.; Kluwer Academic Publishers: Boston, MA, USA, 2000; pp. 175–202. [Google Scholar]
- Eklund, P.C.; Rao, A.M. (Eds.) Fullerene Polymers and Fullerene Polymer Composites; Springer: Berlin, Germany, 2000. [Google Scholar]
- Rosseinsky, M.J. Fullerene intercalation chemistry. J. Mater. Chem. 1995, 5, 1497–1513. [Google Scholar] [CrossRef]
- Bondi, A. Van der waals volumes and radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Brouet, V.; Alloul, H.; Yoshinari, Y.; Forro, L. NMR Evidence for 1D Antiferromagnetic Properties in Cs1C60 and Rb1C60 Polymers. Phys. Rev. Lett. 1996, 76, 3638–3641. [Google Scholar] [CrossRef] [PubMed]
- Schirber, J.E.; Morosin, B.; Kwei, G.H.; Yildirim, T.; Fischer, J.E.; Jorgensen, J.D. Superconductivity in the polymeric phase of Na2CsC60. Physica C 2001, 353, 207–212. [Google Scholar] [CrossRef]
- Kozhemyakina, N.V.; Amsharov, K.Y.; Nuss, J.; Jansen, M. Synthesis and Structure analysis of (K[DB18 C6])4(C60)5∙12THF containing C60 in three different bonding states. Chem. Eur. J. 2011, 17, 1798–1805. [Google Scholar] [CrossRef] [PubMed]
- Konarev, D.V.; Khasanov, S.S.; Saito, G.; Lyubovskaya, R.N. Design of molecular and ionic complexes of fullerene C60 with metal(II) octaethylporphyrins, MIIOEP (M = Zn, Co, Fe, and Mn) containing coordination M−N(ligand) and M−C(C60–) bonds. Cryst. Growth Des. 2009, 9, 1170–1181. [Google Scholar] [CrossRef]
- Konarev, D.V.; Khasanov, S.S.; Mukhamadieva, G.R.; Zorina, L.V.; Otsuka, A.; Yamochi, H.; Saito, G.; Lyubovskaya, R.N. Magnetic and structural transitions at dimerization of C60•− in ionic fullerene complexes with metalloporphyrins: {(TMP+)2·MIITPP}·(C60−)2·(C6H4Cl2)2·(C6H5CN)2 (M = Zn and Mn). Inorg. Chem. 2010, 49, 3881–3887. [Google Scholar] [CrossRef] [PubMed]
- Konarev, D.V.; Khasanov, S.S.; Kuzmin, A.V.; Otsuka, A.; Yamochi, H.; Saito, G.; Lyubovskaya, R.N. Effective magnetic coupling with strong spin frustration in (Ph3MeP+)(C60•−) and reversible C60•− dimerization in (Ph3MeP+)(C60•−)·C6H5CN. Effect of solvent on structure and properties. New J. Chem. 2016, 40, 2792–2798. [Google Scholar] [CrossRef]
- Konarev, D.V.; Khasanov, S.S.; Otsuka, A.; Yamochi, H.; Saito, G.; Lyubovskaya, R.N. Effect of the cooling rate on dimerization of C60•− in fullerene salt (DMI+)2·(C60•−)·{Cd(Et2NCS2)2I−}. Inorg. Chem. 2012, 51, 3420–3426. [Google Scholar] [CrossRef] [PubMed]
- Pénicaud, A.; Peréz-Benítez, A.; Gleason, V.R.; Muñoz, P.E.; Escudero, R. Electrocrystallizing C60: Synthesis, single crystal X-ray structure, and magnetic (ESR, SQUID) characterization of [(C6H5)4P]2[C60][I]x. J. Am. Chem. Soc. 1993, 115, 10392–10393. [Google Scholar] [CrossRef]
- Bilow, U.; Jansen, M. Electrocrystallisation and crystal structure determination of Ph4PC60·Ph4PCl. J. Chem. Soc. Chem. Commun. 1994, 403–404. [Google Scholar] [CrossRef]
- Bilow, U.; Jansen, M. Electrocrystallization of fullerides. Z. Anorg. Allg. Chem. 1995, 621, 982–986. [Google Scholar] [CrossRef]
- Gritsenko, V.V.; Dyachenko, O.A.; Shilov, G.V.; Spitsyna, N.G.; Yagubskii, E.B. Crystal and molecular structures of new fullerides, (Ph4P)2C60Hal (Hal = Br or I) and (Ph4As)2C60Cl. Rus. Chem. Bull. 1997, 46, 1878–1882. [Google Scholar] [CrossRef]
- Kobayashi, H.; Moriyama, H.; Kobayashi, A.; Watanabe, T. Synthesis and characterization of some fulleride compounds by electrocrystallization of C60. Synth. Met. 1995, 70, 1451–1452. [Google Scholar] [CrossRef]
- Hong, J.; Shores, M.P.; Elliott, C.M. Establishment of structure-conductivity relationship for Tris(2,2′-bipyridine) ruthenium ionic C60 salts. Inorg. Chem. 2010, 49, 11378–11385. [Google Scholar] [CrossRef] [PubMed]
- Fässler, T.F.; Hoffmann, R.; Hoffmann, S.; Wörle, M. Triple-decker type coordination of a fullerene trianion in [K([18]crown-6)]3[η6,η6-C60](η3-C6H5CH3)2—Single crystal structure and magnetic properties. Angew. Chem. Int. Ed. 2000, 39, 2091–2094. [Google Scholar] [CrossRef]
- Boeddinghaus, M.B.; Salzinger, M.; Fässler, T.F. Synthesis, X-ray single-crystal structure determination, and magnetic properties of [Rb(benzo[18]crown-6)]+ salts containing well-ordered fulleride trianions C603−. Chem. Eur. J. 2009, 15, 3261–3267. [Google Scholar] [CrossRef] [PubMed]
- Fässler, T.F.; Spiekermann, A.; Spahr, M.E.; Nesper, R. Unprecedented layered structure of a fulleride: synthesis, structure, and magnetic properties of a potassium-containing salt with a C602− counterion. Angew. Chem. Int. Ed. Engl. 1997, 36, 486–488. [Google Scholar] [CrossRef]
- Janiak, C.; Mühle, S.; Hemling, H.; Köhler, K. The solid-state structure of K3C60(THF)14. Polyhedron 1996, 15, 1559–1563. [Google Scholar] [CrossRef]
- Kosaka, M.; Tanigaki, K.; Prassides, K.; Margadonna, S.; Lappas, A.; Brown, C.M.; Fitch, A.N. Superconductivity in LixCsC60 fullerides. Phys. Rev. B 1999, 59, R6628–R6630. [Google Scholar] [CrossRef]
- Tanigaki, K.; Prassides, K. Conducting and superconducting properties of alkali-metal C60 fullerides. J. Mater. Chem. 1995, 5, 1515–1527. [Google Scholar] [CrossRef]
- Tanigaki, K.; Hirosawa, I.; Ebbesen, T.W.; Mizuki, J.; Shimakawa, Y.; Kubo, Y.; Tsai, J.S.; Kuroshima, S. Superconductivity in sodium- and lithium-containing alkali-metal fullerides. Nature 1992, 356, 419–421. [Google Scholar] [CrossRef]
- Takabayashi, Y.; Ganin, A.Y.; Jeglič, P.; Arčon, D.; Takano, T.; Iwasa, Y.; Ohishi, Y.; Takata, M.; Takeshita, N.; Prassides, K.; et al. The disorder-free Non-BCS superconductor Cs3C60 emerges from an antiferromagnetic insulator parent state. Science 2009, 323, 1585–1590. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, Y.; Shibasaki, S.; Kubozono, Y.; Kambe, T. Antiferromagnetic resonance in the Mott insulator fcc-Cs3C60. J. Phys. Condens. Matter 2013, 25, 366001. [Google Scholar] [CrossRef] [PubMed]
- Ihara, Y.; Alloul, H.; Wzietek, P.; Pontiroli, D.; Mazzani, M.; Riccò, M. NMR Study of the Mott transitions to superconductivity in the two Cs3C60 Phases. Phys. Rev. Lett. 2010, 104, 256402. [Google Scholar] [CrossRef] [PubMed]
- Takenobu, T.; Muro, T.; Iwasa, Y.; Mitani, T. Antiferromagnetism and phase diagram in ammoniated alkali fulleride salts. Phys. Rev. Lett. 2000, 85, 381–384. [Google Scholar] [CrossRef] [PubMed]
- Zhou, O.; Palstra, T.T.M.; Iwasa, Y.; Fleming, R.M.; Hebard, A.F.; Sulewski, P.E.; Murphy, D.W.; Zegarski, B.R. Structural and electronic properties of (NH3)xK3C60. Phys. Rev. B 1995, 52, 483–489. [Google Scholar] [CrossRef]
- Iwasa, Y.; Takenobu, T. Superconductivity, Mott-Hubbard states, and molecular orbital order in intercalated fullerides. J. Phys.: Condens. Matter 2003, 15, R495–R519. [Google Scholar] [CrossRef]
- Welp, U.; Fleshler, S.; Kwok, W.K.; Crabtree, G.W.; Carlson, K.D.; Wang, H.H.; Geiser, U.; Williams, J.M.; Hitsman, V.M. Weak Ferromagnetism in κ-(ET)2Cu[N(CN)2]Cl, where (ET) is Bis(ethylenedithio)tetrathiafulvalene. Phys. Rev. Lett. 1992, 69, 840–843. [Google Scholar] [CrossRef] [PubMed]
- Miyagawa, K.; Kawamoto, A.; Nakazawa, Y.; Kanoda, K. antiferromagnetic ordering and spin structure in the organic conductor, κ-(BEDT-TTF)2Cu[N(CN)2]Cl. Phys. Rev. Lett. 1995, 75, 1174–1177. [Google Scholar] [CrossRef] [PubMed]
- Ito, H.; Asai, T.; Shimizu, Y.; Hayama, H.; Yoshida, Y.; Saito, G. Pressure-induced superconductivity in the antiferromagnet κ-(ET)2CF3SO3 with quasi-one-dimensional triangular spin lattice. Phys. Rev. B 2016, 94, 020503. [Google Scholar] [CrossRef]
- Coldea, R.; Tennant, D.A.; Tsvelik, A.M.; Tylczynski, Z. Experimental realization of a 2D fractional quantum spin liquid. Phys. Rev. Lett. 2001, 86, 1335–1338. [Google Scholar] [CrossRef] [PubMed]
- Antropov, P.V.; Gunnarsson, O.; Jepsen, O. Coulomb integrals and model Hamiltonians for C60. Phys. Rev. B 1992, 46, 13647–13650. [Google Scholar] [CrossRef]
- Pederson, M.R.; Quong, A.A. Polarizabilities, charge states, and vibrational modes of isolated fullerene molecules. Phys. Rev. B 1992, 46, 13584–13591. [Google Scholar] [CrossRef]
- Martin, R.L.; Ritchie, J.P. Coulomb and exchange interactions in C60n−. Phys. Rev. B 1993, 48, 4845–4849. [Google Scholar] [CrossRef]
- Brühwiler, P.A.; Maxwell, A.J.; Nilsson, A.; Mårtensson, N.; Gunnarsson, O. Auger and photoelectron study of the Hubbard U in C60, K3C60, and K6C60. Phys. Rev. B 1993, 48, 18296–18299. [Google Scholar] [CrossRef]
- Lof, R.W.; van Veenendaal, M.A.; Koopmans, B.; Jonkman, H.T.; Sawatzky, G.A. Band gap, excitons, and coulomb interaction in solid C60. Phys. Rev. Lett. 1992, 68, 3924–3927. [Google Scholar] [CrossRef] [PubMed]
- LeBlanc, O.H., Jr. On the Electrical conductivities of tetracyanoquinodimethan anion-radical salt. J. Chem. Phys. 1965, 42, 4307–4308. [Google Scholar] [CrossRef]
- Douthwaite, R.E.; Green, M.A.; Green, M.L.H.; Rosseinsky, M.J. Synthesis, reactivity, structure and electronic properties of [N(CH3)4]C60·1.5thf: Fullerides with simple hexagonal packing. J. Mater. Chem. 1996, 6, 1913–1920. [Google Scholar] [CrossRef]
- Douthwaite, R.E.; Brough, A.R.; Green, M.L.H. Synthesis and characterisation of NaC60·5thf. J. Chem. Soc. Chem. Commun. 1994, 3, 267–268. [Google Scholar] [CrossRef]
- Kromer, A.; Wedig, U.; Roduner, E.; Jansen, M.; Amsharov, K.Y. Counterintuitive anisotropy of electron transport properties in KC60(THF)5∙2THF fulleride. Angew. Chem. Int. Ed. 2013, 52, 12610–12614. [Google Scholar] [CrossRef] [PubMed]
- Kodera, H. Dyson effect in the electron spin resonance of phosphorus doped silicon. J. Phys. Soc. Jpn. 1970, 28, 89–98. [Google Scholar] [CrossRef]
- Saito, G.; Teramoto, T.; Otsuka, A.; Sugita, Y.; Ban, T.; Kusunoki, M.; Sakaguchi, K. Preparation and ionicity of C60 charge transfer complexes. Synth. Met. 1994, 64, 359–368. [Google Scholar] [CrossRef]
- Konarev, D.V.; Khasanov, S.S.; Vorontsov, I.I.; Saito, G.; Antipin, M.Y.; Otsuka, A.; Lyubovskaya, R.N. The formation of a single-bonded (C70−)2 dimer in a new ionic multicomponent complex of cyclotriveratrylene: (Cs+)2(C70−)2·CTV·(DMF)7(C6H6)0.75. Chem. Commun. 2002, 21, 2548–2549. [Google Scholar] [CrossRef]
- Konarev, D.V.; Khasanov, S.S.; Otsuka, A.; Yoshida, Y.; Saito, G. Synthesis and crystal structure of ionic multicomponent complex: {[CrI(PhH)2]•+}2[CoIITPP(C60(CN)2)]− [C60(CN)2]•−·3(o-C6H4Cl2) containing C60(CN)2•− radical anion and σ-bonded diamagnetic CoIITPP(C60(CN)2)− anion. J. Am. Chem. Soc. 2002, 124, 7648–7649. [Google Scholar] [CrossRef] [PubMed]
- Konarev, D.V.; Khasanov, S.S.; Saito, G.; Otsuka, A.; Yoshida, Y.; Lyubovskaya, R.N. Formation of single-bonded (C60−)2 and (C70−)2 dimers in crystalline ionic complexes of fullerenes. J. Am. Chem. Soc. 2003, 125, 10074–10083. [Google Scholar] [CrossRef] [PubMed]
- Konarev, D.V.; Neretin, I.S.; Saito, G.; Slovokhotov, Y.L.; Otsuka, A.; Lyubovskaya, R.N. Multicomponent ionic complexes of cobalt(ii) tetraphenylporphyrin with c60 fullerides—Transition from the σ-bonded [(CoIITPP)·(C60−)] anion to nonbonded CoIITPP and C60•− components. Eur. J. Inorg. Chem. 2004, 2004, 1794–1798. [Google Scholar] [CrossRef]
- Konarev, D.V.; Khasanov, S.S.; Otsuka, A.; Saito, G.; Lyubovskaya, R.N. Ionic fullerene complex (DMI+)3·(C60•−)·(I−)2 with 2H-hexagonal fullerene packing and 3-D DMI+-I− network. CrystEngComm 2009, 11, 811–816. [Google Scholar] [CrossRef]
- Konarev, D.V.; Khasanov, S.S.; Otsuka, A.; Maesato, M.; Saito, G.; Lyubovskaya, R.N. A two-dimensional organic metal based on fullerene. Angew. Chem. Int. Ed. 2010, 49, 4829–4832. [Google Scholar] [CrossRef] [PubMed]
- Konarev, D.V.; Khasanov, S.S.; Otsuka, A.; Yamochi, H.; Saito, G.; Lyubovskaya, R.N. Strong Antiferromagnetic coupling of spins in the (MDABCO+)(C60•−) salt with 3D close packing of the C60•− radical anions (MDABCO+: N-Methyldiazabicyclooctanium Cation). Chem. Asian J. 2014, 9, 1629–1635. [Google Scholar] [CrossRef] [PubMed]
- Konarev, D.V.; Kuzmin, A.V.; Khasanov, S.S.; Ishikawa, M.; Otsuka, A.; Yamochi, H.; Saito, G.; Lyubovskaya, R.N. Structure and magnetic properties of the ionic fullerene salt (TMP+)·(C60•−)·C6H5CN containing layers of monomeric C60•− radical anions. New J. Chem. 2013, 37, 2521–2527. [Google Scholar] [CrossRef]
- Konarev, D.V.; Khasanov, S.S.; Otsuka, A.; Ishikawa, M.; Yamochi, H.; Saito, G.; Lyubovskaya, R.N. Formation of hexagonal fullerene layers from neutral and negatively charged fullerenes in {(Ph3P)3Au+}2(C60•−)2(C60)·C6H4Cl2 containing gold cations with the C3v symmetry. Inorg. Chem. 2014, 53, 6850–6855. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, Y.; Ito, H.; Maesato, M.; Shimizu, Y.; Hayama, H.; Hiramatsu, T.; Nakamura, Y.; Kishida, H.; Koretsune, T.; Hotta, C.; et al. Spin-disordered quantum phases in a quasi-one-dimensional triangular lattice. Nat. Phys. 2015, 11, 679–683. [Google Scholar] [CrossRef]
- Sugano, T.; Saito, G.; Kinoshita, M. Conduction-electron-spin resonance in organic conductors: α and β phases of di[bis(ethylenedithiolo)tetrathiafulvalene]triiodide [(BEDT-TTF)2I3]. Phys. Rev. B 1986, 34, 117–125. [Google Scholar] [CrossRef]
- Yagubskii, E.B.; Shchegolev, I.F.; Laukhin, V.N.; Kononovich, P.A.; Karstovnik, M.V.; Zvarykina, A.V.; Buravov, L.I. Normal-pressure superconductivity in an organic metal (BEDT-TTF)2I3 [bis (ethylene dithiolo) tetrathiof ulvalene triiodide]. JETP Lett. 1984, 39, 12–16. [Google Scholar]
- Yildirim, T.; Fischer, J.E.; Harris, A.B.; Stephens, P.W.; Liu, D.; Brard, L.; Strongin, R.M.; Smith, A.B. Orientational phase transition in NaxC60 (1 <x <3). Phys. Rev. Lett. 1993, 71, 1383–1386. [Google Scholar] [PubMed]
- Prassides, K.; Christides, C.; Thomas, I.M.; Mizuki, J.; Tanigaki, K.; Hirosawa, I.; Ebbesen, T.W. Crystal structure, bonding, and phase transition of the superconducting Na2CsC60 fulleride. Science 1994, 263, 950–954. [Google Scholar] [CrossRef] [PubMed]
- Mihailovic, D.; Arcon, D.; Verturini, P.; Blinc, R.; Omerzu, A.; Cevc, P. Orientational and magnetic ordering of buckyballs in TDAE-C60. Science 1995, 268, 400–402. [Google Scholar] [CrossRef] [PubMed]
- Akada, M.; Yamamoto, T.; Kumashiro, R.; Hojyo, A.; Matsui, H.; Toyota, N.; Lu, J.P.; Tanigaki, K. Erectric transport and modulated density of states in rotational order and disorder in Na2CsC60. In Multifunctional Conducting Molecular Materials; Saito, G., Wudl, F., Haddon, R.C., Tanigaki, K., Enoki, T., Katz, H.E., Maesato, M., Eds.; RSC Publishing: Cambridge, UK, 2007; pp. 191–197. [Google Scholar]
- Brouet, V.; Alloul, H.; Quéré, F.; Baumgartner, G.; Folló, L. Detection by NMR of a “Local Spin Gap” in quenched CsC60. Phys. Rev. Lett. 1999, 82, 2131–2134. [Google Scholar] [CrossRef]
- Pinterić, M.; Lazić, P.; Pustogow, A.; Ivek, T.; Kuveždić, M.; Milat, O.; Gumhalter, B.; Basletić, M.; Čulo, M.; Korin-Hamzić, B.; et al. Anion effects on electronic structure and electrodynamic properties of the Mott insulator κ-(BEDT-TTF)2Ag2(CN)3. Phys. Rev. B 2016, 94, 161105. [Google Scholar] [CrossRef]
- Lines, M.E. The quadratic-layer antiferromagnet. J. Phys. Chem. Solids 1970, 31, 101–116. [Google Scholar] [CrossRef]
- Zong, X.; Suh, B.J.; Niazi, A.; Yan, J.Q.; Schlagel, D.L.; Lograsso, T.A.; Johnston, D.C. 17O and 51V NMR for the zigzag spin-1 chain compound CaV2O4. Phys. Rev. B 2008, 77, 014412. [Google Scholar] [CrossRef]
- Helis, H.M.; Goodman, W.H.; Wilson, R.B.; Morgan, J.A.; Hodgson, D.J. A novel halogen-bridged system: Synthesis and structures of dibromo[2-(2-aminomethyl)pyridine]copper(II) and dibromo(2-methyl- 1,2-diaminopropane)copper(II). Inorg. Chem. 1977, 16, 2412–2416. [Google Scholar] [CrossRef]
- Kikuchi, H.; Nagasawa, H.; Ajiro, Y.; Asano, T.; Goto, T. Susceptibility and high-field magnetization of one-dimensional S = 1/2 Heisenberg antiferromagnet with next-nearest exchange interaction. Physica B 2000, 284–288, 1631–1632. [Google Scholar] [CrossRef]
- Khan, M.I.; Giri, S.; Ayesh, S.; Doedens, R.J. Synthesis and characterization of a new hybrid chain derived from oxovanadyl and molybdate moieties [VIVO(μ3-MoO4)(2,2′-bpy)]: Topological equivalence of {MoO4} and {SO4} motifs. Inorg. Chem. Commun. 2004, 7, 721–724. [Google Scholar] [CrossRef]
- Kikuchi, H.; Ishikawa, Y.; Fujii, Y.; Matsuo, A.; Kindo, K. Magnetic properties of S = 1/2 J1-J2 one-dimensional magnets, VO(XO4)(2,2′-bpy) (X = S, Mo; bpy = bipyridine). J. Phys. Conf. Ser. 2014, 568, 042017. [Google Scholar] [CrossRef]
- Hosokoshi, Y.; Katoh, K.; Inoue, K.; Goto, T. Construction of a quantum-spin system of S = 1/2 antiferromagnetic chain with the next-nearest-neighbor interactions. J. Phys. Soc. Jpn. 1999, 68, 2910–2913. [Google Scholar] [CrossRef]
- Nomura, K.; Okamoto, K. Phase diagram of S = 1/2 antiferromagnetic XXZ chain with next-nearest-neighbor interactions. J. Phys. Soc. Jpn. 1993, 62, 1123–1126. [Google Scholar] [CrossRef]
- Maeshima, N.; Okunishi, K. Antiferromagnetic zigzag spin chain in magnetic fields at finite temperatures. Phys. Rev. B 2000, 62, 934–939. [Google Scholar] [CrossRef]
- Troyer, M.; Zhitomirsky, M.E.; Ueda, K. Nearly critical ground state of LaCuO2.5. Phys. Rev. B 1997, 55, R6117–R6120. [Google Scholar] [CrossRef]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otsuka, A.; Konarev, D.V.; Lyubovskaya, R.N.; Khasanov, S.S.; Maesato, M.; Yoshida, Y.; Saito, G. Design of Spin-Frustrated Monomer-Type C60•? Mott Insulator. Crystals 2018, 8, 115. https://doi.org/10.3390/cryst8030115
Otsuka A, Konarev DV, Lyubovskaya RN, Khasanov SS, Maesato M, Yoshida Y, Saito G. Design of Spin-Frustrated Monomer-Type C60•? Mott Insulator. Crystals. 2018; 8(3):115. https://doi.org/10.3390/cryst8030115
Chicago/Turabian StyleOtsuka, Akihiro, Dmitri V. Konarev, Rimma N. Lyubovskaya, Salavat S. Khasanov, Mitsuhiko Maesato, Yukihiro Yoshida, and Gunzi Saito. 2018. "Design of Spin-Frustrated Monomer-Type C60•? Mott Insulator" Crystals 8, no. 3: 115. https://doi.org/10.3390/cryst8030115
APA StyleOtsuka, A., Konarev, D. V., Lyubovskaya, R. N., Khasanov, S. S., Maesato, M., Yoshida, Y., & Saito, G. (2018). Design of Spin-Frustrated Monomer-Type C60•? Mott Insulator. Crystals, 8(3), 115. https://doi.org/10.3390/cryst8030115




