Ferroelectric Relaxor Quantum Crystals

Abstract

A discussion is given of ferroelectrics (FEs) that have their Curie temperatures T_c very near absolute zero. These have differences in their dynamics in comparison with higher-temperature systems, since domain wall motion occurs via quantum mechanical tunneling and not by thermally activated diffusion. Emphasis in the present paper is on FEs that have relaxor characteristics. In such systems, the temperature at which the isothermal electric susceptibility ε(T,f) peaks is a strong function of frequency, and it decreases with decreasing frequency. This is due to glassy viscosity and is symbolic of non-equilibrium dynamics, usually described by a Vogel-Fulcher equation. It permits an extra dimension with which to examine the transitions. The second half of this paper reviews domain wall instabilities and asks about their presence in QCP ferroelectrics, which has not yet been reported and may be unobservable due to the absence of thermal diffusion of walls near T = 0; in this respect, we note that diffusion does exist in ferroelectric relaxors, even at T = 0, by virtue of their glassy, viscous dynamics.

1. Introduction

There are few simple stoichiometric ferroelectrics in which the Curie transition temperature from ferroelectric to paraelectric is very near absolute zero, but a few include potassium lithium tantalate (K₃Li₂Ta₅O₁₅) at T_c = 7 K, lead pyrochlore at T_c = 15.4 K, and O-18 strontium titanate (T_c = ca. 35 K); in addition, sometimes substitutional methods can lower the transition by hundreds of degrees to zero. Examples include hexaferrites [1,2,3,4,5,6,7,8,9,10], tris-sarcosine calcium chloride [11], and a few others. These systems are of general interest, but the interest rises with the degree of complexity, and one kind of additional complexity is provided by the glassy, viscous nature of some ferroelectrics. These systems also exhibit a peak in the isothermal electrical susceptibility (dielectric constant) with temperature, but the value of that temperature varies with frequency, decreasing tens or even hundreds of degrees with decreasing frequency. Typically, measurements are made via dielectric constant and loss data, or by resonant ultrasonic attenuation (RUS), and in the former case, the frequency range of interest varies from a few Hz to a few MHz. With decreasing frequency, the amplitude of the dielectric constant also increases; both this increase and the shift in response peak are typical of viscous materials, and a semi-empirical formula (Vogel-Fulcher Equation) is commonly used to fit the data. This equation has an attempt frequency f₀ for restricted ionic jumps, an activation energy E_a, a high-temperature onset T_c (which coincides with a maximum in the real part of the dielectric constant), and a low-temperature freezing temperature T_f. Note that in the context of quantum critical points, T_c can be finite but T_f < 0, implying that there is a characteristic frequency at which the dielectric constant is maximal exactly at T = 0. There is no term yet in the literature for this frequency; we would suggest the term “zero-Kelvin frequency” or perhaps “QCP frequency”.

Most important in the present context is the argument by Tokura’s group that ferroelectric QCPs have no creep and no classical diffusion. This would appear to rule out domain instabilities such as wrinkling and folding in ferroelectric QCPs, based upon the models of Turing and Hohenberg. However, it is in this respect that relaxor QCPs are special: By definition, their ground states are glassy and viscous, and hence certainly permit some diffusion. The presence of a glassy ground state at T = 0 is remarkable in many ways.

Vogel-Fulcher: 𝑓 = 𝑓₀ exp [−E_a/k(T_c − T_𝑓)]

(1)

Here, f is the probe frequency; f₀ is an attempt frequency (typically of order an optical phonon frequency); T_c is the temperature at which the dielectric constant peaks at high frequencies (typically 1 MHz); T_f is a freezing temperature at which the dielectric constant would peak at very low frequencies (dc); k is the Boltzmann constant; and E_a is an activation energy. In fitting data, the temperature at which the dielectric constant is maximum is usually graphed versus f.

The present author has recently co-authored a lengthy review on ferroelectric QCPs [12], and so readers are referred to it for a general discussion and comparison with the more frequently studied magnetic QCPs. In addition, a detailed study of KLT and lead pyrochlore relaxor QCPs has also been presented [13].

The basic physics idea for QCP transitions is:

• Classical phase transitions at normal temperatures: Spatial fluctuations of the order parameter are separable from temporal fluctuations.
• Quantum Critical Points: Because momentum p and position x do not commute, spatial and temporal fluctuations are mixed together.

Terminology: d + 1 dimensions (space and time).

2. Materials and Methods

The technique used in our work is dielectric constant measurements of single crystals, ceramic pellets, and thin films. These are standard techniques, but there are artifacts to be avoided [14].

3. Results

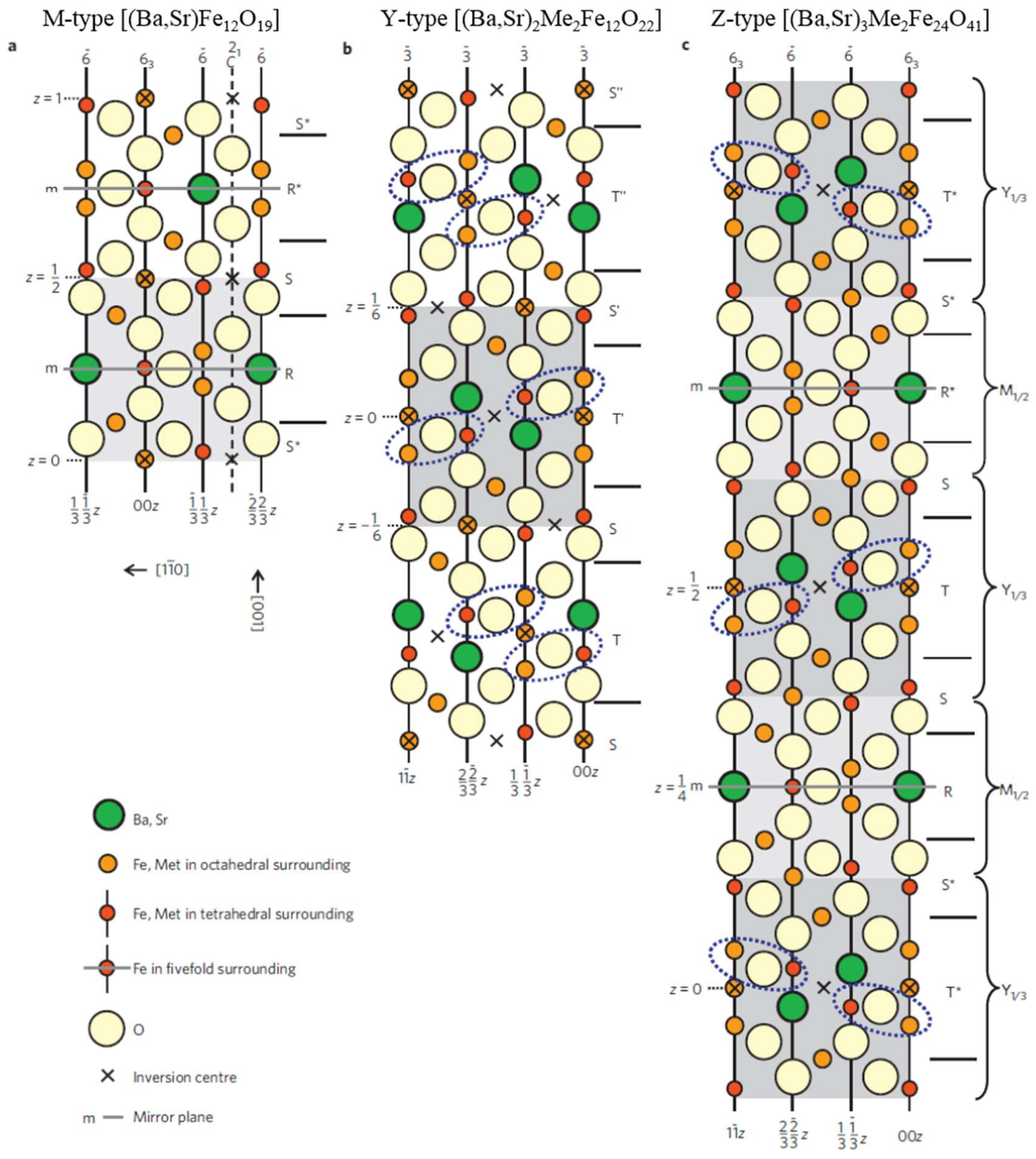
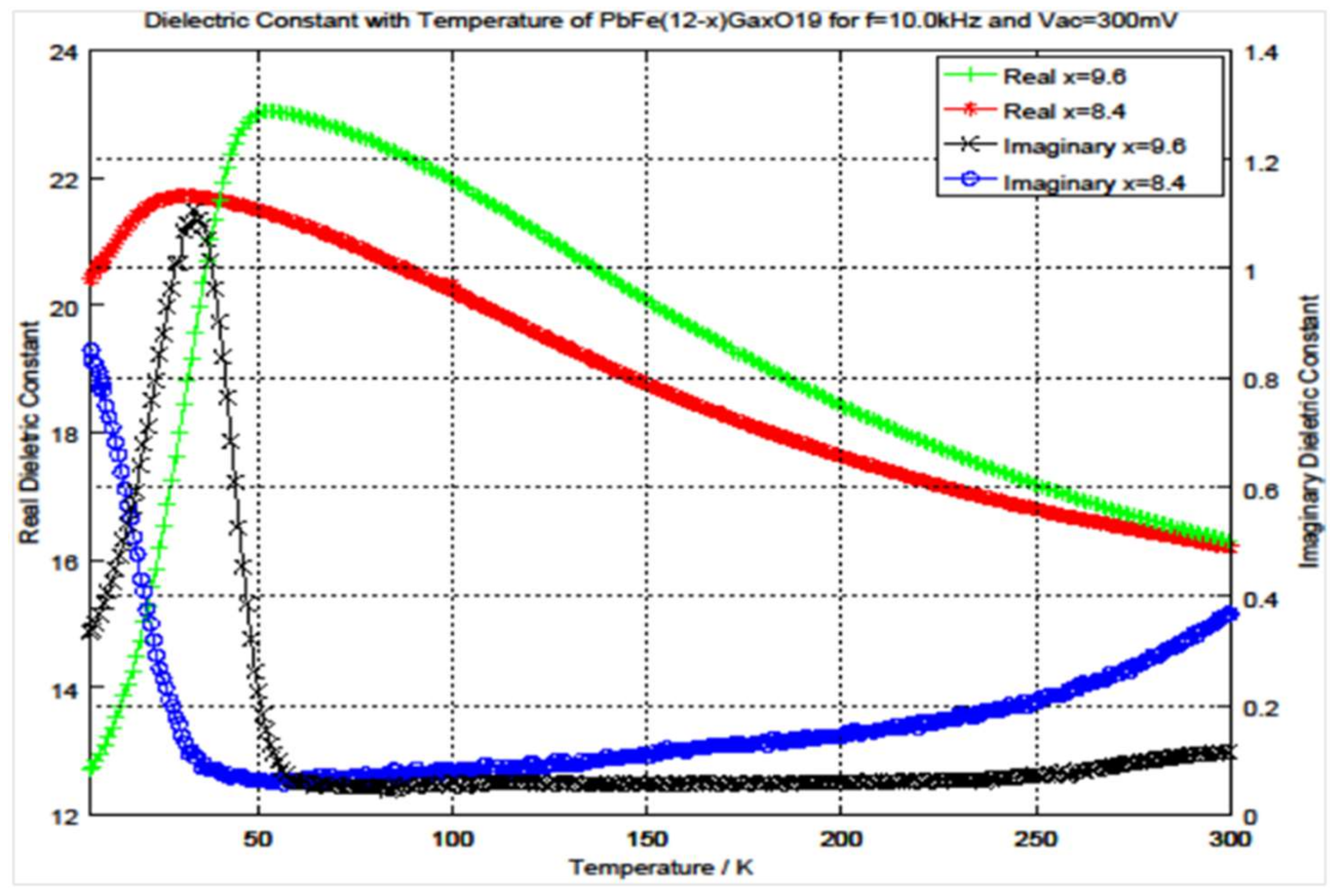
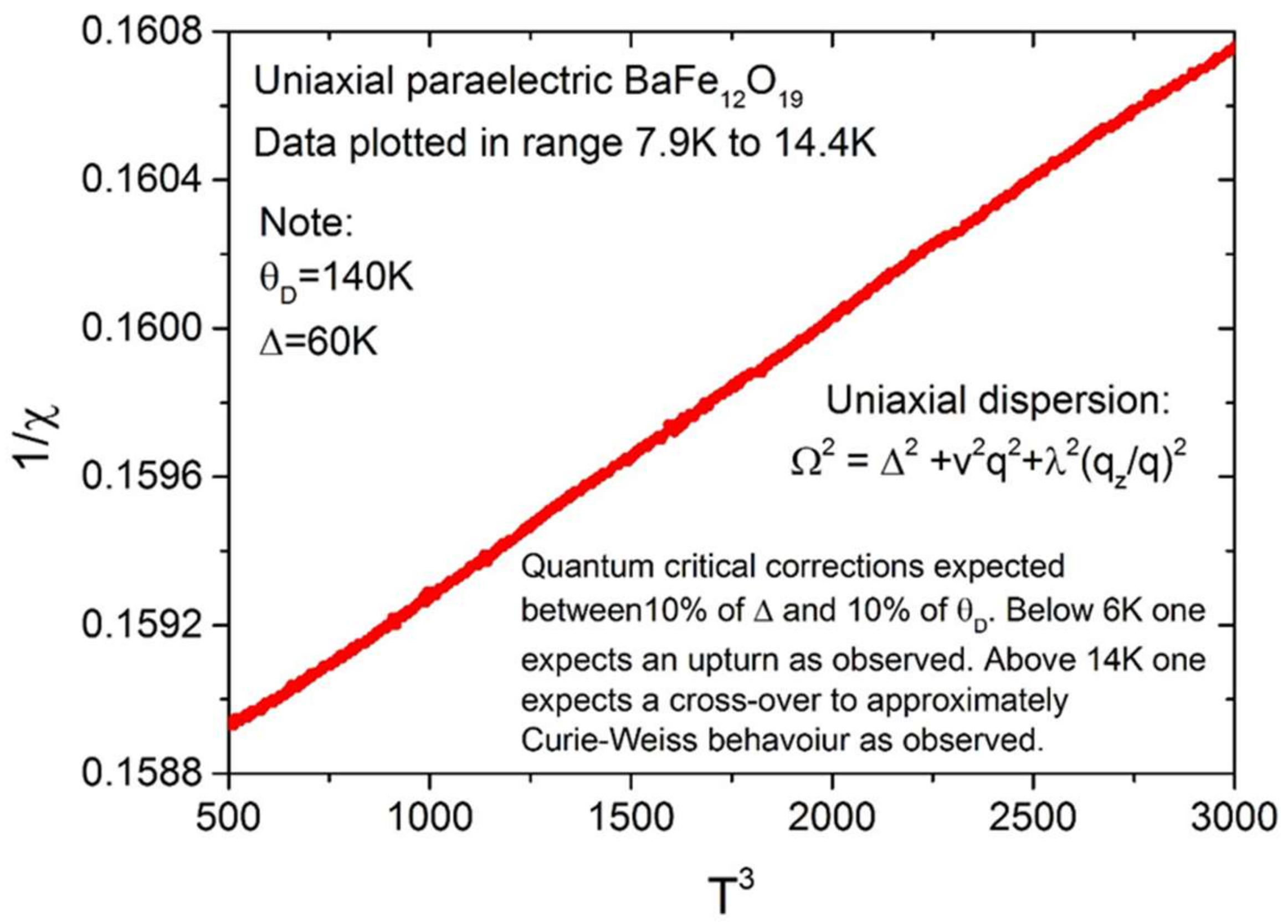
3.1. Hexaferrites

The hexaferrites come in three families, illustrated in Figure 1 [15]. Our interest has been in the M-type, particularly BaFe₁₂O₁₉, SrFe₁₂O₁₉, and PbFe₁₂O₁₉. Its dielectric constants versus temperature for two Ga-percentages are shown in Figure 2. Additionally, in Figure 3 we see how these change with applied frequency from 100 Hz to 1 MHz. The fitted curves are Vogel-Fulcher equations.

Additionally, Figure 4 shows that the dielectric constant varies as T-cubed in such a uniaxial system.

This exponent is different from the quadratic dependence observed in pseudocubic QCPs, seen in, for example, SrTiO₃ or KTaO₃) and was predicted by Khmelnitskii in 1970 [18]. It follows from the general equation

$$\delta {\chi }^{-1}~{{\displaystyle \int }}_0^{q_c}\frac{q^{2}n\left({\mathsf{\Omega }}_q\right)}{{\mathsf{\Omega }}_q}dq$$

(2)

in which χ is the isothermal electric susceptibility and Ω is the phonon frequency, and the phonon dispersion with wave vector q is assumed to be

$${{\mathsf{\Omega }}_q}^2={\mathsf{\Delta }}^2+v^2{q}^2+{\lambda }^2{\left(\frac{q_z}{q}\right)}^2$$

(3)

The key result is γ = (d + z − 2)/z, in which z = 1 is the exponent describing how Ωq behaves (linear acoustic phonon) for small q in ferroelectrics, and hence the behaviour of 1/χ is cubic (d = 4 for uniaxial ferroelectrics). By comparison, most magnetic insulators have the magnon frequency vary as q² for small q, and hence z = 2.

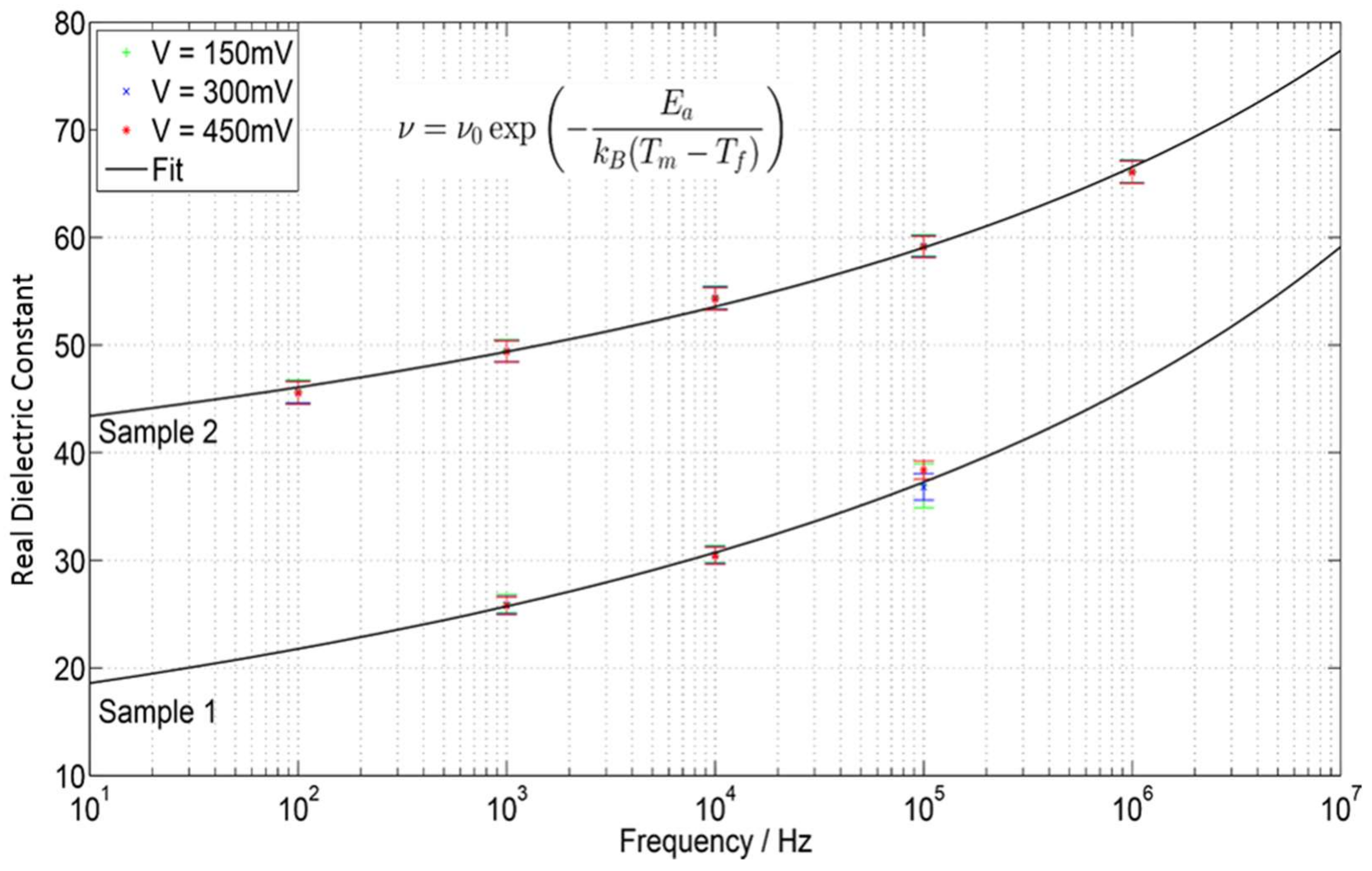
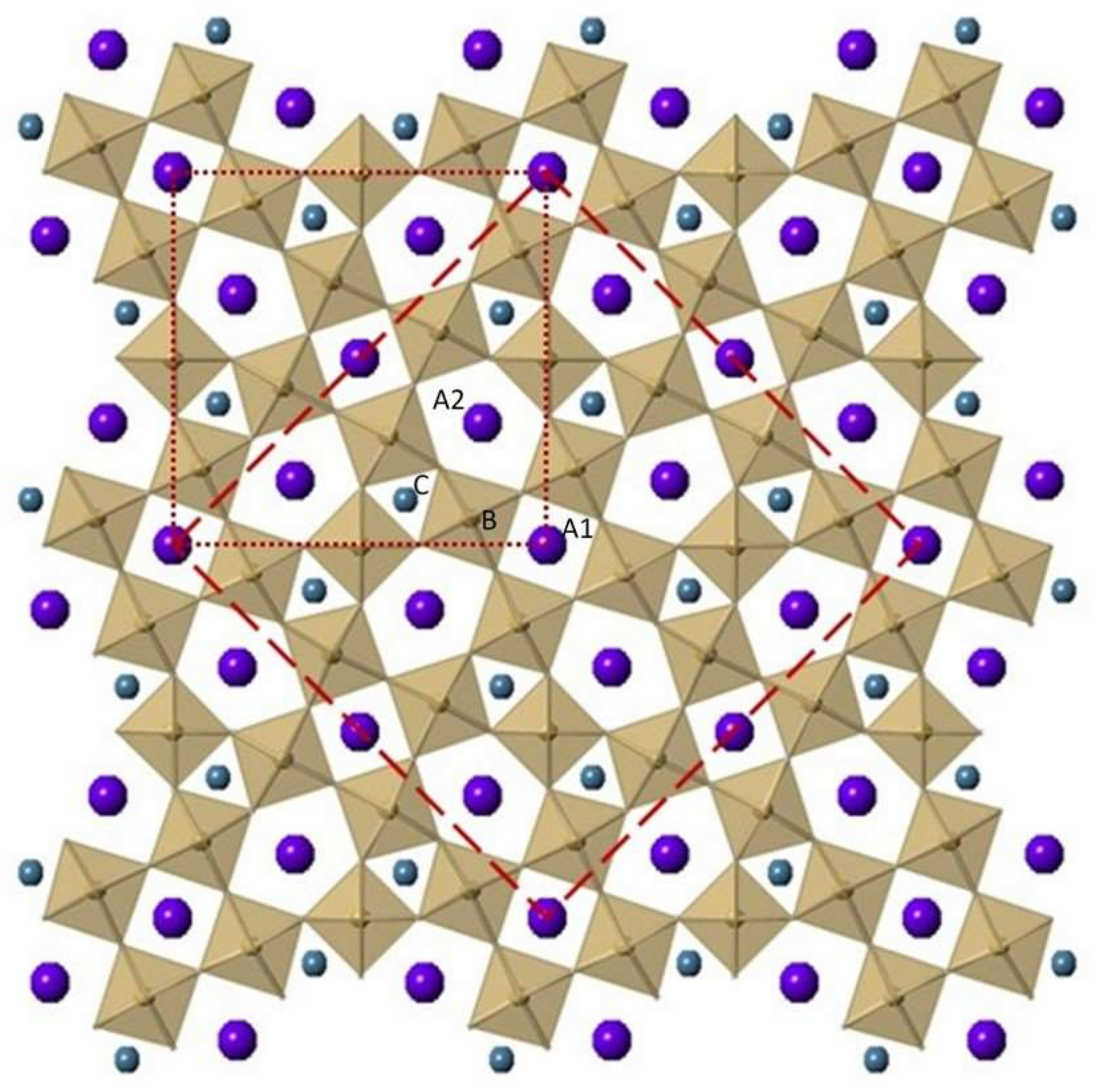
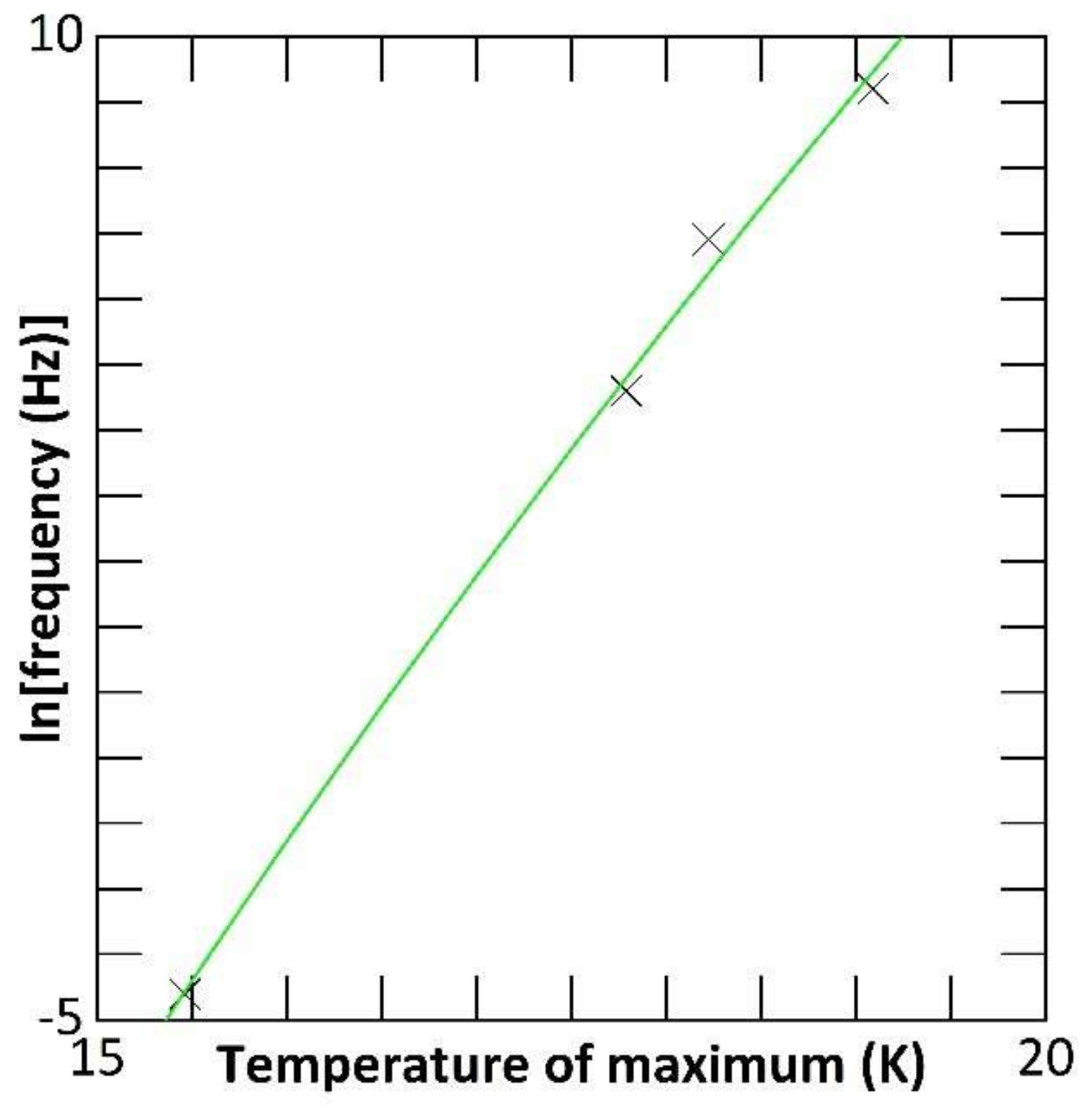
3.2. Newest QCP Relaxor Work: K₃Li₂Ta₅O₁₅ (“KLT”) and Lead Pyrochlore.

Potassium lithium tantalate is a so-called “stuffed” tungsten bronze, which means that its small triangular channels (c-sites) are occupied by Li (Figure 5). The figure illustrates both the tetragonal and orthorhombic primitive cells proposed and the triangular Li sites. KLT and its isomorphic niobate are the only tungsten bronzes in which this channel is occupied. It has a reported tetragonal-orthorhombic ferroelectric phase transition at T_c = 7 K, but this transition is not always manifest in different kinds of experiments. We show in the graphical abstract here that this is because the transition is that of a relaxor QCP. Hence, if measurements are made via resonant ultrasonic spectroscopy or dielectric studies in the 300 kHz regime, a phase transition is measured (up to T = 40 K), whereas if a dc technique is used, such as specific heat, no transition is observed in this temperature range [13].

The situation in lead pyrochlore is rather more confusing. Many years ago a presumably ferroelectric transition was reported at T_c = 15.4 K [19,20]. However, subsequent work showed that this temperature marked a relaxation onset [21]. This was before the era of relaxor ferroelectrics, and so these authors assumed that this is not a structural phase transition but merely the relaxation of a point defect. Indeed, the polarization measured is small (nC/cm² rather than μC/cm²). However, a hint that the anomaly is relaxor ferroelectricity comes from the rarely cited high pressure work of Jayaraman et al. [22], who found a phase transition at modest pressure and ambient temperature in a rare lead pyrochlore single crystal.

Our fit to the lead pyrochlore relaxation, Figure 6, yields a freezing temperature of T_f = −14 K (below absolute zero) [13]. Note that the frequency f₀ in the fit is unreliable; the data fitting is not sensitive to this value, and the fit simply shows that it is very large.

4. Discussion

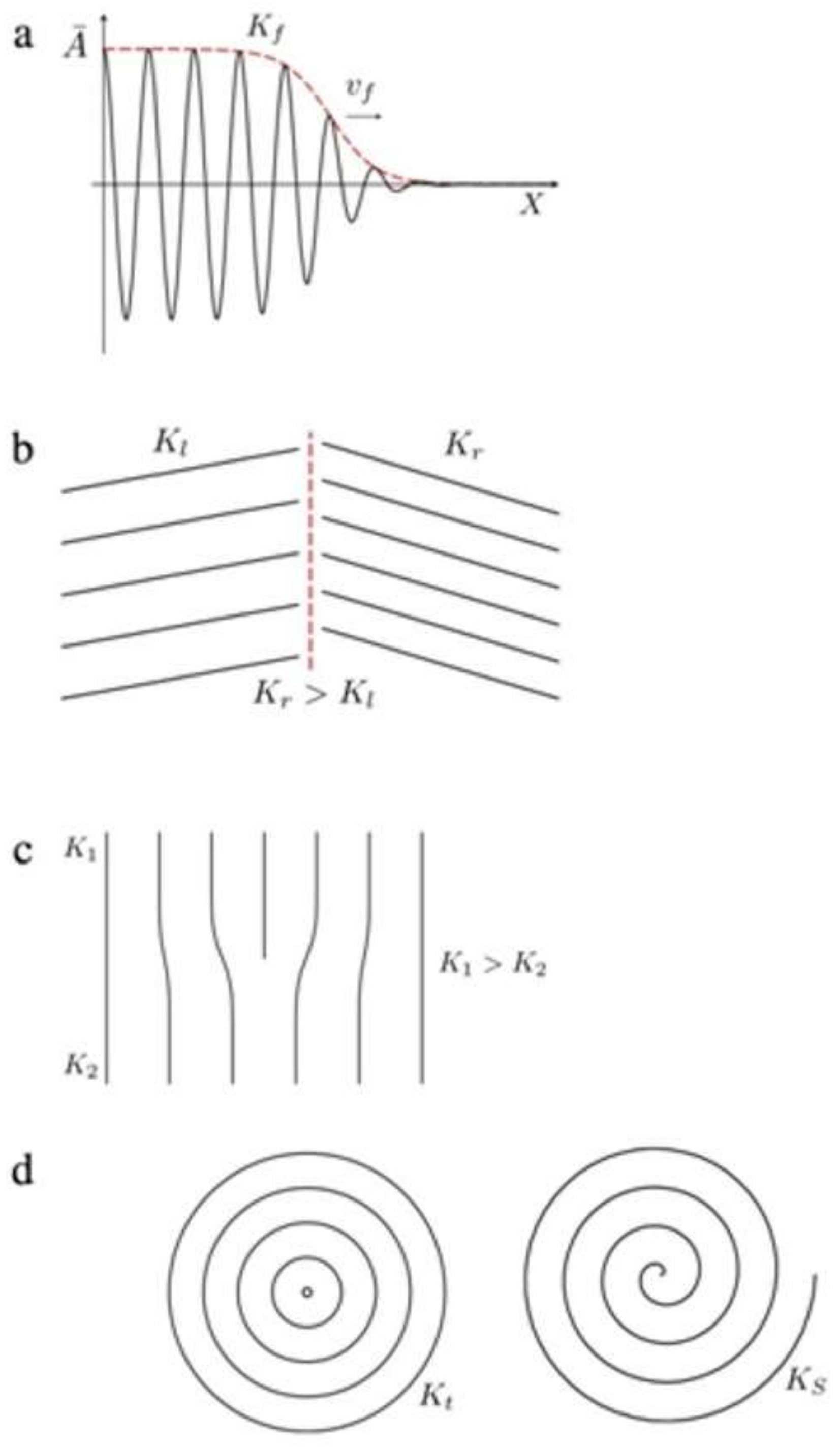
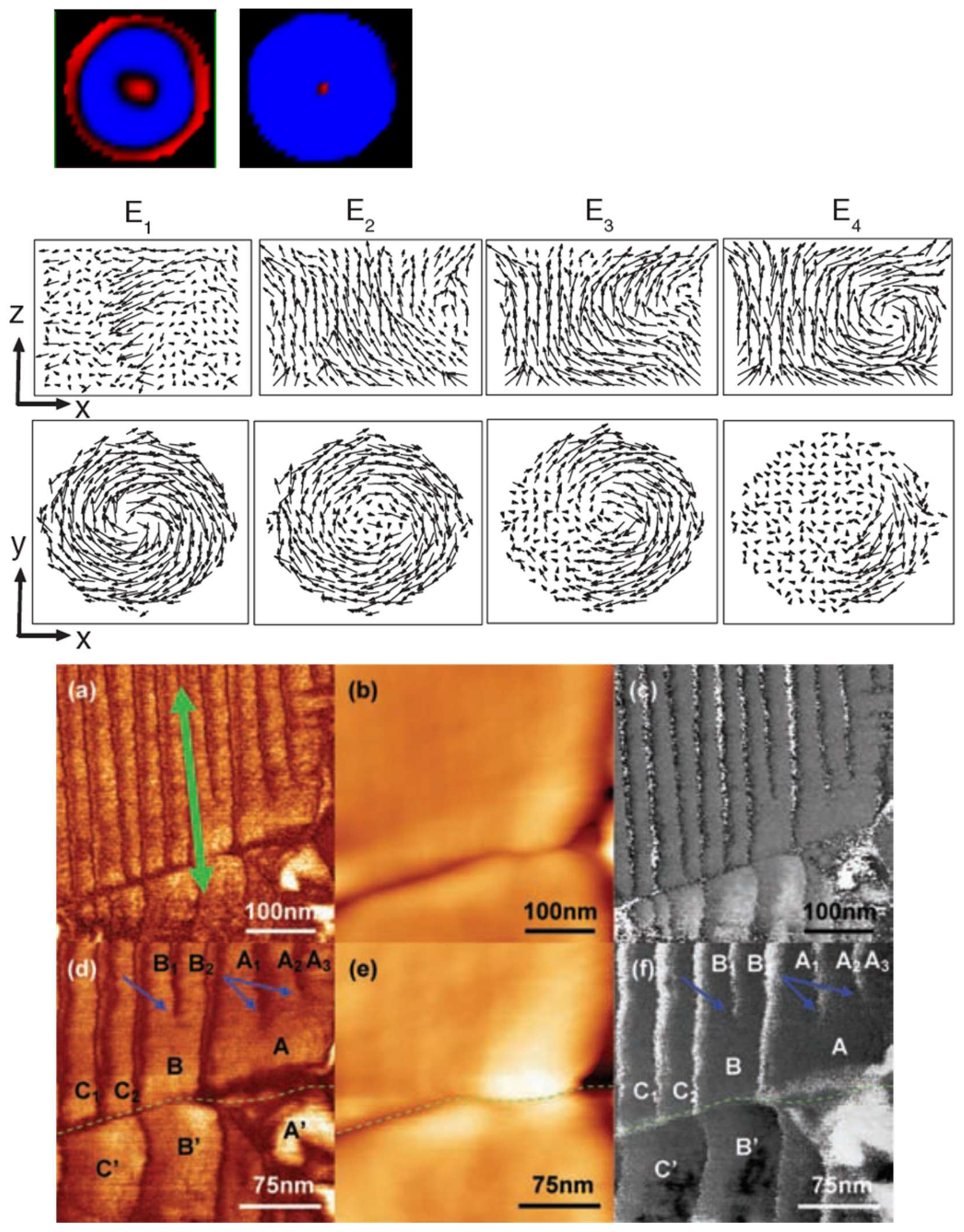
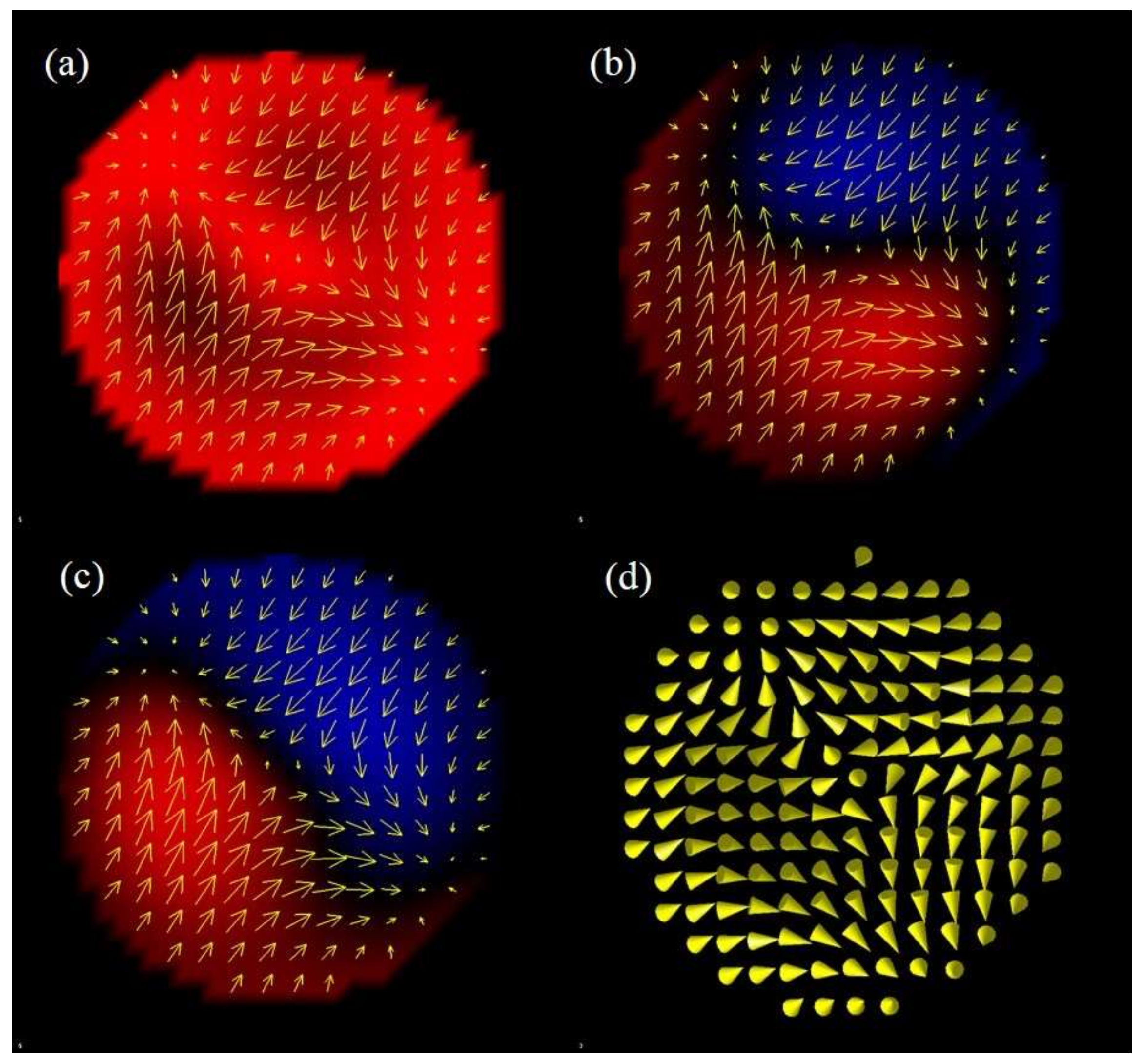
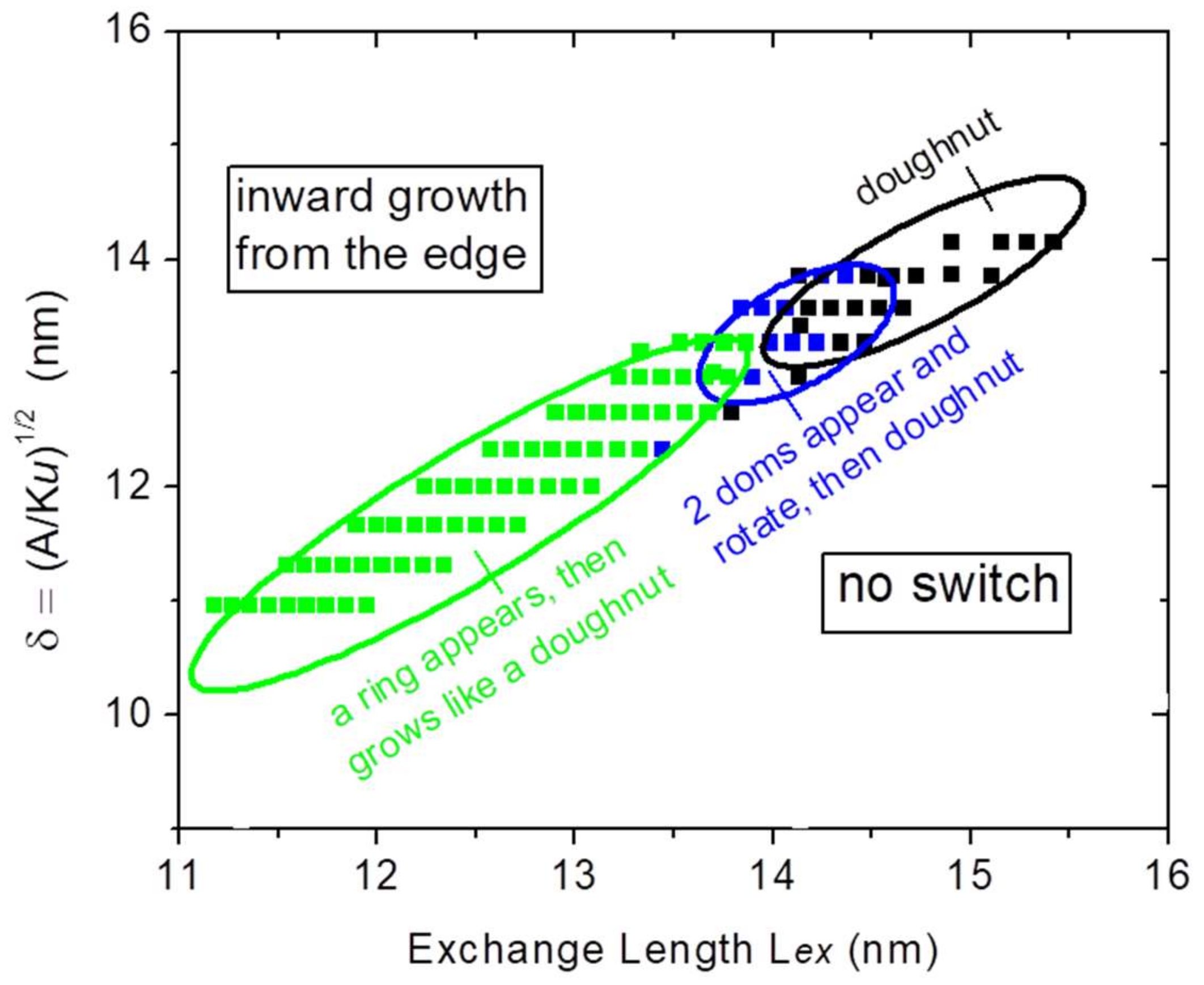
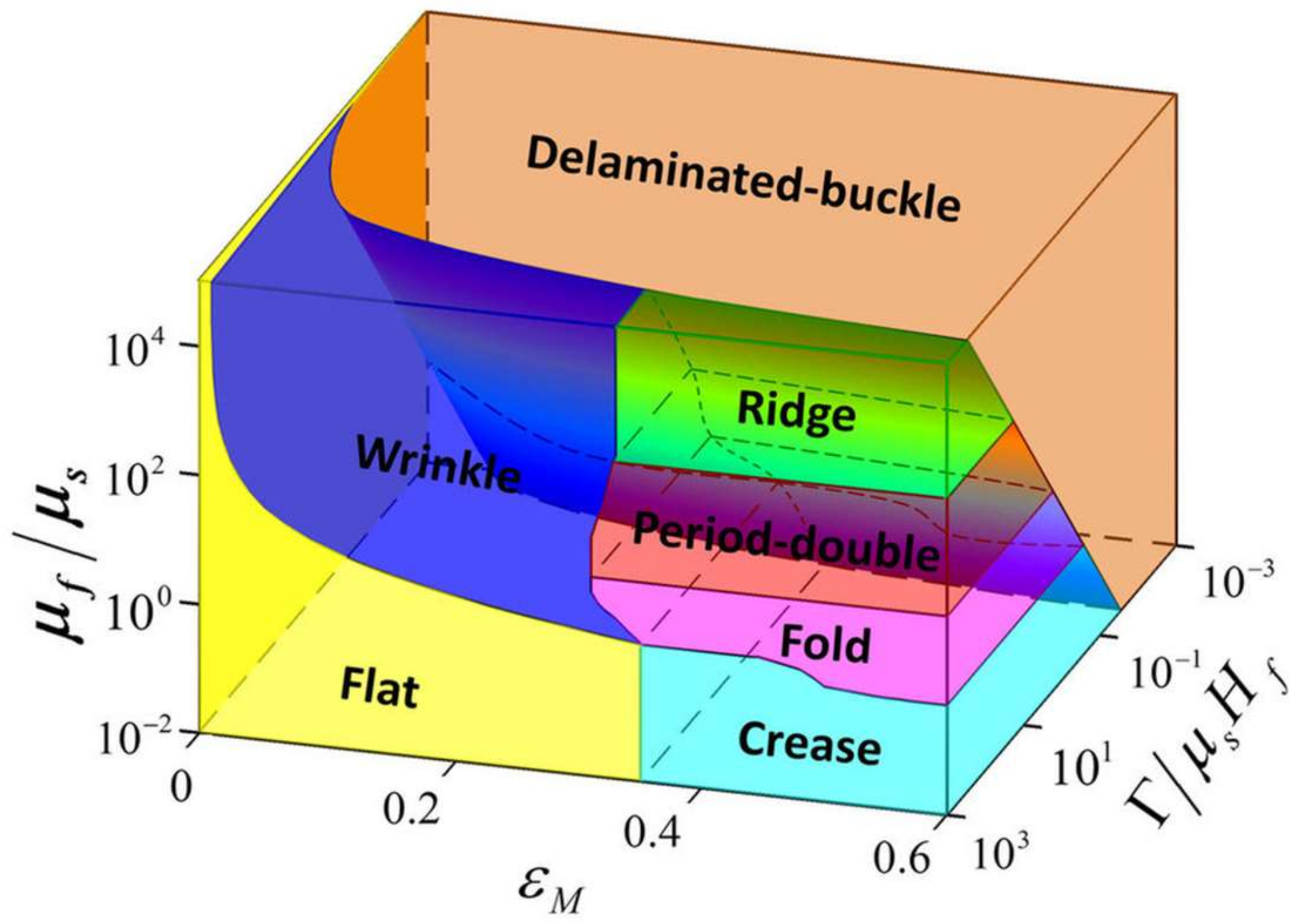
Absence of Thermal Diffusion of Domain Walls in QCPs: Absence of Turing Patterns in Ferroelectric Domains?

Having presented the basic ideas about QCP ferroelectrics and, especially, QCP relaxors, let us turn to predictions of very specific differences in relaxor QCPs compared with other ferroelectric QCPs. The case we shall consider is nonlinear domain processes, including folding, wrinkling, creasing, and period doubling, a subject of current interest [23,24,25]. In particular, we show below that these instabilities arise from diffusion of domain walls, but Tokura’s group has recently established that there is no thermal diffusion of domain walls for QCPs systems near T = 0 (only tunnelling, with wall tunnelling mass ca. 1 m (proton) = ca. 2000 m (e) [26,27]).

There are reasons to believe that the domain dynamics of ferroelectric crystals may be very different for QCP systems. This is because many interesting domain properties, such as wrinkling, folding, and period doubling, rely of diffusion, whereas domain wall motion at very low temperatures arises instead from quantum tunneling, and thermally activated creep plays a negligible role.

Therefore, in the section below we briefly review these domain instabilities and comment on how they might differ or be absent in QCPs. We hope that this will stimulate researchers to look for such domain patterns in QCP ferroelectrics at cryogenic temperatures, which thus far have not been reported.

We show explicitly that the domain patterns in ferroelastic/ferroelectric crystals are those predicted by the Turing pattern model, with four basic structures: Chevron boundaries (with or without domain width change), dislocation zipping and unzipping (with velocities measured), bull’s eye circular patterns, and spiral patterns. These all can be described by reaction diffusion equations, but the terms required in a Landau-Ginzburg approach differ, with, for example, complex coefficients required for spiral patterns and real coefficients for chevron patterns. There is a close analogy between spiral domains and Zhabotinskii-Belousov patterns, and between bull’s eye circular patterns and Rayleigh-Bernard instabilities or Taylor-Couette instabilities with rotating inner cylinders, but not with each other. The evolution of these patterns with increasing strain (e.g., wrinkling/folding or folding/period-doubling) is well described by the model of Wang and Zhao, but the question of whether there is a separate rippling-to-wrinkling transition remains moot. Because these processes require diffusion, they should be absent (or qualitatively different) near Quantum Critical points.

Alan Turing is perhaps best known for his work in solving the Enigma code in the 1940s and for his pioneering work on artificial intelligence, but he was also a superb theoretical biologist. Among his important contributions was the development of reaction-diffusion models later used to explain patterning in chemical reactions, including the famous Zhabotinskii-Belousov reaction [28].

The idea that diffusion would destabilize a uniform distribution of atoms or molecules in nature is somewhat paradoxical and counter-intuitive, because diffusion usually stabilizes things. However, simple reaction-diffusion equations predict many observed patterns in chemistry and biology.

Starting with an equation of form

du/dt = f(u) + D ∇²u

(4)

for two components

du₁/dt = f₁(u₁,u₂₎ + D₁ ∇²u₁

(5)

du₂/dt = f₂(u₁,u₂) + D₂ ∇²u₂

(6)

It can be shown that there is a threshold for a static pattern instability for a certain ratio D₁ > D₂. Here, one component u₁ is termed an activator and the other an inhibitor. In fact, the static pattern predicted by this approach, termed type I-s (s for static) [29,30], is rarely observed, because most chemical reactions involve diffusion coefficients D₁ and D₂ that are close in magnitude; however, specific reagents have been studied in a successful attempt to produce such patterns.

Although these static patterns are not common in nature, the non-static oscillatory patterns are. These are often labelled as type III-o (o for oscillatory) in the Turing scheme, which separates instabilities into those that are static in both space and time (s), those that are static in space but oscillate in time (I-o), and those that oscillate in both space and time (III-o). The spiral domain instabilities, like the Zhabotinskii-Belousov instability, oscillate in both space and time.

There are a total of four patterns predicted for domain instabilities (shown below from Hohenbrg and Krekhov, Figure 7,), and we have recently illustrated all four experimentally [31]. Note that the chevron pattern (next to top panel) can maintain domain width on both sides of the reflection plane or change width; this width change can be an integer ratio (doubling, tripling…), but it can be a non-integer ratio also, resulting in incommensurate domain structures. Of these four patterns, the chevron and dislocation patters are described by Hohenberg as arising from Turing static instabilities, meaning static in both space and time; however, recent unpublished work by A. Hershovitz and Y. Ivry measure the zipping and unzipping velocity of the dislocation mechanism, so in that sense they are not truly static.

The bull’s eye pattern (Figure 7d and Figure 8) is analogous to the Taylor-Couette instability with rotating central cylinder [32], and the spiral pattern is related to the Zhabotinskii-Belousov instability [33,34], but oddly enough, the bull’s eye and spiral patterns are not related to each other. These two instabilities are described as non-static by Hohenberg et al. and are termed oscillatory in the Turing descriptions (oscillatory-I and oscillatory-III, respectively); the bull’s eye is static in space and oscillatory in time, and the spiral is oscillatory in both space and time. In the context of quantum critical systems, the latter two are therefore more dependent upon diffusion and hence less likely than chevrons or dislocation twinning dislocations to arise at cryogenic temperatures. A rather complete description of circular instabilities, which resemble first-order Bessel functions and patterns of vibration on a drum head, has been given by Baudry et al. [35,36,37].

These circular and spiral patterns do evolve with time initially after they are formed, Figure 9 and Figure 10. Figure 9 below shows in-plane patterns modelled from such data [38]. There is a Yin-and-Yan geometry emerging. As time evolves, this pattern rotates clockwise or counterclockwise.

Note that the oscillatory instabilities can also occur in the context of faceting of ferroelectric nano-crystals [40,41,42]. These references illustrate some data for a PZT disc ca. 10 nm in diameter in a TEM beam, monitored during beam exposure time of a few seconds. Note the domain wall realignment and the oscillatory faceting and de-faceting. The latter is modelled in Ref. [42,43,44]. Unlike the thermally activated creep processes, these faceting rearrangements are electric-field driven and hence are expected to persist in QCP cryogenic systems. The measured velocities are typically 1 nm/s.

This faceting can be more complex, with various high-symmetry polygonal structures observed in ferroelectrics of crystallographic low (C₂) symmetry, as shown in Figure 11; Lukyanchuk et al. give a complete model for this phenomenon [45].

The following question remains unanswered: Although most investigators agree that there is a well-defined wrinkling-to-folding phase transition (Wang and Zhao [46], Figure 12; Metaxas et al. [47]), some recent researchers have inferred the existence of a preliminary precursor ripple-to-wrinkle transition [48]—How do these nonlinear phenomena behave at cryogenic temperatures in QCP ferroelectrics, where the domain walls move slowly via quantum mechanical tunneling and not thermally activated diffusion?

In the previous study, we illustrated such wrinkles (first found by Gruverman [49,50] in lead germanate domain walls in his 1990 thesis (Univ. Ekaterinburg)), measured their velocities, and related them to capillary waves [44,45].

The extension of the present work is as follows.

The present interest is in extending this work from single nonlinear domain instabilities (Figure 7) to arrays of vortex structures [39,40,51]. In addition, the existing theory is limited to two-dimensional structures, and it would be of interest to extend the modelling, for example, from flat [2D] cycloids to low-aspect ratio [3D] helices [52,53]. Note that helices have handedness (left-handed or right-handed), whereas cycloids with clockwise phase shifts of Θ degrees are topologically equivalent to counter-clockwise shifts of 360-Θ degrees. Very recently, the non-planar helical characteristics of vortex arrays have been demonstrated; hence, they are not cycloids [52].

5. Conclusions

Ferroelectric crystals with Curie temperatures very near T = 0 are fascinating new examples of quantum crystals. Their domains move via quantum tunnelling rather than thermally activated creep; therefore, they lack the diffusivity requisite for Turing-type instabilities (folding, period doubling, wrinkling…). They also have a wider range of critical upper and lower dimensionalities than magnets, arising from the fact that their unstable Goldstone bosons are acoustic modes with energies linear in wave vector q, in contrast to magnons and their quadratic q-dependence. In the special case of relaxor ferroelectric QCPs, the relaxor characteristic arises from a glassy viscosity and give researchers an extra dimension over which to probe dynamics, most easily in the case of isothermal electric susceptibility (dielectric constant ε(T,f)), whose peak can be tuned exactly through T = 0 in the 10 Hz to 1 MHz range of applied ac probe voltages.

Now, let us remind ourselves of Tokura’s argument that ferroelectric QCPs have no creep and no classical diffusion. This would appear to rule out domain instabilities such as wrinkling and folding in ferroelectric QCPs, based upon the models of Turing and, later, by Hohenberg et al. However, this is, in this respect, why relaxor QCPs are special: their ground states are glassy and viscous and hence certainly permit some diffusion. The presence of a glassy ground state at T = 0 is remarkable in many ways, and certainly relaxors are not in true thermal equilibrium.

An obvious extension is to magnetoelectric QCPs, and some work on the BaFe₁₂O₁₉ hexaferrite family has already been reported [1,2,3,4,5,6,7,8,9,10,54,55,56,57,58,59,60,61]. This material is very popular, because it is the usual material in magnetic-stripe credit cards, with >$1 billion/year in sales as a magnetic compound [60,61].

An alternative approach to the general problem of domain wall instabilities would be to look for the analogues of other known variants in such things as Taylor-Couette flow, which has at least five known instabilities [62,63], not just the one (“bull’s eye”) mentioned here (one of these is a toroid, which is similar to that described in Figure 8a and Figure 10 above).