A Numerical Method for Flexural Vibration Band Gaps in A Phononic Crystal Beam with Locally Resonant Oscillators
Abstract
:1. Introduction
- (1)
- Based on the differential quadrature method, we propose a numerical method for calculating the flexural vibration band gaps of a locally resonant beam. In this paper, the differential quadrature method is applied to calculate the band gaps of locally resonant structures for the first time.
- (2)
- By using an unconventional matrix-partitioning method and a variable substitution method, we can transform the problem of solving the dispersion relation into a standard quadratic eigenvalue problem, and the problem of the non-linear term after using the DQM method can be solved easily.
- (3)
- Compared with the plane wave expansion method and the finite element method, the high accuracy and computational efficiency of the present method are demonstrated.
- (4)
- The proposed method has high precision and a rapid speed of convergence.
2. Method
2.1. Differential Quadrature Method
2.2. Unconventional Matrix-Partitioning Method & Variable Substitution Method
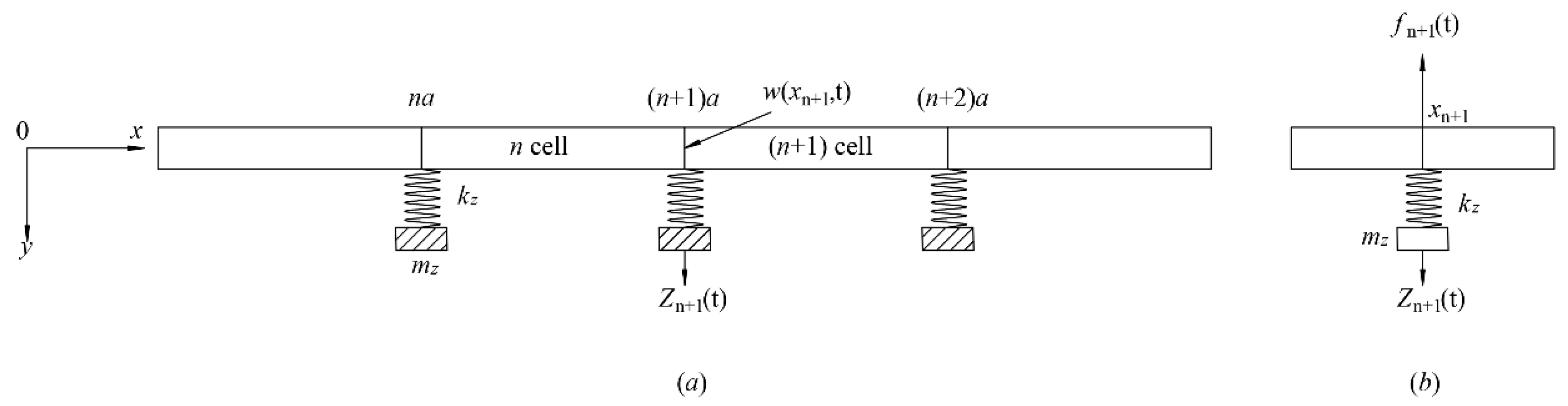
3. Locally Resonant (LR) Beam Models and Solutions
3.1. Euler–Bernoulli Model & Solution Procedures
3.2. Timoshenko Model & Solution Procedures
4. Numerical Results and Discussions
4.1. Convergence Study
4.2. Validation
4.3. Method Advantages
4.4. Parameter Studies
4.4.1. Effects of Shear Deformation and Rotary Inertia
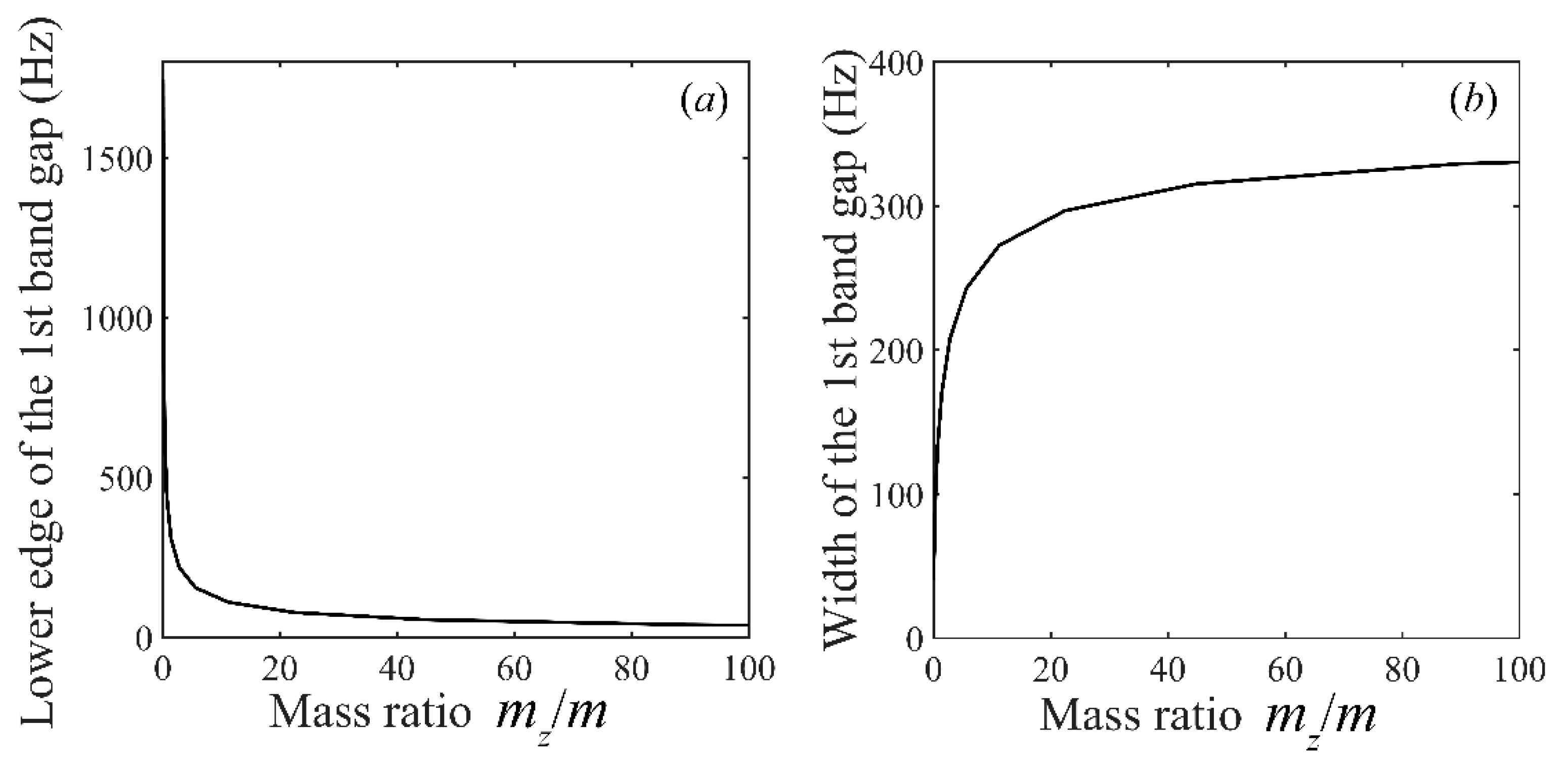
4.4.2. Effects of Lumped Mass mz
4.4.3. Effects of the Spring Stiffness Coefficient kz
4.4.4. Effects of the Lattice Constant a
5. Conclusions
- (1)
- The governing equation and periodic boundary conditions are discretized by the DQM method. The matrix equation is transformed into a standard quadratic eigenvalue problem by the partitioned matrix operation and variable substitution. Thus, the dispersion relationship and the band gap characteristics of a locally resonant beam can be solved. By extending the proposed method further, it can also be suitable for 2-dimensional or 3-dimensional LR structures.
- (2)
- By comparing with the results of the existing literature, the validity of the proposed method is developed from both propagation modes and evanescent modes. Convergence studies indicate that accurate enough results could be got when the number of discrete points Nx ≥ 8.
- (3)
- By comparing with the plane wave expansion method and the finite element method, the high accuracy and computational efficiency of the present method are demonstrated.
- (4)
- The parametric analysis shows that the width of the 1st band gap can be widened by increasing the mass ratio or the stiffness ratio or decreasing the lattice constant. In addition, one can decrease the lower edge of the 1st band gap by increasing the mass ratio or decreasing the stiffness ratio. The starting frequency of the LR band gap has nothing to do with the lattice constant because it is defined by the resonant frequency of the LR oscillator. The band gap frequency range calculated by the Timoshenko beam theory is lower than that calculated by the Euler–Bernoulli beam theory.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Sigalas, M.M.; Economou, E.N. Elastic and acoustic wave band structure. J. Sound Vibr 1992, 158, 377–382. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Sala, R.; Sancho, J.; Sánchez, J.V.; Gómez, V.; Llinares, J.; Meseguer, F. Sound attenuation by sculpture. Nature 1995, 378, 241. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Martínez, G.; Dobrzynski, L.; Djafari-Rouhani, B. Theory of acoustic band structure of periodic elastic composites. Phys. Rev. B 1994, 49, 2313–2322. [Google Scholar] [CrossRef] [PubMed]
- Vasseur, J.O.; Deymier, P.A.; Chenni, B.; Djafari-Rouhani, B.; Dobrzynski, L.; Prevost, D. Experimental and theoretical evidence for the existence of absolute acoustic band gaps in two-dimensional solid phononic crystals. Phys. Rev. Lett. 2001, 86, 3012. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, Y.; Tomoyasu, Y.; Tamura, S.I. Band structure of acoustic waves in phononic lattices: Two-dimensional composites with large acoustic mismatch. Phys. Rev. B 2000, 62, 7387–7392. [Google Scholar] [CrossRef] [Green Version]
- Wu, F.G.; Hou, Z.L.; Liu, Z.Y.; Liu, Y.Y. Acoustic band gaps in two-dimensional rectangular arrays of liquid cylinders. Solid State Commun. 2002, 123, 239–242. [Google Scholar] [CrossRef]
- Xiang, H.J.; Shi, Z.F. Analysis of flexural vibration band gaps in periodic beams using differential quadrature method. Comput. Struct. 2009, 87, 1559–1566. [Google Scholar] [CrossRef]
- Cheng, Z.B.; Xu, Y.G.; Zhang, L.L. Analysis of flexural wave bandgaps in periodic plate structures using differential quadrature element method. Int. J. Mech. Sci. 2015, 100, 112–125. [Google Scholar] [CrossRef]
- Miranda Jr, E.J.P.; Dos Santos, J.M.C. Flexural wave band gaps in phononic crystal euler-bernoulli beams using wave finite element and plane wave expansion methods. Mater. Res.-Ibero-Am. J. Mater. 2017, 20, 729–742. [Google Scholar] [CrossRef]
- Han, L.; Zhang, Y.; Ni, Z.Q.; Zhang, Z.M.; Jiang, L.H. A modified transfer matrix method for the study of the bending vibration band structure in phononic crystal Euler beams. Phys. B Condens. Matter 2012, 407, 4579–4583. [Google Scholar] [CrossRef]
- Hajhosseini, M.; Rafeeyan, M.; Ebrahimi, S. Vibration band gap analysis of a new periodic beam model using GDQR method. Mech. Res. Commun. 2017, 79, 43–50. [Google Scholar] [CrossRef]
- Zhang, Y.; Ni, Z.Q.; Han, L.; Zhang, Z.M.; Jiang, L.H. Flexural vibrations band gaps in phononic crystal timoshenko beam by plane wave expansion method. Optoelectron. Adv. Mater.-Rapid Commun. 2012, 6, 1049–1053. [Google Scholar]
- De Miranda Júnior, E.J.P.; Dos Santos, J.M.C. Band structure in carbon nanostructure phononic crystals. Mater. Res. 2017, 20, 572–579. [Google Scholar] [CrossRef]
- Chen, H.; Fung, K.H.; Ma, H.; Chan, C.T. Polarization gaps and negative group velocity in chiral phononic crystals: Layer multiple scattering method. Phys. Rev. B 2008, 77, 224304. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Srivastava, A. Combining plane wave expansion and variational techniques for fast phononic computations. J Eng. Mech. 2017, 143. [Google Scholar] [CrossRef]
- Yao, L.; Huang, G.; Chen, H.; Barnhart, M.V. A modified smoothed finite element method (M-SFEM) for analyzing the band gap in phononic crystals. Acta Mech. 2019, 1–15. [Google Scholar] [CrossRef]
- Wormser, M.; Wein, F.; Stingl, M.; Körner, C. Design and additive manufacturing of 3D phononic band gap structures based on gradient based optimization. Materials 2017, 10, 1125. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Wang, X.; Wang, M.Y. An analysis of flexural wave band gaps of locally resonant beams with continuum beam resonators. Meccanica 2016, 51, 171–178. [Google Scholar] [CrossRef]
- Yu, D.L.; Liu, Y.Z.; Zhao, H.G.; Wang, G.; Qiu, J. Flexural vibration band gaps in Euler-Bernoulli beams with locally resonant structures with two degrees of freedom. Phys. Rev. B 2006, 73, 064301. [Google Scholar] [CrossRef]
- Wang, G.; Wen, X.S.; Wen, J.H.; Liu, Y.Z. Quasi-one-dimensional periodic structure with locally resonant band gap. J. Appl. Mech. 2006, 73, 167–170. [Google Scholar] [CrossRef]
- Wang, G.; Yu, D.L.; Wen, J.H.; Liu, Y.Z.; Wen, X.S. One-dimensional phononic crystals with locally resonant structures. Phys. Lett. A 2004, 327, 512–521. [Google Scholar] [CrossRef]
- Miranda, E.J.P.; Dos Santos, J.M.C. Evanescent Bloch waves and complex band structure in magnetoelectroelastic phononic crystals. Mech. Syst. Signal Process. 2018, 112, 280–304. [Google Scholar] [CrossRef]
- Nobrega, E.D.; Gautier, F.; Pelat, A.; Dos Santos, J.M.C. Vibration band gaps for elastic metamaterial rods using wave finite element method. Mech. Syst. Signal Process. 2016, 79, 192–202. [Google Scholar] [CrossRef]
- Li, F.L.; Wang, Y.S.; Zhang, C.; Yu, G.L. Boundary element method for band gap calculations of two-dimensional solid phononic crystals. Eng. Anal. Bound. Elem. 2013, 37, 225–235. [Google Scholar] [CrossRef]
- Camley, R.E.; Djafari Rouhani, B.; Dobrzynski, L.; Maradudin, A.A. Transverse elastic waves in periodically layered infinite, semi-infinite, and slab media. J. Vac. Sci. Technol. B 1983, 1, 371–375. [Google Scholar] [CrossRef]
- Sigalas, M.M.; Soukoulis, C.M. Elastic-wave propagation through disordered and/or absorptive layered systems. Phys. Rev. B 1995, 51, 2780–2789. [Google Scholar] [CrossRef] [PubMed]
- Kafesaki, M.; Penciu, R.S.; Economou, E.N. Air bubbles in water: A strongly multiple scattering medium for acoustic waves. Phys. Rev. Lett. 2000, 84, 6050–6053. [Google Scholar] [CrossRef]
- Economou, E.N.; Zdetsis, A. Classical wave propagation in periodic structures. Phys. Rev. B 1989, 40, 1334–1337. [Google Scholar] [CrossRef]
- Cao, Y.; Hou, Z.; Liu, Y. Convergence problem of plane-wave expansion method for phononic crystals. Phys. Lett. A 2004, 327, 247–253. [Google Scholar] [CrossRef]
- Sigalas, M.M.; Garcı, A.N. Theoretical study of three dimensional elastic band gaps with the finite-difference time-domain method. J. Appl. Phys. 2000, 87, 3122–3125. [Google Scholar] [CrossRef]
- Kafesaki, M.; Sigalas, M.M.; García, N. Frequency modulation in the transmittivity of wave guides in elastic-wave band-gap materials. Phys. Rev. Lett. 2000, 85, 4044–4047. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.Y.; Chan, C.T.; Sheng, P.; Goertzen, A.L.; Page, J.H. Elastic wave scattering by periodic structures of spherical objects: Theory and experiment. Phys. Rev. B 2000, 62, 2446–2457. [Google Scholar] [CrossRef] [Green Version]
- Psarobas, I.E.; Stefanou, N.; Modinos, A. Scattering of elastic waves by periodic arrays of spherical bodies. Phys. Rev. B 2000, 62, 278–291. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Wen, X.S.; Wen, J.H.; Shao, L.H.; Liu, Y.Z. Two-dimensional locally resonant phononic crystals with binary structures. Phys. Rev. Lett. 2004, 93, 154302. [Google Scholar] [CrossRef]
- Wang, G.; Wen, J.H.; Liu, Y.Z.; Wen, X.S. Lumped-mass method for the study of band structure in two-dimensional phononic crystals. Phys. Rev. B 2004, 69, 184302. [Google Scholar] [CrossRef]
- Huang, Y.; Li, J.; Chen, W.; Bao, R. Tunable bandgaps in soft phononic plates with spring-mass-like resonators. Int. J. Mech. Sci. 2019, 151, 300–313. [Google Scholar] [CrossRef]
- Zhao, H.J.; Guo, H.W.; Gao, M.X.; Liu, R.Q.; Deng, Z.Q. Vibration band gaps in double-vibrator pillared phononic crystal plate. J. Appl. Phys. 2016, 119. [Google Scholar] [CrossRef]
- Khelif, A.; Aoubiza, B.; Mohammadi, S.; Adibi, A.; Laude, V. Complete band gaps in two-dimensional phononic crystal slabs. Phys. Review E 2006, 74. [Google Scholar] [CrossRef]
- Liang, X.; Kou, H.L.; Wang, L.Z.; Palmer, A.C.; Wang, Z.Y.; Liu, G.H. Three-dimensional transient analysis of functionally graded material annular sector plate under various boundary conditions. Compos. Struct. 2015, 132, 584–596. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Vosoughi, A.R. DQM large amplitude vibration of composite beams on nonlinear elastic foundations with restrained edges. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 906–915. [Google Scholar] [CrossRef]
- Doyle, J.F. Wave Propagation in Structures, 2nd ed.; Springer: New York, NY, USA, 1997; p. 335. [Google Scholar]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Son: New York, NY, USA, 2005; p. 406. [Google Scholar]
- Yu, D.L.; Liu, Y.Z.; Wang, G.; Zhao, H.G.; Qiu, J. Flexural vibration band gaps in Timoshenko beams with locally resonant structures. J. Appl. Phys. 2006, 100, 124901. [Google Scholar] [CrossRef]
- Yu, D.L.; Wen, J.H.; Zhao, H.G.; Liu, Y.Z.; Wen, X.S. Vibration reduction by using the idea of phononic crystals in a pipe-conveying fluid. J. Sound Vibr. 2008, 318, 193–205. [Google Scholar] [CrossRef]






| Parameters | Items | Values |
|---|---|---|
| ρAl | Aluminum density (kg/m3) | 2600 |
| EAl | Elastic modulus of aluminum (Pa) | 7 × 1010 |
| ρrubber | Rubber density (kg/m3) | 1300 |
| Erubber | Elastic modulus of rubber (Pa) | 7.7 × 105 |
| Grubber | Shear modulus of rubber (Pa) | 2.6 × 105 |
| ρCu | Copper density (kg/m3) | 8950 |
| Wave Vector k | Present Frequency (Hz) | ||||
|---|---|---|---|---|---|
| Nx = 6 | Nx = 7 | Nx = 8 | Nx = 9 | Nx = 15 | |
| 0.0 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.3 | 277.547 | 277.635 | 277.638 | 277.638 | 277.638 |
| 0.5 | 304.968 | 304.972 | 304.973 | 304.973 | 304.973 |
| 0.7 | 308.056 | 308.057 | 308.057 | 308.057 | 308.057 |
| 1.0 | 308.722 | 308.722 | 308.722 | 308.722 | 308.722 |
| Method | Band Gaps (Hz) | |||||
|---|---|---|---|---|---|---|
| First | Second | Third | ||||
| Lower | Upper | Lower | Upper | Lower | Upper | |
| Present | 616.378 | 1097.33 | 3038.92 | 6334.27 | 9601.44 | 11929.7 |
| FEM | 616.379 | 1097.33 | 3038.94 | 6334.57 | 9602.36 | 11931.3 |
| MTM | 616 | 1098 | 3038 | 6335 | 9601 | 11930 |
| PWE | 617 | 1103 | 3053 | 6358 | 9662 | 11931 |
| Method | Present | FEM |
|---|---|---|
| Simulation time | 8.8438 | 17.0781 |
| Memory | 154584 | 160380 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, X.; Wang, T.; Jiang, X.; Liu, Z.; Ruan, Y.; Deng, Y. A Numerical Method for Flexural Vibration Band Gaps in A Phononic Crystal Beam with Locally Resonant Oscillators. Crystals 2019, 9, 293. https://doi.org/10.3390/cryst9060293
Liang X, Wang T, Jiang X, Liu Z, Ruan Y, Deng Y. A Numerical Method for Flexural Vibration Band Gaps in A Phononic Crystal Beam with Locally Resonant Oscillators. Crystals. 2019; 9(6):293. https://doi.org/10.3390/cryst9060293
Chicago/Turabian StyleLiang, Xu, Titao Wang, Xue Jiang, Zhen Liu, Yongdu Ruan, and Yu Deng. 2019. "A Numerical Method for Flexural Vibration Band Gaps in A Phononic Crystal Beam with Locally Resonant Oscillators" Crystals 9, no. 6: 293. https://doi.org/10.3390/cryst9060293





